Содержание
| Вид материала | Анализ |
СодержаниеТаблица 11 Факторные нагрузки после вращения Таблица 12 Двухпараметрическая модель регрессии прибыли Вывод итогов Регрессионная статистика Вывод остатка |
- Содержание дисциплины наименование тем, их содержание, объем в часах лекционных занятий, 200.99kb.
- Содержание рабочей программы Содержание обучения по профессиональному модулю (ПМ) Наименование, 139.63kb.
- Заключительный отчет июль 2010 содержание содержание 1 список аббревиатур 3 введение, 6029.85kb.
- 5. Содержание родительского правоотношения Содержание правоотношения, 110.97kb.
- Содержание введение, 1420.36kb.
- Сборник статей Содержание, 1251.1kb.
- Сборник статей Содержание, 1248.25kb.
- Анонсы ведущих периодических изданий содержание выпуска, 806.18kb.
- Вопросы к экзамену по дисциплине «Коммерческая деятельность», 28.08kb.
- Конспект лекций содержание содержание 3 налог на прибыль организаций 5 Плательщики, 795.2kb.
Таблица 11
Факторные нагрузки после вращения
| Факторные нагрузки (Варимакс нормализованный) | ||
| Метод главных компонент | ||
| | | |
| | Фактор | Фактор |
| | 1 | 2 |
| Прибыль | 0,857651 | -0,50455 |
| Покупатели и заказчики | 0,487053 | -0,87331 |
| Векселя к получению | -0,89093 | 0,451333 |
| Прочие дебиторы | -0,83954 | 0,533379 |
| Объясн. | 2,471361 | 1,505431 |
| Уд. Вес | 0,61784 | 0,376358 |
Теперь можно сделать определённые выводы из полученных результатов анализа факторных нагрузок после вращения.
Два фактора объединяют 99% признаков. Первый фактор объединяет прибыль, векселя к получению и прочих дебиторов, второй фактор объединяет покупателей и заказчиков.
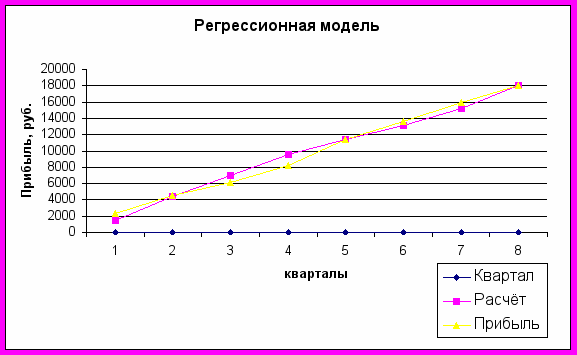
Линейная двухпараметрическая модель регрессии.
В таблице 12 приводятся данные по построению и анализу двухпараметрической модели регрессии прибыли.
Таблица 12
Двухпараметрическая модель регрессии прибыли
| ВЫВОД ИТОГОВ | | | | | | | | |
| | | | | | | | | |
| Регрессионная статистика | | | | | | | | |
| Множественный R | 0,990379 | | | | | | | |
| R-квадрат | 0,98085 | | | | | | | |
| Нормированный R-квадрат | 0,973191 | | | | | | | |
| Стандартная ошибка | 920,4427 | | | | | | | |
| Наблюдения | 8 | | | | | | | |
| | | | | | | | | |
| Дисперсионный анализ | | | | | | | ||
| | df | SS | MS | F | Значимость F | | | |
| Регрессия | 2 | 2,17E+08 | 1,08E+08 | 128,0512 | 5,07E-05 | | | |
| Остаток | 5 | 4236073 | 847214,7 | | | | | |
| Итого | 7 | 2,21E+08 | | | | | | |
| | | | | | | | | |
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | 18042,3 | 741,6122 | 24,32848 | 2,19E-06 | 16135,93 | 19948,67 | 16135,93 | 19948,67 |
| Векселя к получению | -0,14247 | 0,063317 | -2,25014 | 0,074264 | -0,30523 | 0,020289 | -0,30523 | 0,020289 |
| Прочие дебиторы | -19,7114 | 68,99516 | -0,28569 | 0,786571 | -197,069 | 157,646 | -197,069 | 157,646 |
| ВЫВОД ОСТАТКА | | | | | | | | |
| Наблюдение | Предсказанное Прибыль | Остатки | Стандартные остатки | | | | | |
| 1 | 1499,71 | 825,29 | 1,060899 | | | | | |
| 2 | 4368,247 | 229,7535 | 0,295345 | | | | | |
| 3 | 7007,596 | -879,596 | -1,13071 | | | | | |
| 4 | 9621,393 | -1380,39 | -1,77448 | | | | | |
| 5 | 11446,76 | 9,244232 | 0,011883 | | | | | |
| 6 | 13120,68 | 466,3191 | 0,599447 | | | | | |
| 7 | 15235,32 | 776,6812 | 0,998413 | | | | | |
| 8 | 18042,3 | -47,2992 | -0,0608 | | | | | |
Оценим адекватность и точность полученной модели регрессии.
Среднее остатков: -0.00075
Среднее квадратичное: 777.91597
Критерий Стьюдента: 0.00000
Критерий поворотных точек: 2 < 2 не выполняется
Критерий Дарбина-Уотсона: 1.33655
Первый коэф. автокорреляции: 0.42721
Наибольшее значение остатка: 825.29000
Наименьшее значение остатка: -1380.39300
R/S критерий 2.83537
Средняя относительная ошибка: 10.02793 %
Проведём анализ полученных результатов.
С
реднее значение ряда остатков близко к нулю, это очевидно, так как для построения регрессионной модели использовался метод наименьших квадратов, предполагающий минимизацию суммы квадратов остатков.
Для проверки равенства нулю математического ожидания ряда остатков применялся критерий Стьюдента. Для доверительной вероятности 70% и количества наблюдений 8 табличное значение tтабл = 1.05. В данном случае tнабл = 0.0000, то есть гипотеза о равенстве нулю математического ожидания распределения ряда остатков принимается.
Проверка случайности уровней остатков ряда проводится на основе критерия поворотных точек. Для количества наблюдений, равного 8, необходимо, чтобы было не меньше 2 поворотных точек. В нашем случае их 2, то есть гипотеза о случайности ряда остатков не принимается.
При проверке независимости (отсутствия автокорреляции) определялось отсутствие в ряде остатков систематической составляющей с помощью d – критерия Дарбина – Уотсона. Для линейной модели в качестве критических возьмём d1 = 1.08, d2 = 1.36. Так как у нас d находится в пределах от 1.08 до 1.36 то гипотезу об отсутствии автокорреляции принять нельзя и надо воспользоваться другими критериями.
Таким же образом можно проверить отсутствие автокорреляции по первому коэффициенту автокорреляции. Если количество наблюдений меньше 15, то в качестве табличного значения берём rтабл = 0.36. Так как в нашем случае |r(1)| > rтабл, то гипотеза об отсутствии автокорреляции в ряде остатков не подтверждается.
Соответствие ряда остатков нормальному закону распределения определялось при помощи R/S критерия. Для 5% доверительной вероятности интервал для этого критерия будет 2.7 – 3.7. Как видно, в нашем случае данный критерий выполняется, то есть можно говорить о нормальности распределения ряда остатков.
Для характеристики точности модели воспользуемся средней относительной ошибкой. Если ошибка менее 10%, это говорит об удовлетворительной точности полученной модели. В данном случае это имеет место, то есть наша модель имеет удовлетворительную точность.
Из полученных выше результатов можно сделать следующие выводы. Отбор наиболее значимых факторов проведён удачно, построенная линейная двухпараметрическая регрессионная модель адекватно отражает фактические результаты и может использоваться для исследований и прогнозов.
