Методика выполнения работы открыть рабочее окно программы matlab. Изучить теоретические сведения о пакете
| Вид материала | Лабораторная работа |
- Для запуска программы необходимо предварительно запустить пакет matlab. Основное окно, 415.08kb.
- 1. Теоретические сведения, 771.46kb.
- Методические указания по выполнению лабораторной работы №6 по курсу "Цифровая обработка, 222.67kb.
- Валерий Семенович Черкасский программа курса, 25.75kb.
- Задачи: изучить теоретические основы устройства и принципы работы батареек; изучить, 128.44kb.
- Инструкция по настройке доступа к сети Интернет для стационарных компьютеров в компьютерных, 58.1kb.
- Инструкция по настройке доступа к сети Интернет для стационарных компьютеров в компьютерных, 74.36kb.
- «Информационные технологии в налогообложении» Лекция 2 Автоматизированное рабочее место, 191.87kb.
- «Насосы и насосные станции», 197.77kb.
- Методика выполнения работы : Вариант Влияние легирующих элементов на структуру конструкционных, 128.12kb.
Красноярский государственный университет цветных металлов и золота
Кафедра автоматизации производственных процессов
ЦМ   | Дисциплина “Применение ЭВМ в СУ” Красноярск 2005 г. |
Лабораторная работа № 8
“Изучение пакета AutotunerPID Toolkit системы MATLAB для
моделирования, имитирования и анализа систем управления“
ЦЕЛЬ РАБОТЫ
1. Ознакомиться с составом и назначением программного пакета AutotunerPID Toolkit.
2. Ознакомиться с основными методами и примерами использования программного пакета AutotunerPID Toolkit для моделирования и анализа систем управления.
3. Освоить расчет, настройку и анализ одноконтурных САР в среде AutotunerPID Toolkit системы MATLAB.
МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ
- Открыть рабочее окно программы MATLAB .
- Изучить теоретические сведения о пакете AutotunerPID Toolkit
- Закончив изучение теоретических сведений о пакете AutotunerPID Toolkit, выполнить задание по моделированию СУ.
Теоретические сведения
AutotunerPID Toolkit позволяет:
- экспериментировать с хорошо изученными методами настройки, и знакомится с ними;
- понимать различные стадии, которые формируют процедуру автонастройки, и связь между ними, а также предоставляет возможности проведения сеанса автонастройки эффективно и сознательно;
- учиться выбирать определенный метод автонастройки, основанный на параметрах процесса;
- сравнивать результаты различных методов по опыту, как с точки зрения полученных результатов так и эксперимента (то есть, рассматривая такие факты как время настройки, сбой процесса, и т.д), учиться диагностировать результаты сеанса настройки и, когда возможно, получить из них информацию о дальнейшем процессе.
1 Блок автонастройки
Блок автонастройки – это устройство, способное вычислять параметры регулятора, связанного с объектом управления автоматически и, по возможности, без какого-либо вмешательства человека, кроме запуска процесса.
Основные шаги процесса настройки следующие:
- наблюдение за ходом процесса, подача на него каких-либо входных сигналов и составление на основе этих данных описания поведения процесса;
- определение желательного поведения замкнутого контура на основе полученного описания процесса;
- вычисление параметров регулятора, обеспечивающих желательное поведения замкнутого контура.
Формализация этих шагов дает метод настройки. Тогда Автонастройка – это выполнение метода настройки автоматически.
"Описание" процесса может быть получено двумя способами:
- первый подход заключается в идентификации модели процесса на основе данных, где модель означает нечто, что можно смоделировать, и что отображает динамику процесса достаточно точно, чтобы позволить предсказывать его поведение, как только регулятор настроен (блок автонастройки, основанный на модели);
- другой подход заключается в использовании данных процесса непосредственно для последующей настройки (блок автонастройки, не основанный на модели). Важным аспектом является то, что эти представления не могут быть смоделированы. Блоки настройки, не основанные на модели также называют блоками автонастройки, основанными на характеристиках.
Правила настройки могут быть разработаны несколькими способами:
- выбор параметров регулятора таким образом, чтобы ожидаемое поведение замкнутого контура (предсказанное с помощью модели процесса) было насколько это возможно близко к поведению эталонной модели (основанная на модели, отслеживающая модель автонастройка);
- вычисление параметров регулятора так, чтобы замкнутая система удовлетворяла некоторым характеристикам временной или частотной области (основанная на модели, отслеживающая характеристики автонастройка).
2 ISA-PID регулятор
В литературе можно найти несколько структур ПИД-регулятора. Регулятор, использованный в этом приложении – это так называемый "ISA-PID" регулятор, который широко распространен в промышленности. Закон управления ISA-PID, имеет следующий вид:
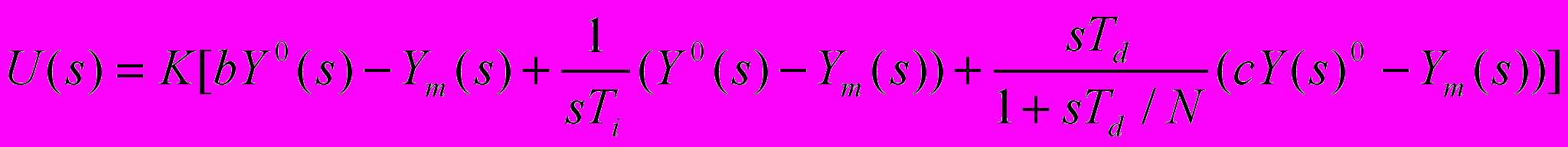
где Y0(s), Ym (s) и U (s), соответственно, преобразование Лапласа заданного значения (SP), (измерение) регулируемой величины или значение процесса (PV) и сигнала управления или переменная управления (CV), K – коэффициент усиления ПИД-регулятора,Ti – постоянная интегрирования, и Td – постоянная дифференцирования.
В выражение ISA-PID входят веса заданного значения b и c воздействия по отклонению и воздействия по производной.
Традиционно, b играет роль ограничителя шага управления, который может увеличиться в результате ошибки шага, в то время как c должен ограничивать импульс управления, который может увеличиться вследствие ошибки шага даже с соответствующим контроллером. Однако, в контексте автонастройки b и c могут играть более обширную и гибкую роль. Дифференциальная часть сделана более точной путем добавления полюса с постоянной времени, пропорциональной Td и параметру N.
3 Идентификация процесса
Первый шаг в процесс автонастройки - определение подходящего описания объекта управления. Далее приводятся два наиболее часто используемых метода поиска этого описания. Первый, так называемый Метод Областей, обеспечивает описание процесса основанное на модели. Он основан на эксперименте с разомкнутым контуром. Второй, называемый Методом Реле, обеспечивает описание модели, основанное на характеристиках. Он основан на эксперименте с замкнутым контуром.
Метод Областей
Метод областей принадлежит к так называемым описаниям процесса, основанным на модели, так как он идентифицирует модель объекта с помощью простого эксперимент, выполняемого над объектом. В большом разнообразии циклов процесса, модель, воспринимаемая регулятором, может быть описана асимптотически устойчивой, строго правильной передаточной функцией, которая может быть довольно точно смоделирована с помощью модели первого порядка с запаздыванием (МППсЗ).
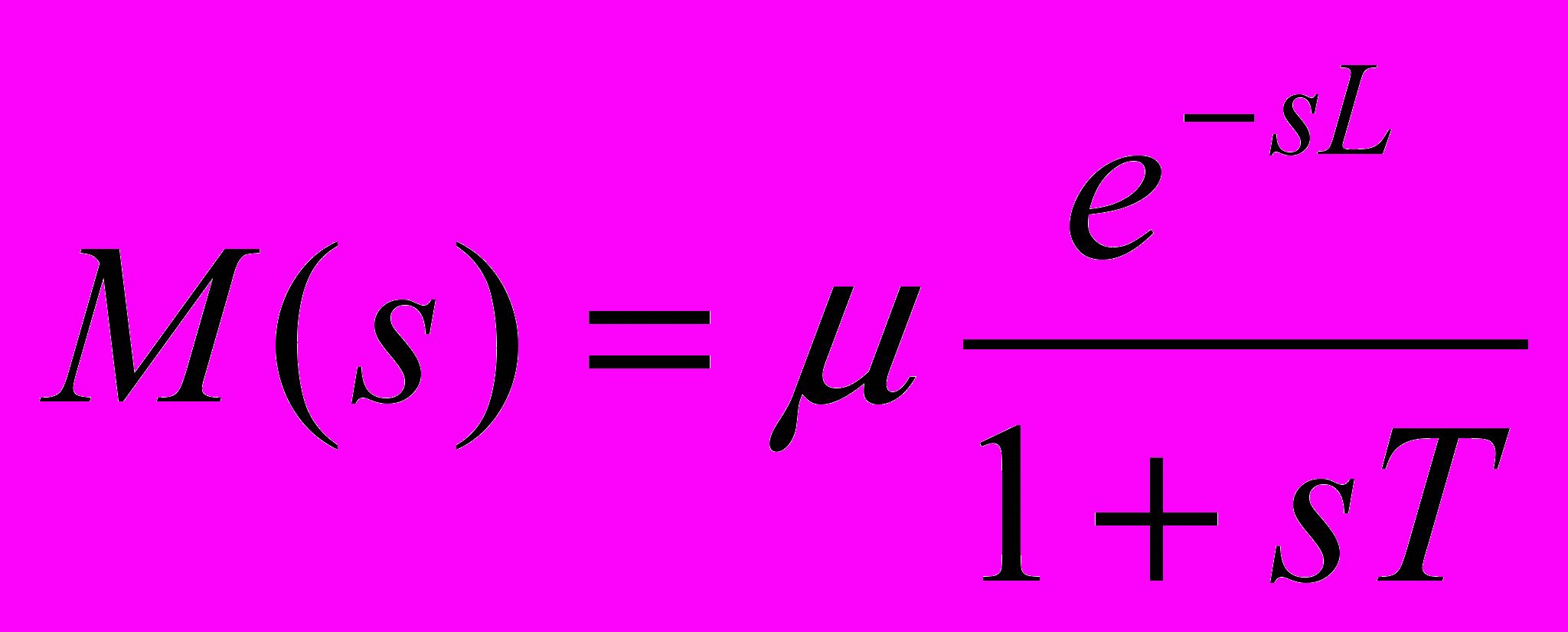
По данной переходной характеристики ys(t) нужно сначала вычислить коэффициент усиления , разделив суммарное отклонение характеристики на амплитуду входного сигнала As, и единичную переходную характеристику Yus(t)=Ys(s)/As
Затем, обозначив время окончания эксперимента как tend, то есть принимая, что при t=tend Yus(t) = , необходимо вычислить последовательно три величины, которые и дают название методу.
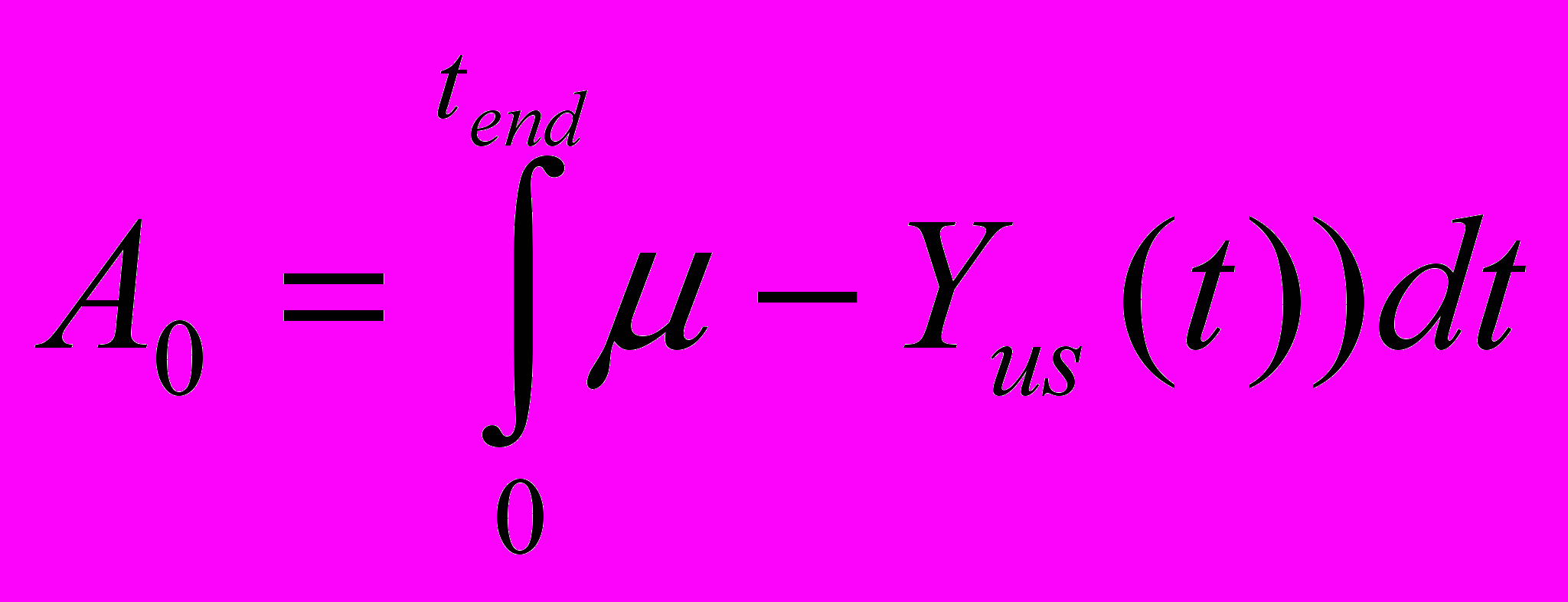 ,
, 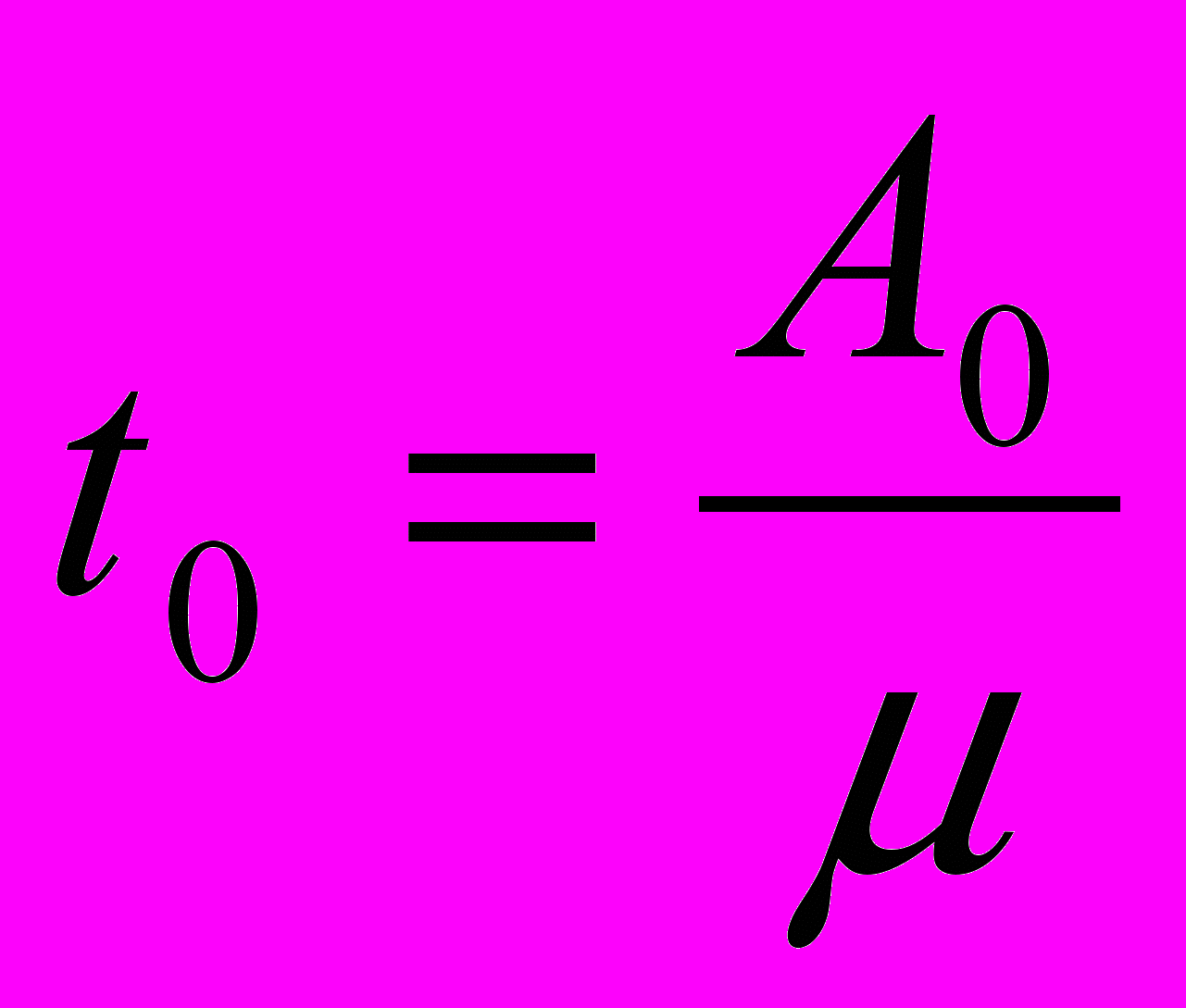 ,
, 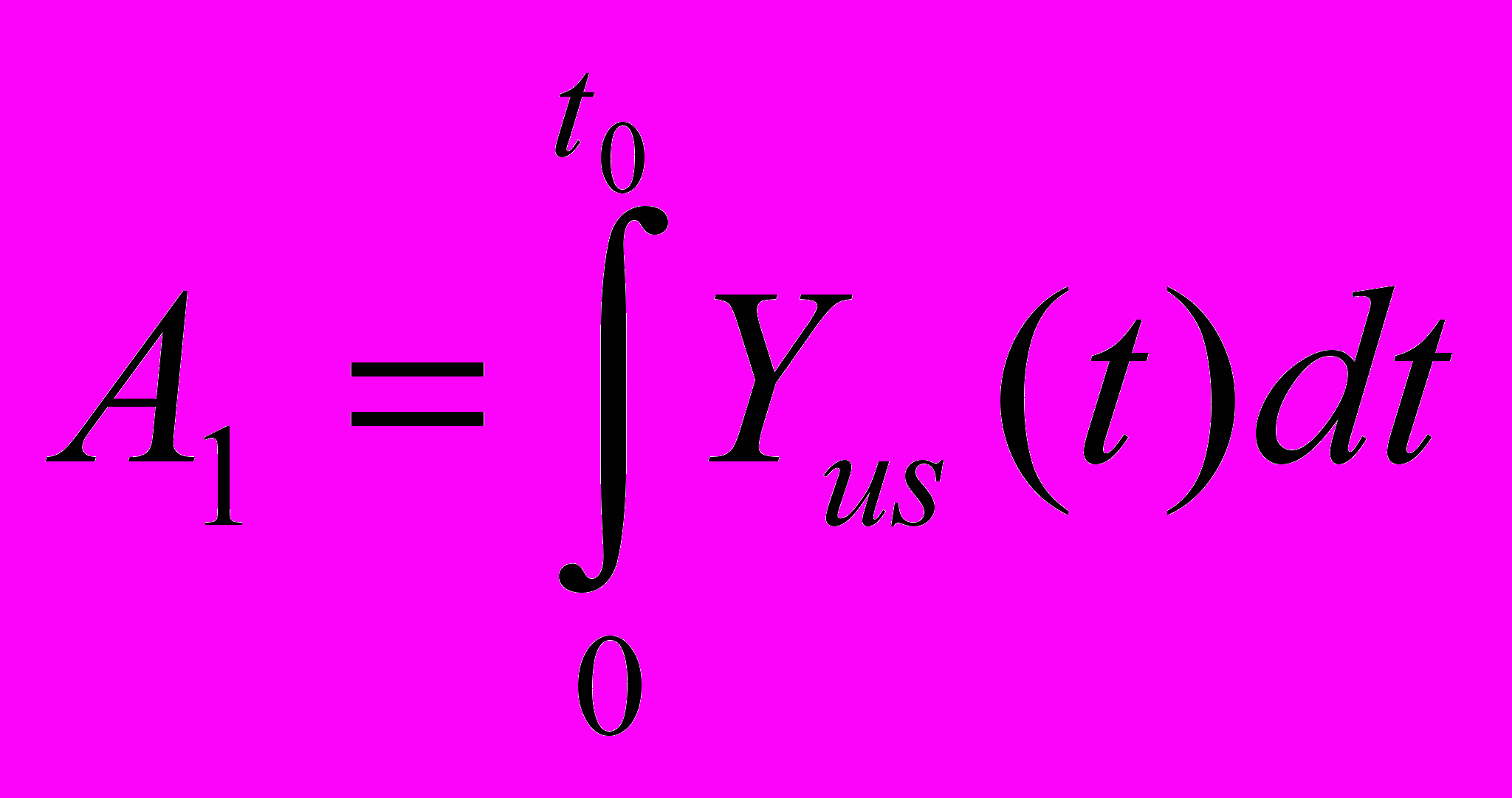
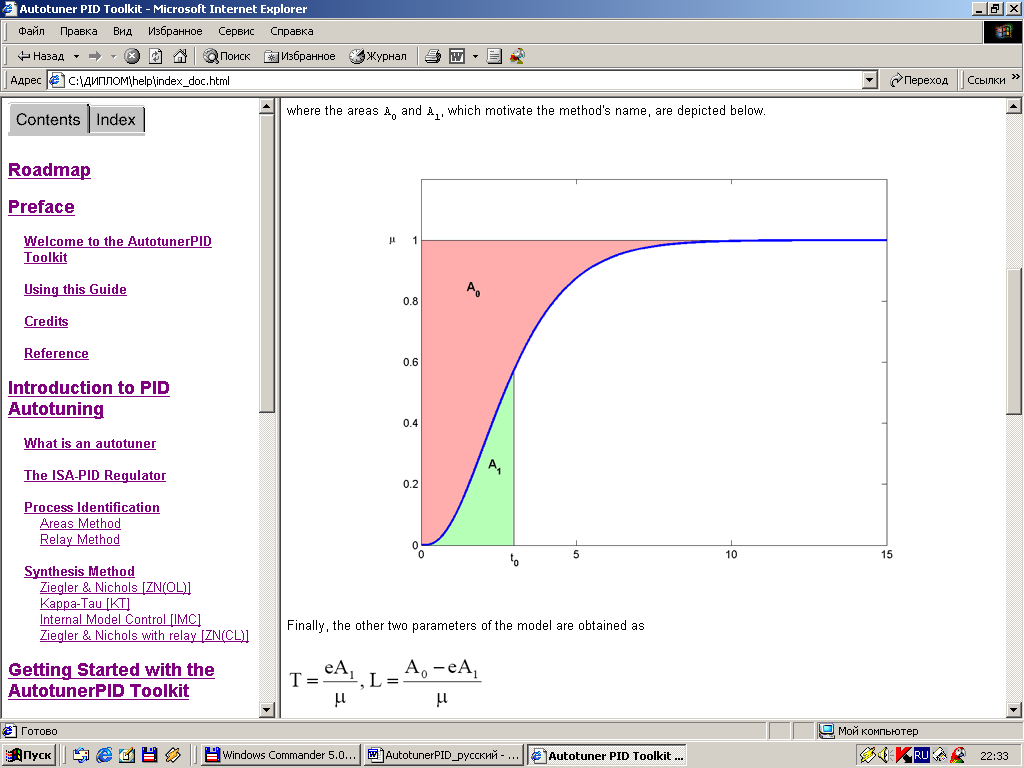
Рисунок 1 Метод областей
Наконец, можно получить другие два параметра модели в виде
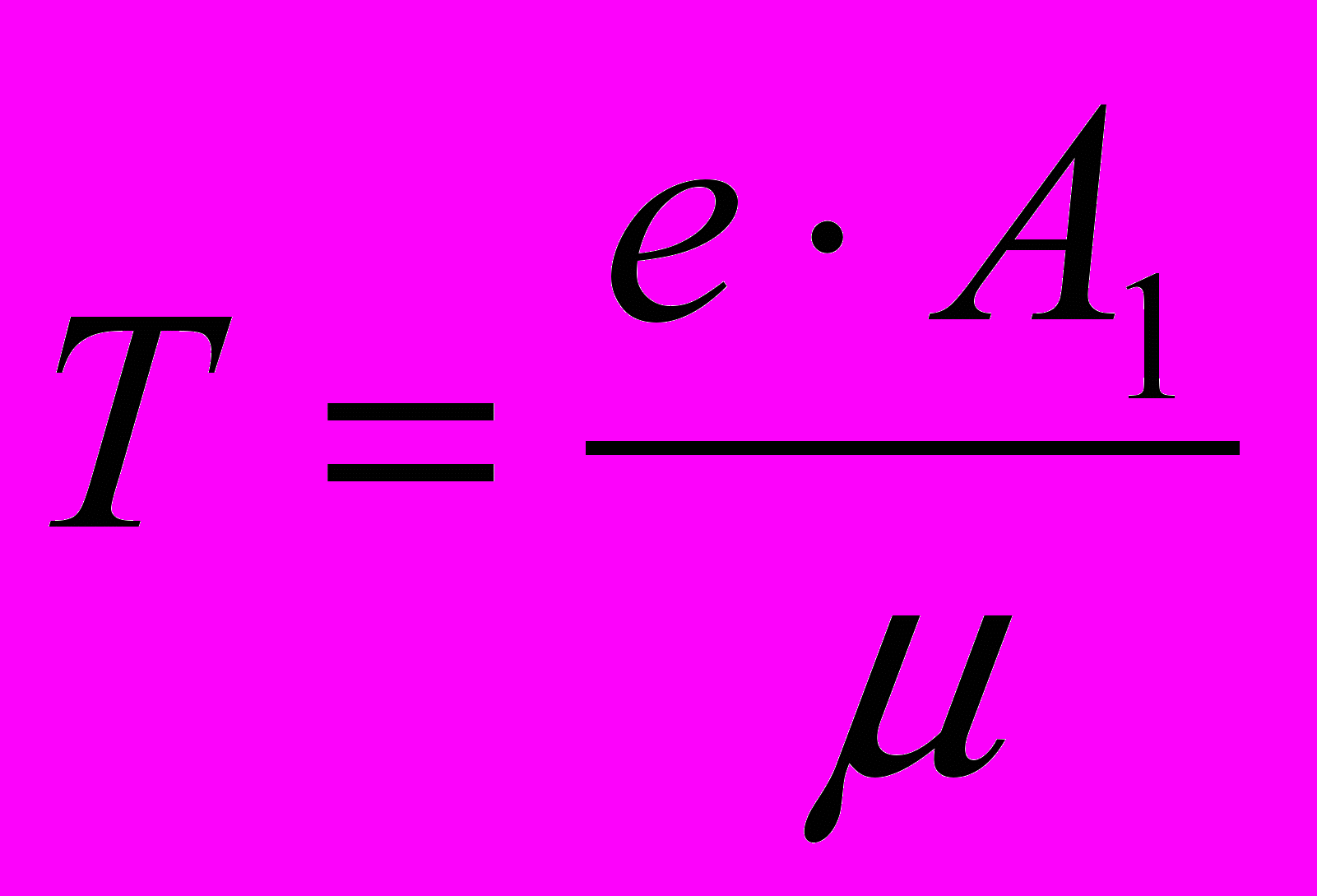 ,
, 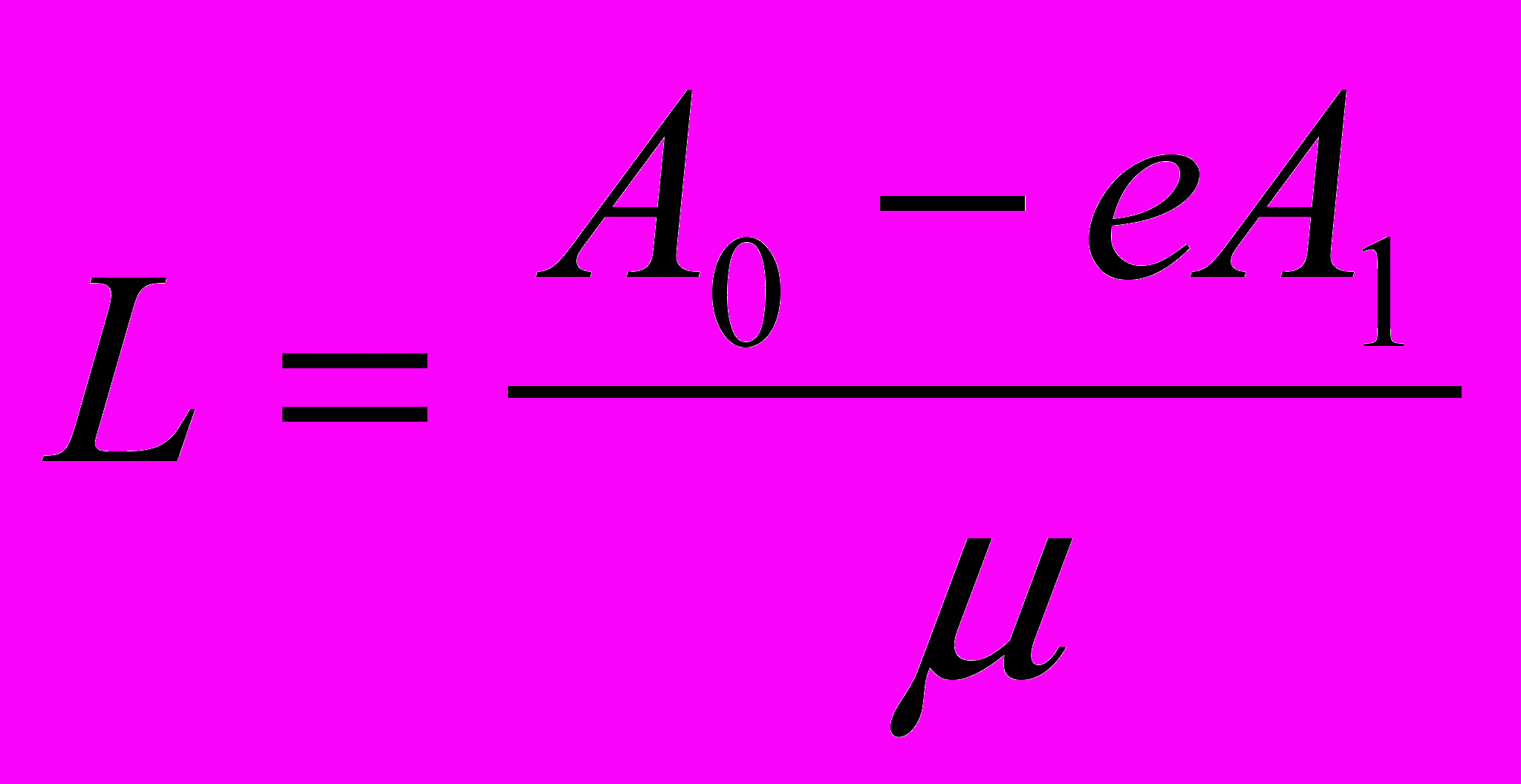
где установка L=0, если вычисленное значение отрицательное (что может случиться, если реальное запаздывание мало).
Метод областей очень эффективный, нечувствителен к шуму (так как использует интегрирование) и весьма точный. Кроме того, он может оценивать запаздывание, не требуя от пользователя дополнительных сведений о начале процесса.
Метод реле
Метод идентификации реле принадлежит к так называемым описаниям процесса, основанным на характеристиках, так как он идентифицирует набор отличительных характеристик модели, а не саму (простую) модель.
Главная идея при идентификации реле состоит в том, что почти в любом устойчивом процессе, при наличии обратной связи, возникает придельный цикл, с помощью которого просто получить некоторые характеристики временной и (особенно) частотной области.
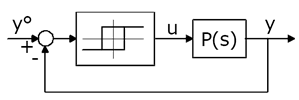
Рисунок 2 Схема системы с реле
Если в процесс с годографом Найквиста P(j) ввести релейную обратную связь с амплитудой D (то есть чей вывод - ±D) и запаздыванием E (то есть чьи точки переключающие находятся в ±E), то в ней возникают постоянные колебания выходного сигнала.
Эти колебания имеют частоту ox, где P(j) пересекает местоположение критической точки реле, которое является прямой, параллельной реальной отрицательной оси, расположенной в третьем квадранте комплексной плоскости и зависит от типа запаздывания.
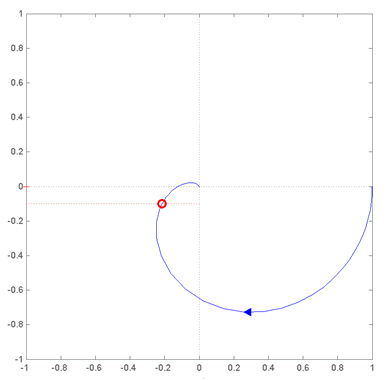
Действительная ось
Рисунок 3 Годограф Найквиста
Это позволяет выделять одну точку процесса на годографе Найквиста P(j) (точка, обозначенная выше кругом). Ее величина связана с амплитудой колебаний А регулируемой величины выражением |G(jox)|=pA/4D, а ее фаза может быть легко выведена, зная, что ее вещественная часть –pE/4D. Кроме того, можно легко вычислить период колебаний.
4 Методы синтеза
После того, как была определена модель (или некоторая характеристика) объекта, второй шаг заключается в настройки параметров ПИД-регулятора так, чтобы достигнуть наилучшего качества. Далее приведен краткий обзор методов синтеза, используемых в приложении.
Методы:
- Циглера-Никольса с Идентификацией Шага [разомкнутый контур].
- Каппа-Тау [KT].
- Внутреннее Управление Моделью[ВУМ].
- Циглера-Никольса с Идентификацией Реле [ЗН (замкнутый контур)].
Метод Циглера-Никольса с идентификацией шага [ZN (OL)]
Первый метод Циглера-Никольса настраивает параметр ПИД-регулятора согласно следующей таблице, на основе параметров, определенных для модели МППсЗ
Таблица 1 Параметры регулятора
| Закон регулирования | К | Ti | Td |
| P | T/mL | 0 | 0 |
| PI | 0.9T/mL | 3L | 0 |
| PID | 1.2T/mL | 2L | 0.5L |
В оригинальной версии метода формулы настройки даются относительно некоторой характеристики процесса, идентифицированного в пределах точек, где тангенс переходной характеристики в точке максимальной кривизны пересекает переходную характеристику. Однако здесь используется измененная версия, так как она более устойчива к шуму.
Метод Каппа-Тау [KT]
Метод Каппа-Taу вычисляет параметры ISA-PID закона управления 2-й степени свободы, кроме N и в случае дифференцирования выхода (то есть c=0). Он требует идентифицировать МППсЗ модель, если процесс не интегрирующий, или МППсЗ плюс коэффициент 1/s, если интегрирующий (пока не рассматривается в данном приложении).
Тогда необходимую информацию получают на основе параметров модели , T и L и требований ПИ или ПИД-регулятора. Дальнейшее описание заключается в определении требуемого запаса устойчивости по амплитуде Ms по формуле
 .
.Рекомендуется принимать следующие значения: 1.4 (осторожная настройка) или 2.0 (более агрессивная настройка). Определение нормированного коэффициента процесса и нормированного запаздывания осуществляется по формулам
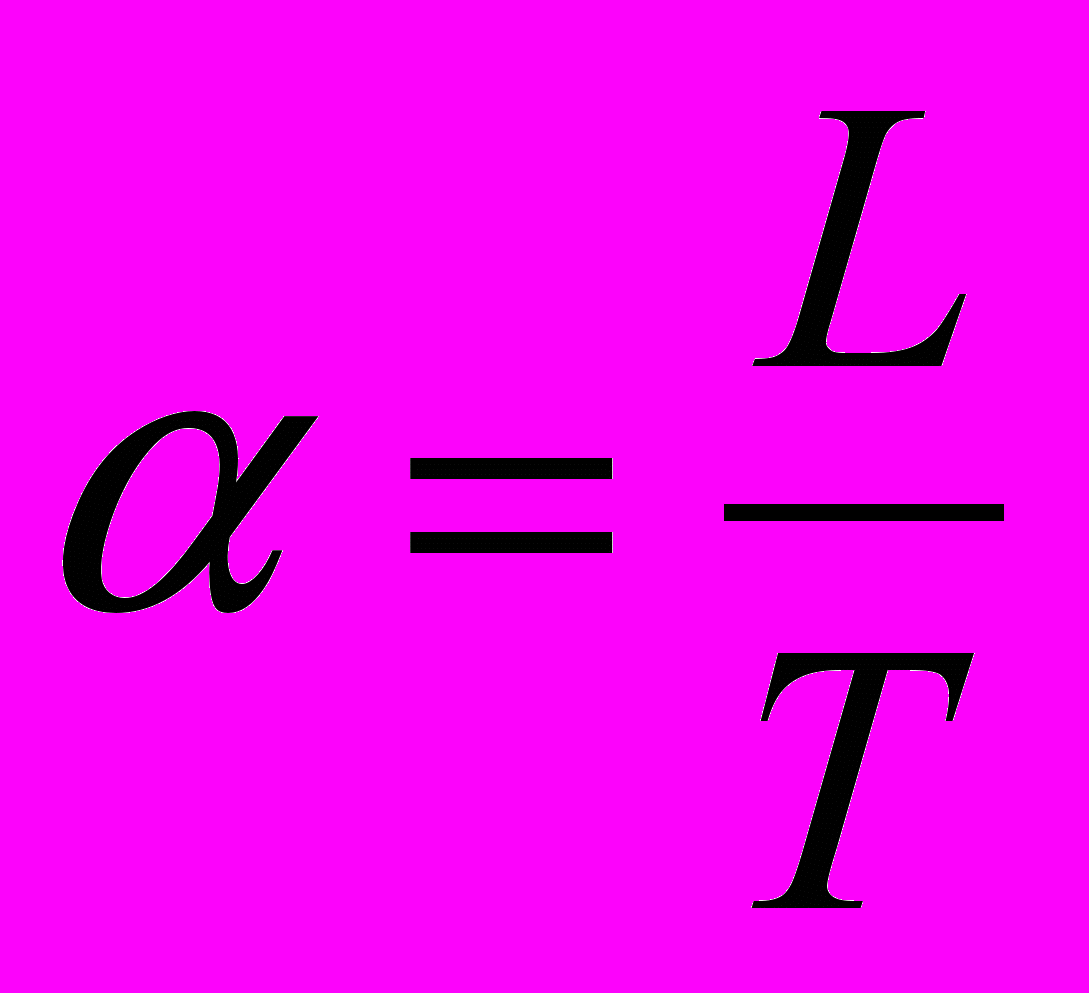 ,
, 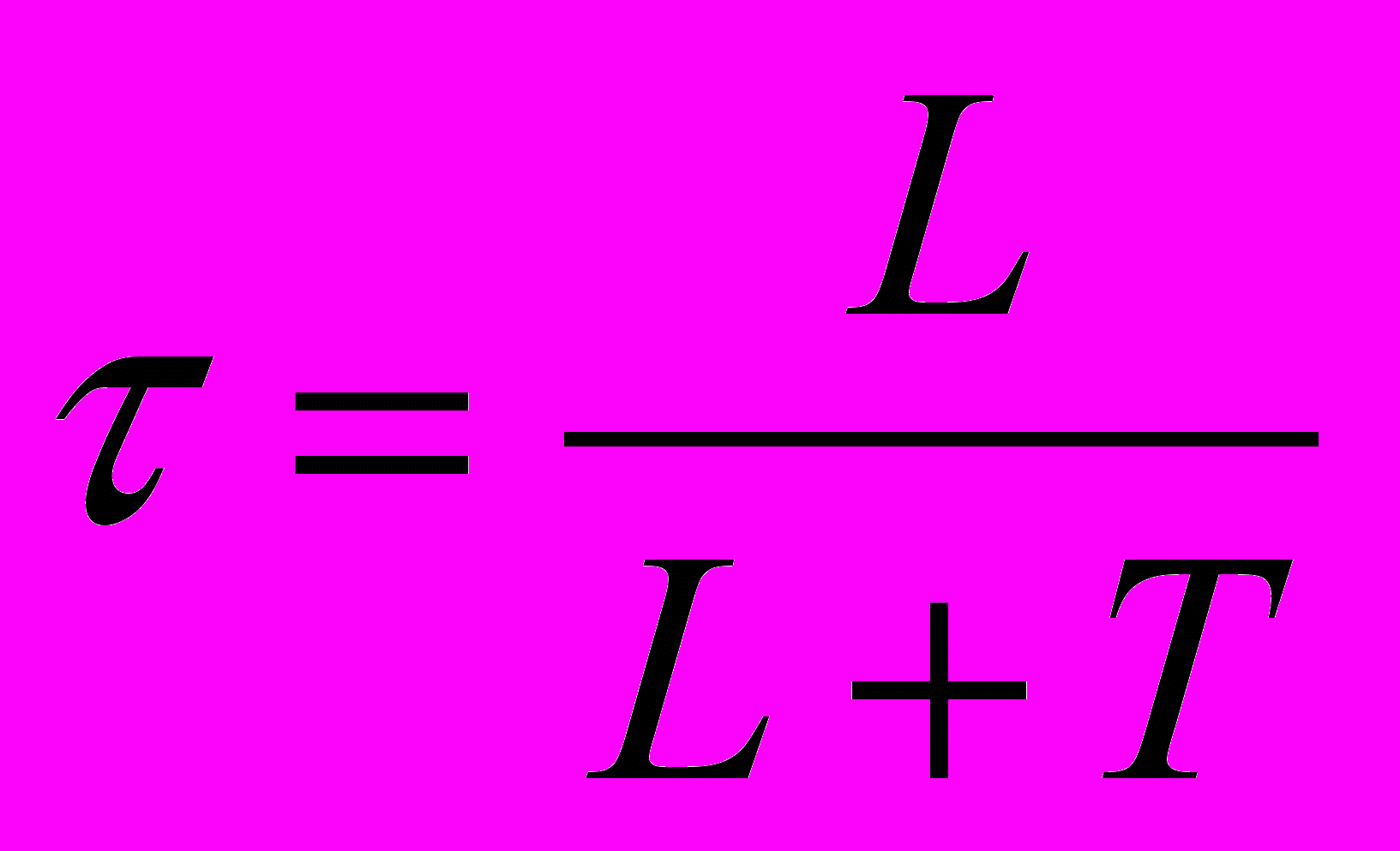 . Параметры ПИД-регулятора определяются по формулам
. Параметры ПИД-регулятора определяются по формулам 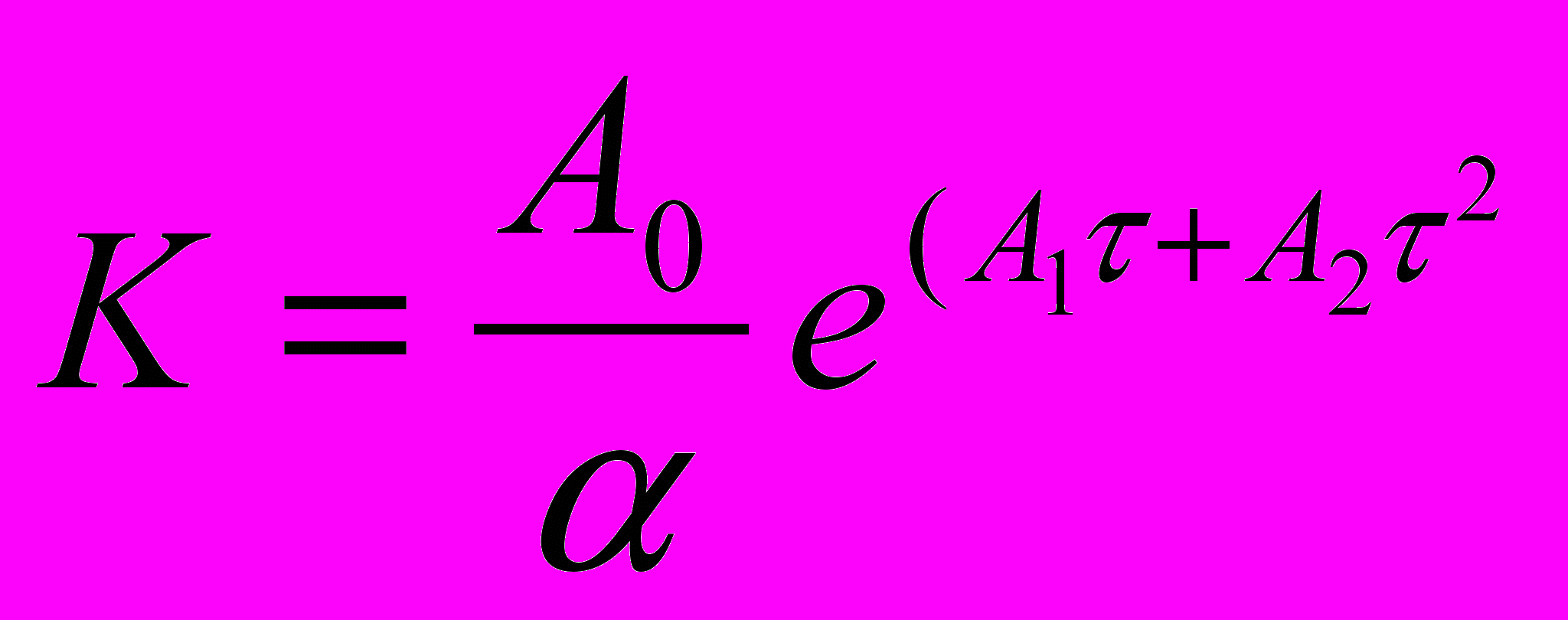 ,
, 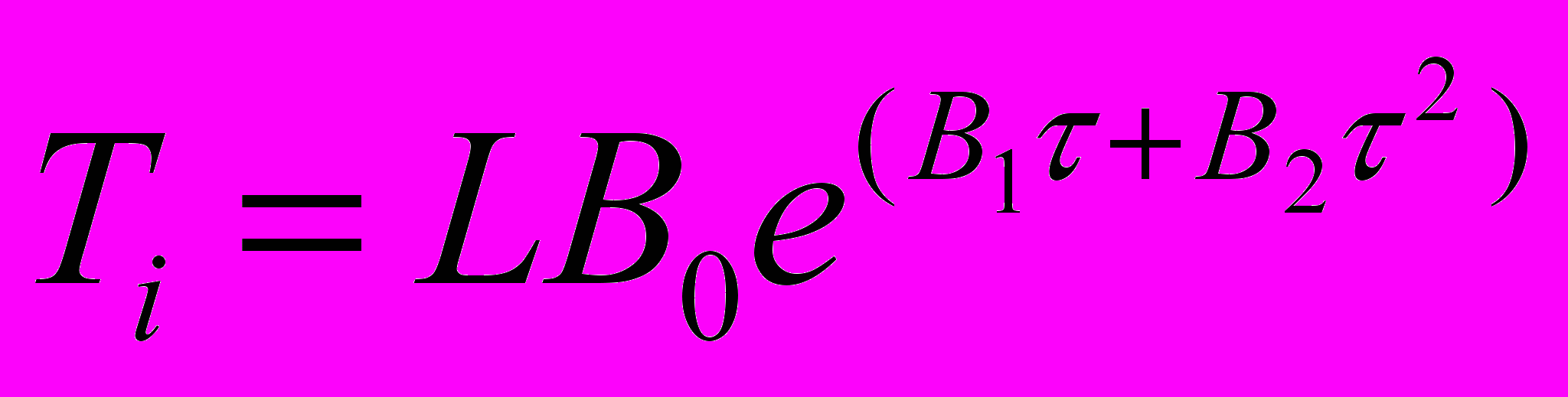 ,
, 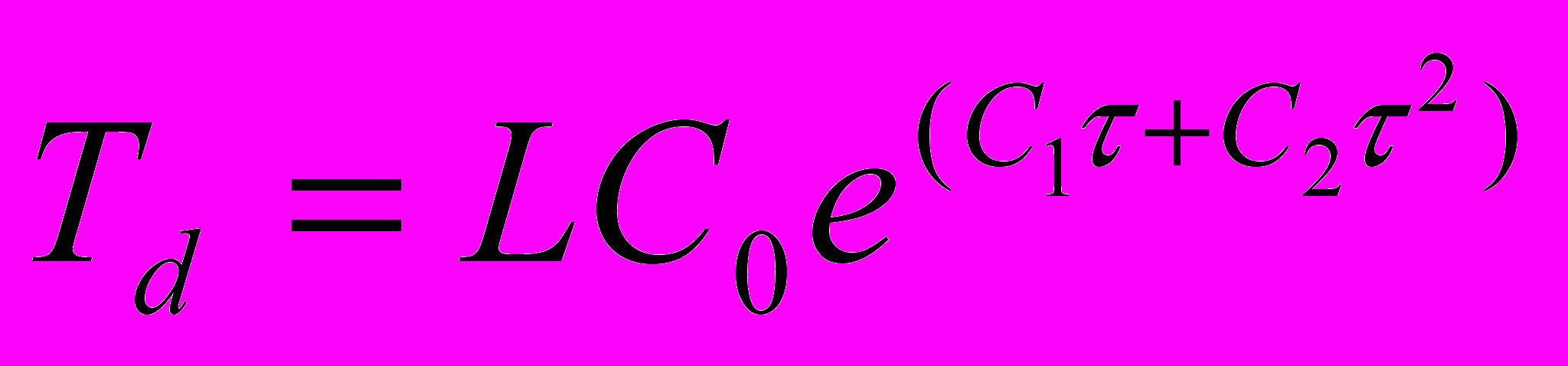 ,
, 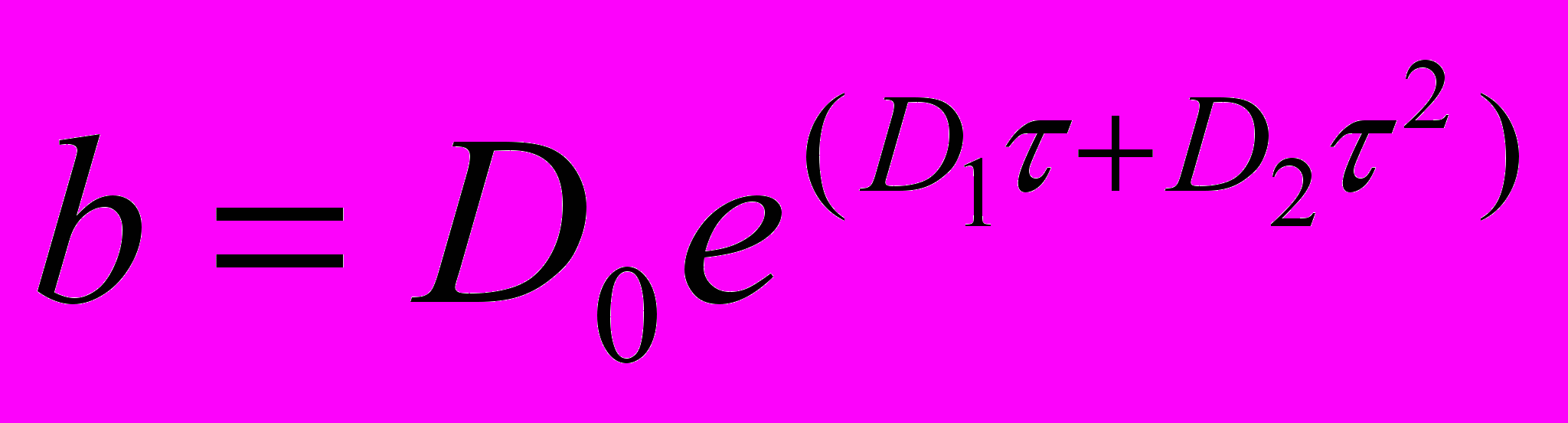 .
.Коэффициенты Аi, Вi, Ci, Di берут из следующей таблицы. Эти коэффициенты были получены с помощью метода доменантого полюса при анализе многих различных процессов с дальнейшей интерполяцией результатов для получения компактных соотношений настройки. Таким образом, этот метод является отслеживающим модель методом с особым образом использованной интерполяцией. Одной из важных особенностей является то, что нормированное запаздывание, иногда называемое "индексом управляемости", может использоваться как мера того, насколько трудно управлять процессом.
Таблица 2 Параметры регулятора
| Structure | PI | PI | PID | PID |
| Ms | 1.4 | 2.0 | 1.4 | 2.0 |
| A0 | 0.29 | 0.78 | 3.8 | 8.4 |
| A1 | -2.7 | -4.1 | -8.4 | -9.6 |
| A2 | 3.7 | 5.7 | 7.3 | 9.8 |
| B0 | 8.9 | 8.9 | 5.2 | 3.2 |
| B1 | -6.6 | -6.6 | -2.5 | -1.5 |
| B2 | 3.0 | 3.0 | -1.4 | -0.93 |
| C0 | 0 | 0 | 0.89 | 0.86 |
| C1 | 0 | 0 | -0.37 | -1.9 |
| C2 | 0 | 0 | -4.1 | -0.44 |
| D0 | 0.81 | 0.48 | 0.4 | 0.22 |
| D1 | 0.73 | 0.78 | 0.18 | 0.65 |
| D2 | 1.9 | -0.45 | 2.8 | 0.051 |
Внутреннее управление моделью [IMC]
Чтобы Объяснить главную идею, лежащую в основе метода внутреннего управления моделью, рассмотрим следующую блок-схему
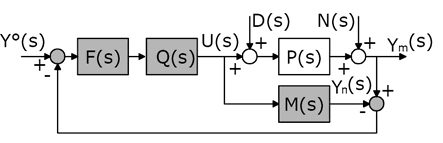
Рисунок 4 Блок-схема внутреннего управления моделью
где P (s) – передаточная функция процесса (считаем его асимптотически устойчивым, таким образом исключая интегрирующие процессы), М(s) - модель процесса, Q(s) и F(s) – произвольные (на этой стадии) асимптотически устойчивые передаточные функции; Ym (s) и Yn (s) - истинная (измеренная) и номинальная регулируемые величины.
Переходя к его практическому использованию следует сказать, что ВУМ метод синтеза - процедура 2-х шаговая. Сначала определяется Q(s) как приближенная инверсия М(s), а именно ее минимально фазовой части. Затем, чтобы гарантировать робастность, вводится “IMC” фильтр низкой частоты F(s). Структура и параметры F(s) выбраны так, чтобы достигнуть разумного равновесия между помехоустойчивостью и качеством.
В идеальном случае T (s) = F (s) Q (s) М(s), ВУМ – отслеживающий модель метод, пытающийся (грубо говоря) компенсировать М(S) Q (s) так, чтобы наложить динамику замкнутого контура F(s).
При выполнении синтеза, метод состоит из идентификации модели FOPDT и последующего применение ВУМ методики, выбирая
 ,
, 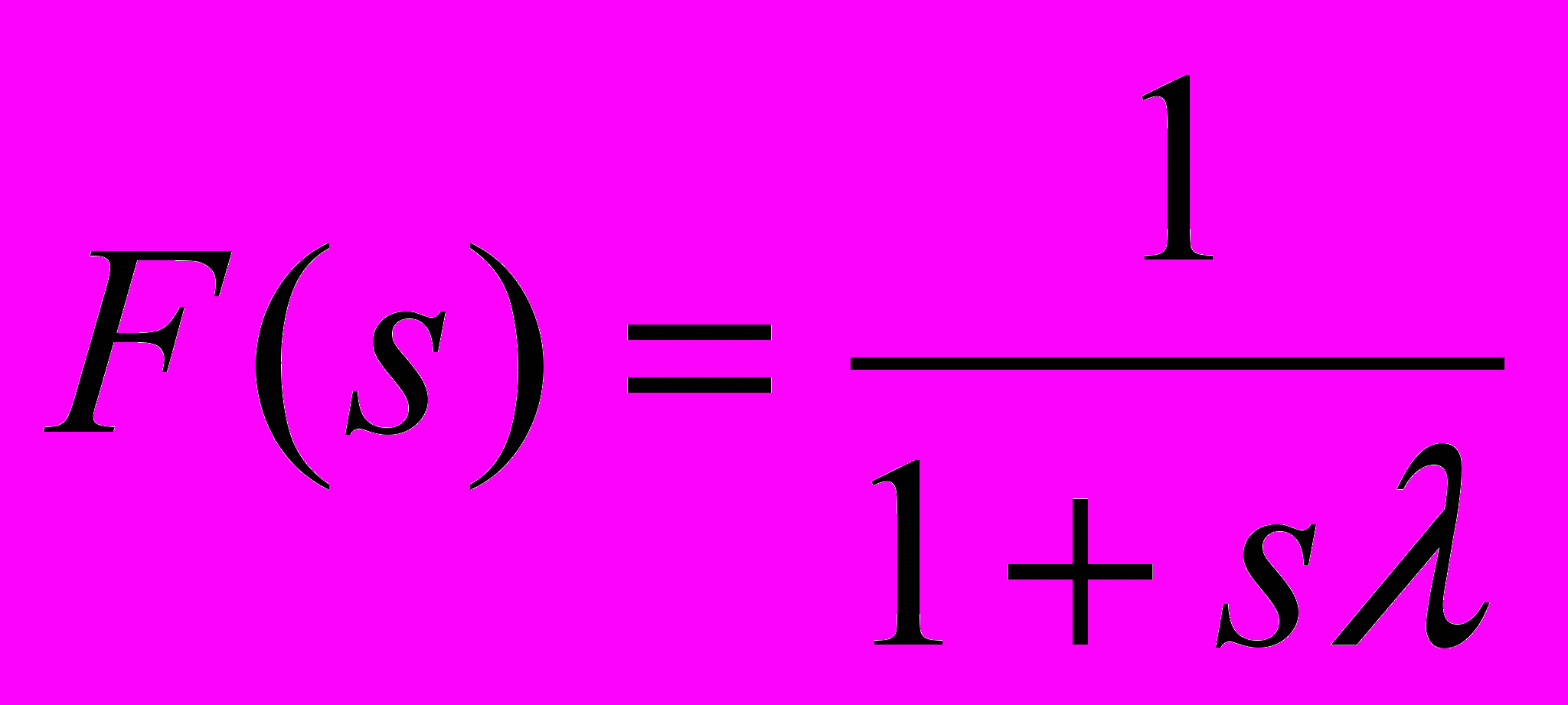
и заменяя запаздывание процесса его(1,1) аппроксимацией Паде (1-sL/2)/(1+sL/2). ПИД-регулятор в этом случае имеет вид
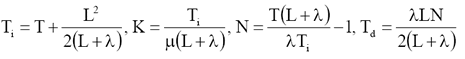
Основной трудностью при использовании метода ВУМ-ПИД является выбор параметра , который является ключевым при определении соотношения устойчивости, робастности и качества.
Метод Циглера-Никольса с идентификацией реле [ZN(CL)]
Второй метод Циглера-Никольса настраивает параметры ПИД-регулятора согласно следующей таблице, на основе точки частотной характеристики, определенной при эксперименте с реле. Период колебания обозначен как Tu, а коэффициент усиления Ku = 4As/pi*A.
Таблица 3 Параметры регулятора
-
Закон регулирования
K
Ti
Td
Р
0.5Ku
0
0
PI
0.4Ku
0.8Tu
0
PID
0.6Ku
0.5Tu
0.125Tu
В оригинальной версии метода идентификация точки требует применения пропорционального управления и увеличения коэффициента усиления контроллера, пока выход процесса не достигнет незатухающих колебаний. Однако это опасная практика, так как при этом модель находится около предела устойчивости.
5 Схема системы управления
AutotunerPID Toolkit моделирует единичный SISO контур управления, который состоит из ПИД-регулятора с блоком автонастройки, объекта управления, фильтра низких частот и некоторых вспомогательных блоков для управления процессом моделирования.
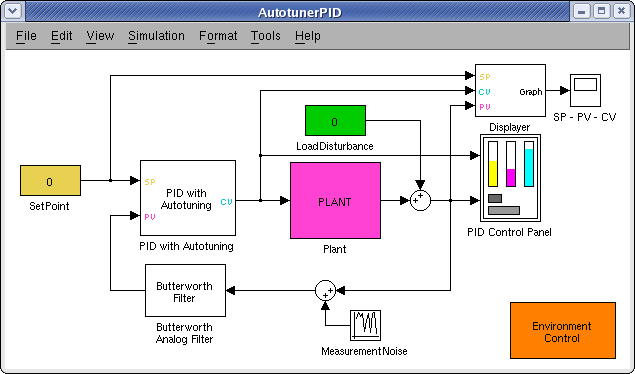
Рисунок 5 Основной интерфейс AutotunerPID Toolkit
6 ПИД-регулятор с автонастройкой
Регулятор – это подсистема, образованная двумя S-функциями: pid_isatd.m, которая обеспечивает выполнение дискретного ISA-PID, и pid_autotuner.m, которая отвечает за процесс автонастройки.
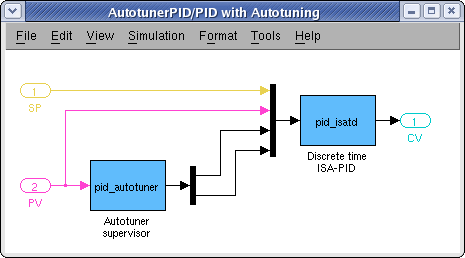
Рисунок 6 Схема ПИД-регулятора с автонастройкой
7 Дискретный ISA-PID (pid_isatd)
Дискретный ISA-PID включает фильтр коррекции по производной и вес заданного значения (но не вес коррекции по производной, который задан c=0). Кроме того ПИД-регулятор включает в себя ограничитель верхнего и нижнего значений управляющего воздействия и безударное переключение с автоматического на ручной режим. Структура такого "промышленного ПИД-регулятора" более сложна чем структура "схоластического" и близко воспроизводит функционирование регуляторов, используемых на практике.
8 Диспетчер блока автонастройки (pid_autotuner)
Диспетчер блока автонастройки управляет процессом автонастройки, главным образом выполняя идентификацию модели процесса (idareas.m) или набора характеристик (pid_autotuner) и синтезируя новые параметры с помощью описанных методов (pid_tuning.m). Кроме того, возможно задать ПИ-регулятор или ПИД, или структура может быть автоматически выбрана диспетчером (pid_structure.m).
9 Задание параметров регулятора
Параметры регулятора могут быть инициализированы через маску блока PID with Autotuning.
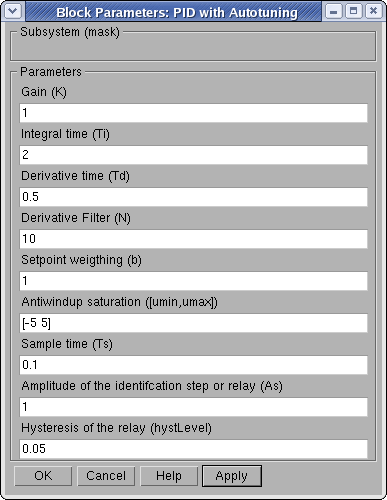
Рисунок 7 Параметры ПИД-регулятора
Эта маска состоит из нескольких разделов:
Начальные параметры ПИД-регулятора.
Эта часть маски позволяет устанавливать начальное значение параметров ISA-PID (K, Ti, Td, N, b). Вес воздействия по производной задан (c=0), так что этот параметр не отображается в маске.
Ограничитель крайних значений.
Нижний и верхний пределы управляющего воздействия задаются как вектор в соответствующем текстовом поле. Чтобы отключить ограничение, устанавливают следующие приделы [-inf, inf].
Время преобразования.
Выбор времени преобразования связан с характеристиками процесса. Вообще, маленькое время преобразования подразумевает, что процесс моделирования будет протекать медленно, в то время как большое значение времени преобразования означает быстрое моделирование. Однако, дискретизация ПИД-регулятора вызывает появление задержки в контуре, которая растет с ростом времени преобразования, так что реальное поведение систем управления может сильно отличаться от ожидаемого (вычисленного относительно непрерывного регулятора).
Идентификация
Последняя часть маски позволяет устанавливать параметры идентификации:
- амплитуда шага управления для эксперимента с разомкнутым контуром или амплитуда реле (положительная и отрицательная) для эксперимента с замкнутым контуром;
- уровень запаздывания реле, включенного, чтобы снизить вероятность ложного срабатывания из-за помех измерения в эксперименте с замкнутым контуром.
10 Объект управления
Объект управления – это подсистема, которая моделирует контролируемый процесс.
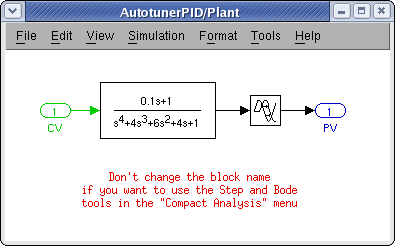
Рисунок 8 Схема объекта управления
Структуру объекта управления специально была оставлена открытой. Таким образом, можно вводить свой собственный объект управления в имитатор безо всяких ограничений: объект может быть линейным или нелинейным, непрерывным или дискретным и так далее. Однако, сравнительный анализ переходных характеристик и диаграмм Боде доступен только для линейных объектов (по очевидным причинам).
Обратите внимание, что сравнительный анализ доступен только когда не выполняется моделирование и для линейных объектов. Кроме того, имена блоков в подсистеме Plant не должны меняться, так как они используются как ссылки в функциях, выполняющих этот анализ.
11 Панель управления ПИД-регулятора
PID Control Panel выполнена с помощью замаскированной S-функции (autogui.m), которая использует основные графические элементы среды MATLAB, чтобы создать графический интерфейс пользователя, который довольно точно воспроизводит панель управления настоящего промышленного ПИД-регулятора. Цель этого интерфейса состоит в том, чтобы обеспечить все вводы и выводы, типичные для реального промышленного ПИД-регулятора.
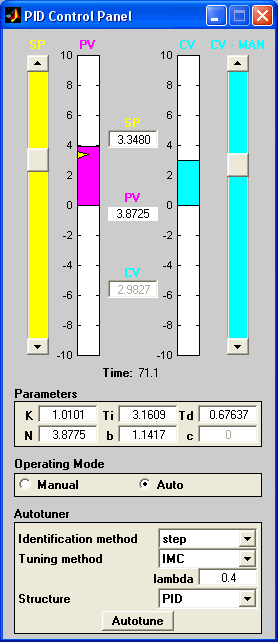
Рисунок 9 Панель управления ПИД-регулятора
Рассмотрим характеристики этого интерфейса, который главным образом разбит на четыре области.
Управления процессом
Верхняя часть графического интерфейса пользователя используется для взаимодействия с системой управления:
- Изменение заданного значения (SP) с помощью движка SP или текстового поля SP. Значение заданного значения также показывается графически желтым треугольником на оси PV.
- Отслеживание регулируемой величины (PV) на оси PV или в текстовом поле PV.
- Отслеживание значения управляющего воздействия (CV) на оси CV или в текстовом поле CV, когда регулятор работает в автоматическом режиме или изменение CV с помощью ползунка CV-MAN или в текстовом поле CV, когда регулятор работает в ручном режиме.
Параметры (parameters)
В этой области показываются текущие значения шести параметров ISA-PID (K, Ti, Td, N, b, c). Все параметры доступны для редактирования кроме веса воздействия по производной, который является постоянным (c=0). Изменения оказывают воздействие на систему немедленно.
Рабочий режим (Operating Mode)
Эта область позволяет управлять режимом работы системы с ПИД-регулятором. В автоматическом режиме (Auto) значение управляющего воздействия вычисляется ПИД-регулятором, и ползунок CV-MAN и область редактирования CV недоступны. В ручном режиме (Manua) CV задается вручную пользователем с помощью ползунка CV-MAN или текстовой области CV.
Автонастройка может быть выполнена как в ручном, так и в автоматическом режиме. В первом случае, однако, ПИД-регулятор не переключается к автоматическому режиму после завершения процесса автонастройки.
Блок автонастройки (Autotuner)
Он управляет процессом автонастройки с помощью следующих параметров:
- identification method: всплывающее меню, которое позволяет выбирать желаемый метод идентификации (Step, Relay);
- Tuning method: всплывающее меню, которое позволяет выбирать желаемый метода настройки (IMC,КТ,ZN (OL),ZN (CL)). Если выбран метод IMC,то должен быть выбран параметр lambda. Если выбран метод KT,то параметр М3 должны быть выбраны между двумя значениями (1.4 и 2.0);
- Structure: всплывающее меню, которое позволяет выбрать структуру регулятора: ПИ, ПИД или авто (программа автоматически выбирает "лучший");
- Autotune button: используется, чтобы запустить процесс автонастройки (включая идентификацию и синтез параметров). В конце процесса автонастройки параметры ПИД-регулятора обновляются. В течение автонастройки интерфейс "заморожен", чтобы предотвратить изменения параметров ПИД-регулятора или режима работы.
12 Панель среды
Environment Panel выполнен с помощью замаскированной S-функции (envgui.m). Она управляет параметрами моделирования, которые не находятся под прямым управлением пользователя, поэтому они не могут быть включены в панель управления ПИД-регулятора. Например, могут быть включены измеримый шум или ступенчатое воздействие на нагружение.
Кроме того, с помощью панели среды управления можно выполнять сравнительный анализ всех методов автонастройки как во временной, так и в частотной области.
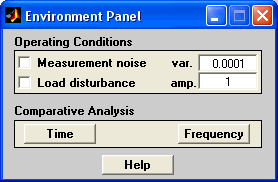
Рисунок 10 Панель среды
Рассмотрим характеристики этого интерфейса, который разбит на три области:
Режимы работы (Operating Conditions).
С ее помощью управляют средой моделирования через следующие параметры настройки:
- Measurement Noise: меню переключателя, которое позволяет накладывать заданные помехи на параметры процесса с определяемой пользователем дисперсией;
- Load Disturbance: меню переключателя, которое позволяет вводить ступенчатое воздействие в процесс с определяемой пользователем амплитудой.
Сравнительный Анализ (Comparative Analysis).
Эта область включает инструментальные средства анализа как во временной, так и в частотной областях. В частности, анализ временной области сравнивает переходные процессы в заданной точке и в нагружении для ПИД-регулятора, настроенного с помощью всех доступных методов. Анализ частотной области, вместо этого, выдает диаграмму Боде разомкнутого контура системы управления вместе с диаграммой Боде дополнительной чувствительности и функции чувствительности.
13 Аналоговый фильтр Баттерворта
Фильтр низкой частоты Баттерворта используется в контуре управления в качестве сглаживающего фильтра а также для уменьшения действия помех при измерении. Порядок и ширина полосы пропускания фильтра может задаваться пользователем (butterdesign.m).
Параметры аналогового фильтра Баттерворта низкой частоты могут быть инициализированы через маску блока Butterworth Analog Filter.
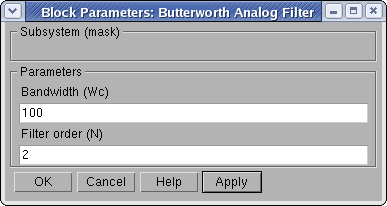
Рисунок 11 Параметры фильтра
Вообще, порядок фильтра должен быть достаточно малым, чтобы дополнительный сдвиг по фазе оставался низким (обычно 2 или 3). Также ширина полосы пропускания не должна быть слишком маленькой, даже если действие помех лучше всего подавляется именно при малой ширине полосы пропускания.
14 Сервисные блоки
Остальные блоки используются для того, чтобы организовать полностью функциональную среду.
- set-point: заданное значение регулируемой величины;
- load disturbance: значение, добавляемое к выводу объекта управления;
- measurement noise: белый Гауссов шум, который накладывается на параметр значения процесса;
- SP-PV-CV: блок устройства наблюдения, который выводит на экран величину заданного значения SP (желтый), значения процесса (регулируемой величины) PV (пурпурный), управляющего воздействия CV (голубой).
15 Начало моделирования
Параметры моделирования могут быть откорректированы пользователем как через классическое меню Simulink, так и с помощью набора блочных масок.
Процесс моделирование начинается, останавливается и приостанавливается с помощью классического меню Simulink или кнопками панели.
Параметры моделирования задаются в диалоговом окне Simulation Parameters, доступном через меню Simulation. В частности, время останова задано очень большим, чтобы воспроизвести эффект непрерывного моделирования, в то время как в качестве решающего устройства задано ode45, чтобы позволить использование объекта управления с общей структурой.
Практическое задание
- Запустите AutotunerPID Toolkit. Для этого в окне Current Directory основного интерфейса MATLAB запустить файл AutotunerPID\ AutotunerPID.mdl.
- По данным таблица 1 в соответствии с номером варианта создайте модель объекта управления второго порядка. Для этого дважды щелкните мышкой по блоку Plant. В появившемся окне сначала дважды щелкните мышкой по блоку передаточной функции и введите числитель и знаменатель. Затем аналогичным образом задайте запаздывание.
- Задайте приближенные параметры (коэффициент усиления, время интегрирования и время дифференцирования) ПИД-регулятора, рассчитанные по формулам таблицы 2 и отключите ограничение управляющего воздействия. Для этого дважды щелкните мышкой по блоку PID with Autotuning и в появившемся окне в строке Antiwindup saturation задайте пределы [-inf, inf]. Параметры регулятора задаются в строках Gain, Integral Time и Derivative time соответственно.
- Запустите моделирование, нажав на панели кнопку
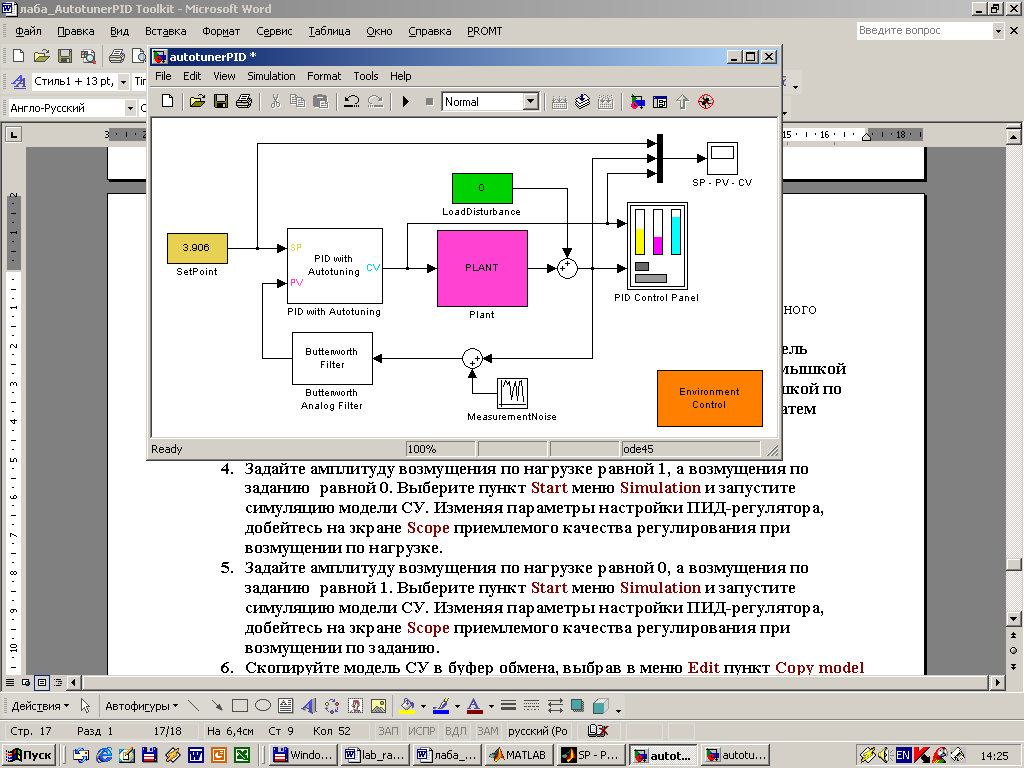
- Определите задающее воздействие, передвигая ползунок SP вверх или вниз и рассчитайте оптимальные настройки регулятора. Для этого в поле Autotuner панели регулятора в строке identification method задайте метод идентификации, в строке tuning method задайте метод настройки, в окне structure выберите структуру регулятора и нажмите кнопку Autotune. Попробуйте различные комбинации.
- Сравните переходные процессы в системе с регуляторами, рассчитанными разными методами. Для этого на панели среды в области Comparative Analyze нажмите кнопку Time.
На титульном листе отчета укажите свою фамилию, группу и номер варианта.
Таблица 1.
| № варианта | Параметры объекта регулирования | |||
| Kоб | T1об, с | Т2об, с | об, с | |
| 1 | 0,9 | 2,4 | 0,8 | 0,1 |
| 2 | 1,1 | 23 | 7 | 2 |
| 3 | 52 | 55 | 17 | 8 |
| 4 | 35 | 21 | 7 | 3 |
| 5 | 6 | 62 | 18 | 9 |
| 6 | 2,7 | 23 | 10 | 5 |
| 7 | 0,75 | 14 | 5 | 1,2 |
| 8 | 0,8 | 3,5 | 1,1 | 0,1 |
| 9 | 2,4 | 17 | 6,3 | 0,5 |
| 10 | 0,12 | 19,5 | 4,7 | 2,2 |
| 11 | 1,6 | 31 | 9,6 | 1 |
| 12 | 0,32 | 17 | 4,3 | 1,5 |
| 13 | 1,8 | 37 | 10 | 1,6 |
| 14 | 54 | 64 | 22 | 2,5 |
| 15 | 61 | 21 | 7,4 | 4,2 |
| 16 | 2,3 | 8 | 2,7 | 0,5 |
| 17 | 0,6 | 3,1 | 1,2 | 0,2 |
| 18 | 1,2 | 22 | 6,8 | 1,2 |
| 19 | 51 | 58 | 15 | 4,4 |
| 20 | 33 | 23 | 8 | 1,5 |
| 21 | 6,5 | 64 | 17 | 6 |
| 22 | 3,0 | 25 | 11 | 2 |
| 23 | 0,7 | 15 | 6,1 | 1,3 |
| 24 | 0,9 | 3,7 | 1,3 | 0,2 |
| 25 | 2,2 | 17,6 | 7,3 | 1,8 |
| 26 | 6,1 | 6 | 1,4 | 0,2 |
| 27 | 2,5 | 8,4 | 2,6 | 0,5 |
| 28 | 0,6 | 5,1 | 1,2 | 0,16 |
| 29 | 1,4 | 25 | 6,8 | 0,8 |
| 30 | 54 | 55 | 13 | 2,4 |
Оптимальные параметры настройки регуляторов для статических
объектов первого порядка с запаздыванием
| Тип регулятора | Параметры настройки | Тип переходного процесса | ||
| апериодический | с 20%-м перерегулированием | с min 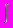 y2 dt y2 dt | ||
| И- | Кр | 1/(4,5 A) * | 1/(1,7A) | 1/(1,7 A) |
| П- | Кр | 0,3 В * | 0,7 В | 0,9 В |
| | Кр | 0,6 В | 0,7 В | 1,0 В |
| ПИ- | Ти | 0,6 Тоб | 0,7 Тоб | 1,0 Тоб |
| | Кр | 0,95 В | 1,2 В | 1,4 В |
| ПИД- | Ти | 2,4 об | 2,0 об | 1,3 об |
| | Тд | 0,4 об | 0,4 об | 0,5 об |
| * Примечание: А = КобТоб; В = Тоб/(Кобоб). | ||||
Контрольные вопросы для защиты
- Состав и назначение пакета AutotunerPID Toolkit.
- Структура регулятора ISA-PID.
- Структура и назначение блоков в AutotunerPID Toolkit.
- Методы идентификации (метод областей, метод реле).
- Методы синтеза.
- Расчет настроек регулятора в AutotunerPID Toolkit.
- Сравнительный анализ методов расчета в AutotunerPID Toolkit.
