А. М. Дымков расчет и конструирование трансформаторов допущено Министерством высшего и среднего специального образования СССР в качестве учебник

Вид материала

Учебник

Содержание Глава v расчет режима нагрузки трансформатора § 5.2. расчет потерь короткого замыкания PK=Ir= δsПρ•(1/sП)= ρδsПl. § 5.3. расчет добавочных потерь и потерь в отводах § 5.4. потоки рассеяния при нагрузке трансформатора § 5.5. вывод расчетной формулы напряжения рассеяния Рис. 5.3. Эскиз, поясняющий вывод формулы напряжения рассеяния UP= IωDСРΔKp/806eωH0 § 5.6. расчет напряжения короткого замыкания Контрольные вопросы

Подобный материал:

• Г. Г. Почепцов Теоретическая грамматика современного английского языка Допущено Министерством, 6142.76kb.
• В. Г. Атаманюк л. Г. Ширшев н. И. Акимов гражданская оборона под ред. Д. И. Михаилика, 5139.16kb.
• A. A. Sankin a course in modern english lexicology second edition revised and Enlarged, 3317.48kb.
• Автоматизация, 5864.91kb.
• Н. Ф. Колесницкого Допущено Министерством просвещения СССР в качестве учебник, 9117.6kb.
• В. В. Виноградов Очерки по истории русского литературного языка XVII-XIX веков издание, 11316.28kb.
• А. Б. Долгопольский пособие по устному переводу с испанского языка для институтов, 1733.75kb.
• В. К. Чернышева, Э. Я. Левина, Г. Г. Джанполадян,, 563.03kb.
• В. И. Королева Москва Магистр 2007 Допущено Министерством образования Российской Федерации, 4142.55kb.
• Ю. А. Бабаева Допущено Министерством образования Российской Федерации в качестве учебник, 7583.21kb.

ГЛАВА V

РАСЧЕТ РЕЖИМА НАГРУЗКИ ТРАНСФОРМАТОРА

§ 5.1. ЭКСПЛУАТАЦИОННЫЕ ПАРАМЕТРЫ (ХАРАКТЕРИСТИКИ) ТРАНСФОРМАТОРА ПО ГОСТу ПРИ ЕГО НАГРУЗКЕ: ПОТЕРИ И НАПРЯЖЕНИЕ КОРОТКОГО ЗАМЫКАНИЯ, ИЗМЕНЕНИЕ НАПРЯЖЕНИЯ И К. П. Д.

Рассмотрим кратко физические процессы, возникающие в трансформаторе при его нагрузке.

Токовая нагрузка трансформатора определяется сопротивлением любого вида: активным, индуктивным, емкостным или смешанным, включаемым на зажимы его вторичной обмотки. Вследствие включения сопротивления в образовавшейся замкнутой цепи появится вторичный нагрузочный ток

I₂=U₂/ Z₂

где Z₂ — полное сопротивление цепи.

Вторичный ток I₂ создает намагничивающую силу (ампер-витки) I₂ω₂, которая должна возбудить в магнитопроводе некоторый магнитный поток Ф_н. Согласно правилу Ленца этот поток в охватывающей его первичной обмотке вызовет первичную намагничивающую силу I’₁ω₁ равную по величине I₂ω₂. Намагничивающая сила согласно тому же правилу создает магнитный поток — Ф_н, т.е. поток, равный и направленный противоположно потоку Ф_н. Магнитные потоки взаимно уничтожаются, но в первичной обмотке появляется нагрузочный ток

I₁= I₂ω₂/ω₁

Таким образом, при включении со вторичной стороны трансформатора нагрузки появляются нагрузочные токи в обеих его обмотках, направленные противоположно друг другу.

В силовых трансформаторах без большой погрешности полагают, что первичное и вторичное напряжения пропорциональны числам витков обмоток, поэтому

I’₁ = I₂ω₂/ω₁ = I₂U₂/U₁ или U₁ I’₁ = U₂ I₂

Отсюда следует, что первичная и вторичная мощности равны, и это согласуется с законом сохранения энергии.

Трансформатор, потребляя с первичной стороны электрическую энергию одного напряжения U₁ отдает эту же энергию (за вычетом потерь) со вторичной стороны, но только при другом напряжении U₂.

Так как в первичной обмотке имеется также и ток холостого хода I₀, то общий первичный ток I₁ при нагрузке трансформатора должен быть равен сумме (в общем случае геометрической) нагрузочного тока I’₁ и тока холостого хода I₀, т. е.

İ₁ =İ'₁+ İ₀

Но так как ток холостого хода составляет всего несколько процентов от номинального нагрузочного тока и, кроме того, оба тока складываются под некоторым углом друг к другу, то обычно током холостого хода пренебрегают и полагают, что I₁≈ I’₁.

Нагрузочные токи I₁ и I₂, проходя по обмоткам трансформатора, вызывают в них активные падения напряжения U_a1= I₁r₁ и U_a2= I₂r₂ и индуктивные падения напряжения P_k1 и P_k2.

Активные падения напряжения возникают вследствие электрических (джоулевых) потерь в обмотках, равных P_K1= I²₁r₁ и Р_к2 = I²₂r₂. Потери в обмотках Р_к1 и Р_к2 в сумме составляют основную часть потерь коротксго замыкания Р_к трансформатора.

Индуктивные падения напряжения возникают вследствие наличия магнитных потоков рассеяния, охватывающих каждую из обмоток в отдельности. Индуктивные падения напряжения компенсируют э. д. с. рассеяния E_р1 и E_р2, т. е. U_р1= — Е_р1 и U_p2= — Е_р2.

В приведенном трансформаторе полное активное падение напряжения равно сумме активных падений напряжения в обеих обмотках, т. е.

U_a=U_a1+ U_a2

Аналогичным образом полное индуктивное падение напряжения равно сумме индуктивных падений напряжения, т. е.

U_p=U_p1+ U_p2

На векторной диаграмме приведенного трансформатора геометрическая сумма активного и индуктивного падений напряжения, векторы которых находятся под углом 90° друг к другу, составляет полное падение напряжения, называемое напряжением короткого замыкания U_K трансформатора, следовательно,

_______

U_k=√U²_a+ U²_p (5.1)

Потери и напряжение короткого замыкания являются важными эксплуатационными параметрами (характеристиками) трансформаторов, поэтому они нормируются ГОСТами. Их значения приведены выше, в табл. 2.1 и 2.2.

От величины потерь и напряжения короткого замыкания зависит величина к. п. д. и изменения напряжения трансформатора, расчет которых приводится далее.

§ 5.2. РАСЧЕТ ПОТЕРЬ КОРОТКОГО ЗАМЫКАНИЯ

Потерями короткого замыкания Р_к называется мощность, определяемая по ваттметру при проведении опыта короткого замыкания (см. § 5.6).

Основную часть потерь короткого замыкания, как было сказано выше, составляют электрические потери в обмотках или, точнее, в обмоточных проводах. Кроме электрических потерь в обмотках, в состав потерь короткого замыкания входят также добавочные потери в проводах, стенках бака и деталях конструкции и потери в отводах.

Электрические потери в обмотках, вызванные нагрузочными токами в них, рассчитываются по основной формуле мощности электрического тока, затрачиваемой в цепи

P=I²r.

В заводской практике часто пользуются преобразованной формулой, в которую входят плотность тока δ и вес обмоточного провода G_o,

P_K=I²r= δ²s²_Пρ•(1/s_П)= ρδs_Пl.

Так как G₀=γs_Пl•10^-3 и s_Пl = G₀•10^-3/γ , то

P_K=(ρ/γ)δ²G₀•10³=К_П δ²G₀, вт (5.2)

где s_П— сечение провода, мм²; l — длина провода, м;

ρ — удельное сопротивление меди (или алюминия), Ом•мм²/м;

γ— удельный вес, кГ/дм³; G_o— вес обмоточного провода, кГ.

Значение коэффициента К_П берется из табл. 5.1.

Таблица 5.1

Материал провода	Значение КП при температуре
	20° С	75°С
Медь…………………. Алюминий…………...	1,97 11,2	2,4 13,6

Так как плотности тока и вес провода у первичной и вторичной обмоток отличаются между собой, то потери в обмотках рассчитываются для каждой из обмоток отдельно и затем суммируются.

§ 5.3. РАСЧЕТ ДОБАВОЧНЫХ ПОТЕРЬ И ПОТЕРЬ В ОТВОДАХ

Добавочные потери при нагрузке трансформатора возникают как в самой обмотке, так и в отдельных деталях конструкций, главным образом в стенках бака. Эти потери возникают от вихревых токов, наводимых в проводах обмотки и в стенках бака потоками рассеяния.

При расчете добавочных потерь предполагается, что магнитные линии поля рассеяния Ф_р проходят параллельно главному каналу, одновременно пронизывая и обе обмотки, как это показано на рис. 5.2.

Так как обмоточные провода имеют некоторую толщину в радиальном направлении, то они пронизываются магнитным потоком рассеяния и вследствие этого в них возникают добавочные потери от вихревых токов. Эти дополнительные потери учитываются коэффициентом К_Ф, на который множатся основные (джоулевы) потери в обмоточных проводах.

Теоретический расчет коэффициента К_ф представляет собой относительно сложную проблему и поэтому для его определения применяют различные полуэмпирические формулы.

Для силовых трансформаторов с обмотками из прямоугольного провода

К_Ф=1+[(m²-0,2)/9](a')⁴, (5.3)

где m — число слоев катушки;

а' — приведенный радиальный размер провода, равный

a'=(a/1,03)√(b/b_ИЗ)•(f/50)•K_P

а — радиальный размер провода, см;

b — осевой размер голого провода, см;

b_ИЗ— то же, изолированного провода, см;

К_р— коэффициент Роговского (см. § 5.4);

f— частота, Гц.

Для обмоток из круглого провода диаметра d

К_Ф=1+[(m²-0,2)/15,25](d')⁴, (5.4)

где d' — приведенный диаметр провода, равный

d'=(d/1,03)√(d/d_ИЗ)•(f/50)•K_P

d_ИЗ—диаметр изолированного провода, см.

При диаметре провода до 3,5 мм (большие диаметры применяются редко, обычно в таких случаях переходят на прямоугольный провод) процент добавочных потерь относительно мал, поэтому при круглых проводах добавочными потерями пренебрегают.

При расчете добавочных потерь следует учитывать, что их величина в слое проводов, прилежащем к главному каналу рассеяния, получается примерно в 3 раза большей, чем средняя величина, определяемая по вышеприведенным формулам, что может привести к повышенному нагреву этого слоя.

Кроме того, за счет искривления магнитного потока рассеяния на выходе из обмотки могут возникнуть местные перегревы при большом осевом размере провода, что необходимо учитывать при расчете потерь трансформаторов большой мощности.

Из рассмотрения вышеприведенных формул видно, что величина добавочных потерь очень сильно (в четвертой степени) зависит от радиального размера провода. Поэтому следует избегать применения слишком толстых, массивных проводов, а если это требуется из необходимости иметь большое общее сечение обмоточного провода, то следует применять несколько параллельных проводов с их транспозицией (перемещением) (см. далее винтовые обмотки).

Кроме добавочных потерь в обмоточных проводах, потоки рассеяния вызывают также добавочные потери в стенках бака, прессующих ярмовых балках и других массивных частях конструкции трансформатора. Эти потери возникают как от вихревых токов, так и от перемагничивания.

Теоретический расчет этих потерь также очень затруднителен, так как обычно неизвестно точное направление магнитного поля рассеяния и его конфигурация.

Для силовых трансформаторов габарита 1 добавочные потери в стенках бака Р_б ввиду их относительно небольшой величины обычно не учитываются. Для трансформаторов большей мощности существует несколько предложенных эмпирических формул для их расчета. Для трансформаторов габаритов II и III наиболее простой является формула

Р₆ = 0,007 S^1.5 вт (5.5)

Потери в отводах между обмотками и вводами (проходными изоляторами) являются частью потерь короткого замыкания и должны быть учтены при расчете последних.

Потери в отводах могут быть точно определены после конструктивной разработки трансформатора, т. е. когда известны длина и сечение отводов. Однако величину этих потерь хотя бы приблизительно желательно знать заранее, чтобы не вносить коррективы в расчет обмоток после разработки конструкции.

Данные отводов уже выполненных серийных конструкций однотипных по мощности силовых трансформаторов в части потерь существенно не отличаются между собой. Поэтому предварительная величина потерь в отводах Р_отв трехфазного трансформатора с достаточным приближением может быть определена по эмпирической формуле

Р_отв = 0,05I⁴√S вт, (5.6)

где I — линейный ток обмотки, а.

Как можно видеть из приведенной формулы, величина Р_отв при токе, не превышающем 100—200 а, относительно мала, поэтому потери в отводах силовых трансформаторов габаритов II и III практически достаточно определять только для обмоток НН.

§ 5.4. ПОТОКИ РАССЕЯНИЯ ПРИ НАГРУЗКЕ ТРАНСФОРМАТОРА

При нагрузке трансформатора в его обмотках возникают нагрузочные токи, создающие соответствующие намагничивающие силы I₁ω₁ и I₂ω₂.



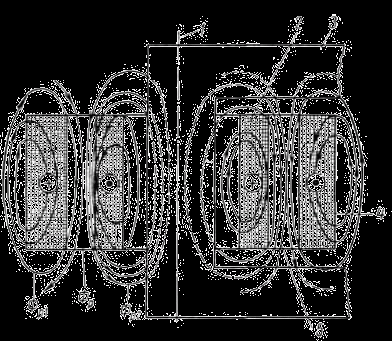
Рис. 5.1. Магнитные потоки рассеяния при нагрузке трансформатора:

1 — общалось стержня и обмоток трансформатора; 2 — вторичная обмотка; 3 — магнитопровод; 4 — первичная обмотка; 5 - канал между обмотками.

Вследствие этого вокруг каждой из обмоток образуются потоки рассеяния, как это показано на рис. 5.1. Так как токи в первичной и вторичной обмотках согласно правилу Ленца направлены в противоположные стороны, то оба потока рассеяния, создаваемые намагничивающими силами обеих обмоток, складываются в общий поток рассеяния Ф_р, проходящий через промежуток между обмотками, называемый главным каналом рассеяния. Ввиду наличия потоков должно существовать некоторое реактивное падение напряжения, обозначаемое U_p1 и U_p2. На векторной диаграмме треугольника короткого замыкания векторы U_p1 и U_p2 падений напряжения повернуты на угол 90º в сторону опережения по отношению к векторам U_a1 и U_a2 активного падения напряжения, совпадающим с направлением векторов нагрузочных токов.

Для расчета реактивного падения напряжения, или иначе напряжения рассеяния, необходимо знать магнитное сопротивление потоку рассеяния данного трансформатора.

Так как расчет действительного потока рассеяния ввиду сложности его формы крайне затруднителен, то вместо него производится расчет более простого, фиктивного, потока рассеяния Ф_ф, эквивалентного действительному. Направление магнитных линий фиктивного потока принято прямолинейным.

Форма фиктивного потока принята как наиболее простая цилиндрическая, с направлением магнитных линий, параллельным оси обмоток. Длина фиктивного потока согласно теоретическим исследованиям проф. Роговского при этом получается лишь на немного большей длины обмоток, так как основное магнитное сопротивление потоку рассеяния заключается в наиболее насыщенной его части, т. е. в главном канале. Вне обмоток поток рассеяния имеет относительно малую плотность и частично проходит по стальным частям трансформатора и поэтому встречает малое сопротивление.



Рис. 5.2. Фиктивный поток рассеяния, эквивалентный действительному, но имеющий более простую форму.

На рис. 5.2 изображен фиктивный поток рассеяния для концентрического расположения обмоток, когда последние имеют цилиндрическую форму и одинаковую длину.

Разность между длиной Н_о обмотки и длиной 1_р фиктивного потока учитывается особым коэффициентом К_р Роговского,

Н_о = К_р I_р,

К_р=(а+а₁+а₂)/π Н_о (5.7)

а — радиальный размер главного канала, см;

а₁ и а₂— радиальные размеры обмоток, см;

Н₀— осевой размер обмотки, см.

§ 5.5. ВЫВОД РАСЧЕТНОЙ ФОРМУЛЫ НАПРЯЖЕНИЯ РАССЕЯНИЯ

Напряжение рассеяния определяется по основной формуле напряжения трансформатора

U_р = 4,44fωФ_р•10^-4 в,

где Ф_р — общий поток рассеяния, проходящий вдоль обмоток и сцепленный с одним витком обмотки.

Индукция В_р в любой точке магнитного поля пропорциональна намагничивающей силе (ампер-виткам), охватывающей эту точку или, для трансформатора, цилиндрическую поверхность, проведенную через какую-либо магнитную линию потока рассеяния.

На рис. 5.3 изображены в разрезе обе обмотки и диаграмма распределения магнитной индукции, поясняющие вывод формулы напряжения рассеяния.

Как было сказано выше, первичная и вторичная намагничивающие силы равны между собой и направлены противоположно, т. е.

I₁ω₁+ I₂ω₂ = 0.

По краям зоны обмоток (точки О₁ и О₂) индукция равна нулю, так как нет ампер-витков, охватывающих силовые линии, находящиеся на крайних поверхностях обмоток. В толще катушек индукция будет увеличиваться по направлению от края катушки к главному каналу,

потому что поток создается теми ампер-витками, которые охватывают данную магнитную линию или с которыми сцеплена магнитная линия.

Наибольшая индукция потока рассеяния будет в главном канале и она будет одинаковой по всей ширине канала. Обычно предполагается, чтобы не усложнять хода рассуждений, что ампер-витки по сечению обмотки распределены с равномерной плотностью. Тогда распределение ампер-витков, а следовательно, и индукции В_р в радиальном направлении зоны обмоток может быть изображено диаграммой в виде трапеции, называемой трапецией Каппа, как это показано на рис. 5.2 и 5.3.

Произведение ωФ_р= ωB_РF называется потокосцеплением. Так как значения ω и В_Р являются величинами переменными, то общее потокосцепление определяется как сумма элементарных потокосцеплений

ωФ_р=Σ ω_ХB_ХdF_X



Рис. 5.3. Эскиз, поясняющий вывод формулы напряжения рассеяния

Для облегчения расчет производится раздельно по каждому из трех отдельных участков зоны обмоток с радиальными размерами а₁, а и а₂, для которых находится значение потокосцепления.

На среднем участке а (главного канала) ампер-витки и поток постоянны по величине, так как ω и В_р не меняют своих значений, поэтому потокосцепление на этом участке будет

(ωФ_р)_a = ωB_РF_a = ωB_Рπ D_cpa,

где F_a= πD_cpa — площадь сечения участка а, см²;

D_cp — средний диаметр главного канала рассеяния, см.

Любая магнитная линия участка а будет сцеплена со всеми витками либо первичной обмотки I, либо вторичной обмотки II.

Расчет потокосцепления на участке a₁ производится путем интегрирования элементарных потокосцеплений на этом участке.

Выделим в обмотке I элементарную зону в виде силовой трубки (цилиндра) с толщиной стенки dx, на расстоянии х от точки O₁, находящейся на крайней поверхности обмотки I, которая будет являться началом координат.

Магнитный поток этой трубки

dФ_x = B_xdF_x = В_p (х/а₁)π (D₁— a₁ + 2x) dx.

где D₁ — средний диаметр обмотки I, см.

Этот магнитный поток сцеплен с витками ω_x= ω₁(х/а₁) , расположенными на рис. 5.3 влево от зоны dx.

Следовательно, общее потокосцепление на участке a₁



Для удобства интегрирования полученный интеграл разбивается на два интеграла. В первый интеграл из членов, заключенных в скобки, войдут члены D₁—a₁, а во второй — 2х.

После вынесения постоянных величин за знак интеграла получим:

1)

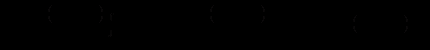
2)

Отсюда потокосцепление на участке а_х будет равно сумме полученных результатов, т. е.



Аналогичным образом определяется общее потокосцепление на участке а2 (приводится без вывода)



где D₂— средний диаметр обмотки II, см.

Число витков ω₂ обмотки II приведено к числу витков да, обмотки I через обычную формулу приведения

ω'₂ = ω₂ E₁/E₂ = ω₁.

Таким образом, общее потокосцепление всей зоны обмоток будет равно сумме потокосцеплений трех участков, т. е.

ωФ_р = (ωФ_р)_а + (ωФ_р)_а1 + (ωФ_р)_а2 = ω₁В_pπ[(D_СРа +(D₁+a₁/2)(a₁/3) +(D₂ - a₂/2)(a₂/3)]

У силовых трансформаторов, класс напряжения которых не превышает 35 кв, радиальные размеры обмоток ВН и НН мало отличаются друг от друга, поэтому с достаточной для практических расчетов точностью можно положить, что a₁≈a₂. Это сильно упростит полученное выражение для потокосцепления.

Раскрыв круглые скобки и заменив D₁ и D₂ соответственно через D_cp—а—а₁ и D_cp+a+a₂, будем иметь:

ωФ_р = ω₁В_pπ[(D_СРа +(D_СР –a - a₁/2)(a₁/3) +(D_СР +a + a₂/2)(a₂/3)]=

ω₁В_pπD_СР [(a+ (a₁+a₂)/3)) + (a/3)(a₂ – a₁)+ (a²₂ - a²₁) /6]

Легко видеть, что при a₁≈a₂, т. е. а₂ - a₁≈0, два последних члена малы, и поэтому ими можно пренебречь. Благодаря этому выражение в квадратных скобках значительно упрощается:

ωФ_р = ω₁В_pπD_СР (a+ (a₁+a₂)/3)= ω₁В_pπD_СРΔ

где Δ= a+ (a₁+a₂)/3 называется приведенным, или редуцированным каналом рассеяния.

В тех же случаях, когда размеры a₁ и a₂значительно отличаются друг от друга, как, например, в высоковольтных трансформаторах, необходимо выражение в квадратных скобках вычислять точно, без указанного упрощения.

Для воздушной (т. е. немагнитной) среды справедлива следующая формула зависимости индукции от намагничивающей силы (ампер-витков) и длины магнитного пути:

В_p=(0,4π√2Iω)/l_P

После подстановки этого выражения формула потокосцепления примет вид

_

ωФ_р =(0,4π²√2I₁ω²₁D_СРΔ)/ l_P

Это выражение следует подставить в формулу напряжения

U_P=4,44fωФ_р10^-4 =(4,44f0,4 π²√2 I₁ω²₁D_СРΔ•10^-4)/ l_P , в

Сделав замену l_p=H₀/K₀ и 4,44 = π²√2 и выразив напряжение

рассеяния в % от номинального напряжения (умножив на 100), получим

U_P=100/U₁= (0,8π³f I₁ω²₁D_СРΔK_p•10^-4)/H₀=(2480f I₁ω²₁D_СРΔK_p•10^-4)/H₀•U₁, %

И, наконец, сделав последнюю подстановку f = 50 гц и U₁/ω₁ =e_ω в/виток, окончательно получим практическую формулу для расчета напряжения рассеяни

U_P= IωD_СРΔK_p/806e_ωH₀, %

При расчете трансформатора обычно бывает необходимо получить заданное значение напряжения рассеяния.

Рассмотрение полученной формулы показывает, что при необходимости изменения расчетного значения U_р наиболее целесообразно в первую очередь изменять размер а — ширину главного канала рассеяния. Если это почему-либо сделать нельзя (например, по изоляционным соображениям или если размер а надо слишком намного увеличивать), то следует либо изменять высоту обмотки Н_о, либо изменять число витков w, хотя это требует уже полного перерасчета трансформатора.

§ 5.6. РАСЧЕТ НАПРЯЖЕНИЯ КОРОТКОГО ЗАМЫКАНИЯ

Напряжение короткого замыкания трансформатора, представляющее полное падение напряжения в нем, измеряется у готового трансформатора при опыте короткого замыкания.

Опыт короткого замыкания заключается в том, что вторичную обмотку (обычно НН) замыкают накоротко, а к первичной обмотке через регулятор напряжения РН подводят напряжение. Схема опыта короткого замыкания изображена на рис. 15.5.

Напряжение поднимают от нуля до тех пор, пока амперметр не покажет номинальное значение тока I₁.Так как вторичная обмотка,ставляет собой замкнутый контур, то в ней также возникнет локальный ток I₂(I₁ω₁= I₂ω₂).

Ввиду отсутствия внешней вторичной цепи мощность, которую по-.ажет ваттметр, называется мощностью, или потерями, короткого замыкания Р_к, которые состоят, как было сказано в § 5.2, из потерь в обмоточных проводах, добавочных потерь и потерь в отводах.



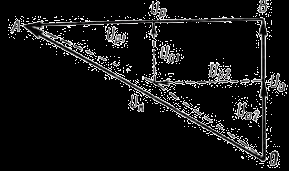
Рис. 5.4. Треугольник короткого замыкания (векторная диаграмма)

Напряжение, которое необходимо подвести к одной из обмоток трансформатора, чтобы в ней установился ток, соответствующий номинальной мощности, при замкнутой накоротко второй обмотке называется напряжением короткого замыкания.
Это напряжение U_K компенсирует активные и реактивные падения напряжения в обеих обмотках, вызванные токами I₁ и I₂, и поэтому является полным падением напряжения в трансформаторе. Напряжение короткого замыкания составляет несколько процентов

от номинального напряжения (от 5,5 до 7,5% для трансформаторов габаритов I—II—III напряжением до 35 кв). Так как насыщение магнито-провода, а следовательно, потери и ток холостого хода будут при этом весьма малы, то последними при расчете U_K можно пренебречь.

Векторная диаграмма короткого замыкания трансформатора может быть получена из упрощенной векторной диаграммы приведенного трансформатора, в которой вектор вторичного напряжения Ич равен нулю. Треугольник ЛВО, построенный на катетах, равных суммам активных и реактивиых падений напряжения обеих обмоток, называется треугольником короткого замыкания (см. рис. 5.4).

Напряжение короткого замыкания U_K, а также и его составляющие U_а и U_p удобнее выражать в % от номинального напряжения. Расчет напряжения рассеяния U_p уже был рассмотрен в § 5.5.

Активная составляющая U_а зависит от величины потерь короткого замыкания и ее формула выводится следующим образом. Для каждой из обмоток на основании закона Ома

U_a1=I₁r₁ и U_a1=I₁r₁,

или, выразив падения напряжения в % от номинального,

u_a1=U_a1/U₁•100= (I₁r₁/U₁)•100= (I²₁r₁/ U₁I²₁)•100=(P_k1/S)•100%;

u_a2=U_a2/U₂•100= (I₂r₂/U₂)•100= (I²₂r₂/ U₂I²₂)•100=(P_k2/S)•100%;

u_a= u_a1+ u_a2= [(P_k1+ P_k2) /S]•100%

Потери Р_к обычно выражаются в вт, а мощность — в ква, поэтому окончательно

u_a= (P_k /1000S)•100=P_k /10S, % (5.9)

Так как в треугольнике короткого замыкания напряжение короткого замыкания Pк является гипотенузой, то через свои составляющие это напряжение, очевидно, будет выражено формулой

U_K=√U²_a+U²_p

Соотношения между Ua и Up различны и зависят от мощности трансформатора. У самых малых трансформаторов (мощностью до 1 ква) реактивная составляющая мала, и напряжение U_K можно считать равным U_a. С ростом мощности значение U_p относительно увеличивается, и у самых крупных трансформаторов, наоборот, напряжение U_K становится уже почти равным реактивной составляющей Up.

Контрольные вопросы

• Что является нагрузкой трансформатора?
  
• Почему при нагрузке вторичной обмотки трансформатора в первичной обмотке также появляется нагрузочный ток?
  
• Почему потери, возникающие при нагрузке трансформатора, называются потерями короткого замыкания?
  
• Где и отчего возникают добавочные потери?
  
• Что такое реактивное падение напряжения и отчего оно возникает?
  
• Что такое приведенный канал рассеяния и коэффициент Роговского?
  

Напишите их формулы.

• Напишите расчетную формулу напряжения рассеяния.
  

Что такое напряжение короткого замыкания?

Что такое треугольник короткого замыкания?