Конкурс «vii всероссийская дистанционная неделя Математики»
| Вид материала | Конкурс |
- Конкурс «vii всероссийская дистанционная неделя Математики», 107.17kb.
- Vii-я Всероссийская дистанционная эвристическая олимпиада по литературе (стихи), 39.73kb.
- Дундукова Татьяна Алексеевна Учитель математики Романчева Ирина Викторовна Учитель, 11.44kb.
- Неделя математики, информатики и физики, 57.9kb.
- Автор: учитель математики Смирнова Неделя математики в школе. Открытие недели, 74.01kb.
- Всероссийская дистанционная викторина "Обитатели морских глубин" (5-9 кл.), 18.46kb.
- 2и 3 ступени обучения, 109.81kb.
- Iii-я Всероссийская дистанционная эвристическая олимпиада по компьютерной грамотности, 31.89kb.
- Предметная неделя по математике: а Понедельник открытие недели математики. Сообщение, 338.26kb.
- Г в Твери прошёл VII международный конкурс, 33.52kb.
Центр «СНЕЙЛ»
Дистанционный конкурс «VII Всероссийская дистанционная неделя Математики»
216, Команда №1 7Акласса , ГБОУ «Средняя общеобразовательная школа №644», г. Санкт-Петербург, 7А класс, e-mail: tp60@mail.ru
Исследовательская работа
Математика и Литература. Три главные точки соприкосновения?!
Команда «Дружбы круг»
Наша эмблема:
Наш девиз:
Чтобы добиться результата
Не стоит быть в углах квадрата.
Протяни же руку, друг!
Создадим мы дружбы круг.
Введение.
Математика и Литература. Казалось бы, что может быть общего между этими разными науками? Наша команда решила доказать, как же близки эти, на первый взгляд, несовместимые предметы.
В первую очередь мы решили провести опрос среди друзей в социальной сети. Фотография ниже доказывает, что опрос был. В него входил только один вопрос: Математика и Литература. Есть ли что-то общее между ними?
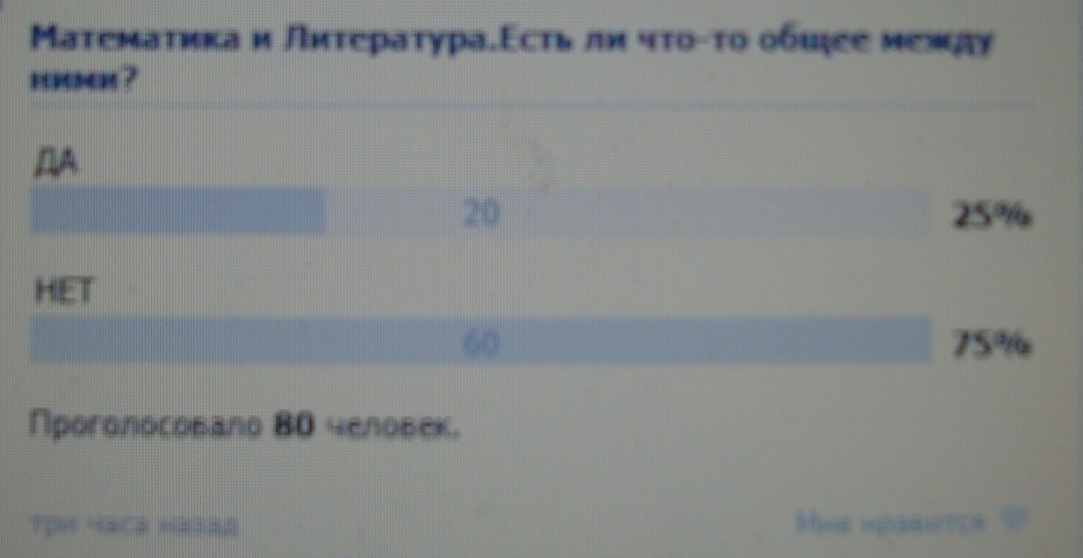ЧИСТО ДЛЯ ОЛИМПИАДЫ)Математика и Литература.Есть ли что-то общее между ними?
ЧИСТО ДЛЯ ОЛИМПИАДЫ)
Математика и Литература.Есть ли что-то общее между ними?
После таких неутешительных выводов мы убедились, что выбранная нами тема необычайно актуальна. В наше время чтению книг, не говоря уже о заинтересованностью математикой, подростки уделяют внимания намного меньше, чем развлечениям. Новое поколение не чувствует красоту, всё необычайное проходит мимо ребят, не оставляя ни единого открытия. Надеемся, что наша исследовательская работа откроет глаза подростков, приоткроет занавес в новый мир. Вступить в него могут только они сами, покоряя новые высоты. Все наши рассуждения, предположения и выводы представлены ниже.
Цель работы:
-рассмотреть актуальность выбранной темы; -доказать, что математика и литература имеют точки соприкосновения; -доказать важность их взаимодействия друг с другом; -показать, насколько интересной может быть математика и литература.
1. Гипотеза первая: математика не менее поэтична и красива, чем литература.
Великий русский поэт и литератор Александр Сергеевич Пушкин считал, что «вдохновение нужно в геометрии не меньше, чем в поэзии». А как же иначе?
Красота точных линий, плавных изгибов и остроты углов сравнимы лишь с нежными переливами стихотворных строк, совершенной чёткостью, размеренностью рифм и живыми, захватывающими книжными сюжетами. Самым ярким доказательством красоты математики и литературы является “золотое сечение”. Это понятие ввел Леонардо да Винчи.
Суть золотой пропорции заключается в следующем: если целое разделить на две части, то отношение большей части к меньшей равно отношению целого к большей части.
Ученые считают автором “золотого деления” Пифагора, другие утверждают, что греческий философ и математик позаимствовал знания у египтян и вавилонян, которые пользовались золотыми пропорциями для создания огромных фигур фараонов и богов. Установленные каноны позволяли по одной части определить целое и размеры других частей.
В фасаде Парфенона присутствуют золотые пропорции. В Помпейском циркуле также заложены пропорции золотого деления.
Платон рассказывал, что Вселенная устроена согласно золотому сечению, Аристотель нашел соответствие золотого сечения этическому закону. После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и другие учёные.
Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей теории исследователь отводил золотому сечению.
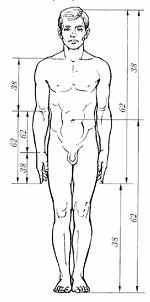
Теория Альбрехта Дюрера.
Так как же связывает «золотое сечение» литературу и математику? Необходимо отметить, что литература - это особый вид искусства, поэтому нельзя подходить к анализу художественных произведений только с точки зрения математических формул, логики. В основе литературного произведения лежат принципы гармонии и красоты, следовательно, и золотая пропорция. Это проявляется в:
- чередовании ударных и безударных слогов (ритм),
- проявлении законов симметрии,
- композиционном построении произведений,
- в эмоциональной насыщенности и т.д.
Андрей Чернов, исследуя памятник древнерусской литературы ХП века “Слово о полку Игореве”, пришел к выводу, что структура произведения подчиняется математическим законам: в основе лежит круговая композиция.Если число стихов во всех трех частях (804) разделить на число стихов в первой и последней части (256), получается 3,14, т.е. число
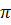.Академик АН СССР Г.В.Церетели, изучая структуру поэмы Шота Руставели “Витязь в тигровой шкуре”, написанную катренами, каждый стих которой состоит из 16 слогов и делится на равные полустишия по 8 слогов с цезурой (слоговой раздел, пауза) между полустишиями, пришел к выводу, что поэма построена по принципу золотого сечения. Проявляется симметрия в строках, построенных по формуле (16=8+8, 8+8) и золотое сечение в ассиметричных строках (16=8+8, 8=5+3=3+5).
На примере «золотого сечения» становится ясно, что математика и литература связанны теснее, чем кажется. Ещё Жуковский говорил: «математике есть своя красота, как в живописи и поэзии».
2. Гипотеза вторая: логическое мышление.
«..человека, умеющего наблюдать и анализировать, обмануть просто невозможно. Его выводы будут безошибочны, как теорема Евклида.»
Артур Конан Дойль
Читая книгу, погружаясь в мир фантазии, казалось бы, очень далёкий от алгебры и геометрии, мы невольно обращаемся к своему личному математическому или логическому опыту, который помогает нам увидеть причинно-следственные связи, на которых основан текст. Чаще всего мы логически рассуждаем именно при чтении детективных романов. Вы подумайте, какая связь между алгеброй и детективами! Читая очередную историю о раскрытии какого-нибудь преступления, непременно пытаешься угадать, кто же все-таки преступник. Если попробовать вместе с писателем распутывать цепочку событий, подмечая малейшие детали, сопоставляя их между собой с помощью построения логических цепочек, то со временем таким образом можно научиться раскрывать преступление самому, раньше сыщиков. В этом деле поможет логическое мышление – способность думать и размышлять. А ведь уравнение - это тот же детективный роман, где требуется обнаружить неизвестное, распутывать цепочку математических событий. Формулы скоро забудутся, но останется способность к логическому мышлению, а это очень важный навык, который пригодится в жизни. Занимательные книги по многим предметам сделают интересными школьные учебники и убедят в том, что учиться весело. Без знаний, которые мы получаем в школе, не может обойтись ни один нормальный человек. Поэтому мы ещё раз советуем всем своим ровесникам: читать и рассуждать как можно больше.
3. Гипотеза третья: поэты вдохновляются математикой.
Начиная с числа Пи и завершая числами Фибоначчи, воображение поэтов всегда одолевала красота чисел – и математики возвращали им должное в виде математических стихов.
Первые продвижения математике в литературу начались именно через поэзию. Первые рывки в поэзию шли рука об руку с первыми проявлениями симпатии к числам. С раннего детства мы учились считать, стараясь срифмовать неизвестные доселе числа. Каждый ребёнок начинает познание мира через образы, привлекая числа, которые находятся в определенной последовательности, соединяя тем самым, слова друг с другом. На примере рассказов об «Алисе» Льюиса Кэрролла, включающих в себя 71-у цифру Пи в каждом двустишье, мы всё больше убеждаемся в связи цифр и рифм. Кажется, что поэзия и математика не могут сочетаться в одном ключе, но это легко опровергнуть. Во все времена было много поэтов, увлекающихся математикой – такие как Льюис Кэрролл или Омар Хайам.
Не менее интересна тема фиб – так называемая поэтическая форма (шесть линий, 20 слогов), придуманная Грегори Пинкусом, которая основана на последовательности Фибоначчи. Таким образом, слоги в каждой линии употребляются как 1, 1, 2, 3, 5, 8. Оригинальный Фиб Пинкуса лишний раз подтверждает пользу и возможность взаимодействия поэзии и математики.
Например, анализ стихотворений А.С. Пушкина с этой точки зрения показал, что поэт явно предпочитает размеры в 5, 8, 13, 21 и 34 строк (числа Фибоначчи).
Числа Фибоначчи в творчестве А.С.Пушкина часто определяют внутреннюю композицию стихотворений. Кульминацией является точка деления произведения по законам золотого сечения. Из 106 произведений в 54 встречается деление, равное числам Фибоначчи: 3, 5, 8, 13, 21, 34, 55.
Н. Васютинский нашел проявление золотой пропорции в произведении «Евгений Онегин». Исследователя заинтересовала 8 глава, которая, по его мнению, является самой яркой в произведении: «Кульминацией главы является объяснение Евгения в любви к Татьяне - строка "Бледнеть и гаснуть ... вот блаженство!". Эта строка делит всю восьмую главу на две части - в первой 477 строк, а во второй - 295 строк. Их отношение равно 1,617! Тончайшее соответствие величине золотой пропорции! Это великое чудо гармонии, совершенное гением Пушкина!»
Арифметическая прогрессия находит практическое применение в искусстве стихосложения. Обратимся к литературе и вспомним два стихотворных размера “ямб” и “хорей”. Ямб – стихотворный метр с ударениями на чётных слогах стиха.
Мой дЯдя сАмых чЕстных прАвил.(А.С.Пушкин). Ударными являются 2-й, 4-й, 6-й, 8-й и так далее слоги.
Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2,4,6,8,…
Двусложный размер – ямб – придает нерифмованным строчкам стихотворения четкость, чеканность. Ломоносов самым подходящим размером считал ЯМБ, полагая, сто стихи, составленные из ямбических стоп “матери благородство, великолепие, высоту умножают”. Известное преувеличение, конечно, в таком утверждении имеется. Однако настойчивая пропаганда Ломоносовым преимущества ямбического стиха пошла на пользу русской поэзии. В ямбической организации она обретала и лёгкость, и “скорость”, и способность передавать достаточно разнообразные состояния. 80% стихов А.С.Пушкина написаны ямбом.
Хорей – стихотворный размер с ударением на нечетных слогах стиха.
Я пропАл , как звЕрь в загОне.(Б.Л.Пастернак)
Номера ударных слогов также образуют арифметическую прогрессию, но ее первый член равен единице, а разность по-прежнему равна двум:
1,3,5,7,…
4.Не менее важные точки соприкосновения.
Наша команда нашла ещё много необычных деталей, связывающих математику и литературу. Наиболее интересные мы выписали в отдельный список:
1. Многие термины встречаются как в математике, так и в литературе: гипербола, парабола, метр, параллелизм.
2. Результат работы писателя и результат умножения - произведение.
3.Математика и литература схожи тем, что требуют творческого подхода к изучению жизни, смелости мысли, безудержной фантазии, тонкого наблюдения, интуиции.
4. К художественному произведению и решению задачи (уравнения и т.п.) предъявляют одинаковые требования - правильность, ясность, точность.
5. Математик А.Маркушевич писал:
«Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели».
Но как заинтересовать ребёнка математикой? Ответ прост: при помощи литературы.
Сказка входит в мир ребёнка с самых ранних лет. Она привлекает волшебством, оптимизмом, чувством справедливости. Благодаря литературе можно развивать в ребёнке математические способности, прививать любовь к этой науке. Вот они, наши первые сказки, в которых математическое начало уже в самом названии: «Волк и семеро козлят», «Три медведя», «Три поросёнка», «Цветик - семицветик» и многие другие.
Таким образом, мы наблюдаем, как литература и математика взявшись за руки, помогают в умственном воспитании и развитии интеллекта детей. 6. Нельзя написать точную, но в то же время стилистически грамотную задачу без доли вдохновения. Литература и тут протягивает руку помощи математике. 7. Мило. Цифровые стихи, обладающие особым обаянием, ритмом и своеобразной энергетикой. 17 30 48 Я к Вам пишу - чего же боле?
140 10 01 Что я могу ещё сказать?
126 138 Теперь, я знаю, в Вашей воле
140 3 501 Меня презреньем наказать.
Вывод
Итог работы:
- доказали актуальность выбранной темы на примере опроса; -привели все три точки соприкосновения математики и литературы; -смогли доказать важность взаимодействия математики и литературы; -провели исследовательскую работу, которая оказалась увлекательной и захватывающей для нас.
ВЫВОД.
МАТЕМАТИКА, ДРУЗЬЯ, В НАШЕМ МИРЕ ТАК ВАЖНА!
ЛИТЕРАТУРА ТОЖЕ!
ИЗ-ЗА ТОГО, МОЛ, ЧТО ГЛАВНЕЙ, ЧТО В НАШЕЙ ЖИЗНИ ВСЁ Ж НУЖНЕЙ?-
ССОРИТЬСЯ НЕГОЖЕ.
КОГДА ВОЗНИК ВОПРОС О ТОМ -
«ИХ ЧТО, СОПРИКАСАЮТ ?!...»,
ПРИШЛИ МЫ К ВЫВОДУ:
ОНИ ДРУГ ДРУГА ДОПОЛНЯЮТ!
Сазыкина Злата.
Ссылки.
ссылка скрыта
ссылка скрыта
ссылка скрыта
ссылка скрыта