Xxxvii всероссийской олимпиады школьников по математике
| Вид материала | Документы |
- Администрация города белгорода управление образования, 818.87kb.
- Протоко л заседания Центрального оргкомитета всероссийской олимпиады школьников, 273.34kb.
- Методические рекомендации по подготовке заданий школьного и муниципального этапов всероссийской, 649.53kb.
- Методические рекомендации по подготовке заданий школьного и муниципального этапов всероссийской, 647.3kb.
- Методика и система оценивания олимпиадных заданий муниципального этапа Всероссийской, 761.17kb.
- Итоговая таблица результатов регионального этапа всероссийской олимпиады школьников, 192.75kb.
- Список участников муниципального этапа всероссийской олимпиады школьников по математике, 133.45kb.
- Список участников муниципального этапа всероссийской олимпиады школьников по математике, 118.47kb.
- Приказ 24 ноября 2010г №627-од Об итогах муниципального этапа всероссийской олимпиады, 557.23kb.
- Положение о школьном, муниципальном, региональном этапах всероссийской олимпиады школьников, 117.5kb.
III. Результаты выполнения заданий на краевом этапе
XXXVII Всероссийской олимпиады школьников по математике
Задания и рекомендации для проведения краевого этапа олимпиады по математике, а также критерии оценивания работ были подготовлены Центральной методической комиссией по математике Всероссийской олимпиады школьников.
Каждому из участников олимпиады предстояло за два дня решить по 8 заданий.
Анализ решаемости задач краевого этапа
52 Всероссийской олимпиады школьников по математике
(январь 2011 г.)
9 класс
1. Количественные показатели
| 9 класс- 11 чел | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 |
| Выполнили | 0 – 0% | 4 – 36% | 2 – 18% | 1 – 9% | 2 – 18% | 1 – 9% | 1 – 9% | 0 – 0% |
| Приступили | 11 – 100 % | 5 – 45% | 7 – 64% | 5 – 45% | 6 – 55% | 3 – 27% | 6 – 55% | 7 – 64% |
| Не выполняли | 0 – 0% | 3 – 27% | 3 –- 27% | 6 – 55% | 4– 36% | 8 – 73% | 5 – 45% | 4 – 36% |
Диаграмма 1
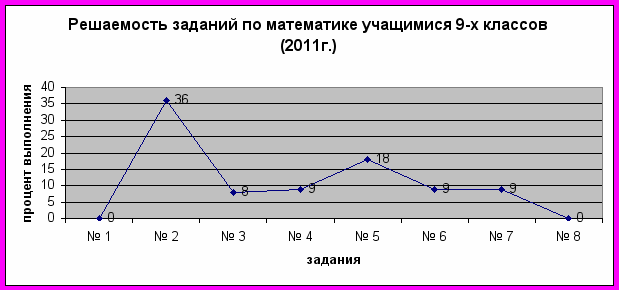
2. Анализ решений и допущенных ошибок
Задача 9.1. Задание на исследование решений алгебраической системы уравнений. Приступили к решению все участники, но никто не сумел получить верный ответ, хотя все смогли выполнить необходимую формализацию и основные преобразования. Основная причина – отсутствие опыта в решении подобных задач.
Задача 9.2. Геометрическая задача на доказательство параллельности. Решение основано на признаке параллельности и свойствах вписанных углов. Справились 36%, 45% приступали к решению.
Задача 9.3. Логическая задача на геометрическом материале. Участники предлагали различные варианты решения, как правило, основанные на рассмотрении различных частных случаев. Главная трудность – перейти от частных примеров к общему методу доказательства. С ней справились два человека из 11. Основная причина невысокой решаемости – отсутствие опыта в решении подобных задач.
Задача 9.4. Задание на доказательство неравенства, содержащего три числа. Приступила к решению половина участников. Основной момент в полном решении – рассмотреть два способа упорядочения трех чисел. Это сделал только один участник. Остальные не обратили внимания на такой нюанс.
Задача 9.5. Классическое задание на признак делимости. К сожалению, большинство участников олимпиады были сбиты с толку и пытались представить ответ в виде некоторой сложной формулы. Правильно решили задачу только два участника.
Задача 9.6. Геометрическая задача, основанная на симметрии. В решении использовано свойство диаметра окружности. Догадался применить это свойство только один участник. Основная трудность связана с тем, что девятиклассники не умеют применять знания из геометрии для доказательства (в основном решаются вычислительные задачи).
Задача 9.7. «Классическая» задача на делимость. Главный момент в решении – доказать, что наименьшее из чисел в условиях задачи – четное простое (то есть 2). Полностью доказательство сумел привести только один участник. Половина участников сумели формализовать задачу, но не довели решение до конца.
Задача 9.8. Задание предполагает получение оценки и доказательство существования решения для этой оценки. Треть участников не сумели понять условия задачи (вместо случая «в худшем» рассмотрели случай «в лучшем»). Остальные получили оценку (102 части), но не смоги доказать возможность построить прямоугольник при любом разбиении.
10 класс
1. Количественные показатели
| 10 класс- 20 чел | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 |
| Выполнили | 5 – 25% | 3 – 15% | 2 – 10% | 0 – 0% | 4– 20% | 3– 15% | 3 – 15% | 1 – 5% |
| Приступили | 13 – 65% | 12 – 60% | 3 – 15% | 7 – 35% | 11 – 55% | 8 – 40% | 8 – 40% | 10 – 50 % |
| Не выполняли | 2 – 10% | 5 – 25% | 15 – 75% | 13 – 65% | 5 – 20% | 9 – 45% | 9 – 45% | 9 – 45% |
Диаграмма 2
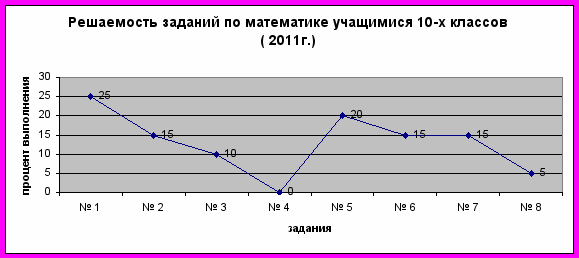
2. Анализ решений и ошибок
Задача 10.1. Логическая задача на оценку скорости движения. Основная сложность – дать обоснование в общем случае. К сожалению, 65% участников не смогли оторвать свои обоснования от конкретных примеров. Некоторые вместо прямого утверждения доказывали обратное, что гораздо проще.
Задача 10.2. Геометрическая задача на признак вписанного четырехугольника. В решении используются свойства вписанных углов. Полностью справились трое (15%) участников.
Задача 10.3. Задача на доказательство, в решении которой используется четность и принцип Дирихле. Правильно решили двое (10%). Остальные не смогли получить точные оценки.
Задача 10.4. Задание на многочлены. Используя условия задачи требуется доказать совпадение корней трех уравнений. Для этого требуется провести специальные преобразования, группировки и проанализировать два случая. К сожалению, никто не решил задачу.
Задача 10.5. Классическое задание на признак делимости. К сожалению, большинство участников олимпиады были сбиты с толку и пытались представить ответ в виде некоторой сложной формулы. Правильно решили задачу четыре участника.
Задача 10.6. Логическая задача на оценку. Решение основано на упорядочении чисел и исследовании нескольких ключевых равенств. Полностью справились трое (15%), остальные продвинулись в той или иной мере, но не смогли точно закончить решение.
Задача 10.7. Геометрическая задача на доказательство коллинеарности трех точек. При решении существенно используется тот факт, что некоторая вспомогательная фигура по условию является ромбом. Используя этот факт трое участников (15%) получили полное решение. Остальные не пытались учитывать данное свойство. Важное значении в решении этой задачи имел аккуратно выполненный чертеж.
Задача 10.8. Задание предполагает получение оценки и доказательство существования решения для этой оценки. Треть участников не сумели понять условия задачи (вместо случая «в худшем» рассмотрели случай «в лучшем»). Половина участников получили оценку (102 части) но не смоги доказать возможность построить прямоугольник при любом разбиении. Полностью решил задачу только один участник.
11 класс
1. Количественные показатели
| 11 класс – 18 чел | №1 | №2 | №3 | №4 | №5 | №6 | №7 | №8 |
| Выполнили | 6 – 33% | 5 – 28% | 2 – 18% | 0 – 0% | 1 – 6% | 1 – 6% | 0 – 0% | 0 – 0% |
| Приступили | 10 – 56% | 11 – 61% | 12 – 67% | 11 – 61% | 15 – 83% | 10 – 56% | 14 – 78% | 11 – 61% |
| Не выполняли | 3 – 17% | 3 – 17% | 3 – 17% | 8 – 44% | 3 – 17% | 7 – 39% | 4 – 22% | 7 – 39% |
Диаграмма 3
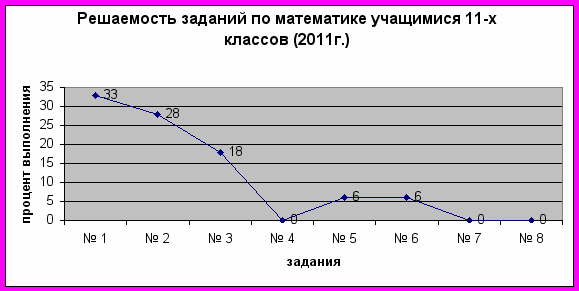
2. Анализ решений и допущенных ошибок
Задача 11.1. Комбинированная задача на тригонометрические тождества и свойства рациональных чисел. В решении используется формула, преобразования суммы косинусов в произведение. Этой формулой воспользовалась треть участников и получила правильное решение.
Задача 11.2. Задача на ненулевые целые числа. Для решения нужно определиться с количеством возможных отрицательных чисел, доказать, что оно одно и большое по модулю. Из этого легко доказывается основное утверждение. С задачей справилось около трети (28%) участников. Остальные либо не смогли обосновать, что отрицательное число единственное, либо не поняли, что модуль этого числа больше произведения модулей остальных чисел.
Задача 11.3. Геометрическая задача на доказательство. В решении используется свойство точки пересечения медиан и свойство вписанного и центрального углов. С решением справилось только два участника.
Задача 11.4. Логическая задача с элементами графов. Решение основано на методе математической индукции. Основная трудность в решении – выполнение индуктивного перехода. Никто из участников не справился с полным решением. Но больше половины участников сумели получить оценку количества рейсов.
Задача 11.5. Классическое задание на признак делимости. К сожалению, большинство участников олимпиады были сбиты с толку и пытались представить ответ в виде некоторой сложной формулы. Правильно решил задачу один участник.
Задача 11.6. Геометрическая задача на доказательство. Решение может быть основано либо на свойстве биссектрис, либо на свойстве серединных перпендикуляров. Задачу решил один человек. Остальные не смогли использовать все пункты условия.
Задача 11.7. Комбинаторно-геометрическая задача. Решение основано на свойстве вписанной окружности правильного многоугольника. Два этапа: получить точную оценку на количество окружностей и привести пример, удовлетворяющий условиям.
Задача 11.8. Задача на доказательство алгебраического неравенства. Решение основано на применении бинома Ньютона после выполнения некоторых манипуляций. Были попытки применить эту формулу, но без предварительных преобразований они оказались безрезультатными.
Диаграмма 4
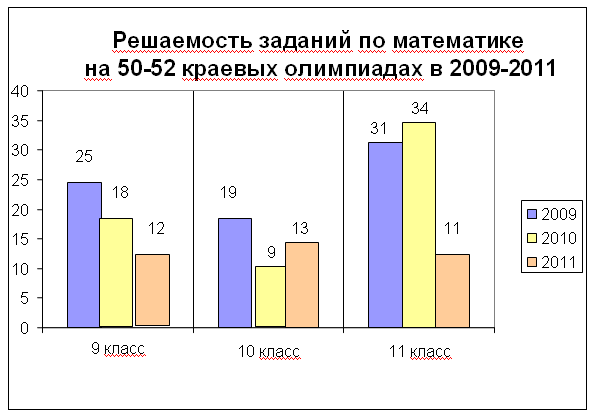
На диаграмме 4 в сравнении приведена решаемость задач на олимпиадах в 2009-2011 годах. Из этой диаграммы видно, что положительная динамика наблюдается только в 10-х классах по сравнению с прошлым годом. Следует отметить, что нынешние 9-ти и 11-ти классники в этом году показали более низкие результаты, чем в прошлом. В 9-х классах решаемость задач оказалась ниже на 6%, а в 11-х – на 23%. Если сравнить результаты нынешних 11-ти классников с соответствующими результатами двух прошлых лет, то в 2010г. решаемость задач была ниже на 16%, а в 2011 году результат стал выше на 2% по сравнению с прошлым годом. Причиной снижения решаемости задач в 2011году учащимися 9-х и 10-х классов можно объяснить несколькими причинами.
- Учащиеся 9 классов плохо подготовлены к решению задач на доказательство. Необходимо разбирать большое количество примеров и обязательно письменно оформлять решение.
- Олимпиадные задачи для десятиклассников в значительной мере опираются на специфические знания из математики, частично уходящие за пределы стандартной программы. Поэтому десятиклассники должны больше внимания уделять комбинаторике, графам, неравенствам и другим темам.
- Учащиеся одиннадцатого класса испытывают большие трудности при решении геометрических задач (планиметрии). Им необходимо повторять геометрию, уделяя особое внимание задачам на доказательство.
- В целом следует обратить внимание на методы формализации условий и на работу с условиями в целом. Часто участники олимпиады пытаются решать задачу, не используя всех данных в ней условий.
Таблица 8
| № п/п | Ф.И.О. | Кол-во час в матем. в нед. | Авторы учебников математики | Специальная подготовка к олимпиаде | Систематичность подготовки | Место на муниц. олимпиаде | Место на кр. олимпиаде |
| 9 класс | |||||||
| 1 | Бондаренко Григорий | 5 | Никольский Атанасян | сам-но по допол. литер., консультации учителя, заочная ФМШ при МГУ | постоянно | победи тель | |
| 2 | Жагалкович Полина | 8 | Виленкин Атанасян | сам-но по допол. литер., консультации учителя | постоянно | призер | |
| 3 | Евгеньев Александр | 8 | Никольский Атанасян | сам-но по дополнит.литер., систематич. подготовка в школе 2ч, ФМШ | постоянно. | призер | |
| 4 | Кочкарь Роман | 8 | Виленкин Атанасян | систематич. подготовка в школе 2ч, курсы при вузе | постоянно | победи тель | призер |
| 5 | Костриков Вячеслав | 8 | Виленкин Шарыгин | систематич. подготовка в школе 2ч, ФМШ курсы при вузе | постоянно | призер | призер |
| 6 | Лосев Иван | 8 | Виленкин Шарыгин | систематич. подготовка в школе 2ч, курсы при вузе, ФМШ | постоянно | призер | |
| 7 | Молчанова Анна | 5 | Макарычев Атанасян | сам-но по допол. литер., Интернет | постоянно | победи тель | |
| 8 | Саргина Анна | 7 | Макарычев Атанасян | сам-но по допол. литер., консультации учителя, ФМШ | постоянно | победи тель | |
| 9 | Тимошко Андрей | 6 | Макарычев Атанасян | систематич шк. ф-в 1,5ч сам-но по допол. литер., Интернет | постоянно. | победи тель | |
| 10 | Туров Евгений | 8 | Виленкин Атанасян | сам-но по допол. литер., консультации учителя, ФМШ | постоянно. | победитель | победитель |
| 11 | Шолохов Алексей | 8 | Виленкин Атанасян | сам-но по допол. литер., систематич. подготовка в школе 2ч | постоянно | призер | |
| 10 класс | |||||||
| 1 | Анисимов Александр | 9 | Никольский Атанасян | систематич шк. ф-в 2ч, сам-но по дополнит.литер, курсы при вузе | постоянно | призер | |
| 2 | Благодатских Александр | 6 | Атанасян Атанасян | сам-но по дополнит.литер., консультации учителя | постоянно | участник | |
| 3 | Блажнов Алексей | 9 | Виленкин Атанасян | сам-но по дополнит.литер, совместно с учителем, ФМШ, Интернет | постоянно | победи тель | призер |
| 4 | Диодорова Владислава | 9 | Колягин Атанасян | сам-но по дополнит.литер, совместно с учителем, Интернет | постоянно | призер | |
| 5 | Зернова Наталья | 6 | Никольский Атанасян | сам-но по дополнит.литер, консультации учителя | постоянно | победи тель | |
| 6 | Ершов Вячеслав | 9 | Никольский Атанасян | сам-но по дополнит.литер., Интернет | постоянно. | победи тель | |
| 7 | Егоров Александр | 6 | Виленкин Атанасян | сам-но по дополнит.литер, консультации учителя | постоянно. | участник | |
| 8 | Ким Александр | 6 | Колягин Атанасян | сам-но по дополнит.литер., консультации учителя, Интернет | постоянно. | призер | |
| 9 | Левашов Никита | 5 | Виленкин Атанасян | сам-но по дополнит.литер., ФМШ | постоянно. | участник | |
| 10 | Мачкарина Полина | 6 | Никольский Атанасян | консультации учителя, сам-но по дополнит.литер., ФМШ | постоянно | призер | |
| 11 | Миргородский Юрий | 9 | Никольский Атанасян | сам-но по дополнит.литер, ФМШ | постоянно | призер | |
| 12 | Некрасов Илья | 9 | Виленкин Атанасян | систематич шк. ф-в, сам-но по дополнит.литер., Интернет, ФМШ | постоянно | победи тель | победи тель |
| 13 | Петренко Ксения | 6 | Никольский Атанасян | систематич шк. ф-в 2 ч сам-но по дополнит.литер. | постоянно | победи тель | |
| 14 | Подледнева Маргарита | 6 | Колягин Атанасян | сам-но по дополнит.литер., курсы при вузе | постоянно | участник | |
| 15 | Сухарь Ксения | 6 | Колягин Атанасян | сам-но по дополнит.литер, курсы при вузе, ФМШ | постоянно | участник | |
| 16 | Соловьев Александр | 9 | Виленкин Атанасян | систематич шк. ф-в, сам-но по дополнит.литер., Интернет, ФМШ | постоянно | призер | призер |
| 17 | Тур Дмитрий | 9 | Никольский Атанасян | сам-но по дополнит.литер, курсы при вузе, ФМШ | постоянно | призер | призер |
| 18 | Ткаченко Роман | 9 | Виленкин Атанасян | систематич шк. ф-в, сам-но по дополнит.литер., Интернет, ФМШ | постоянно | призер | |
| 19 | Хороших Мария | 8 | Виленкин Атанасян | сам-но по дополнит.литер, курсы при вузе, консультации учителя | постоянно | призер | |
| 20 | Ященко Юрий | 9 | Виленкин Атанасян | систематич шк. ф-в, сам-но по дополнит.литер., Интернет, ФМШ | постоянно | победи тель | призер |
| 11 класс | |||||||
| 1 | Брюханов Александр | 9 | Виленкин Атанасян | систематич шк. ф-в, сам-но по дополнит.литер., Интернет, ФМШ | постоянно | призер | призер |
| 2 | Гавриков Александр | 9 | Никольский Атанасян | систематич шк. ф-в, сам-но по дополнит.литер., Интернет, ФМШ | постоянно | победи тель | призер |
| 3 | Гайдар Владимир | 5 | Колягин Атанасян | сам-но по дополнит.литер. | перед олимпиадой (за 3мес) | победи тель | |
| 4 | Грифлюк Полина | 5 | Колягин Атанасян | совместно с учителем | постоянно | участник | |
| 5 | Дьякова Анастасия | 6 | Никольский Атанасян | сам-но по дополнит.литер, занятия с учителем, Интернет | постоянно | победи тель | |
| 6 | Другова Кристина | 9 | Виленкин Атанасян | сам-но по дополнит.литер., консультации учителя, ФМШ. Интернет | постоянно | участник | |
| 7 | Карпов Иван | 9 | Виленкин Атанасян | сам-но по дополнит.литер., ф-в., ФМШ, | постоянно | участник | |
| 8 | Литвинов Владимир | 9 | Виленкин Атанасян | сам-но по дополнит.литер. | постоянно | победи тель | победи тель |
| 9 | Моисеенко Анастасия | 9 | Виленкин Атанасян | сам-но по дополнит.литер, занятия с учителем, ФМШ, Интернет | постоянно | призер | призер |
| 10 | Первых Александр | 6 | Никольский Атанасян | сам-но по дополнит.литер, ФМШ | постоянно | участник | |
| 11 | Сущинская Светлана | 8 | Никольский Атанасян | сам-но по дополнит.литер, занятия с учителем при вузе, ФМШ | постоянно | призер | призер |
| 12 | Сырова Екатерина | 5 | Колягин Атанасян | занятия с учителем | постоянно | участник | |
| 13 | Сажнев Егор | 6 | Колягин Атанасян | сам-но по дополнит.литер, Интернет | постоянно | призер | |
| 14 | Трач Ростислав | 6 | Колягин Атанасян | сам-но по дополнит.литер, Интернет | постоянно | участник | |
| 15 | Феофанов Михаил | 6 | Никольский Атанасян | сам-но по дополнит.литер, занятия с учителем, ФМШ | постоянно | призер | |
| 16 | Чернова Елена | 9 | Виленкин Атанасян | сам-но по дополнит.литер, занятия с учителем, ФМШ | постоянно | призер | |
| 17 | Чуднова Елена | 6 | Колягин Атанасян | сам-но по дополнит.литер. | постоянно | участник | |
| 18 | Чжен Евгений | 9 | Никольский Смирнов | сам-но по дополнит.литер, ФМШ | постоянно | участник | |
В таблице №8 приведены сведения о количестве часов математики в неделю и учебниках, по которым занимаются учащиеся в школе. Из этих данных следует, что 25 из 49 участников обучаются по учебникам, специально предназначенным для классов с углубленной подготовкой по математике.
Также обращает на себя внимание тот факт, что наиболее высоких результатов достигли те участники, у которых недельная нагрузка по математике составляет 6-9 часов.
