Деление многочленов. Алгоритм евклида деление многочленов
| Вид материала | Документы |
- Элективный курс «Отработка основных методов и приёмов решения уравнений» 10класс. 2010/2011, 51.02kb.
- Программа Учебный курс предпрофильной подготовки «Деление многочленов. Теорема Безу»., 55.16kb.
- Разложение многочленов на множители” (7 класс), 38kb.
- План-конспект открытого урока по теме: «Разложение многочленов на множители», 74.23kb.
- Деление клетки Размножение. Размножение клеток, 116.15kb.
- Опрацювати тему «Подовження м’яких приголосних звуків І позначення їх на письмі» (стор., 39.49kb.
- Тема : Деление клетки основа размножения, роста и развития организмов, 105.53kb.
- Расширенный алгоритм Евклида, 78.19kb.
- 1. Римский гражданский процесс: понятие, формы, основные черты. Деление гражданского, 313.96kb.
- Тема №1 ономастика в цикле языковедческих дисциплин вопросы, 518.88kb.
ДЕЛЕНИЕ МНОГОЧЛЕНОВ. АЛГОРИТМ ЕВКЛИДА
§1. Деление многочленов
При делении многочлены представляются в канонической форме и располагаются по убывающим степеням какой-либо буквы, относительно которой определяется степень делимого и делителя. Степень делимого должна быть больше или равна степени делителя.
Результатом деления является единственная пара многочленов – частное и остаток, которые должны удовлетворять равенству:
< делимое > = < делитель > < частное > + < остаток >.
Если многочлен степени n Pn(x) является делимым,
многочлен степени m Rk(x)является делителем (n m),
многочлен Qn – m(x) – частное. Степень этого многочлена равна раз-ности степеней делимого и делителя,
а многочлен степени k Rk(x) является остатком (k < m).
То равенство
Pn(x) = Fm(x) Qn – m(x) + Rk(x) (1.1)
должно выполняться тождественно, то есть, оставаться справедливым при любых действительных значениях х.
Ещё раз отметим, что степень остатка k должна быть меньше степени делителя m. Назначение остатка – дополнить произведение многочленов Fm(x) и Qn – m(x) до многочлена, равного делимому.
Если произведение многочленов Fm(x) Qn – m(x) дает многочлен, равный делимому, то остаток R = 0. В этом случае говорят, что деление производится без остатка.
Алгоритм деления многочленов рассмотрим на конкретном примере.
Пусть требуется разделить многочлен (5х5 + х3 + 1) на многочлен (х3 + 2).
1. Разделим старший член делимого 5х5 на старший член делителя х3:
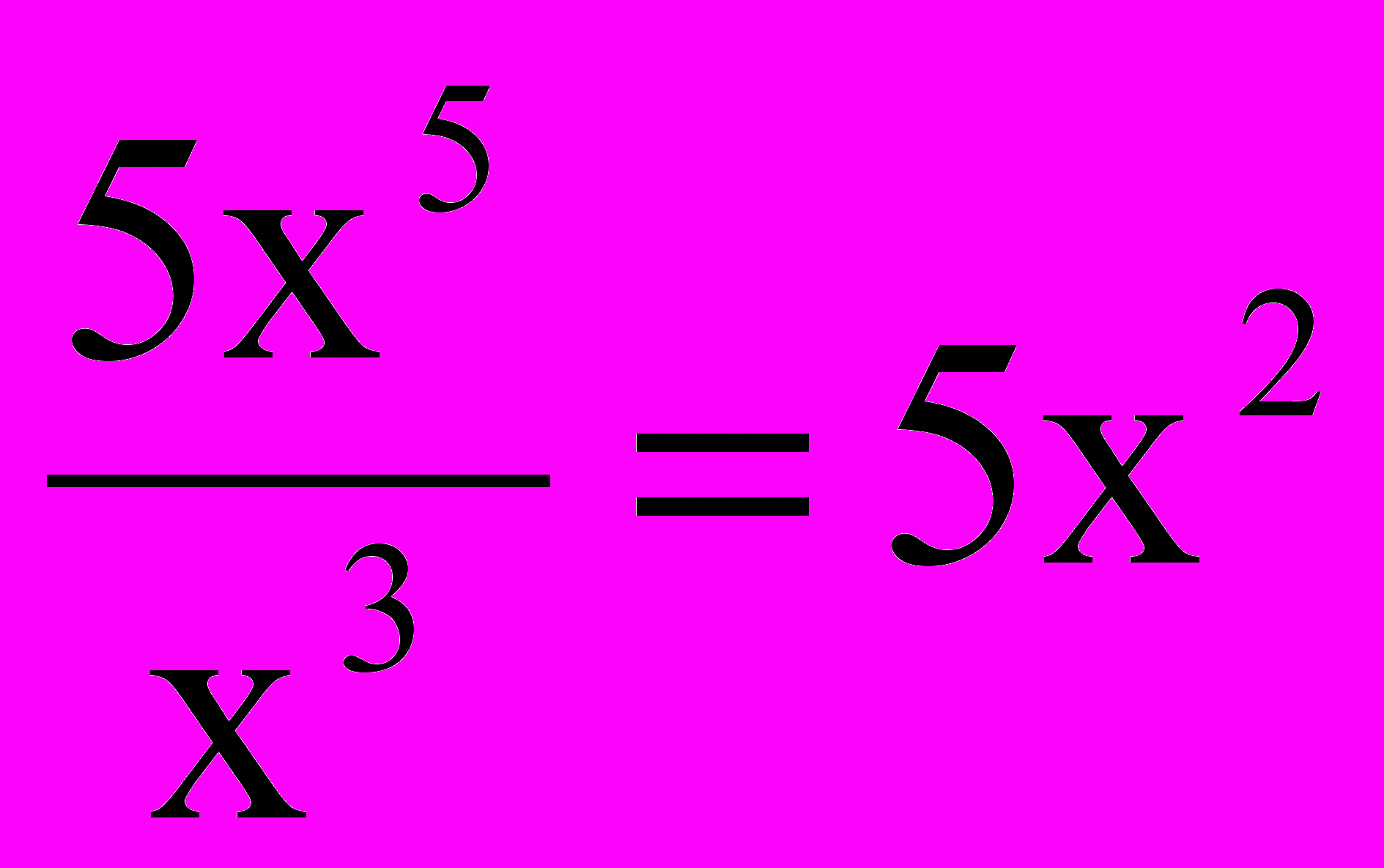 .
.Ниже будет показано, что так находится первый член частного.
2. На очередное (поначалу первое) слагаемое частного умножается делитель и это произведение вычитается из делимого:
5х5 + х3 + 1 – 5х2(х3 + 2) = х3 – 10х2 + 1.
3. Делимое можно представить в виде
5х5 + х3 + 1 = 5х2(х3 + 2) + (х3 – 10х2 + 1). (1.2)
Если в действии (2) степень разности окажется больше или равна степени делителя (как в рассматриваемом примере), то с этой разностью действия, указанные выше, повторяются. При этом
- Старший член разности х3 делится на старший член делителя х3:
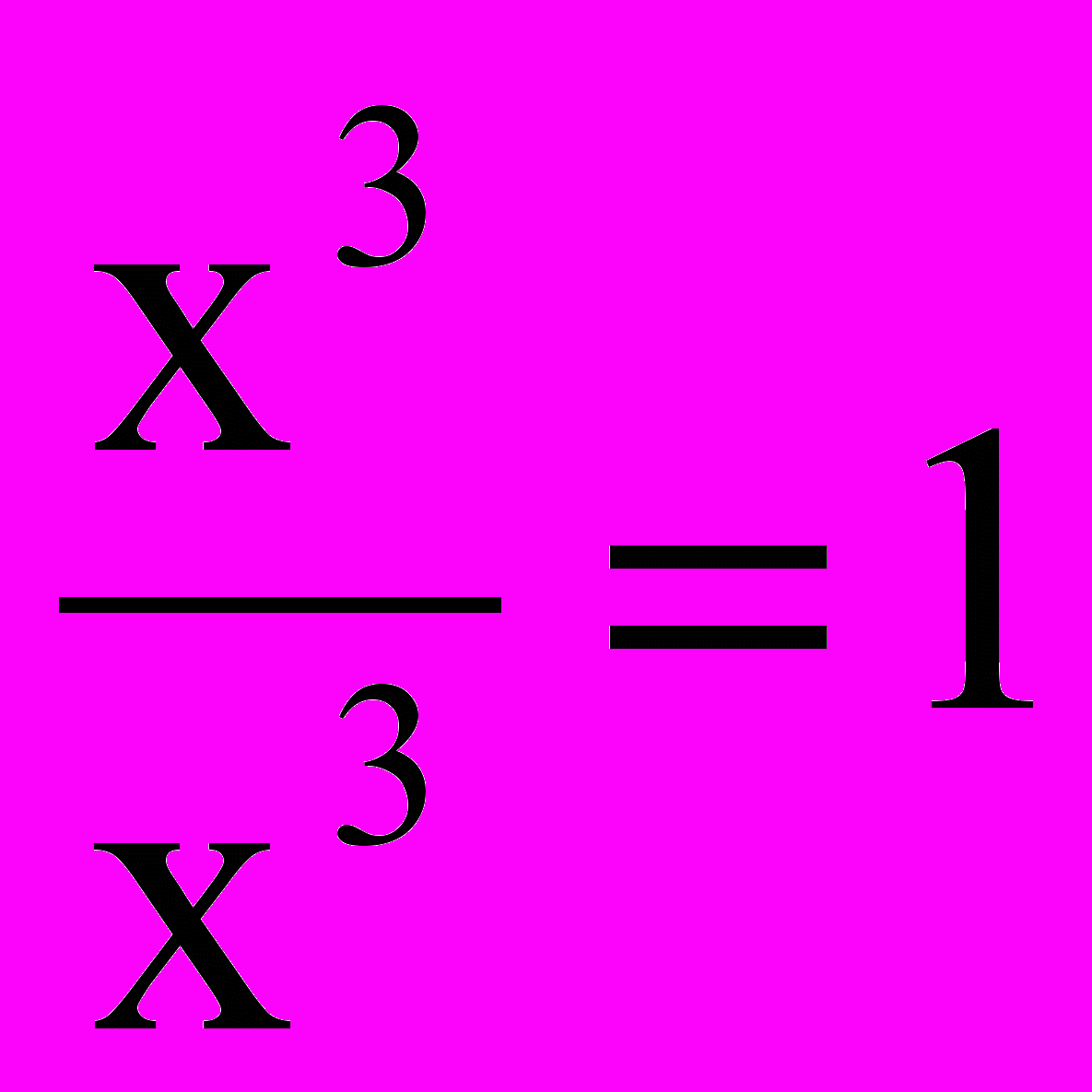 .
.Ниже будет показано, что таким образом находится второе слагаемое в частном.
2. На очередное (теперь уже, второе) слагаемое частного умножается делитель и это произведение вычитается из последней разности
х3 – 10х2 + 1 – 1(х3 + 2) = – 10х2 – 1.
3. Тогда, последнюю разность можно представить в виде
х3 – 10х2 + 1 = 1(х3 + 2) + (–10х2 + 1). (1.3)
Если степень очередной разности окажется меньше степени делителя (как при повторе в действии (2)), то деление завершено с остатком, равным последней разности.
Для подтверждения того, что частное является суммой (5х2 + 1), подставим в равенство (1.2) результат преобразования многочлена х3 – 10х2 + 1 (см.(1.3)): 5х5 + х3 + 1 = 5х2(х3 + 2) + 1(х3 + 2) + (– 10х2 – 1). Тогда, после вынесения общего множителя (х3 + 2) за скобки, получим окончательно
5х5 + х3 + 1 = (х3 + 2)(5х2 + 1) + (– 10х2 – 1).
Что, в соответствии с равенством (1.1), следует рассматривать как результат деления многочлена (5х5 + х3 + 1) на многочлен (х3 + 2) с частным (5х2 + 1) и остатком (– 10х2 – 1).
Указанные действия принято оформлять в виде схемы, которая называется «деление уголком». При этом, в записи делимого и последующих разностей желательно производить члены суммы по всем убывающим степеням аргумента без пропуска.

– –
5х5 + 0х4 + х3 + 0х2 + 0х + 1 х3 + 2
5х5 +10х2 5х2 + 1
– –
х3 –10х2 + 0х + 1
 х3 + 2
х3 + 2–10х2 + 0х – 1

 Мы видим, что деление многочленов сводится к последовательному повторению действий:
Мы видим, что деление многочленов сводится к последовательному повторению действий:- в начале алгоритма старший член делимого, в последующем, старший член очередной разности делится на старший член делителя;
- результат деления дает очередное слагаемое в частном, на которое умножается делитель. Полученное произведение записывается под делимым или очередной разностью;
- из верхнего многочлена вычитается нижний многочлен и, если степень полученной разности больше или равна степени делителя, то с нею повторяются действия 1, 2, 3.
Если же степень полученной разности меньше степени делителя, то деление завершено. При этом последняя разность является остатком.
Пример №1
6
–

 х3 + х2 – 3х – 2 2х2 – х – 1
х3 + х2 – 3х – 2 2х2 – х – 1 6х3 3х2 3х 3х + 2
–
4х2 + 0х – 2
 4х2 2х 2
4х2 2х 22х
Таким образом, 6х3 + х2 – 3х – 2 = (2х2 – х – 1)( 3х + 2) + 2х.
Пример №2


–
a5 + b5 a + b
 a5
a5  a4b a4 –a3b + a2b2 – ab3 + b4
a4b a4 –a3b + a2b2 – ab3 + b4– a4b + b5
 a4b a3b2
a4b a3b2–
a3b2 + b5
 a3b2
a3b2  a2b3
a2b3– a2b3 + b5
 a2b3 ab4
a2b3 ab4+ ab4 + b5
 – ab4
– ab4 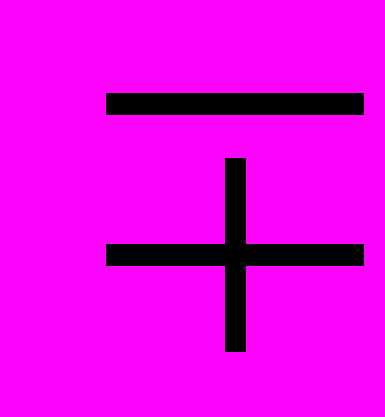 b5
b50
Таким образом, a5 + b5 = (a + b)(a4 –a3b + a2b2 – ab3 + b4).
Пример №3


–
х5 – у5 х – у
 х5
х5 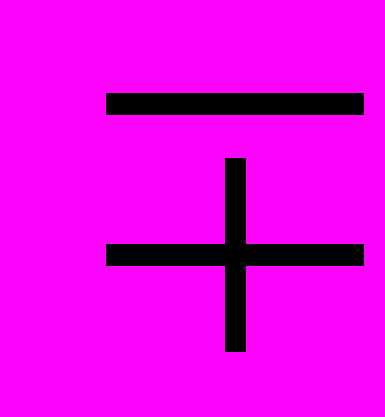 х4у х4 + х3у + х2у2 + ху3 + у4
х4у х4 + х3у + х2у2 + ху3 + у4–
х4у – у5
 х4у х3у2
х4у х3у2–
х3у2 – у5
 х3у2 х2у3
х3у2 х2у3–
х2у3 – у5
 х2у3 ху4
х2у3 ху4–
ху4 – у5
 ху4 – у5
ху4 – у50
Таким образом, х5 – у5 = (х – у)( х4 + х3у + х2у2 + ху3 + у4).
Обобщением результатов, полученных в примерах 2 и 3, являются две формулы сокращенного умножения:
(х + а)(х2n – х2n–1a + х2n–2a2 – … + a2n) = х2n+1 + a2n + 1;
(х – a)(х2n + х2n–1a + х2n–2a2 + … + a2n) = х2n+1 – a2n + 1, где nN.
Упражнения
Выполнить действия
1. (– 2х5 + х4 + 2х3 – 4х2 + 2х + 4) : (х3 + 2).
Ответ: – 2х2 + х +2 – частное, 0 – остаток.
2. (х4 – 3х2 + 3х + 2) : (х – 1).
Ответ: х3 + х2 – 2х + 1– частное, 3 – остаток.
3. (х2 + х5 + х3 + 1) : (1 + х + х2).
Ответ: х3 – х2 + х + 1– частное, 2х – остаток.
4. (х4 + х2у2 + у4) : (х2 + ху + у2).
Ответ: х2 – ху + у2– частное, 0 – остаток.
5. (a3 + b3 + c3 – 3abc) : (a + b + c).
Ответ: a2 – (b + c)a + (b2 – bc + c2) – частное, 0 – остаток.
§2. Нахождение наибольшего общего делителя двух многочленов
1. Алгоритм Евклида
Если каждый из двух многочленов делится без остатка на третий, то этот третий многочлен называется общим делителем первых двух.
Наибольшим общим делителем (НОД) двух многочленов называется их общий делитель наибольшей степени.
Заметим, что любое число неравное нулю является общим делителем двух любых многочленов. Поэтому, всякое неравное нулю число называется тривиальным общим делителем данных многочленов.
Алгоритм Евклида предлагает последовательность действий, которая или приводит к нахождению НОД двух данных многочленов, или показывает, что такой делитель в виде многочлена первой или большей степени не существует.
Алгоритм Евклида реализуется в виде последовательности делений. В первом делении многочлен большей степени рассматривается как делимое, а меньшей – как делитель. Если многочлены, для которых находится НОД, имеют одинаковые степени, то делимое и делитель выбираются произвольно.
Если при очередном делении многочлен в остатке имеет степень больше или равную 1, то делитель становится делимым, а остаток – делителем.
Если при очередном делении многочленов получен остаток, равный нулю, то НОД данных многочленов найден. Им является делитель при последнем делении.
Если же при очередном делении многочленов остаток оказывается числом неравным нулю, то для данных многочленов не существует НОД помимо тривиальных.
Пример №1
Сократить дробь
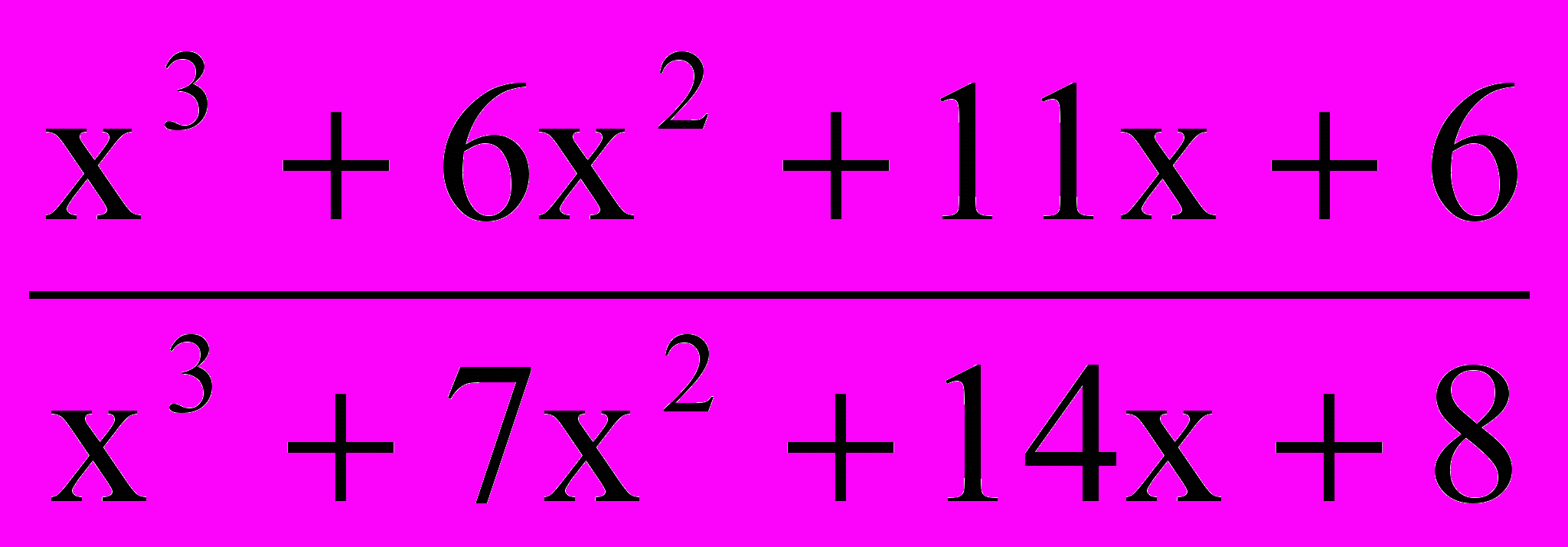 .
.Решение
Найдем НОД данных многочленов, применяя алгоритм Евклида
1
– – – –

 ) х3 + 6х2 + 11х + 6 х3 + 7х2 + 14х + 8
) х3 + 6х2 + 11х + 6 х3 + 7х2 + 14х + 8  х3 + 7х2 + 14х + 8 1
х3 + 7х2 + 14х + 8 1– х2 – 3х – 2
2


– – –
) х3 + 7х2 + 14х + 8 – х2 – 3х – 2
 х3 + 3х2 + 2х – х – 4
х3 + 3х2 + 2х – х – 4– – –
4х2 + 12х + 8
 4х2 + 12х + 8
4х2 + 12х + 80
Следовательно, многочлен (– х2 – 3х – 2) является НОД числителя и знамена-теля данной дроби. Результат деления знаменателя на этот многочлен известен. Найдем результат деления числителя.

 х3 + 6х2 + 11х + 6 – х2 – 3х – 2
х3 + 6х2 + 11х + 6 – х2 – 3х – 2 х3 + 3х2 + 2х – х – 3
х3 + 3х2 + 2х – х – 3– – –
3х2 + 9х + 6
 3х2 + 9х + 6
3х2 + 9х + 60
Т
– – –
аким образом,
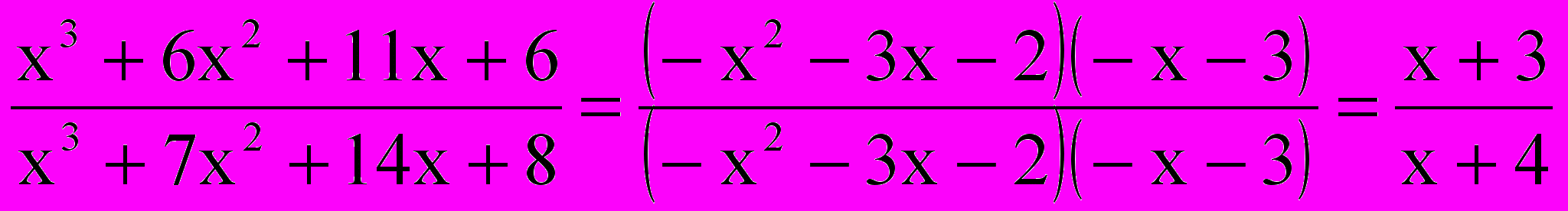
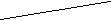
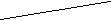 .
.Ответ:
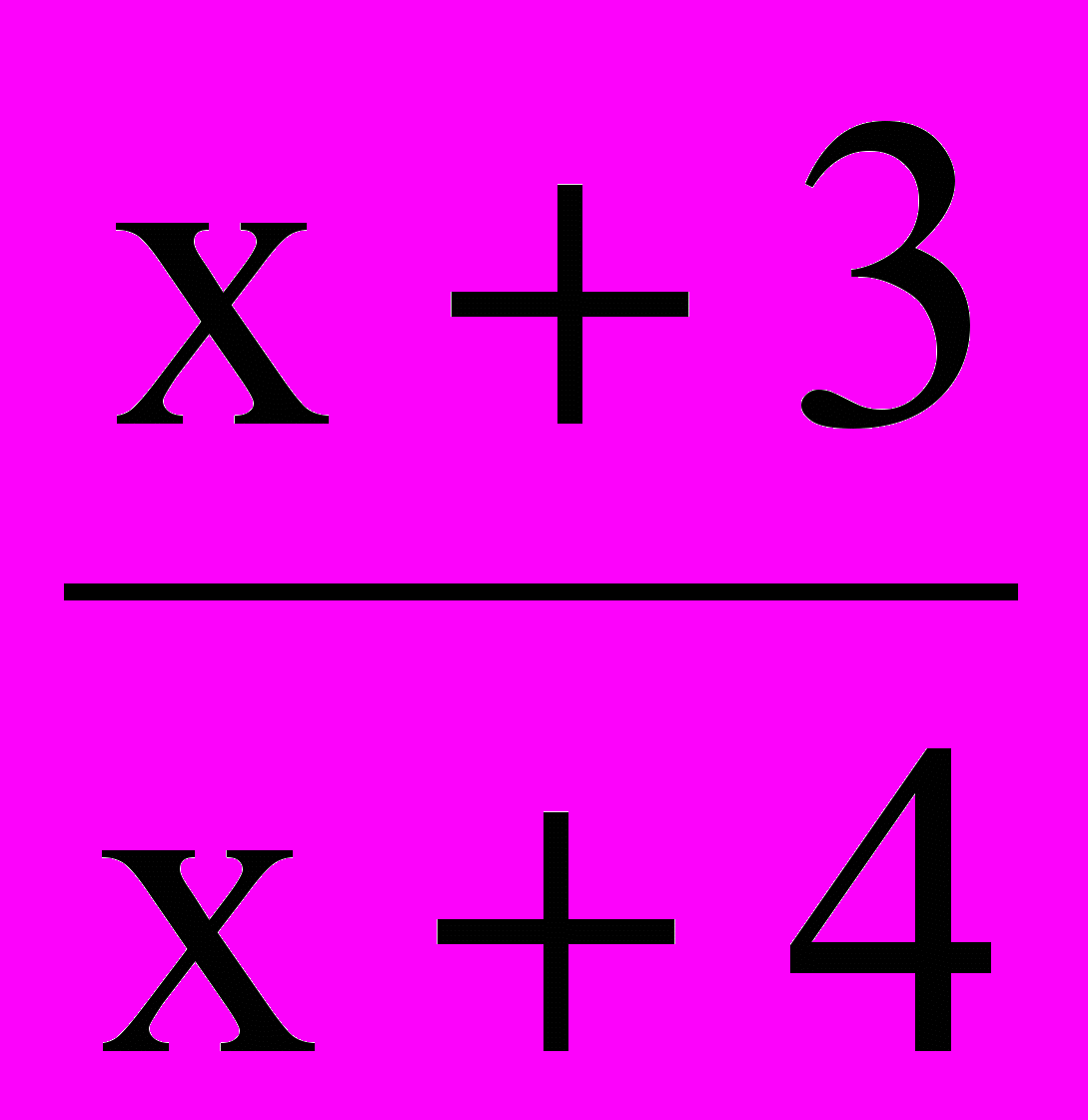 .
.2. Возможности упрощения вычислений НОД в алгоритме Евклида
Теорема
При умножении делимого на число не равное нулю частное и остаток умножаются на такое же число.
Доказательство
Пусть P – делимое, F – делитель, Q – частное, R – остаток. Тогда,
P = FQ + R.
Умножая данное тождество на число 0, получим
P = F(Q) + R,
где многочлен P можно рассматривать как делимое, а многочлены Q и R – как частное и остаток, полученные при делении многочлена P на многочлен F. Таким образом, при умножении делимого на число 0, частное и остаток так же умножаются на , ч.т.д
Следствие
Умножение делителя на число 0 можно рассматривать как умножение делимого на число
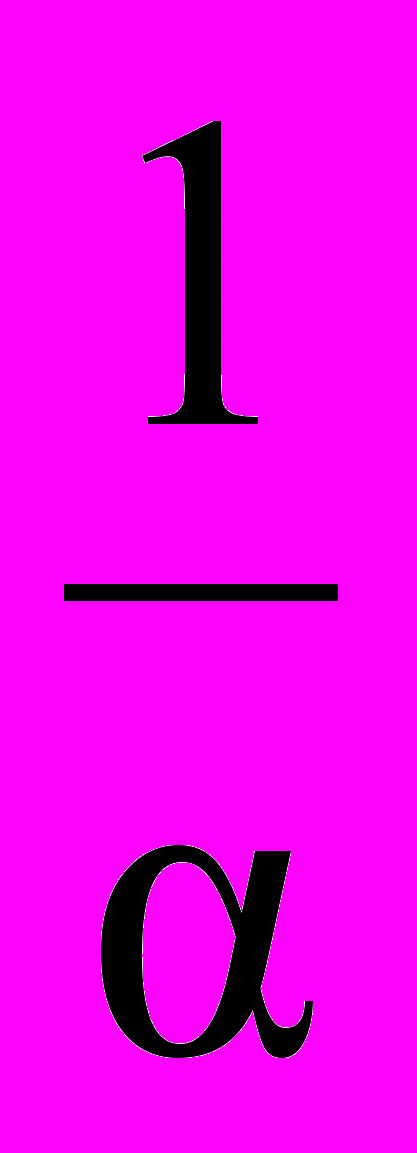 .
.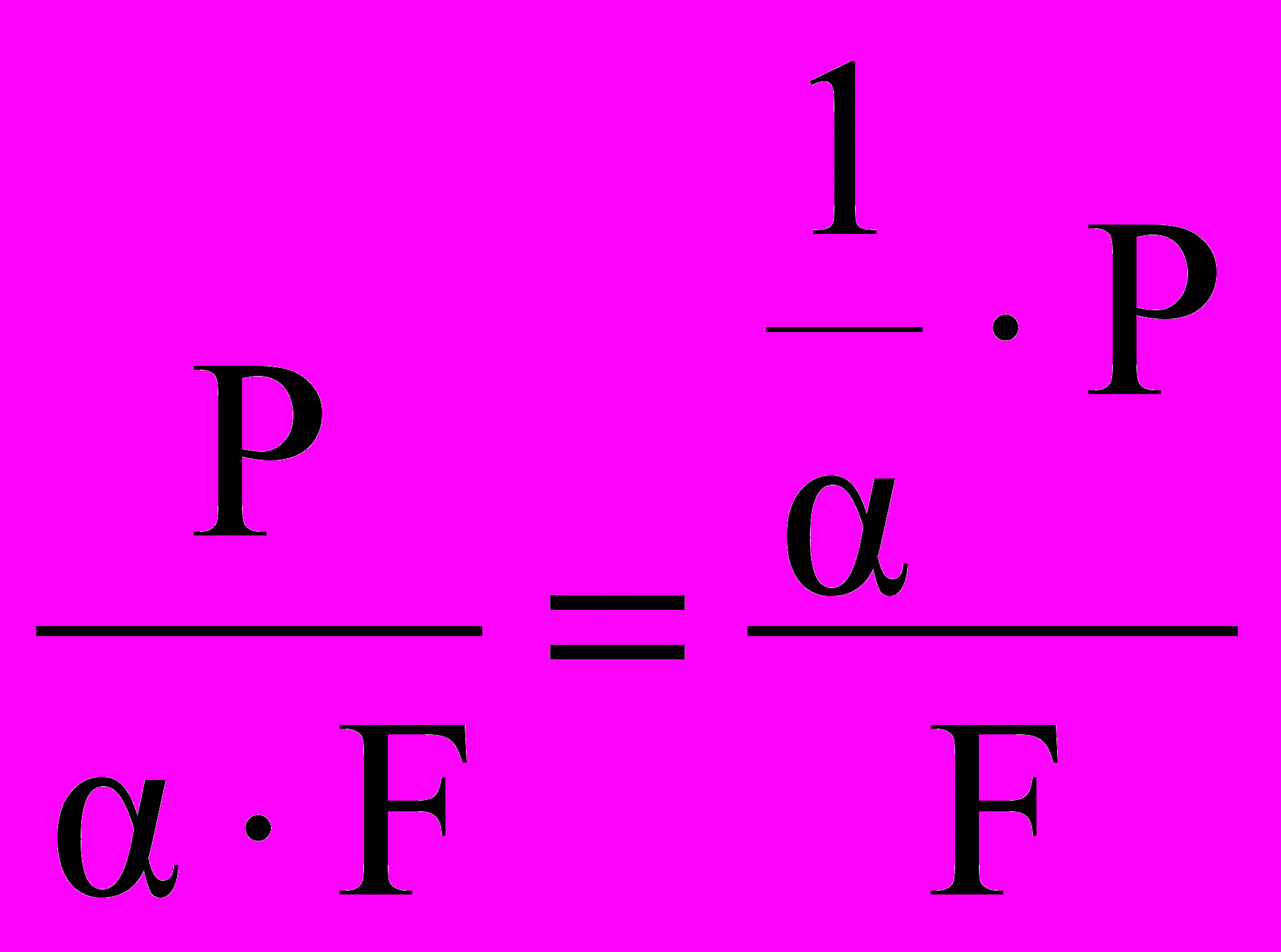 .
.Следовательно, при умножении делителя на число 0 частное и остаток умножается на
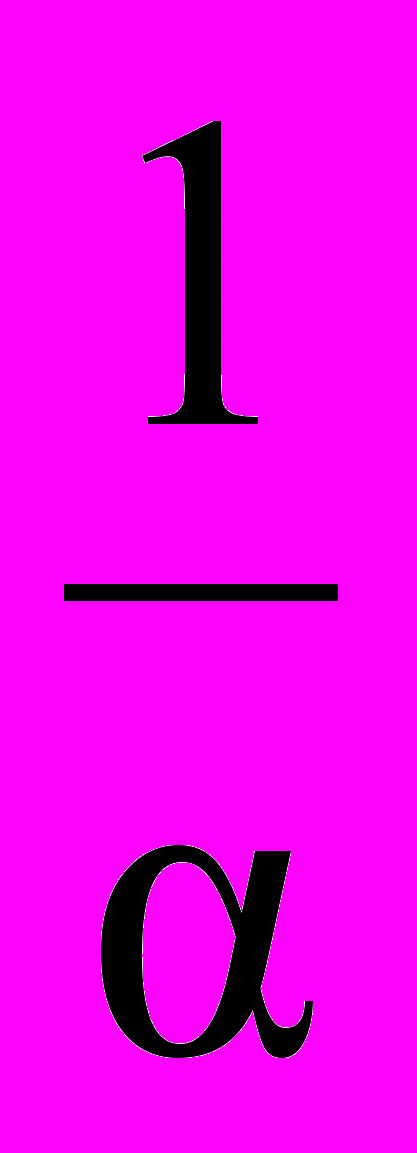 .
.Пример №2
Найти частное Q и остаток R при делении многочленов

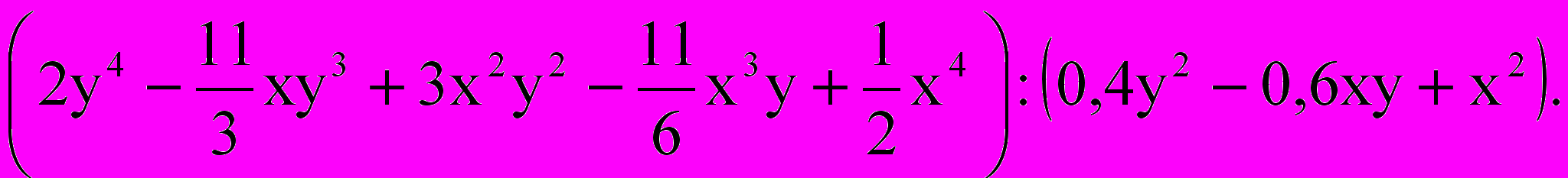
Решение
Для перехода в делимом и делителе к целым коэффициентам умножим делимое на 6, что приведет к умножению на 6 искомого частного Q и остатка R. После чего, умножим делитель на 5, что приведет к умножению частного 6Q и остатка 6R на
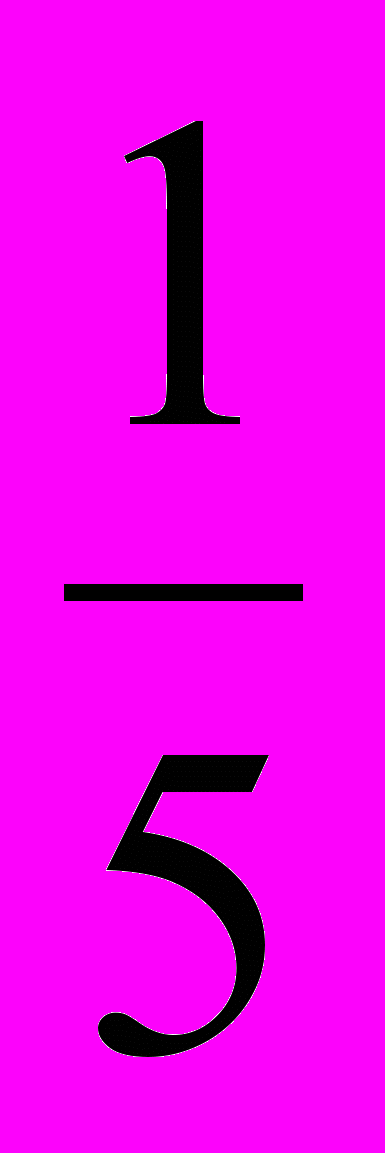 . В итоге, частное и остаток, полученные при делении многочленов с целыми коэффициентами, в
. В итоге, частное и остаток, полученные при делении многочленов с целыми коэффициентами, в 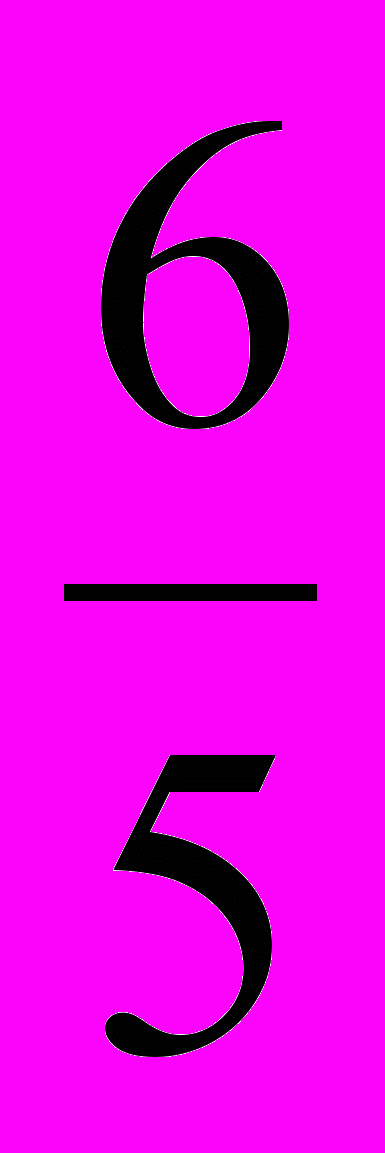 раз будут отличаться от искомых значений частного Q и остатка R, полученных при делении данных многочленов.
раз будут отличаться от искомых значений частного Q и остатка R, полученных при делении данных многочленов.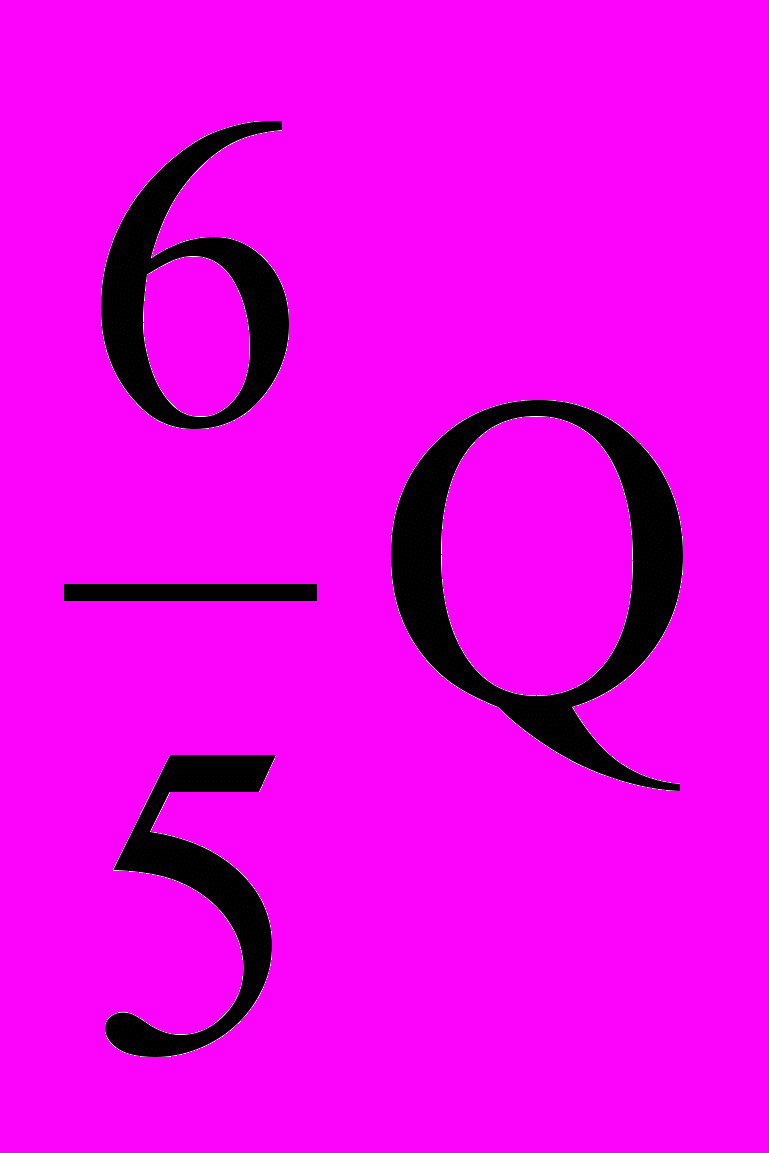


–
12у4 – 22ху3 + 18х2у2 – 11х3у + 3х4 2у2 – 3ху + 5х2
 12у4 18ху3
12у4 18ху3  30х2у2 6у2 – 2ху – 9х2 =
30х2у2 6у2 – 2ху – 9х2 = – 4ху3 – 12х2у2 – 11х3у + 3х4
 4ху3
4ху3  6х2у2 10х3у
6х2у2 10х3у– 18х2у2 – х3у + 3х4
 18х2у2
18х2у2 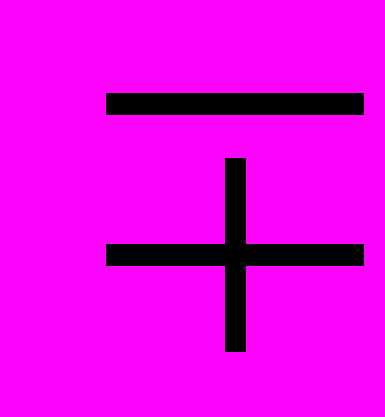 27х3у 45х4
27х3у 45х4– 28х3у + 48х4 =
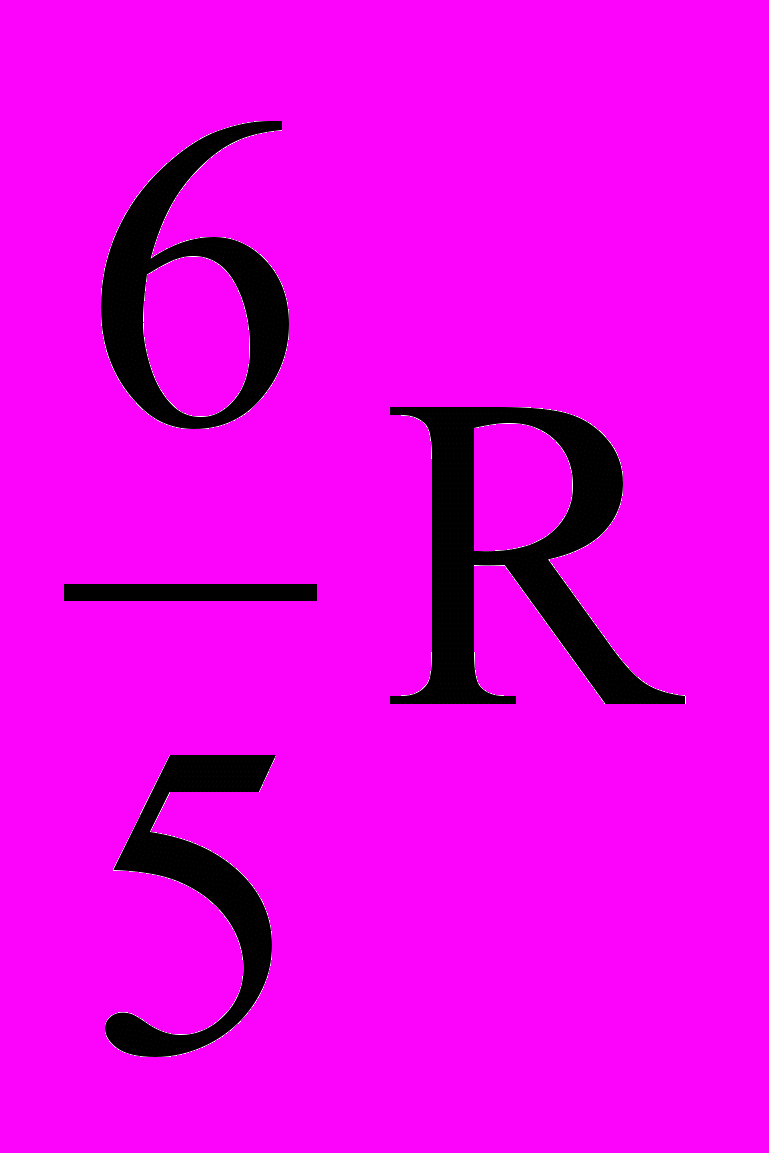
Следовательно,
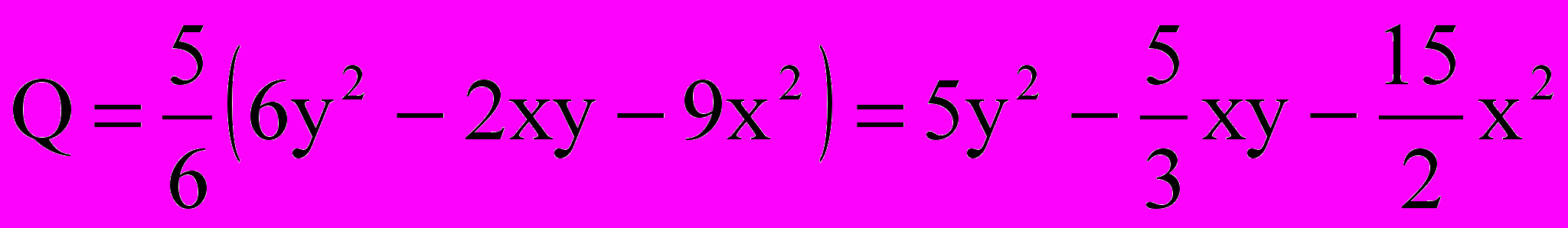 ;
;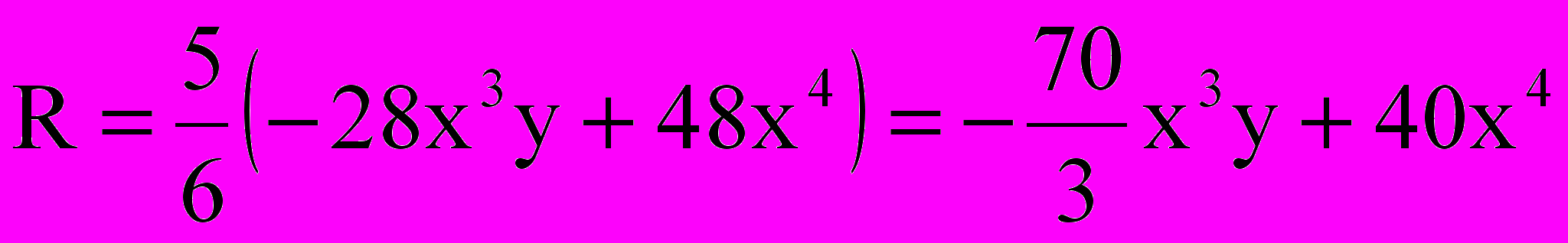 .
.Ответ:
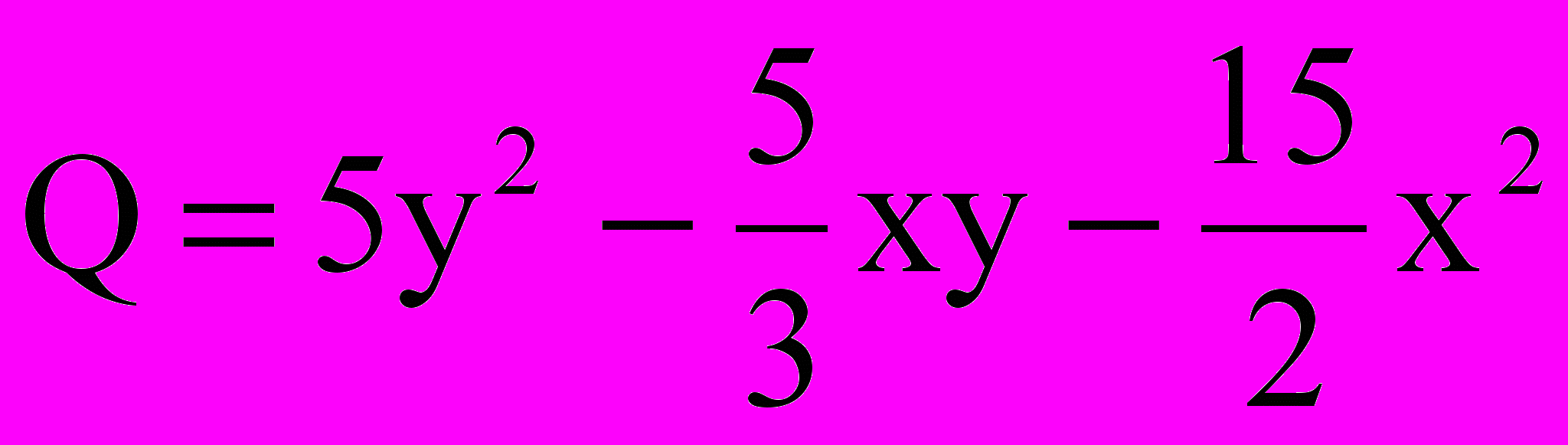 ,
, 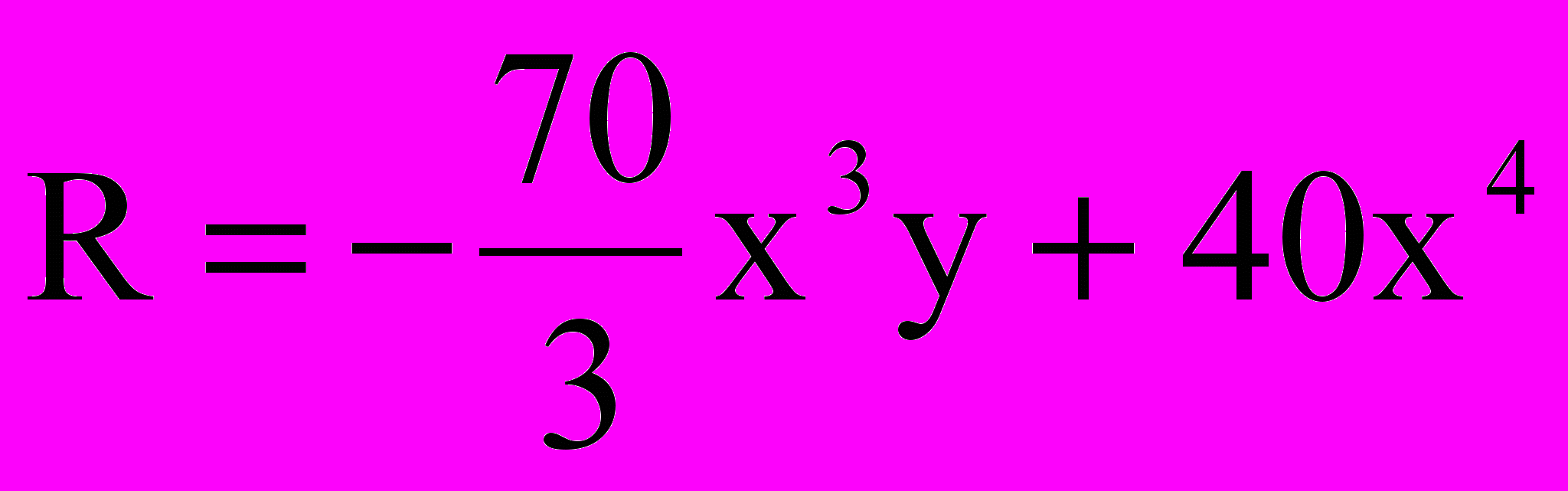 .
.Заметим, что если наибольший общий делитель данных многочленов найден, то, умножая его на любое число, не равное нулю, мы также получим наибольший делитель этих многочленов. Это обстоятельство дает возможность упрощать вычисления в алгоритме Евклида. А именно, перед очередным делением делимое или делитель можно умножать на числа, подобранные специальным образом так, чтобы коэффициент первого слагаемого в частном был числом целым. Как показано выше, умножение делимого и делителя приведет к соответствующему изменению частного остатка, но такому, что в итоге НОД данных многочленов умножится на некоторое равное нулю число, что допустимо.
Пример №3
Сократить дробь
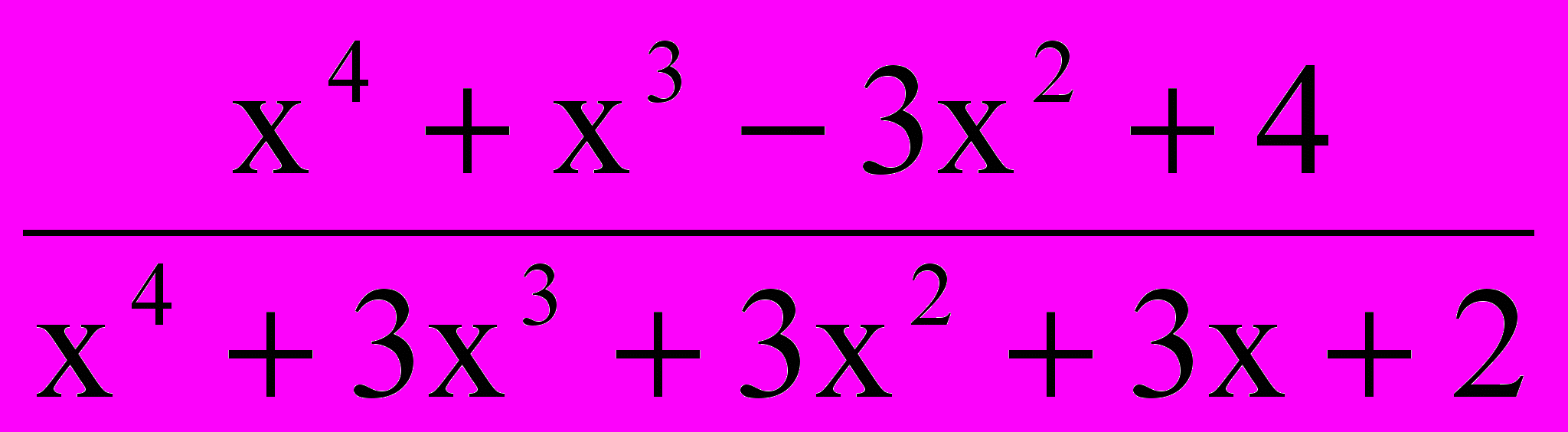 .
.Решение
Применяя алгоритм Евклида, получим
1


–
) х4 + 3х3 + 3х2 + 3х + 2 х4 + х3 – 3х2 + 4
х4
 х3 3х2
х3 3х2  4 1
4 12х3 + 6х2 + 3х – 2
2


 ) 2(х4 + х3 – 3х2 + 4) = 2х4 + 2х3 – 6х2 + 8 2х3 + 6х2 + 3х – 2
) 2(х4 + х3 – 3х2 + 4) = 2х4 + 2х3 – 6х2 + 8 2х3 + 6х2 + 3х – 2 2х4
2х4  6х3
6х3 3х2 2х х – 2
3х2 2х х – 2– 4х3 – 9х2 + 2х + 8
 4х3 12х2 6х
4х3 12х2 6х 4
43х2 + 8х + 4
3
–

–
) 3(2х3 + 6х2 + 3х – 2) = 6х3 + 18х2 + 9х – 6 3х2 + 8х + 4

 6х3
6х3 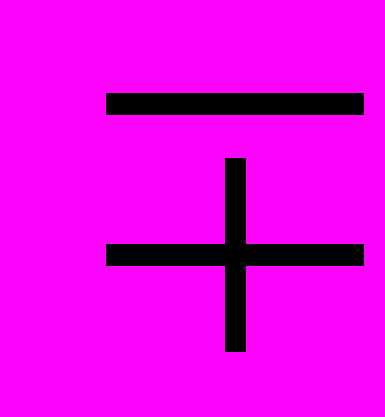 16х2
16х2 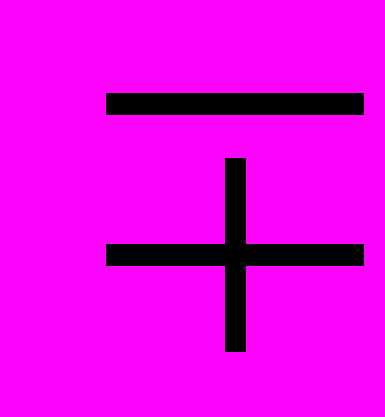 8х 2х +
8х 2х + 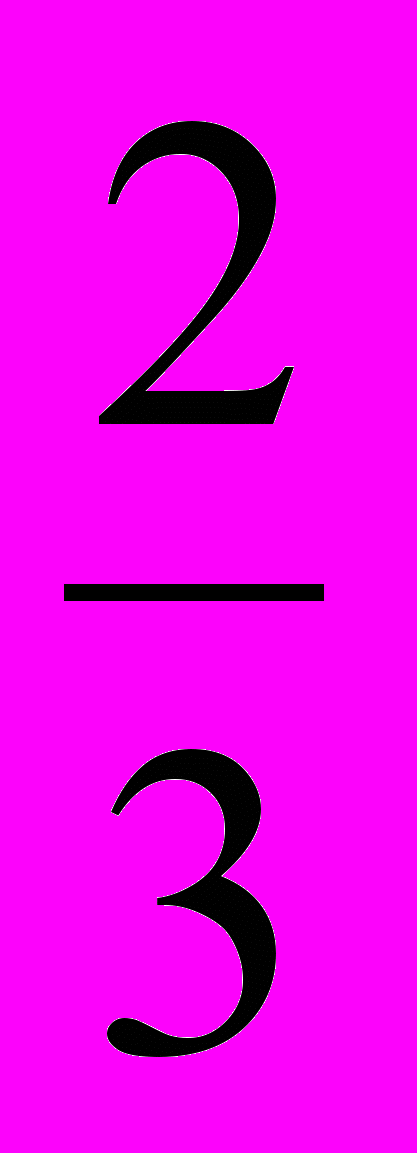
–
2х2 + х – 6
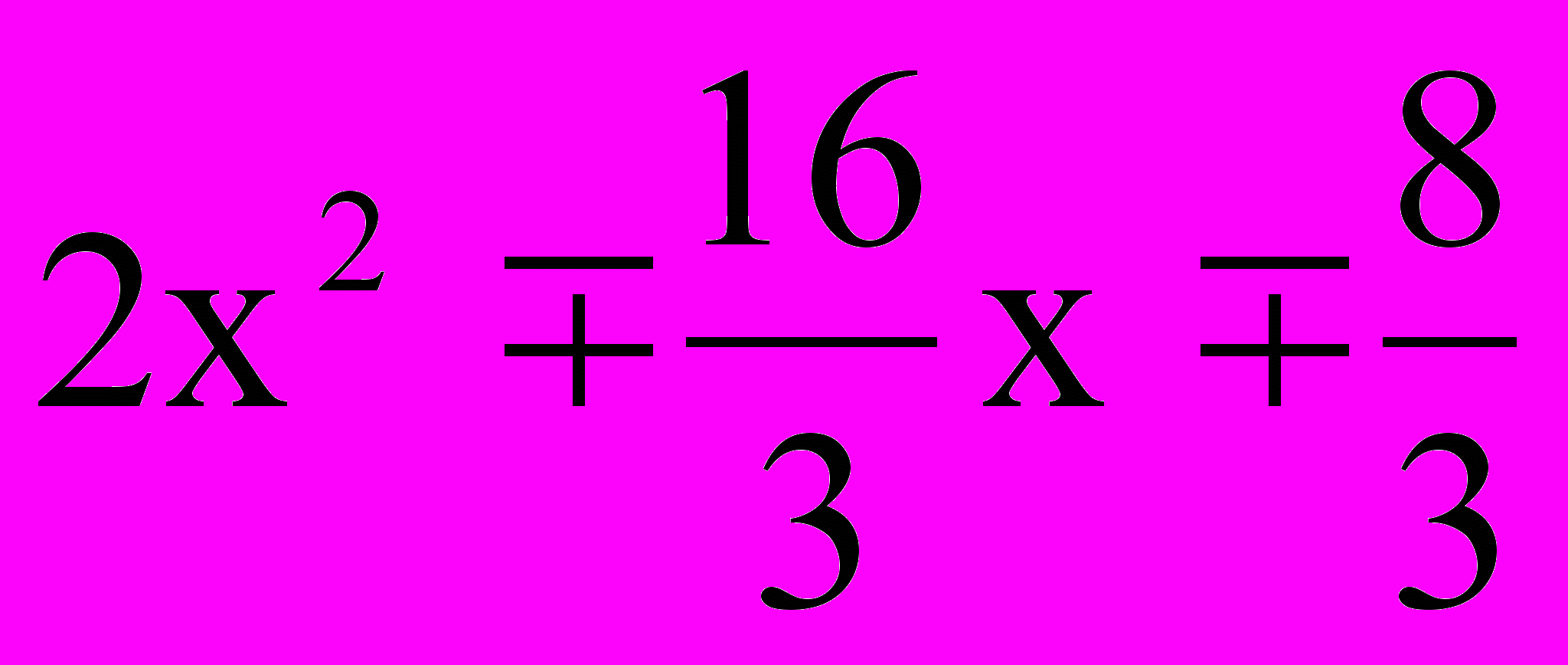

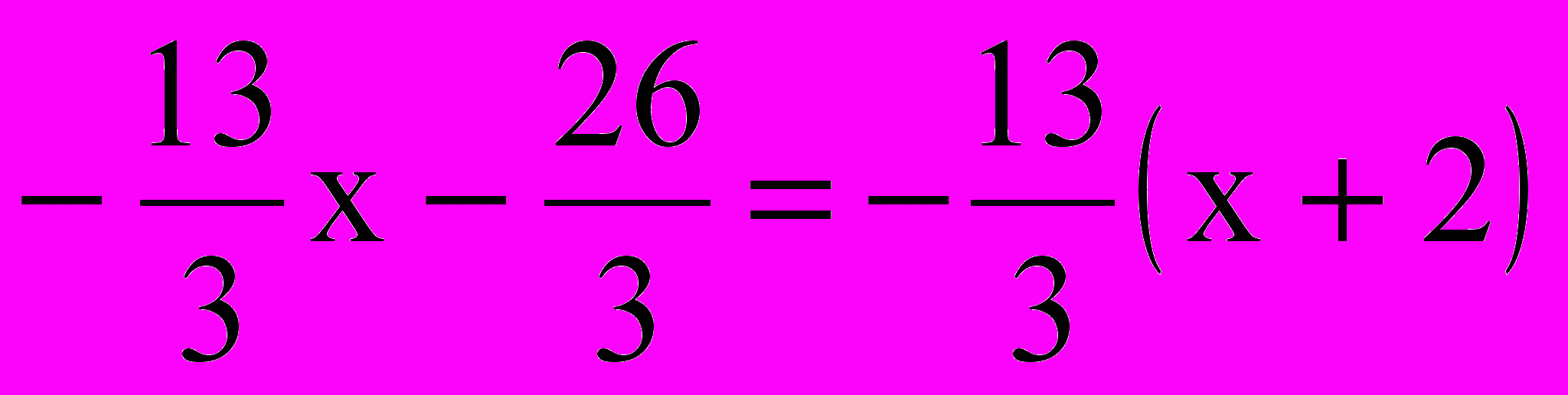
4


–
) 3х2 + 8х + 4 х + 2
 3х2
3х2 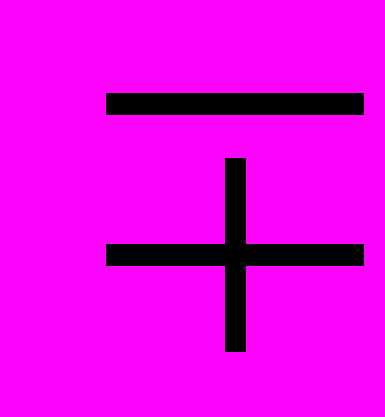 6х 3х + 2
6х 3х + 2–
2х + 4
 2х + 4
2х + 40
Следовательно, многочлен (х + 2) является НОД числителя и знаменателя данной дроби. При этом,


–
х4 + 3х3 + 3х2 + 3х + 2 х + 2
 х4
х4 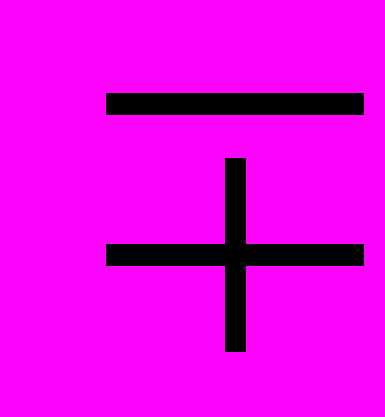 2х3 х3 + х2 + х + 1
2х3 х3 + х2 + х + 1–
х3 + 3х2 + 3х + 2
 х3
х3 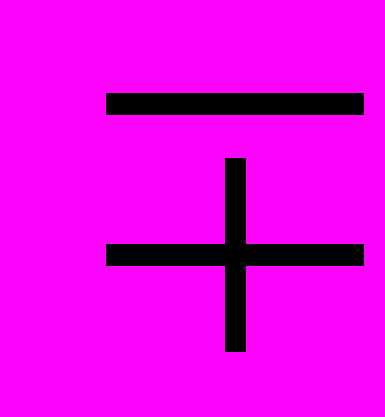 2х2
2х2 х2 + 3х + 2
 х2
х2 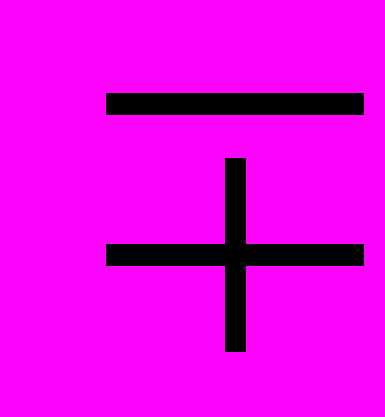 2х
2хх + 2
 х
х 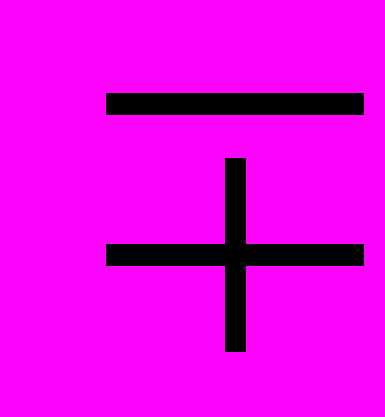 2
20
х

–
 4 + х3 – 3х2 + 4 х + 2
4 + х3 – 3х2 + 4 х + 2 х
 4 +2х3 х3 – х2 – х + 2
4 +2х3 х3 – х2 – х + 2– х3 – 3х2 + 4
 х3 2х2
х3 2х2 – х2 + 4
 х2 2х
х2 2х–
2х 4
 2х + 4
2х + 40
Таким образом,
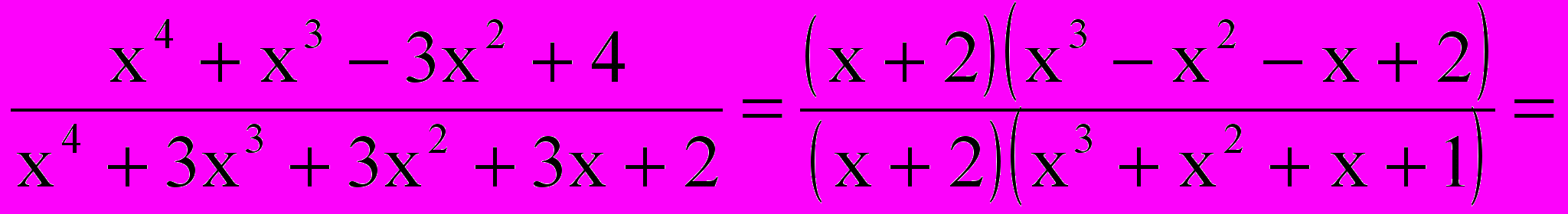
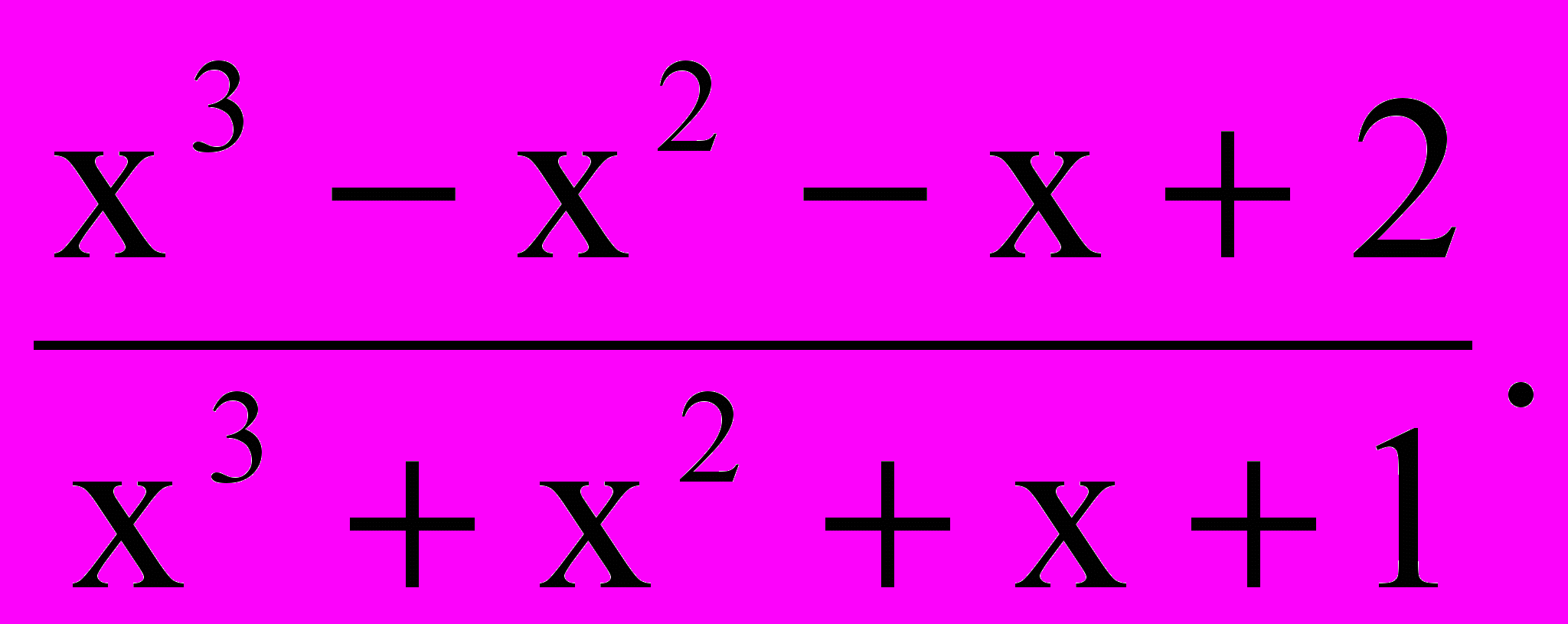
 Ответ:
Ответ: 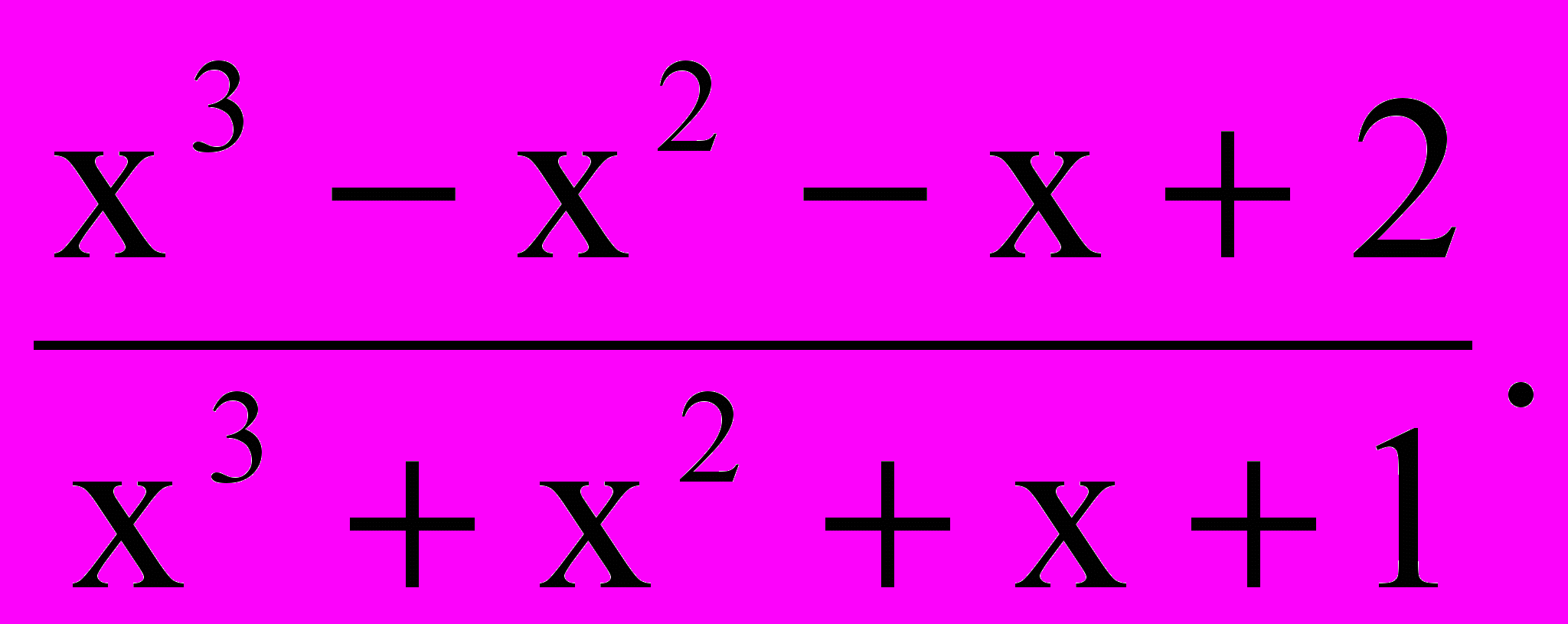
Упражнения
Сократить дроби
1.
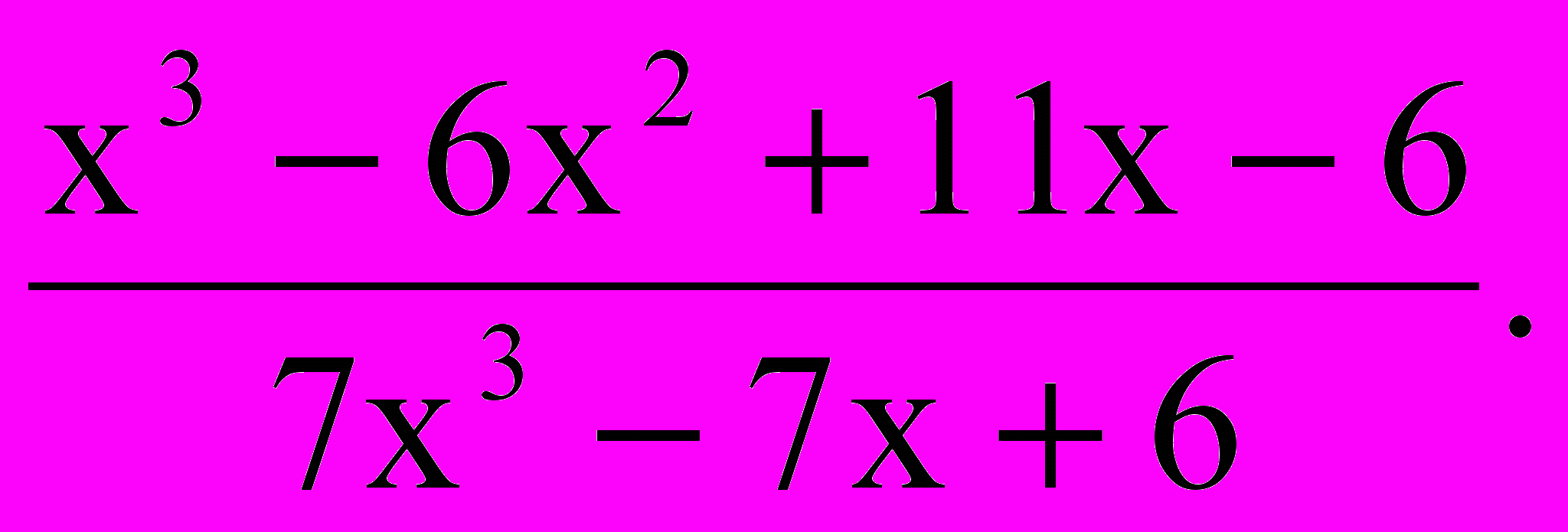 Ответ:
Ответ: 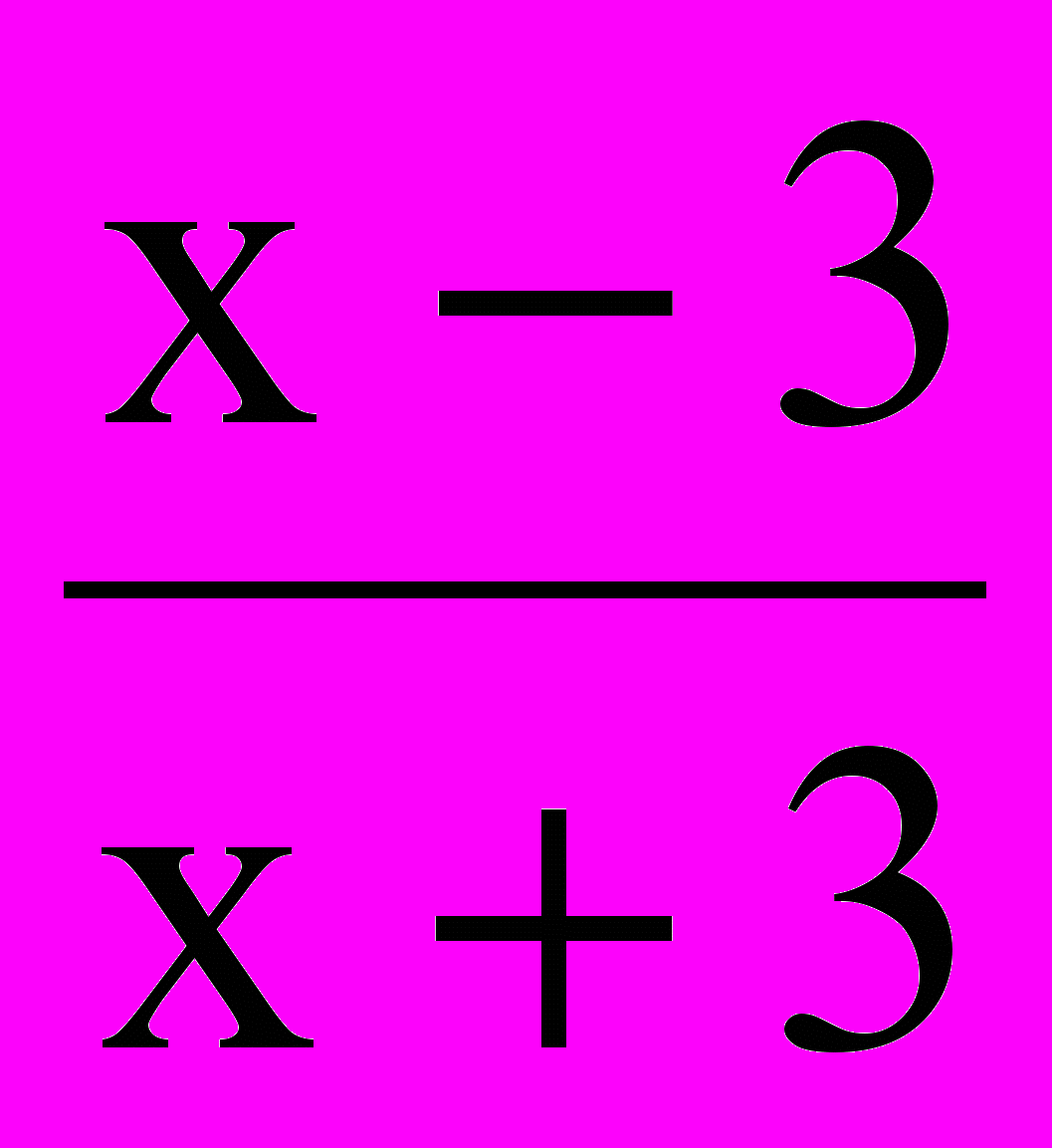 .
.2.
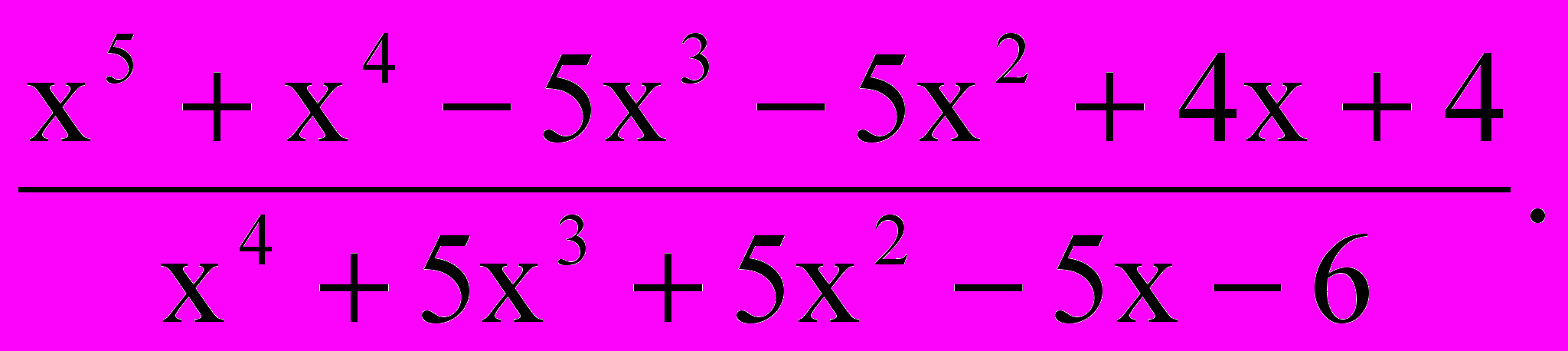 Ответ:
Ответ: 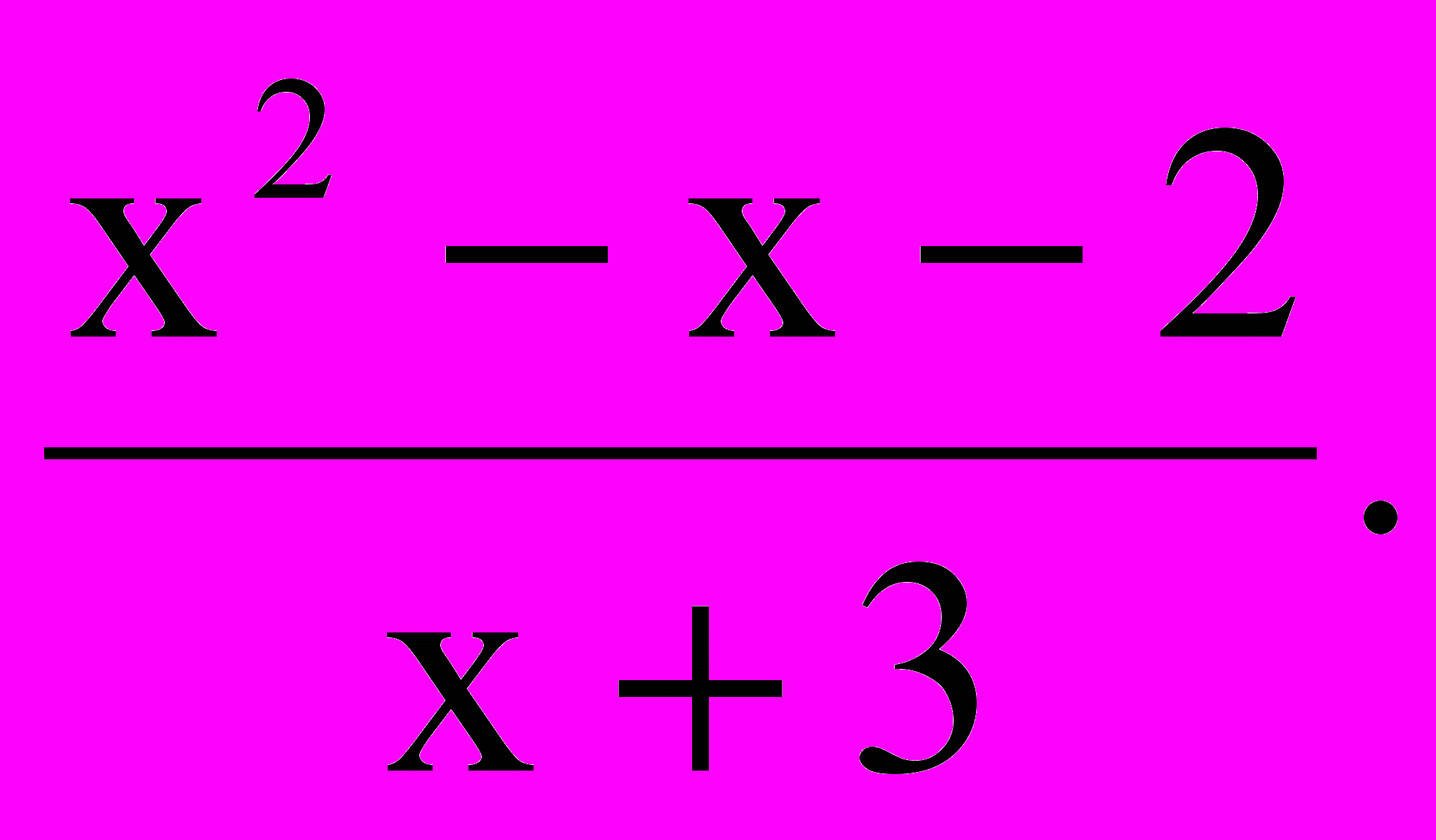
3.
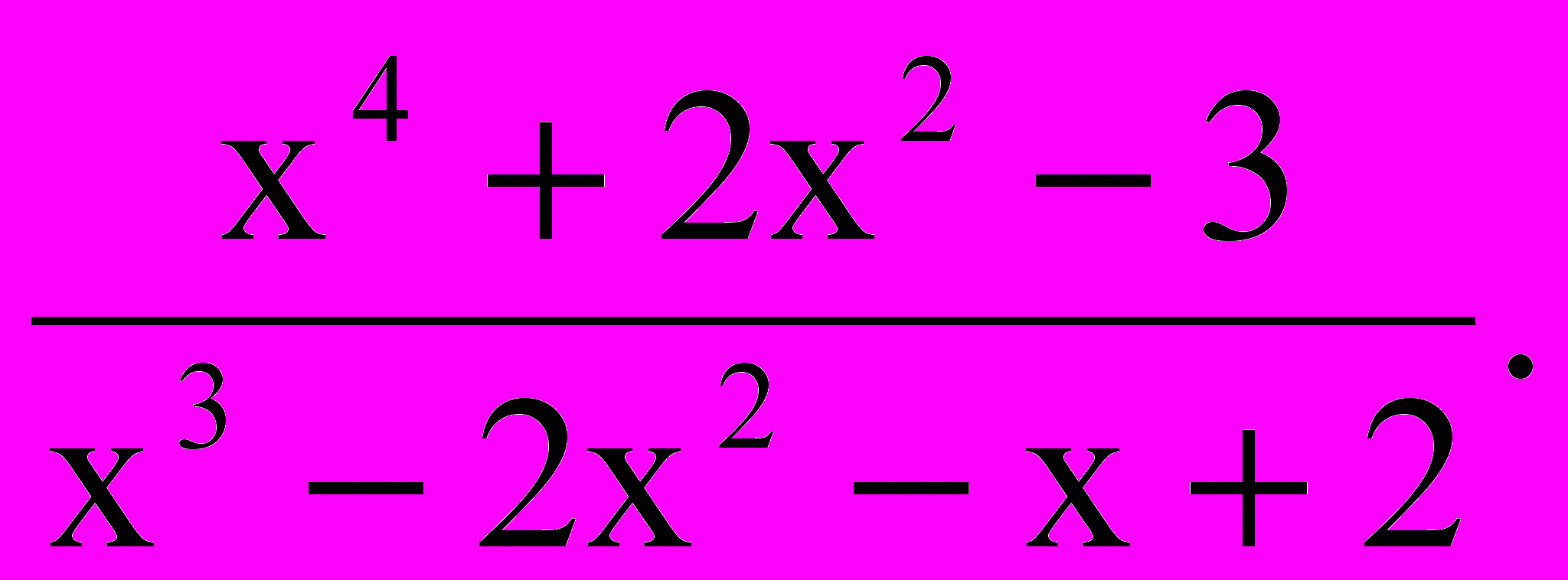 Ответ:
Ответ: 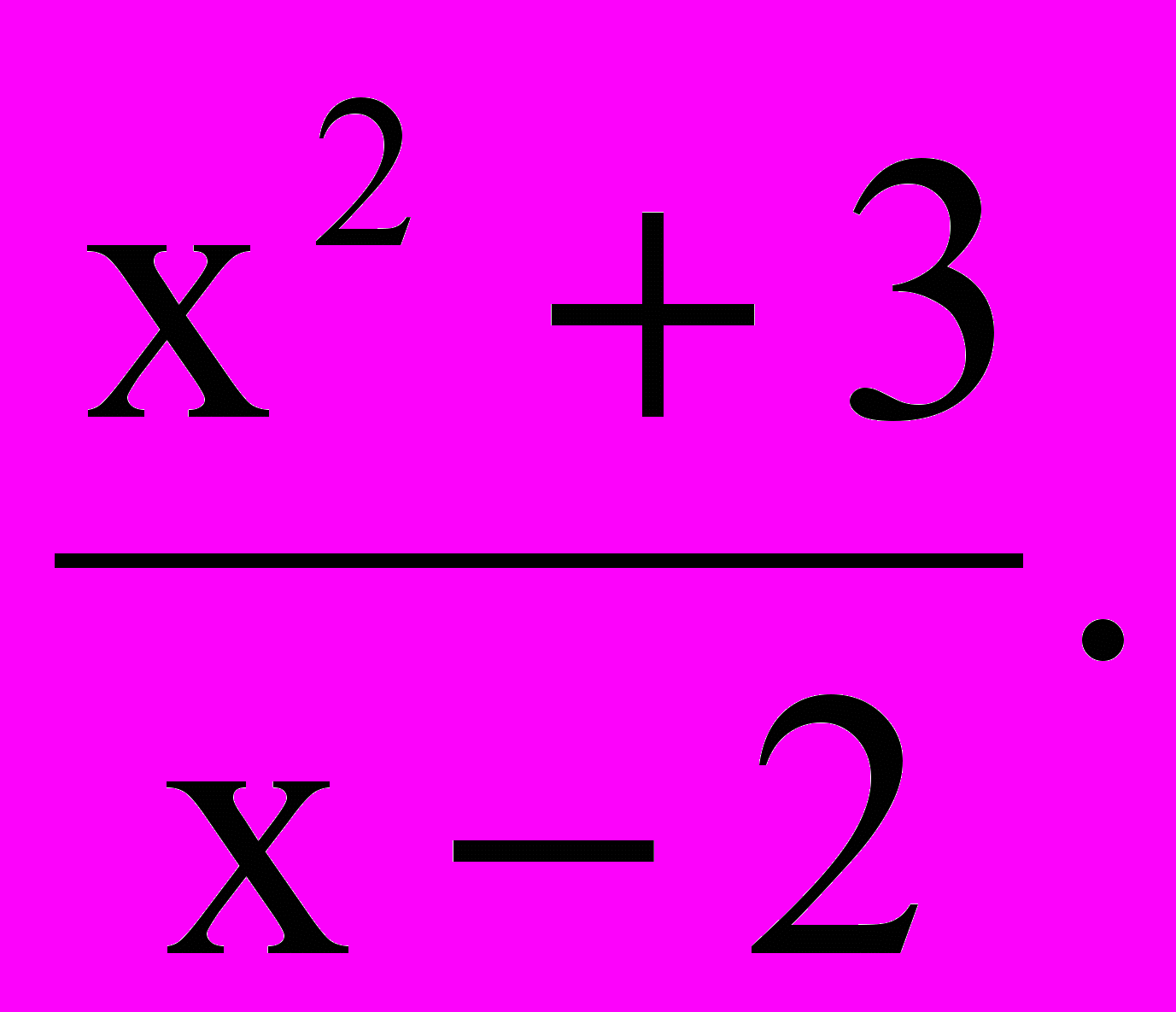
4.
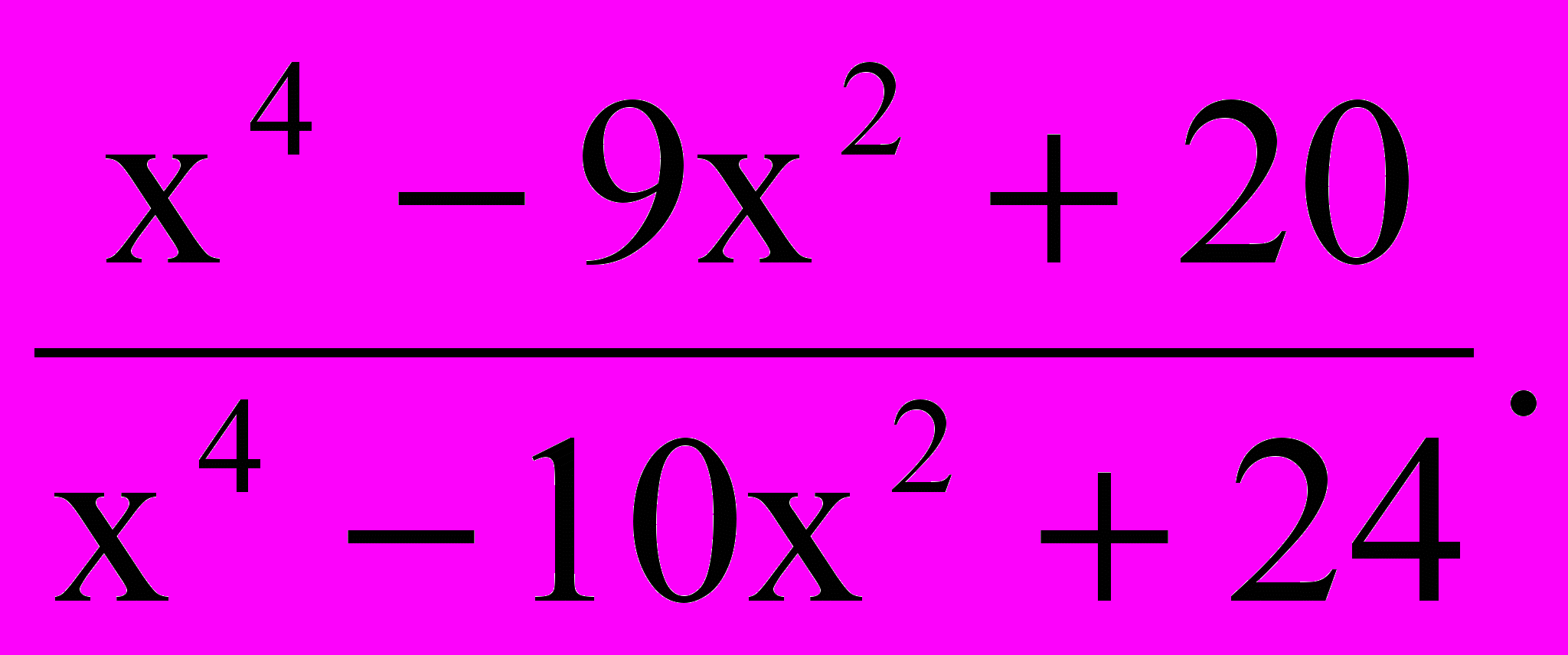 Ответ:
Ответ: 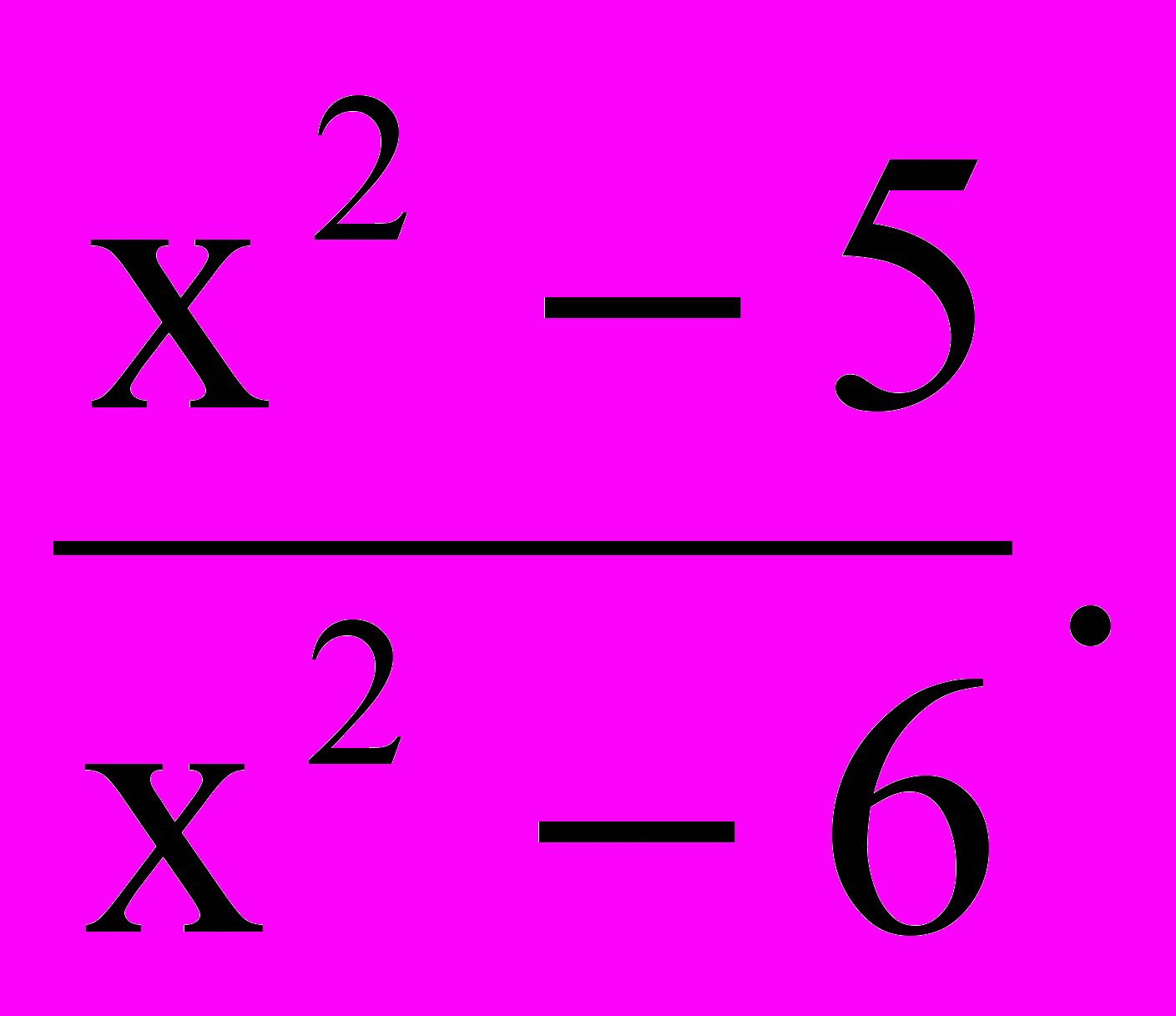
5.
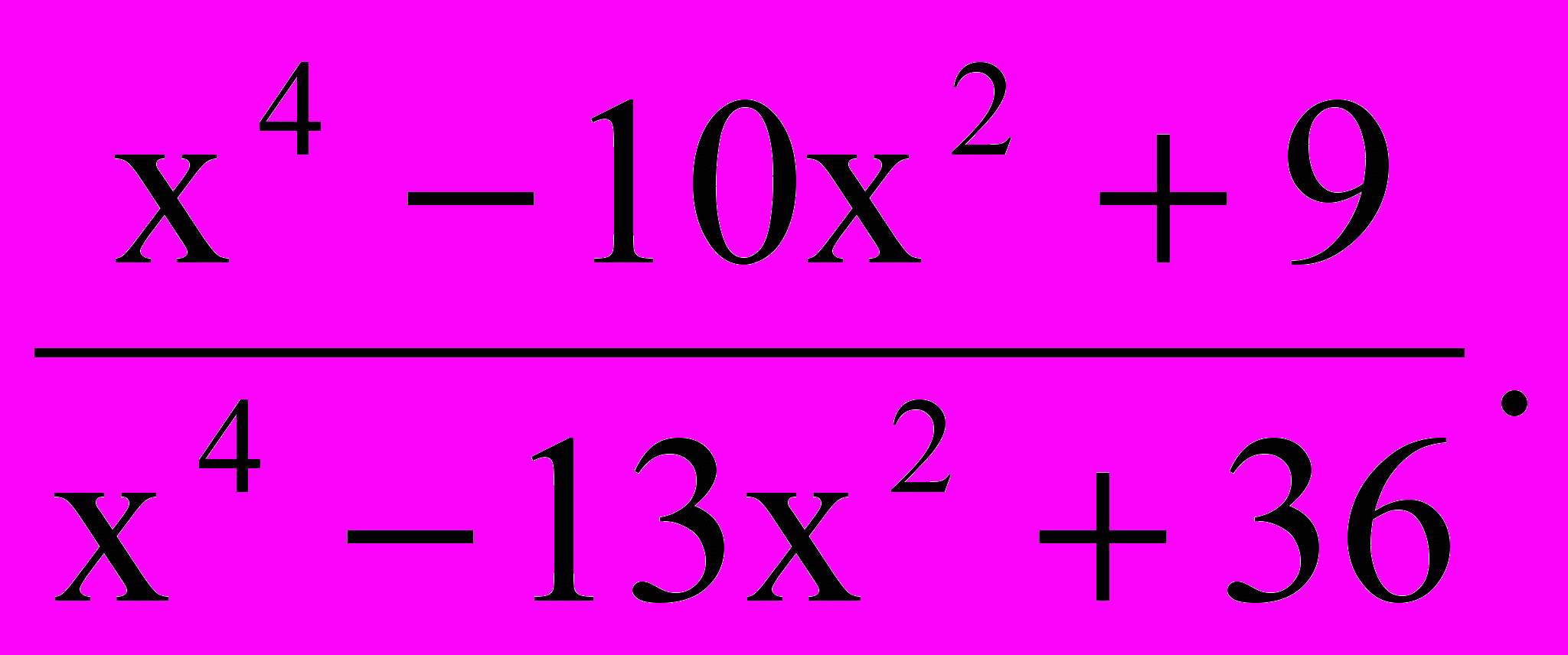 Ответ:
Ответ: 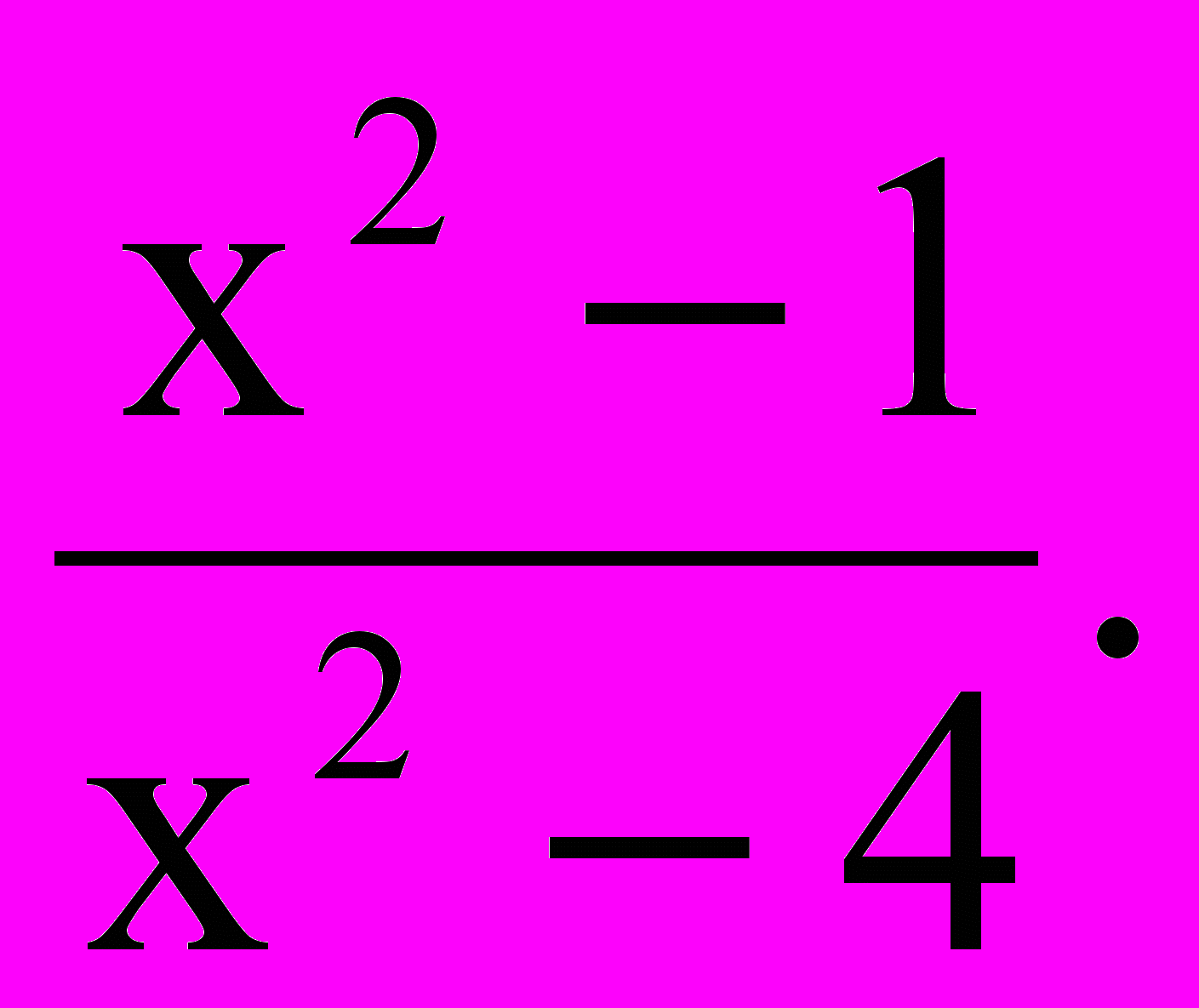
§3. Нахождение НОД двух натуральных чисел
Число является частным случаем многочлена. Поэтому, алгоритм нахождения НОД двух натуральных чисел не отличается от рассмотренного алгоритма определения НОД двух многочленов. При этом, большее из заданных чисел становится делимым, а меньшее – делителем. И, подобно тому, как признаком отсутствия НОД двух многочленов является появление остатка в виде числа неравного нулю – тривиального делителя любого многочлена, признаком отсутствия НОД двух натуральных чисел является появление 1 в остатке – тривиального делителя любого натурального числа.
Пример №1
Найти НОД двух чисел 323 и 247
Решение
1





 ) 323 247 2) 247 76 3) 76 19
) 323 247 2) 247 76 3) 76 19

 247 1 228 3 76 4
247 1 228 3 76 476 19 0
Ответ: НОД 323; 247 = 19.
Пример №2
Найти НОД двух чисел 323 и 107
Решение
1



 ) 323 107 2) 107 2
) 323 107 2) 107 2 
 321 3 100 53
321 3 100 53 2 7
 6
61 не существует
Ответ: НОД 323; 107 не существует.
Упражнения
