Построение оптимальных безусловных диагностических тестов при интеллектуальном анализе данных и знаний*
| Вид материала | Документы |
- Построение функциональных диагностических тестов конвейеризованных risc процессоров, 188.67kb.
- Моделирование потоков работ в задаче приведения данных, 72.4kb.
- Аппаратно-программный комплекс >14. Атлас 15. Атласная информационная система >16., 68.1kb.
- Дискретных Марковских Цепей) в анализе данных. Пример применения. (лекция, 7.29kb.
- Кулик Б. А., Зуенко А. А., Фридман А. Я. Алгебраический подход к интеллектуальной обработке, 13.89kb.
- 1. Введение Основы анализа данных. Методология построения моделей сложных систем. Модель, 399.94kb.
- Готовления препаратов из лекарственных средств и вспомогательных веществ путем придания, 256.6kb.
- Удовлетворение потребностей детей, подростков и молодежи в интеллектуальном, творческом,, 11.52kb.
- Рефератов, историй болезни, литературы, обучающих программ, тестов, 180.34kb.
- Экспертные системы и базы знаний, 42.45kb.
,УДК 681.5:681.327.12.001.362
ПОСТРОЕНИЕ ОПТИМАЛЬНЫХ БЕЗУСЛОВНЫХ ДИАГНОСТИЧЕСКИХ ТЕСТОВ ПРИ ИНТЕЛЛЕКТУАЛЬНОМ АНАЛИЗЕ ДАННЫХ И ЗНАНИЙ*
A.И. Гедике 1, А.E. Янковская 2
Предлагается алгоритм построения подмножества оптимальных по ряду критериев безусловных диагностических тестов при интеллектуальном анализе данных и знаний. Подмножество оптимальных тестов используется для принятия решений в интеллектуальных тестовых распознающих системах с матричным представлением данных и знаний. Приводятся подходы к решению задачи, ее постановка, алгоритм решения.
Введение
Актуальность разработки эффективных алгоритмов анализа данных и знаний, используемых в интеллектуальных системах (ИС) принятия решений не вызывает сомнения. Одно из направлений создания ИС базируется на тестовых методах распознавания образов, в рамках которого одним из перспективных является подход [Янковская, 2000], основанный на построении безусловных диагностических тестов (БДТ), развиваемый в лаборатории интеллектуальных систем Томского государственного архитектурно-строительного университета (ЛИС ТГАСУ). Данный подход ориентирован на матричное представление данных и знаний об изучаемых объектах из рассматриваемой проблемной области и включает построение всех минимальных и безызбыточных БДТ (МБДТ и ББДТ).
Однако, в задачах большой размерности не только число ББДТ, но и число МБДТ может быть достаточно велико, а выбор "хороших" тестов [Ермаков А.Е. и др., 2002] не приводит к построению оптимальных решений, что обосновано в публикациях [Янковская, 2002; Yankovskaya et al., 2004;]. Поэтому возникает необходимость нахождения подмножества безусловных диагностических тестов, оптимальных по ряду критериев (ОБДТ), т.е. решения многокритериальной оптимизационной задачи.
В публикациях [Yankovskaya et al., 2004; Колесникова и др., 2005] приводятся алгоритмы выбора оптимального подмножества тестов из множества всех построенных тестов. В отличие от вышеупомянутых алгоритмов предлагаемый алгоритм предназначен для построения заданного количества ОБДТ c наименьшим числом входящих в тесты признаков (критерий 1) и наибольшим их суммарным весом (критерий 2), минимальной суммарной стоимостью измерения значений этих признаков (критерий 3) и минимальным суммарным ущербом (риском), наносимым при их измерении (критерий 4).
К сожалению, у авторов отсутствует информация об исследованиях по построению ОБДТ с учетом нескольких критериев оптимальности, за исключением приведенных в публикациях [Янковская, 2002; Колесникова и др., 2005]. Из других авторов наиболее близким по способу решения алгоритмом, в котором учитывается только один критерий, является алгоритм, представленный в статье [Новоселов, 1966].
1. Представление данных и знаний
Для представления данных и знаний об изучаемых объектах используется матричная модель, включающая матрицу описаний (Q), задающую описания объектов в пространстве характеристических признаков, и матрицу различений (R), разбивающую объекты на классы эквивалентности по каждому механизму классификации в пространстве классификационных признаков [Янковская, 2000].
Строки булевой матрицы Q сопоставляются изучаемым объектам, столбцы характеристическим признакам. Строки целочисленной матрицы R сопоставляются строкам матрицы Q, столбцы классификационным признакам.
Описание каждого образа задается подмножеством строк матрицы Q, которым сопоставлены одинаковые строки матрицы R.
Для представления условий различимости изучаемых объектов, принадлежащих разным образам, по матрицам Q и R строится безызбыточная (не содержащая поглощающих строк) булева матрица импликаций (U), столбцы которой сопоставляются признакам, задающим описания объектов (столбцам матрицы Q), строки результатам сравнения пар типа образ-образ, объект-образ и объект-объект из разных образов. Элемент строки матрицы U принимает единичное значение, если соответствующий признак является различающим для данной пары, и нулевое значение в противном случае. Таким образом, матрица U задает условия различимости любой пары объектов, принадлежащих разным образам, описания которых представлены матрицами Q и R.
При построении матрицы U вычисляются весовые коэффициенты признаков
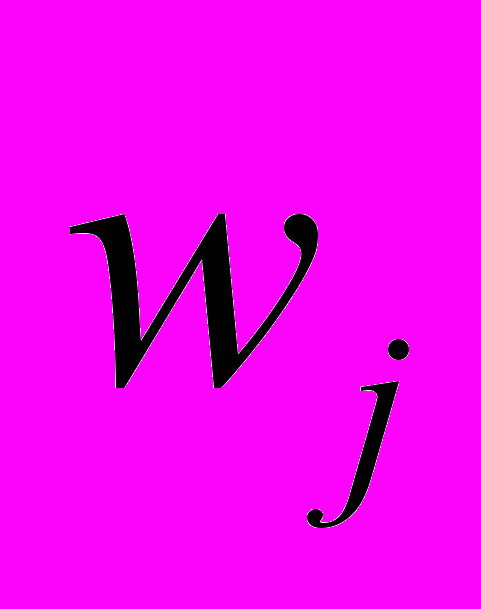 ( j=1,…,m, где m число признаков), характеризующие вклад каждого признака в различимость объектов из разных образов.
( j=1,…,m, где m число признаков), характеризующие вклад каждого признака в различимость объектов из разных образов.Построенные тесты представляются строками матрицы тестов T.
2. Подходы к построению ОБДТ и постановка задачи
Задачи построения всех МБДТ и ББДТ сводятся к задачам нахождения всех кратчайших и всех безызбыточных столбцовых покрытий (КСП и БСП) булевой матрицы U, для решения которых были разработаны соответствующие алгоритмы [Yankovskaya et al., 1999; Гедике и др., 2005].
Оба алгоритма основаны на применении ряда специальных правил и оригинальной разметки столбцов булевой матрицы, используемых в процессе построения и обхода дерева поиска, что позволяет существенно сократить число переборов путем отсечения неоптимальных путей в дереве поиска. Аналогично задача построения ОБДТ сводится к нахождению оптимальных столбцовых покрытий (ОБП) матрицы U.
Для учета нескольких критериев оптимальности основными являются следующие подходы:
- Упорядочить критерии по убыванию значимости и последовательно применять их в установленном порядке.
- Выполнить свертку критериев, т.е. заменить многокритериальную задачу оптимизации однокритериальной задачей.
В данной работе предлагается первым учитывать критерий 1, затем учитывать критерий 2 и, наконец, учитывать свертку критериев 3 и 4.
Обозначим через l число признаков, входящих в каждый (по критерию 1) i-й ОБДТ, а через ni1,ni2,…nil соответствующие им номера. И пусть известны весовые коэффициенты признаков
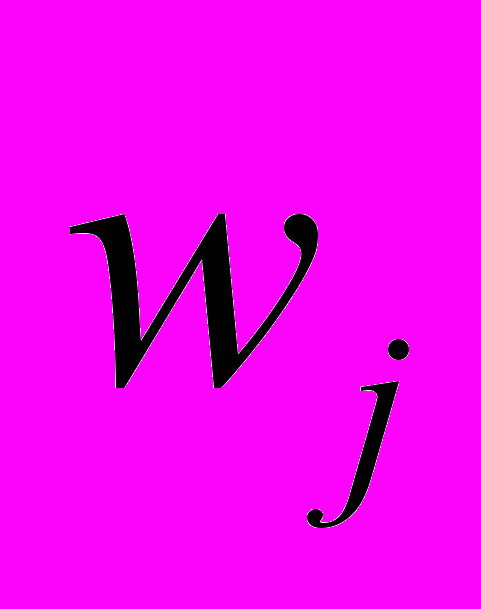 (j=1,…m), а также коэффициенты
(j=1,…m), а также коэффициенты 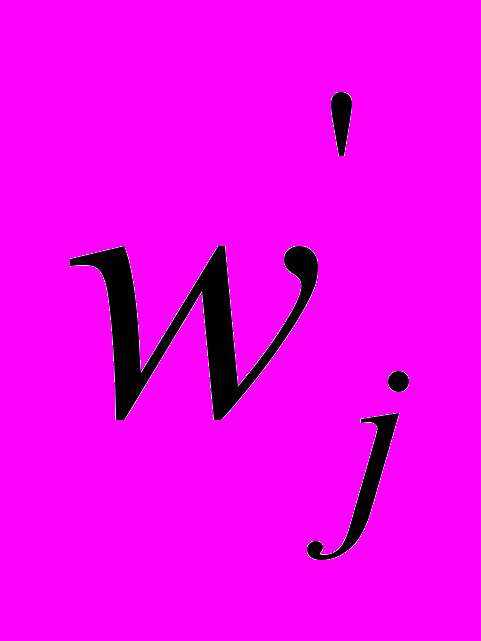 и
и 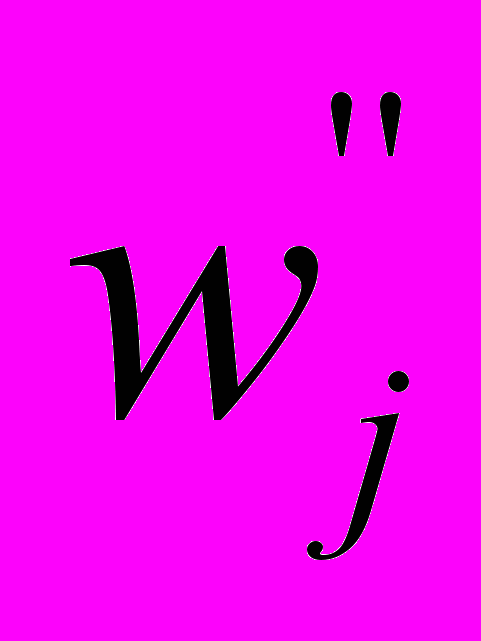 , задающие соответственно стоимость измерения значения j-го признака и ущерб (риск), наносимый при его измерении.
, задающие соответственно стоимость измерения значения j-го признака и ущерб (риск), наносимый при его измерении.Тогда для каждого i-го ОБДТ можно вычислить вес теста
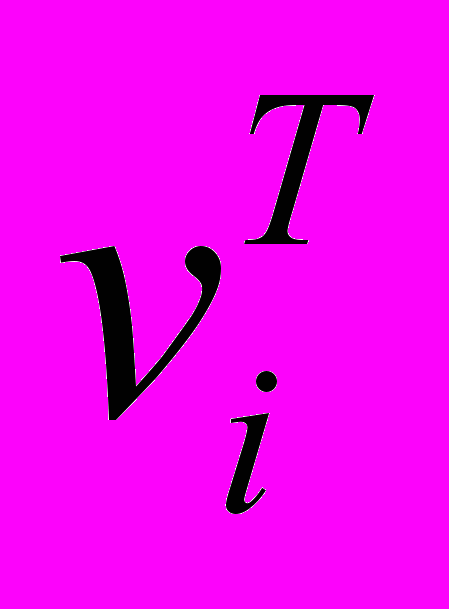 и коэффициент свертки
и коэффициент свертки 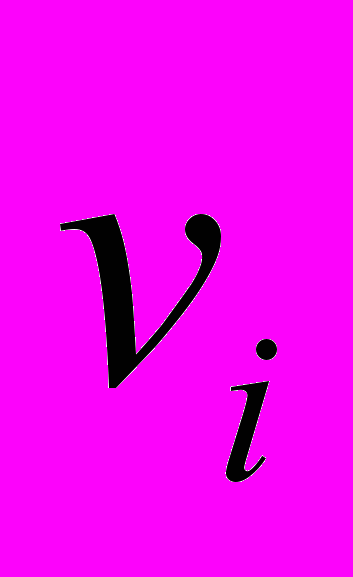 по формулам:
по формулам: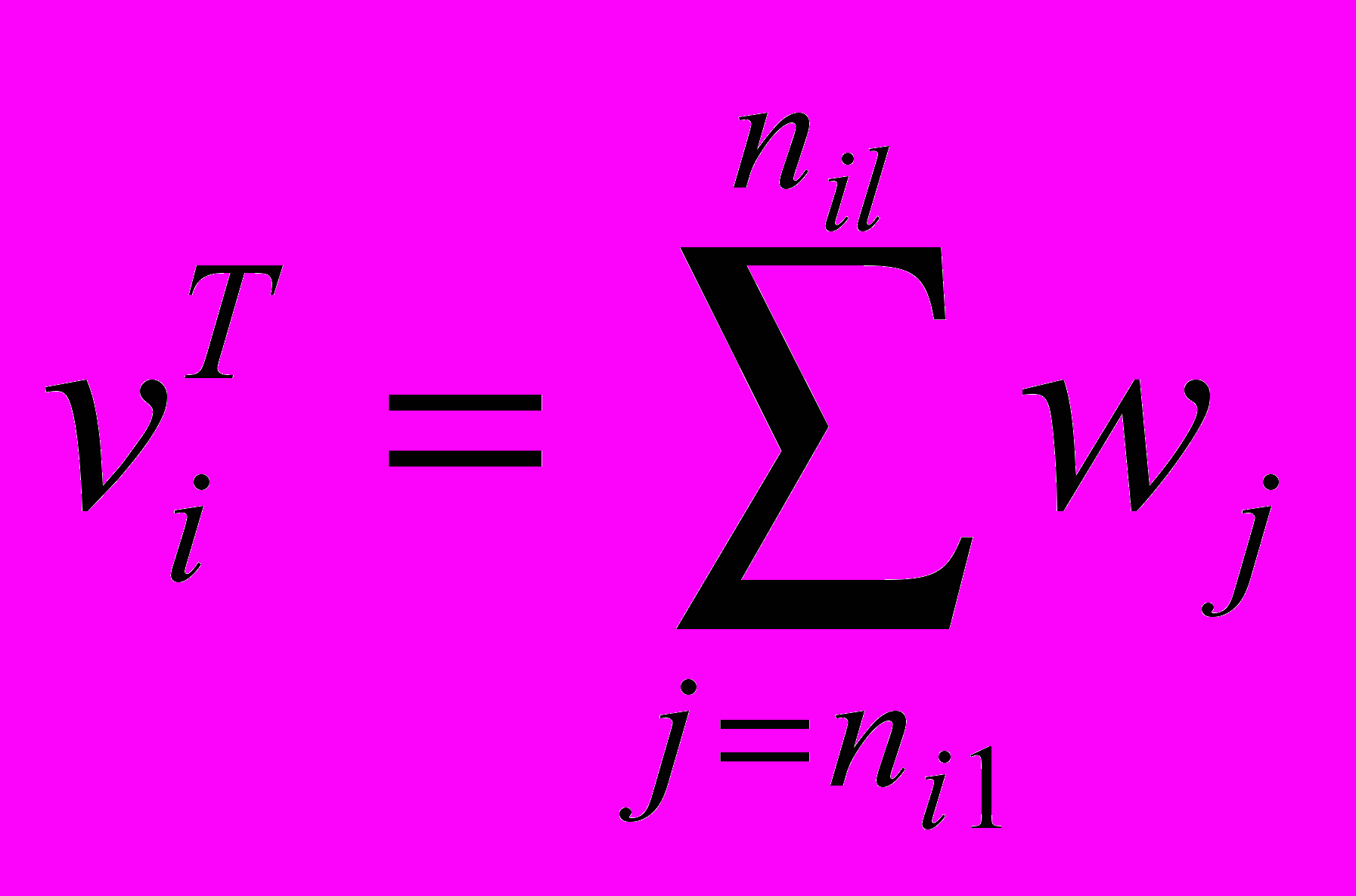 (1)
(1) 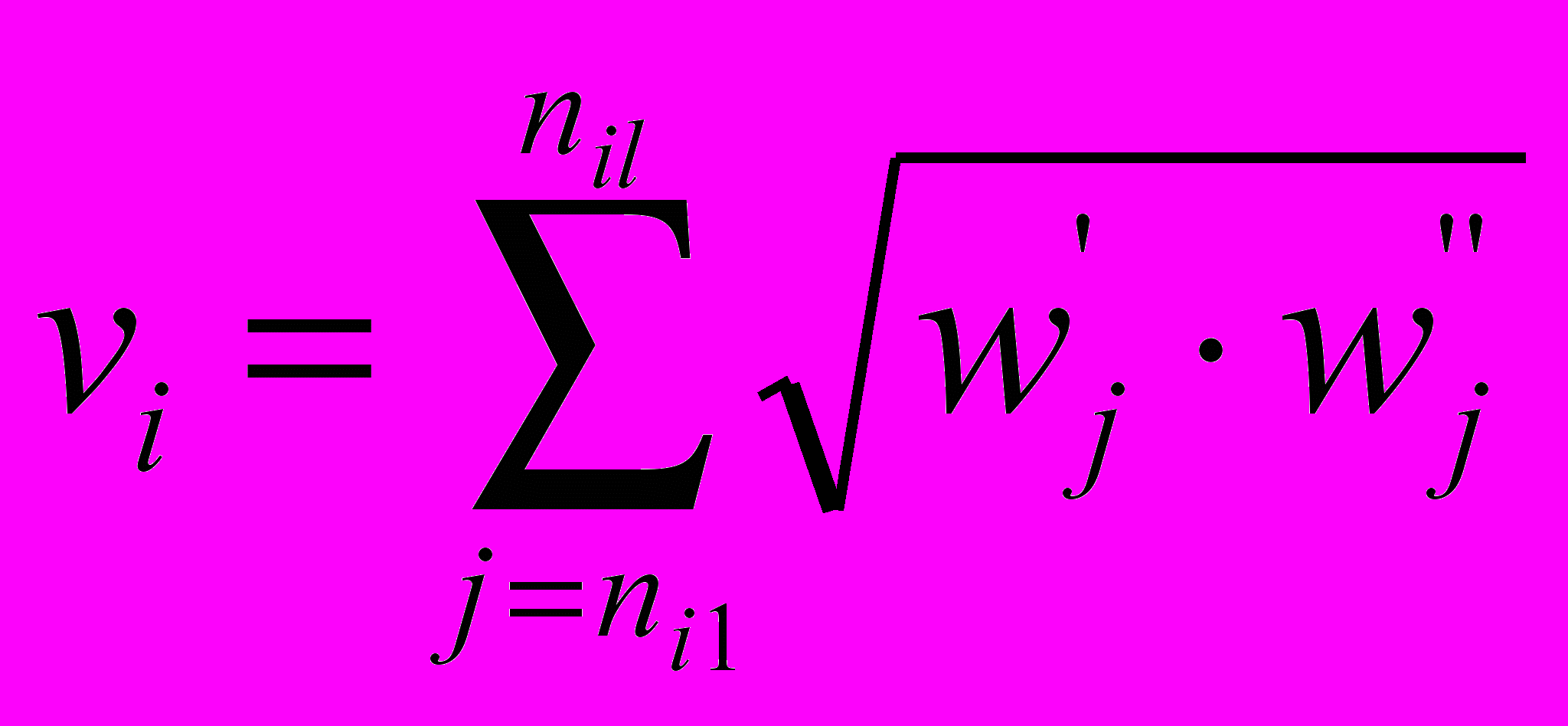 (2)
(2)Сформулируем задачу построения ОБДТ следующим образом.
Пусть заданы булева матрица U размерности
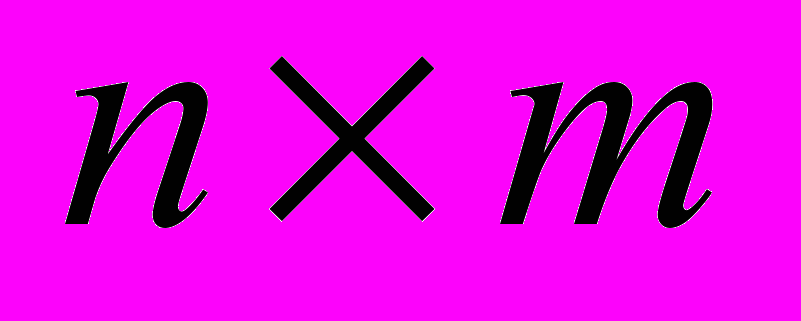 , где n число строк, m число столбцов; коэффициенты
, где n число строк, m число столбцов; коэффициенты 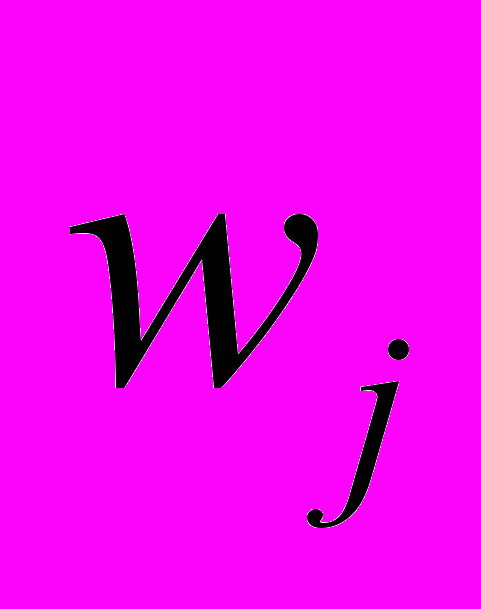 ,
, 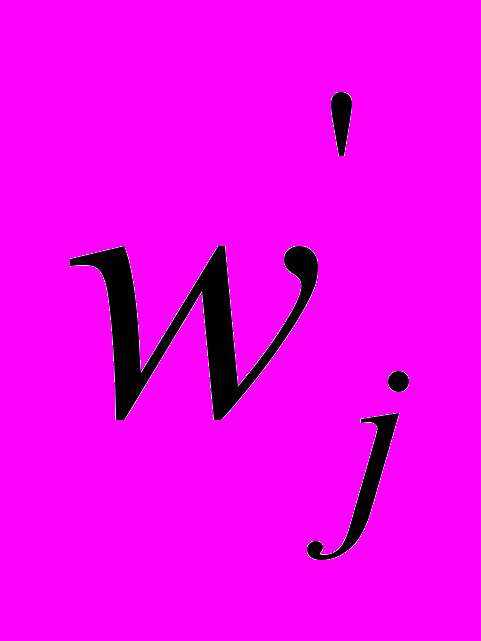 и
и 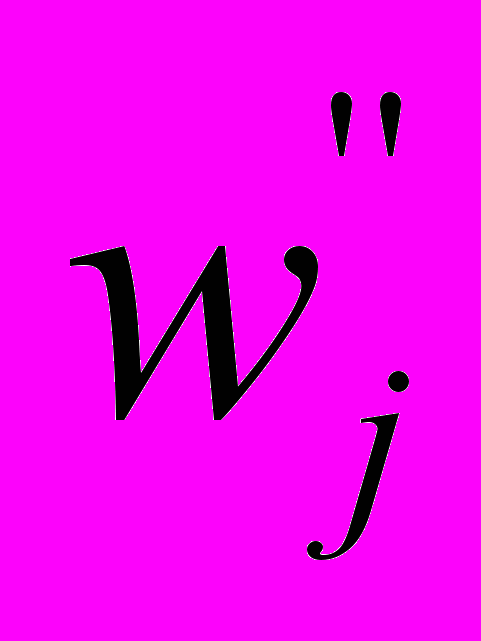 (j=1,…m); максимально допустимое число строк матрицы тестов T (
(j=1,…m); максимально допустимое число строк матрицы тестов T (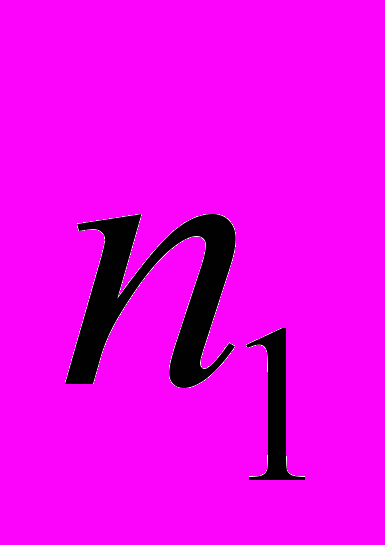 ); число искомых ОБДТ (
); число искомых ОБДТ (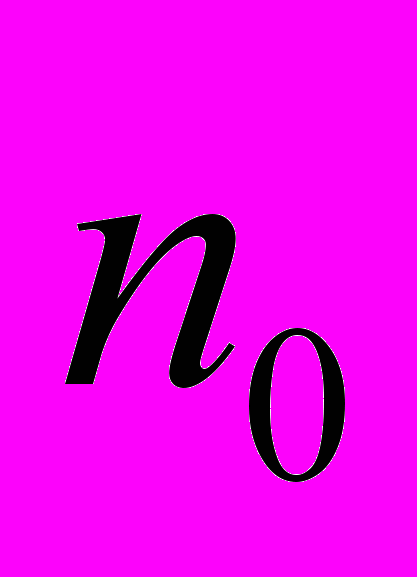 ). При этом
). При этом 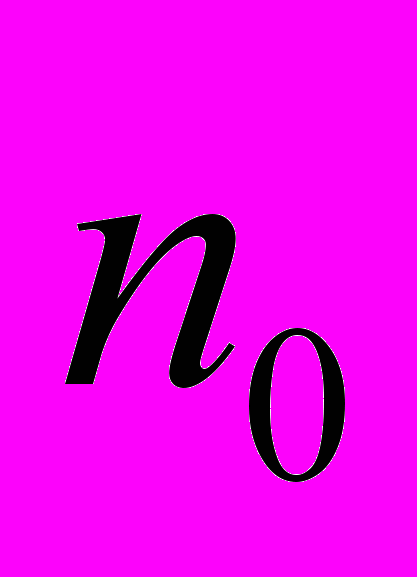 <<
<<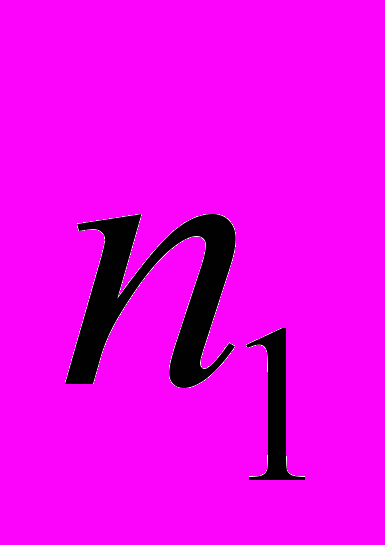 .
.Требуется найти
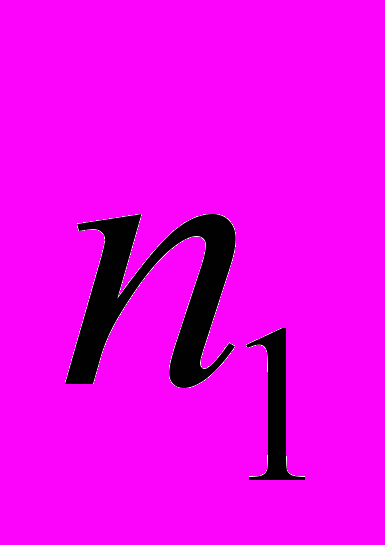 ОСП из всех КСП матрицы U с наибольшими
ОСП из всех КСП матрицы U с наибольшими 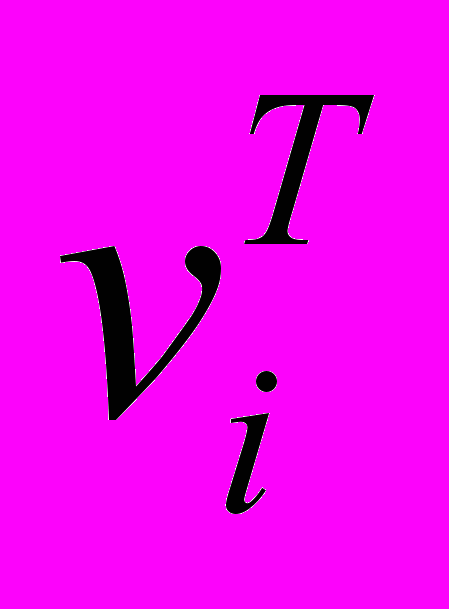 , а среди них
, а среди них 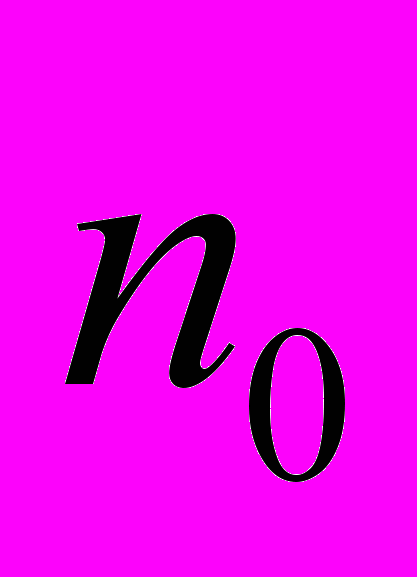 строк матрицы тестов T с минимальными
строк матрицы тестов T с минимальными 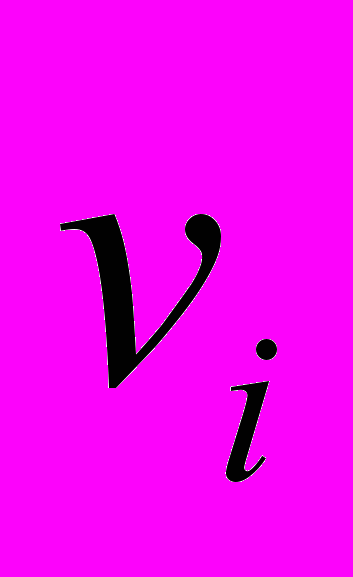 .
.Из вышеизложенного следует, что каждому ОСП соответствует ОБДТ, задающее необходимые и достаточные условия различимости любой пары объектов из разных образов, представленных матрицами Q и R.
3. Алгоритм
Дерево поиска заданного числа ОСП строится в виде иерархической системы подматриц матрицы U.
Правило выделения подматрицы по j-му столбцу (j=1,…,m) состоит в удалении j-го столбца и всех строк, содержащих единицы в j-ом столбце.
В полном дереве поиска 0-му уровню (корню) сопоставляется матрица U, вершинам 1-го уровня подматрицы, выделенные по каждому столбцу из матрицы U, вершинам i-го уровня (i=2,3,…) подматрицы, выделенные по каждому столбцу из подматриц (i-1)-го уровня, концевым вершинам (листьям) подматрицы, состоящие из одного столбца. Каждой вершине i-го уровня (i=1,2,…) присваивается значение, равное номеру столбца, по которому была выделена сопоставленная этой вершине подматрица, а каждому листу значение, равное номеру сопоставленного ему столбца. Множество значений вершин, входящих в некоторый путь от корня к листу, задает столбцовое покрытие. Если пути состоят из вершин с одинаковыми значениями, но следующих в различном порядке, то они задают одни и те же столбцовые покрытия и считаются повторяющимися. Если ни одно подмножество множества значений вершин некоторого неповторяющегося пути не совпадает ни с одним множеством значений вершин других неповторяющихся путей, то такой путь является безызбыточным и задает БСП. Безызбыточные пути минимальной длины l называются кратчайшими и задают КСП мощности l. Совокупность признаков, сопоставленных КСП, является МБДТ.
Очевидно, что построение полного дерева поиска с последующим нахождением в нем всех неповторяющихся безызбыточных путей, а среди них оптимальных, сопряжено с большими вычислительными затратами.
Однако, при построении только тех ветвей дерева поиска, которым соответствуют неповторяющиеся оптимальные пути, возникают вопросы: как строить неповторяющиеся пути, можно ли строить пути без выделения подматриц, по каким критериям выбирать столбцы для выделения подматриц, чтобы очередной построенный путь был оптимальным?
Для разрешения этих вопросов в каждой вершине, на каждом i-м (i=0,1,…) уровне дерева поиска предлагается применять следующие правила относительно соответствующих этим вершинам текущих подматриц, обозначаемых далее
 .
.Правило 1. Нулевые столбцы удаляются.
Правило 2. Из каждой группы одинаковых столбцов удаляются (с запоминанием их номеров) все, кроме одного.
Правило 3. Если есть строки, содержащие одну единицу, то соответствующие этим единицам столбцы выбираются (они обязательно входят в КСП) для построения вершины (i+1)-го уровня.
Правило 4. Если правило 3 неприменимо и есть один столбец с наибольшим числом единиц, то именно этот столбец выбирается для построения вершины (i+1)-го уровня (так как в соответствующей ей подматрице остается наименьшее число строк, оставшихся непокрытыми).
Правило 5. Если правило 3 неприменимо и есть несколько столбцов с наибольшим числом единиц, то для каждого из них нужно строить вершины (i+1)-го уровня. К каждой из них следует последовательно применить правила 1-5 и выбрать тот столбец, при удалении которого остается наименьшее число строк в одной из подматриц среди всех подматриц, сопоставленных вершинам (i+1)-го уровня.
Правило 6. Каждый столбец выбирается для выделения подматрицы при построении вершины (i+1)-го уровня только один раз.
Правило 7. Если длина очередного строящегося пути превысит длину ранее построенных путей (критерий 1 не выполняется), то построение соответствующего ему столбцового покрытия прекращается.
Правило 8. Если длина очередного построенного пути окажется меньше длины ранее построенных путей (критерий 1 выполняется), то все соответствующие им столбцовые покрытия отбрасываются.
Правило 9. Если число ранее построенных столбцовых покрытий равно заданному числу
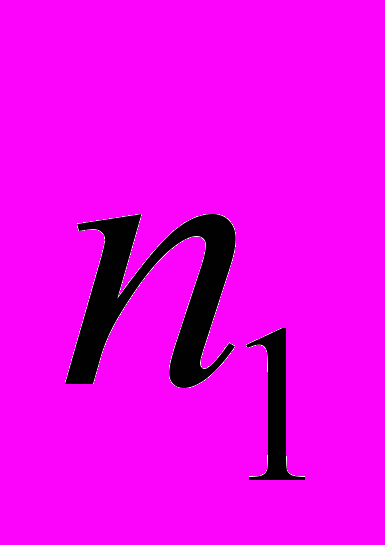 и очередное построенное покрытие удовлетворяет критерию 2, то ранее построенное покрытие с наибольшим суммарным весом заменяется очередным, иначе очередное покрытие отбрасывается.
и очередное построенное покрытие удовлетворяет критерию 2, то ранее построенное покрытие с наибольшим суммарным весом заменяется очередным, иначе очередное покрытие отбрасывается.Правило 10. Для каждого построенного покрытия вычисляются веса тестов по формуле 1 и коэффициенты свертки по формуле 2.
Правило 11. Покрытия добавляются в матрицу T в порядке убывания соответствующих им весов тестов.
Правило возврата с (i+1) на i-й уровень. Текущей становится вершина i-го уровня (по которой была выделена только что обработанная вершина (i+1)-го уровня). В соответствующей ей подматрице
 по номерам удаленных равных столбцов строятся пути без выделения подматриц, и удаляется столбец, по которому была построена вершина (i+1)-го уровня.
по номерам удаленных равных столбцов строятся пути без выделения подматриц, и удаляется столбец, по которому была построена вершина (i+1)-го уровня.В предлагаемом алгоритме эффективное применение данных правил в вершинах дерева поиска обеспечивается специальной разметкой нулевых и равных столбцов, а также столбцов, по которым выделяются подматрицы.
Замечание 1. При применении правила возврата в очередной выделенной подматрице могут появиться нулевые строки, не покрываемые ни одним столбцом. Тогда ни один путь, проходящий через сопоставленную ей вершину, не задает столбцовое покрытие, и все соответствующие этим путям ветви дерева поиска подлежат отсечению.
Замечание 2. При рекурсивном применении правила 5 порождается ветвящийся процесс, реализация которого при глубине рекурсии больше двух требует параллельных вычислений. В настоящий момент алгоритм программно реализован с использованием упрощенного правила 5, в котором глубина рекурсии не превышает два. Если при этом есть столбцы, для которых его снова нужно применять, то выбирается левый из них.
Замечание 3. Поскольку не доказано, что при применении правил 1-5 первый построенный путь будет минимальным, применяется Правило 8.
Алгоритм поиска
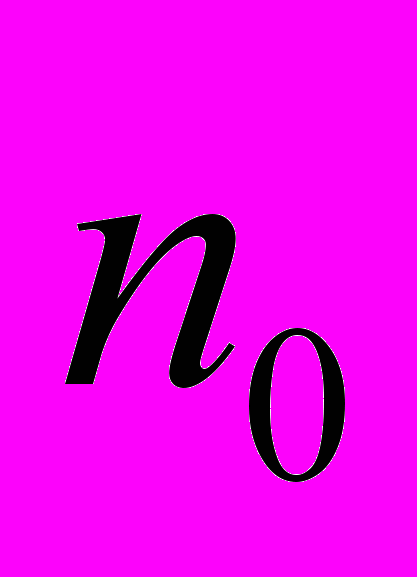 (из
(из 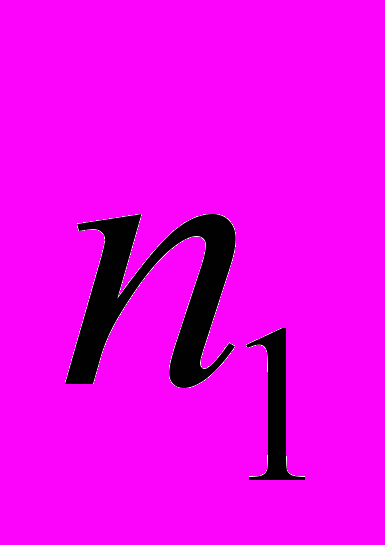 ) ОСП состоит из следующих пунктов:
) ОСП состоит из следующих пунктов: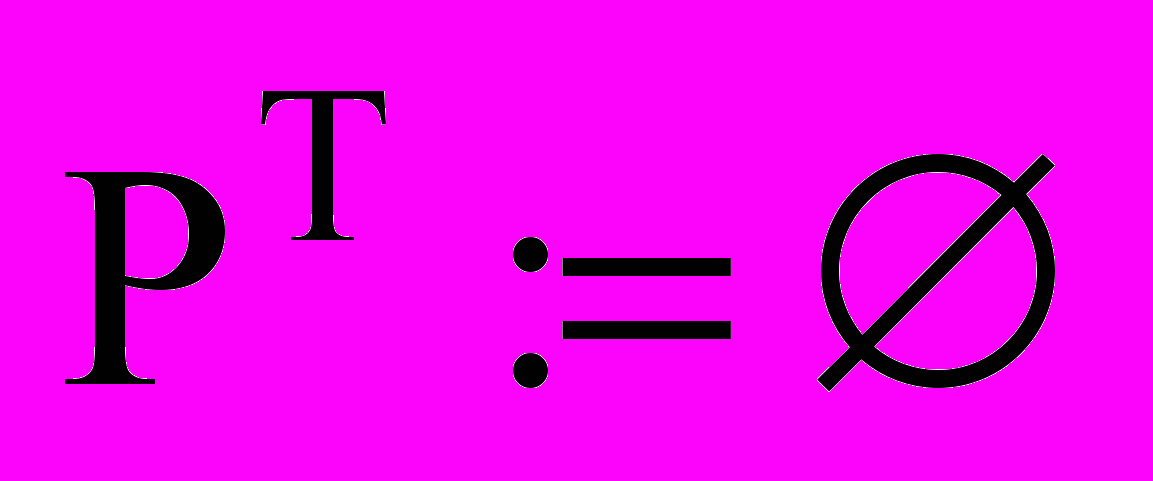 (
( строящееся столбцовое покрытие), i
строящееся столбцовое покрытие), i 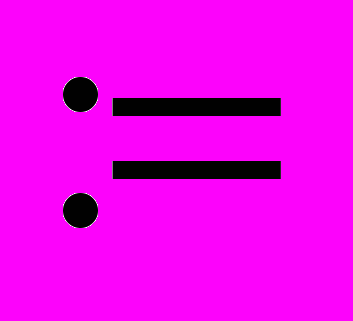 0,
0, 
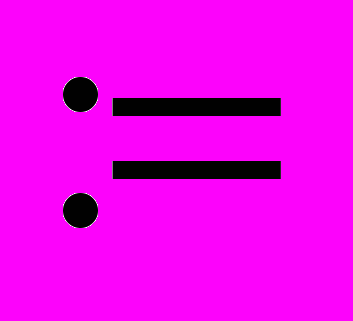 U.
U.
- Если в
 есть нулевые строки (замечание 1), то выполняется переход к п. 14.
есть нулевые строки (замечание 1), то выполняется переход к п. 14.
- Если к неотмеченным столбцам
 применимо правило 1, то соответствующие столбцы отмечаются символом "–".
применимо правило 1, то соответствующие столбцы отмечаются символом "–".
- Если к неотмеченным столбцам
 применимо правило 2, то в каждой группе равных столбцов левый из них отмечается символом "+", а остальные символом "–" и их номера запоминаются.
применимо правило 2, то в каждой группе равных столбцов левый из них отмечается символом "+", а остальные символом "–" и их номера запоминаются.
- Если к неотмеченным столбцам
 применимо правило 3, то соответствующие столбцы отмечаются символом "*", их номера включаются в
применимо правило 3, то соответствующие столбцы отмечаются символом "*", их номера включаются в  и выполняется переход к п. 8.
и выполняется переход к п. 8.
- Если к неотмеченным столбцам
 применимо правило 4, то соответствующий столбец отмечается символом "*", его номер включается в
применимо правило 4, то соответствующий столбец отмечается символом "*", его номер включается в  и выполняется переход к п. 8.
и выполняется переход к п. 8.
- К неотмеченным столбцам
 применяется правило 5 (либо упрощенное правило 5 в силу замечания 2), соответствующий столбец отмечается символом "*" и его номер включается в
применяется правило 5 (либо упрощенное правило 5 в силу замечания 2), соответствующий столбец отмечается символом "*" и его номер включается в  .
.
- Если применимо правило 7, то выполняется переход к п. 12.
- Если в
 есть неотмеченные столбцы, то
есть неотмеченные столбцы, то  запоминается и выполняется переход к п. 13.
запоминается и выполняется переход к п. 13.
- Если применимо правило 8, то оно применяется.
 запоминается в матрице T (с учетом правил 9-11). Если i<1, то для каждого столбца, отмеченного символом "+", по номерам равных ему столбцов строятся и запоминаются в матрице T равномощные столбцовые покрытия (с учетом правил 9-11) и выполняется переход к п. 15.
запоминается в матрице T (с учетом правил 9-11). Если i<1, то для каждого столбца, отмеченного символом "+", по номерам равных ему столбцов строятся и запоминаются в матрице T равномощные столбцовые покрытия (с учетом правил 9-11) и выполняется переход к п. 15.
- Применяется правило возврата (при этом для каждого столбца, отмеченного символом "+", по номерам равных ему столбцов строятся и запоминаются матрице T равномощные столбцовые покрытия (с учетом правил 9-11), а столбцы, отмеченные символом "*", и соответствующие им столбцы, отмеченные символом "+", переотмечаются (в соответствии с правилом 6) символом "–") и
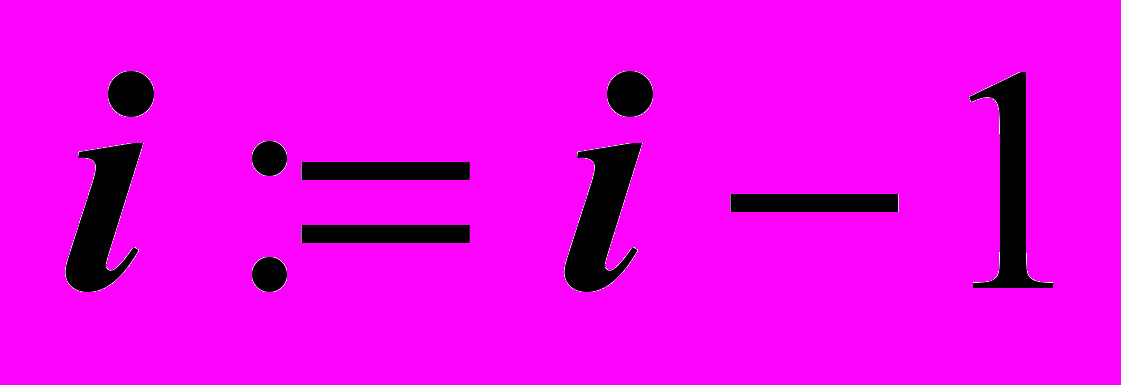 . Восстанавливается
. Восстанавливается  , соответствующее
, соответствующее  . Если в
. Если в  есть неотмеченные столбцы, то выполняется переход к п. 2, иначе, выполняется переход к п. 12.
есть неотмеченные столбцы, то выполняется переход к п. 2, иначе, выполняется переход к п. 12.
- Применяется правило выделения подматрицы по всем столбцам, отмеченным символом "*" с одновременным удалением столбцов, отмеченных символами "–" и "+",
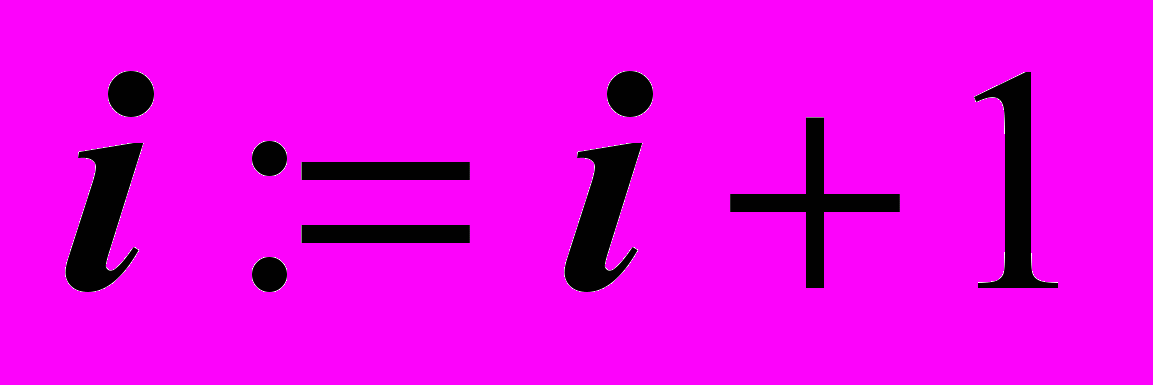 и выполняется переход к п. 2.
и выполняется переход к п. 2.
- Если i>0, то выполняется переход к п. 12.
- Из матрицы T удаляется
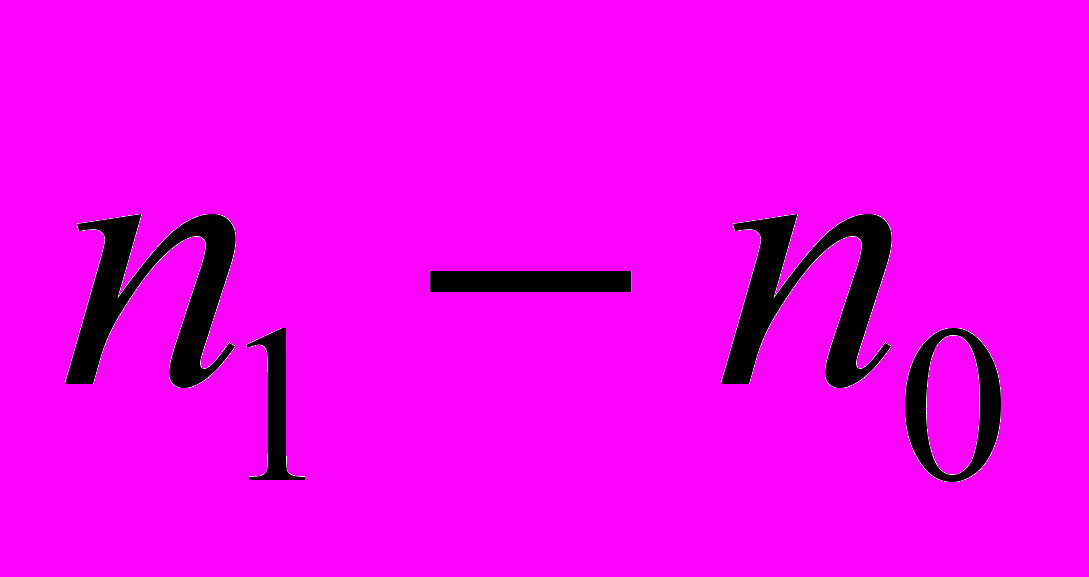 строк с наибольшими значениями коэффициентов свертки
строк с наибольшими значениями коэффициентов свертки 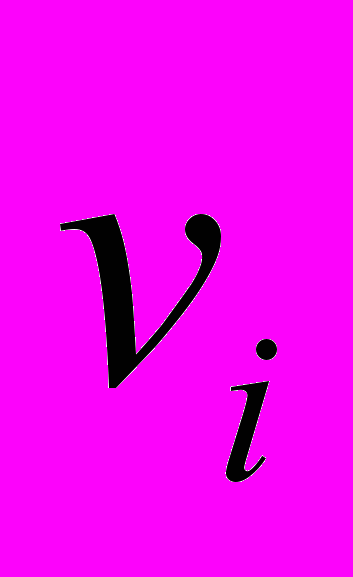 .
.
- Конец алгоритма.
Рамки публикации не позволяют привести иллюстративный пример.
Заключение
Приведенный алгоритм построения ОБДТ программно реализован, апробирован и включен в состав интеллектуального инструментального средства (ИИС) ИМСЛОГ [Yankovskaya et al., 2003] в виде динамически подключаемых модулей.
Применение ОБДТ повышает качество принимаемых на их основе решений в прикладных ИС различного назначения, создаваемых с использованием ИИС ИМСЛОГ, в частности, в информационной системе диагностики и коррекции состояний коммуникативного стресса (ДИАКОР-КС) [Янковская и др., 2006].
Дальнейшие исследования связаны с учетом большего числа критериев и проведением сравнительного анализа с ранее разработанными алгоритмами [Колесникова и др., 2005].
Список литературы
[Гедике и др., 2005] Гедике А.И., Янковская А.Е. Построение всех безызбыточных безусловных диагностических тестов в интеллектуальном инструментальном средстве ИМСЛОГ/ Интеллектуальные системы (AIS'05), Интеллектуальные САПР (CAD-2005). Тр. Междунар. научно-техн. конф. Т. 1. Москва: Физматлит. 2005.
[Ермаков А.Е. и др., 2002] Ермаков А.Е., Найденова К.А. Пошаговый алгоритм построения хороших классификационных диагностических тестов как модель правдоподобных рассуждений/ VIII нац. конф. с междунар. уч. по искусственному интеллекту (КИИ-2002). Сб. науч. трудов. Т. 1. Москва: Физматлит. 2002.
[Колесникова и др., 2005] Колесникова С.И., Можейко В.И., Цой Ю.Р., Янковская А.Е. Алгоритмы выбора оптимального множества безызбыточных диагностических тестов в интеллектуальных системах поддержки принятия решений/ Системный анализ и информационные технологии (САИТ-2005). Тр. Первой междунар. конф. Т.1. М.: КомКнига, 2005.
[Новоселов, 1966] Новоселов В.Г. Нахождение -минимальных покрытий// Тр. Сибирского физико-технического института. 1966. Вып. 48.
[Янковская, 2000] Янковская А.Е. Логические тесты и средства когнитивной графики в интеллектуальной системе/ Новые информационный технологии в исследовании дискретных структур. Докл. 3-ей Всеросс. конф. с междунар. уч. Томск: Изд-во СО РАН. 2000.
[Янковская, 2002] Янковская А.Е. Построение логических тестов с заданными свойствами и логико-комбинаторное распознавание на них/ Интеллектуализация обработки информации (ИОИ-2002). Тез. докл. междунар. науч. конф. Симферополь, 2002.
[Янковская и др., 2006] Янковская А.Е., Гедике А.И., Аметов Р.В., Муратова Е.А. Математические основы и программная реализация интеллектуальной информационной системы ДИАКОР-КС/ Актуальные проблемы математики, механики, информатики. Матер. междунар. науч.-метод. конф. Пермь. 2006.
[Yankovskaya et al., 1999] Yankovskaya A., Gedike A. Finding of All Shortest Column Coverings of Large Dimension Boolean Matrices/ Proceedings of the First International Workshop on Multi-Architecture Low Power Design (MALOPD). Moscow. 1999.
[Yankovskaya et al., 2003] Yankovskaya A.E., Gedike A.I., Ametov R.V., Bleikher A.M. IMSLOG-2002 Software Tool for Supporting Information Technologies of Test Pattern Recognition// Pattern Recognition and Image Analysis. 2003. Vol. 13, No. 4.
[Yankovskaya et al., 2004] Yankovskaya A.E., Mozheiko V.I. Optimization of a set of tests selection satisfying the criteria prescribed/ 7th International Conference on Pattern Recognition and Image Analysis: New Information Technologies (PRIA-7-2004). Conference Proceedings. Vol. I. St. Petersburg: SPbETU, 2004.
* Работа выполнена при финансовой поддержке РФФИ (проект № 07-01-00452) и РГНФ (проект № 06-06-12603)
1 634003, Томск, Соляная пл. 2, ТГАСУ, , gai@tsuab.ru
2 634050, Томск Соляная пл. 2, ТГАСУ yank@tsuab.ru
