Лабораторный компьютерный практикум

Вид материала

Практикум

Содержание Задание. Энтропия. Б). Задайте число частиц равное 4 В). Задайте число частиц равное 8 Г). Задайте число частиц равное 16 Лабораторная работа № 10. Форма отчета.

Подобный материал:

• А. М. Горького Кафедра алгебры и дискретной математики Щербакова В. А. Лабораторный, 418.72kb.
• Липатов Петр Иванович, учитель биологии; Липатова Людмила Николаевна, учитель биологии, 620.01kb.
• Практикум по химии Анкудимова И. А., Гладышева, 2202.13kb.
• Учебно-методический комплекс дисциплины «лабораторный практикум по бухгалтерскому учету, 3221.38kb.
• Практикум, методическое руководство, компьютерный практикум на cd rom по информатике, 353.2kb.
• Жигалов М. С., Мойсеяк М. Б. Лабораторный практикум по технохимическому контролю чайного, 572.07kb.
• Своей целью лабораторный комплекс ставит глубокое знакомство студентов с системой межпроцессных, 17.55kb.
• Московский инженерно-физический институт, 1479.21kb.
• Утверждаю: Декан Физико-технического факультета, 146.47kb.
• Лабораторные работы, 281.72kb.

Задание. Энтропия.

Ознакомьтесь с теоретической частью работы.


Откройте рабочее окно.

А). Нажмите кнопку Пуск и запустите движение частиц. Из-за перегородки частицы будет только в правой части объема, поэтому на графике это будет соответствовать максимальному отклонению от равномерного распределения частиц в двух половинах объема или упорядоченному состоянию в целом. Удалите перегородку и через некоторое время нажмите клавишу Стоп, а затем Пуск, чтобы очистить третью колонку таблицы. Пронаблюдайте за графиком отклонения распределения частиц от равномерного распределения. Дождитесь, когда график заполнит все окно и движение частиц остановится. Из третьей колонки таблицы выпишите время нахождения системы в состояниях с распределением частиц 0:2; 1:1 и 2:0 (первая цифра число частиц слева, вторая - справа) и общее время наблюдения T. Снова нажмите кнопку Пуск и повторите эту процедуру 2 - 3 раза. По проведенным измерениям, найдите среднее время t_сред. нахождения системы в каждом из трех состояний.

Различные состояния системы могут осуществляться с той или иной вероятностью. Вероятность i-го состояния p_i определяется как предел отношения времени t_i , в течение которого система находится в данном состоянии, к полному времени T наблюдения над системой при неограниченном увеличении T.



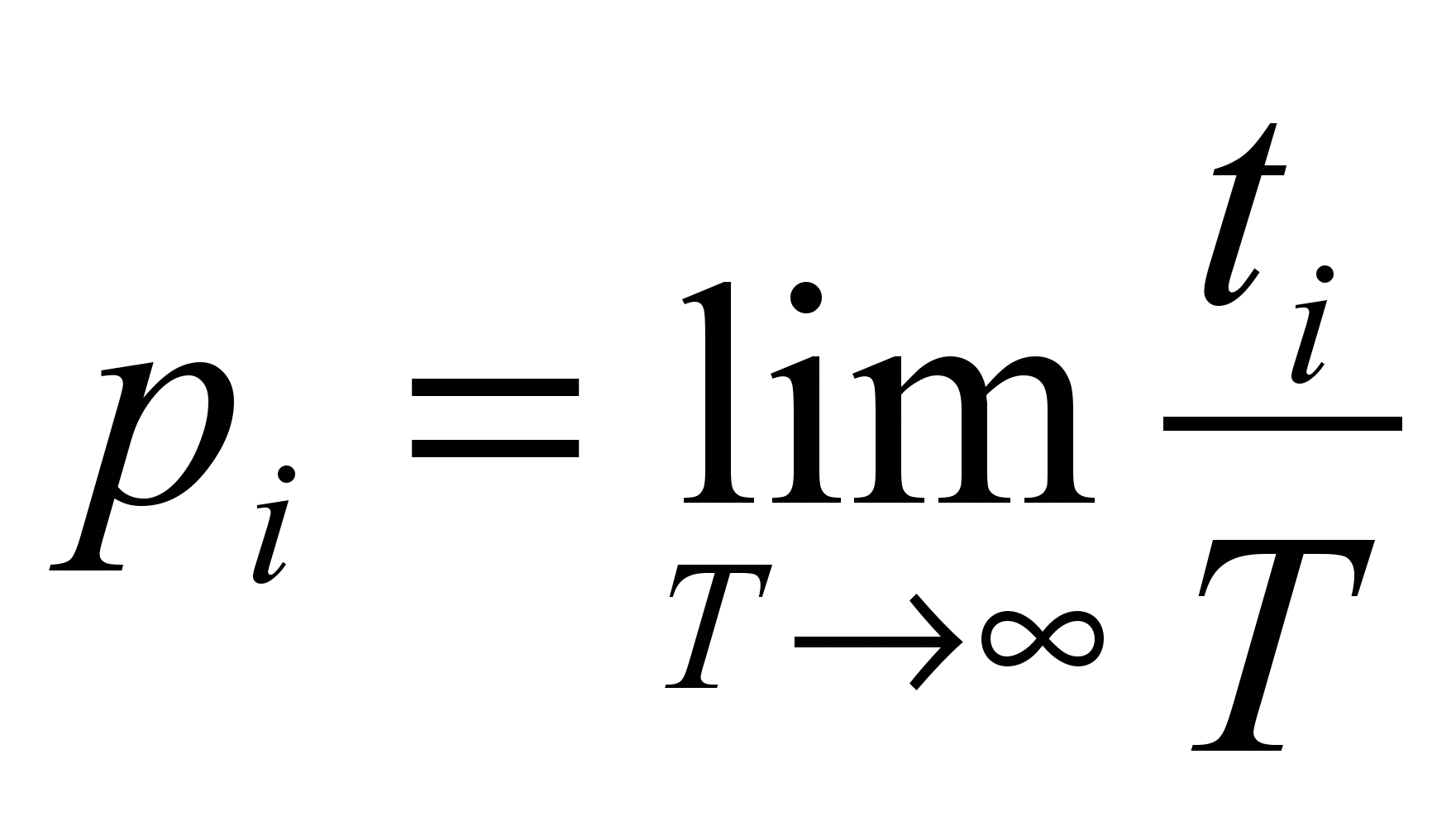
При ограниченном времени наблюдения T, отношение t_i/T называют относительной частотой (h_i), которую используют для оценки соответствующей вероятности.

Разделив t_сред. на общее время наблюдения, рассчитайте относительную частоту h_i нахождения системы в каждом из трех состояний и заполните таблицу:

Состояние	0:2	1:1	2:0
tсред.
hi

Оцените вероятность нахождения системы в этих состояниях и сравните полученный результат с данными приведенными в теоретической части. Какое состояние из трех состояний наименее упорядоченное и наиболее вероятное?


Б). Задайте число частиц равное 4. Повторите то же самое, что и в пункте А, но уже для 4-х частиц. После удаления перегородки подождите, пока частицы не распределятся во всем объеме, и не забудьте нажать клавишу Стоп, а затем Пуск, чтобы очистить третью колонку таблицы. Заполните таблицу:

Состояние	0:4	1:3	2:2	3:1	4:0
tсред.
hi

Как изменилась, по сравнению с предыдущим случаем, вероятность того, что все частицы будут находиться в одной половине объема? Используя формулы в теоретической части, найдите эту вероятность и сравните с приведенным в таблице значением. Используя относительную частоту состояния 2:2 из заполненной вами таблицы, оцените число способов (или термодинамическую вероятность W), которым можно реализовать это состояние.


В). Задайте число частиц равное 8. Повторите то же самое, что и в предыдущих заданиях, но уже для 8-ми частиц. После удаления перегородки подождите, пока частицы не распределятся во всем объеме, и не забудьте нажать клавишу Стоп, а затем Пуск, чтобы очистить третью колонку таблицы. Заполните таблицу:

Состояние	0:8	1:7	2:6	3:5	4:4	5:3	6:2	7:1	8:0
tсред.
hi

Используя относительную частоту состояния 4:4 из заполненной вами таблицы, оцените число способов (или термодинамическую вероятность W), которым можно реализовать это состояние.


Г). Задайте число частиц равное 16. Повторите то же самое, что и в предыдущих заданиях, но уже для 16-ти частиц. После удаления перегородки подождите, пока частицы не распределятся во всем объеме, и не забудьте нажать клавишу Стоп, а затем Пуск, чтобы очистить третью колонку таблицы. Заполните таблицу:

Состояние

0:16

1:15

2:14

3:13

4:12

5:11

6:10

7:9

8:8

9:7

10:6

11:5

12:4

13:3

14:2

15:1

16:0

tсред.

hi

Используя относительную частоту состояния 8:8 из заполненной вами таблицы, оцените число способов (или термодинамическую вероятность W), которым можно реализовать это состояние. На основании табличных данных постройте график, на котором по горизонтальной оси отметьте через равные промежутки все возможные состояния системы от 0:16 до 16:0, а по вертикальной, соответствующую этим состояниям вероятность.


Д). Сравните между собой все рассмотренные случаи. Как меняется вероятность нахождения данной системы в упорядоченном состоянии с увеличением числа частиц? Почему, с точки зрения вероятностного подхода, когда мы убираем перегородку, газ, содержащий большое количество частиц занимает весь объем и не может самопроизвольно собраться в одной половине? Когда в этом случае система в целом находится в более упорядоченном состоянии до удаления перегородки или после? Как при этом меняется энтропия системы? Возможен ли самопроизвольный переход изучаемой системы на некоторое время в упорядоченное состояние в случае малого количества частиц (например, 2-х)? Можно ли в этом случае говорить о законе возрастания энтропии или он проявляется только для систем с большим количеством частиц?


Е). В рассматриваемых случаях объем газа после удаления перегородки увеличивался в два раза. Термодинамическая вероятность W~V^N, где V - объем, а N -число частиц. Найдите изменение энтропии для случая 16 частиц при расширении газа. В процессах смешения двух газов, расширении газа после удаления перегородки или в процессе теплопередачи, вначале в системах можно выделить отличающиеся части: один газ - другой газ; есть газ - нет газа; более горячая - менее горячая. В конце этих процессов выделить отличающиеся части нельзя. На этих примерах поясните, почему энтропия является мерой беспорядка и хаоса? Мы нагреваем лед, он тает, охлаждаем воду - она замерзает. Отрытые это системы или нет? Как меняется степень упорядоченности и энтропия в первом и во втором случае? Сделайте вывод о том, как может меняться энтропия в открытых системах? Человек сжигая бензин в двигателе автомобиля, преобразует энергию хаотического теплового движения в упорядоченное механическое движение автомобиля. С другой стороны органический углерод, содержащийся в бензине, окисляется до углекислого газа и разлетается в атмосфере, кроме этого, и большая часть тепловой энергии передается окружающей среде. Увеличивается при этом энтропия или уменьшается в целом, включая окружающую среду. Как хозяйственная деятельность человека влияет на биосферу?


Лабораторная работа № 10. Форма отчета.