Решение экономических задач компьютерными средствами > Информатика в экономике: Учебное пособие
| Вид материала | Решение |
- Литература Информатика в экономике: Учебное пособие, 756kb.
- Дружининская Ирина Михайловна Хованская Ирина Аскольдовна Матвеев Виктор Федорович, 426.6kb.
- «Машины и технология обработки металлов давлением», 10.97kb.
- Решение математических и экономических задач средствами matlab, 11.27kb.
- Решение инженерных задач в системе matlab практическое пособие по курсу "Информатика", 407.62kb.
- С. А. Бартенев история экономических учений в вопросах и ответах Предисловие Предлагаемое, 2413.78kb.
- С. А. Бартенев история экономических учений в вопросах и ответах Предисловие Предлагаемое, 2413.67kb.
- Учебное пособие для студентов специальностей «Прикладная информатика в экономике» и«Менеджмент, 1982.74kb.
- I. Решение логических задач средствами алгебры логики 22 >II. Решение логических задач, 486.64kb.
- Общий курс физики т-1 Механика: учебное пособие М.: Физматлит, 2002. Сивухин Д. В.,, 679.32kb.
Тема 5. Решение экономических задач компьютерными средствами
1. Информатика в экономике: Учебное пособие/Под ред. Б.Е. Одинцова, А.Н. Романова. – М.: Вузовский учебник, 2008.
2. Информатика: Базовый курс: Учебное пособие/Под ред. С.В. Симоновича. – СПб.: Питер, 2009.
3. Информатика. Общий курс: Учебник/Соавт.:А.Н. Гуда, М.А. Бутакова, Н.М. Нечитайло, А.В. Чернов; Под общ. ред. В.И. Колесникова. – М.: Дашков и К, 2009.
4. Информатика для экономистов: Учебник/Под ред. Матюшка В.М. - М.: Инфра-М, 2006.
5. Экономическая информатика: Введение в экономический анализ информационных систем.- М.: ИНФРА-М, 2005.
- Понятие и классификация моделей объектов, процессов и систем
Главная же причина создания моделей состоит в бесконечной сложности окружающего человека мира, в котором изучаемые им процессы и объекты имеют огромное количество свойств и взаимосвязей. Чтобы понять, как действует реальный объект, приходится вместо него рассматривать его упрощенное представление – модель.
Модель (лат. modulus) – это упрощенный объект-заменитель объекта-оригинала, в котором отражаются его существенные особенности (свойства). Чем меньше подробностей оригинала отражено в модели, тем она проще.
Существуют
Образные (материальные, предметные) – это физические модели. Они воспроизводят геометрические и физические свойства оригинала и всегда имеют материальное воплощение, отражая внешние свойства и частично внутренние устройства объекта-оригинала. Примерами здесь могут служить детские игрушки, скелет человека, макет солнечной системы и т.д.
Класс образных (материальных) моделей можно разделить на подклассы: опытные, учебные и игровые. Опытные модели – это уменьшенные искусственно созданные копии каких-либо реальных процессов (аэродинамическая труба, воссоздающая движение воздуха, синхрофазотрон, воссоздающий реальное движение частиц), учебные - наглядные пособия, тренажеры, обучающие программы, игровые модели - экономические, спортивные, деловые, бытовые.
Некоторые классы моделей
Знаковые (абстрактные) модели, в отличие от образных (материальных) не имеют внешнего (реального) сходства с оригиналом. Их основу составляет теоретический метод познания окружающей среды и по признаку формы воплощения они бывают: вербальные (мысленные), математические и информационные.
Вербальные (мысленные) модели формируются в воображении человека в виде некоторого образа, который затем выражается (вербализуется) в словесной форме.
Логико-лингвистические модели – это особая форма вербализации связей между объектами. Цель создания такого рода моделей состоит в описании объектов и связей таким образом, чтобы его преобразование и обработка могла осуществляться логическими средствами. Примером такой модели может служить запись
В настоящее время модели подобного рода развились в семантические сети, нечеткие выводы, в которых особое место занимает понятие «лингвистическая переменная».
С усложнением сфер моделирования, и, как правило, невозможностью натурного воспроизведения требуемых свойств оригинала, стало развиваться математическое моделирование.
Под математическим моделированием подразумевается процесс установления соответствия реальному объекту математического объекта, отражающего цели моделирования.
Математические модели воспроизводят реальные объекты и их связи с помощью математических символов (алгебраических, дифференциальных и конечно-разностных уравнений, предикатов и т.д.). Такого рода модели исследуются либо аналитически, (стремление получить явные зависимости для искомых величин) либо численно (при отсутствии общего решения отыскивается частное).
Математические модели, в соответствии с природой воспроизводимых процессов, можно разделить на детерминированные, вероятностные (стохастические) и имитационные (компьютерные).
Некоторые знания об окружающем мире условно можно характеризовать как определенные, отражающие вполне устоявшиеся взаимосвязи объектов, что подтверждается практикой. Модели, которые воспроизводят эти связи, обычно называются детерминированными, так как отражают причинно-следственные отношения между объектами или процессами. Задавая в этих моделях причину (исходные данные, значение переменных, значение параметров и т.д.) можно определить следствие (скорость, рентабельность, индекс валют и т.д.). Детерминированные модели можно разделить на дискретные и непрерывные.
Дискретные детерминированные модели воспроизводят процессы в отдельные промежутки времени. Например, формула расчета рентабельности, предназначенная для определения показателя на конец месяца, является дискретной детерминированной моделью, так как все переменные рассматриваются в качестве фиксированных величин на некотором промежутке времени.
Непрерывные детерминированные модели отражают процессы в любой момент времени. Для этого довольно используют дифференциальные уравнения. С их помощью выражается движение маятника, скорость изменения прибыли, зависящей от объемов продаж и т.д.
Стохастические модели воспроизводят вероятностные процессы и события. Если имеет место процесс, дальнейшая эволюция которого определяется только состоянием в предшествующий момент, а переход из состояния в состояние происходит в дискретные моменты времени, то воспроизводят с помощью цепей Маркова.
Стохастические модели оперируют вероятностями, которые не всегда можно получить, поэтому вместо них часто используют статистические модели. В основе такого моделирования лежит понятие парной регрессии – уравнения связи, которое может иметь разное количество переменны.
Известны линейные и нелинейные регрессии:
линейная:
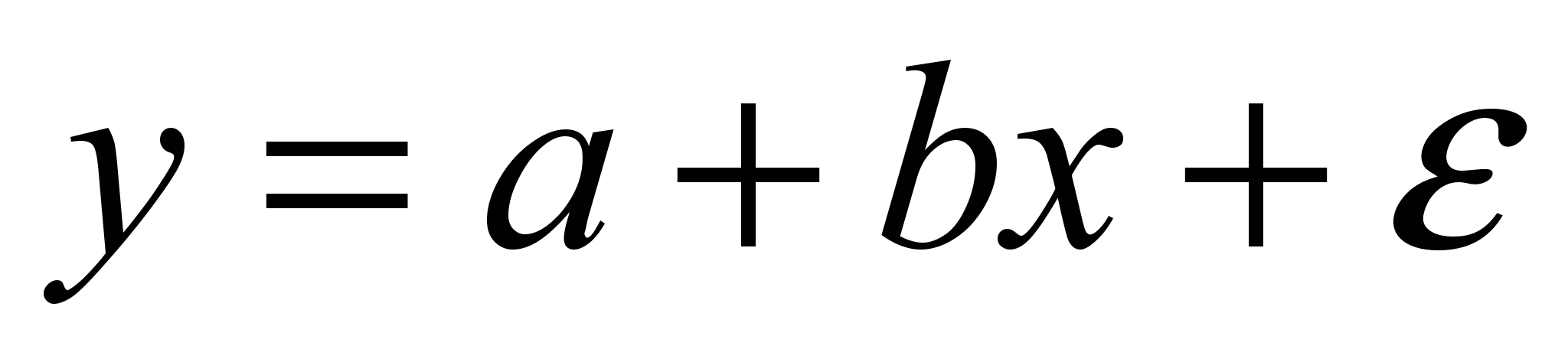; нелинейная:
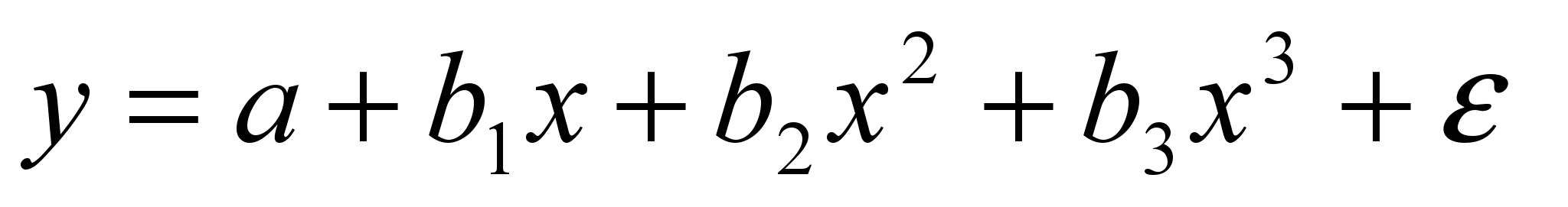(полином);
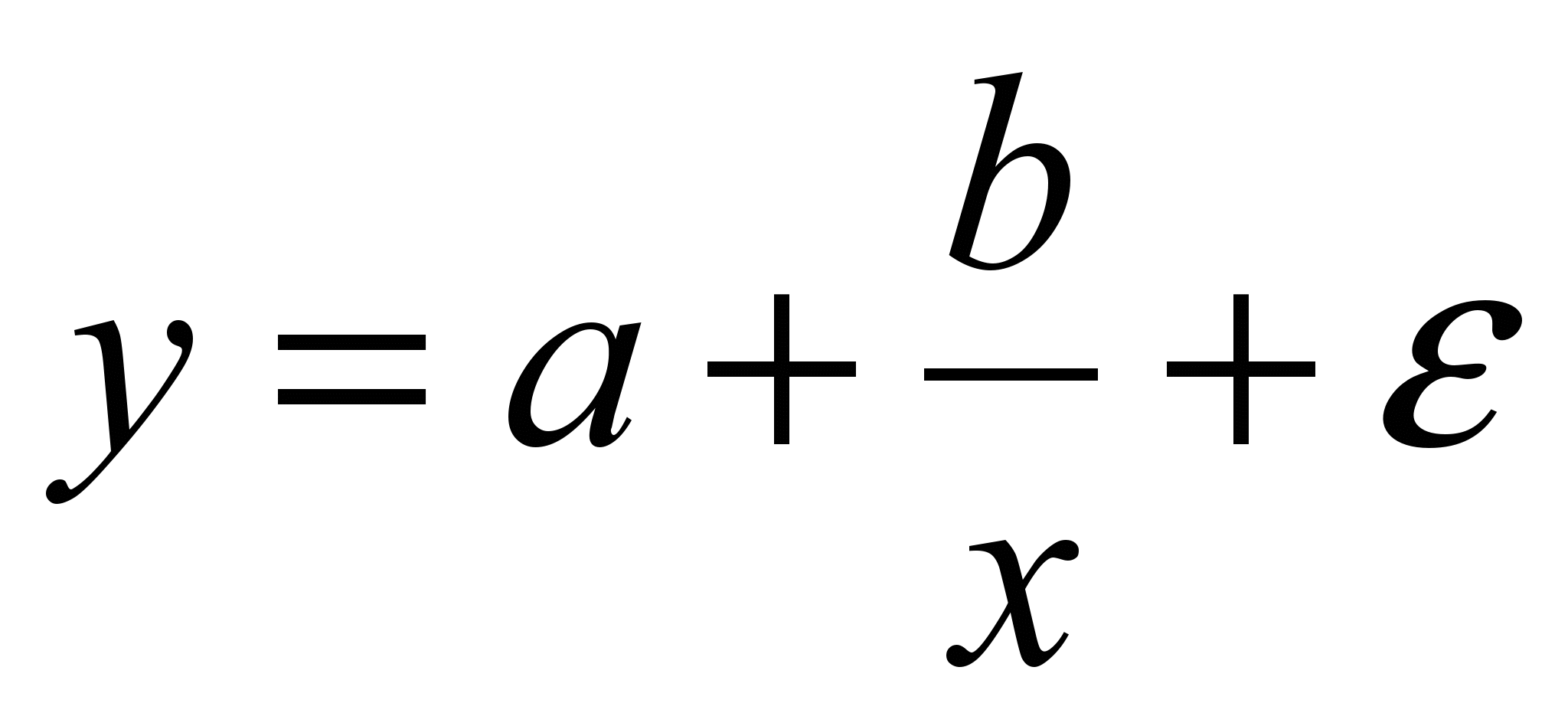(гипербола).Имитационные модели. Моделирование сложных объектов и процессов сталкивается с трудностями как на этапе составления соответствующих детерминированных или стохастических уравнений, так и на этапе их решения. Основное препятствие состоит в формализации и математическом описании общесистемных ситуаций на базе умозрительного анализа взаимозависимостей составляющих их событий.
Такого рода трудности стимулировали разработку иного пути воспроизведения связей сложных объектов: это конструирование общесистемных ситуаций на компьютере, то есть имитирование моделируемого процесса.
Для этого необходимо:
а) необходимо задать границы пространства состояний объекта,
б) описание перемещения изучаемой точки,
в) указать правила расчета распределения вероятности скачка состояния при выходе точки за границу пространства,
г) указать правила расчета распределения вероятности скачка точки при поступлении входного сигнала,
д) указать правила расчета координат выходного сигнала.
Важная особенность моделей такого рода состоит в получении информации о состоянии объекта в произвольный момент времени. Сегодня достаточно широко используются модели, имитирующие природные аномалии, техногенные катастрофы, распространение заболеваний и т.д.
Информационные модели. Наибольшие трудности в обработке информации на компьютере встречаются на начальном этапе, предназначенном для приведения неформального описания экономических процессов (бизнес-процессов) к формальному. Нужная степень формализации достигается путем постепенной последовательной смены одного описания другим. Первое описание, как правило, выполняется в виде информационной модели, видов которых существует достаточно много, а последнее - на одном из языков программирования. Поэтому особое место в информатике занимают информационные модели, которые рассмотрим более подробно.
Информационные модели отражают информационные потоки между различными объектами. Они состоят из:
а) идентификаторов объектов;
б) идентификаторов потоков данных;
в) объемных, временных, частотных и других характеристик, как самих объектов, так и входящих и исходящих потоков данных;
г) последовательности процедур обработки потоков данных.
Цель информационного моделирования состоит в отражении в наглядной форме процессы сбора внешней и внутренней информации, ее регистрации на машинных носителях, передачи, обработки с указанием последовательности расчетов и использования.
Особенность такого рода моделей заключается в их графическом представлении, но при этом имеется возможность матричного или аналитического способа их отображения.
Наиболее распространенными графическими формами информационных моделей являются: диаграммы потоков данных (DFD), диаграммы IDEF1, сети Петри, сети управления и планирования, модели баз данных, модели баз знаний и т.д.
В информатике особенно широко используются такие информационные модели как табличные, иерархические и сетевые. Табличные модели отображают объекты и их свойства в виде списка, а их значения размещаются в ячейках прямоугольной формы. Наименования однотипных объектов размещены в первом столбце (или строке), а значения их свойств размещаются в следующих столбцах (или строках). Иерархические модели предназначены для выражения отношений соподчинения между объектами. Объект нижнего уровня может входить в состав только одного элемента более высокого уровня. Сетевые модели необходимы для отражения систем, в которых связи между элементами имеют сложную структуру.
Перечисленные информационные модели используются также и для создания и функционирования баз знаний – деревьев вывода, семантических сетей, деревьев целей, фреймов и т.д.
Заканчивая описание наиболее популярных моделей, используемых в практике управления, следует отметить, что большинство из них, так или иначе, реализуется с помощью компьютеров, то есть преобразуются в компьютерную модель. Поэтому далее необходимо рассмотреть сущность и этапы создания таковой.
Компьютерное моделирование
Компьютерная модель является представлением процесса обработки информации об объекте на алгоритмическом или программном языке, позволяющим использовать компьютер в практике управления.
Для того, чтобы создать такую модель, как правило, необходимо
1) выполнить постановку задачи,
2) создать собственно компьютерную модель,
3) затем осуществить компьютерный эксперимент и, наконец,
4) сделать анализ полученных результатов.
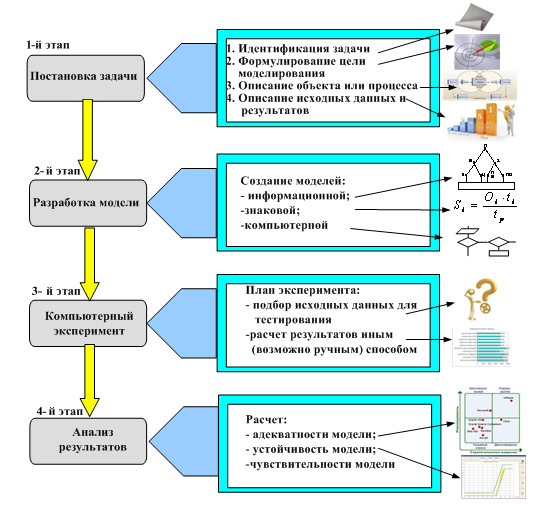
Этапы компьютерного моделирования
. Анализ результатов
Анализ результатов полученных с помощью созданной модели - заключительный этап моделирования. По полученным расчетным данным проверяется, насколько результаты соответствуют целям моделирования. Для модели определяют ее:
- адекватность;
- устойчивость;
- чувствительность.
Адекватность - это степень соответствия модели и реального объекта (процесса) в важных интервалах параметров и исходных данных заданной точности. Модель может быть адекватна для одного диапазона одних параметров и неадекватна для других. В результате анализа адекватности определяют также область адекватности, т.е. диапазон тех значений исходных данных и параметров, где модель соответствует объекту. При планировании эксперимента и обработке результатов поиск границ области адекватности обязателен.
Для определения адекватности можно использовать характеристики модели, которые делят на три группы:
- корректность;
- достоверность;
- устойчивость.
Характеристика адекватности связана с корректностью модели, если сравнение модели производится с набором требований, предъявляемых к полученным результатам. Для характеристики адекватности, описывающей корректность, может использоваться эталонная модель, представленная неким стандартом - описанием способа получения нужных значений характеристик или критерием оценки достоверности или описанием принадлежности некоторому отношению (или истинности соответствующего предиката) и др.
Адекватность модели может также характеризоваться достоверностью, если с ее помощью оценивается «близость» значений некоторых характеристик модели и реальных характеристик объекта.
Устойчивость модели – это уровень изменения выходных параметров при изменении входных. Если в модели при малых изменениях входных параметров сильно меняются выходные, то имеет место высокий уровень ее чувствительности. В различных ситуациях может быть либо слишком высокая чувствительность, либо недостаточная. Высокая чувствительность модели ведет к неустойчивости результатов, низкая - к тому, что ее параметры являются несущественными, что указывает на необходимость их дополнительного изучения.
Если полученные результаты не соответствуют целям поставленной задачи, значит, на предыдущих этапах были или неправильно отобраны свойства объекта или допущены ошибки в формулах на этапе формализации или использован неудачный метод или не та среда моделирования и т.д. В этом случае модель корректируется.
- Модели и структуры данных
С точки зрения компьютерной обработки различают структурированные и неструктурированные сообщения (исходные данные).
Неструктурированные вводятся, хранятся и передаются на естественном языке, а структурированные – на искусственном.
Понятие “структура” используется в том случае, если возникла необходимость представить множество каких-либо элементов и отношений (связей) между ними.
Поэтому обработка данных с помощью компьютера требует определения их структуры, то есть порядка размещения однотипных связанных данных в его памяти.
Структура данных зависит от цели их обработки и специфики отражаемых реальных объектов или событий. В дальнейшем под структурой данных будет пониматься совокупность элементов данных, между которыми указаны связи (отношения). Связи между элементами устанавливают порядок доступа к ним в процессе обработки. Элементы данных размещаются в ячейках памяти, имеющих адреса.
Так как структура данных указывает на способ их организации в памяти компьютера, поэтому, как правило, под структурой данных подразумевают структуру хранения данных. Известны следующие типовые структуры данных: линейные (одномерный массив, двумерный массив), и нелинейные (списочные структуры, древовидные и сетевые).
Линейные одномерные массивы
Данная структура предполагает размещение элементов данных в непрерывной последовательности ячеек памяти компьютера
Наиболее важными из однородных (линейных) структур данных являются очередь и стек. Очередь содержит элементы, выстроенные друг за другом в цепочку, у которой есть начало и конец. Добавлять новые элементы можно только в конец очереди, забирать элементы можно только из начала.
Двумерные массивы
На рис. 6.10б указан способ хранения данных в виде двумерного массива. Он применяется в том случае, если длина строки или столбца известны. Как правило, при обработке двумерных массивов известны и номера строк и номера столбцов (матрицы). Тогда для поиска нужного элемента достаточно указать номер строки и номер столбца.
Нелинейные структуры
Списочные структуры
Довольно часто данные в компьютере располагаются не в последовательных ячейках, а в произвольных частях памяти. Для того, что бы задать связь между различными элементами данных применяют указатели. Списочная линейная структура представлена на рис. 6.10а. В ней первая ячейка содержит адрес первого элемента данных, вторая элемент данных и адрес следующего элемента данных и т.д. Последняя ячейка содержит элемент данных и указатель конца списка.
Двухсвязный линейный список представлен на рис. 6.10б. Каждый элемент списка, кроме первого и последнего, содержит три поля, первое и третье из которых имеют указатели на предыдущий и последующий элементы.
Цикличный линейный список, представленный на рис. 6.10в, позволяет организовать переход с последнего элемента списка на первый. Образуется кольцо, выход из которого возможен после получения некоторого сигнала.
Рис. 6.10. Списочная структура данных: линейная (а), двухсвязная (б), циклическая (в)
Древовидная структура используется в случае необходимости отражения отношений соподчиненности между объектами или процессами. Деревом называется множество элементов, называемых узлами, таких, что:
- между узлами имеет место отношение типа «исходный - порожденный».
- Есть только один узел, не имеющий исходного – корень.
- Все узлы, за исключением корня, имеют только один исходный.
- Ни один порожденный узел не может стать исходным.
На рис. 6.11 представлено две формы моделирования иерархических отношений: иерархическое дерево, отражающее отношение соподчиненности (а) и структура данных, позволяющая отразить эти отношения в памяти компьютера (б).
Узел иерархической структуры данных в данном случае содержит три поля: одно для размещения собственно данных и два для указателей (на подчиненный и на соседний узел).
В информатике существует ряд разновидностей деревьев.
Рис. 6.11. Древовидная структура: а) иерархическая структура, б) древовидная структура данных
Бинарное дерево
Особое значение прибрели бинарные деревья (binary tree)) упорядоченное дерево, каждая вершина которого или пустая или состоит из одного корня и двух бинарных поддеревьев.
Сетевая структура представляет собой структуру наиболее общего вида, так как способна воспроизводить большинство связей между объектами. На рис. 6.14а представлена сеть автомобильных дорог, а на рис. 6.14б структура данных, позволяющая представить эту сеть в памяти компьютера. Для этого в сети используется два типа узлов: те, что отражают название города (тип 1), и те, что отражают расстояние между ними (тип 2). На рис. 6.14в указано содержание узла типа 1, а на рис. 6.17г – типа 2.
Рис. 6.14. Сеть автомобильных дорог- а), сетевая структура данных - б), содержание узлов первого типа - в), содержание узлов второго типа - г)
С понятием «структура данных» тесно связано понятие «модель данных», что можно представить следующим образом:
Модель данных - это структура данных с заданными над ними операциями для обработки. Содержательно структура данных является составной частью модели данных.
Различают следующие базовые модели данных: реляционные (двумерные массивы), иерархические и сетевые. Кроме перечисленных известно множество моделей, отражающих цели их создателей (сущность-связь, бинарные модели, семантические сети и т.д.).
Реляционная модель основывается на понятии “отношение”, и представляется совокупностью таблиц. На рис. 6.15 приведены базовые понятия данной модели.
Рис. 6.15. Основные понятия реляционной модели базы данных
Домен – это множество значений, принимаемых свойствами (характеристиками) отражаемого объекта.
Атрибут – это имя множества значений, входящих в домен. Атрибуты используются в качества средства для обращения к доменам.
Кортеж – это множество элементов из доменов, составляющих одну строку отношения (таблицы).
Отношение – это множество кортежей, отражающих свойства объекта.
Таблицы, входящие в реляционную модель, строятся в рамках ограничений, диктуемых операциями их обработки. Это следующие ограничения:
- таблица должна иметь имя (например, ДЕТАЛЬ, ПОСТАВЩИК, ПОСТАВКИ);
- таблица должна быть простой, то есть не содержать составных столбцов, например, у поставщика должен быть только один номер телефона;
- в таблице не должно быть одинаковых строк;
- должен быть известен первичный ключ, используемый для поиска или выполнения других логических операций.
В компьютере таблицы реляционной модели обрабатываются с помощью операций реляционной алгебры.
- Понятие алгоритма, его свойства и способы описания
Алгоритм – это точное предписание о выполнении в определенном порядке некоторой системы операций (шагов) для решения всех задач некоторого типа.
Точно указать шаги в алгоритме с помощью естественного языка, в силу его неоднозначности, достаточно сложно. Поэтому обращаются к символьным, то есть искусственным языкам. Наиболее распространенными формами искусственных языков, используемых для представления алгоритмов, являются:
- формульное описание, предназначенное для представления процесса решения несложных задач, базирующихся на локальных вычислениях;
- задание алгоритмов в виде блок-схем, широко распространенное для представления большого числа логических условий;
- словесное описание правил в виде фраз естественного языка с ограниченным синтаксисом.