Курс, 524 группа Адаптация комплекса программ M2dgd для работы на мвс с использованием среды параллельного программирования ost павлухин Павел
| Вид материала | Документы |
- Рабочая программа учебной дисциплины (модуля) Технологии параллельного программирования, 79.5kb.
- Лекция Языки и системы программирования. Структура данных, 436.98kb.
- Программа по курсу: современные технологии параллельного программирования (по выбору), 69.72kb.
- 1. Теоретические сведения, 771.46kb.
- Рабочая учебная программа по дисциплине «Технология программирования» Направление №230100, 109.02kb.
- Методические указания по выполнению контрольной работы с использованием компьютерных, 1010.76kb.
- Учебной дисциплины «Технология программирования и работ на эвм» для направления 010100., 38.85kb.
- Адаптация персонала, 260.18kb.
- Лекция 3 Инструментальное по. Классификация языков программирования, 90.16kb.
- Эволюция языков программирования, 493.92kb.
Московский Государственный Университет им. М. В. Ломоносова
Механико-математический факультет
Кафедра вычислительной механики
5 курс, 524 группа

Адаптация комплекса программ M2DGD для работы на МВС с использованием среды параллельного программирования OST
Павлухин Павел
Научный руководитель: д. ф-м. н. Меньшов И. С.
17.05.2010
Введение
В течение последних лет в области высокопроизводительных вычислений сложилась следующая картина: интенсивное нарищивание вычислительной мощности, приходящейся на одно ядро в CPU, приостановилось, т.к. производство процессоров «уперлось» в частотные ограничения на отметке 3 — 4 Ггц. Даже переход на более совершенный техпроцесс (с 0.65мкм на 0.32мкм) не дает значительного увеличения частоты, которая последние пять лет остается практически на одном и том же уровне. Отчасти наращивание вычислительных мощностей происходит за счет совершенствования архитектуры самих CPU, но после появления семейства CoreDuo, когда его представитель работал на 50 — 100% быстрее своего предшественника Pentium 4(D) с той же частотой, таких значительхых рывков по производительности больше не было. Увеличение вычислительных мощностей как в сфере ПК, так и в сфере МВС стало происходить в основном за счет увеличения количества ядер в одном CPU и увеличения числа самих CPU в системе. За последние 5 лет количество ядер в однопроцессорной системе увеличилось до 6 на текущий момент, причем в ОС они могут представляться 12 ядрами(используя технологию Hiper-Threading, которая каждое ядро процессора представляет двумя «виртуальными», благодаря этому достигается прирост до 25% в некоторых приложениях, использующих многопоточность). Для современных МВС количество ядер измеряется уже даже не тысячами, а десятками тысяч.
С другой стороны, объем вычислений в современных прикладных задачах в масштабах предприятия таков, что на одном ядре эти задачи считались бы месяцами и годами. К тому же объем данных в них нередко в несколько раз превышает объем оперативной памяти, доступной на одном узле в МВС.
Поэтому особую важность в параллельном программировании на сегодняшний день имеют два направления: адаптация для счета с использованием нескольких CPU уже существующих расчетных задач, которые выполняются в рамках одного процесса на одном CPU, и создание алгоритмов, учитывающих изначальный параллелизм физических задач, когда значение величин в каждой точке пространства определяется лишь ближайшим его окружением-”соседями” и переносящих этот параллелизм на программно-аппаратный уровень. Данная работа будет посвящена первому направлению, а именно параллельной реализации задачи M2DGD в среде OST, так же будет сделано сравнение разработанного алгоритма в вышеназванной программной среде с реализацией на C/C++/MPI [1, 2].
Наряду с созданием алгоритмов для параллельных вычислений остается важным также и вопрос об их программно-аппаратной реализации и используемых при этом сред и инструментов. На сегодняшний день самой распространенной технологией, используемой для программ, одновременно выполняющихся на нескольких процессорах, является MPI (Message Passing Interface), с помощью которой организуется обмен сообщениями между параллельно выполняющимися процессами. Основной ее недостаток состоит в том, что непосредственно организация удаленных вызовов — часть, относящаяся к системному программированию, - целиком ложится на плечи прикладного программиста, причем от задачи к задаче ему необходимо каждый раз ее реализовывать. Назначение связей между процессами, синхронизация времени их выполнения — все это должен организовывать сам прикладной программист. Основная идея OST (Object, Space, Time), предлагаемая как альтернатива MPI, - «вынести за скобки» системную часть и предоставить прикладному программисту удобные средства для назначения связей между частями параллельно выполняющихся программ, синхронизации вычислений и межпроцессных обменов в рамках модели объектно-ориентированного программирования, сведя при этом программирование распределенных частей задачи к локальному с обращением к объектам- ”соседям”.
1. Описание последовательного алгоритма M2DGD
M2DGD(Menshov 2 Dimensional Gas Dynamics) – комплекс программ для решения нестационарных двумерных задач газовой динамики в рамках модели уравнений Навье-Стокса, основанный на модификации метода LU-SGS решения систем алгебраических уравнений [2]. Пространственная дискретизация исходных дифференциальных уравнений выполняется методом конечного объема. Используются оригинальные интерполяционные схемы восполнения сеточных функций на неструктурированных произвольных (в том числе некомформных) сетках для повышения порядка пространственной аппроксимации. Численные потоки определяются методом Годунова по точному решению нелинейной задачи Римана. Для интегрирования уравнений по времени используется оригинальная гибридная явно-неявная схема, обладающая свойством абсолютной устойчивости при условии минимального вклада диссипативной неявной компоненты и вторым порядком аппроксимации при переходе на явную компоненту [1]. Эта схема позволяет эффективно решать задачи на сетках с сильной пространственной неоднородностью (с большим относительным удлинением в одном из направлений), которые неизбежно возникают при решении задач в рамках уравнений Навье-Стокса. Основные характеристики алгоритма:
• применим как к структурированным, так и неструктурированным сеткам,
• второй порядок точности по времени и пространству,
• высокая надежность: абсолютно устойчив по отношению к выбору шага по времени.
Дискретная модель, в конечном счете, неявная и сводится к решению большой разреженной СЛАУ
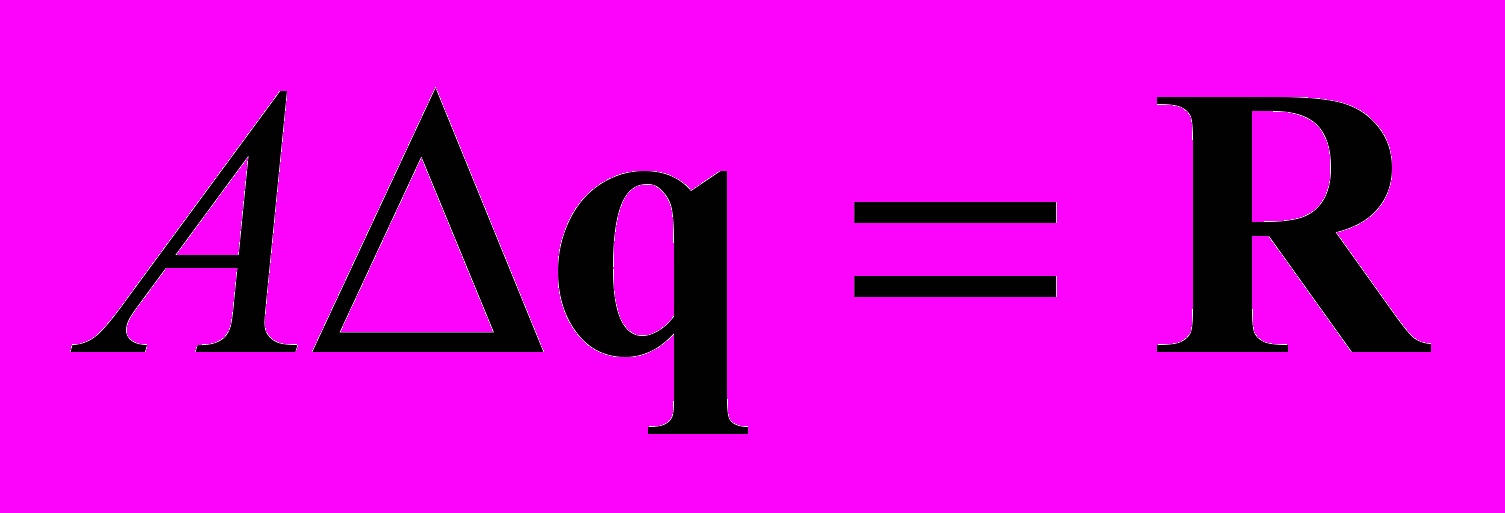
которая решается методом LU-SGS (Lower-Upper Symmetric Gauss-Seidel) - приближенной факторизацией матрицы
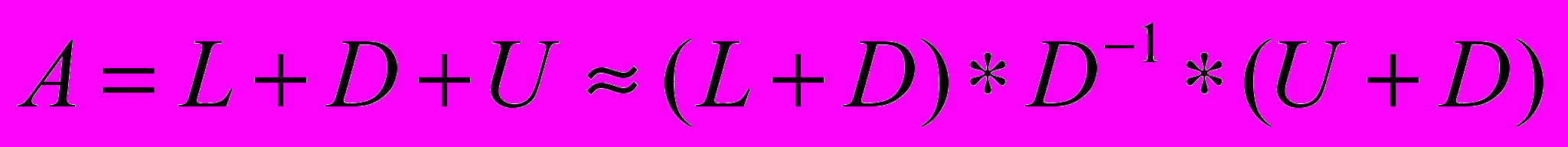
и решению двух систем с нижней и верхней треугольной матрицей, которые решаются в 2 прохода:
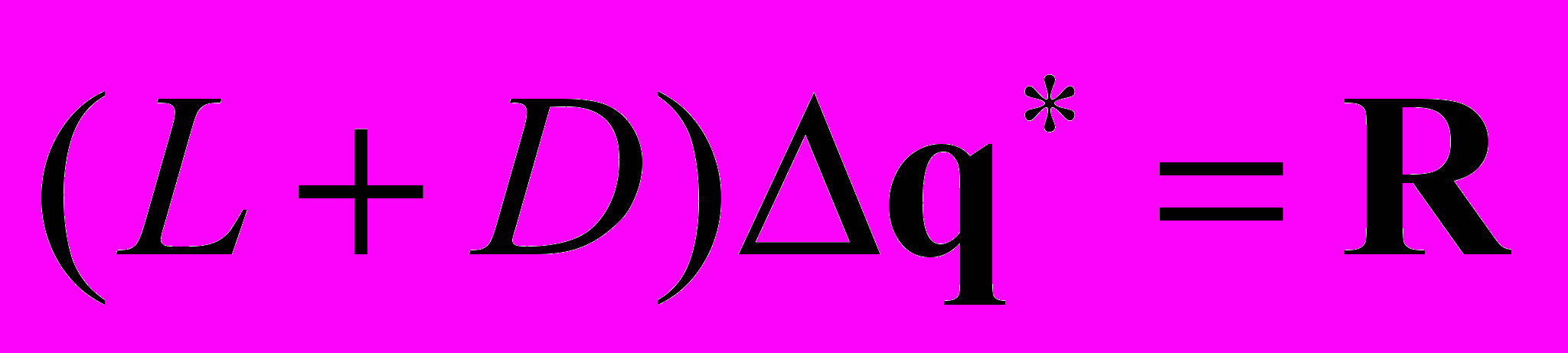
(forward)
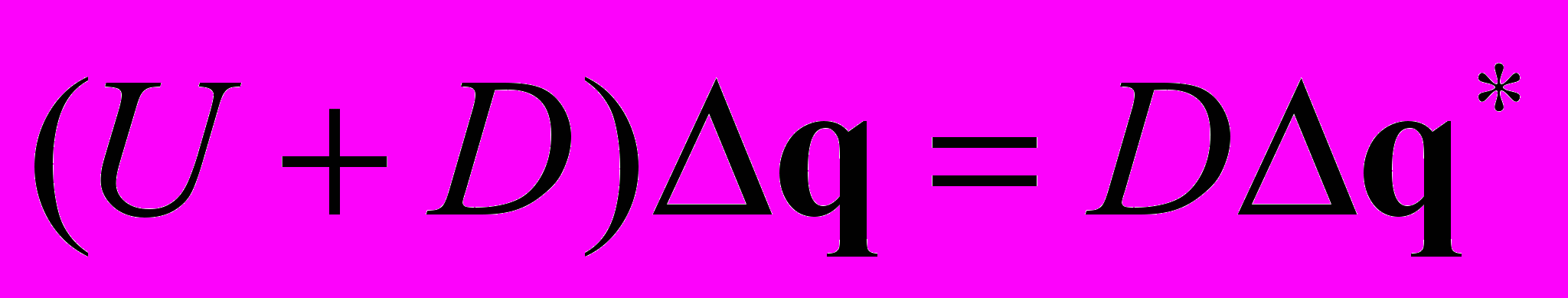
(backward)
где forward и backward – названия обходов области с сеточным разбиением для соответствующей СЛАУ.
Этот метод приводит к неявной схеме, но при этом с нижней и верхней треугольной матрицами, это будет существенно для предлагаемой ниже параллельной версии этого метода.
Расчетная область задачи делится на подобласти, на каждой из которой строится сеточное разбиение, при этом каждая такая подобласть с разбиением топологически эквивалентна четырехугольнику, для каждой ее стороны задается граничное условие, определяемое индексом — типом граничного условия и вектором граничных условий с четырьмя компонентами: давление, 2 компоненты скорости и плотность (в случае необходимости):
3 – для граничных условий типа стенка (нулевая скорость и нулевая производная от давления по нормальному к границе направлению;
4 – для граничных условий, задающих все параметры (плотность, 2 компоненты вектора скорости и давление) на границе;
5 – для граничного условия экстраполяция нулевого порядка (простой снос значений из прилегающей ячейки на границу;
6 – для граничного условия «ось симметрии»
7 – для характеристического граничного условия (т.н. неотражающее условие на основе римановских инвариантов для выходных границ с дозвуковым потоком).
Под ячейкой в дальнейшем изложении подразумевается элемент сеточного разбиения (четырехугольник) с приписанными ему соответствующими вершинами и осредненным значением вектора-решения на этом элементе.
После полного определения расчетной области для численного метода она представляет из себя 2 матрицы: одна с координатами узлов сеточного разбиения, другая — с осредненными значениями вектора решения на соответствующих элементах; к каждой физической границе приписывается тип граничного условия и вектор граничных условий (рис. 1).
Базовый вектор решения q состоит из 4-х компонент и включает либо примитивные переменные (плотность , х-компонента вектора скорости Ux, y-компонента вектора скорости Uy, давление P), либо консервативные переменные (, Ux, Uy, E), где Е – полная удельная энергия. Полный вектор решения f состоит из 33-х компонент и включает кроме базовых дополнительные переменные, необходимые для проведения расчета.
Весь комплекс программ написан на языках C и Fortran. Общая схема работы вычислительного ядра представляется в виде:
do is=1,NSTEP
do it=1,MAXITER
call omega(dt)
call slope(1)
call predicval(2)
call forward(dt,dtpseudo)
call backward(dt,dtpseudo)
call updateiter
end do
call updatetime
lstep=lstep+1
time=time+dt
end do
NSTEP задает число шагов по времени, которые необходимо выполнить, MAXITER определяет число итераций внутри одного шага по времени, dt – шаг по времени, dtpseudo – шаг по псевдовремени. При вызове каждой процедуры (omega,slope,predicval,forward,backward,updateiter,updatetime) осуществляется полный обход по всем ячейкам расчетной области. Для получения данных о ячейке используется функция getnewcell, написанная на C, которая через параметры-ссылки передает информацию о геометрии ячейки и вектор решения f, приписанный этой ячейке. Для записи нового значения f используется C-функция setcurval, которая обновляет этот вектор для текущей ячейки. Часть процедур использует данные из ячеек-соседей, определяемых по обычной дискретной двумерной топологии (т.е. для текущей ячейки в общем случае имеется 4 соседних: ”снизу”, ”справа”, ”сверху”, ”слева”), для получения данных из таких ячеек используется C-функция getnewneib, которая вызывается каждый раз для получения очередного соседа до тех пор, пока после своего очередного вызова она не передаст через параметр флаг R=-1, означающий, что обход всех соседей для текущей ячейки закончен. Для записи вектора f в текущую ячейку-сосед используется C-функция setneighval. Для процедур forward и backward, в которых происходит решение указанных выше СЛАУ, устанавливается неизменяемый во время счета линейный порядок обхода всех ячеек области: все ячейки нумеруются числами от 1 до N (N – число всех ячеек в расчетной области), порядок при этом выбирается произвольным образом, что также будет существенно при построении параллельного алгоритма; обход ячеек в forward осуществляется по возрастанию номеров ячеек, в backward – строго по убыванию, т.е. в обратном порядке. В начале каждой процедуры вызывается rescell – она устанавливает текущей ячейку с первым номером.
Omega – подготовительная процедура, при обходе по ячейкам не использует и не обновляет данные в ячейках-соседях; простой обход ячеек от 1 до N.
Slope, predicval – также подготовительные процедуры, но уже используют данные ячеек-соседей, при этом не важно, была обсчитана ячейка-сосед в этой процедуре на текущей итерации или еще не обсчитана, при этом данные в ячейки-соседи не пишутся (ячейка считается обчитанной для данной процедуры в текущей итерации, если данные о ней уже передавались для обсчета посредством вызова getnewcell из данной процедуры, иначе ячейка не обсчитана).
Forward – основная процедура; при обходе по соседям: если сосед был обсчитан, то выполняется один блок вычислений, если еще не обсчитан – другой блок, после проделанных вычислений обновляются вектор текущей ячейки и, если сосед еще не был обсчитан, вектор ячейки-соседа.
Backward – основная процедура; при обходе по соседям: если сосед был обсчитан, то выполняется один блок вычислений, если еще не обсчитан – другой блок, после проделанных вычислений обновляется только вектор текущей ячейки.
Updateiter, updatetime – вспомогательные процедуры, при обходе по ячейкам не используют и не обновляют данные в ячейках-соседях; простой обход ячеек от 1 до N.
2. Сложности распараллеливания M2DGD
Рассмотрим простейший случай, когда область поделена на две части (блок 1 и блок 2) и вычисления ведутся параллельно на двух процессорах, счет на каждом из них ведется над своей частью области с обращением за соседними ячейками в другую часть, когда это необходимо. Если использовать какой-либо простой порядок обхода ячеек, одинаковый в двух блоках (например, ”слева-направо”, ”сверху-вниз”), то при запуске одной и той же задачи несколько раз могут, вообще говоря, получаться разные результаты. Действительно, при запросе соседних ячеек из блока 2 граничными ячейками из блока 1 получаемые ячейки из первого блока могут быть как обсчитанными, так еще и не обсчитанными, т.е. иметь разные значения вектора f (рис. 2а,б).
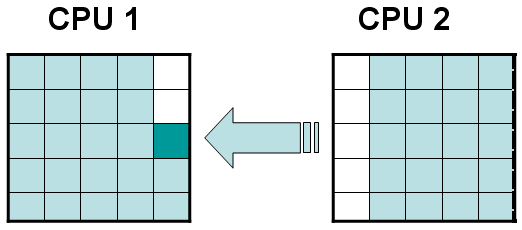
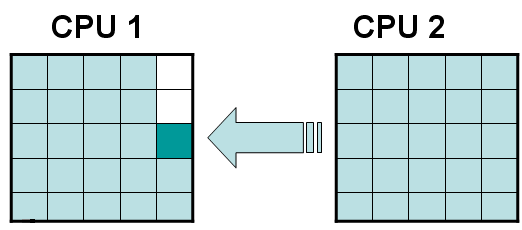
а) б)
Рис. 2 а) получаемые ячейки из блока 2 еще не посчитаны, б) получаемые ячейки из блока 2 уже посчитаны
Поэтому рассмотренный выше случай являет собой пример некорректного алгоритма, параллельно работающая программа должна выдавать всегда один и тот же постоянный результат, который получается таким же, как и в случае работы последовательной программы. Ясно, что для выполнения этого свойства все обходы в блоках параллельной программы должны быть эквивалентны некоторому обходу в последовательном решении. Это означает, что задавать линейную нумерацию ячеек нужно не в пределах одного блока, а глобально для всех блоков, из которых состоит расчетная область, тем самым определяя однозначно статус ячеек (обсчитана/не обсчитана), получаемых из соседних блоков. Но при этом наряду с проблемой корректности счета необходимо учитывать и эффективность счета получаемого алгоритма. Рассмотрим работу параллельной программы, пронумеровав от 1 до N1 ячейки в блоке 1 ”снизу-вверх” и ”слева-направо” и от N1+1 до N1+N2 в блоке 2 тем же образом (N1 – число ячеек в блоке 1, N2 – число ячеек в блоке 2). При такой нумерации для граничных ячеек блока 2 всегда должны доставляться уже обсчитанные ячейки из блока 1 (т.к. номера ячеек в блоке 1 меньше номеров ячеек в блоке 2 и при последовательном обходе этих двух блоков ячейки в блоке 1 всегда обсчитываются первыми). Поэтому при одновременном запуске процедуры forward в этих блоках в первом из них будет идти счет, а во втором процесс будет ожидать завершения обсчета граничных ячеек-соседей в первом, причем это время ожидания будет практически равно времени работы forward в блоке 1; после того, как второй блок наконец получит обсчитанные ячейки из блока 1, в нем (во втором блоке) будет идти счет, а в первом блоке процесс будет ожидать окончания счета во втором, причем опять это время будет почти равно времени счета forward во втором блоке (для корректной работы следующей процедуры необходимо, чтобы счет текущей процедуры также завершился и в соседних блоках). Из-за этих простоев общее время счета на двух процессорах будет мало отличаться от времени последовательного счета на одном процессоре (forward и backward, для которой так же важен порядок обхода, составляют основную часть времени счета на одной итерации).
Из сказанного выше вытекает, что для корректного счета задачи на нескольких процессорах необходимо однозначно определить статус получаемых (передаваемых) ячеек (обсчитаны/не обсчитаны), что эквивалентно заданию глобальной последовательной нумерации ячеек, а для повышения эффективности счета (уменьшения простоев) использовать более сложные обходы в блоках. Описание такого алгоритма дается ниже.
3. Параллельная реализация M2DGD
Необходимо заметить, что внутренние части блоков (часть блока без ячеек, расположенных на границе (по периметру) блока) напрямую не связаны соотношениями ячеек ”обсчитаны/не обсчитаны”, поэтому обходы на таких частях можно проводить параллельно, сохраняя при этом корректность счета, основная проблема здесь – упорядочить вычисления в граничных ячейках блоков с минимальными потерями в эффективности счета. Как видно из примера выше, одинаковый обход во всех блоках практически не дает выигрыша по времени счета задачи на нескольких процессорах (для конфигурации из 2 блоков одинаковые обходы в них с эффективным счетом построить можно, но в общем случае при разбиении области на NxM блоков с одинаковыми обходами появляются простои). Организовать корректный и эффективный счет на нескольких блоках можно, разделя все блоки определенным образом на два класса – black и white (выбор таких названий станет понятен чуть позже), задав в них разные обходы ячеек. Усложнение порядка обхода связано только с двумя процедурами – forward и backward, для которых является существенным обсчитанность/необсчитанность соседних ячеек, для всех прочих процедур это не важно, поэтому для них можно использовать одинаковый (несмотря на разделение на два класса) ”простой” порядок обхода, не заботясь о том, были или не были обсчитаны в текущей процедуре полученные из соседнего блока ячейки.
Итак, распределим на два класса параллельно обсчитывающиеся блоки так, чтобы они образовали «шахматную доску», т.е. чтобы у каждого блока black все соседи были из класса white, а у каждого блока white все соседи были из black (соседство блоков определяется так же, как и соседство ячеек) (рис. 3).
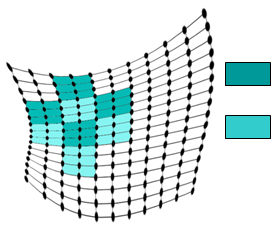
Black
White
Рис 3. Распределение по классам блоков
Среда OST предполагает использование объектно-ориентированного подхода для написания прикладных задач, поэтому естественным выглядит представление счета M2DGD в виде объектов, распределенных по имеющимся процессорам, каждый объект при этом содержит блок ячеек и методы, отвечающие как непосредственно за счет в блоке, так и за обмен ячейками между объектами-соседями (соседство объектов определяется по соседству содержащихся в них блоков).
Для того, чтобы упорядочить и синхронизировать вычислительные операции, введем логическое время (прикладного) объекта – числовой параметр, разделяющий операции в объекте; все операции по обмену ячейками в соседних объектах в этом случае возможны только при равенстве в них логических времен. Чтобы увеличить свое логическое время, объект вызывает предоставленный монитором OST (элемент среды, контролирующий и обслуживающий прикладные объекты) метод setXYZT, тем самым отправляя заявку в монитор на продвижение своего локального времени, счет в объекте приостанавливается до того момента, пока монитор не подтвердит эту заявку. Монитор ее подтверждает в том случае, если от всех объектов-соседей получены аналогичные заявки или логическое время в соседях больше текущего времени объекта-заявителя. Таким образом, данный алгоритм синхронизации не позволяет счету в каком-либо объекте «убежать вперед, не дожидаясь» своих объектов-соседей.
После разделения блоков (и, соответственно, объектов) на классы, рассмотрим последовательность действий, выполняемых за одну итерацию в паре соседних объектов, которые всегда будут представителями двух разных классов (следует непосредственно из введенного распределения объектов по классам).
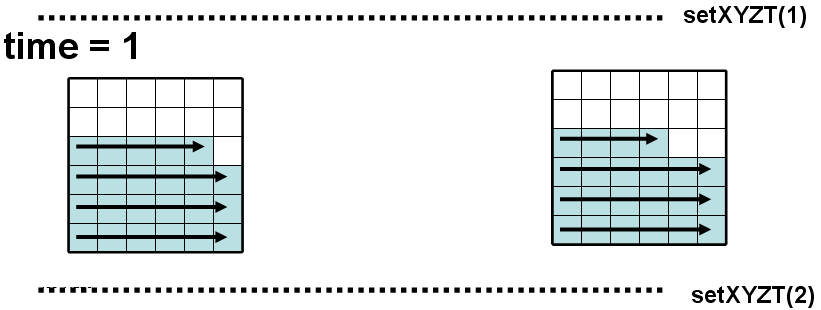
Рис 4. Omega в black и white
После завершения инициализации в объектах устанавливается логическое время time = 1, и вызывается omega, не требующая данных от ячеек-соседей, поэтому никаких обменов между объектами не происходит; в объектах используется одинаковый обход «слева-направо, снизу-вверх» (назовем его simplesweep), после завершения omega в монитор из объектов направляются заявки на продвижение логического времени. Исходная область делится на блоки так, чтобы число ячеек в них было по возможности равным, либо отличалось не значительно, и сами блоки были приближены к квадратным (за счет чего уменьшается относительная часть пересылаемых ячеек). Поэтому заявки в монитор от двух объектов поступят почти в одно и то же время и простои из-за ожидания счета в соседнем объекте будут сведены к минимуму.
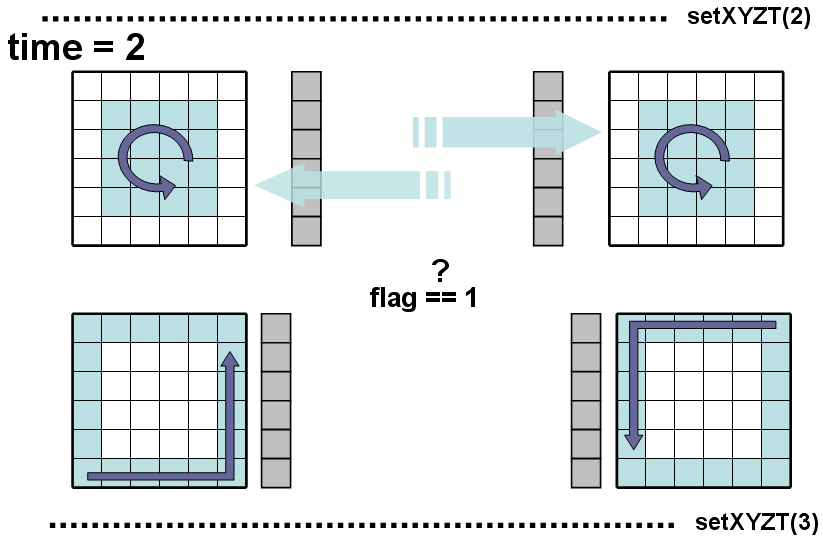
Рис 5. Slope в black и white
После подтверждения заявок монитором на time=2 из каждого объекта отсылаются граничные ячейки соответствующим соседям и запускается slope с обходом по внутренним ячейкам, исключая граничные (innersweep). Затем выполняется проверка флага, сигнализирующего о том, что граничные ячейки от соседей получены, иначе происходит приостановка в объекте и последующая проверка флага через некоторый интервал времени. Так как процесс пересылки ячеек требует значительно меньше ресурсов CPU и занимает меньшее время по сравнению со счетом внутренних ячеек в блоке, то к моменту проверки флага, как правило, нужные граничные ячейки будут получены и без простоев продолжится счет omega с обходом по граничным ячейкам (ringsweep), при этом будут использоваться данные полученных от объектов-соседей ячеек. В завершении в монитор почти в одно и то же время поступают заявки на продвижение времени из обоих объектов.
Работа predicval при time=3 полностью аналогична работе slope при time=2, после ее завершения отправляются заявки на продвижение времени в объектах.
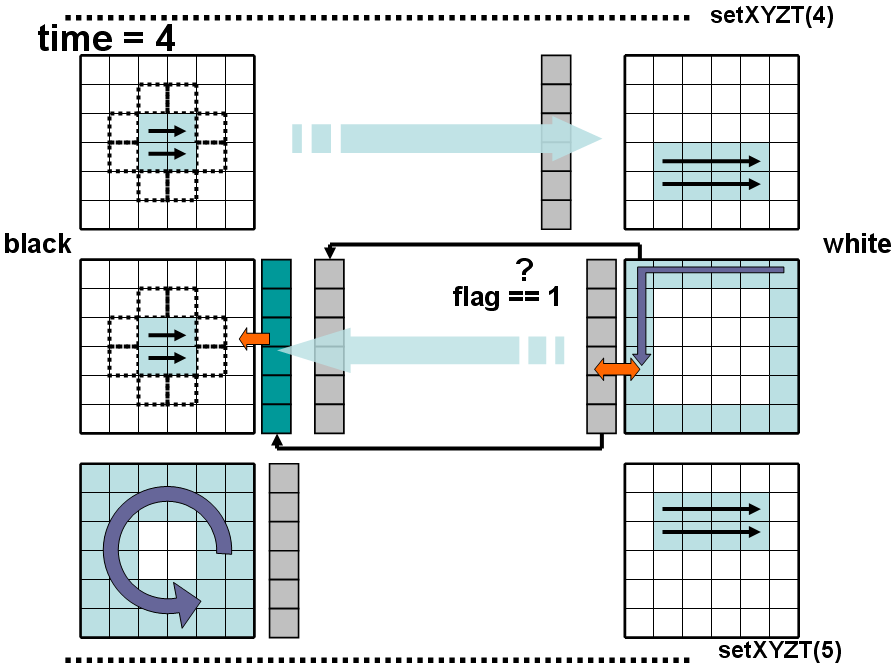
Рис 6. Forward в black и white
При работе forward в объектах уже используются разные обходы; необходимо однозначно определить статус передаваемых ячеек (обсчитаны/не обсчитаны). В объекте white запускается forward с обходом по внутренним ячейкам (downinnersweep), но только по «нижней» их половине, т.е. обход будет сделан только по части внутренних ячеек. Из black отсылается в white соответствующая граничная часть ячеек, которые являются соответствующими соседями для ячеек из white, при этом отсылаемые ячейки для white не являются обсчитанными. В black запускается обход по всем ячейкам, кроме граничных и кроме ячеек, являющихся соседними к граничным внутри блока, т. е. обход по всем ячейкам, кроме «двойного» периметра ячеек (smallinnersweep). Если бы был выбран обход innersweep, то изменялись бы и граничные ячейки, и возникали ситуации, когда они (граничные ячейки) отсылались бы в white как с обновленными компонентами (после вызова setneighval для граничной ячейки из обхода innersweep), так и с необновленными. При обходе же smallinnersweep граничные ячейки остаются неизмененными (рис. 6, все изменяемые ячейки показаны пунктиром) и таковыми передаются соседним объектам. В white после завершения обхода downinnersweep проверяется флаг, сигнализирующий о том, что ячейки из соседнего объекта получены (это, как правило, так и будет – по соображениям, описанным выше) и запускается forward по граничным ячейкам(ringsweep), причем используется копия К ячеек полученных из black, в этой копии также обновляются ячейки (полученные из black, они еще не обсчитаны). После завершения этого обхода из white в black отправляются граничные ячейки блока white, которые являются соседями для соответствующих ячеек из black, и обновленная копия К ячеек из black. В black граничные ячейки обновляются из присланной копии К (операция корректна, т.к. никаких действий над граничными ячейками в black при time=4 еще не производилось). Затем в white запускается forward с завершающим обходом оставшейся «верхней» половины внутренних ячеек upinnersweep и подается в монитор заявка на продвижение времени в white. В black по флагу проверяется, обновились ли граничные ячейки в блоке и присланы ли ячейки из соседних white-блоков, которые уже являются обсчитанными. После подтверждения этого запускается forward с обходом bigringsweep по оставшимся ячейкам из «двойного» периметра блока black с обращениями к присланным посчитанным ячейкам из white. По завершении обхода подается заявка в монитор на продвижение времени в black.
При работе backward в каждом объекте используется обход, обратный таковому при forward, при этом все так же вычисления будут зависеть от обсчитанности/необсчитанности ячеек-соседей, но сами они (ячейки-соседи) уже не обновляются, происходит запись только в текущую ячейку.
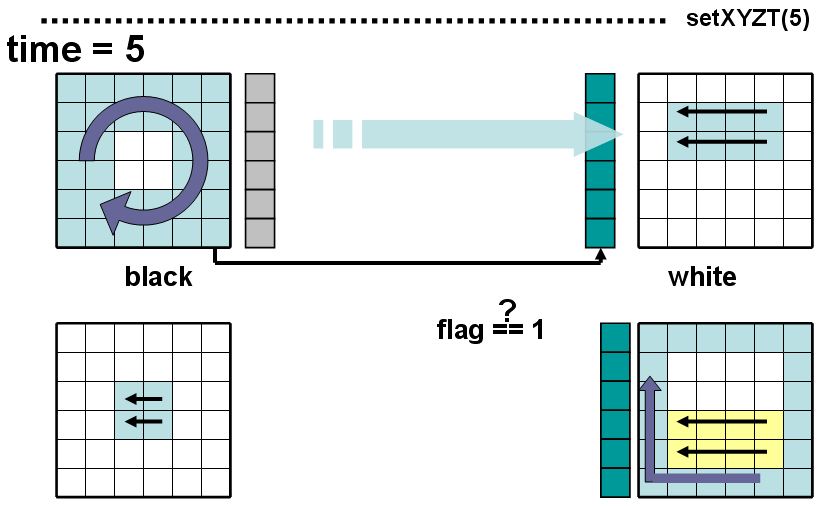
Рис 7. Backward в black и white
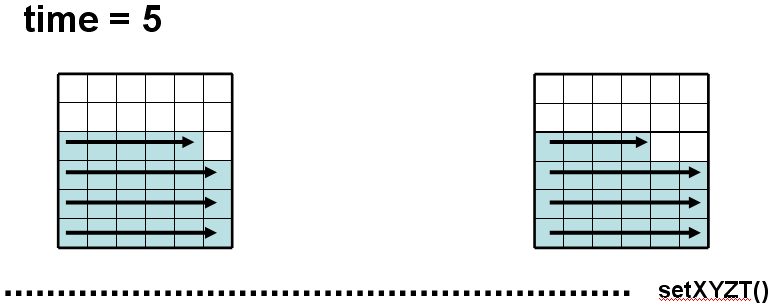
Рис 8. Updateiter, updatetime в black и white
При time=5 в black запускается backward по обходу, обратному bigringsweep – bigringsweepback, используя при этом ячейки от соседей black, полученных еще при time=4, т.к. эти ячейки для black в backward будут со статусом «не обсчитаны» и обновлять их не требуется, поскольку имеющаяся копия совпадает с соответствующими ячейками в white. После завершения обхода bigringsweepback из black в white отправляются только ячейки блока black, которые являются соседними для соответствующих ячеек в white и в black запускается backward для оставшихся внутренних ячеек с обходом smallinnersweepback, обратным smallinnersweep. В white запускается backward с обходом upinnersweepback (обратный для upinnersweep), затем проверяется по флагу, получены ли соседи для граничных ячеек блока white из black, и, в случае подтверждения, запускается backward c обратным обходом по граничным ячейкам white – ringsweepback, с использованием ячеек-соседей, полученных из black. В заключении backward обсчитывает оставшиеся ячейки с обходом downinnersweepback, обратным downinnersweep. После этих процедур в объектах запускаются с одинаковым обходом simplesweep updateiter и updatetime (если текущая итерация – последняя на шаге по времени), не требующие обращания к соседям.
Описанный алгоритм эффективно работает на блоках с примерно равным числом ячеек, поскольку время счета между двумя вызовами setXYZT для всех объектов будет мало отличаться и они не будут значительным образом тормозить счет друг друга. Корректность алгоритма обеспечивается механизмом синхронизации, предоставляемым OST (вызовы между объектами, выполняющими разные процедуры (например, slope и predicval), т.е. находящимися в разных логических временах, блокируются монитором до совпадения их времен) и существованием эквивалентного обхода всей области при последовательной работе M2DGD. Существование такого обхода необходимо только для forward и backward, поскольку для всех других рассмотренных процедур он не важен. Построим такой обход, например, для области с 2х2 блоками:
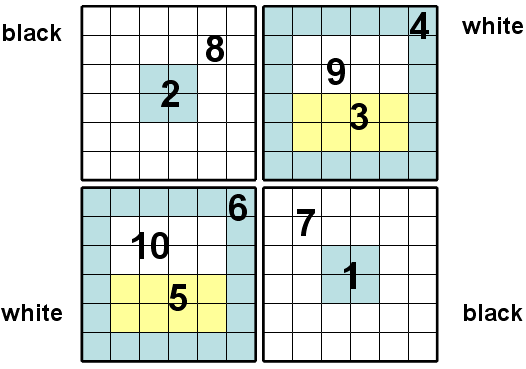
Рис 9. Эквивалентный последовательный обход
Числами обозначена последовательность обхода в forward частей области, каждая часть соответствует обходу в параллельном счете: 1, 2 – smallinnersweep; 3, 5 – downinnersweep; 4, 6 – ringsweep; 7, 8 – bigringsweep, 9, 10 – upinnersweep. При параллельном счете в black запускается счет в 1 и 2, используя при этом не обсчитанные еще ячейки из 7 и 8; в white считается 3 и 5, используя также необсчитанные ячейки из 4, 9, 6, 10; затем, используя полученные из 7 и 8 необсчитанные еще соответствующие копии граничных ячеек, в white считается 4 и 6, используя соответственно уже обсчитанные ячейки из 3 и 5, а также еще не обсчитанные из 9 и 10, 7 и 8 (копии). Обновленные копии отсылаются обратно для обновления своих оригиналов, что соответствует обходу 4 и 6 в последовательном случае с обновлением соседних ячеек в 7 и 8. После, в white счет 9 и 10 с использованием уже посчитанных 3 и 4, 5 и 6. В black считаются 7 и 8, используя уже полученные обсчитанные копии из 4 и 6. Таким образом, работа параллельного алгоритма эквивалентна работе последовательного с соответствующим обходом. Для backward обход осуществляется в порядке убывания номеров частей области; аналогично показывается эквивалентность последовательного и параллельного алгоритмов. В случае произвольной конфигурации NxM блоков последовательный обход строится следующим образом: сначала обходятся все части smallinnersweep во всех black в произвольном порядке, затем в каждом white upinnersweep и ringsweep (последовательность обхода самих блоков white произвольная), после обходятся все bigringsweep в black произвольным образом, затем оставшиеся части downinnersweep в white (также произвольно). Нетрудно видеть, что этот обход будет эквивалентным для параллельного алгоритма.
