Высокочастотные микрофильтры

Вид материала

Документы

Содержание Моделирование резонаторов Стержневой резонатор с продольной волной Стержневой резонатор с волной кручения Круговые и прямоугольные мембраны

Подобный материал:

• Высокочастотные микрофильтры, 146.79kb.
• Задачи по теме Высокочастотные, 34.16kb.
• 1. общие положения, 728.02kb.
• Мощные высокочастотные транзисторы, 2370.77kb.
• Одним из важнейших направлений астрономии в течение последнего времени является обработка, 72.97kb.
• Аннотация проведенных научных исследований в 2011 г по Договору от 25 ноября 2010, 182.98kb.
• Е. А. Земская использует понятие ключевые слова единицы, которые обозначают явления, 89.78kb.
• Для сотовых сетей связи (мобильные телефоны, а также модемы, применяемые в сотовых, 307.64kb.

ВЫСОКОЧАСТОТНЫЕ МИКРОФИЛЬТРЫ

Часть 1


Миниатюризация фильтров является технически сложной задачей, которой в последние годы уделяется большое внимание. Фильтры оказывают влияние на распространение механических волн при их прохождении между входными и выходными портами. Колебания – пример таких механических волн. К этому классу устройств от­носятся и фильтры, работающие с акустическими волнами, кото­рые могут рассматриваться, как разновидность механических волн. В составе некоторых фильтров нет механических компонентов, но если они изготавливаются методами микротехнологий, они также относятся к микрофильтрам. Объединяющим элементом всех ми­крофильтров является технология их производства.

В устройствах связи используются несколько типов фильтров. В зависимости от полосы частот, которую они пропускают, их мож­но разделить на:

- фильтры высоких частот,

- фильтры нижних частот,

- полосовые фильтры,

- режекторные.

Однако в большинстве случаев в устройствах связи используются полосовые фильтры с очень узкой полосой пропускания и резким спадом частотной характеристики. Далее будут приведены некото­рые рабочие параметры фильтров.

Самая важная характеристика фильтра— вносимые потери, ко­торые определяются в виде отношения сигнала на выходе фильтра к сигналу на его входе. Разработчики стремятся к минимизации этого параметра внутри полосы пропускания. Добротность филь­тра Q является характеристикой его полосы пропускания, которая выражается через отношение энергий, накопленной и рассеянной в течение одного периода. Ее часто определяют в следующем виде:

(1)

где f₀ – центральная частота, а Δf = f₂ – f₁. Отсюда вид­но, что добротность показывает эффективность работы фильтра в терминах его частотных характеристик. Существует еще несколько характеристик, используемых для описания фильтров:

- Спад частотной характеристики – скорость перехода пе­редаточной характеристики фильтра из зоны пропускания в полосу подавления,

- Коэффициент подавления сигнала в полосе заграждения – сигнал, проходящий через фильтр на частотах вне его полосы пропускания. Этот коэффициент выражается в децибелах и часто соотносится с минимальным уровнем вносимых потерь.

На рис. 1 графически представлены параметры фильтра.

На рис. 2 показана схема типовой современной персональной системы связи. Такие системы способны работать со множеством каналов связи, функционирующих одновременно.

Выбор требуемого канала осуществляется при помощи полосовых фильтров. Чем боль­ше каналов расположено внутри ограниченного частотного спектра, тем строже следующие требования к полосе пропускания фильтра:

- очень низкий уровень вносимых потерь,

- быстрый спад частотной характеристики,

- высокий коэффициент подавления сигнала вне полосы пропус­кания.

Для разных частотных диапазонов устройства беспроводной свя­зи используют различные реализации фильтров. Самыми простыми фильтрами являются схемы, состоящие из сосредоточенных кату­шек индуктивности и конденсаторов. Но на практике такие филь­тры используются в ВЧ устройствах нечасто из-за сравнительно низких значений добротности. Другой подход – применение циф­ровых фильтров, построенных на основе быстродействующих про­цессоров и современных алгоритмов цифровой обработки сигналов. Однако такие фильтры ограничены максимальной частотой выбор­ки, что особенно сказывается на высоких частотах. Поэтому тре­буется разработка альтернативных схем фильтров.




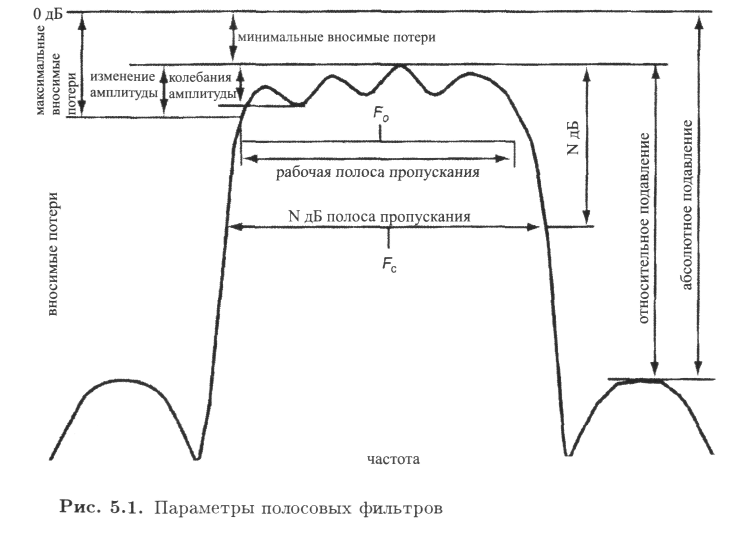
Рис. 1. Параметры фильтров




Рис. 2. Блок-схема беспроводного приемопередатчика


С самого начала развития телекоммуникационной техники для получения требуемых характеристик, например, высокой добротно­сти, использовались различные электромеханические фильтры, ко­торые, как правило, состоят из электромеханических преобразова­телей: одного на входе, другого на выходе, соединенных линией передач. Используемые механические и электромеханические ком­поненты обычно обладают сильным резонансом, что объясняется высокой добротностью таких фильтров. Для моделирования элек­тромеханических фильтров чаще всего применяется эквивалентная схема, которая может быть переведена в электрическую форму для упрощения проектирования и оптимизации. Для простоты анализа предполагается, что преобразователи не имеют никаких потерь.

Высокодобротные фильтры, имеющие в своем составе механиче­ские резонансные элементы, широко используются во многих систе­мах связи и радарах, работающих в килогерцовом частотном диапа­зоне. При увеличении частоты размеры фильтров уменьшаются и, в конце концов, их становится практически невозможно изготовить. Поэтому ВЧ электромеханические фильтры очень дороги и не при­годны для массового производства. Поскольку для широкого рас­пространения современных телекоммуникационных устройств не­обходимо снижать их стоимость, требуется разработка принципи­ально новых схем, способных заменить механические фильтры.

Принципы действия механических фильтров могут быть приме­нены к миниатюрным устройствам, способным работать на более высоких частотах. Такие фильтры работают на частотах до десят­ков МГц и при правильном монтаже обладают добротностью бо­лее 1000. В таких устройствах элек­трическая энергия превращается в форму механической энергии, например, в колебания электромеханического преобразователя на входе фильтра. Полученная механическая энергия через механиче­скую линию передач поступает на второй электромеханический пре­образователь, превращающий ее обратно в электрическую энергию. Механические и электромеханические компоненты, используемые в таких фильтрах, обычно имеют высокую частотную чувствитель­ность. Их механический резонанс определяет рабочую полосу ча­стот всего устройства. При небольших изменениях такие фильтры могут работать в области очень высоких частот (ОВЧ).

Существующие технологии позволяют изготавливать микрофиль­тры, работающие на частотах порядка 100 МГц, и планарные рас­пределенные фильтры – до частот нескольких ГГц. Фильтры и резонаторы на поверхностных акустических волнах (ПАВ) пере­крывают этот диапазон и позволяют реализовывать высокодоброт­ные устройства с рабочими частотами до 2 ГГц. В состав таких устройств входит встречно-штыревой (гребенча­тый) преобразователь (ВШП), запускающий поверхностные акусти­ческие волны по пьезоэлектрической подложке. На выходе устрой­ства, как правило, стоит аналогичный преобразователь, превраща­ющий акустические волны в электрические сигналы. Такие устрой­ства очень чувствительны к изменению частоты и поэтому могут использоваться в конструкциях фильтров. В настоящее время при помощи современных методов микрообработки возможно прецизионное изготовление таких планарных устройств. Предельно допустимые характеристики рассматриваемых устройств, как пра­вило, объясняются технологическими ограничениями. Для более высоких частот используются фильтры на объемных акустических волнах (ОАВ). Благодаря обоим типам фильтров: на ПАВ и ОАВ, стал возможным прогресс в развитии современных микросистем связи.

В ВЧ и СВЧ диапазонах для реализации фильтров широко ис­пользуются распределенные компоненты. Добротность фильтров при таком подходе ограничивается паразитными эффектами. Планар­ные фильтры на тонких диэлектрических мембранах обладают низ­кими потерями и подходят для недорогих, компактных и быстро­действующих монолитных СВЧ схем.


Моделирование механических фильтров


Рассматриваемые преобразователи ведут себя как резонаторы и для их анализа используются элек­трические и механические характеристики. Важными механически­ми характеристиками фильтров являются резонансная частота и добротность. Для улучшения рабочих характеристик фильтров не­сколько резонаторов могут объединяться вместе при помощи соеди­нительных элементов, например, проводов. Количество используе­мых резонаторов сильно влияет на форму рабочих характеристик фильтра, поскольку их резонансная частота определяет централь­ную частоту полосы пропускания фильтра. При увеличении экви­валентной массы резонаторов или коэффициента упругости соеди­нительных проводов происходит уменьшение полосы пропускания фильтра.

Несмотря на разную форму резонаторов, используемых в микро­устройствах, понимание их принципа действия помогает при про­ектировании фильтров на их основе.


Моделирование резонаторов


Механические свойства резонаторов зависят от их формы, типа ис­пользуемых материалов и от соответствующего вида колебаний. Су­ществует несколько классических описаний резонансных колебаний балок, стержней, тонких пластин и дисков, полезных при разработ­ке фильтров. В случаях, когда один из размеров резонатора сильно отличается от остальных двух, его математический анализ срав­нительно прост. Для таких резонаторов несложно вывести уравне­ния для описания продольных, крутильных, изгибных и радиальных колебаний. Для толстых резонаторов такой анализ уже весьма не­прост.

Для упрощенного анализа примем несколько предположений:

- Колебания имеют небольшую амплитуду, а зависимость де­формации от напряжений является линейной;

- В системе нет внутренних потерь и внешнего затухания коле­баний из-за сопротивления воздуха и т.д;

- Силой тяжести и магнитными силами можно пренебречь.

Анализ резонаторов проводится в следующей последовательности действий:

1⁰. Составляются дифференциальные уравнения, описывающие рас­пространение волны внутри резонатора. Они, как правило, имеют второй или четвертый порядок по пространственным координатам и второй порядок по времени.

2⁰. Для исключения зависимости от времени уравнения решаются для синусоидальных колебаний, которые записываются в век­торном виде.

3⁰. Решения уравнений представляются в виде тригонометриче­ских и гиперболических функций или функций Бесселя.

4⁰. Для исключения констант в решения уравнений подставляют­ся граничные условия. Определяются выражения частоты для разных типов волн.

5⁰. Полученные выражения подставляются в исходное дифферен­циальное уравнение и находится зависимость между номером волны и частотой.

6⁰. При помощи этой зависимости и уравнения для частоты опре­деляется резонансная частота для различных типов волн коле­баний.

7⁰. Находится эквивалентная масса в виде эквивалентной сосредо­точенной массы, помещенной в определенном месте на резона­торе, которая соответствует кинетической энергии элемента с распределенными параметрами, вибрирующего на заданном типе волны и резонансной частоте.


Стержневой резонатор с продольной волной


На рис. 3 показана схема возникновения продольной волны в тон­ком стержне. Материал стержня имеет плотность ρ и модуль Юнга Е. Уравнение волны в этом случае можно записать в виде:

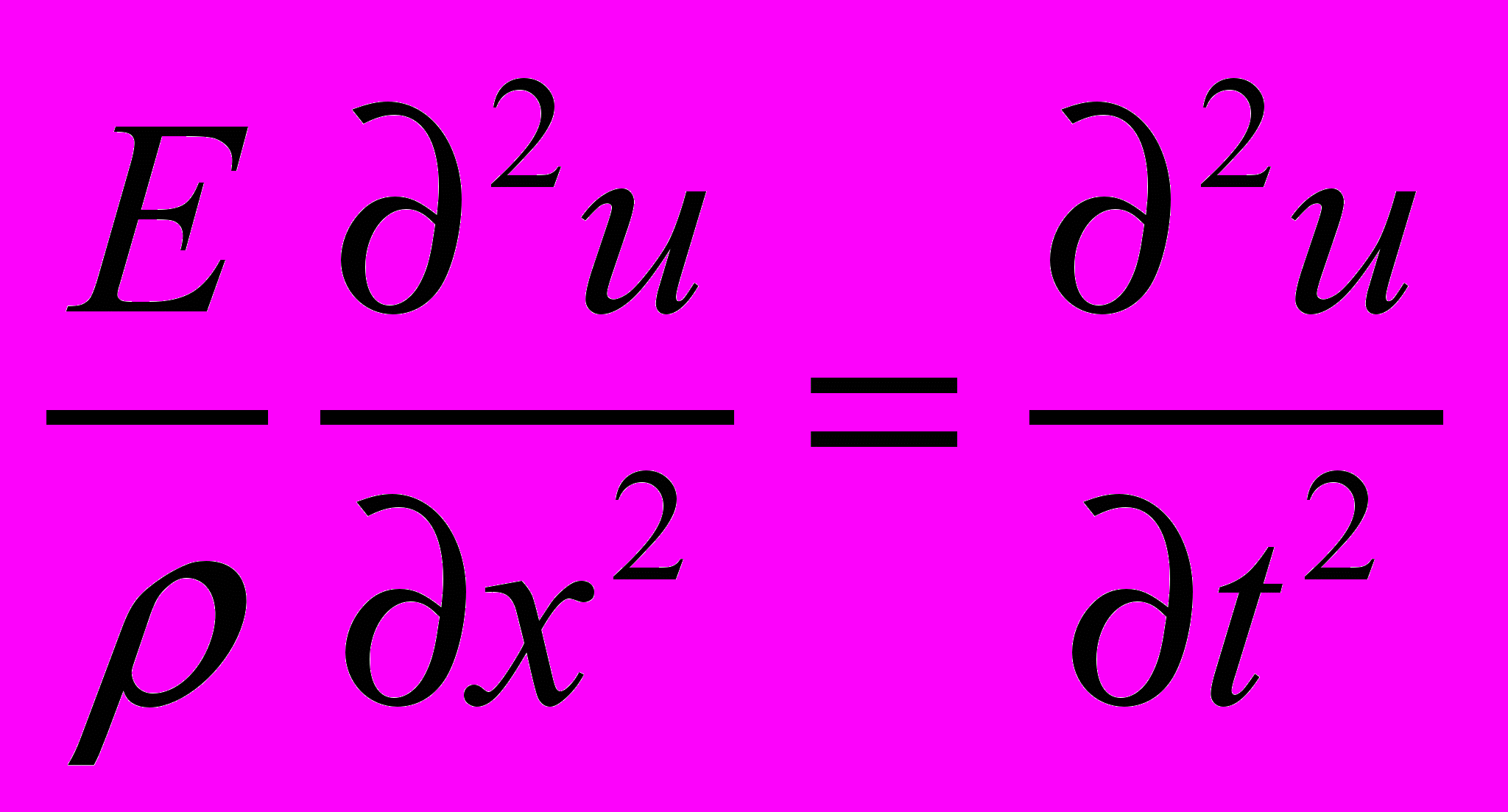(2)

где u показано на рис. 3. Используя векторную запись для исключе­ния временной зависимости, найдем решение уравнения (2) в виде тригонометрических функций. Считая, что оба конца стержня сво­бодны, уравнение для частоты будет следующим:

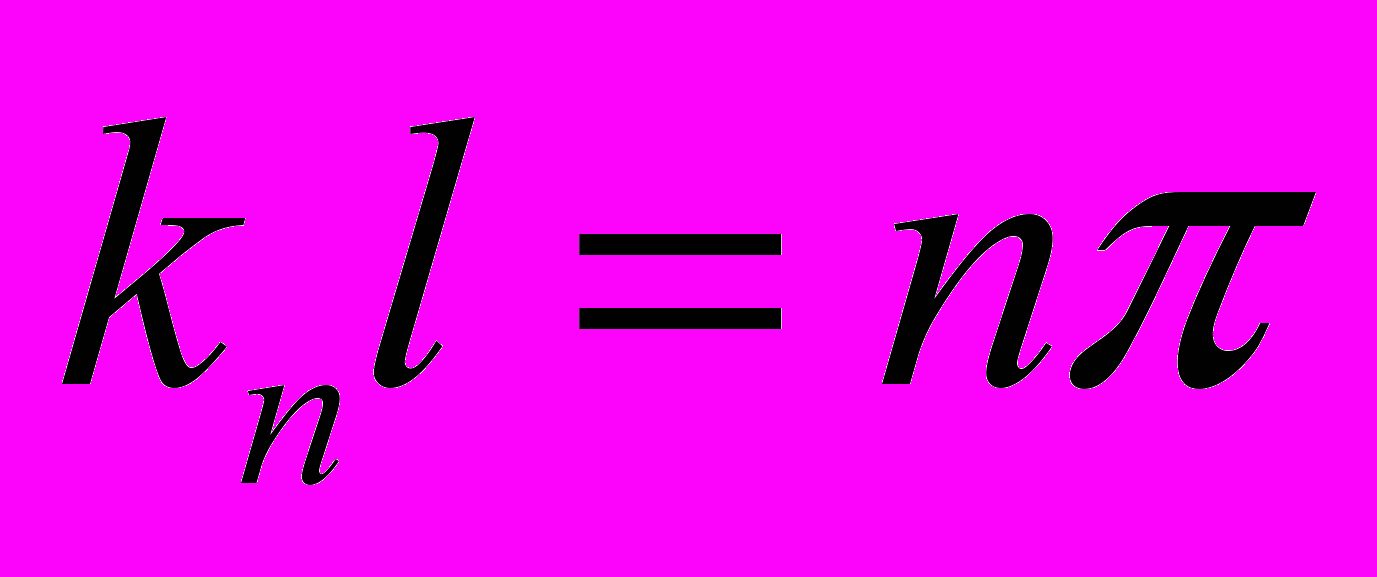
(3)

Из уравнения волны находится зависимость между константой распространения волны и частотой ω:

(4)

Отсюда выводится выражение для резонансной частоты:

(5)

Перемещение u_n(х) для n-ой волны можно записать в виде:

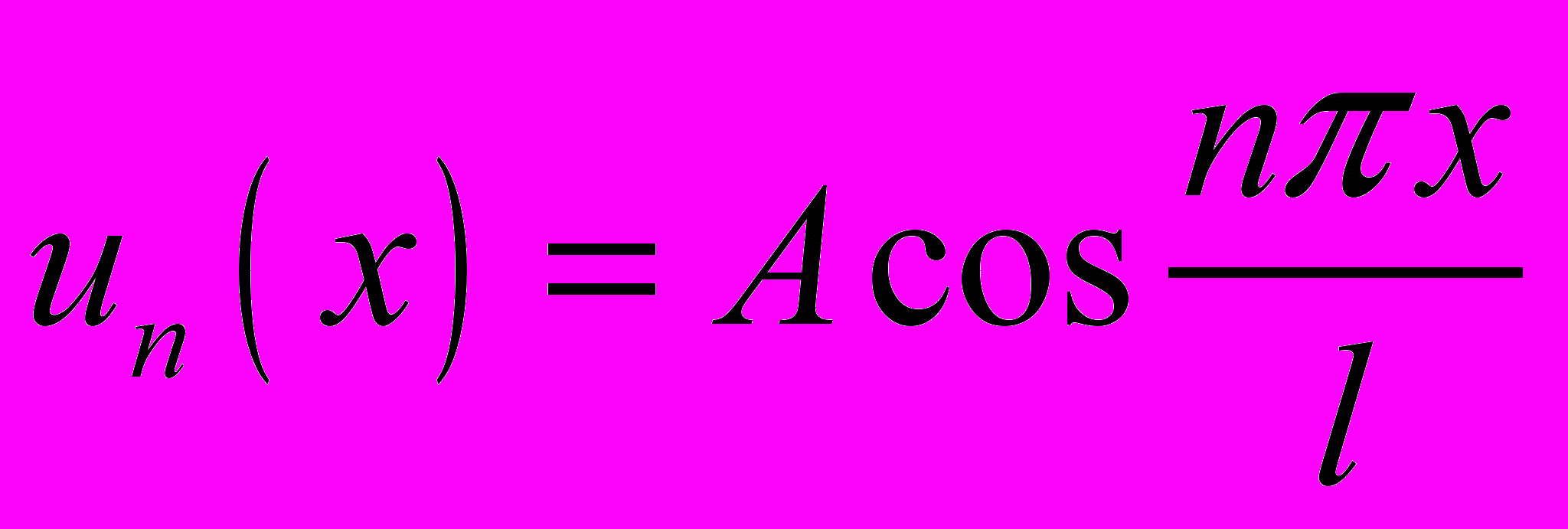(6)

где А – константа.




Рис. 3. Резонатор с продольной волной колебаний


Для продольной волны в тонком стержне выражение для экви­валентной массы имеет вид:

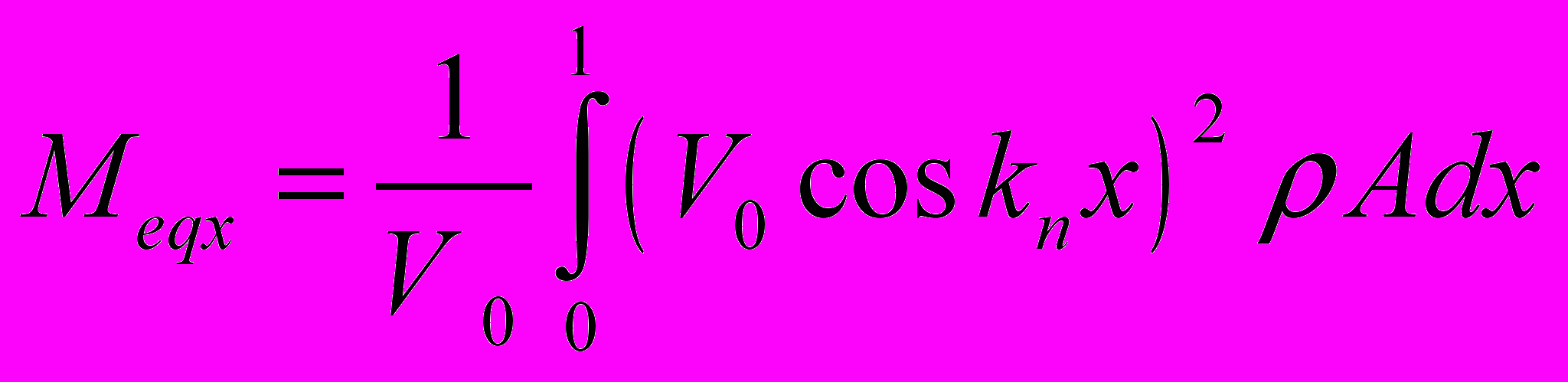(7)

где V₀ – скорость при х = 0.

Если радиус стержня больше десятой части длины волны, в урав­нении для перемещения необходимо учитывать радиальные измене­ния. Тогда выражение для резонансной частоты принимает вид:

(8)


Стержневой резонатор с волной кручения


На рис. 4 показана схема возникновения волны кручения в стерж­не. Уравнение волны в этом случае совпадает с уравнением про­дольной волны. Угловое перемещение и резонансная частота имеют следующий вид:

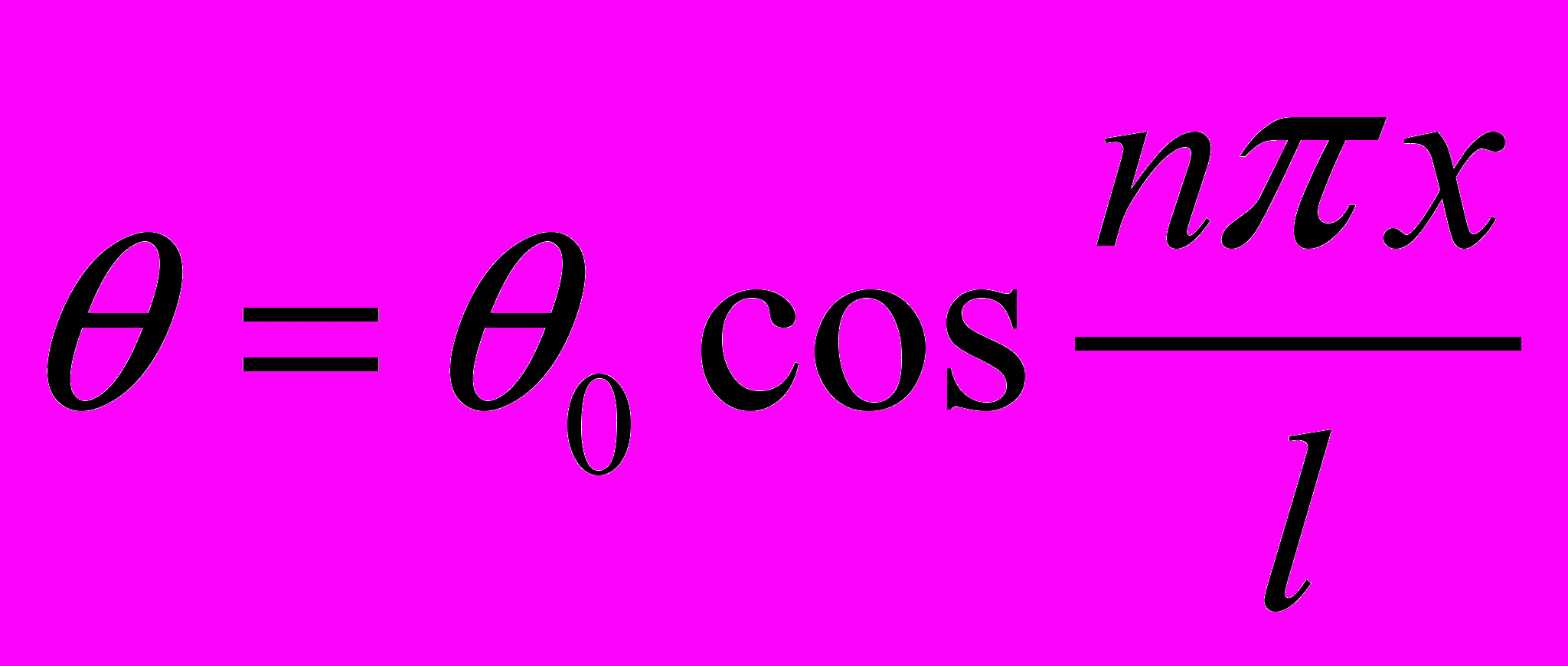(9)

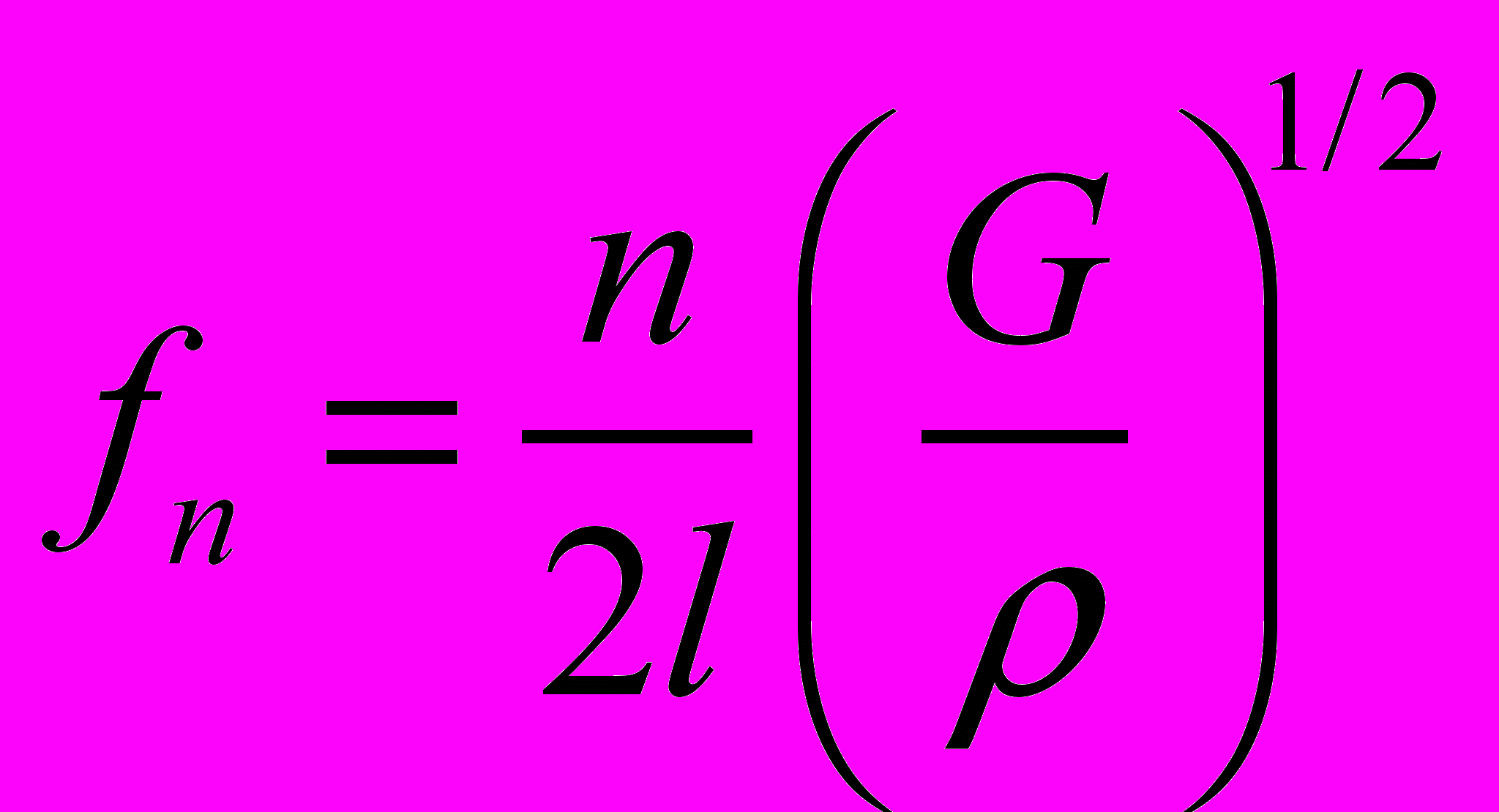(10)

где G – модуль кручения, θ₀ – угловое перемещение на конце стержня. Выражение для эквивалентной массы записывается как:

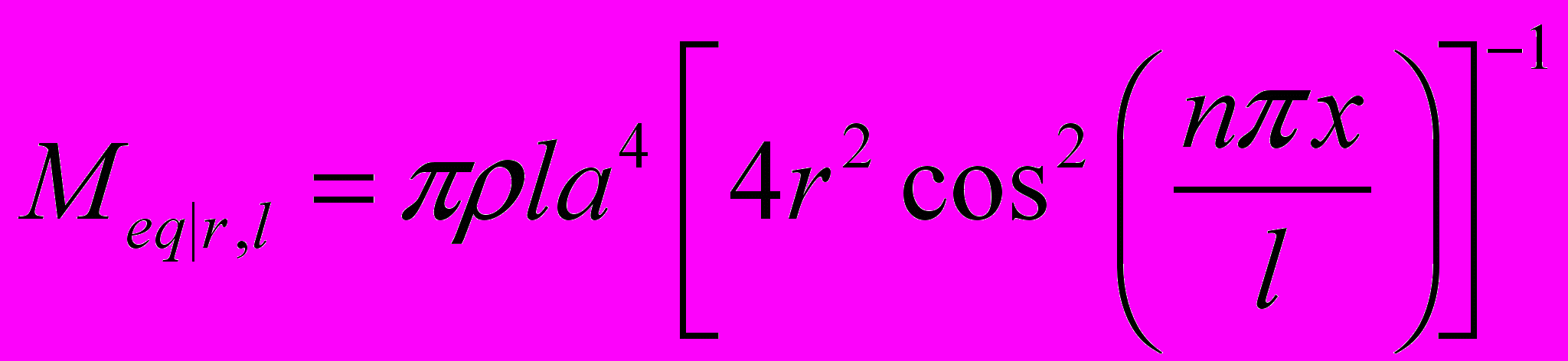(11)




Рис. 4. Резонатор с волной кручения


Стержневой резонатор с волной изгиба


Схема возникновения волны изгиба в стержневом резонаторе пока­зана на рис. 5. Уравнение имеет вид:

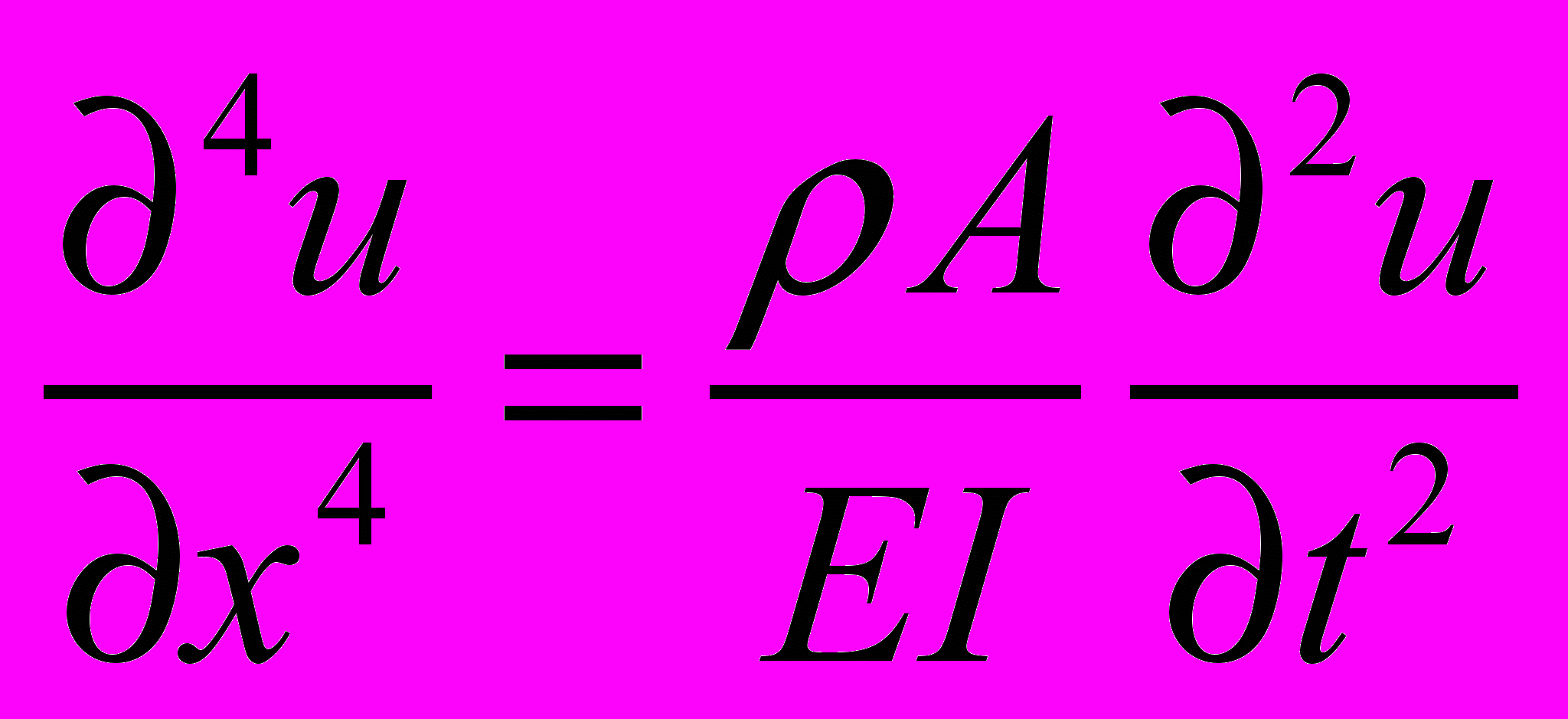(12)

где I – изгибающий момент инерции, который для прямоугольного стержня шириной w и толщиной h равен:

(13)

а для круглого стержня радиуса а –

(14)

Если оба конца стержня свободны или, наоборот, закреплены, уравнение для частоты находится из выражения:

(15)



Рис.5. Волна изгиба в стержневом резонаторе


Корни этого уравнения равны: к₁₁ = 4.73, к₂₁ = 7.853, к₃₁ = 10.996, к₄₁ = 14.137, ....

Дисперсионная зависимость между константой распространения волны и частотой имеет вид:

(16)

Отсюда находится выражение для резонансной частоты волны из­гиба:

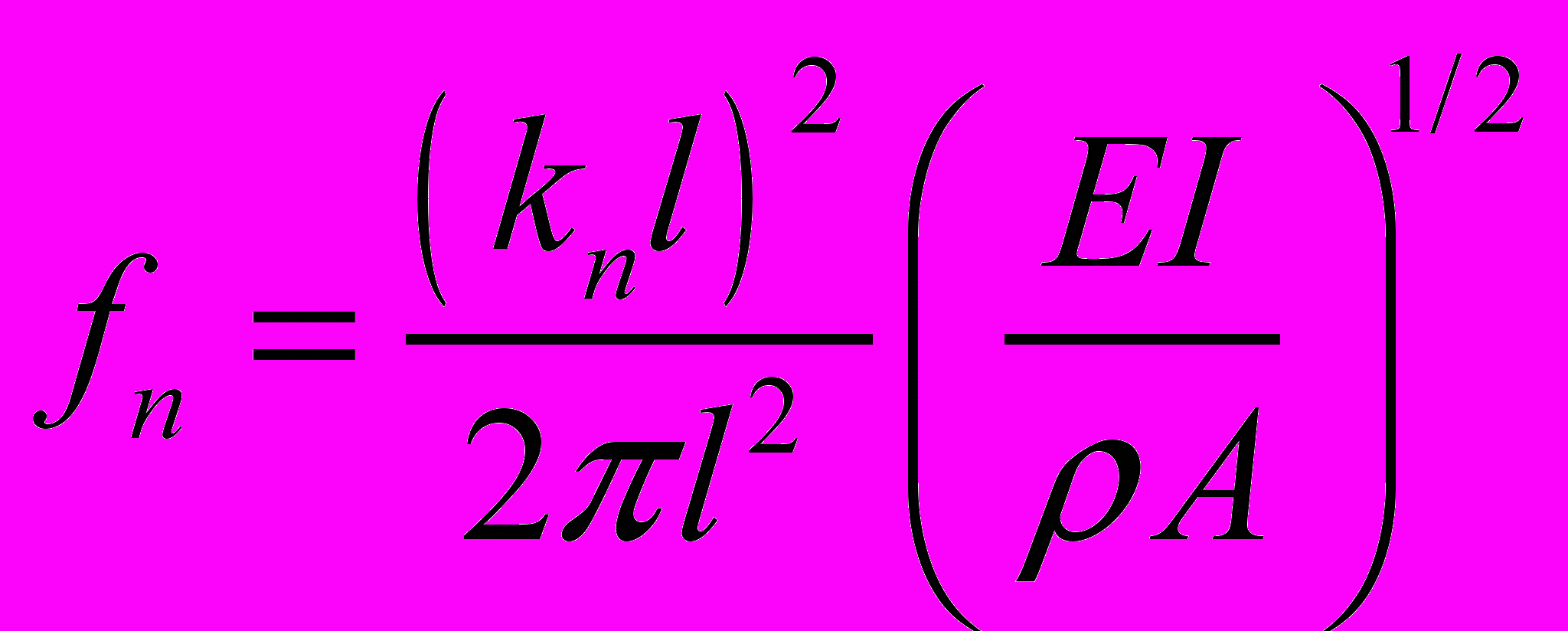(17)

Уравнение для эквивалентной массы имеет следующий вид:

(18)


Резонаторы с изгибающимся диском


На рис. 6 показана схема возникновения волны изгиба в дисковом резонаторе. Ее уравнение в прямоугольных координатах имеет вид:

(19)

Это уравнение проще всего решать в цилиндрической системе ко­ординат:

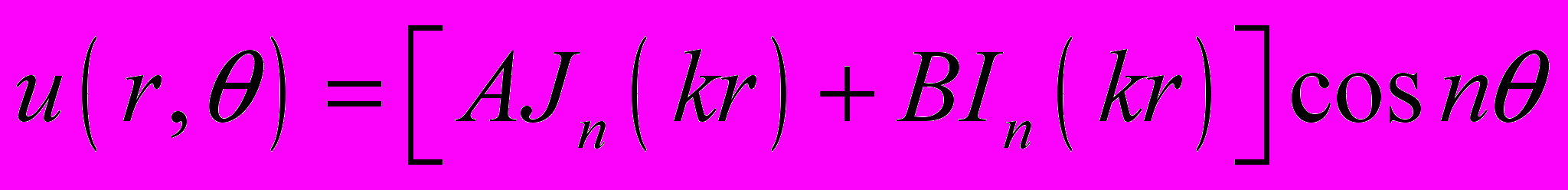(20)

Найденное выражение для частоты можно записать как:

(21)

Дисперсионная зависимость в данном случае имеет вид:

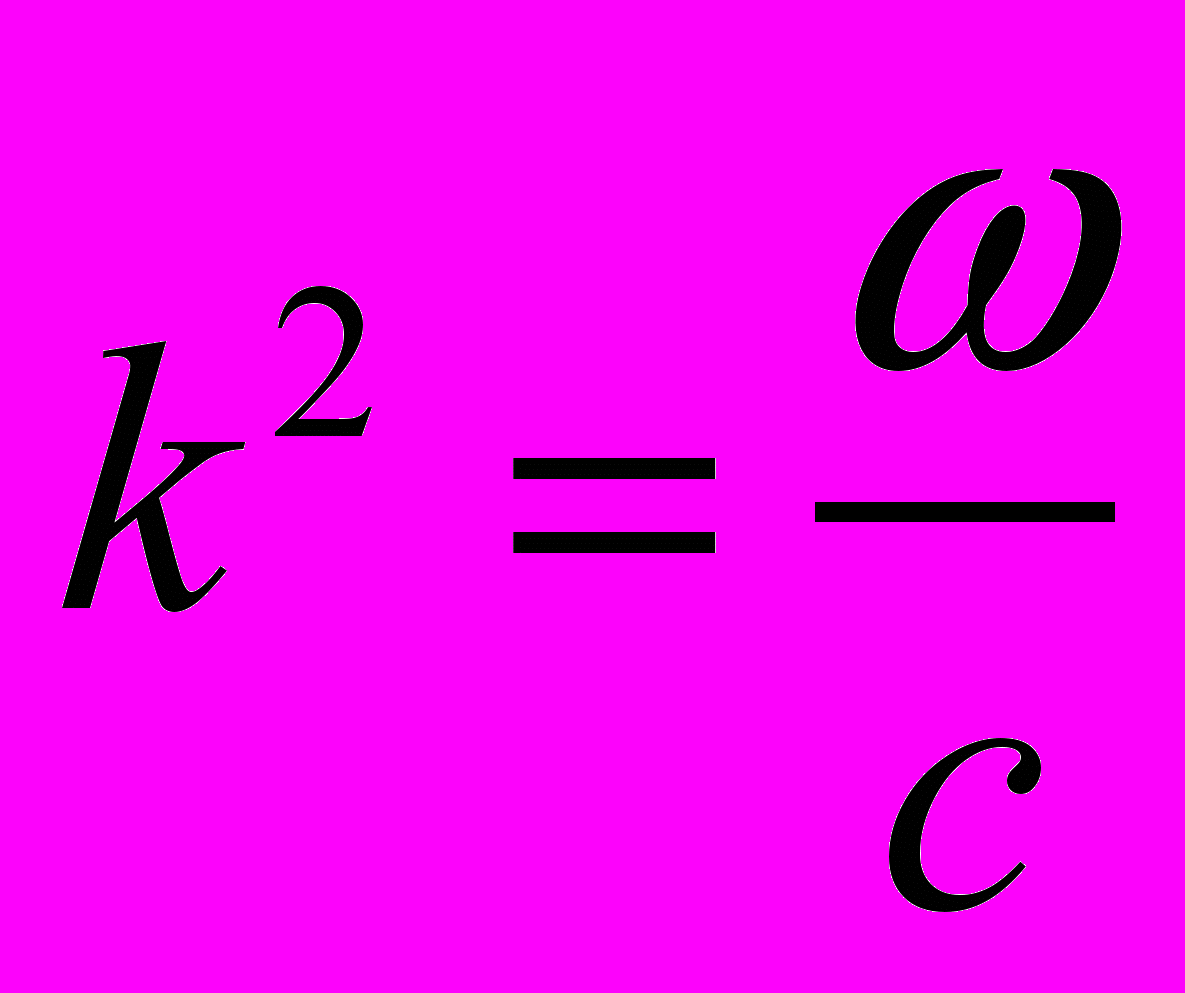(22)

Отсюда находится выражение для резонансной частоты:

(23)

Здесь индекс s соответствует центральной волне с круговой поля­ризацией изгибных колебаний. Уравнение для перемещения имеет вид:

(24)

Рис.6. Волна изгиба в диске


При s = l эквивалентная масса определяется выражением:

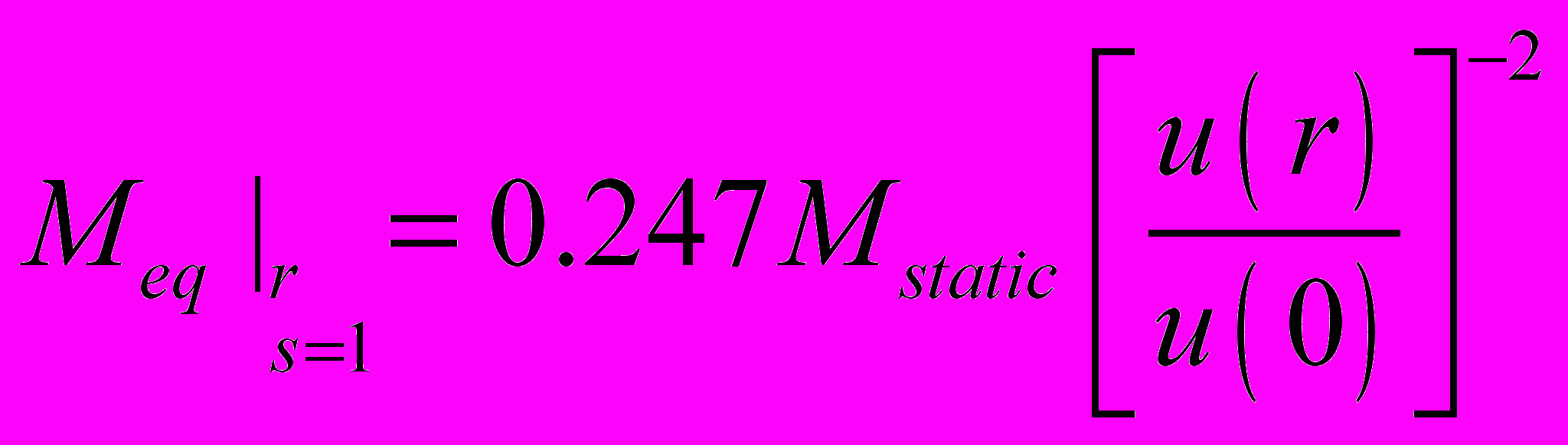(25)


Толстые диски и пластины


Дифференциальное уравнение, соответствующее колебаниям тол­стой круглой пластины, записывается как:

(26)

где ρ – плотность материала, h – толщина пластины, a D – ее диаметр.

Дисперсионная зависимость имеет вид:

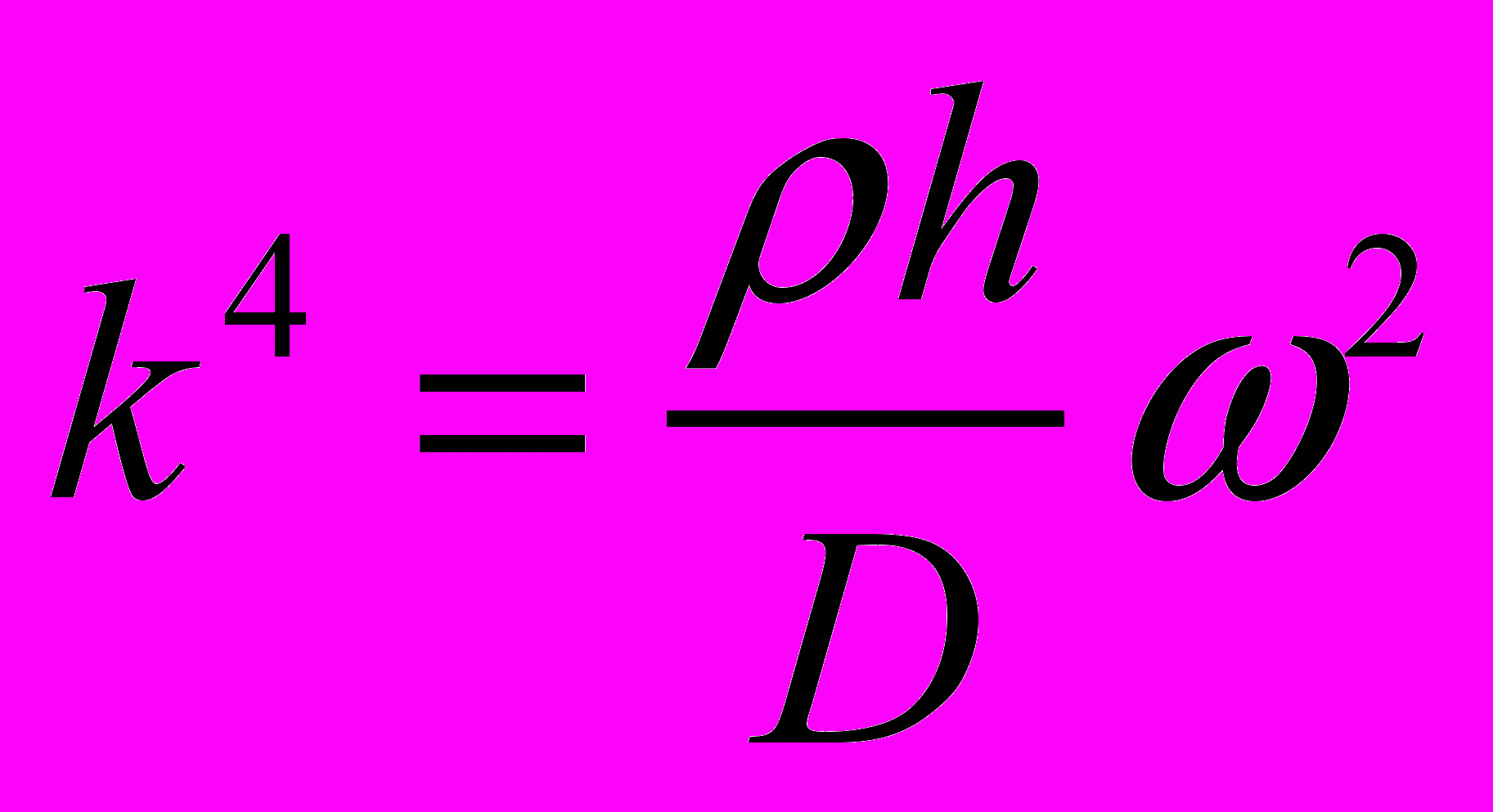(27)

а резонансная частота задается выражением:

(28)

Здесь α_n – корни характеристического уравнения

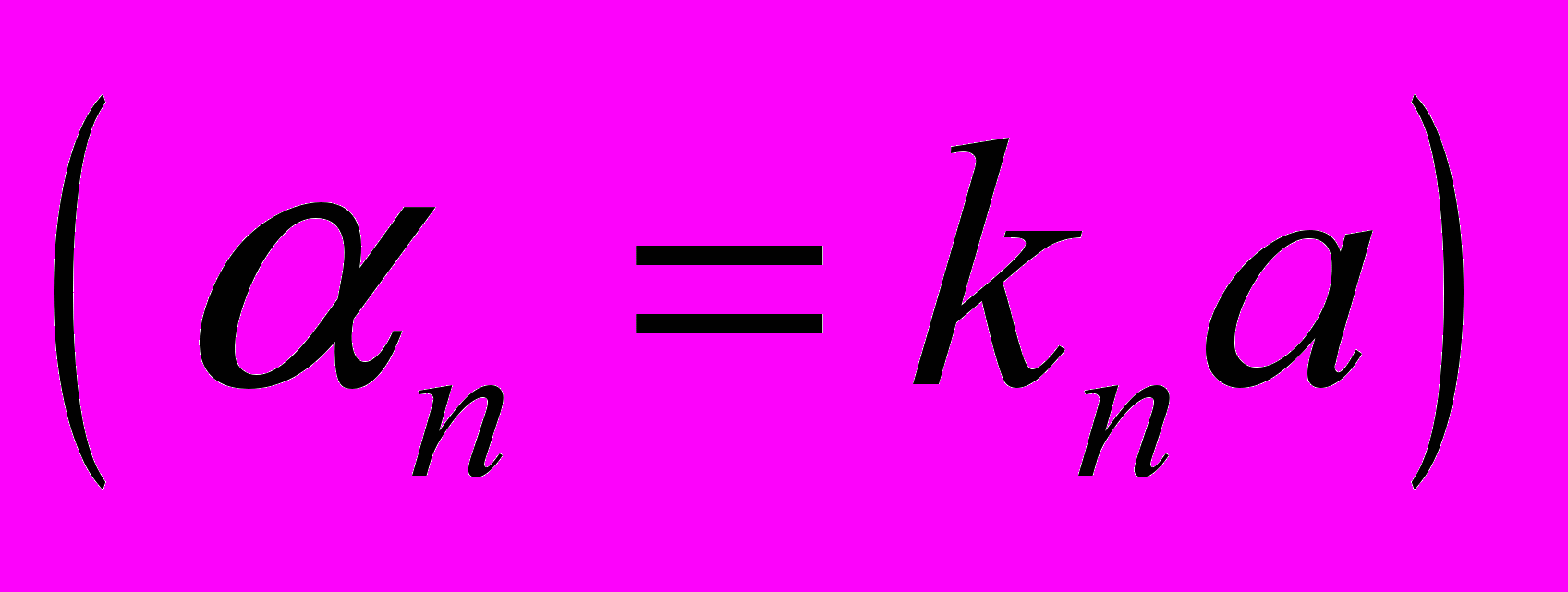
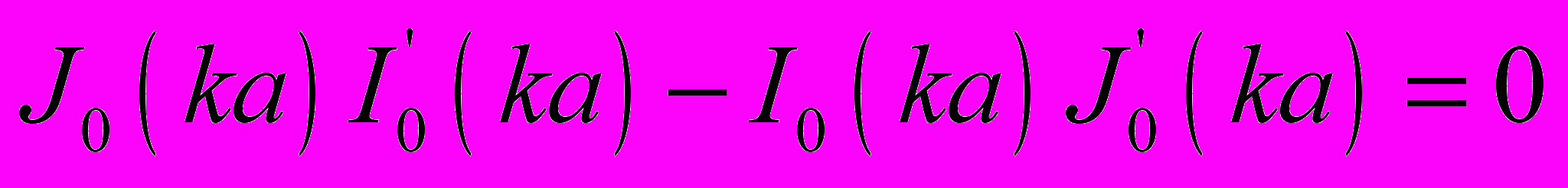(29)

Перемещение определяется как:

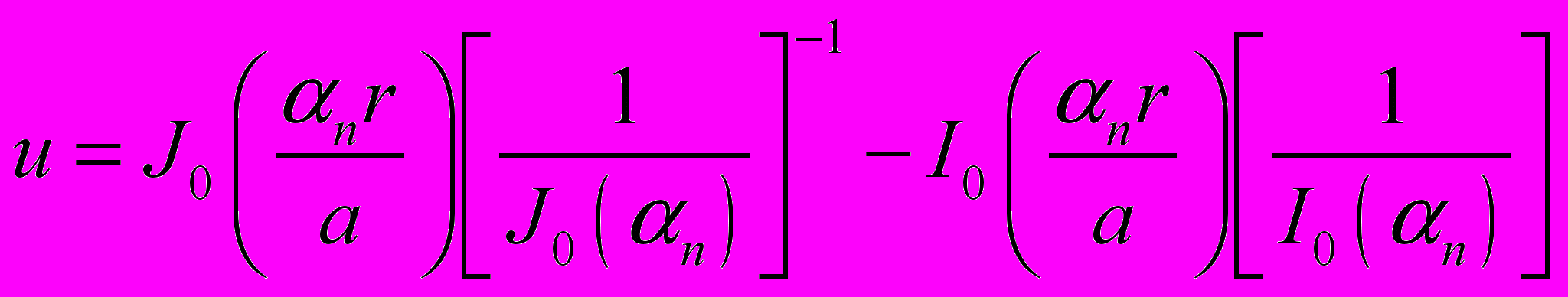(30)


Круговые и прямоугольные мембраны


Для круговой мембраны радиуса а двумерное уравнение распро­странения волны в полярных координатах с началом координат в центре мембраны имеет вид:

(31)

где ρ’’ – масса на единицу площади мембраны, F' – напряжение на ее краях. Дисперсионное соотношение для этого случая записы­вается как:

(32)

Решение дифференциального уравнения в пространстве имеет сле­дующий вид:

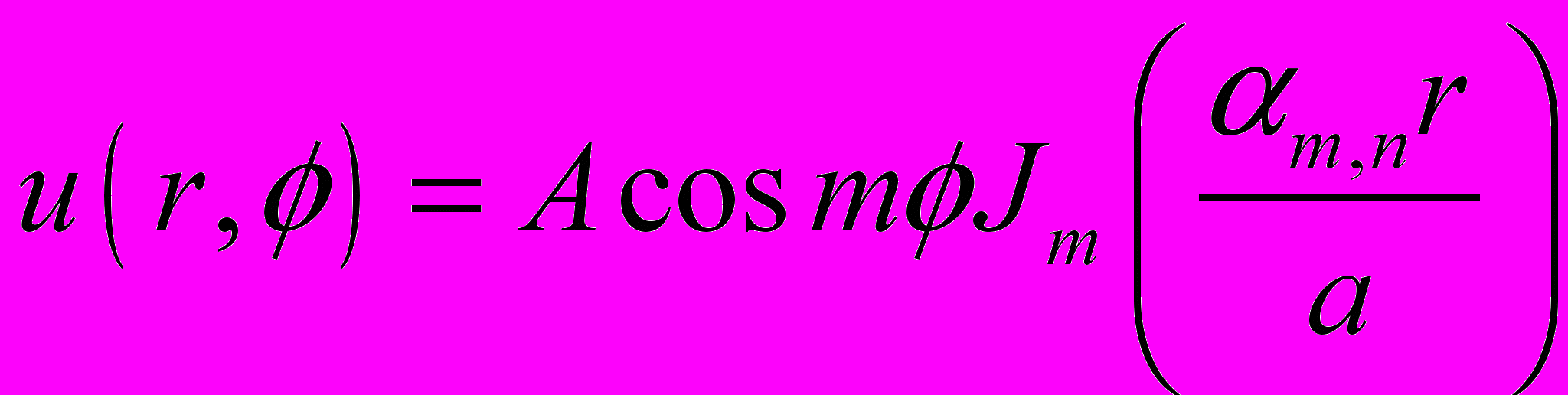(33)

где А – произвольная константа, α_m,n – значения а при J_m(αa) = 0, удовлетворяющие граничным условиям. Тогда резонансная частота задается следующим выражением:

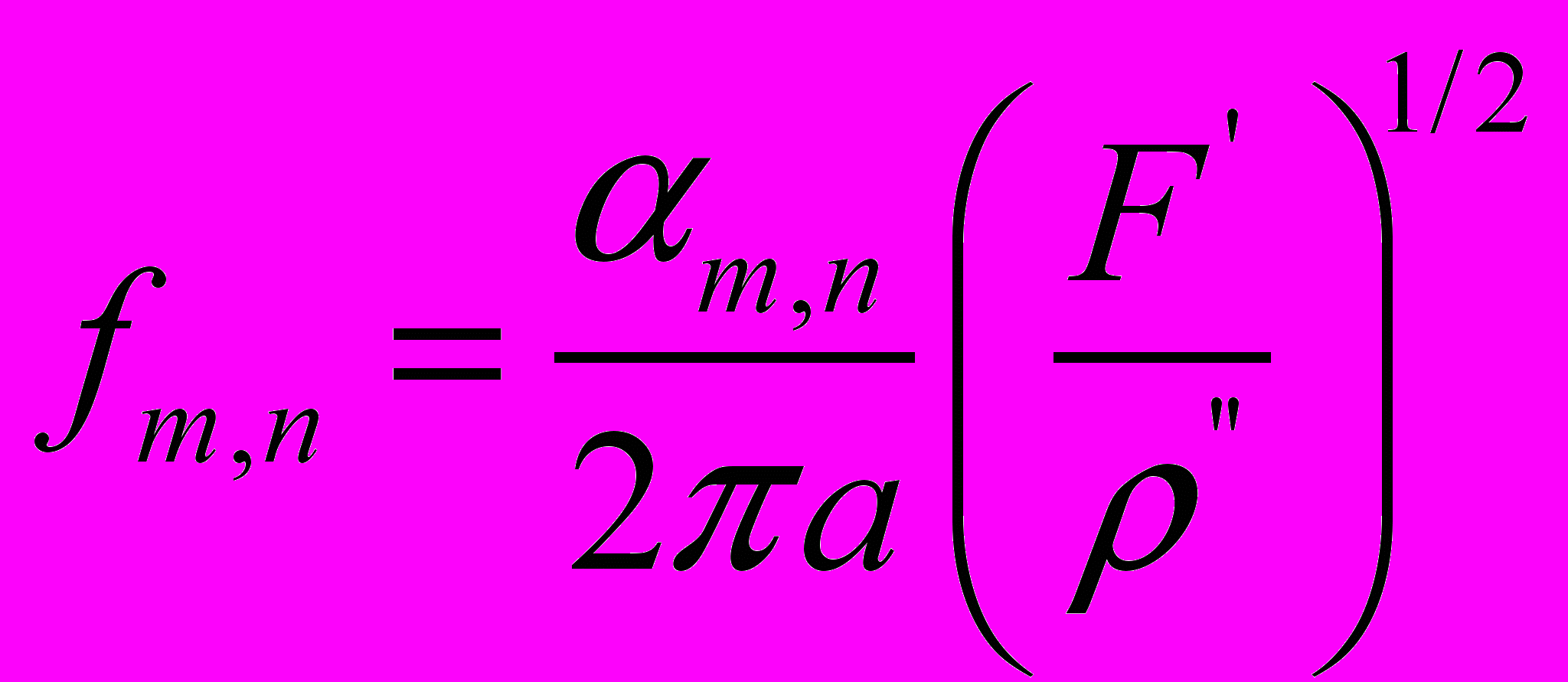(34)

Для первых пяти значений резонансной частоты волновые коэффици­енты в уравнении (5.34) равны: α₀₁ = 2.406, α₀₂ = 5.52, α₀₃ = 8.654, α₀₄ = 11.792 и α₀₅ = 14.931.

При применении прямоугольной мембраны дифференциальное уравнение меняется. В декартовых координатах его решение имеет вид:

(35)

где а и b – размеры мембраны в направлениях x и y, А – кон­станта, тип положительные целые числа, которые не могут одновременно равняться нулю.

Резонансная частота определяется выражением:

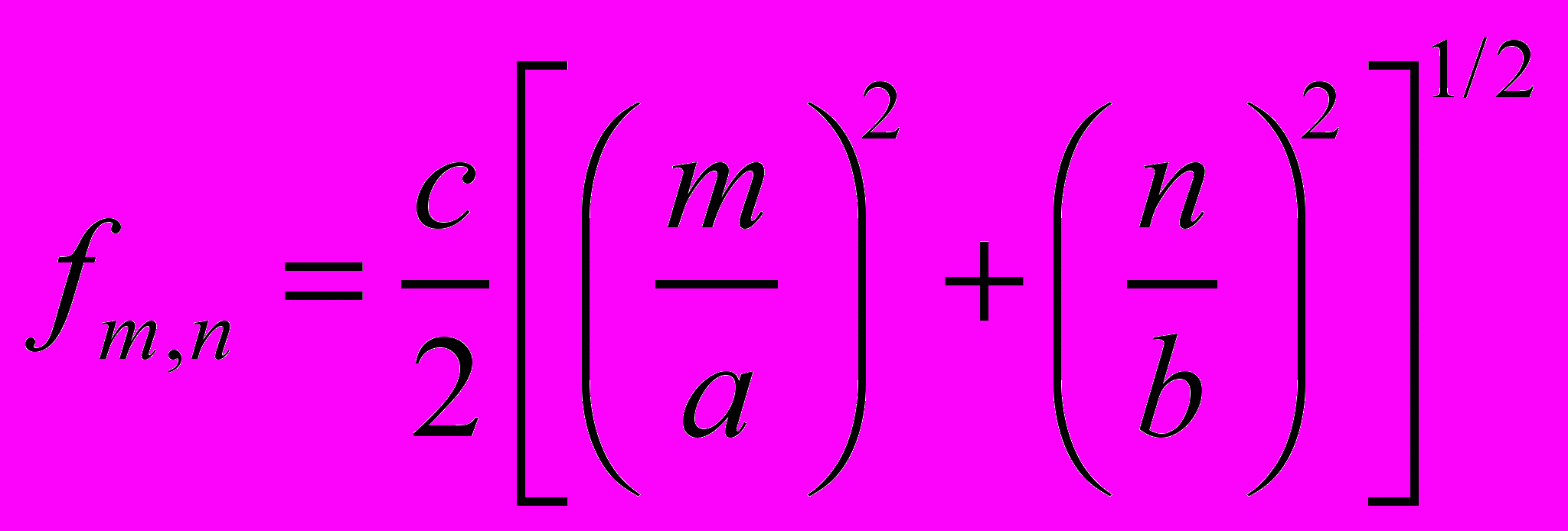(36)

Контрольные вопросы

1. Характеристики и параметры полосковых фильтров.
   
2. Моделирование резонаторов (предположения, последовательность действий).
   
3. Стержневой резонатор с продольной волной. Схема. Математическая модель.
   
4. Стержневой резонатор с волной кручения. Схема. Математическая модель.
   
5. Стержневой резонатор с волной изгиба. Схема. Математическая модель.