Одним из важнейших направлений астрономии в течение последнего времени является обработка астрономических изображений, т е

Вид материала

Документы

Содержание S=0: for k=1 то 6: a=rnd: s=s+rnd-rnd: next k

Подобный материал:

• Примерная рабочая программа по дисциплине «Компьютерная обработка изображений» Факультет:, 75.51kb.
• Белорусский государственный университет применение информационных технологий при анализе, 187.23kb.
• Обработка и передача изображений, 213.76kb.
• Программа элективного курса «робототехника», 222.82kb.
• Переработка побочных продуктов процесса совместного получения оксида пропилена и стирола, 129.08kb.
• Электролиз введение, 421.2kb.
• -, 147.54kb.
• Реферат по физике на тему: Дережинского Сергея «а» класс, 410.05kb.
• Акция "Служим Беларуси", 191.56kb.
• Всероссийская политическая партия «единая россия» партийный проект, 147.37kb.

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ И ОБРАБОТКА АСТРОНОМИЧЕСКИХ ИЗОБРАЖЕНИЙ


Халак Василий


Научный руководитель: И.Л.Андронов,

доцент кафедры астрономии ОГУ


Одним из важнейших направлений астрономии в течение последнего времени является обработка астрономических изображений, т.е. оп­ределение средней освещенности в зависимости от координат изобра­жения. Классический методом является метод наименьших квадратов, позволяющий описывать данную зависимость гладкой функцией, "гася­щей" высокочастотные шумы, связанные с погрешностью наблюдений.

Поскольку двумерное изображение, заданное в дискретных точках, можно представить в виде наложения одномерных "разрезов", рас­смотрим для начала аппроксимацию функции z(x,у) по одной оси при фиксированном y:

z^*(x) = a₀ + a₁ cos x + a₂ cos2x + ... a_k coskx + (1)

+ b₁ sin x + b₂ sin2x + ... b_k sinkx

Поскольку значения z(x) заданы в дискретных точках x_j=lj/n, где

n - число точек, а l - масштабный коэффициент, значения неизвест­ных a₀,...,a_k,b₁,...,b_k, согласно методу наименьших квадратов равны (для =2/n):



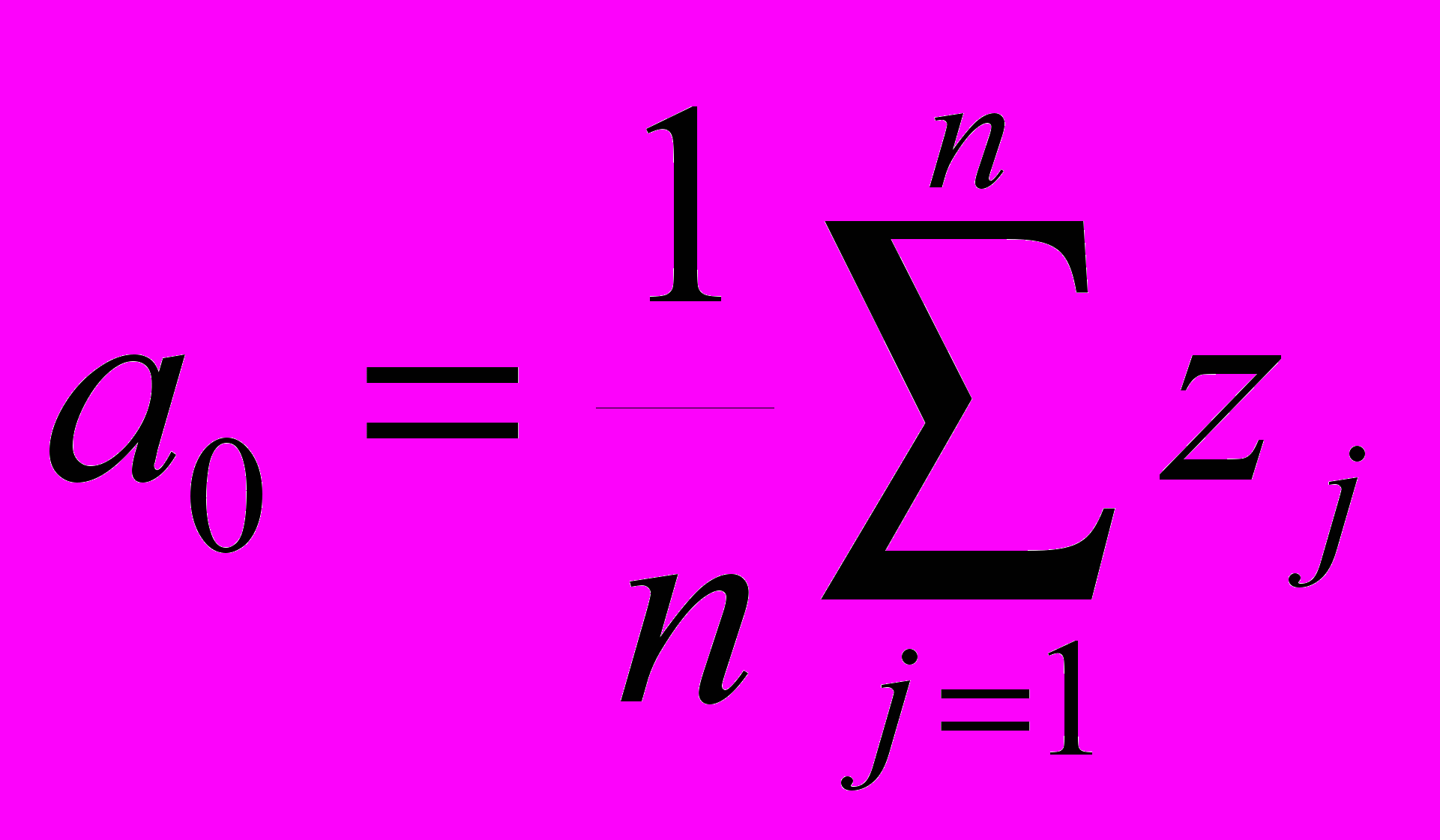
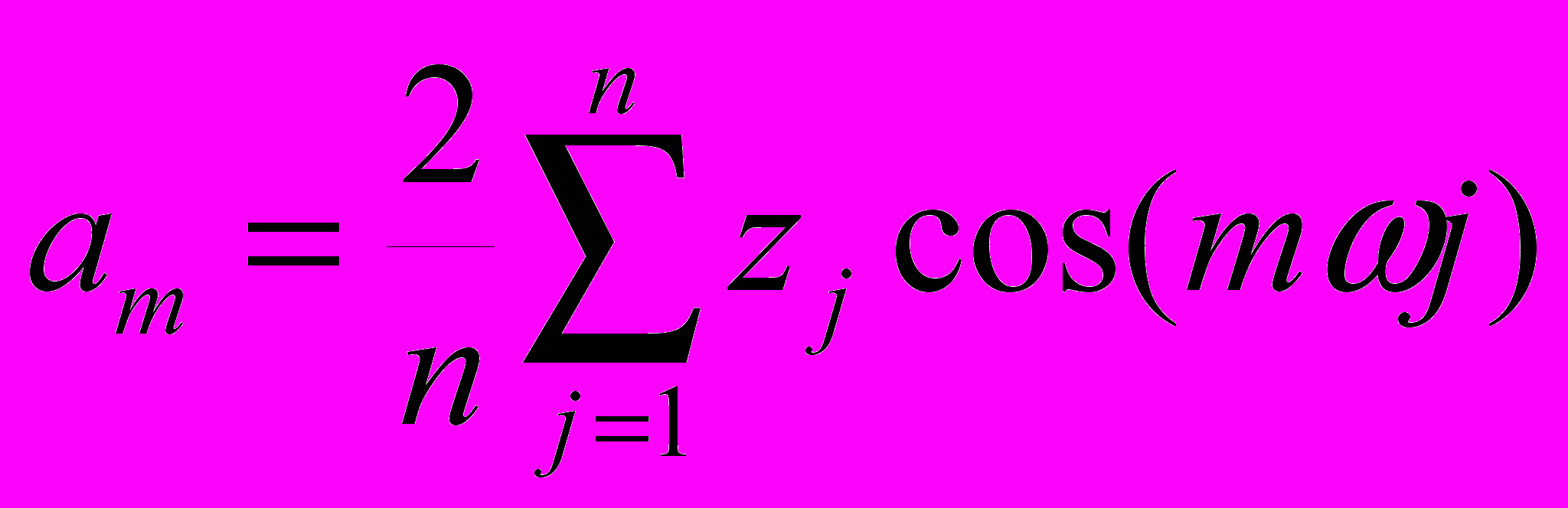(2)



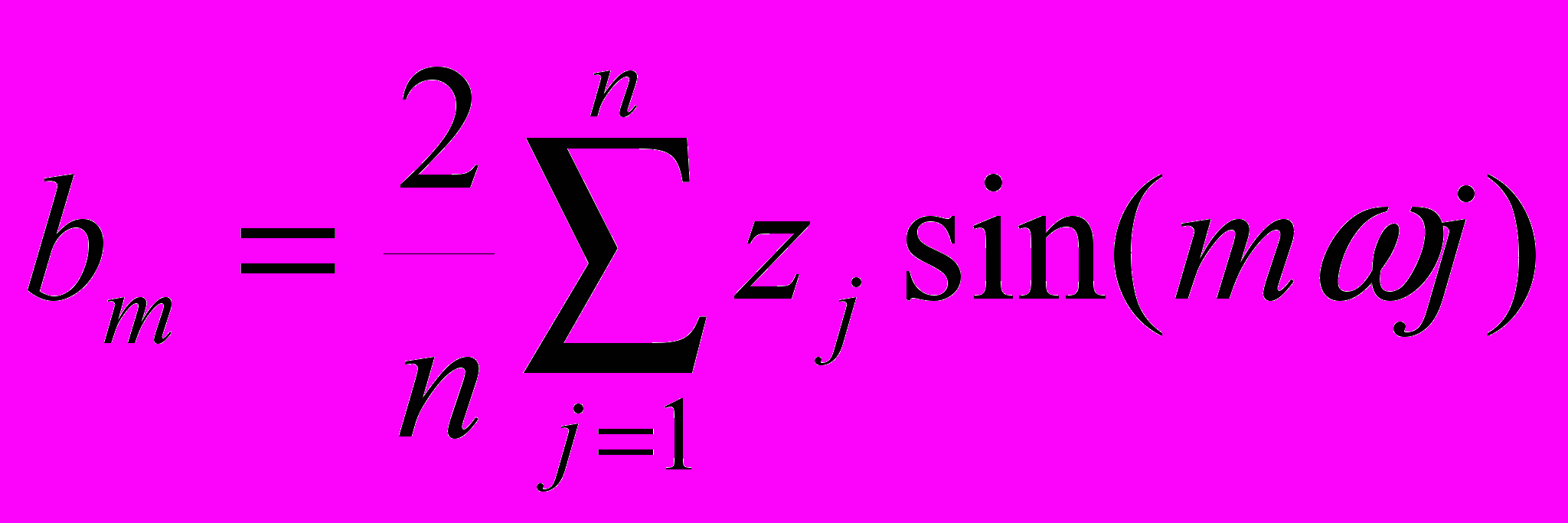
Соотношения 2 справедливы для всех m=1,...,k(n-1)/2 при нечетных значениях n. При четных n, b_k=0, а a_k следует разделить пополам по сравнению с формулой (2).

Нами была исследована зависимость формы сглаженной кривой (1) от числа гармоник k.Вычисления проводились первоначально на каль­куляторе, а затем была составлена программа на языке GW-Basic для ПЭВМ. В качестве примера мы задавали значения z(x_j)=z_j, равные

z_j = A exp(-j-B)²/C ) + D RND_j (3)

и варьировали значения коэффициентов A,B,C,D. Здесь RND_j - случай­ное число. Также строились зависимост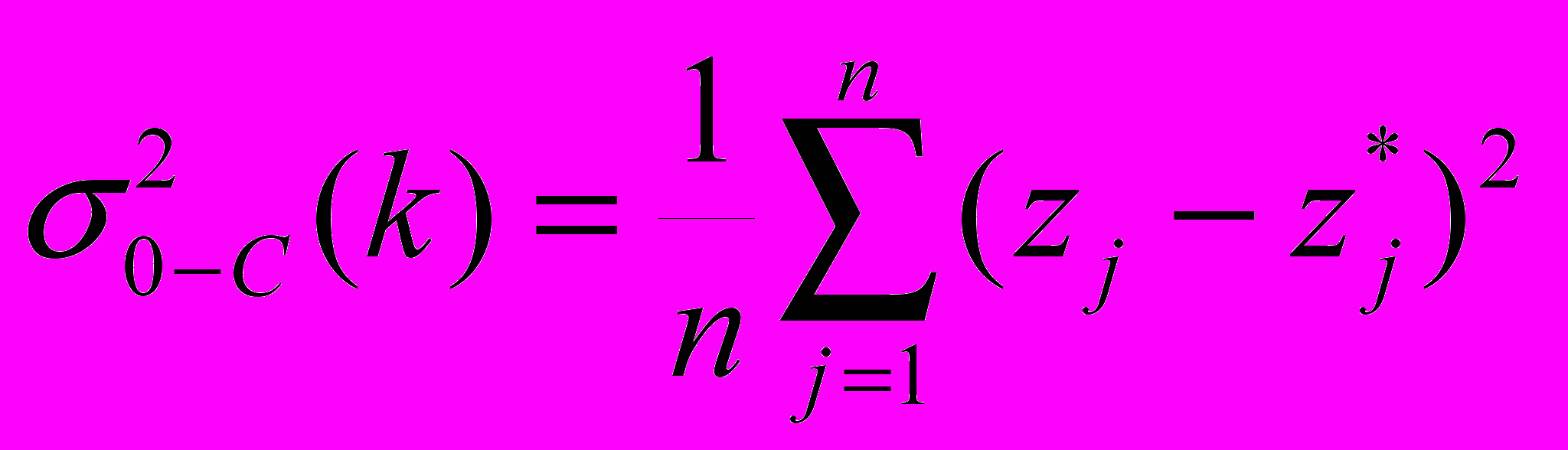и и 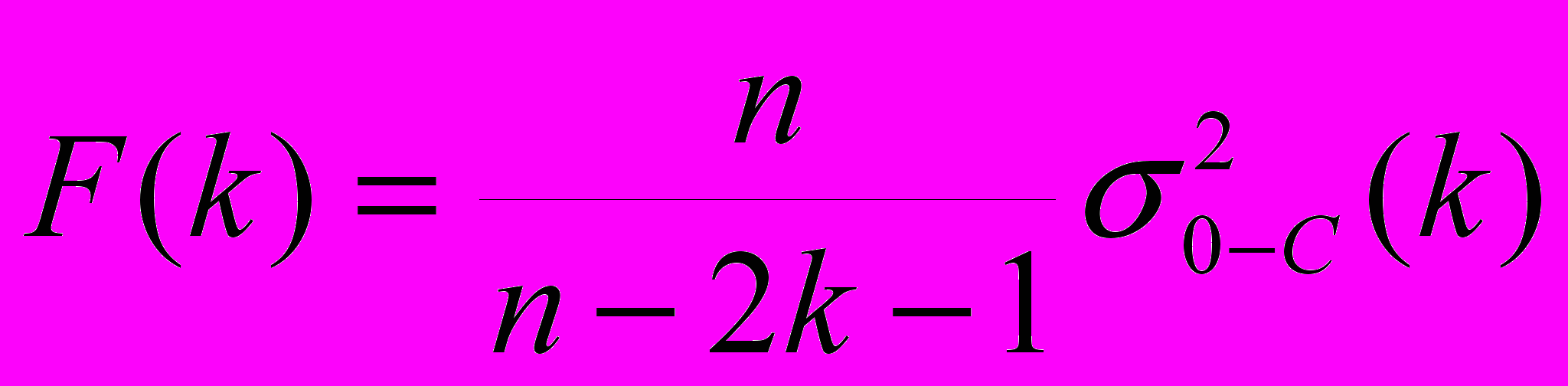от величины k.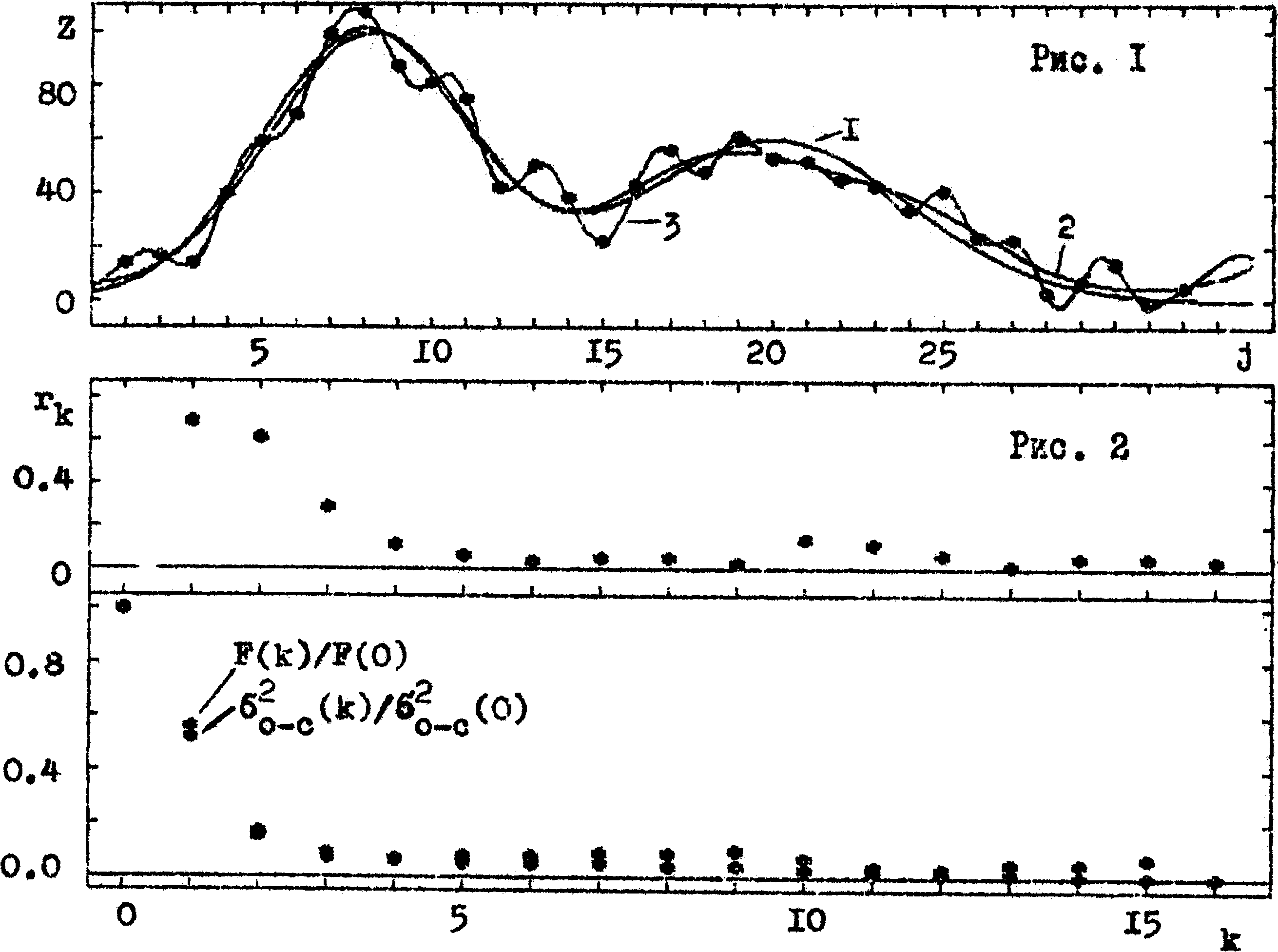




На рисунке I показан график пробной функции

z(x)= 100*exp(-(x-8)²/18) + 60* exp(-(x-20)²/32)

(линия I), ее значения в точках x_j=j, искаженные добавкой 10*RND

(кружки), аппроксимации по формуле (1) для k=4 (сглаживающая линия 2) и k=16 (интерполирующая линия 3). Как видно из рисунка, значе­ние k=4 достаточно для построения гладкой кривой, с хорошей точно­стью описывающей сумму двух экспонент. Небольшое систематическое отличие для 19<x<23 от "истинной кривой" I связано со случайным "выпадением вниз" четырех точек подряд. В качестве генератора слу­чайных чисел использовалась последовательность команд на языке бейсик, вызывающих встроенный генератор случайных чисел RND:

S=0: FOR K=1 ТО 6: A=RND: S=S+RND-RND: NEXT K

При каждом вызове значение RND меняется в интервале от 0 до 1, а сумма S близка к нормально распределенной случайной величине c нулевым средним и единичной дисперсией.

На рис.2 показаны зависимости относительной амплитуды

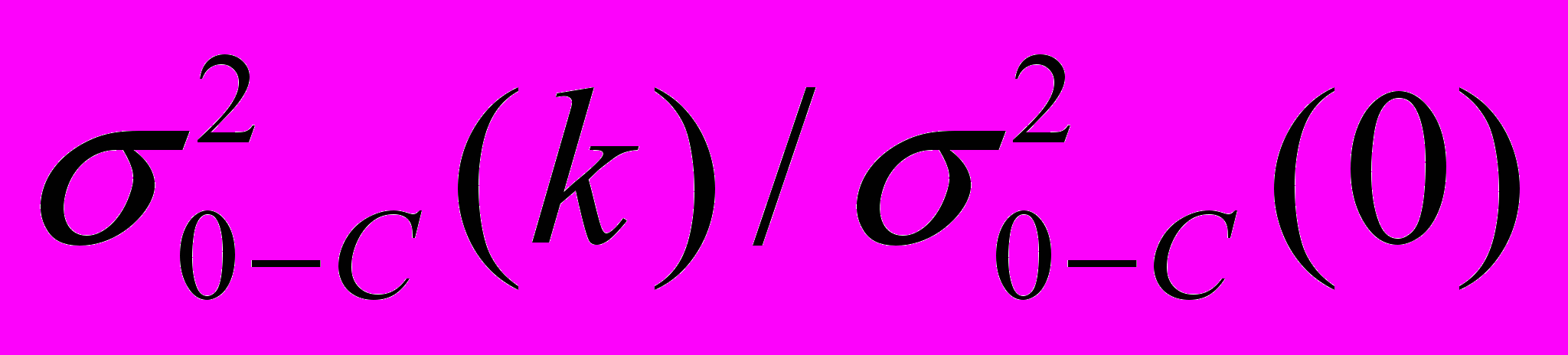, параметров и

F(k)/F(0). Как видно из рисунка, при k>4 значение последнего па­раметра меняется незначительно, образует "плато", поэтому гармо­никами с k>4 можно пренебречь, как отражающими высокочастотные шумы. Это же видно и по резкому уменьшению амплитуд r_k.


ОБЛАСТНАЯ СТАНЦИЯ ЮНЫХ ТЕХНИКОВ им.АКАДЕМИИ НАУК УКРАИНЫ
ОБЛАСТНОЙ ИНСТИТУТ УСОВЕРШЕНСТВОВАНИЯ УЧИТЕЛЕЙ, ПЕРВЫЕ ШАГИ,
Выпуск V, Одесса, 1992г. Подписано к печати 18.06.92г. Формат 60х94 1/16