Мезоны со скрытым «очарованием»

Вид материала

Документы

Содержание Частная теория относитель­ности Частотная модуляция ЧАСТОТНО-КОНТРАСТНАЯ ХАРАКТЕРИСТИКА (функция передачи модуляции) Рис. 1. Принципиальная схема конденса­торного частотомера. Рис. 2. Блок-схема цифрового частотомера. В. П. Кузнецов. Рис. 1. Движение заряж. ч-цы в среде со скоро­стью v Рис. 2. Движение заряж. ч-цы в среде со скоростью v>u. Угол между направлениями волново­го вектора возникающего из­лучения и ско Черенковский счётчик Z — заряд ч-цы (в ед. элемен­тарного электрич. заряда). В Ч. с. свет излучается только ч-цами, ско­рости к-рых v c Черная дыра Черное излучение Черное тело Четность уровня Числа заполнения Чистое состояние

Подобный материал:

• 1. Некоторые характеристики и свойства микрообъектов, 610.11kb.
• Мой путь я не магиня, но очарованием добьюсь того же Миру мир, 6.5kb.
• Программа курса лекций, 75.02kb.
• Барионы и мезоны. Метастабильные адроны и резонансы. Странные и очарованные адроны., 22.91kb.
• Пояснительная записка Знания дети удивления и любопытства, 216.78kb.
• Москва. Золотое кольцо очарование старины, 72.69kb.
• Производительности, 244.32kb.
• «Тайны бытия в поэзии символизма в творчестве К. Д. Бальмонта», 162.29kb.
• Часы раннего утра наполнены особой свежестью и своим непередаваемым очарованием, 2340.28kb.
• Л. Б. Вишня Борис Годунов. Реферат, 335.66kb.

Ч

«ЧАРМ»

ЧАРМОНИЙ

ЧАС

ЧАСТНАЯ ТЕОРИЯ ОТНОСИТЕЛЬ­НОСТИ

ЧАСТОТА КОЛЕБАНИЙ

ЧАСТОТНАЯ МОДУЛЯЦИЯ

ЧАСТОТНО-КОНТРАСТНАЯ ХАРАКТЕРИСТИКА

ЧАСТОТОМЕР

ЧЕРЕНКОВА — ВАВИЛОВА ИЗЛУЧЕНИЕ

ЧЕРЕНКОВСКИЙ СЧЁТЧИК

ЧЕРНАЯ ДЫРА

ЧЕРНОЕ ИЗЛУЧЕНИЕ

ЧЕРНОЕ ТЕЛО

ЧЕТНОСТЬ

ЧЕТНОСТЬ УРОВНЯ

ЧИСЛА ЗАПОЛНЕНИЯ

ЧИСТОЕ СОСТОЯНИЕ

ЧУВСТВИТЕЛЬНОСТЬ

«ЧАРМ» , то же, что «очарование».

ЧАРМОНИЙ (от англ. charm — оча­рование), то же, что мезоны со скрытым «очарованием».

ЧАС (ч, h), внесистемная ед. времени, равная 60 мин или 3600 секундам. В часовой мере принято выражать небесные координаты светил в астро­номии: прямое восхождение и часовые углы. При этом большой круг сферы делится на 24 ч; т. о., 1ч=15°.

ЧАСТНАЯ ТЕОРИЯ ОТНОСИТЕЛЬ­НОСТИ, специальная теория отно­сительности; см. Относительности теория.

ЧАСТОТА КОЛЕБАНИЙ, величина, обратная периоду колебаний T(f=1/Т), т. е. равная числу периодов колебаний (числу колебаний), совер­шаемых в единицу времени. Обычно Ч. к. измеряется в герцах: 1 Гц соответствует одному колебанию в секунду. Часто используется также величина =2f, наз. циклической или круговой частотой. В случае гар­монич. волновых процессов

u(x, t)=Acos(t± kx),

где А — амплитуда колебаний, t — время, х — координата. Круговая Ч. к. связана с волновым числом k и фазо­вой скоростью v соотношением =kv.

ЧАСТОТНАЯ МОДУЛЯЦИЯ, вид мо­дуляции колебаний, при к-рой часто­та высокочастотного колебания изме­няется во времени по закону, соответ­ствующему передаваемому сигналу.

ЧАСТОТНО-КОНТРАСТНАЯ ХАРАКТЕРИСТИКА (функция передачи модуляции), ф-ция, с помощью к-рой

оценивают «резкостные» св-ва изобра­жающих оптич. систем и отд. элемен­тов таких систем. Ч.-к. х. есть преобра­зование Фурье т. н. функции рассеяния линии, описываю­щей характер «расплывания» изобра­жения одной отдельно взятой тонкой линии. Ч.-к. х. даёт более полную информацию о св-вах изображающей системы, чем разрешающая способ­ность, характеризуя возможности си­стемы адекватно передавать в изобра­жении детали объекта любых разме­ров, а не только самые малые. Особое значение приобрёл метод Ч.-к. х. в связи с развитием космич. съёмки и др. спец. видов получения оптич. изображений. См. также Изображение оптическое.

ЧАСТОТОМЕР, прибор для измере­ния частоты периодич. процессов (гл. обр. частоты электрич. сигналов). Раз­личают Ч. с электроизмерит. меха­низмами, электронные аналоговые и цифровые Ч. Одним из простейших явл. Ч. с вибрационным электроизме­рительным механизмом. Большинство стрелочных Ч. с электроизмерит. механизмом строится на основе логометра (электродинамич., ферродинамич., эл.-магн., выпрямительного). Электрич. цепи, соединённые последо­вательно с катушками логометра, обеспечивают изменение соотношений токов или сдвига фаз между ними с изменением частоты входного сигнала в результате соответствующего подбо­ра реактивных элементов (конденсаторов, катушек индуктивности). Ч. с электроизмерит. механизмами приме­няются для измерений частот от 35 до 2000 Гц (осн. погрешность в % от верхнего предела измерений 0,5 — 4%).

Упрощённая схема электронного аналогового конденсаторного Ч. изоб­ражена на рис. 1. Формирователь создаёт последовательность импуль­сов тока с пост. амплитудой, длитель­ность к-рых и, соответственно, дли­тельность паузы между к-рыми равна полупериоду напряжения U_f, частота колебаний к-рого измеряется.



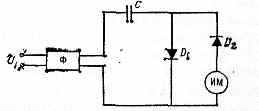
Рис. 1. Принципиальная схема конденса­торного частотомера.


За время действия импульса тока конден­сатор С заряжается через диод D₁ (ток через измерит. механизм ИМ благодаря диоду D₂ практически ра­вен нулю) до макс. напряжения. За время паузы конденсатор С полно­стью разряжается через ИМ и диод D₂. В силу инерционности магнитоэлектрич. измерит. механизма его показа­ния будут определяться ср. значением тока разряда конденсатора, к-рый пропорционален частоте напряжения U_f. Конденсаторные Ч. применяются

849


для измерения частоты в диапазоне 10 Гц — 200 кГц с осн. относит. погрешностью 1—3%. Для измерения более высоких частот (до 80 ГГц) применяют электронные аналоговые Ч. (резонансные, гетеродинные и др.) с осн. относит. погрешностью до 0,0005%.

Цифровые Ч. осн. на подсчёте числа периодов сигнала, частота к-рого измеряется за строго определённый



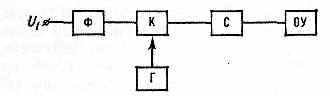
Рис. 2. Блок-схема цифрового частотомера.


промежуток времени (рис. 2). Форми­рователь импульсов (Ф) преобразует периодически изменяющийся сигнал в последовательность импульсов, пе­риод к-рых совпадает с периодом исследуемого сигнала U_f. Ключ (К) пропускает импульсы от формирова­теля на счётчик (С) за промежуток времени, заданный генератором (Г). Результаты подсчёта числа импульсов выдаются отсчётным устройством (ОУ). Цифровые Ч. охватывают диапазон измерений от 10^-1 Гц до 500 МГц с осн. относительной погрешностью до 10^-7'%.

в Электрические измерения, под ред. А. В. Фремке и Е. М. Душина, 5 изд., Л., 1980; Мирский Г. Я., Радиоэлектрон­ные измерения, 3 изд., М., 1975; Справоч­ник по электроизмерительным приборам, 2 изд., Л., 1977; Осипов К. Д., Пасынков В. В., Справочник по радио­измерительным приборам, ч. 2, М., 1960.

В. П. Кузнецов.

ЧЕРЕНКОВА — ВАВИЛОВА ИЗЛУЧЕНИЕ (Черенкова -- Вавилова эффект), излучение света электри­чески заряженной ч-цей, возникающее при её движении в среде с пост. ско­ростью v, превышающей фазовую ско­рость света в этой среде (скорость рас­пространения световых волн). Обна­ружено в 1934 при исследовании П. А. Черенковым -люминесценции р-ров как слабое голубое свечение жидкостей под действием -лучей. Эксперименты Черенкова, предпри­нятые по инициативе С. И. Вавилова, выявили характерные особенности из­лучения: 1) свечение наблюдается у всех чистых прозрачных жидкостей, причём его яркость мало зависит от их хим. состава; 2) излучение имеет поляризацию с преим. ориентацией вектора напряжённости электрич. поля вдоль направления первичного пучка; 3) в отличие от люминесценции, не наблюдается ни температурного, ни примесного тушения. На основании этих данных Вавилов сделал осново­полагающее утверждение, что обна­руженное явление — не люминесцен­ция, свет же излучают движущиеся в жидкости быстрые эл-ны, образую­щиеся при облучении в-ва. Ч.— В. и.

характерно не только для жидкостей, но и для тв. тел и газов. Свечение, вызываемое -излучением, нек-рые учёные наблюдали и раньше (напр., франц. учёный М. Л. Малле, в 1926 — 1929 получивший фотографии его спек­тра). Однако оставалось непонятным то, что наблюдаемое излучение — но­вое, ещё не изучавшееся явление; не было установлено и наиб. характерное его св-во, обнаруженное Черенко­вым в 1936,— направленность под ост­рым углом к скорости ч-цы.

Механизм Ч.— В. и. был выяснен в работе И. Е. Тамма и И. М. Франка (1937), содержавшей и количеств. тео­рию, основанную на ур-ниях классич. электродинамики. К тем же резуль­татам привело и квант. рассмотрение (В. Л. Гинзбург, 1940).

Условие возникновения Ч.— В. и. и его направленность могут быть пояснены с помощью Гюйгенса принципа.



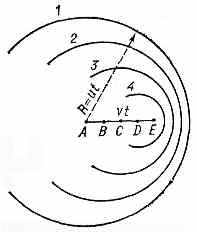
Рис. 1. Движение заряж. ч-цы в среде со скоро­стью v


Каждую точку (А, В, С, D на рис. 1 и 2) траектории заряж. ч-цы следует считать источником волны, возникаю­щей в момент прохождения через неё ч-цы. В оптически изотропной среде такие парциальные волны будут сфе­рическими, распрост­раняющимися со ско­ростью u=c/n, где n — показатель пре­ломления среды. До­пустим, что ч-ца, дви­гаясь равномерно и



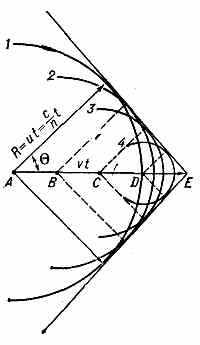
Рис. 2. Движение заряж. ч-цы в среде со скоростью v>u. Угол между направлениями волново­го вектора возникающего из­лучения и скоростью ч-цы ра­вен .

прямолинейно со скоростью v, в момент наблюдения находилась в точке Е. За время t до этого она проходила через точку A (AE=vt). Волна, испущенная из А, к моменту наблюдения пред­ставится сферой радиуса R=ut; на рис. 1 и 2 ей соответствует окружность 1, а волнам, испущенным из В, С, D,—

окружности 2, 3, 4. По принципу Гюйгенса в результате интерференции парциальные волны гасят друг друга всюду за исключением их общей огибающей, к-рой соответствует волн. поверхность света, распространяюще­гося в среде.

Пусть v < и (рис. 1), тогда свето­вые волны будут обгонять ч-цу на тем большее расстояние, чем раньше они испущены. Общей огибающей пар­циальные волны при этом не имеют — все окружности 1, 2, 3, 4 лежат одна внутри другой; следовательно, элект­рич. заряд при равномерном и прямо­линейном движении со скоростью v
Если же ч-ца движется быстрее, чем распространяются световые волны, т. е. при

v>u = c/n, или n>1 (1)

(где =v/c), то соответствующие вол­нам сферы пересекаются (рис. 2), их общая огибающая (волновая поверх­ность) представляет собой конус с вершиной в точке Е, совпадающей с мгновенным положением ч-цы, а нор­мали к образующим конуса определя­ют волн. векторы, т. е. направления распространения света. Угол 6, к-рый составляет волн. вектор с направле­нием движения ч-цы (см. рис. 2), удов­летворяет отношению:

cos=u/v=c/nv=l/n. (2)

Такой же метод рассмотрения можно провести и для оптически анизотроп­ной среды (в частности, для проз­рачных кристаллов), в к-рой парциа­льные волны не явл. сферами. В этом случае обыкновенному и необыкновен­ному лучам будут соответствовать разные конусы и излучение будет возникать под разными углами 6 к направлению распространения ч-цы, согласно соотношению (2). Условие (1) для оптически анизотропных сред формулируется неск, иначе. Во всех случаях осн. ф-лы теории хорошо согласуются с опытом.

Расчёт показывает, что в оптически изотропной среде ч-ца с зарядом е, прошедшая расстояние в 1 см со скоростью v > и, излучает энергию:



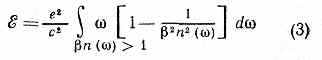
(=2c/ — круговая частота света,  — дл. волны излучаемого света в вакууме). Подынтегральное выраже­ние отражает распределение энергии в спектре Ч.— В. и.

В жидкостях и тв. в-вах условие (1) начинает выполняться для эл-нов уже при энергиях ~10⁵ эВ, для протонов, масса к-рых в ~2000 раз больше элект­ронной,— при энергиях ~10⁸ эВ. На основе Ч.— В. и. разработаны широко применяемые эксперим. методы для регистрации ч-ц высоких энергий, измерения их скорости. Приборы, применяемые для этой цели, наз. черенковскими счётчиками. Эти методы

850


позволяют также рассчитывать массу ч-ц (это, напр., было использовано при открытии антипротона).

Ч.— В. и. может наблюдаться в чистом виде только в идеальных слу­чаях, когда заряж. ч-ца движется с пост. скоростью в радиаторе неогранич. длины. В тонком радиаторе, удовлетворяющем условию (1), Ч.— В. и. неотделимо от переходного излу­чения, возникающего при пересече­нии ч-цей границы раздела 2 сред с разными коэфф. преломления.

В 1940 Э. Ферми обобщил теорию Ч.— В. и., приняв во внимание, что реальная среда обладает способностью поглощать свет по крайней мере в нек-рых областях спектра. Получен­ные им результаты внесли существ. уточнения в теорию ионизац. потерь заряж. ч-цами (эффект поляризации среды).

Ч.— В. и. явл. примером оптики «сверхсветовых» скоростей и имеет принципиальное значение. Ч.— В. и. экспериментально и теоретически изу­чено не только в оптически изотроп­ных средах, но и в кристаллах, теоре­тически рассмотрено излучение элек­трич. и магн. диполей и мультиполей. Ожидаемые св-ва излучения движуще­гося магн. заряда были использованы для поисков магнитного монополя. Рас­смотрено излучение ч-цы в канале внутри среды (напр., излучение пучка ч-ц внутри волновода) и др. Новые особенности приобретает Доплера эф­фект в среде: появляются т. н. ано­мальный и сложный Доплера эффекты. Можно полагать, что всякая система ч-ц, способная взаимодействовать с эл.-магн. полем, будет излучать свет за счёт своей кинетич. энергии, если её скорость превышает фазовую ско­рость света.

Теор. представления, лежащие в основе Ч.— В. и., тесно связаны с др. явлениями, имеющими важное зна­чение в совр. физике (волны Маха в акустике, вопросы устойчивости дви­жения ч-ц в плазме и генерации в ней волн, нек-рые проблемы теории ускорителей, а также генерация и усиление эл.-магн. волн).

• Черенков П. А., Видимое свечение чистых жидкостей под действием -радиации. «Доклады АН СССР», 1934, т. 2, в. 8, с. 451—57; Вавилов С. И., О возможных причинах синего -свечения жидкостей, там же с. 457—61; Тамм И. Е., Франк И.М., Когерентное излучение быстрого электрона в среде, там же, 1937, т. 14, в. 3, с. 107— 112; Черенков П. А., Т а м м И. Е., Франк И. М., Нобелевские лекции, М., 1960; Джелли Дж., Черенков­ское излучение и его применения, пер. с англ., М., 1960; 3 р е л о в В. П., Излуче­ние Вавилова — Черенкова и его примене­ние в физике высоких энергий, т. 1—2, М., 1968.

И. М. Франк.

ЧЕРЕНКОВСКИЙ СЧЁТЧИК, де­тектор для регистрации заряж. ч-ц, в к-ром используется Черенкова Вавилова излучение. При движении заряж. ч-цы в среде со скоростью v, превышающей фазовую скорость света c/n в данной среде (n — показатель преломления среды), ч-ца излучает в направлении, составляющем угол  с

её траекторией. Угол  связан со ско­ростью ч-цы v и показателем прелом­ления среды га соотношением:

cos=c/vn=1/n, =v/c. (1)

Интенсивность W черенковского излучения на 1 см пути заряж. ч-цы в интервале длин волн от ₁ до ₂ выражается соотношением:



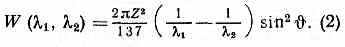
Здесь Z — заряд ч-цы (в ед. элемен­тарного электрич. заряда). В Ч. с. свет излучается только ч-цами, ско­рости к-рых v c/n ( 1/n), причём излучение происходит одновременно с прохождением ч-цы под углом  к её траектории. С ростом v (надпороговой) растут угол  и интенсивность из­лучения. Для предельных скоростей, близких к скорости света 1-1, угол  достигает предельного значе­ния:

_мaкс=arccos(1/n). (3)

Осн. элементы Ч. с.: радиатор (в-во, в к-ром v >с/n), оптич. система, фо­кусирующая свет, и один или неск. фотоэлектронных умножителей (ФЭУ), преобразующих световой сигнал в электрический (см. рис.). Радиаторы изготавливают из тв., жидких и газообразных в-в.



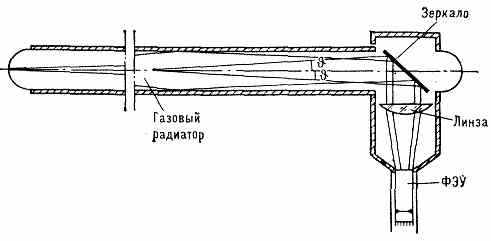
Схема стандартного газового порогового черенковского счётчика. Черенковское излу­чение собирается на катод ФЭУ с помощью оптич. системы, состоящей из плоского зер­кала и кварцевой линзы.


Они должны быть прозрачны к черенковскому излуче­нию и иметь низкий уровень сцинтил­ляций, создающих фоновые сигналы. Для регистрации ч-ц, обладающих сравнительно небольшой скоростью, используются органич. стекло (n=1,5), свинцовое стекло (n=1,5) и вода (n=1,33).

Ч. с. широко применяются в экс­периментах на ускорителях заряж. ч-ц. С ростом энергии ускорителей и, следовательно, с ростом энергии ч-ц особенно широкое применение полу­чили газовые Ч. с., к-рые могут выде­лять ч-цы ультрарелятивистских ско­ростей, для к-рых (1-)<<1. Угол  в газе очень мал (n близко к 1), мала и интенсивность излучения на ед. пути заряж. ч-цы. Чтобы получить вспыш­ку света, достаточную для регистра­ции, приходится увеличивать длину газовых Ч. с. до 10 м и более. Газовые Ч. с. позволяют плавно менять га изменением давления газа.

Существуют Ч. с. 3 типов: порого­вые, дифференциальные и счётчики

полного поглощения. Осн. хар-ками Ч. с. являются эффективность реги­страции и разрешающая способность по скорости ч-ц, т. е. способность счётчика разделять две ч-цы, движу­щиеся с близкими скоростями. Поро­говый Ч. с. должен регистрировать все ч-цы со скоростями, большими нек-­рой (пороговой). Дифф. Ч. с. регист­рируют ч-цы, движущиеся в интервале скоростей от v₁ до v₂. В традиц. дифф. Ч. с. это достигается выделением оп­тич. системой света, излучаемого в интервале соответствующих углов от ₁ до ₂. Линза или сферич. зерка­ло, помещённое на пути черенковского излучения, фокусирует свет, излу­чённый под углом О, в кольцо с радиу­сом R=f, где f — фокусное расстоя­ние линзы или зеркала. Если в фокусе системы поместить щелевую кольце­вую диафрагму, а за диафрагмой один или неск. ФЭУ, то в такой системе свет будет зарегистрирован только для ч-ц, излучающих свет в определённом ин­тервале углов, т. е. имеющих скоро­сти, лежащие в заданном диапазоне. В дифф. Ч. с. с прецизионной оптич. системой можно выделить ч-цы, к-рые по величине  отличаются всего на 10^-6 от др. ч-ц. Такие Ч. с. требуют особого контроля давления газа и фор­мирования параллельного пучка ч-ц. Ч. с. полного по­глощения предназна­чены для регистрации и спектрометрии элек­тронов и -квантов. В отличие от рас­смотренных Ч. с., в к-рых частица теряла в радиаторе ничтож­но малую долю энер­гии, Ч. с. полного поглощения содержит блок радиаторов

большой толщины, в котором электрон или -квант образует электронно-фотонную лавину и теряет всю (или большую часть) энергию. Как правило, радиаторы в этом случае изготавли­вают из стекла с большим содержанием Pb; при толщине 40 см в нём может пра­ктически полностью тормозиться элек­трон с энергией до 10 ГэВ. Кол-во света, излучаемого в Ч. с. полного поглощения, пропорционально энергии первичного электрона или -кванта. Разрешающая способность Ч. с. пол­ного поглощения (по энергии) зави­сит от энергии ξ ч-цы и для самых чувствительных ФЭУ может быть вы­ражена ф-лой: ξ=(8—12)% ξ, где ξ— энергия электрона в ГэВ.

• Джелли Дж., Черенковское излу­чение и его применения, пер. с англ., М., 1960; 3 р е л о в В. П., Излучение Вави­лова — Черенкова и его применение в фи­зике высоких энергий, т. 1—2, М., 1968.

В. С. Кафтанов.

ЧЕРНАЯ ДЫРА, космич. объект, возникающий в результате сжатия те-

851


ла гравитац. силами до размеров, меньших его гравитационного радиуса r_g=2/c² (где М— масса тела, G— гравитац. постоянная, с — численное значение скорости света). Предсказа­ние о существовании во Вселенной Ч. д. сделано на основе общей теории относительности (ОТО). Согласно ОТО, с приближением размера небесного тела к r_g сила тяготения стремится к бесконечности. Однако противодей­ствующие сжатию силы упругости даже при очень высокой плотности в-ва в малом объёме, характеризуемом r_g, остаются конечными. Поэтому в-во тела, достигшего размеров гравитац. радиуса, должно неудержимо сжи­маться к центру (испытывать реляти­вистский гравитационный коллапс). Один возможный путь образования Ч. д. указывает теория эволюции звёзд. Ч. д. может стать звезда, в недрах к-рой угасли термоядерные источники энергии. В таких звёздах с массой М>M_{критич.}=1,5—3 М_солн силы внутр. давления уже не могут противостоять силам гравитации. В-во звезды устремляется к центру и практически за время свободного падения достигает гравитац. радиуса и насту­пает гравитац. «самозамыкание» звез­ды. Осн. св-во звезды, поверхность к-рой достигла сферы с радиусом r_g (сферы Шварцшильда), состоит в том, что никакие сигналы (свет, ч-цы), испускаемые в пределах сферы Шварцшильда, не могут выйти наружу и достигнуть внеш. наблюдателя (рис.).




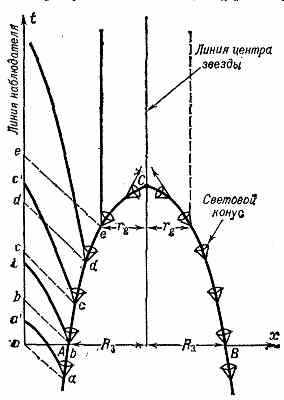
Проотранствевно-временной график грави­тац. коллапса звезды и образования чёрной дыры в системе отсчёта удалённого наблюда­теля: t — время, х — одна из пространств. осей, АВ=2 R_з — диаметр звезды в один из моментов времени. АС и ВС — линии дви­жения поверхности звезды. Действие тяго­тения приводит к тому, что к наблюдателю сигнала из точек а, b, с, d, e,... приходят не через равные промежутки ab=bc=cd=de=..., а с запаздыванием (аа', bb', cc' и т. д.). С момента е, когда радиус звезды становится равным её гравитац. радиусу r_g, свет пере­стаёт выходить из-под сферы Шварцшильда. Наблюдатель видит звезду «застывшей» на стадии de.


Границу области, за к-рую не выходит свет, наз. горизонтом Ч. д. Сохраняющиеся у Ч. д. внеш. прояв­ления связаны с существованием у неё гравитац. поля, момента враще­ния и электрич. заряда, если сколлапсировавшая звезда была заряжена. На больших расстояниях гравитац. поле Ч. д. не отличается от полей обычных звёзд, и движение др. тел, взаимодействующих с Ч. д., подчиня­ется законам механики Ньютона. Вблизи Ч. д. характер гравитац. поля определяется ОТО. Рядом особенно­стей обладает гравитац. поле враща­ющейся Ч. д. (поле Керра). У вра­щающейся Ч. д. вне горизонта суще­ствует особая область — эргосфера. В-во, попадающее в эргосферу, неизбежно начинает вращаться вокруг Ч. д. Наличие эргосферы может при­вести к потере чёрной дырой энергии вращения. Это возможно, напр., в случае, когда нек-рое тело, влетев в эргосферу, распадается на две части, причём одна из них продолжает па­дение на Ч. д., а другая вылетает из эргосферы по направлению вращения. Энергия вылетающей части может при определ. условиях превышать первонач. энергию всего тела.

Таким способом Ч. д. может терять энергию и при образовании в её эргосфере пары ч-ц (ч-цы и антич-цы), если одна из ч-ц поглощается Ч. д., а др. вылетает из эргосферы наружу. Ч. д. может терять энергию вращения не только с вылетающими из эргосфе­ры ч-цами, но и в процессах т. н. сверхизлучательного рассеяния внеш. эл.-магн. и гравитац. излучений. Подсчитано, что энергия рассеянной эл.-магн. волны может увеличиться за счёт энергии вращения Ч. д. на 4,4%, а энергия рассеянной гравитац. вол­ны — на 138%. Энергетич. потери Ч. д., связанные с уменьшением её вращат. момента, могут составить 29% от её полной энергии, т. е. 0,29 Мс². Указанные выше процессы происходят только около вращающихся Ч. д. Но даже в отсутствии вращения нали­чие горизонта ведёт к квантовомеханич. процессу рождения ч-ц и антич-ц вблизи Ч. д. за счёт энергии её грави­тац. поля. В результате Ч. д. должна излучать, причём как абс. чёрное тело с темп-рой T_э=10²⁶/М (в Кельвинах). Этот механизм излучения Ч. д. был рассмотрен англ. физиком С. Хоукингом в 1974. Интенсивность черно-тельного излучения Ч. д. низка, т. к. T_э мала (для Ч. д. массой M=3M_солнТ_э~10^-7К). За счёт излучения Ч. д. большой массы уменьшается очень медленно. Но с уменьшением М темп-ра Ч. д. повышается, процесс её «ис­парения» ускоряется, завершаясь своеобразным взрывом и, возможно, полным исчезновением. Кроме Ч. д., возникающих в процессе эволюции звёзд, теория рассматривает Ч. д.,

образовавшиеся на ранних (горячих и сверхплотных) стадиях развития Вселенной. Эти первичные Ч. д. с массой, меньшей 10¹⁵ г, к нашему времени должны были испариться, а существенно более массивные — остаться практически неизменными.

Поиски Ч. д. как первичных, так и звёздного происхождения -- важней­шая проблема совр. астрономии. Наи­более вероятно обнаружение Ч. д. в тесных двойных звёздных системах, в к-рых один компонент — Ч. д., а другой - - звезда-гигант, в-во к-рой перетекает к Ч. д. Вблизи Ч. д. из перетекающего в-ва образуется враща­ющийся газовый диск. Трение между слоями диска, движущимися с разл. скоростями, приводит к значит. ра­зогреву в-ва (до десятков млн. град) и появлению рентг. теплового излу­чения. Неск. источников космич. рентг. излучения имеют, по-видимому, подобное строение. В одном из них— источнике Лебедь Х-1 —масса звёзд-компонентов составляет примерно 25М_солн и 10М_солн (соответственно для оптически наблюдаемой звезды-сверх­гиганта и для невидимой звезды — источника рентг. излучения). Компакт­ная звезда с массой ~10М_солн не может быть нейтронной звездой. Поэтому предполагают, что в этой системе аст­рономы впервые открыли кандидата в Ч. д. Предполагается также, что в активных ядрах галактик и в квазарах могут находиться сверхмассивные Ч. д. (М ~10⁶—10⁸М_солн,), наблюдае­мая активность этих объектов возмож­но обусловлена аккрецией на Ч. д. окружающего газа.

• Зельдович Я. Б., Новиков, И. Д., Теория тяготения и эволюция звезд, М., 1971; Шкловский И. С., Звезды. Их рождение, жизнь и смерть, 2 изд., М., 1977; Происхождение и эволюция га­лактик и звезд, М., 1976; Ф р о л о в В. П., Черные дыры и квантовые процессы в них, «УФН», 1976, т. 118, в. 3; П е н р о у з Р., «Черные дыры», пер. с англ., «УФН», 1973, т. 109, в. 2.

ЧЕРНОЕ ИЗЛУЧЕНИЕ, тепловое излучение абсолютно чёрного тела. Явл. равновесным излучением. Не зави­сит от природы излучающего в-ва и определяется его темп-рой. Св-ва Ч. и. подчиняются Планка закону излу­чения, Стефана — Больцмана закону излучения и др. законам теплового излучения.

ЧЕРНОЕ ТЕЛО, то же, что абсолют­но чёрное тело.

ЧЕТНОСТЬ, квантовомеханич. хар-ка состояния микрочастицы (молеку­лы, атома, ат. ядра, элем. ч-цы), отображающая св-ва симметрии волн. ф-ции этой ч-цы относительно зерк. отражений (пространственной ин­версии). В процессах, обусловленных сильным и эл.-магн. вз-ствиями, имеет место закон сохранения Ч.: физ. система, обладавшая в нач. со­стояния зерк. симметрией определ. типа, сохраняет эту симметрию во все последующие моменты времени. Сохранение Ч. приводит к ряду от-

852


бора правил для эл.-магн. излучения атомов и ат. ядер, для яд. реакций и реакций взаимопревращений элем. ч-ц.

Закон сохранения Ч. можно проил­люстрировать на примере излучаю­щей антенны, у к-рой геом. форма и распределение токов в каждый момент времени обладают зерк. симметрией. Согласно закону сохранения Ч., та­кой же симметрией будет обладать диаграмма направленности излучения антенны.

В слабом взаимодействии, обуслов­ливающем, в частности, бета-распад ядер, закон сохранения Ч. наруша­ется. Возможность такого нарушения была предсказана в 1956 кит. физи­ками Ли Цзундао и Янг Чжень-нином и подтверждена экспериментально в 1957 By Цзяньсюн с сотрудниками (США) в -распаде ядер, а также Л. Ледерманом с сотрудниками (США) в распаде мюона. Ю. Г. Абов, В. М. Лобашёв и др. обнаружили сла­бое несохранение Ч. при нуклон-нуклонном вз-ствии. Имеются эксперим. указания на слабое несохране­ние Ч. в эл.-магн. излучении атомов.



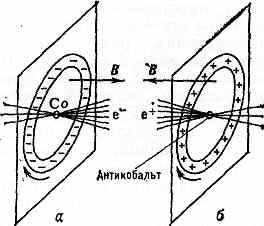
На рис. а изображена схема опыта By. Образец, содержащий радиоакт. изотоп ⁶⁰Со, помещён в магн. поле кругового тока (В — магн. индукция). Это поле ориентирует магн. моменты ядер кобальта вдоль В (установка помещена в криостат при темп-ре ок. 1 К). Маленькой стрелкой указа­но направление скоростей эл-нов внутри проводника с током. Как и в примере с антенной, вся система зеркально симметрична относительно плоскости, в к-рой течёт круговой ток. При выполнении закона сохра­нения Ч. интенсивность излучения эл-нов -распада должна быть оди­наковой по обе стороны этой плоско­сти. В эксперименте же наблюдалась резкая асимметрия: по одну сторону плоскости испускалось на 40% больше эл-нов, чем по другую. Т. о., из опыта By следует, что изучаемая система не обладает зерк. симметрией.

Ещё в 1952 амер. физик Э. Вигнер с сотрудниками отметили возможность того, что при зерк. отражении эл-ны переходят в положительно заряж. ч-цы той же массы — позитроны и вообще все ч-цы переходят в соответ­ствующие античастицы. Зерк. отра­жение, сопровождающееся заменой всех ч-ц системы на античастицы,

было названо Л. Д. Ландау комбини­рованной инверсией. Симметрия зако­нов природы относительно комбини­рованной инверсии приводит для истинно нейтральных частиц и систем к закону сохранения комбини­рованной чётности. При замене закона сохранения Ч. на закон сохранения комбинированной Ч. схе­ма опыта By перестаёт быть зеркально симметричной, т. к. зерк. отображе­нием этого опыта (рис., б) будет позитронный -распад ядра антикобаль­та (состоящего из антипротонов и анти­нейтронов) в магн. поле кругового тока позитронов антивещества про­водника. (Поскольку заряд позитрона положителен, при том же направле­нии носителей заряда проводника знак тока изменится, что приведёт к изме­нению знака В.)

Сильное нарушение закона сохра­нения Ч. установлено для всех про­цессов слабого вз-ствия.

В квант. теории Ч. явл. физ. ве­личиной, характеризующей основные и возбуждённые состояния микроча­стиц. При соблюдении закона сохра­нения Ч. последняя может иметь только два значения: +1 и -1. Под влиянием слабого вз-ствия к состоя­нию с данной Ч. добавляется малая примесь состояния с противоположной Ч. В атомах и в ат. ядрах эта примесь не превышает 10^-6—10^-7 (однако в ядрах могут быть спец. причины уси­ления эффектов несохранения чёт­ности на неск. порядков). Поэтому каждая ч-ца с хорошей точностью обладает определённой внутрен­ней чётностью Р, равной либо + 1, либо -1. Ч-цы с Р=+1 наз. чётными, а с Р=-1 —нечётными. Напр., °-мезон нечётен. Внутр. Ч. ч-ц с полуцелым спином — фермионов неопределённы, но они противополож­ны Ч. соответствующих античастиц. Это обусловливает, напр., отрицат. внутр. Ч. мезонов, составленных из кварка и антикварка с нулевым орбит. моментом (, К, , ,  и т. д.). Для ч-ц с целым спином (бозонов) Ч. ч-цы и античастицы одинакова. Ч. системы из ч-ц с орбит. моментами ћl₁,. . ., ћl_n равна

P₁...P_n(-1)^l1+...ln

где Р₁, . . ., Р_n — внутр. Ч. ч-ц системы, l₁ . . ., l_n — неотрицат. це­лые числа.

У квантов эл.-магн. поля (фотонов) не существует ни внутр. Ч., ни орбит. момента. Ч. фотона определяется его мультипольностью (см. Мультиполь). Ч. электрического 2^l-поля равна (-1)_l, а Ч. магнитного 2^l-поля равна (-1)^l+1. Поэтому Ч. физ. микроси­стемы сохраняется при испускании или поглощении электрич. мультипольного фотона с чётным l или магн. мультипольного фотона с нечётным l, а в остальных случаях меняется на противоположную. Это приводит к правилам отбора по Ч. для эл.-магнитного излучения молекул, атомов и ядер.

• Ли Цзун-дао, Янг Чжень-нин, Вопрос о сохранении четности в сла­бых взаимодействиях, в кн.: Новые свойст­ва симметрии элементарных частиц, пер. с англ., М., 1957; By Цзянь-сюн [и др.], Экспериментальная проверка сохра­нения четности при -распаде, там же, с. 69; Абов Ю. Г. [и др.], Repeated experiment to observe the weak nucleon—nucleon in­teraction, «Physics Letters», 1968, v. 27B, № 1, p. 16; Лобашов В. М., Экс­перименты по обнаружению несохранения четности в ядерных силах, «Вестник АН СССР», 1969, № 2; By Ц., Нарушение сохранения четности, в кн.: Альфа-, бета- и гамма-спектроскопия, под ред. К. Зигбана, пер. с англ., в. 4, М., 1969, гл. 24Г, § 20—21; Широков Ю. М., Юдин Н. П., Ядерная физика, 2 изд., М., 1980 (Общий курс физики); Барков Л. М., Золоторев М.С.,Хриплович И.Б., Наблюдение несохранения чётности в ато­мах, «УФН», 1980, т. 132, в. 3.

Ю. М. Широков.

ЧЕТНОСТЬ УРОВНЯ, чётность состояния физ. системы (чётность волн. ф-ции), соответствующего данному уровню энергии. Такая хар-ка уров­ней возможна для системы ч-ц, между к-рыми действуют эл.-магн. или яд. силы, сохраняющие чётность. При учёте слабого взаимодействия к состоя­нию с данной чётностью добавляется незначит. примесь состояния с проти­воположной чётностью (в атомах и ат. ядрах относит. величина такой при­меси обычно невелика: ~10^-6—10^-7). Если уровень энергии вырожден так, что ему принадлежат волн. ф-ции с разной чётностью (как, напр., для возбуждённых уровней атома водоро­да), то возможны состояния, описыва­емые суперпозицией таких волн. ф-ций, т. е. вырожд. уровень может не обладать определ. чётностью (да­же если действующие в системе силы

сохраняют чётность).

С. С. Герштейн.

ЧИСЛА ЗАПОЛНЕНИЯ в квантовой механике и квантовой статистике, числа, указывающие степень заполне­ния квант. состояний ч-цами квантовомеханич. системы многих тождест­венных частиц. Для систем ч-ц с полу­целым спином (фермионов) Ч. з. могут принимать лишь два значения: 0 для свободных состояний и 1 для за­нятых, для систем ч-ц с целым спином (бозонов) — любые целые числа: 0, 1, 2, ... Сумма всех Ч. з. должна быть равна числу ч-ц системы. С по­мощью Ч. з. можно описывать и чис­ла элем. возбуждений (квазичастиц) квантованных полей; в этом случае их сумма не фиксирована. Средние по статистически равновесному состоя­нию Ч. з. идеальных квант. газов определяются ф-циями распределения Ферми — Дирака и Бозе — Эйнштей­на (см. Ферми — Дирака статистика, Бозе — Эйнштейна статистика). Понятие Ч. з. лежит в основе метода вторичного квантования, к-рый наз. также представлением Ч. з.

Д. Н. Зубарев.

ЧИСТОЕ СОСТОЯНИЕ, состояние квантовомеханич. системы, к-рое ха-

853


рактеризуется заданием полного на­бора возможных значений динамич. переменных, определяющих состояние системы. Ч. с. описывается волновой функцией от этих переменных и явл. одним из осн. понятий квант. меха­ники. Суперпозиция волн. ф-ций (т. е. их сумма с произвольными комп­лексными коэфф.) также описывает

Ч. с. системы. Обычно Ч. с. называют просто квантовомеханическим состоянием, хотя в квант. механике есть более общий слу­чай — смешанное состояние.

ЧУВСТВИТЕЛЬНОСТЬ измеритель­ного прибора, свойство измерит. прибора, выражаемое отношением линейного (l) или углового () перемещения указателя по шкале при­бора (сигнала на выходе прибора) к вызвавшему его изменению x изме­ряемой величины х. Различают абс. Ч. измерит. прибора S=l/x: или /x, где x; выражено в единицах измеряемой величины, и относит. Ч. S0=l/(x/x) или /(x/x)

К. П. Широков.