Geum.ru

Программа курса лекций

Вид материалаПрограмма курса

Содержание


Теория сильных взаимодействий
Подобный материал:

Теория сильных взаимодействий

Программа курса лекций
(1 год магистратуры, 2 сем., 32 ч., экзамен)


Профессор Фадин Виктор Сергеевич
  1. Кварковая модель адронов. Мезоны и барионы как составные кварковые состояния. Триплет "легких" кварков, унитарная симметрия.
  2. Новое квантовое число - цвет. Причины для его введениия: симметрия барионной волновой функции, "асимптотика" сечения e+e– аннигиляции в адроны, время жизни 0 -мезона. Невылетание цвета, белые состояния.
  3. Модель векторной доминантности в области умеренных энергий.
  4. Квантовая хромодинамика. Построение лагранжиана КХД из принципа калибровочной инвариантности.
  5. Трудности с каноническим квантованием. Добавление в лагранжиан члена, фиксирующего калибровку. "Духи" Фаддеева-Попова. Правила Фейнмана.
  6. Основные процессы КХД: , , , .
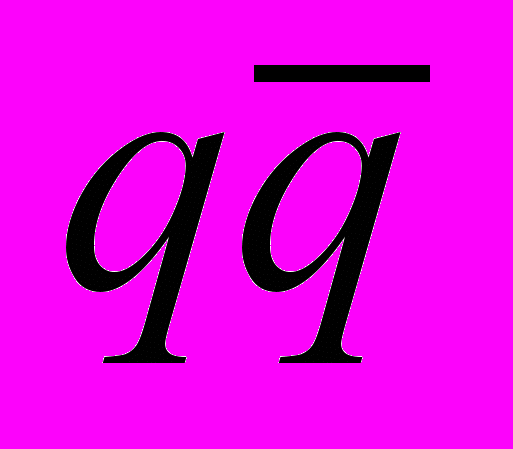
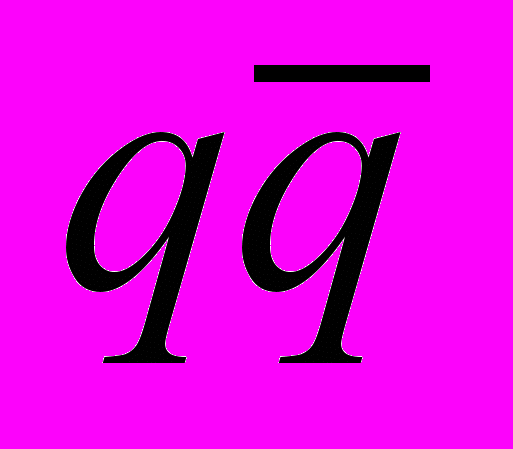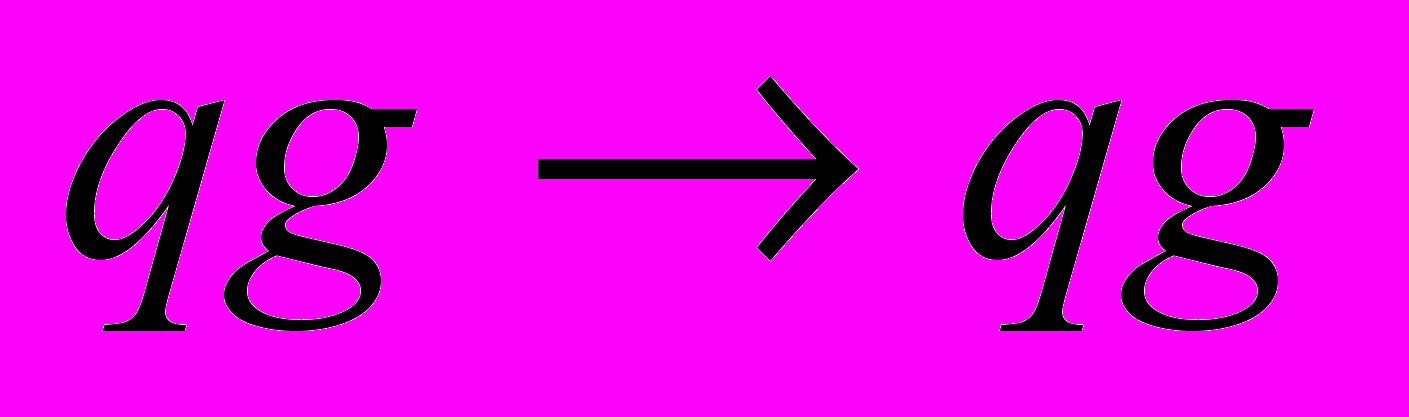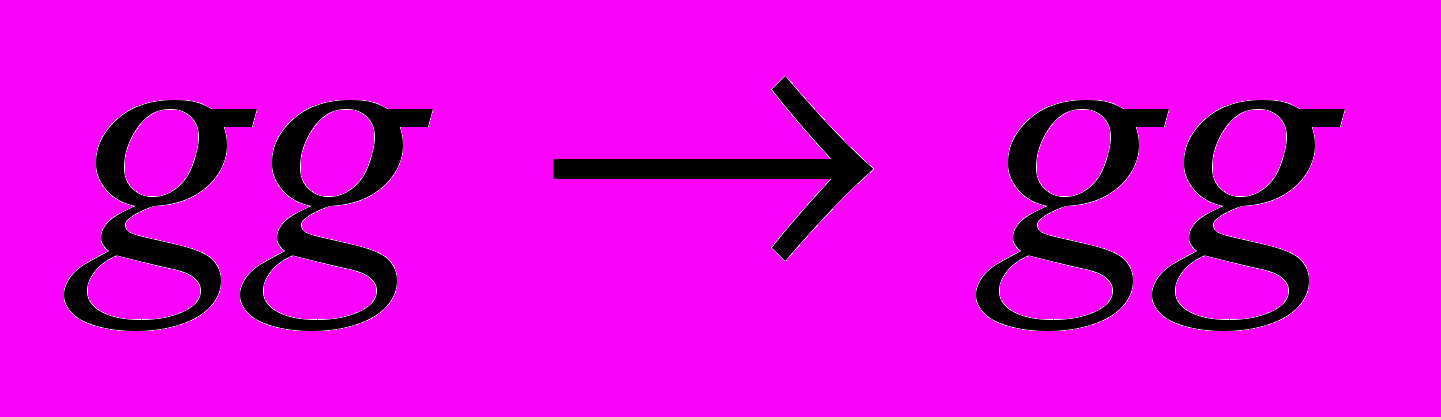  7. "Бегущая" константа связи. Асимптотическая свобода в КХД. "Кварковый счет" для рассеяния адронов на большие углы.
  8. Тяжелые кварконии. Спектроскопия состояний. Аннигиляционные каналы распада. Определение величины константы связи. Потенциальные модели, спиновые эффекты, радиационные переходы.
  9. Упругое и глубоко неупругое рассеяние лептонов на адронах. Формакторы адронов. Структурные функции, скейлинг.
  10. Кварк - партонная модель. Эволюция кварковых и глюонных распределений в адронах. Уравнения ДГЛАП для партонных распределений.
  11. Операторное разложение и моменты структурных функций. Ренормгруппа, уравнения ренормгруппы для моментов структурных функций.
  12. Электрон-позитронная аннигиляция в адроны. Асимптотика полного сечения. Кварковые и глюонные струи.
  13. Оператор поляризации вакуума в КХД. Дисперсионные соотношения. Дисперсионные правила сумм.
  14. Непертурбативные эффекты в КХД. Вакуум в КХД.
  15. Спонтанное нарушение киральной симметрии. Теорема Голдстоуна.
  16. Соотношение Голдбергера-Треймана. Частичное сохранение аксиального тока. Массы кварков.
  17. Великое объединение. SU(5)-модель. Распад протона.

Литература

    1. М.Пескин, Д. Шредер, Введение в квантовую теорию поля. Москва- Ижевск, 2001г.
    2. Волошин М.Б., Тер-Мартиросян К.А. Теория калибровочных взаимодей­ствий элементарных частиц. "Энергоатомиздат", Москва,1984.
    3. Т.-П. Ченг, Л.-Ф. Ли. Калибровочные теории в физике элементарных частиц. "Мир", Москва, 1987.
    4. К. Хуанг. Кварки, лептоны и калибровочные поля. "Мир", Москва, 1985.
    5. T. Muta. Foundation of Quantum Chromodynamics, "World Scientific", Singapore, 1987.

Теория сильных взаимодействий

Программа семинаров
(1 год магистратуры, 2 сем., 32 ч., зачет)


Профессор Фадин Виктор Сергеевич
  1. Изотопическая симметрия. G-четность.
  2. SU(3)-симметрия. Спин-тензорный формализм. Массовые формулы.
  3. Соотношения между ширинами распадов векторных и псевдоскалярных мезонов в SU(3)-симметрии и модели векторной доминантности. Сечения e+e– аннигиляции в резонансной области.
  4. Процесс . Hесокращение вкладов продольных и временных глюонов при фейнмановском суммировании по поляризациям.
  5. Сечения процессов , , , .
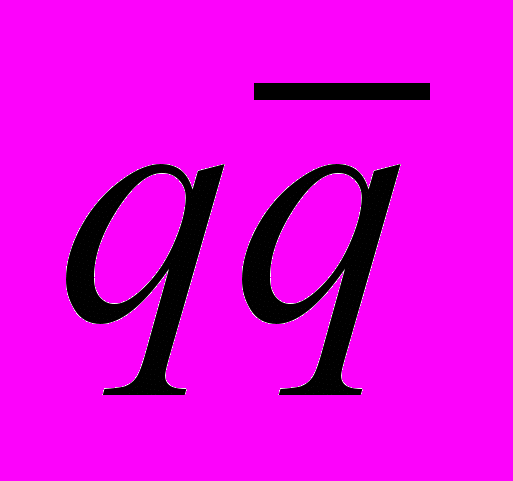
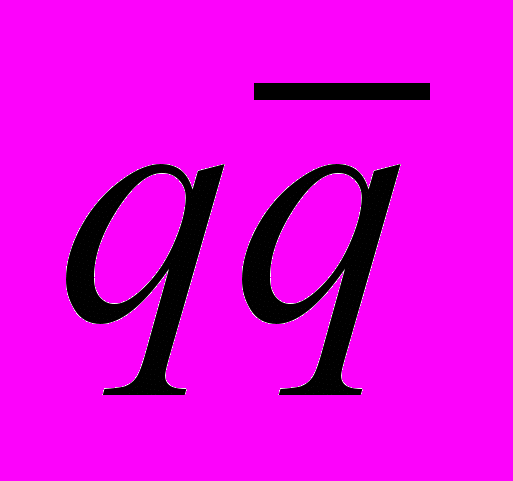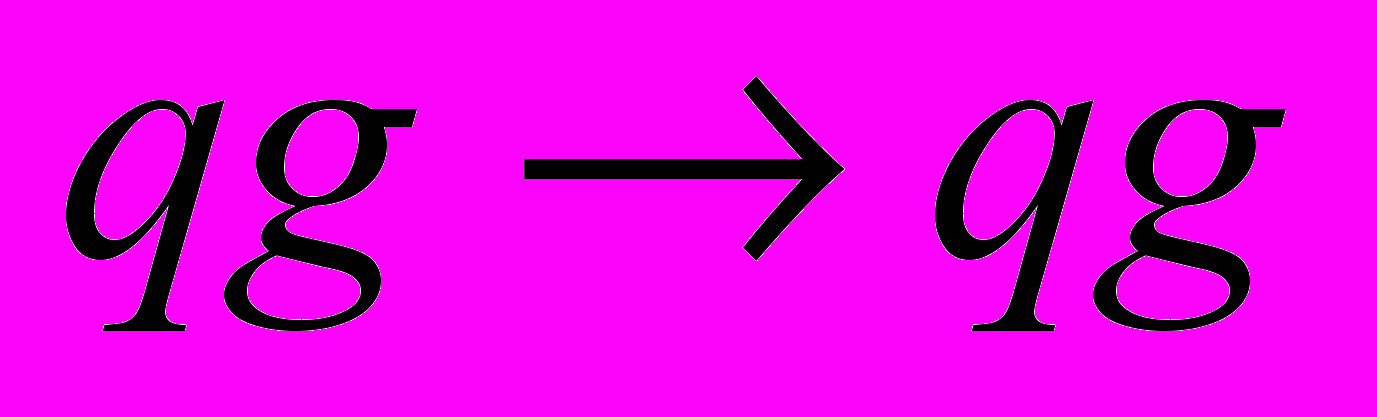  6. Сечения рассеяния адронов на большие углы.
  7. Потенциал взаимодействия тяжелых кварков в теории возмущений КХД.   Определение величины константы связи из распадов тяжелых кваркониев. Ширины радиационных распадов.
  8. Сечения глубоко неупругого рассеяния лептонов на адронах через структурные функции. Структурные функции в партонной модели.
  9. Правила сумм для глубоко неупругого рассеяния: Бьеркена, Адлера, Гросса и Левеллина Смитта, Готтфрида, Эллиса и Яффе.
  10. Ядра Алтарелли-Паризи. Аномальные размерности операторов твиста 2. Моменты структурных функций и партонные распределения.
  11. Сечения e+e– аннигиляции в кварки и глюоны в однопетлевом приближении.
  12. Поляризационный оператор во внешнем поле – квадратичная по полю поправка.
  13. Аномалия Адлера-Белла-Джакива. Матричный элемент дивергенции аксиального тока для перехода |вакуум>|два фотона> в однопетлевом приближении с регуляризацией Паули-Вилларса.
  14. Общий вид матричного элемента аксиального тока между нуклонными состояниями. Проверка соотношения Голдбергера-Треймана.
  15. Соотношения между массами псевдоскалярного октета из ЧСАТ и алгебра токов. Время жизни пи-мезона.
  16. SU(5)-модель «великого объединения». Квантование заряда. Величина угла Вайнберга. Эффективный лагранжиан для распада протона. Время жизни протона.

Задания


Задание №1
  1. Расмотpеть pаспады ,  0, , , f - мезонов на , ,  ,  , ,  .
    1. Составить таблицу, в котоpой указать запpещенные pаспады, отметив, сохpанением какой из величин I, P, C, T, G они запpещены.

      Частица
      IG JP C






      



























      0



































































      F




















    2. Для pазpешенных двухчастичных pаспадов выписать pелятивистски инваpиантные матpичные элементы и опpеделить из сpавнения с экспеpиментальными данными численные значения безpазмеpных констант pаспадов. Константы pаспадов делать безpазмеpными пользуясь массой pаспадающейсячастицы.
  2. Hайти SU(3)- соотношение между амплитудами pаспадов ,  и сpавнить его с экспеpиментальными данными. Учесть - ' смешивание, угол котоpого опpеделить из массовых фоpмул.
  3. Hаписать инваpиантные амплитуды pадиационных pаспадов нонета вектоpных мезонов VP, вычислить веpоятности и сpавнить полученные pезультаты с экспеpиментальными значениями. Пpовеpить пpедсказания вектоpной доминантности, сpавнивая веpоятности пpоцессов    и    .
  1. Найти форму спектра фотонов в процессax e+e–   f    , e+e–   a   и сравнить с экспериментальными данными ВЭПП-2М. Матpичные элементы процессов f  , a   выписать пользуясь pелятивистской и калибровочной инваpиантностью. Значения входящих констант связи оценить в кварковой модели.

Задание №2
  1. Используя размерностную регуляризацию вычислить в кулоновской калибровке расходящуюся часть поляризационного оператора глюона в однопетлевом приближении.
  2. Вычислить аномальную размерность октетного оператора твиста 2 со спином N.
  3. Пользуясь уравнениями ДГЛАП определить поведение моментов партонных распределений при N1. Найти отсюда асимптотическое поведение структурных функций при x  0.

Литература

  1. М.Пескин, Д. Шредер, Введение в квантовую теорию поля. Москва- Ижевск, 2001г.
  2. Волошин М.Б., Тер-Мартиросян К.А. Теория калибровочных взаимодей­ствий элементарных частиц. "Энергоатомиздат", Москва,1984.
  3. Т.-П. Ченг, Л.-Ф. Ли. Калибровочные теории в физике элементарных частиц. "Мир", Москва, 1987.
  4. К. Хуанг. Кварки, лептоны и калибровочные поля. "Мир", Москва, 1985.
  5. T. Muta. Foundation of Quantum Chromodynamics, "World Scientific", Singapore, 1987.