Правила організації та проведення Міжнародного чемпіонату з розв’язування логічних математичних задач Оргкомітет конкурсу
| Вид материала | Конкурс |
- Правила організації та проведення Міжнародного чемпіонату з розв’язування логічних, 90.4kb.
- Методика розв’язування олімпіадних задач з логічним навантаженням. Геометричні інваріанти, 399.86kb.
- Р. Шпакович Бобер – 2009 Відповіді та вказівки до розв’язування завдань Зміст, 316.81kb.
- Розв'язування дослідницьких задач з фізики із застосуванням нових інформаційних технологій, 137.39kb.
- Автономної Республіки Крим, управління освіти І науки обласних, Київської та Севастопольської, 169.82kb.
- Міністерство освіти І науки України Кіровоградський державний педагогічний університет, 1297.75kb.
- Про графічний спосіб розв’язання математичних задач, 262.98kb.
- Матеріали для проведення математичного тижня в школі, 340.44kb.
- Урок на тему: " Розв’язування задач на розрахунок електроенергії, що споживається побутовими, 122.51kb.
- Методика навчання розв’язуванню планіметричних задач на побудову із використанням комп’ютера., 256kb.
Правила
організації та проведення
Міжнародного чемпіонату з розв’язування логічних математичних задач
- Оргкомітет конкурсу
24 Міжнародний чемпіонат з розв’язування логічних математичних задач на території України проводиться у відповідності до наказу МОН України №159 від 23.02. 2009р. та додатків до нього.
Організація та проведення в Україні Міжнародного чемпіонату з розв’язування логічних математичних задач покладається на Центральний організаційний комітет, який діє на базі Центру по інтеграції до європейського та світового освітнього простору.
До повноважень Центрального оргкомітету належить, зокрема, вирішення питань щодо проведення конкурсу, перевірка робіт учасників, формування списків учасників півфіналів та фіналів, формування команди – учасниці суперфіналу в м. Парижі, оприлюднення результатів.
ПРЕДСТАВНИКОМ ЦЕНТРАЛЬНОГО ОРГКОМІТЕТУ В ХАРКІВСЬКІЙ ОБЛАСТІ Є КРИЖАНОВСЬКИЙ ОЛЕКСАНДР ФЕЛІКСОВИЧ,
e-mail: plushakaf@mail.ru або plushakaf@yandex.ru .
- Участь у конкурсі та порядок проведення конкурсу
Змагання проводяться під егідою Міжнародного комітету математичних змагань (м. Париж).
Кожен з Чемпіонатів проводиться в чотири етапи за текстами Міжнародного комітету.
I етап – чвертьфінал (заочний тур, проходить в грудні 2009 – січні 2010 року),
II етап – півфінал ( очний тур, кінець березня 2010 року),
III етап – національний фінал ( очний тур, травень 2010 року).
IV етап – міжнародний суперфінал ( традиційно проводиться в м. Парижі впродовж двох днів в кінці серпня 2010 року).
У чвертьфіналі можуть брати участь всі бажаючі за такими віковими категоріями:
- 1 – 3 класи ( 5 задач з №1 по №5 )
- 4 – 5 класи ( 8 задач з №1 по №8 )
- 6 – 7 класи ( 11 задач з №1 по №11 )
- 8 – 9 класи ( 15 задач з №1 по №15 )
- 10 – 11 класи ( 18 задач з №1 по №18 )
Чвертьфінал у регіонах проводять координатори або вчителі відповідної школи. Допускається і персональна заявка та учать учня в чвертьфіналі. Для участі в чвертьфіналі ПРЕДСТАВНИК ЦЕНТРАЛЬНОГО ОРГКОМІТЕТУ заповнює заявку на участь і надсилає її на адресу Центрального оргкомітету разом з роботами чвертьфіналістів та копією поштового переказу благочинної пожертви не пізніше 31 січня 2010 року.
РОБОТИ ТА БЛАГОЧИННУ ПОЖЕРТВУ ТРЕБА НАДАТИ ПРЕДСТАВНИКУ ЦЕНТРАЛЬНОГО ОРГКОМІТЕТУ НЕ ПІЗНІШЕ 25 СІЧНЯ 2009 РОКУ.
Рекомендована благочинна пожертва за участь у чвертьфіналі складає 4 гривні 50 копійок від кожного учасника та повністю використовується для покриття витрат на організацію та проведення конкурсу.
Переможці чвертьфіналу, яких визначає Центральний оргкомітет, запрошуються до участі в очному півфіналі, що проводиться координаторами в регіонах за текстами, наданими Центральним оргкомітетом, в березні 2010 року.
ПРОВЕДЕННЯ ПІВФІНАЛЬОГО ТУРУ В ХАРКІВСЬКЙ ОБЛАСТІ ВІДБУДЕТЬСЯ НА БАЗІ ХАРКІВСЬКОГО НВК №45 «АКАДЕМІЧНА ГІМНАЗІЯ».
Роботи півфіналістів відправляються в Центральний оргкомітет на перевірку в день проведення півфіналу. Переможці півфіналу, яких визначає Центральний оргкомітет, запрошуються на участь у Всеукраїнському фіналі, що проходитиме в травні в м. Вінниці. Міжнародний суперфінал проходитиме в кінці серпня 2010 року в м. Парижі.
Час для виконання завдань суперфіналів, фіналів, півфіналів наступний:
- 1 – 3 класи – 1 година,
- 4 – 5 класи – 1 година 30 хвилин,
- 6 – 7 класи – 2 години,
- 8 – 9 класи - 2 години 30 хвилин,
- 10 – 11 класи – 3 години .
Місцеві осередки отримують завдання заочного чвертьфіналу 1 грудня 2009 року.
Завдання очного напівфіналу отримують в переддень напівфіналу.
Перед початком проведення чемпіонату координатори проводять детальний інструктаж учасників щодо правил проведення чемпіонату та оформлення розв’язань.
Головна вимога до учасників напівфіналів – самостійна чесна робота над завданнями. Учасники напівфіналів сидять по одному за партами.
Користуватися калькулятором, підручниками та математичними таблицями категорично забороняється.
Роботи учасників Чемпіонату зберігаються до 1 вересня 2010 року.
- Правила оформлення та оцінювання робіт
Учасник чвертьфіналу наводить повне розв’язання (українською або російською мовою) до кожної запропонованої задачі.
Учасник півфіналів та фіналів до запропонованих задач вказує лише відповідь ( без будь- яких обґрунтувань).
За вимогою умови задачі, необхідно вказувати кількість розв’язків задачі та навести два з них. Правильний розв’язок задачі оцінюється одним балом, але кожна задача має свій вказаний коефіцієнт складності, який теж враховується. У випадку, коли задача має декілька розв’язків, але знайдені не всі, то зараховується лише коефіцієнт задачі. Всі місця в турнірній таблиці розподіляються одноосібно. Якщо учасники розв’язали однакову кількість задач, то перемога присуджується тому, хто розв’язав задачі з вищою сумою коефіцієнтів. Якщо ж і сума коефіцієнтів однакова, то переможцем півфіналів та фіналів стає той, хто для розв’язування витратив меншу кількість часу ( при здачі учасниками півфіналів та фіналів виконаних робіт, члени оргкомітету фіксують час здачі роботи).
- Відзначення учасників Чемпіонату
Відзначення учасників Чемпіонату здійснюється за рахунок благодійних внесків учасників та залучених спонсорських коштів на місцях.
Кожному учаснику фіналу вручається спеціальний диплом учасника Міжнародного чемпіонату з розв’язування логічних математичних задач. Переможцям в кожній з категорій вручаються відповідно золота, срібна та бронзова медалі.
- Підбиття підсумків Чемпіонату
Результати чвертьфіналу та списки півфіналістів надсилаються в регіони Центральним оргкомітетом до кінця лютого 2010 року.
Результати півфіналу та списки фіналістів надсилаються в регіони Центральним оргкомітетом до кінця квітня 2010 року.
Результати Всеукраїнського фіналу оголошуються в день його проведення після перевірки робіт.
Команда учасників Міжнародного суперфіналу формується з переможців Всеукраїнського фіналу за підсумками проведення відбіркових зборів в червні 2010 року.
Всі питання щодо участі в чемпіонаті можна узгодити з представником Центрального Організаційного комітету в Харківській області Крижановським Олександром Феліксовичем за вказаними адресами електронної пошти.
24 Міжнародний чемпіонат
з розв’язування логічних та математичних задач
Заочний тур, чвертьфінал
1. Розглянемо малюнок
. В першому квадраті є дві фішки, а в четвертому 10 фішок. За один хід дозволяється перемістити лише одну фішку з будь-якого квадрату в сусідній квадрат, що має з даним квадратом спільну сторону. Потрібно отримати таке розміщення фішок, щоб у кожному квадраті була б хоча б одна фішка та у всіх квадратах була різна кількість фішок. Яка мінімальна кількість ходів потрібна для цього?2. Чотири дівчинки та чотири хлопчики святкують день народження в танцювальній студії. В кожному танці приймає участь деяка кількість пар учасників ( склад пари: одна дівчинка та один хлопчик). Через годину запитали хлопчиків про кількість танців, які вони танцювали і отримали такі відповіді: 2, 0, 0 та 10. Троє з дівчаток відповіли на це ж питання так: 1, 2, 3. Якою була відповідь четвертої дівчинки?
3. Яку найбільшу кількість квадратів можна побачити на малюнку?
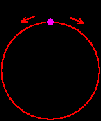
4. Починаючи з 7 годин ранку автобуси від’їжджають від вокзалу (на малюнку Gare), кожні 20 хвилин та рухаються в напрямку годинникової стрілки. А починаючи з 7 годин 10 хвилин відкривається і другий напрямок руху автобусів – проти годинникової стрілки. Ці автобуси також від’їжджають кожні 20 хвилин. Кожен автобус рухається по маршруту рівно 40 хвилин і повертається на вокзал. Скільки автобусів на маршруті зустріне автобус, який виїде о 8 годині?
5. Марійка виписує всі чотирицифрові числа, в записі яких обов’язково присутні лише цифри 2, 1, 0, кожна як мінімум один раз. Наприклад: 1200 або 2010 чи 1210. Потім вона вибирає з усіх записаних чисел найбільше та найменше і обчислює різницю між найбільшим та найменшим. Якою буде ця різниця? (У жодного з чотирицифрових чисел запис не починається з нуля).
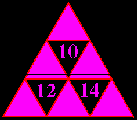
6. Впишіть всі цифри від 1 до 6, кожна по одному разу, в маленькі білі трикутники ( одну цифру в один трикутник). При цьому повинна бути виконана умова, що кожне з чисел, які записані в маленьких чорних трикутниках, рівне сумі цифр в білих трикутниках, що його оточують.
7. Код сейфу є шестицифровим числом в якому використана кожна з шести цифр від 1 до 6 рівно по одному разу. Відомо, що код є число парне, а також відомо, що для кожної пари сусідніх цифр коду одна з цифр ділиться на іншу без остачі. Вкажіть код сейфу.
8. Викресліть три значки в наступному записі 2 х 3 х 4 х 5 х 6 х 7 так, щоб результат був 2010. Значком, який викреслюють може бути будь-яка цифра чи знак множення. Якщо наприклад ви викреслите знак множення "х" між числами 2 та 3, то це число буде читатись як 23.
9. 28 томів універсальної енциклопедії розміщенні в довільному порядку на полиці. Рухом тома називають виймання тома з полиці і переставляння його на край в кінець не рухаючи інші томи на полиці. Скільки треба зробити таких рухів з томами, щоб навіть в "самому гіршому" випадку початкового розміщення томів, розташувати їх в порядку зростання зліва направо?
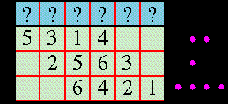
10. В школі телепатії вчитель написав шість цифр - від 1 до 6, кожну рівно по одному разу в таблицю. Потім свій запис закрив смужкою зі знаками питань. Своїм трьом кращим учням 1 класу навчання вчитель запропонував відгадати які числа він записав. Кожен з трьох учнів записав чотири цифри в своєму рядку, напроти цифр вчителя. Після чого вчитель відмітив не порядок вгаданих, а кількість вірно вгаданих цифр, що стоять на тих же місцях, як поставив вчитель, знаком - "•". Кількість вгаданих цифр, які належать до даної четвірки, але знаходяться на інших місцях в межах даної четвірки цифр він відмітив "○". Вкажи всі шість цифр в порядку запису вчителем.
11. Артур вибрав шестицифровий код для свого комп’ютера. Всі цифри коду різні, тобто жодна не зустрічається більше одного разу. АВСДЕЖ – код комп’ютера. Відомо, що цифра А є середнє арифметичне між числами В та СД ( СД - двоцифрове число). АС є середнім арифметичним між числами ВЕ та ЖЕ (всі три числа двоцифрові). Запис жодного з чисел не починається з нуля. Запишіть шестицифровий код Артура для комп’ютера.
12. Дано деякий опуклий чотирикутник. Розглянемо всі можливі трикутники з вершинами у вершинах чотирикутника. Площа найбільшого з трикутників дорівнює 2010 см2, а площа найменшого з трикутників дорівнює 201 см2. Яка може бути найбільша площа початкового чотирикутника? Відповідь дайте у см2.
13. Деякий куб розрізали 7 разів горизонтальними та вертикальними розрізами на прямокутні паралелепіпеди без перестановки частин під час розрізання. Загальна площа поверхні цих частин 500 см2. Знайти довжину ребра куба. Відповідь записати в сантиметрах.
14. Анатолій знайшов цікаве чотирицифрове число. Коли його помножити на 6, то отримаємо чотирицифрове число, записане тими ж цифрами, але в іншому порядку. Вкажіть число, яке знайшов Анатолій.
15. Михайлик написав дуже велике число, потім помножив його на 5. В результаті отримав сорокацифрове число, в записі якого міститься тридцять цифр 5, та десять цифр 7. Вкажіть суму цифр числа, яке написав Михайлик.
16. Антон має три квадрати, вирізані з паперу. Сторони квадратів 6см, 8см, 10см відповідно. Він їх розміщує на столі без накладання один на одного, таким чином, щоб вони попарно дотикались сторонами. Яка мінімальна площа трикутника, вершинами якого є центри цих квадратів?
17. Дідусь, займаючись з онуком математикою, знайшли число, яке має незвичайні властивості: перша цифра числа не нуль і відмінна від останньої цифри числа; якщо цифру одиниць перемістити з свого місця на початок числа, а інші залишити на своїх місцях, то нове число буде більшим ніж початкове в кількість разів, яка дорівнює останній цифрі початкового числа. Яке найменше з усіх можливих чисел, що знайшли дідусь з онуком, має ці властивості?
18. Петро та Сергій - два молодих математики, які полюбляють посміятися один з одного 1-го квітня, зустріли свою подругу Жозефіну. Вона вибрала деякі два числа з проміжку від 1 до 100 включно. Записала їх добуток і суму на окремих листочках. Листок з добутком віддала Сергію, а Петру - листок з написаною сумою. «Хто з вас може відгадати числа, які я вибрала?» - запитала Жозефіна.
- Результату добутку недостатньо, - відповів Петро.
- Я це знав, - відповів Сергій.
На наступний день Жозефіна повідомила математикам, що напередодні вона помилково листок для Сергія віддала Петру і навпаки.
«Але і цього мені недостатньо для визначення чисел, - повідомив Сергій, - проте я знаю, що цього достатньо, щоб ці числа відгадав Петро».
«Тоді я знаю ці числа», - відповів Петро.
«То тепер і я знаю ці числа», - повідомив Сергій.
Вкажи ці числа в порядку зростання.