Правила організації та проведення Міжнародного чемпіонату з розв’язування логічних математичних задач Оргкомітет конкурсу
| Вид материала | Конкурс |
- Правила організації та проведення Міжнародного чемпіонату з розв’язування логічних, 84.21kb.
- Методика розв’язування олімпіадних задач з логічним навантаженням. Геометричні інваріанти, 399.86kb.
- Р. Шпакович Бобер – 2009 Відповіді та вказівки до розв’язування завдань Зміст, 316.81kb.
- Розв'язування дослідницьких задач з фізики із застосуванням нових інформаційних технологій, 137.39kb.
- Автономної Республіки Крим, управління освіти І науки обласних, Київської та Севастопольської, 169.82kb.
- Міністерство освіти І науки України Кіровоградський державний педагогічний університет, 1297.75kb.
- Про графічний спосіб розв’язання математичних задач, 262.98kb.
- Матеріали для проведення математичного тижня в школі, 340.44kb.
- Урок на тему: " Розв’язування задач на розрахунок електроенергії, що споживається побутовими, 122.51kb.
- Методика навчання розв’язуванню планіметричних задач на побудову із використанням комп’ютера., 256kb.
Правила
організації та проведення
Міжнародного чемпіонату з розв’язування логічних математичних задач
Оргкомітет конкурсу
26 Міжнародний чемпіонат з розв’язування логічних математичних задач на території України проводиться у відповідності до наказу МОН України №159 від 23.02. 2009р. та додатків до нього.
Організація та проведення в Україні Міжнародного чемпіонату з розв’язування логічних математичних задач покладається на Центральний організаційний комітет, який діє на базі Центру по інтеграції до європейського та світового освітнього простору.
До повноважень Центрального оргкомітету належить, зокрема, вирішення питань щодо проведення конкурсу, перевірка робіт учасників, формування списків учасників півфіналів та фіналів, формування команди – учасниці суперфіналу в м. Парижі, оприлюднення результатів.
ПРЕДСТАВНИКОМ ЦЕНТРАЛЬНОГО ОРГКОМІТЕТУ В ХАРКІВСЬКІЙ ОБЛАСТІ Є КРИЖАНОВСЬКИЙ ОЛЕКСАНДР ФЕЛІКСОВИЧ,
e-mail: plushakaf@mail.ru або plushakaf@yandex.ru .
- Участь у конкурсі та порядок проведення конкурсу
Змагання проводяться під егідою Міжнародного комітету математичних змагань (м. Париж).
Кожен з Чемпіонатів проводиться в чотири етапи за текстами Міжнародного комітету.
I етап – чвертьфінал (заочний тур, проходить в грудні 2011 – січні 2012 року),
II етап – півфінал ( очний тур, кінець березня 2012 року),
III етап – національний фінал ( очний тур, травень 2012 року).
IV етап – міжнародний суперфінал ( традиційно проводиться в м. Парижі впродовж двох днів в кінці серпня 2012 року).
У чвертьфіналі можуть брати участь всі бажаючі за такими віковими категоріями:
- 1 – 3 класи ( 5 задач з №1 по №5 )
- 4 – 5 класи ( 8 задач з №1 по №8 )
- 6 – 7 класи ( 11 задач з №1 по №11 )
- 8 – 9 класи ( 15 задач з №1 по №15 )
- 10 – 11 класи ( 18 задач з №1 по №18 )
Чвертьфінал у регіонах проводять координатори або вчителі відповідної школи. Допускається і персональна заявка та учать учня в чвертьфіналі. Для участі в чвертьфіналі ПРЕДСТАВНИК ЦЕНТРАЛЬНОГО ОРГКОМІТЕТУ заповнює заявку на участь і надсилає її на адресу Центрального оргкомітету разом з роботами чвертьфіналістів та копією поштового переказу благочинної пожертви не пізніше 29 січня 2012 року.
РОБОТИ ТА БЛАГОЧИННУ ПОЖЕРТВУ ТРЕБА НАДАТИ ПРЕДСТАВНИКУ ЦЕНТРАЛЬНОГО ОРГКОМІТЕТУ НЕ ПІЗНІШЕ 22 СІЧНЯ 2012 РОКУ.
Рекомендована благочинна пожертва за участь у чвертьфіналі складає 4 гривні 50 копійок від кожного учасника та повністю використовується для покриття витрат на організацію та проведення конкурсу.
Переможці чвертьфіналу, яких визначає Центральний оргкомітет, запрошуються до участі в очному півфіналі, що проводиться координаторами в регіонах за текстами, наданими Центральним оргкомітетом, в березні 2012 року.
ПРОВЕДЕННЯ ПІВФІНАЛЬОГО ТУРУ В ХАРКІВСЬКЙ ОБЛАСТІ ВІДБУДЕТЬСЯ НА БАЗІ ХАРКІВСЬКОГО НВК №45 «АКАДЕМІЧНА ГІМНАЗІЯ».
Роботи півфіналістів відправляються в Центральний оргкомітет на перевірку в день проведення півфіналу. Переможці півфіналу, яких визначає Центральний оргкомітет, запрошуються на участь у Всеукраїнському фіналі, що проходитиме в травні в м. Вінниці. Міжнародний суперфінал проходитиме в кінці серпня 2012 року в м. Парижі.
Час для виконання завдань суперфіналів, фіналів, півфіналів наступний:
- 1 – 3 класи – 1 година,
- 4 – 5 класи – 1 година 30 хвилин,
- 6 – 7 класи – 2 години,
- 8 – 9 класи - 2 години 30 хвилин,
- 10 – 11 класи – 3 години .
Місцеві осередки отримують завдання заочного чвертьфіналу 27 листопада 2011 року.
Завдання очного напівфіналу отримують в переддень напівфіналу.
Перед початком проведення чемпіонату координатори проводять детальний інструктаж учасників щодо правил проведення чемпіонату та оформлення розв’язань.
Головна вимога до учасників напівфіналів – самостійна чесна робота над завданнями. Учасники напівфіналів сидять по одному за партами.
Користуватися калькулятором, підручниками та математичними таблицями категорично забороняється.
Роботи учасників Чемпіонату зберігаються до 1 вересня 2012 року.
- Правила оформлення та оцінювання робіт
Учасник чвертьфіналу наводить повне розв’язання (українською або російською мовою) до кожної запропонованої задачі.
Учасник півфіналів та фіналів до запропонованих задач вказує лише відповідь ( без будь-яких обґрунтувань).
За вимогою умови задачі, необхідно вказувати кількість розв’язків задачі та навести два з них. Правильний розв’язок задачі оцінюється одним балом, але кожна задача має свій вказаний коефіцієнт складності, який теж враховується. У випадку, коли задача має декілька розв’язків, але знайдені не всі, то зараховується лише коефіцієнт задачі. Всі місця в турнірній таблиці розподіляються одноосібно. Якщо учасники розв’язали однакову кількість задач, то перемога присуджується тому, хто розв’язав задачі з вищою сумою коефіцієнтів. Якщо ж і сума коефіцієнтів однакова, то переможцем півфіналів та фіналів стає той, хто для розв’язування витратив меншу кількість часу ( при здачі учасниками півфіналів та фіналів виконаних робіт, члени оргкомітету фіксують час здачі роботи).
- Відзначення учасників Чемпіонату
Відзначення учасників Чемпіонату здійснюється за рахунок благодійних внесків учасників та залучених спонсорських коштів на місцях.
Кожному учаснику фіналу вручається спеціальний диплом учасника Міжнародного чемпіонату з розв’язування логічних математичних задач. Переможцям в кожній з категорій вручаються відповідно золота, срібна та бронзова медалі.
- Підбиття підсумків Чемпіонату
Результати чвертьфіналу та списки півфіналістів надсилаються в регіони Центральним оргкомітетом в березні 2012 року.
Результати півфіналу та списки фіналістів надсилаються в регіони Центральним оргкомітетом до кінця квітня 2012 року.
Результати Всеукраїнського фіналу оголошуються в день його проведення після перевірки робіт.
Команда учасників Міжнародного суперфіналу формується з переможців Всеукраїнського фіналу за підсумками проведення відбіркових зборів в червні 2012 року.
Всі питання щодо участі в чемпіонаті можна узгодити з представником Центрального Організаційного комітету в Харківській області Крижановським Олександром Феліксовичем за вказаними адресами електронної пошти.
Завдання та правила оформлення буде вивішено найближчим часом на сайті www.qbit.org.ua
26 Міжнародний чемпіонат з розв’язування логічних математичних задач
чвертьфінал (заочний етап )
- Стакан, повністю заповнений водою, має масу 200 грам. Цей самий стакан, наполовину заповнений водою, має масу120 грам. Вкажіть масу пустого стакану.
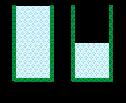
2. Українською мовою число 4 (чотири) записується за допомогою шести букв, серед яких є п’ять різних букв ч, о, т, и, р. Вкажіть число, для запису якого потрібно п’ять букв, серед яких лише чотири різні.
3
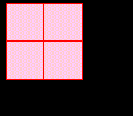 . В кожну клітинку квадрату (див. малюнок), записано число. Сума чисел першого стовпця дорівнює 20. Сума чисел другого стовпця дорівнює 12. Сума чисел першого рядка 13. Яка сума чисел другого рядка?
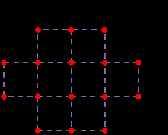
. В кожну клітинку квадрату (див. малюнок), записано число. Сума чисел першого стовпця дорівнює 20. Сума чисел другого стовпця дорівнює 12. Сума чисел першого рядка 13. Яка сума чисел другого рядка?- Ви рухаєтесь по лабіринту( див. малюнок). Вхід - стрілка зверху, вихід - стрілка справа. Рухатись можна лише по пунктирам. Вкажіть маршрут руху по лабіринту так, щоб він проходив через кожну точку сітки рівно по одному разу.
-
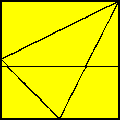
 На яку найбільшу кількість частин можна розділити фігуру (див. малюнок) двома прямими лініями?
На яку найбільшу кількість частин можна розділити фігуру (див. малюнок) двома прямими лініями?
- Я задумав особливе число. Якщо помножити це число на шість, а потім від результату відняти шість, то одержимо результат такий самий, як і у випадку віднімання від задуманого числа семи і множення одержаної різниці на сім. Яке число я задумав?
7. Марія записує початкове число 1. Це перше число. Потім вона рахує кількість щойно записаних цифр 1. Записує результат своїх міркувань. Таким чином наступне її число буде11(одна одиниця). Третім числом буде 21 (тому що дві одиниці). Четверте число буде 1211(тому що в попередньому числі одна двійка та одна одиниця). П’яте число буде 111221(тому що в написанні четвертого числа є одна одиниця одна двійка дві одиниці) і т. д. Якби Марійка написала таким чином 27-ме число, то воно б містило 2012 цифр. Однак Марійка зупинила свій запис на 13-му числі. Вкажіть кількість цифр, яку містить це число.
- У 2012 році в місяці лютому день тижня середа зустрічається 5 разів. У якому найближчому з років майбутнього знову місяць лютий буде містити п’ять днів тижня під назвою «середа»?
- Михайлик відшукав таке чотирицифрове число, сума цифр якого дорівнює 11 і саме число ділиться на 11 націло. Вкажіть число, яке відшукав Михайлик.
- О першій годині дня трикутник, утворений центром годинника та кінцями годинної та хвилинної стрілок є прямокутним. Довжина хвилинної стрілки (більшої з стрілок) дорівнює 20,12 см. Вкажіть відстань між кінцями годинної та хвилинної стрілок в цей момент часу.
- Тетянка задумала двоцифрове число, в якому цифра десятків відмінна від цифри одиниць. Вона обраховує квадрат двоцифрового числа, а потім обраховує квадрат числа, отриманого з початкового, перестановкою цифр. У неї виходить, що обидва результати записуються одними і тими ж цифрами, тільки в іншому порядку. Квадрат якого числа обраховувала Тетянка? Зауваження: розв’язки ав та ва вважаються різними.
12. В коледжі Матмістечка навчається 2012 учнів. 16 учнів цього коледжу серед учнів коледжу мають точно одного родича - брата або сестру. 12 дітей мають рівно два родичі серед учнів коледжу. 8 учнів - рівно 3 родичі і у 5 учнів - рівно чотири родичі. У всіх інших учнів коледжу немає жодного брата або сестри серед учнів коледжу. Яка кількість сімей навчає хоча б одну дитину в коледжі?
- Дівчинка Оксанка пробує обрахувати корінь квадратний з величезного числа 11 111 111 115 555 555 555. Вкажіть найближчий можливий результат, округлений до цілих.
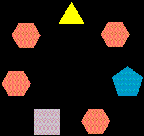
- Розмістіть всі цифри від 1 до 7 у фігурки на колі (по одній цифрі в кожну фігурку) так, щоб виконувались умови:
• цифра в трикутнику дорівнює цифрі старшого розряду добутку цифр в фігурках, з якими трикутник з’єднаний дугою (найближчі сусідні фігурки);
• цифра в квадраті дорівнює цифрі одиниць добутку цифр двох сусідніх з нею фігурок, з якими квадрат з’єднаний;
• цифра в п’ятикутнику дорівнює цифрі старшого розряду суми двох цифр, які знаходяться в двох сусідніх фігурках, з якими п’ятикутник з’єднаний;
• цифра в кожному з шестикутників дорівнює цифрі одиниць суми відповідно двох, трьох чи чотирьох цифр, з якими з’єднаний шестикутник.

- Дано трикутник АВС з основою ВС=2012мм та площею 254 526 048 мм². Є множина трикутників, які мають таку ж основу ВС і таку ж площу. Яке найменше можливе значення периметру серед трикутників цієї множини?
- Запишіть замість зірочок в прикладі на множення цифри 2; 3; 5; 7. Використовуйте лише ці чотири цифри. Зрозуміло, що цифри можуть повторюватись.
- Якщо поділити 3195 на 2011, то отримаємо1,58876...
Якщо поділити 3195 на 2012, то отримаємо1,58797...
В
 обох частках одна і таж ціла частина 1. Вкажіть найбільше натуральне число, яке буде давати одну й ту ж цілу частину при діленні і на 2011, і на 2012.
обох частках одна і таж ціла частина 1. Вкажіть найбільше натуральне число, яке буде давати одну й ту ж цілу частину при діленні і на 2011, і на 2012.- На зображення квадрату, сторона якого дорівнює 2012 мм, наклали зображення розгортки чотиригранника. В цей чотиригранник вписано кулю (всі чотири грані його є дотичними до кулі).
Вкажіть діаметр цієї кулі. Відповідь запишіть в міліметрах та округліть до цілих.
