Методические рекомендации для студентов заочной формы обучения по экономическим специальностям. (Курсовая работа)

Вид материала

Методические рекомендации

Содержание Учёт влияния инфляции в принятии финансовых решений Сложная декурсивная ставка

Подобный материал:

• Методические рекомендации для студентов заочной формы обучения по экономическим специальностям., 395.12kb.
• Методические указания к выполнению лабораторных заданий и контрольной работы по дисциплине, 541.58kb.
• Методические рекомендации для студентов очно-заочной и заочной форм обучения Тематика, 268.03kb.
• Методические рекомендации по выполнению курсовой работы для студентов очной и заочной, 185.53kb.
• Методические рекомендации по выполнению курсовой работы (для студентов заочной формы, 140.99kb.
• Методические рекомендации по выполнению курсовой работы (для студентов заочной формы, 148.36kb.
• Методические указания по выполнению курсового проекта для студентов III курса заочной, 507.48kb.
• Тематический план, рабочая программа и методические рекомендации к семинарским занятиям, 755.58kb.
• Методические указания для студентов заочной формы обучения по специальностям: «Государственное, 151.35kb.
• Методические указания: краткий курс лекций для студентов заочной формы обучения Санкт-Петербург, 1540.61kb.

Учёт влияния инфляции в принятии финансовых решений

Инфляция характеризуется снижением покупательной способности национальной валюты и общим повышением цен.

В различных случаях влияние инфляционного процесса неодинаково.

Для кредитора: теряет часть дохода за счёт обесценения денежных средств.

Для заёмщика: получает возможность погасить задолженность деньгами сниженной покупательной способности.


Механизм влияния инфляции рассматривается в форме простых математических расчётов и преобразований.


Пусть S_ - сумма, покупательная способность которой с учётом инфляции равна покупательной способности суммы S при отсутствии инфляции.

Разница между этими суммами - S;

Отношение S/S – уровень инфляции (в процентах – темп инфляции).





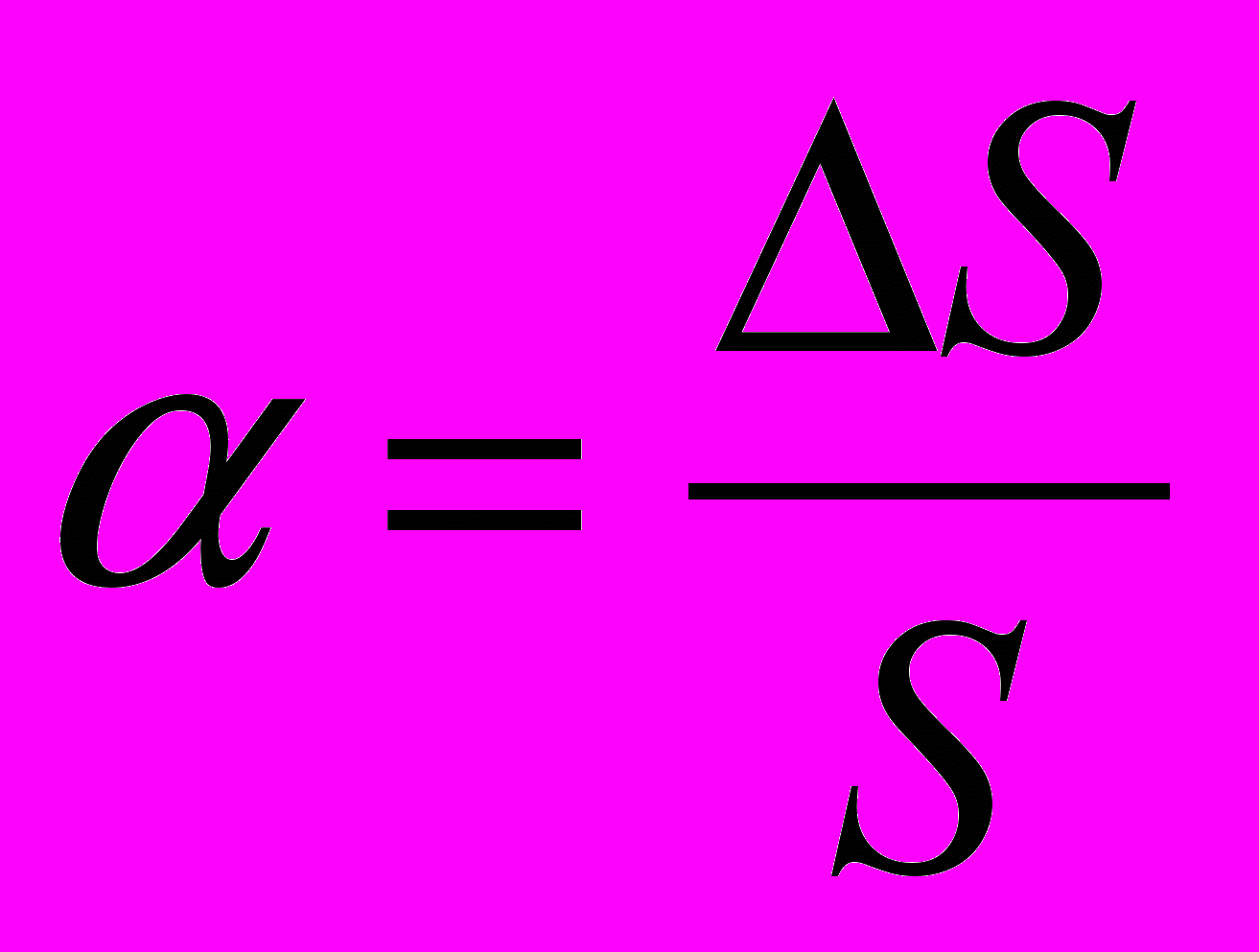
Тогда для определения S_ получаем следующее выражение:





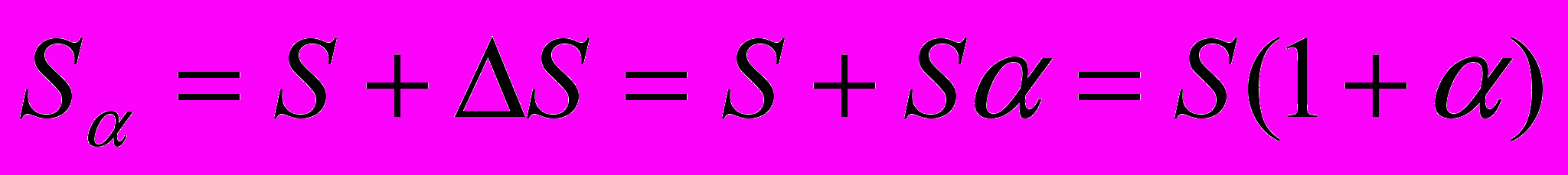
В
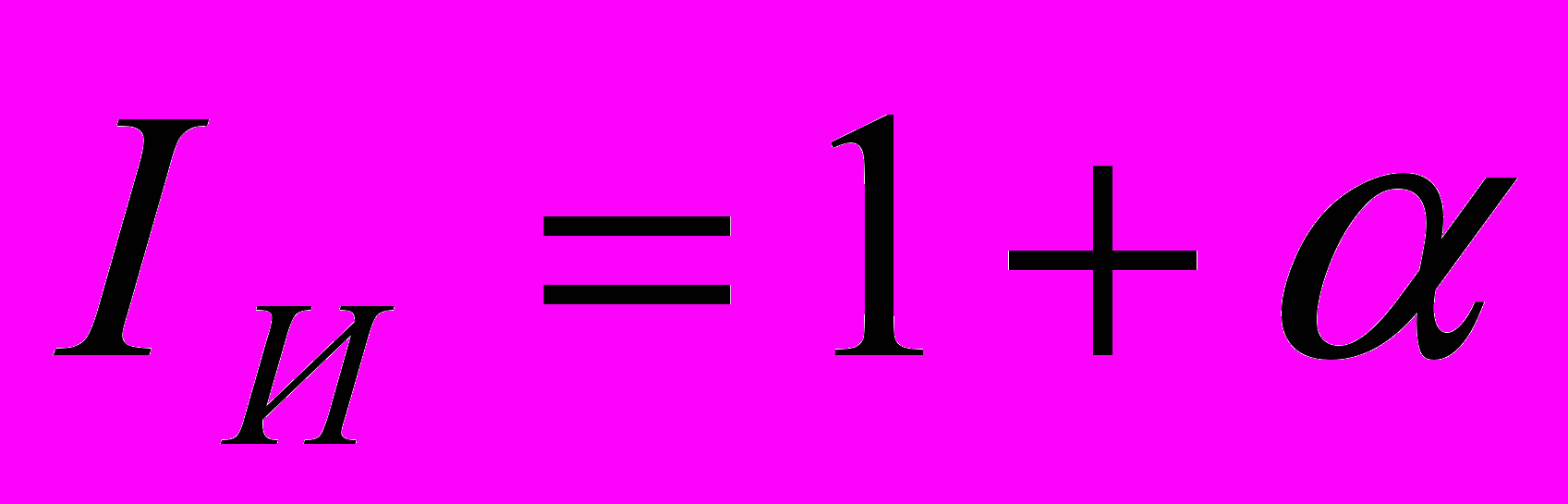
еличину (1+), показывающую, во сколько раз S_ больше S ( т.е. во сколько раз в среднем выросли цены), называют индексом инфляции I_и.


Повышение индекса инфляции за определённый период по сравнению с предыдущим таким же периодом указывает на ускорение инфляции, снижение – на уменьшение её темпов.

Инфляционный рост суммы S при годовом уровне инфляции  подобен наращению суммы S по сложной годовой ставке процентов .


Через год сумма S’_ будет больше суммы S в (1+) раз. По прошествии ещё одного года S”_ будет больше суммы S’_ в (1+) раз, т.е. больше суммы S в (1+)² раз.

Через n лет сумма Sⁿ_=S(1+)ⁿ

Т.е.





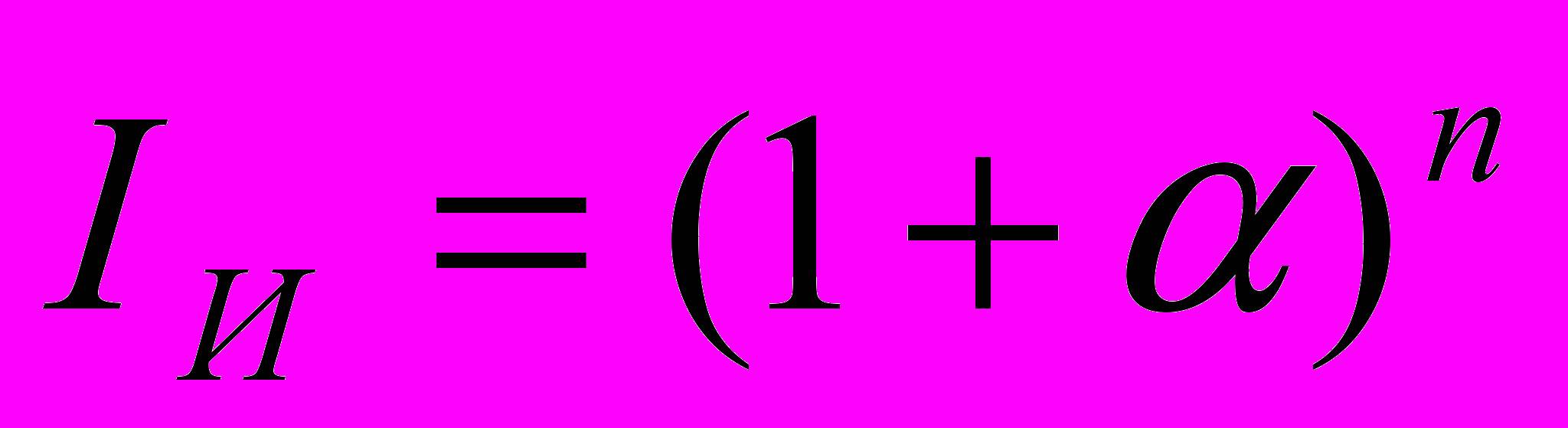
Теперь, на основании изученных в предыдущих параграфах формул, необходимо выяснить, как влияет инфляция на величину процентной ставки и будущую сумму при разных методах начисления процентов.


Если в обычном случае первоначальная сумма P при заданной ставке процентов превращается за определённый период в сумму S, то в условиях инфляции для сохранения покупательной способности на том же уровне она должна превратиться в сумму S_, что требует уже иной процентной ставки.

Такая ставка называется – ставка, учитывающая инфляцию.


Тогда, используя предыдущие обозначения, принимается:

i_ - ставка ссудного процента, учитывающая инфляцию;

d_ - учётная ставка, учитывающая инфляцию;

j_ - номинальная ставка сложного процента, учитывающая инфляцию;

и т.д.


Если задать годовой уровень инфляции  и простую годовую ставку ссудного процента i. Тогда для наращенной суммы S, превращающейся в условиях инфляции в S_, используется формула:





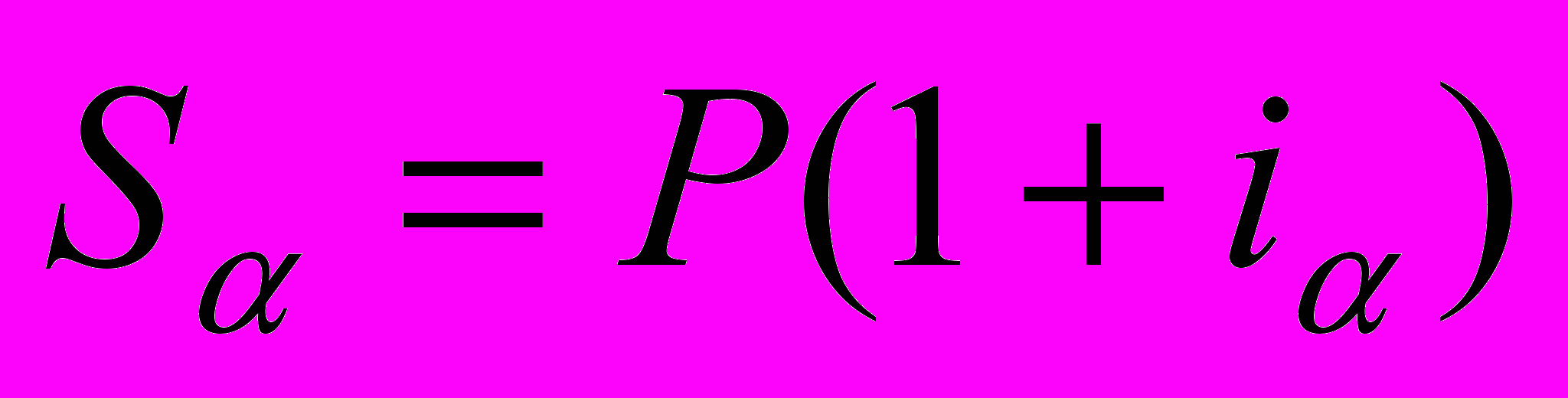
Для данной суммы ещё можно записать следующее соотношение:






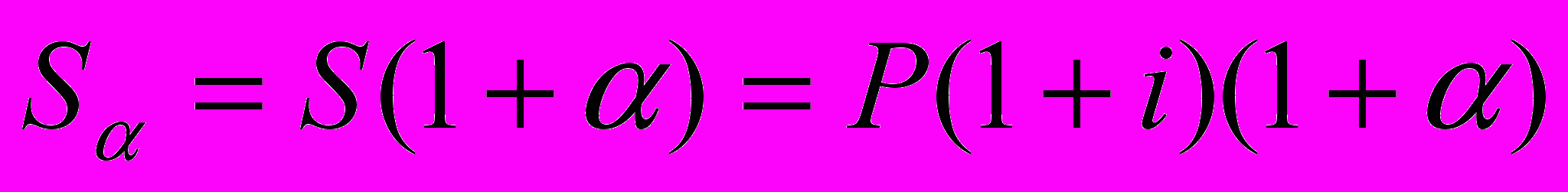
Для этих двух формул можно составить уравнение эквивалентности:





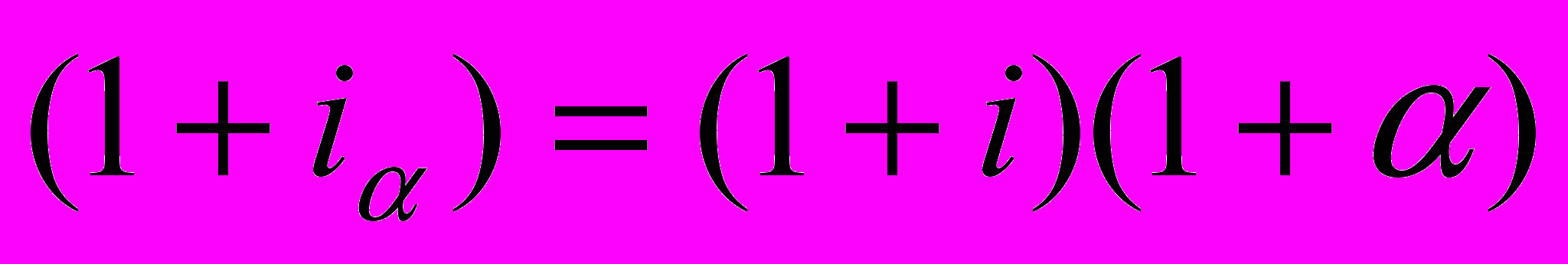
Из этого уравнения следует, что





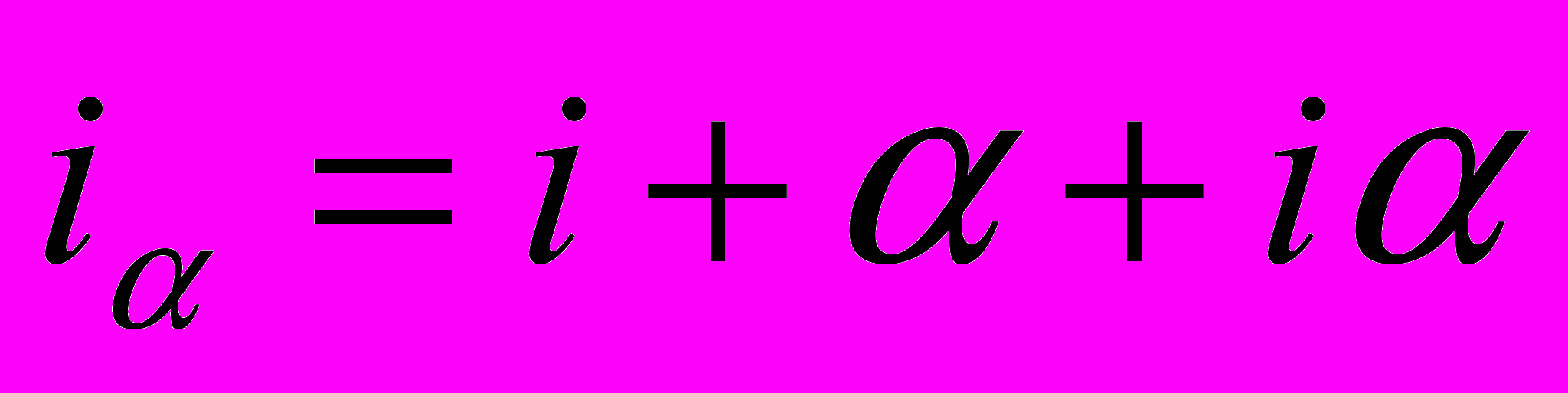
Эта формула называется формулой И. Фишера. В ней сумма +i - величина, которую нужно прибавить к реальной ставке доходности для компенсации инфляционных потерь. Эта величина называется инфляционной премией.

Применение формулы Фишера для различных способов начисления процента за несколько лет позволяет определить ставки с учётом инфляции. При этом всегда удобно пользоваться значением индекса инфляции за весь рассматриваемый период (I_И).


Простая декурсивная ставка:









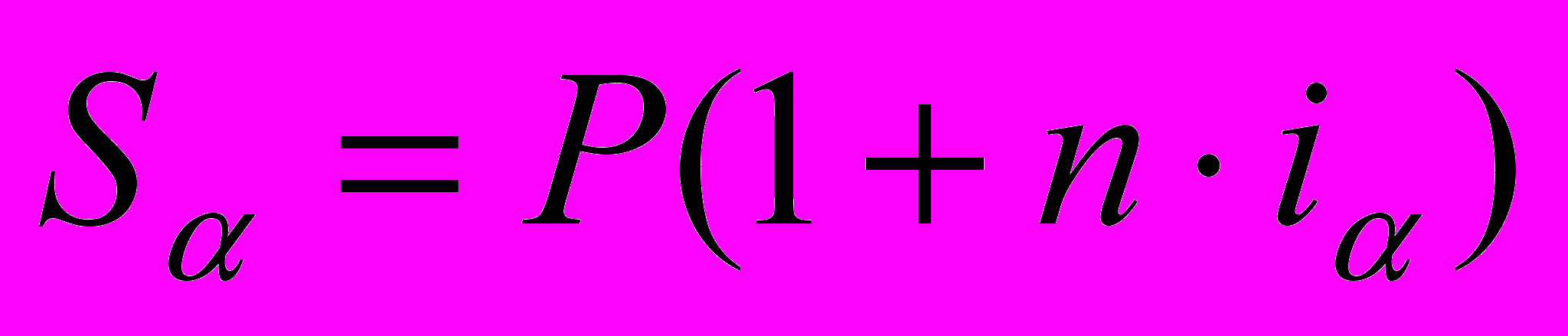
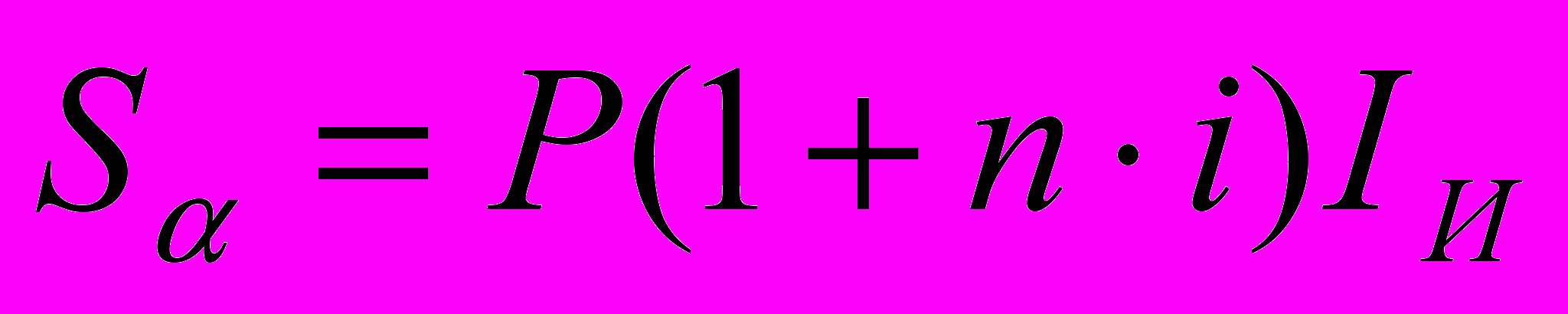
Уравнение эквивалентности:





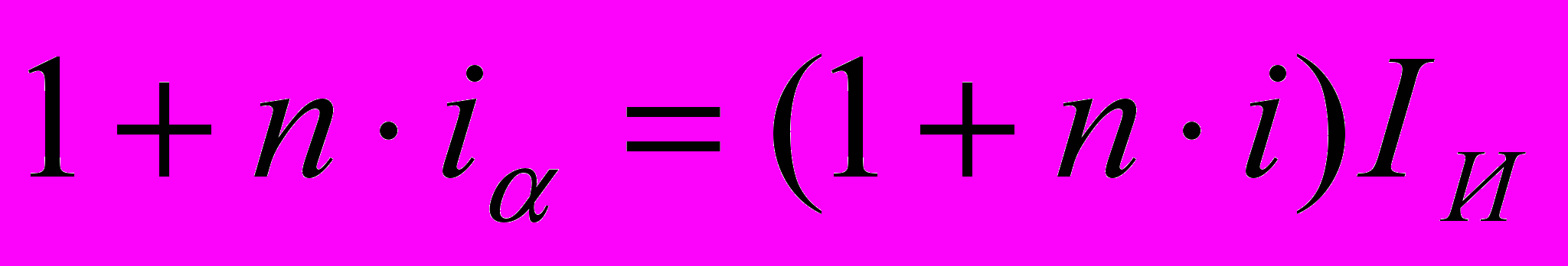
Отсюда:









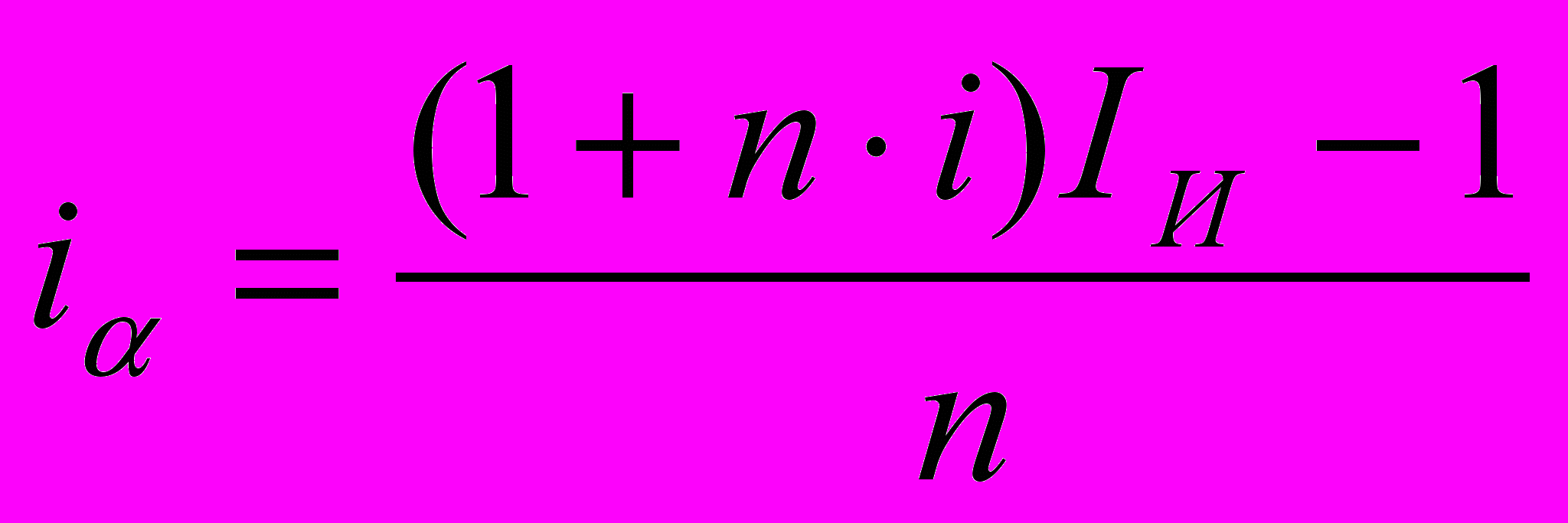
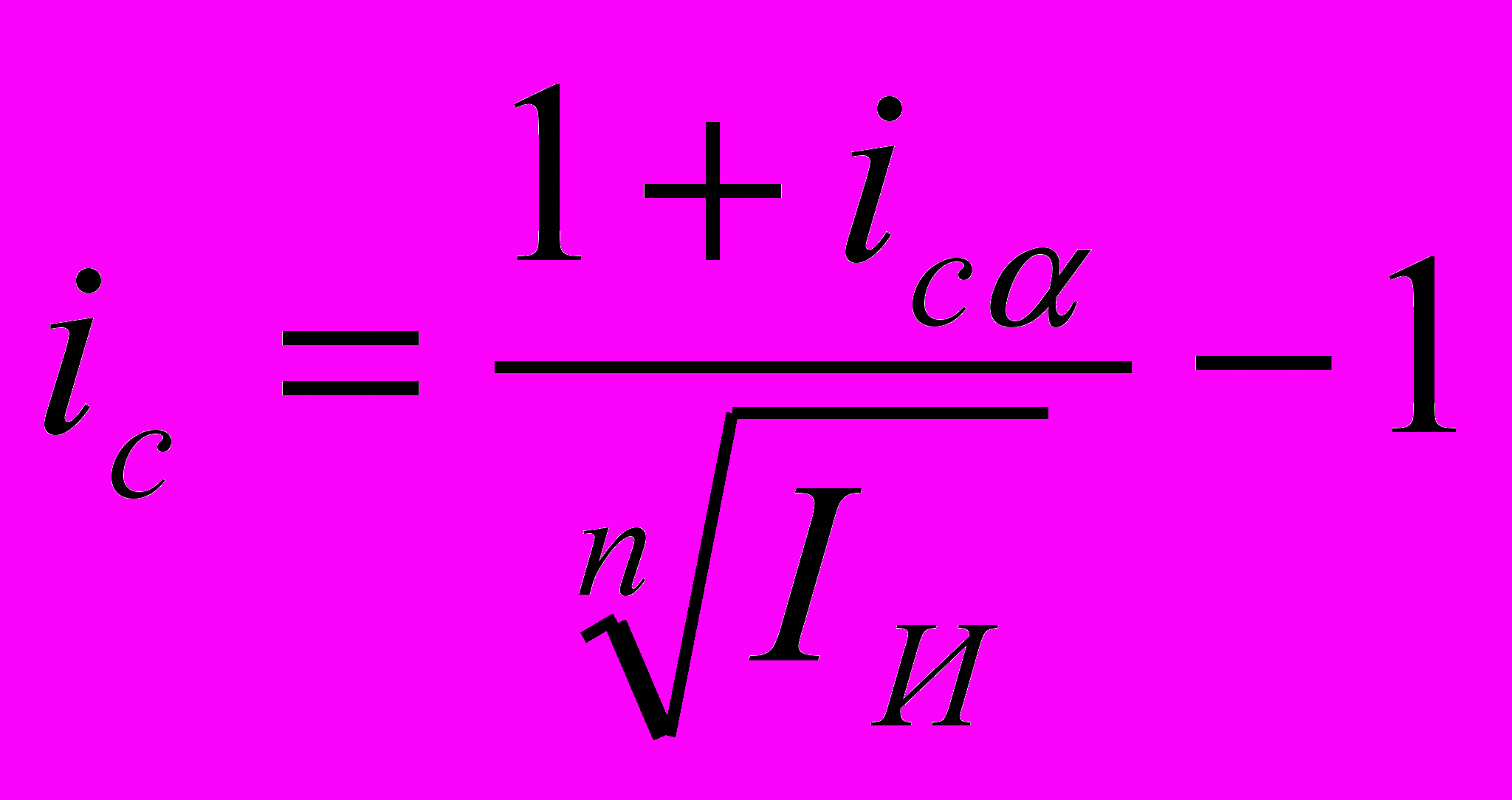
Аналогично находится простая антисипативная ставка, учитывающая инфляцию:





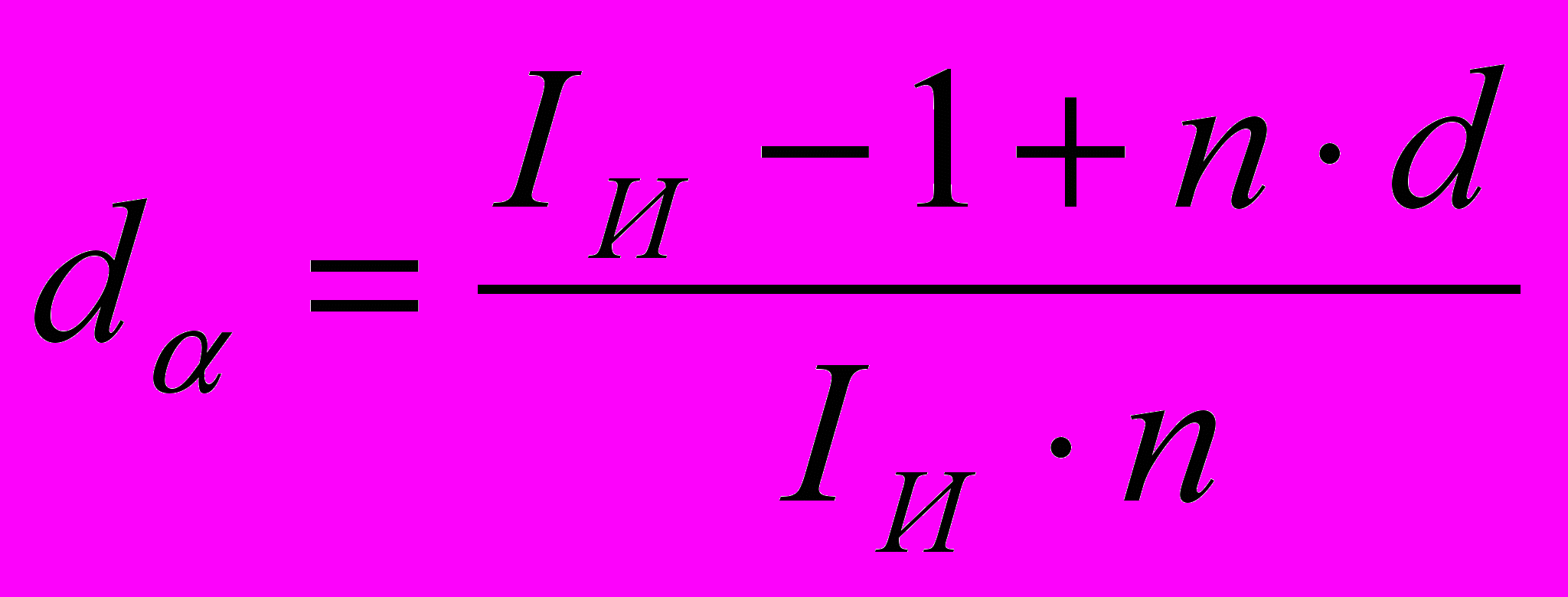
Сложная декурсивная ставка:






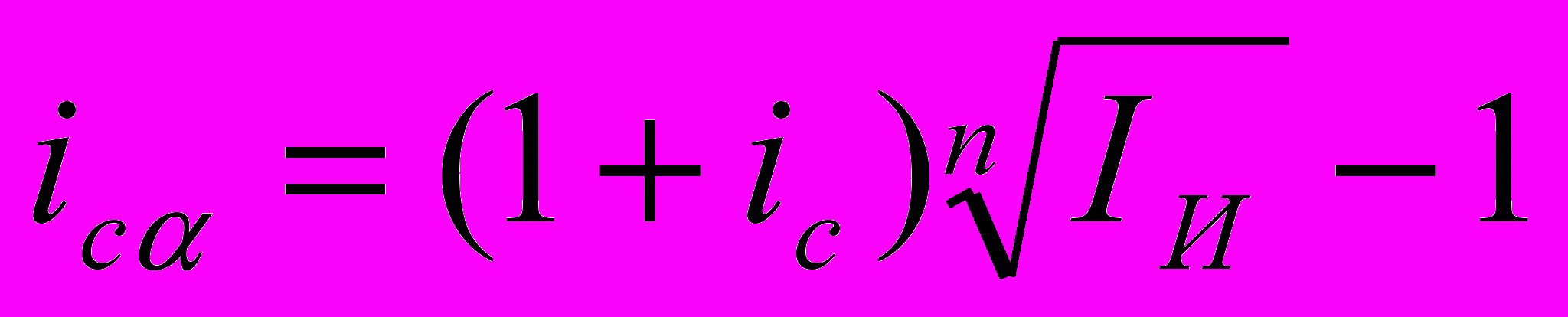
Если начисление процентов происходит несколько раз в год (m раз), то для определения номинальной ставки, учитывающей инфляцию, имеем:





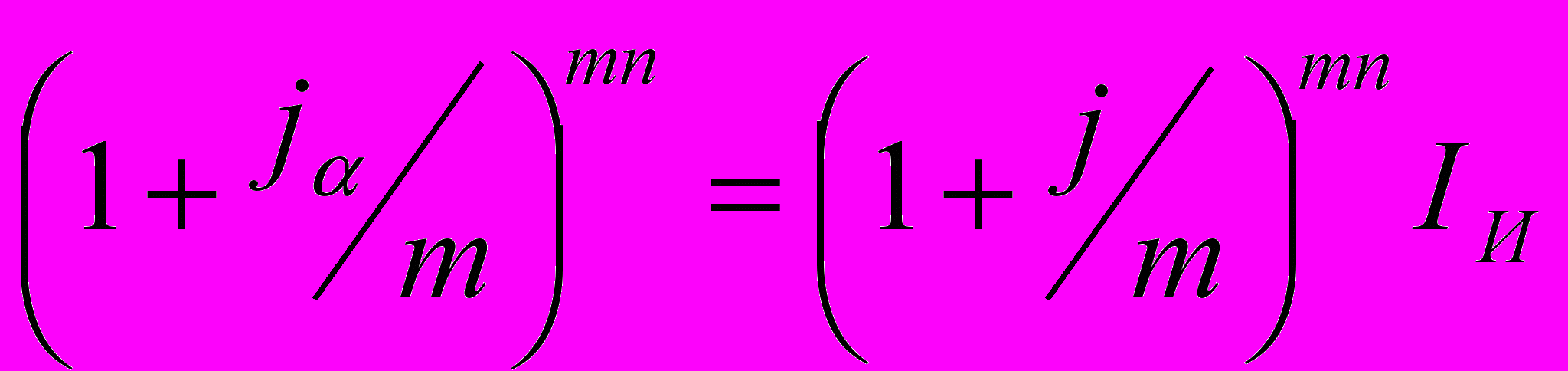
Отсюда:





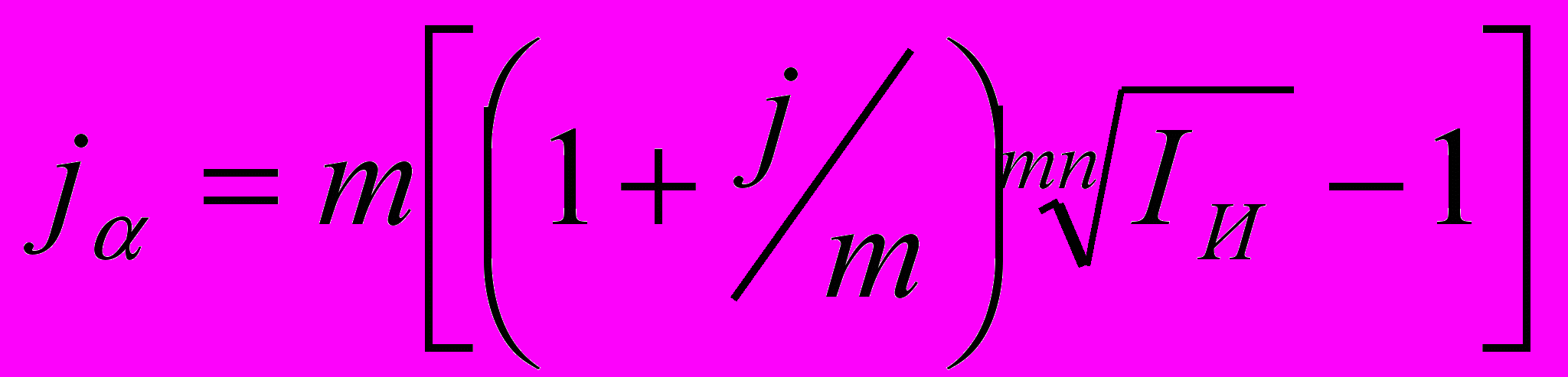
Таким же образом получаем формулы для случая сложных учётных ставок:









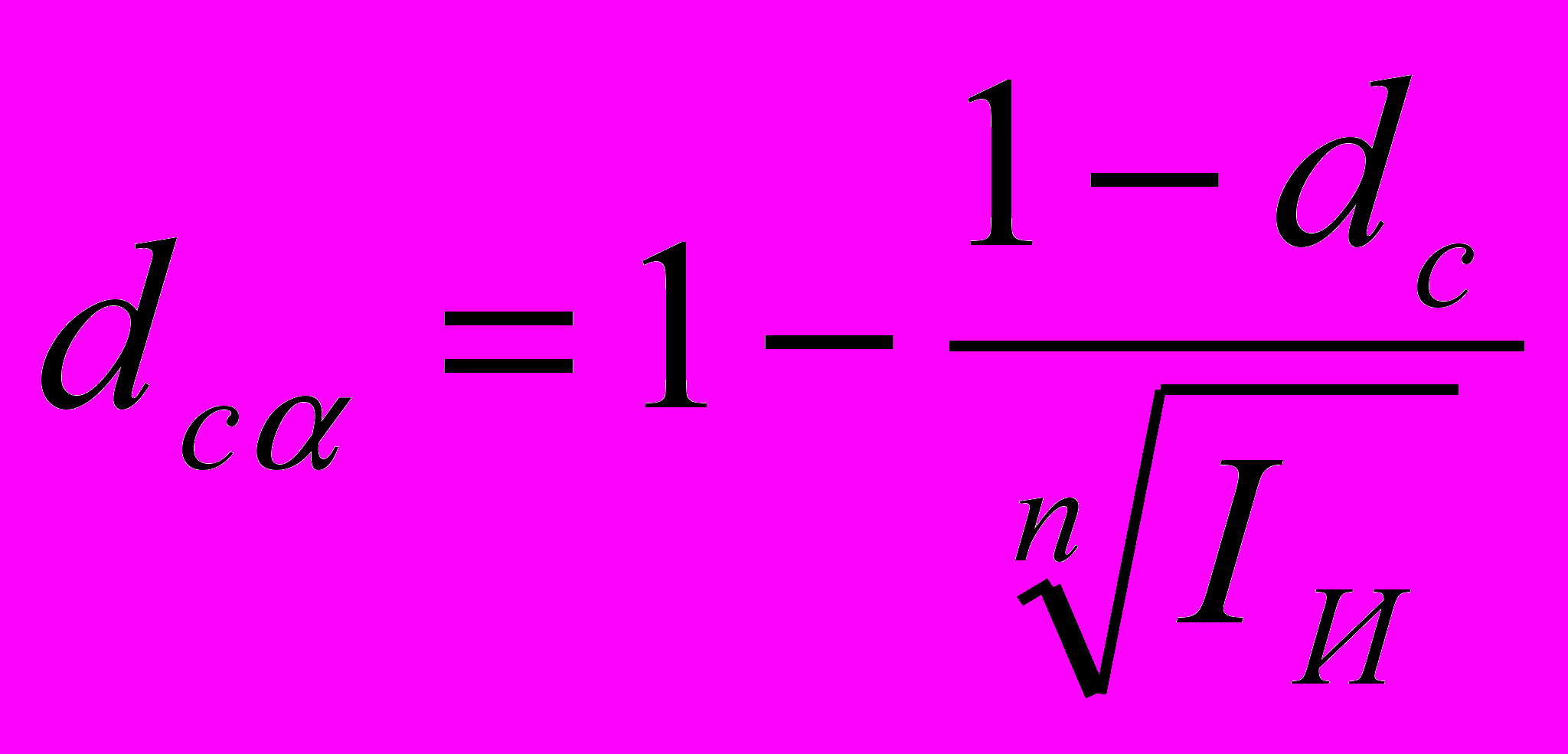
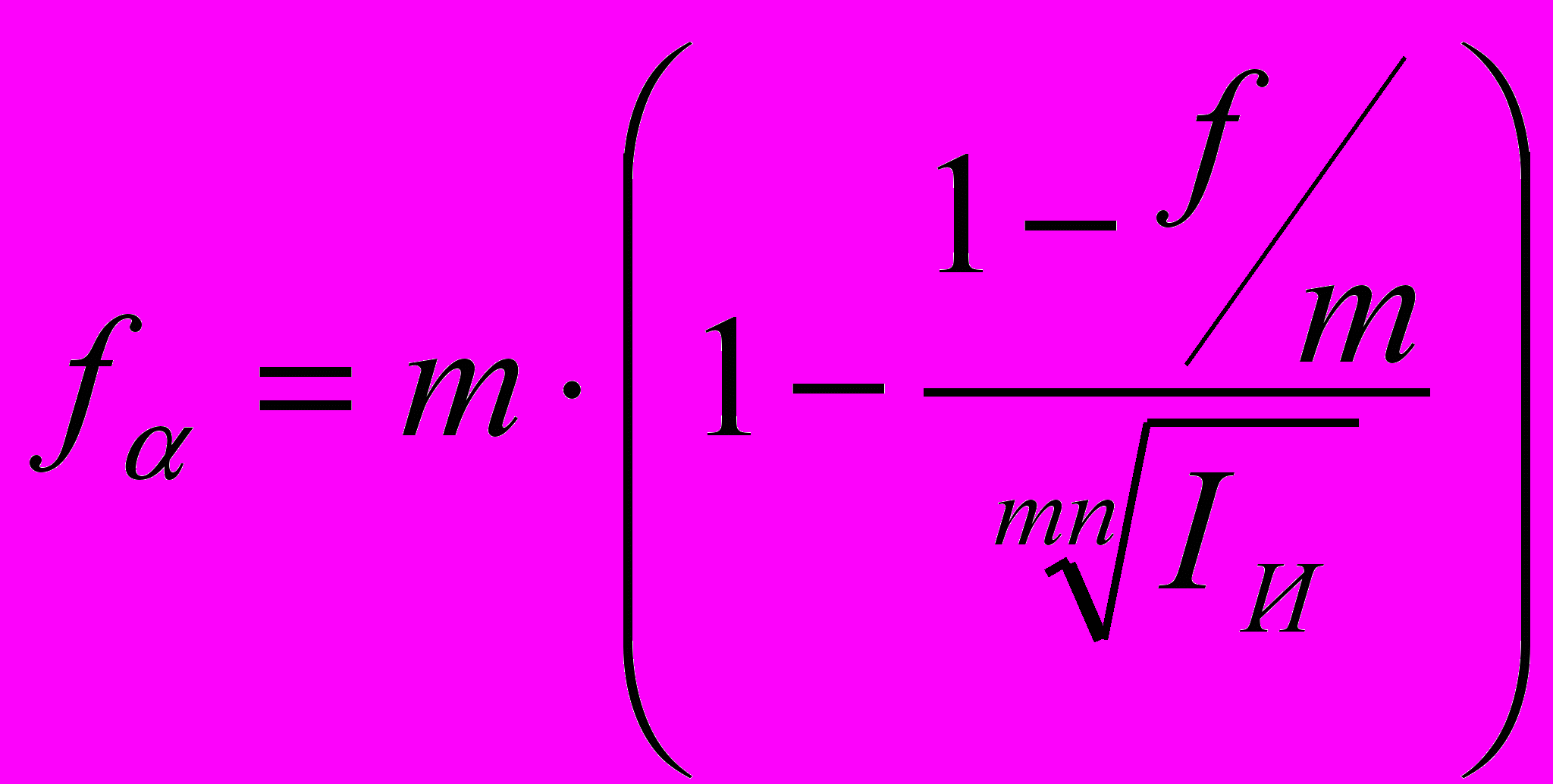
Используя полученные формулы, можно находить процентную ставку, компенсирующую потери от инфляции, когда заданы процентная ставка, обеспечивающая желаемую доходность финансовой операции, и уровень инфляции в течение рассматриваемого периода.

Можно получить формулы, позволяющие определить реальную доходность финансовой операции, когда задан уровень инфляции и ставка процентов, учитывающая инфляцию.

Например, для сложной декурсивной ставки:


Подставив в последнюю формулу вместо индекса инфляции выражение (1+)ⁿ, получим формулу:





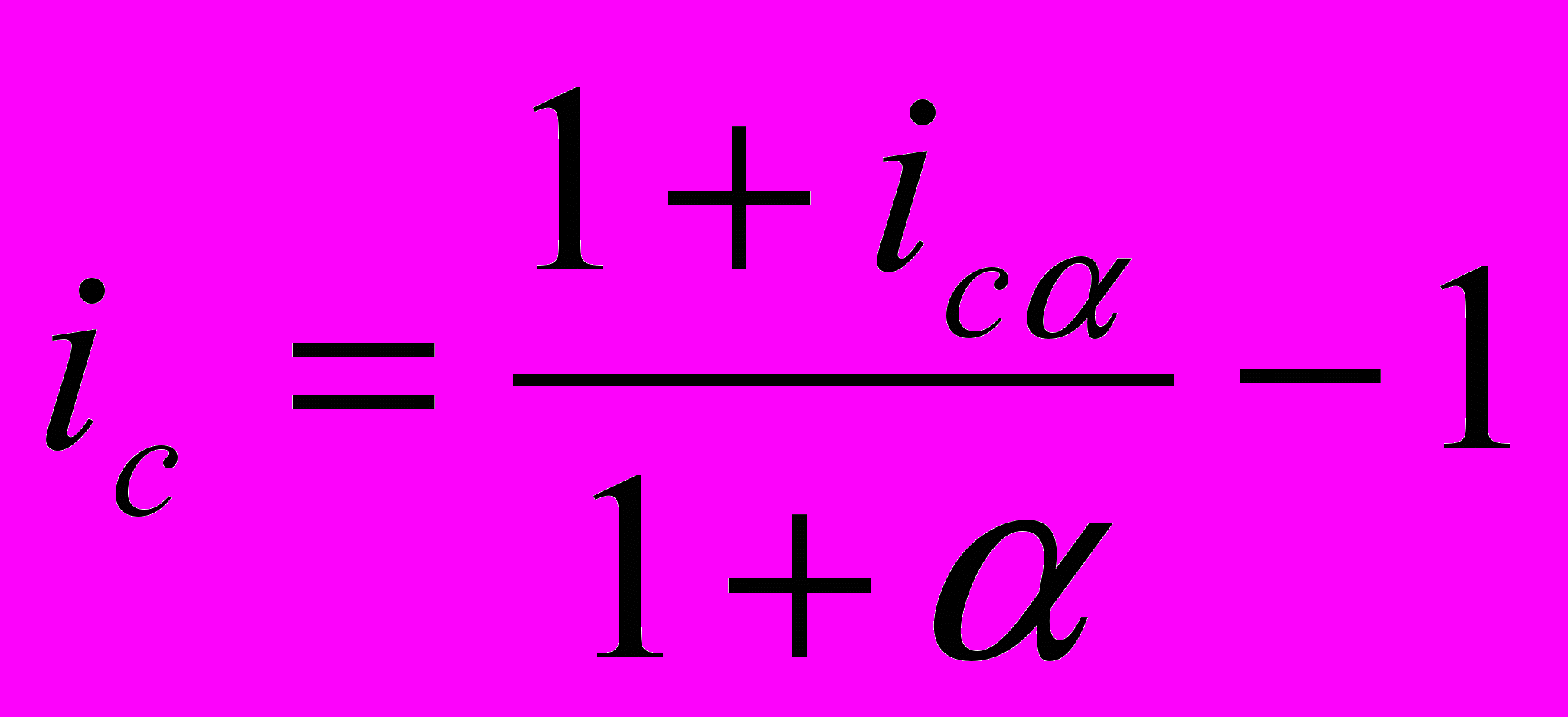
Из этой формулы видно:

• если i_c= (доходность и уровень инфляции равны), то i_c=0, т.е. весь доход поглощается инфляцией;
  
• если i_c< (доходность вложений ниже уровня инфляции), то i_c<0, т.е. операция приносит убыток;
  
• если i_c> (доходность вложений выше уровня инфляции), то i_c>0, т.е. происходит реальный прирост вложенного капитала.