Ученик 10 класса

Вид материала

Документы

Содержание 1. Кем и когда проводился опыт, его историческая цель Д.К. Максвеллу R - универсальная газовая постоянная, е 2. Приборы и материалы, необходимые для постановки опыта, принципиальная схема установки Рис. 3. Схема установки О.Штерна (вид сверху). При покоящейся установке налет серебра образуется точно против щели C Способ нахождения скорости атомов серебра был достаточно прост. Атом,   двигаясь  со   скоростью   υ,   проходил  расстояние 4. Основные результаты опыта Объяснение данных опыта с позиции современных научных теорий

Подобный материал:

• Проекта, 43.2kb.
• Постоева Елизавета Владимировна, ученица 3 класса моу сош №117 Красноармейского района, 208.92kb.
• Сочинение «Я знаю о войне…» Автор: ученик 1-в класса Панин Артём, 10.52kb.
• Платонов Максим Михайлович, ученик 11"В" класса средней школы №20 Лениского района, 120.41kb.
• Награждается ученик класса, 6.35kb.
• 3 класс Ученик(ца) 3 класса, 23.65kb.
• Ученик 9 класса, 341.77kb.
• Николая Васильевича Гоголя. Напомним, что за победу в конкурс, 103.77kb.
• Ученик 11-го класса, 223.07kb.
• Подготовил: ученик 9-ого класса, 157.7kb.

Муниципальное образовательное учреждение

Крещенская средняя общеобразовательная школа.







Выполнил: Ученик 10 класса

Устинов Никита.

Проверил: Учитель физики

Лапина Людмила Фёдоровна.


с. Крещенское – 2009 г.

ОПЫТ ОТТО ШТЕРНА

 (1920 Г.)

                                           

1. КЕМ И КОГДА ПРОВОДИЛСЯ ОПЫТ, ЕГО ИСТОРИЧЕСКАЯ ЦЕЛЬ

Отто Штерн (17.02.1888 - 17.08.1969) – немецкий физик. В 1912 окончил университет в Бреслау (Вроцлаве) и  защитил докторскую диссертацию по физической химии. С 1920 г. доцент, а затем  профессор университета во Франкфурте-на-Майне, с 1922 профессор университета в Ростоке. С 1923 г. профессор и директор Физико-химической лаборатории университета в Гамбурге. С1933 г. жил и работал в США. Профессор Технологического института Карнеги в Питсбурге (1933 - 45 гг.). Проводил исследования  по ядерной физике, квантовой физике, термодинамике. Разработал метод молекулярных пучков, измерил (1920 г.) скорость теплового движения молекул газа (опыт Штерна), доказал (1922  г.) существование пространственного квантования (опыт Штерна - Герлаха). Открыл (1929 г.) дифракцию атомов и молекул; измерил (1933 г.) магнитный момент протона. В 1943 О. Штерн был удостоен Нобелевской премии по физике за вклад в развитие метода молекулярных пучков, открытие и измерение магнитного момента протона.

 

В 1828 г. английский ботаник Роберт Броун (1773 – 1885) заметил, что взвешенные в воде мельчайшие частицы вещества находятся в движении. Они то удаляются, то приближаются друг к другу, то поднимаются вверх, то опускаются вниз. Это движение, отметил ученый, неупорядоченно и  некогда не прекращается. Обнаруженное ученым движение взвешенных частиц  стало называться в его честь броуновским движением.

В конце XIX века исследование броуновского движения приобрело огромное теоретическое значение и привлекло внимание многих  физиков-теоретиков. В рамках сформировавшихся  к тому времени молекулярно-кинетических представлений о строении вещества это движение получает вполне логичное объяснение: броуновская частица движется благодаря непрерывным ударам молекул жидкости, в которой находится взвесь.

Несмотря на правдоподобное объяснение подвижности броуновских частиц никаких  прямых доказательств существования самих молекул и тем более их движения на тот момент времени не существовало. Молекулярно-кинетическая теория вещества базировалась лишь на предположениях и разрабатывалась как в физике, так и в химии только как гипотеза. Молекулы по-прежнему были недоступными непосредственному наблюдению, а  проблема измерения скорости движения невидимых частиц казалась по тем временам просто неразрешимой. Именно поэтому эксперимент, связанный   с  прямым доказательством факта существования молекул и определением скорости их движения,  изначально определялся как один из фундаментальных научных экспериментов. Его решающее значение для науки было очевидно, так как он напрямую подтверждал справедливость молекулярно-кинетической теории строения вещества.

Первые попытки найти  среднюю скорость движения молекул предпринял немецкий физик Рудольф Эммануэль Клаузиус (1822 – 1888).

В разработке кинетической теории газов роль Р. Клаузиуса особенно велика.  Одна из его первых   работ   «О роде движения, который мы называем теплотой» была опубликована в 1857 г. Позднее появился трехтомный труд   «Механическая теория тепла», в котором Р. Клаузиус излагает основные представления новой теории тепловых явлений, названной им «кинетической». Р. Клаузиус изучал тепловое движение молекул в газах, жидкостях и твердых телах. Но существенные результаты он получил только для идеального газа.

Р. Клаузиус  предложил чисто теоретическое решение проблемы измерения скорости движения молекул (1870 г.) Действительно, из уравнения молекулярно-кинетической теории газов известно, что

                                                                    .                                                                    

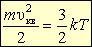Тогда среднеквадратичная скорость равна:

 



 

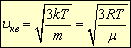
Если учесть, что

,

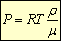то для средней квадратичной скорости можно получить выражение, в которое входят величины измеряемые экспериментально, а именно:

 

,

 

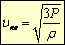где Р – давление, ρ  плотность газа.

Вычисленные Р. Клаузиусом скорости молекул газов оказались неожиданно очень большими. Отметим, что Р. Клаузиус предположил, что все молекулы движутся с одинаковой скоростью, которая зависит от температуры газа. По его расчетам средняя квадратичная скорость молекул кислорода при 0С составила 461 м/с, азота - 402 м/с, а водорода - 1844 м/с.

Сразу возникли вопросы: как, исходя из таких значений скорости молекул газа, объяснить, почему диффузия в газах происходит медленно, а  теплопроводность  газов мала. Р.Клаузиус смог ответить на эти вопросы. Он ввел понятие о средней длине свободного пробега молекулы. Показал, что ее величина зависит от температуры и от плотности газа.

После публикации работы Р. Клаузиуса кинетическая теория теплоты стала быстро развиваться.

Основные заслуги в ее дальнейшем развитии принадлежат Д.К. Максвеллу (1831- 1879 гг.) и Л. Больцману  (1844-1906 гг.).

21 сентября 1859 г. на собрании Британской Ассоциации содействия прогрессу наук Джеймс Клерк Максвелл  сделал доклад «Пояснения к динамической теории газов». Д. Максвелл отметил, что из молекулярной гипотезы «... может быть выведено так много свойств материи, в особенности, если ее рассматривать в газообразной форме, что истинная природа этого движения является предметом естественного интереса».

Д. Максвелл  считал невероятным, что все молекулы движутся с одной скоростью. По его мнению, при каждой заданной температуре большинство молекул обладает скоростями, лежащими в довольно узких пределах, но некоторые молекулы могут двигаться с большей или меньшей скоростью. Более того, считал ученый, в каждом объеме газа при той или иной температуре есть молекулы, обладающие как очень малыми, так и очень большими скоростями. Сталкиваясь между собой, одни молекулы увеличивают скорость, а другие уменьшают. Но если газ находится в стационарном состоянии, то число молекул, обладающих той или иной скоростью, остается постоянным. Исходя из такого представления, Д. Максвелл исследовал вопрос о распределении молекул по скоростям в газе, находящемся в стационарном состоянии.


На основе законов механики он теоретически исследует  движение и столкновение некоторого числа твердых упругих шаров малого размера и приходит к выводу, что в такой системе в результате взаимных столкновений устанавливается распределение «живых сил»(в современной терминологии – кинетической энергии)  между частицами «согласно некоторому правильному закону». При этом возможно определить «среднее число частиц, скорости которых лежат между определенными пределами, хотя скорость каждой отдельной частицы изменяется при каждом столкновении».  Д. Максвелл в качестве общего вывода констатирует, что «скорости распределяются между частицами по тому же закону, по которому распределяются ошибки между наблюдениями в теории «метода наименьших квадратов». Скорости молекул, согласно его расчетам, лежат в пределах от  0   до  , однако число молекул, имеющих очень большие скорости, по мнению Д. Максвелла, сравнительно невелико.

В ходе данных исследований Д.Максвелл ввел в физику понятие вероятности, до этого понятием вероятности оперировали только математики. Примечательно, что в резюме к докладу Д. Максвелл ни слова не говорит об открытом им законе распределения скоростей. Между тем именно в этом открытии сейчас мы видим одну из главных заслуг Д. Максвелла.

Массовость и случайность событий в микромире определяют статистический характер открытого Д.Максвеллом закона.  Согласно этому закону  нельзя сказать, сколько частиц тела имеют определенные скорости или координаты  в данный момент времени (строго говоря, ни одной), можно лишь рассчитать вероятность  нахождения в заданном объеме  той или иной частицы со скоростью из заданного интервала скоростей. Можно также ответить на  вопрос: сколько (приблизительно, но достаточно обоснованно) частиц тела в данный момент имеют скорости и координаты из заданных интервалов. Причем точность ответа на этот вопрос будет  тем выше, чем больше частиц в рассматриваемом объеме.

Вид   функции    распределения   молекул   по скорости движения   Д. Максвелл определил теоретическим  путем (на основе теории вероятностей). Максвелловская функция распределения, называемая законом Максвелла, выражается следующей формулой: 

 

,

 

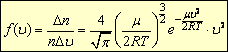где n - общее число молекул,   - молярная масса газа, R - универсальная газовая постоянная, е - основание натурального логарифма.

На основе выведенной им формулы Д. Максвелл смог определить, например, что у молекулы азота при температуре 140° С наиболее вероятная скорость равна 500 м/с. Со скоростью от 300 до 700 м/с движется 59 % молекул. Меньшей скоростью обладает 12,6%, а большей – 28,4 % всех молекул.

Результаты работы Д. Максвелла получили всеобщее признание, но при этом не были   подтверждены   экспериментально. 

О. Штерн в 1920 г., воспользовавшись методом молекулярных пучков, изобретенным французским   физиком   Луи  Дюнойе (1911 г.) измерил скорость газовых  молекул и  на опыте подтвердил полученное Д. Максвеллом распределение молекул газа по скоростям [17, С. 47] .(Результаты опыта Штерна подтвердили правильность оценки средней скорости атомов, которая вытекает из распределения Максвелла. О характере самого распределения этот опыт мог дать лишь весьма приближенные сведения.

Более точно закон распределения был проверен в опытах Ламмерта (1929 г.), в которых молекулярный пучок пропускался через два вращающихся диска с радиальными щелями, смещенными относительно друг друга на некоторый угол. Меняя скорость вращения прибора или угол между щелями, можно выделить  из пучка молекулы, обладающими различными значениями скорости. Результаты опытов Ламмерта и других исследований, предпринимавшихся с той же целью, находятся в полном соответствии с теоретическим законом распределения скоростей молекул Максвелла.)

 

2. ПРИБОРЫ И МАТЕРИАЛЫ, НЕОБХОДИМЫЕ ДЛЯ ПОСТАНОВКИ ОПЫТА, ПРИНЦИПИАЛЬНАЯ СХЕМА УСТАНОВКИ

 

Для постановки опыта по измерению средней скорости движения молекул О. Штерн  спроектировал специальную установку. Прибор состоял из двух жестко соединенных коаксиальных цилиндров с радиусами R и r (рис. 1-3). Во внутреннем цилиндре по оси была расположена платиновая нить А. Исследуемым газом в опыте служили разреженные пары серебра. Атомы получались при испарении слоя серебра, нанесённого на платиновую нить, нагревавшуюся электрическим током. Воздух в  малом цилиндре был откачан, поэтому испарившиеся атомы серебра свободно разлетались от нити  во все стороны.

Вдоль поверхности внутреннего цилиндра была вырезана узкая щель С.  Рядом с щелью располагалась диафрагма, которая позволяла «вырезать» из  потока атомов серебра тонкий пучок. Конструкция диафрагмы D обеспечивала одно и то же направление скорости всем атомам серебра, попадавшим далее в камеру большого цилиндра. Другими словами,  диафрагма фильтровала атомы, движущиеся только в определенном направлении. В вакуумной камере большого цилиндра обеспечивалась высокая степень разреженности (порядка  Па.). Вероятность столкновений атомов серебра с молекулами воздуха была очень мала и, следовательно, была очень невелика вероятность какого-либо отклонения атомов серебра при их равномерном и прямолинейном движении (т.е. рассеяния пучка). На внутренней поверхности внешнего цилиндра помещалась съемная латунная пластинка В. Пластинка имела комнатную температуру. На этой пластинке в области E атомы серебра, охладившись, оседали в виде узкой серебренной полоски.

Специальным устройством  установка  могла приводиться во вращение вокруг собственной оси с  частотой 25-45 оборотов в секунду.

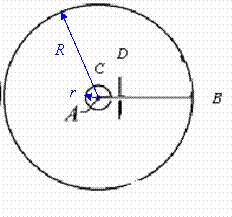Рис. 3. Схема установки О.Штерна (вид сверху). При покоящейся установке налет серебра образуется точно против щели C

 

3. ПОРЯДОК ПРОВЕДЕНИЯ ОПЫТА


Опыт  проводился в следующей последовательности. По платиновой нити, располагающейся по оси малого цилиндра, пропускался электрический ток. Нить нагревалась практически до температуры плавления серебра Т_п = 1234 К, и серебро начинало испаряться. Часть атомов серебра проходило сквозь щель. Отфильтрованные диафрагмой, далее они двигались по радиальным направлениям к внутренней поверхности  большого цилиндра прямолинейно и равномерно со скоростью, соответствующей температуре платиновой нити. Стенка большого цилиндра охлаждалась так, чтобы попадающие на нее атомы «прилипали» к ней, образуя налет серебра в форме щели, но немного больших размеров.


Сначала прибор покоился, и изображение щели на экране (латунной пластинке) приходилось как раз против нее самой (рис. 3). Затем прибор приводился в быстрое вращение вокруг собственной оси  с частотой 1500 - 2700 об/мин и,  результаты опыта существенно изменялись. Каждый атом по-прежнему двигался прямолинейно, но за время, которое требовалось атому, чтобы, пройдя щель, долететь до латунной пластинки, последняя успевала повернуться на некоторый угол, и атом уже прилипал к ней не точно против щели, а несколько в стороне [ там же] (рис. 4).

Смещение полоски серебра при вращении установки позволяло определить величину скорости движения атомов серебра и сравнить ее со значением, полученным теоретическим путем.

Способ нахождения скорости атомов серебра был достаточно прост. Атом,   двигаясь  со   скоростью   υ,   проходил  расстояние:

 

 

 

где R и  r – радиусы внешнего и внутреннего цилиндров, а  τ – время прохождения этого расстояния.

Любая точка внешнего цилиндра  за это время проходила путь:

 

 

 


Решая эти уравнения совместно, О. Штерн определил среднюю скорость движения атомов:



 

Измеряя значения ω, R, r и S можно рассчитать среднюю скорость движения атомов серебра при температуре нити – Т_н. Меняя  температуру накала нити  можно найти температурную зависимость скорости теплового движения атомов.

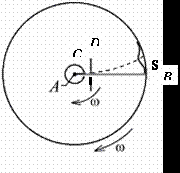Рис. 4. При вращении прибора по часовой стрелке налет  серебра смещается.

Толщина налета серебра определялась  в опыте О.Штерна оптическим методом.

 

4. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ОПЫТА

 

Ширина полоски из серебра при неподвижной установке составила 0,4 мм. При вращении установки смещение полоски также не превысило нескольких долей миллиметра (0,035 – 0,063 см).  По величине смещения полоски серебра  была определена скорость движения атомов, которая  составила около  600  м/с.

Другим важным результатом опыта О. Штерна  явилось то, что  полоска серебра при вращении прибора приобрела принципиально другой вид. Оказалось, что изображение щели не просто сместилось, но  оно стало  еще и  размытым. Если бы все атомы, вылетающие из нити, имели одинаковую скорость, то изображение щели на экране не изменилось бы по форме и размеру, а лишь немного бы сместилось в сторону. Размытость же полоски из серебра позволила О. Штерну сделать заключение о том, что вылетающие из раскаленной нити атомы движутся с разными скоростями. Атомы, движущиеся быстро, смещались меньше, чем атомы движущиеся с меньшей скоростью.

Возникла проблема определения скорости движения атомов серебра. В  этой ситуации можно было определить только смещение для середины изображения щели и, соответственно,  вычислить среднюю скорость движения атомов.

Температура нити в опытах О.Штерна равнялась 1225С, что соответствует среднеквадратичной скорости  = 588 м/с. О.Штерном для этого значения температуры были получены значения скорости движения атомов серебра от 560 до 640 м/с.

Изучение профиля полоски серебра позволило ученому сделать вывод о существовании наиболее вероятной средней скорости движения частиц (т.е. скорости с которой движется наибольшее число молекул).

С ростом температуры профиль полоски серебра смещался меньше, что  убедительно свидетельствовало о зависимости средней скорости движения частиц от температуры металла.

Как видно, результаты  опыта О.Штерна хорошо согласовались с предварительными теоретическими расчетами и выводами

 

5. ОБЪЯСНЕНИЕ ДАННЫХ ОПЫТА С ПОЗИЦИИ СОВРЕМЕННЫХ НАУЧНЫХ ТЕОРИЙ

 

Результаты опыта О. Штерна подтвердили справедливость предсказанного  Р.Клаузиусом  значения скорости движения молекул газа,  послужили  ярким   доказательством  верности  полученного Д. Максвеллом закона распределения числа молекул по скоростям и явились, в конечном счете, блестящим свидетельством правильности молекулярно-кинетических представлений о строении вещества, а также статистического характера закономерностей, которым подчиняется поведение молекулярных систем.

Изобразим полученный Д. Максвеллом результат графически (рис. 5). По оси абсцисс отложим возможные различные значения скоростей молекул V и  интервалов этих скоростей ΔV. По оси ординат отложим ΔN/N·ΔV.

 



 

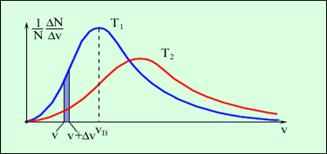
Рис. 5. Распределение молекул по скоростям (Т₂>T₁) [24]

 

Площадь густо заштрихованной фигуры численно равна доле ΔN/N общего числа молекул N со скоростями между V и V + ΔV. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Кривые распределения молекул по скоростям имеют следующие особенности:

        они проходят через начало координат,

        асимптотически приближаются к оси абсцисс при бесконечно больших скоростях,

        имеют максимум,

        асимметричны (слева от максимума кривые идут круче, чем справа).

То, что кривая распределения проходит через начало координат, означает, что неподвижных молекул в газе нет. Из того, что кривая при бесконечно больших скоростях асимптотически приближается к оси абсцисс, следует, что слишком большие скорости молекул маловероятны. Значение наиболее вероятной скорости движения молекул соответствует максимуму кривой распределения .

Вид   функции    распределения   молекул   по скорости движения, которую  Д. Максвелл определил теоретическим  путем, качественно совпал с профилем налета атомов серебра на латунной пластинке в опыте О.Штерна.

Опыт О. Штерна (наряду с опытом Ж. Перрена) был   первым  прямым доказательством справедливости молекулярно-кинетической теории строения вещества. В настоящее время атомно-молекулярное учение подтверждено многочисленными опытами и является общепризнанным.