Академия наук СССР галилео галилей избранные труды в двух томах

Вид материала

Документы

Содержание Диалог о двух главнейших системах мира Асв, относитсльно коих С, и от нее про-'водятся две другие прямые АС Ошибка этого пери­патетика, доказы­вающего ignotum per ignotius. День второй АСВ длиннее прямой AB? AB (что из­вестно из Евклида), то всякий раз, как кривая будет больше обеих прямых АС и СВ С] взяв в месте соприкосновения другую точку D День второй 307 СаЛЬВИаТИ. КаКОВЫ бы ОНИ НИ быЛИ, ОНИ Также МОГуТ ключительнай оо 308 Диалог о двух главнейших системах мира День второй 309 Неправильные фор 310 Диалог о двух главнейших сис темах мира Ьопрос о системе День второй 311 312 Диалог о двух главнейших системах мира

Подобный материал:

• Галилео галилей (Galilei), 238.2kb.
• Галилей галилео галилей галилео, 23.36kb.
• Жизнь и деятельность Галилео Галилея, 159.16kb.
• Галилео Галилей (1564-1642), 46.37kb.
• Отечества избранные психологические труды в 70-ти томах, 4620.69kb.
• Бенедикт спиноза избранные произведения в двух томах том, 8400.08kb.
• А. Н. Леонтьев Избранные психологические произведения, 6448.08kb.
• Вычислительного Центра Академии наук СССР (вц ан ссср) положило начало истории нашего, 230.29kb.
• А. Н. Леонтьев Избранные психологические произведения, 6931kb.
• Основание Петербургской академии наук, 49.85kb.

СаЛЬВИаТИ. В ТаКОМ Же ТОЧНО ПОЛОЖенИИ НаХОДИТСЯ ^И материальная
тт ти-чгт, ,„„ y сфера касается ма-

и ют, кто говорит, что материальная сфера касается материалъ- термальной плоско-ной же плоскости не в одной точке, ибо сказать это — все равно, ™£™^мь™ ^{в однои} что сказать, что сфера не есть сфера. И чтобы в этом убедиться, скажите мне, в чем полагаете вы сущность сферы, т. е. что именно отличает сферу от всех других твердых тел?

804

ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА


ДЕНЬ ВТОРОЙ

305



Сальвиати. Как каким образом? Разве неизвестное по­ложение, которое вы хотите доказать, не состоит в том, что кри­вая АСВ длиннее прямой AB? А средний член, принимаемый в ка­честве известного, не тот ли, что кривая АСВ будет больше, чем АС и СВ вместе, которые, как известно, больше AB? Но, если вам неизвестно, что кривая больше одной прямой AB, разве не будет еще гораздо менее известным, что она больше двух прямых А С и СВ, которые больше одной AB?А вы принимаете это за известное.

Симпличио. Я еще не совсем понимаю, в чем заключает­ся ошибка.

Сальвиати. Если две прямые будут больше AB (что из­вестно из Евклида), то всякий раз, как кривая будет больше обеих прямых АС и СВ, не будет ли она и подавно длиннее одной пря­мой AB?

Симпличио. Да, синьор.

Сальвиати. Что кривая АСВ больше прямой AB,— поло­жение, более известное, нежели средний член, а именно, что та же кривая больше двух прямых А С и СВ, а когда средний член ме­нее известен, чем заключение, это и называется доказательством ignotum perignotius. Но вернемся к нашему положению: с меня достаточно вашего понимания, что прямая есть кратчайшая из всех линий, могущих быть проведенными между двумя точками. Что касается главного положения, то вы утверждаете, что мате­риальная сфера касается плоскости не в одной единственной точ­ке. Каково же будет ее касание?

Симпличио. Оно будет частью ее поверхности.

Сальвиати. Таким же образом место касания и другой сферы, равной первой, будет подобной же частицей ее поверх­ности?

Симпличио. Нет оснований, чтобы было иначе.

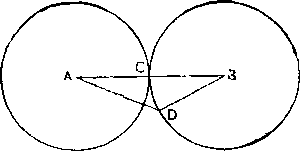
Сальвиати. Значит, и обе сферы при соприкосновении будут соприкасаться двумя оди­наковыми частицами поверхности, потому что, если каждая из них порознь прилегает так к одной и той же плоскости, то необходи­мо, чтобы они прилегали и друг ^к Другу. Итак, представьте себе две соприкасающиеся сферы с центра­ми А и В; соединим их центры прямой линией AB, которая прой­дет через место соприкосновения. Пусть она проходит через точку

20 Галилео Галилей, т. I

Доказательство то­го, что сфера каса­ется плоскости то­лько в одной точке.

306

С] взяв в месте соприкосновения другую точку D, проведем от нее две прямые линии AD и BD так, чтобы образовался треугольник ADB, у которого стороны AD и DB вместе будут равны третьей АСВ, содержащей два полудиаметра, которые по определению сферы все между собой равны. Итак, прямая AB, проведенная между двумя центрами А и В, не будет кратчайшей из всех, поскольку АО и AB вместе равны ей, а это, по вашему же признанию, абсурдно.

Симпличио. Это доказательство относится к сферам аб­страктным, а не материальным.

С а л ь в и а т и. Так скажите же мне, в чем заключается не­правильность моей аргументации, почему заключение не может

почему абстракт- быть распространено на сферы материальные, а относится лишь

абстшпнойло¹- ^к нематериальным и абстрактным?

скости в одной точ- С и м п л и ч и о. Материальные сферы подвержены многим

ке, а материальная, „ ^с тт

конкретная — ш случайностям, которым не подлежат нематериальные. Ие может ли
" ^однои- оказаться, что когда металлическая сфера положена на плоскость,

ее собственный вес давит так, что плоскость несколько подается или же сама сфера при соприкосновении сплющивается? Кроме того, такая плоскость едва ли может быть совершенной, хотя бы только из-за пористости вещества; пожалуй, не менее трудным будет найти и сферу, столь совершенную, чтобы все линии от центра до поверхности были бы у нее совершенно равны.

Сальвиати. О, все это я охотно допускаю, но это весьма далеко от нашей темы. Желая показать мне, что материальная сфера соприкасается с материальной плоскостью не в одной точ­ке, вы пользуетесь сферой, которая не есть сфера, и плоскостью, которая не есть плоскость, поскольку, по вашим словам, или этих вещей в мире нет, или если они и есть, то они портятся при при­менении их к делу. Было бы, значит, правильнее принять заклю­чение, хотя бы условно, а именно, что если бы в природе существо­вали и сохранялись без изменения совершенные сферы и плоско­сти, то они соприкасались бы в одной-единственной точке, а за­тем уже отрицать возможность этого в действительности.

Симпличио. Думаю, что положение философов нужно понимать именно в этом смысле, потому что, несомненно, несо­вершенство материи является причиной того, что вещи, взя­тые конкретно, не соответствуют вещам, рассматриваемым в аб­стракции.

Сальвиати. Как не соответствуют? Наоборот, то, что вы сами сейчас говорите, доказывает, что они в точности соответ­ствуют.

ДЕНЬ ВТОРОЙ 307

Симпличио. Каким образом?

Сальвиати. Не говорите ли вы, что из-за несовершенства материи то тело, которое должно бы быть совершенно сферичным, и та плоскость, которая должна бы быть совершенно плоской, конкретно не оказываются такими, какими вы их представляете себе в абстракции?

Симпличио. Говорю.

Сальвиати. Значит, всякий раз, как вы конкретно при­кладываете материальную сферу к материальной плоскости, вы прикладываете несовершенную сферу к несовершенной плоскости и говорите, что они соприкасаются не в одной-единственной точ­ке. А я вам говорю, что и в абстракции нематериальная сфера, которая является несовершенной сферой, может касаться немате­риальной, также несовершенной плоскости, не одной точкой, а частью поверхности. Так что то, что происходит конкретно, име­ет место и в абстракции. Было бы большой неожиданностью, если бы вычисления и действия, производимые абстрактно над числами, не соответствовали затем конкретно серебряным и золо­тым монетам и товарам. Но знаете ли, синьор Симпличио, что происходит на деле и как для выполнения подсчетов сахара, шел­ка и полотна НеобхОДИМО СКИНУТЬ ВеС ЯЩИКОВ, оберТКИ И ИНОЙ жмвп

тары; так и философ-геометр, желая проверить конкретно резуль- суются с таты, полученные путем абстрактных доказательств, должен сбро- ^ныл<и сить помеху материи, и если он сумеет это сделать, то, уверяю вас, все сойдется не менее точно, чем при арифметических подсче­тах. Итак, ошибки заключаются не в абстрактном, не в кон­кретном, не в геометрии, не в физике, но в вычислителе, который не умеет правильно вычислять. Поэтому, если у вас есть совер­шенные сфера и плоскость, хотя бы и материальные, не сомне­вайтесь, что они соприкасаются в одной точке. А если их невоз­можно получить, то все же утверждение, что sphaera aenea non tangit in puncto, весьма далеко от сути дела. Но я скажу вам бо­лее, синьор Симпличио; если я уступлю вам, признав, что не мо­жет быть ни совершенной материальной сферической фигуры, ни совершенной плоскости, то, как вы полагаете, могут ли суще­ствовать два материальных тела с поверхностью в какой-либо части или каким-либо образом искривленной, если угодно, даже неправильно?

Симпличио. В таких, я думаю, у нас недостатка не будет.

СаЛЬВИаТИ. КаКОВЫ бы ОНИ НИ быЛИ, ОНИ Также МОГуТ ключительнай оо

соприкасаться в одной точке, ибо соприкасаемость в одной точке вовсе не является исключительной привилегией совершенного

20*

308 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА

сферического тела и совершенной плоскости. Напротив, тот, кто

рассмотрит более внимательно этот вопрос, найдет, что гораздо

труднее найти два тела, которые соприкасались бы частью своих

труднее найти фи- поверхностей, нежели единственной точкой, ибо для того, чтобы

УрикасалисКы ча- Д^ве поверхности вполне совпали одна с другой, необходимо, что-

стью своих поверх- бы обе они были совершенно плоскими или, если одна выпукла,

костей, чем сопри- ^г „ '

касающиеся в одной то другая должна быть вогнутой и так, чтобы ее вогнутость в точ-

VY1 ПУ Kf> «-»

ности отвечала выпуклости первой, а такие условия гораздо труднее найти из-за их слишком строгой определенности, чем другие, которые по своей широкой неопределенности бесконечны.

Симпличио. Значит, вы считаете, что два камня или два куска железа, взятые наудачу и приложенные друг к другу, в большинстве случаев соприкасаются в одной точке?

Сальвиати. При случайных сближениях, думаю, что нет, поскольку поверх них обычно имеется хотя бы немного подат­ливой грязи и поскольку при прикладывании их друг к другу не стараются избежать всякого толчка; этого немногого достаточно для того, чтобы одна поверхность несколько уступила другой и по­верхности взаимно формировали друг друга, по крайней мере на маленьком пространстве, вдавливаясь одна в другую; но если по­верхности их будут хорошо отполированы, если оба они будут положены на стол так, чтобы один не давил на другой, а затем ос­торожно придвинуты один к другому, то я не сомневаюсь, что они могли бы прийти в соприкосновение в одной единственной точке.

Сагредо. С вашего разрешения мне необходимо изложить здесь один вопрос, возникший у меня, когда я слышал заявление синьора Симпличио о невозможности найти твердое материальное тело, имеющее совершенно сферическую форму, и видел, что синьор Сальвиати, не противореча, некоторым образом с этим соглашался. Я хотел бы знать, не возникает ли та же трудность при придании твердому телу другой какой-либо формы, или, вер­нее говоря, представляется ли более трудным придать куску мра­мора форму совершенной сферы, чем форму совершенной пира­миды, или совершенного коня, или совершенной саранчи.

Сальвиати. Давая вам ответ, я прежде всего хочу снять с себя упрек в согласии, которое, как вам кажется, я дал синь-

сферическую форму ору Симпличио; это было только временно, потому что я также па-
легче придать, чем о

другую. меревался, прежде чем перейти к другим вопросам, сказать то, что, пожалуй, будет тождественно или весьма сходно с вашей мыслью. Отвечая на ваш первый вопрос, скажу, что из всех форм, какие могут быть приданы твердому телу, сферическая является наиболее легкой, так как она является простейшей и занимает

ДЕНЬ ВТОРОЙ 309

среди телесных фигур то же место, какое круг занимает среди плоских. Вычерчивание круга, как наиболее легкое по сравнению со всеми прочими, одно почитается математиками достойным за­нять место среди постулатов, касающихся черчения всех прочих фигур. И столь легко образование сферы, что если в плоской тулат. пластинке из твердого металла сделано круглое отверстие, в ко­тором будет вращаться какое-нибудь твердое тело, весьма грубо округленное, то оно само собой, без других ухищрений, примет сферическую форму, сколь угодно совершенную, лишь бы такое твердое тело было не меньше сферы, проходящей сквозь этот круг; и, что особенно достойно внимания, это то, что одно и то же отвер­стие может образовать сферы различной величины. Что же касает­ся того, как сделать коня или (как вы говорите) саранчу, то пре­доставляю судить об этом вам самому, знающему, что в мире най- ^руг££^1в_в ^т1а_н ^р.

ДУТСЯ ОЧеНЬ неМНОГИе Ваятели, КОТОрЫе СПОСобнЫ ЭТО СДелаТЬ. гут быть воспроиз-
ДумаЮ, ЧТО В ЭТОМ ЧаСТНОМ ВОПрОСе И СИНЬОр СИМПЛИЧИО Не ра- одного ^Пи^Птого°
ЗОЙДеТСЯ СО МНОЙ ВО МНеНИИ. инструмента.

Симпличио. Не знаю, расхожусь ли я с вами в чем-ни­будь. Мое мнение таково: ни одна из названных фигур не может получиться совершенной, но если говорить о возможном прибли­жении к совершенной степени, то, конечно, несравненно легче придать твердому телу форму сферическую, нежели форму коня или саранчи.

Сагредо. А от чего, думаете вы, эта большая трудность зависит?

Симпличио. Подобно тому, как абсолютная простота и единообразие сферы обусловливают большую легкость ее обра- Неправильные фор зования, так крайняя неправильность делает затруднительным SoXlu*^{0 60СГФО} создание других форм.

Сагредо. Стало быть, раз неправильность есть причина трудности, то и форма камня, разбитого наудачу молотком, веро­ятно, будет принадлежать к числу наиболее трудных для воспро­изведения, поскольку она, пожалуй, еще более неправильна, чем фигура коня?

Симпличио. Так должно быть.

Сагредо. Но скажите мне, та форма, которую имеет ка­мень, какова бы она ни была, является ли для него совершенной или нет?

Симпличио. Та форма, которую он имеет, является столь совершенной, что никакая другая не подойдет к нему столь же точно.

Сагредо. Значит, если среди неправильных и потому труд­ных для воспроизведения форм у нас все же оказывается беско-

310 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИС ТЕМАХ МИРА

нечное множество весьма совершенных, то на каком основании можно утверждать, что форму простейшую и потому легчайшую из всех невозможно встретить?

Сальвиати. Синьоры, с вашего разрешения, мне кажет­ся, что мы вступили в спор, весьма недалекий от пустословия; в то время как наши рассуждения должны были бы касаться вещей серьезных и значительных, мы тратим время в пустых и бессодер­жательных словопрениях. Не будем забывать, что изыскание о строении мира — одна из самых великих и благородных проб-

Ьопрос о системе Л6М, КаКИв ТОЛЬКО СуЩбСТВуЮТ В Природе, Т6М более, ЧТО ОНО В6-

^Ртмъ1х^ивысоких^На Д^{ет также и к} разрешению другой задачи — причины происхож-
проблем. дения морского отлива и прилива, разрешить которую пытались

многие великие люди, жившие до сих пор и которую, пожалуй, ни один не разрешил ²⁵.

Поэтому, если у нас нет более ничего, что можно было бы при­вести для окончательного опровержения возражения, основанно­го на вращении Земли и являющегося последним из аргументов для доказательства ее неподвижности по отношению к собствен­ному центру, то мы можем перейти к исследованию аргументов за и против годового движения.

С а г p e д о. Мне не хотелось бы, синьор Сальвиати, чтобы вы измеряли наши умы мерою вашего; вы, всегда занятый высочай­шими созерцаниями, считаете пустыми и низкими некоторые воп­росы, такие, которые нам кажутся достойной пищей для наших умов; поэтому ради нашего удовлетворения соблаговолите иног­да снизойти до некоторых уступок нашему любопытству. Что ка­сается опровержения последнего возражения, основанного на суточном вращении, то, чтобы удовлетворить меня, достаточно было бы значительно меньшего, чем было здесь сказано; но, во всяком случае, то, что говорилось с таким избытком, показалось мне столь любопытным, что не только не утомило меня, но своей новизной доставило мне удовольствие, больше которого трудно и желать; потому, что если вам остается добавить еще какое-нибудь соображение, приведите его — я, со своей стороны, выслушаю его весьма охотно.

Сальвиати. Я всегда находил величайшее наслаждение, делая свои открытия; после этого наслаждения, являющегося мак­симальным, я испытываю наибольшую радость, делясь ими с не­которыми из друзей, которые их понимают и обнаруживают к ним вкус; и вот, поскольку вы один из них, я, ослабив несколько узду моего тщеславия, которое заставляет меня радоваться, когда я кажусь себе более проницательным чем некоторые другие, по-

ДЕНЬ ВТОРОЙ 311

читающиеся зоркими, приведу в завершение прошлого спора дру­гую ошибку последователей Птолемея и Аристотеля, допущенную в приведенном доказательстве ²⁶.

Сагредо Яс жадностью готов это выслушать.

Сальвиати. Мы до сих пор обходили молчанием и усту­пили Птолемею в качестве явления бесспорного, что при отбра­сывании камня скоростью вращающегося около своего центра колеса причина отбрасывания возрастает настолько, насколько увеличивается скорость вращения. Отсюда вытекало, что раз ско­рость земного вращения несравненно больше скорости любой ма­шины, которую мы можем искусственно вращать, то соответствен­но и отбрасывание камней, животных и т. д. должно было бы быть чрезвычайно сильным. Теперь я замечаю, что в этом рассужде­нии имеется большая ошибка, ибо мы сравниваем между собой эти скорости абсолютно и без различения их. Действительно, если я сравниваю скорости одного и того же колеса или же двух равных колес, то колесо, которое вращается быстрее, отбросит камень с большим импульсом, и при возрастании скорости в той же пропорции будет возрастать и причина отбрасывания, но если скорость будет возрастать не путем увеличения скорости движе­ния колеса, т. е. не путем сообщения ему большего числа оборо­тов в равные промежутки времени, а вследствие удлинения ди­аметра и увеличения самого колеса, так что при сохранении того же самого времени на один оборот как у малого, так и у большо­го колеса скорость у большого будет больше лишь от того, ЧТО его причина отбрасы-

i s* вания не возрастает

окружность больше, то нельзя думать, что причина отбрасыва- пропорционально ния в большем колесе возрастет пропорционально отношению сти^асТобЦслоел2ой

СКОрОСТИ ОКруЖНОСТИ большего КОЛеса К СКОРОСТИ ОКруЖНОСТИ увеличением колеса.

меньшего. Это совершенно неправильно, как нам сразу же пс кажет очень подходящий для этого опыт: камень, который мы мо жем метнуть тростью длиной в локоть, мы не сможем метнуть тростью длиной в шесть локтей, хотя бы движение конца длин­ной трости, т. е. помещенного в ней камня, было вдвое быстрее движения конца трости более короткой, что могло бы произойти, если бы скорость была такова, что за время полного оборота большей трости меньшая совершала их три.

Сагредо. То, что вы, синьор Сальвиати, мне говорите, должно происходить, как я понимаю, именно так, но я не могу столь быстро найти причину, почему одинаковые скорости не ока­зывают одинакового действия при отбрасывании тел, так что дей­ствие скорости меньшего колеса гораздо больше действия скоро­сти колеса большего; прошу вас объяснить мне, как обстоит дело?

312 ДИАЛОГ О ДВУХ ГЛАВНЕЙШИХ СИСТЕМАХ МИРА

Симпличио. Вы, синьор Сагредо, на этот раз оказались непохожим на самого себя: обычно вы сразу все схватываете, а теперь вы прошли мимо ошибки в опыте с тростью, которую я смог подметить; заключается она в различии способа движения при бросании тростью длинной и тростью короткой. Действитель­но, если мы хотим, чтобы камень выскочил из расщепа, то нужно не продолжать равномерное движение, а наоборот, в тот момент, когда оно весьма быстро, удержать руку и умерить скорость тро­сти; благодаря этому камень, уже находящийся в быстром дви­жении, выскакивает и движется с импульсом; но нельзя таким образом задержать большую трость, которая благодаря своей длине и гибкости не вполне повинуется сдерживающей руке и, продолжая сопровождать камень на некоторое расстояние и слег­ка его сдерживая, сохраняет соединение с ним, не испытывая ос­тановки как бы от твердой преграды, которая дала бы ему выс­кочить; если бы обе трости наталкивались на останавливающее¹ их препятствие, я полагаю, что камень одинаково выскочил бы из той и другой трости, поскольку их движения будут одинаково быстры.

Сагредо. С разрешения синьора Сальвиати я кое-что от­вечу синьору Симпличио, поскольку он обратился ко мне; скажу, что в его рассуждении есть и хорошее и плохое: хорошее, потому что почти все верно, плохое, потому что в общем не относится к нашей теме. Совершенно верно, что когда нечто, быстро переме-Если существует щающее камни, наталкивается на неподвижную преграду, пос-SeUww?°mo построй- ледние с импульсом выбрасываются вперед; подобное ежедневно ки, горы и даже, совершается на наших глазах с лодками, которые на быстром