Профессор, Dr. Sc. Habil. Ю
| Вид материала | Документы |
- Федеральное агентство по образованию Государственное образовательное учреждение Высшего, 4583.66kb.
- М. Д. Хуторской, В. П. Зволинский, А. А. Рассказов мониторинг и прогнозирование геофизических, 3335.7kb.
- С этой ссылки можно взять фото, 2277.05kb.
- Платоновские чтения Материалы XIII всероссийской конференции молодых историков г. Самара, 3309.31kb.
- Программа международной конференции «Теория операторов, комплексный анализ и математическое, 269.19kb.
- Сквозная программа учебных и производственных практик методическОе указаниЕ для студентов, 597.46kb.
- Региональное Отделение Российского Философского Общества Саратовский государственный, 223.62kb.
- Программа всероссийской научно-практической конференции «проблемы современной экономики:, 87.2kb.
- Практикум 2 Профессор Ищенко Е. Г.; к э. н., доцент Владимирова, 348.88kb.
- Программа по курсу «Современные проблемы уголовного права», 159kb.
Задача 7. Игральная кость бросается дважды. Определить вероятность того, что по крайней мере один раз появится 6 очков?
Задача 8. Уличный торговец предлагает прохожим иллюстрированную книгу. Из предыдущего опыта ему известно, что в среднем один из 65 прохожих, которым он предлагает книгу, покупает ее. В течение некоторого промежутка времени он предложил книгу 20 прохожим. Чему равна вероятность того, что он продаст им хотя бы одну книгу? Прокомментируйте предположения, которые Вы использовали при решении задачи.
Самостоятельная работа 3. Формула полной вероятности (60 мин)
Задача 1. Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,04, в период экономического кризиса 0,13. Предположим, что вероятность того, что начнется период экономического роста, равна 0,65. Чему равна вероятность того, что случайно выбранный клиент банка не вернет полученный кредит?
Задача 2. Агент по недвижимости пытается продать участок земли под застройку. Он полагает, что участок будет продан в течение ближайших шести месяцев с вероятностью 0,9 (если экономическая ситуация в регионе не будет ухудшаться). Если же экономическая ситуация будет ухудшаться, то вероятность продать участок уменьшится до 0,5. Экономист, консультирующий агента, полагает, что с вероятностью, равной 0,7, экономическая ситуация в регионе в течение следующих шести месяцев будет ухудшаться. Чему равна вероятность того, что участок будет продан в течение ближайших шести месяцев?
Задача 3. Транснациональная компания обсуждает возможности инвестиций в некоторое государство с неустойчивой политической ситуацией. Менеджеры компании считают, что успех предполагаемых инвестиций зависит, в частности, и от политического климата в стране, в которую предполагается вливание инвестиционных средств. Менеджеры оценивают вероятность успеха (в терминах годового дохода от субсидий в течение первого года работы) равной 0,55, если преобладающая политическая ситуация будет благоприятной; равной 0,30, если политическая ситуация будет нейтральной; равной 0,10, если политическая ситуация в течение года будет неблагоприятной. Менеджеры компании также полагают, что вероятности благоприятной, нейтральной и неблагоприятной политических ситуаций соответственно равны: 0,6; 0,2 и 0,2. Чему равна вероятность успеха инвестиций?
Задача 4. На химическом заводе установлена система аварийной сигнализации. Когда возникает аварийная ситуация, звуковой сигнал срабатывает с вероятностью 0,95. Звуковой сигнал может сработать случайно и без аварийной ситуации с вероятностью 0,02. Реальная вероятность аварийной ситуации равна 0,004. Предположим, что звуковой сигнал сработал. Чему равна вероятность реальной аварийной ситуации?
Задача 5. Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго автомата. Первый автомат производит в среднем 60% деталей отличного качества, а второй — 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом? Вторым автоматом?
Задача 6. Среди студентов института по результатам зимней сессии 30% первокурсников имеют только отличные оценки, среди второкурсников таких студентов 35%, на третьем и четвертом курсе их 20% и 15% соответственно. По данным деканатов известно, что на первом курсе 20% студентов сдали сессию только на отличные оценки, на втором — 30%, на третьем — 35%, на четвертом — 40% отличников. Наудачу вызванный студент оказался отличником. Чему равна вероятность того, что он (или она) — третьекурсник.
Задача 7. Детали для обработки поступают из двух заготовительных цехов: из первого цеха — 70%, из второго - 30%, причем продукция первого цеха имеет 10% брака, а продукция второго цеха " 20% брака. Какова вероятность того, что случайно взятая деталь будет без дефектов?
Самостоятельная работа 4. Дискретные случайные величины (120 мин)
Задача 1. Строительная инвестиционная компания в настоящий момент продает акции по 16 условных денежных единиц за штуку. Инвестор планирует покупку пакета акций и предполагает хранение их в течение года. Пусть Х — случайная величина, означающая цену одной акции спустя год. Ряд распределения
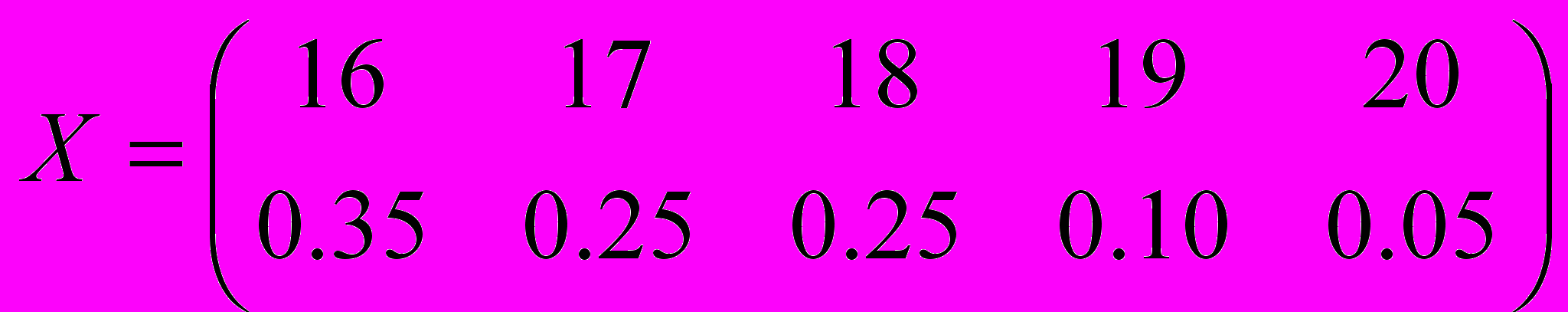.Показать, что заданное распределение обладает всеми свойствами ряда распределения. Чему равно ожидаемое среднее значение цены акции спустя один год?Чему равен ожидаемый средний выигрыш от акции спустя год? Чему равен процент возврата инвестиций, отражаемый этим ожидаемым значением? Определите дисперсию цены акции спустя год. Другая акция с одинаковым ожидаемым значением возврата инвестиций имеет дисперсию, равную 3. Какая из акций лучше в смысле минимизации риска или неопределенности, ассоциируемой с инвестициями?
Задача 2. На факультете в среднем 10% студентов получают неудовлетворительные оценки при сдаче экзамена по статистике. Предположим, что в группе 20 студентов. Чему равна вероятность того, что двое студентов не сдадут экзамен? Чему равна вероятность того, что четверо студентов не сдадут экзамен? Чему равна вероятность того, что трое или больше студентов не сдадут экзамен? Чему равно ожидаемое среднее число студентов, которые не сдадут экзамен?
Задача 3. В случае нормальной настройки автоматического станка только 1% выпускаемых деталей — дефектные. Предположим, что автомат настроен нормально. Из большой партии выпущенных деталей случайно отобраны две. Чему равна вероятность того, что одна из них с дефектом? Из большой партии выпущенных деталей случайно отобраны пять штук. Чему равна вероятность того, что все они без дефектов? Дневной выпуск деталей составил 200 штук. Чему равно ожидаемое среднее число дефектных деталей? Чему равно среднее квадратическое отклонение числа дефектных деталей в партии из 200 деталей?
Задача 4. Торговый агент в среднем контактирует с восемью потенциальными покупателями в день. Из опыта ему известно, что вероятность того, что потенциальный покупатель совершит покупку, равна 0.1.Чему равна для агента вероятность двух продаж в течение одного дня? Чему равна вероятность того, что у агента будут хотя бы две продажи в течение дня? Чему равна вероятность того, что в течение одного дня не будет продаж? Чему равно ожидаемое среднее число продаж в течение дня? Если агент работает пять дней в неделю, какое число продаж он может ожидать?
Задача 5. На торговой базе для продажи приготовлена партия из 10 моторов стоимостью в 100 условных денежных единиц каждый. Если покупатель в приобретенной партии обнаружит хотя бы один неисправный мотор, то ему возвращается его двойная стоимость. Найти ожидаемую чистую прибыль для продавца, если вероятность дефекта для любого мотора равна 0,08.
Задача 6. Доход от некоторого рискованного бизнеса составляет сумму около 1000 условных денежных единиц с заданным рядом распределения:
| X | -2000 | -1000 | 0 | 1000 | 2000 | 3000 |
| P(X)=pi | 0,1 | 0,1 | 0,2 | 0,2 | 0,3 | 0,1 |
Замечание: -2000; —1000 означают убыток. Какой наиболее вероятностный денежный доход рискованного бизнеса? Является ли этот риск вероятностно-успешным? Объясните. Чему равен на длительный период средний доход от этого бизнеса? Какова хорошая мера риска вложений в такое рискованное предприятие? Почему? Вычислите эту меру.
Задача 7. В налоговую инспекцию поступила информация, что в фирме «А» 20% списочного состава - «мертвые души». Проверяющий инспектор отбирает случайным образом 4 наряда на выполненные работы и ищет работников, на которых они были выписаны. Какова вероятность, что среди четырех случайно выбранных нарядов не будет ни одного фиктивного? Будет хотя бы один фиктивный?
Задача 8. Экзаменационный тест имеет 15 вопросов, каждый из которых имеет 5 возможных ответов и только 1 из них — верный. Предположим, что студент, который сдаёт экзамен, не знает ответов на вопросы. Чему равна вероятность, что он правильно ответит, по крайней мере, на 10 вопросов?
Задача 9. Фирма предлагает в продажу со склада партию из 10 компьютеров, 4 из которых — с дефектами. Покупатель приобретает 5 из них, не зная о возможных дефектах. Чему равна вероятность того, что все 5 компьютеров окажутся без дефектов? Ремонт одной дефектной машины будет стоить $50. Найдите математическое ожидание общей средней стоимости ремонта и его дисперсию.
Самостоятельная работа 5. Непрерывные случайные величины (120 мин)
Задача 1. Найдите вероятность того, что стандартная нормально распределенная случайная величина будет иметь значения между -2 и 1.
Задача 2. Найдите вероятность того, что стандартная нормально распределенная случайная величина будет иметь значения, меньшие чем —45.
Задача 3. Насколько вероятно, что стандартная распределенная случайная величина будет иметь значения, меньшие, чем -4?
Задача 4. Найдите стандартную случайную величину, отсекающую площадь 0.575 (слева).
Задача 5. Найдите значение стандартной нормально распределенной случайной величины z, такое, чтобы P(Z>z)=0.28.
Задача 6. Найдите два значения z=z1 и z=z2 такие, чтобы P(-z< Z>z)=0.95
Задача 7. Отклонения стрелки компаса из-за влияния магнитного поля в определенной области Заполярья – случайная величина. X ~N(0; 12). Чему равна вероятность того, что абсолютная величина отклонения в определенный момент времени будет больше, чем 2,4?
Задача 8. Если X ~ N (120; 442), то найдите такое значение х, при котором Р (Х< х) = 0,56.
Задача 9. Еженедельный выпуск продукции на заводе распределен приблизительно по нормальному закону со средним значением a = 134 786 ед. продукции в иедслю и = 13 000 сд. Найдите вероятность того, что еженедельный выпуск продукции: а) превысит 150 000 ед.; б) окажется ниже 100 000 ед. в данную неделю; в) предположим, что возникли трудовые споры и недельный выпуск продукции стал ниже 80 000 ед. Менеджеры обвиняют профсоюзы п беспрецедентном падении выпуска продукции, а профсоюзы утверждают, что выпуск продукции находится в пределах принятого уровня (±3). Доверяете ли Вы профсоюзам?
Задача 10. Мастер, осуществляющий ремонт на дому может появиться в любое время с 10 до 18 ч. Клиент, прождал до 14 ч, отлучился на 1 ч. Какова вероятность, что мастер (приход его обязателен) не застанет его дома?
Задача 11. Кандидат на выборах считает, что 20% избирателей в определенной области поддерживают его избирательную платформу. Если 64 избирателя случайно отобраны из большого числа избирателей данной области, оцените вероятность того, что отобранная доля избирателей, поддерживающих кандидата, не будет отличаться от истинной доли более чем на 0,07.
Задача 12. Срок службы жесткого диска компьютера — случайная величина, подчиняющаяся экспоненциальному распределению со средней в 12 000 ч. Найдите долю жестких дисков, срок службы которых превысит 20 000 ч.
Задача 13. Служащий рекламного агентства утверждает, что время, а течение которого телезрители помнят содержание коммерческого рекламного ролика, подчиняется экспоненциальному закону с
= 0,25 дня. Найдите долю зрителей, способных вспомнить рекламу спустя 7 дней? Задача 14. Компьютерный программист использует экспоненциальное распределение для оценки надежности своих программ. После того как он нашел 10 ошибок, он убедился, что время (в днях) до нахождения следующей ошибки подчиняется экспоненциальному распределению с
= 0,25. Найдите среднее время, потраченное для нахождения первой ошибки, и определите вероятность того, что для нахождения первой ошибки понадобится более 5 дней, а также вероятность того, что на нахождение одиннадцатой ошибки потребуется от 3 до 10 дней? | Statistical tables. Values  | ||||||||||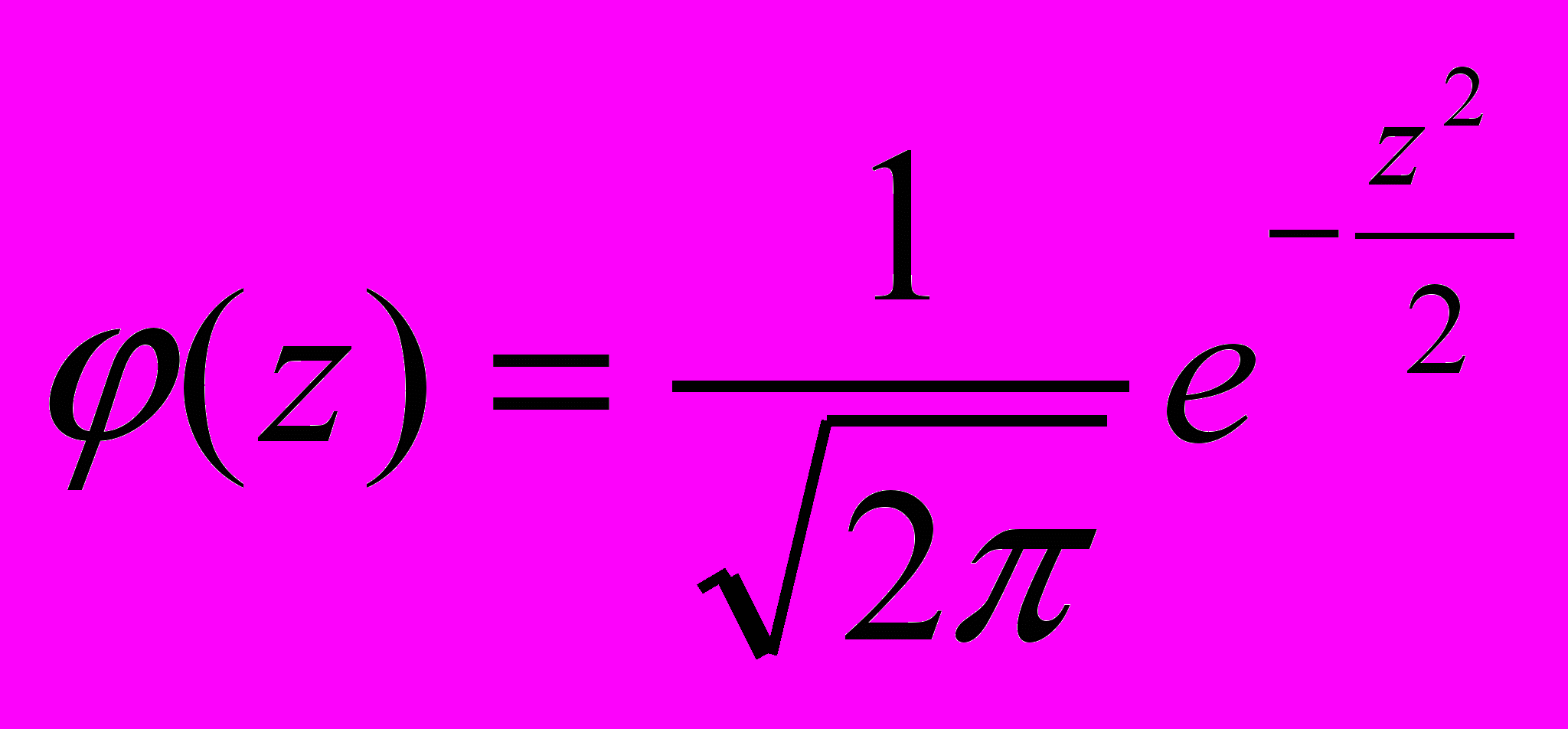
| Integer and tenth | Hundredth | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 0,0 | 0.398 | 0.398 | 0,398 | 0.398 | 0.398 | 0,398 | 0.398 | 0.398 | 0.397 | 0.397 |
| 0.I | 3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0.2 | 3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0.3 | 3814 | 3802 | 3790 | 3778 | 3765 | 3752 | 3739 | 3726 | 3712 | 3697 |
| 0.4 | 3683 | 3668 | 3653 | 3637 | 3621 | 3605 | 3589 | 3572 | 3555 | 3538 |
| 0.5 | 3521 | 3503 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0.6 | 3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0.7 | 3123 | 3101 | 3079 | 3056 | 3034 | 3011 | 2989 | 2966 | 2943 | 2920 |
| 0,8 | 2897 | 2874 | 2850 | 2827 | 2803 | 2780 | 2756 | 2732 | 2709 | 2685 |
| 0.9 | 2661 | 2637 | 2613 | 2589 | 2565 | 2541 | 2516 | 2492 | 2468 | 2444 |
| 1.0 | 0.242 | 0.239 | 0,237 | 0.234 | 0.232 | 0,229 | 0,227 | 0,225 | 0.222 | 0,220 |
| 1,1 | 2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1965 |
| 1,2 | 1942 | 1919 | 1895 | 1872 | 1849 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1.3 | 1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1,4 | 1497 | 1476 | 1456 | 1435 | 1415 | 1394 | 1374 | 1354 | 1334 | 1315 |
| 1.5 | 1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1.6 | 1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1,7 | 0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0848 | 0833 | 0818 | 0804 |
| 1,8 | 079(1 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1,9 | 0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| 2,0 | 0,054 | 0,052 | 0.051 | 0.050 | 0,049 | 0,048 | 0,047 | 0.046 | 0,045 | 0,044 |
| 2.1 | 0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2,2 | 0355 | 0347 | 0339 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2,3 | 0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2.4 | 0224 | 0219 | 02/3 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2.5 | 0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2.6 | 0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2,9 | 0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0046 |
| J, | 0,004 | 0,004 | 0,004 | 0.004 | 0,003 | 0.003 | 0,003 | 0,003 | 0.003 | 0,003 |
| 3,1 | 0033 | 0032 | 0031 | 0030 | 0029 | 0028 | 0027 | 0026 | 0025 | 0025 |
| 3,2 | 0024 | 0023 | 0022 | 0022 | 0021 | 0020 | 0020 | 0019 | 0018 | 0018 |
| 3,3 | 0017 | 0017 | 0016 | 0016 | 0015 | 0015 | 0014 | 0014 | 0013 | 0013 |
| 3.4 | 0012 | 0012 | 0012 | 0011 | 0011 | 0010 | 0010 | 0010 | 0009 | 0009 |
| 3.5 | 0009 | 0008 | 0008 | 0008 | 0008 | 0007 | 00007 | 0007 | 0007 | 0006 |
| 3.6 | 0006 | 0006 | 0006 | 0005 | 0005 | 0005 | 0005 | 0005 | 0005 | 0004 |
| 3. " | 0004 | 0004 | 0004 | 0004 | 0004 | 0004 | 0003 | 0003 | 0003 | 0003 |
| 3.8 | 0003 | 0003 | 0003 | 0003 | 0003 | 0002 | 0002 | 0002 | 0002 | 0002 |
| 3.9 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0001 | 0001 |
| 4.0 | 0.000 | 0,000 | 0.000 | 0.000 | 0,000 | 0,000 | 0.000 | 0,000 | 0,000 | 0.000 |
| 4.1 | 0.0001338 | | ||||||||
| 4.5 | 0.0000160 | | ||||||||
| 5.0 | 0.0000015 | |
| Probability integral  | ||||||||||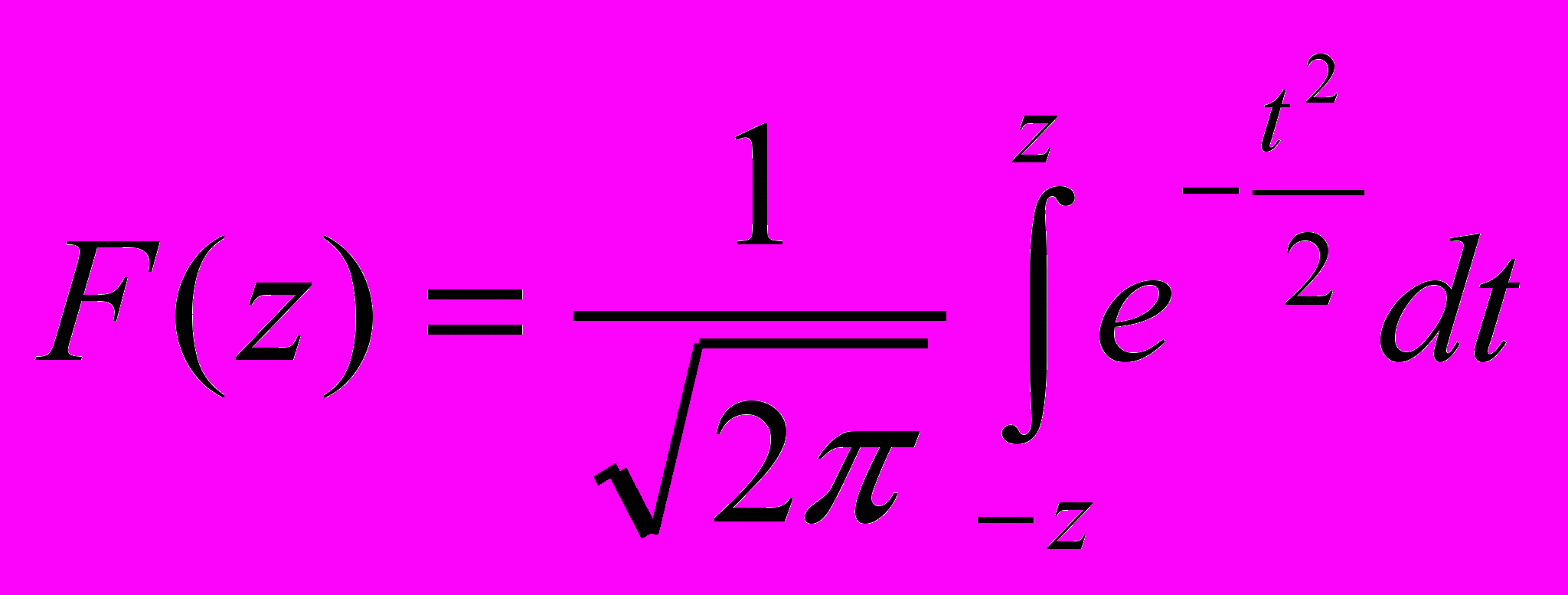
| Z | Hundredth | | | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 0,0 | 0000 | 0080 | 0160 | 0239 | 0319 | 0399 | 0478 | 0558 | 0638 | 0718 |
| 0.1 | 0797 | 0876 | 0955 | 1034 | 1114 | 1192 | 1271 | 1350 | 1428 | 1507 |
| 0,2 | 1585 | 1663 | 1741 | 1819 | 1897 | 1974 | 2051 | 2128 | 2205 | 2282 |
| 0,3 | 2358 | 2434 | 2510 | 2586 | 2661 | 2737 | 2812 | 2886 | 2961 | 3035 |
| 0.4 | 3108 | 3182 | 3255 | 3328 | 3401 | 3473 | 3545 | 3616 | 3688 | 3752 |
| 0,5 | 3829 | 3899 | 3969 | 4039 | 4108 | 4177 | 4245 | 4313 | 4381 | 4448 |
| 0,6 | 4515 | 4581 | 4647 | 4713 | 4778 | 4843 | 4909 | 4971 | 5035 | 5098 |
| 0,7 | 5161 | 5223 | 5285 | 5346 | 5467 | 5497 | 5527 | 5587 | 5646 | 5705 |
| 0,8 | 5763 | 5821 | 5878 | 5935 | 5991 | 6047 | 6102 | 6157 | 6211 | 6265 |
| 0.9 | 6319 | 6372 | 6424 | 6476 | 6528 | 6579 | 6626 | 6679 | 6729 | 6778 |
| 1.0 | 6817 | 6875 | 6923 | 6970 | 7017 | 7063 | 7109 | 7154 | 7199 | 7243 |
| 1.1 | 7287 | 7330 | 7373 | 7415 | 7457 | 7499 | 7540 | 7580 | 7620 | 7660 |
| 1,2 | 7699 | 7737 | 7775 | 7813 | 7850 | 7887 | 7923 | 7959 | 7995 | 8030 |
| 1.3 | 8064 | 8098 | 8132 | 8165 | 8198 | 8230 | 8262 | 8293 | 8324 | 8355 |
| 1.4 | 8385 | 8415 | 8444 | 8474 | 8501 | 8529 | 8557 | 8584 | 8611 | 8638 |
| 1.5 | 8664 | 8690 | 8715 | 8740 | 8764 | 8788 | 8812 | 8836 | 8859 | 8882 |
| 1.6 | 8904 | 8926 | 8948 | 8969 | 8990 | 9011 | 9031 | 9051 | 9070 | 9089 |
| 1.7 | 9108 | 9127 | 9146 | 9164 | 9182 | 9199 | 9216 | 9233 | 9249 | 9265 |
| 1.8 | 9281 | 9297 | 9312 | 9327 | 9342 | 9357 | 9371 | 9385 | 9399 | 9412 |
| 1.9 | 9425 | 9438 | 9451 | 9464 | 9476 | 9488 | 9500 | 9512 | 9523 | 9534 |
| 2.0 | 9545 | 9556 | 9566 | 9576 | 9586 | 9596 | 9608 | 9615 | 9625 | 9634 |
| 2.1 | 9643 | 9652 | 9660 | 9669 | 9676 | 9684 | 9692 | 9700 | 9707 | 9715 |
| 2.2 | 9722 | 9729 | 9736 | 9743 | 9749 | 9755 | 9762 | 9768 | 9774 | 9780 |
| 2.3 | 9785 | 9791 | 9797 | 9802 | 9807 | 9812 | 9817 | 9822 | 9827 | 9832 |
| 2.4 | 9836 | 9840 | 9845 | 9849 | 9853 | 9857 | 9861 | 9866 | 9869 | 9872 |
| 2.5 | 9876 | 9879 | 9883 | 9886 | 9889 | 9892 | 9895 | 9898 | 9901 | 9904 |
| 2.6 | 9907 | 9909 | 9912 | 9915 | 9917 | 9920 | 9924 | 9926 | 9927 | 9929 |
| 2.7 | 9931 | 9933 | 9935 | 9937 | 9939 | 9940 | 9942 | 9944 | 9946 | 9947 |
| 2.8 | 9949 | 9950 | 9952 | 9953 | 9955 | 9956 | 9958 | 9959 | 9960 | 9961 |
| 2.9 | 9963 | 9964 | 9965 | 9966 | 9967 | 9968 | 9969 | 9970 | 9971 | 9972 |
| 3.0 | 99730 | 99739 | 99747 | 99755 | 99763 | 99771 | 99779 | 99786 | 99793 | 99800 |
| 3.1 | 99807 | 99813 | 99819 | 99825 | 99831 | 99837 | 99842 | 99847 | 99853 | 99858 |
| 3.2 | 99863 | 99867 | 99872 | 99876 | 99880 | 99884 | 99888 | 99892 | 9989 | 99900 |
| 3.3 | 99903 | 3.6 | 99911 | 3.9 | 999904 | 4.4 | 9999892 | 5.0 | | 99999943 |
| 3.4 | 99933 | 3,7 | 99937 | 4,0 | 999937 | 4.6 | 9999957 | 5,0 | | 99999996 |
| 3.5 | 99953 | 3.8 | 99957 | 4,2 | 999973 | 4,8 | 9999984 | 6,0 | | 999999998 |