Задача №9

Вид материала

Содержание

Задача № 19
Задача № 29
Задача № 39
Задача № 49
Задача № 59
Задача № 79
Г∞. – предельная адсорбция, С
Задача № 89
Задача № 99
Задача № 109
Задача № 119
Задача № 129

Подобный материал:

Задача № 9

Изменение энтропии будет происходить в три этапа

изменение энтропии при охлаждении жидкого бензола с 320 до 279 К

изменение энтропии при замерзании (фазовом переходе) бензола (фазовом переходе)

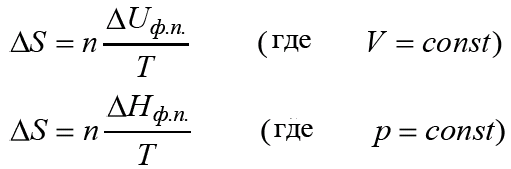
изменение энтропии при охлаждении твердого бензола

Суммарное уравнение:

Находим количесиво моль бензола (n)

n=m/M, где m-масса бензола, M-молярная масса бензола=78 г/моль

n=m/M=50/78=0,64 моль

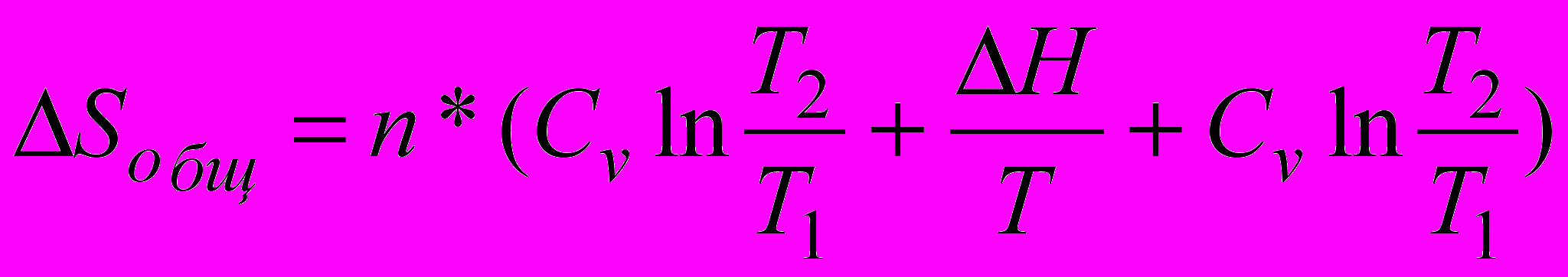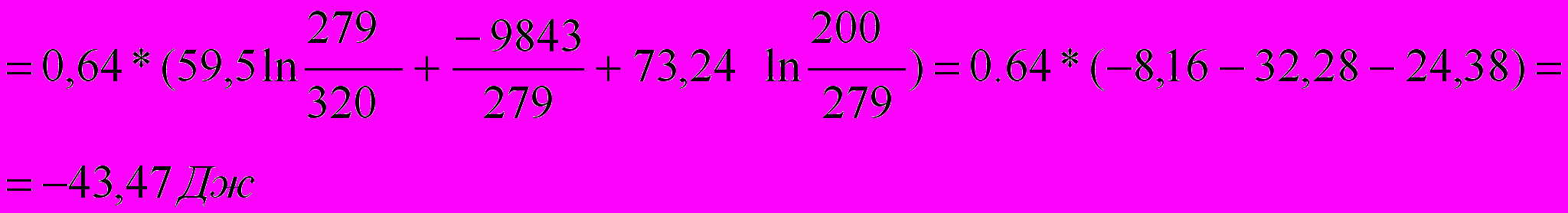
Ответ: -43,47 Дж

Третье начало термодинамики говорит о том, как энтропия ведет себя вблизи абсолютного нуля температур. Третье начало термодинамики относится только к равновесным состояниям

Процессы фазового перехода (плавление, испарение, возгонка) проходят при постоянной температуре (Т=const). Изменение энтропии рассчитывают по уравнениям:

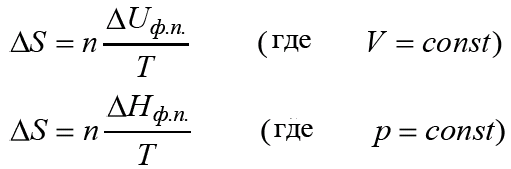
где ΔUф.п. и ΔНф.п. – теплоты фазового перехода, Т – абсолютная температура фазового перехода, n – число моль.

2. Расчет изменения энтропии при нагревании жидких или твердых тел от Т₁ до Т₂

а) процесс протекает при постоянном объеме и теплоемкости (V, CV = const):

б) процесс протекает при постоянном давлении и теплоемкости (р, Cр = const):

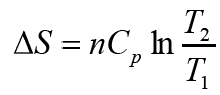
Задача № 19

Молярную массу растворенного вещества (сахара) находим из следующей формулы

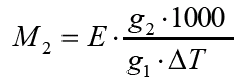
где М₂ – молярная масса растворенного вещества; Е – эбуллиоскопическая постоянная; g₁ – масса растворителя; g₂ – масса растворенного вещества,∆Т – повышение температуры кипения растворителя над раствором.

Находим ∆Т – повышение температуры кипения растворителя относительно чистого растворителя.

∆Т=(0,512*1*1000)/(100*342)=0,015 °С

В преведущей формуле в 100 грамах 1 % раствора g₁ – 99 грам (масса рас творителя); g₂ – 1 грам (масса растворенного вещества).Температура кипения раствора сахара:

Т_{кип.р-ра}=Т_кип_{растворителя}+∆Т=373,15+0,015=373,165 К

Температуры кипения 1%-ных растворов сахара и кухонной соли будут различатся, так как первое вещество неэлектролит, а второе электролит

Для растворов электролитов справедлива формула:

∆Т_кип=К*С_м, где К-эбулиоскопическая константа, См-моляльная концентрация (количество моль растворенного вещества в 1000 грам растворителя)

Моляльная концентрация 1% раствора хлорида натрия:

В 1000 грам растворителя (воды) будет содержатся 10 грам хлорида натрия.

Колисчество моль хлорида натрия

n=m/M, где m-масса хлорида натрия, M-молярная масса хлорида натрия =58,5 г/моль

n=m/M=10/58,5=0,171 моль, соответственно

См=0,171 моль/(1000 г растворителя)

Находим повышение температуры кипения раствора хлорида натрия:

∆Т_кип=К*С_м=0,512*0,171=0,088 °С

Температура кипения раствора хлорида натрия:

Т_{кип.р-ра}=Т_кип_{растворителя}+∆Т=373,15+0,088=373,238 К

Задача № 29

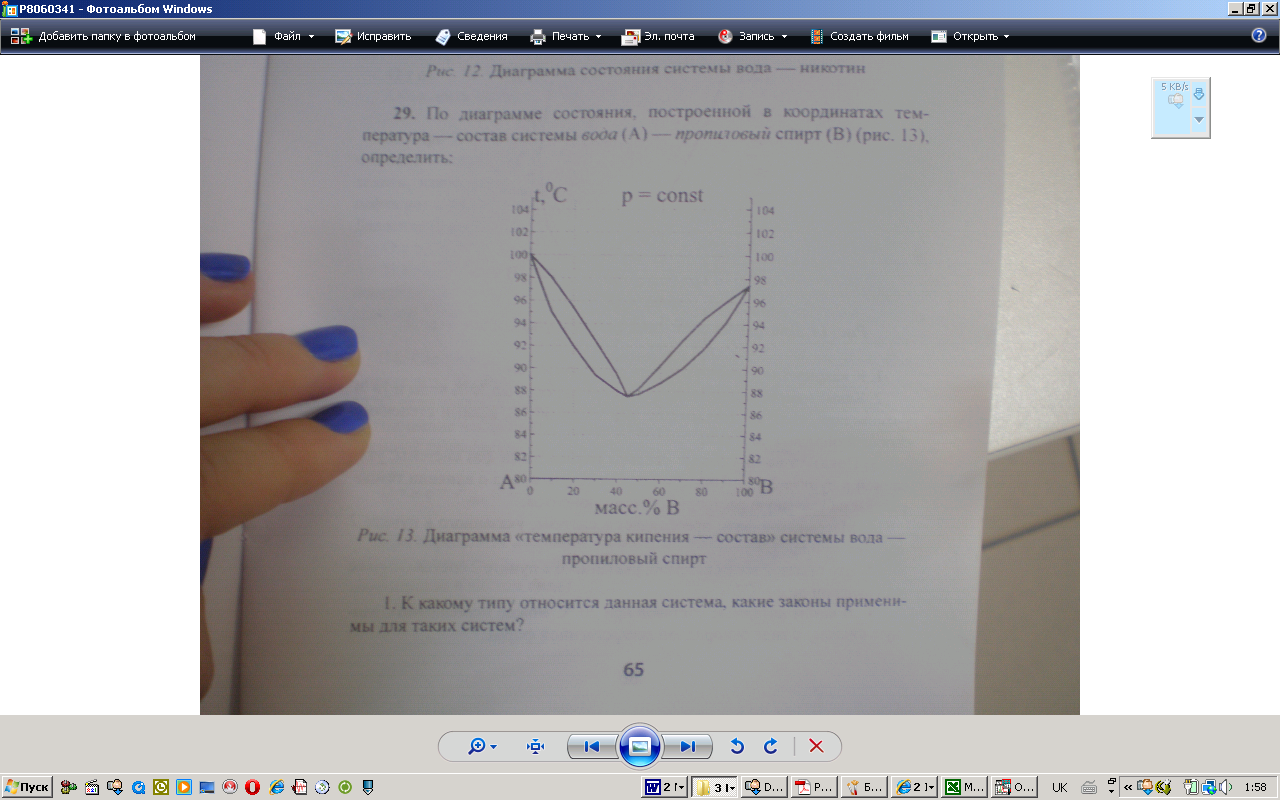
Двохкомпонентная диаграмма, правилао фаз Гиббса
При 92°С. 65% воды, 35 % спирта
Две фазы-=вода и пар. Согласно правилу фаз Гиббса 1 степень свободы
Азеотроп. Пар однородного состава
Химическими
Жидкая фаза 80% воды,20 % спирта; пар-40% спирта ,60% воды

Задача № 39

Коэффициент распределения (К_D ) равняется отношению концентрации вещества в органической и водной фазах:

К_D=

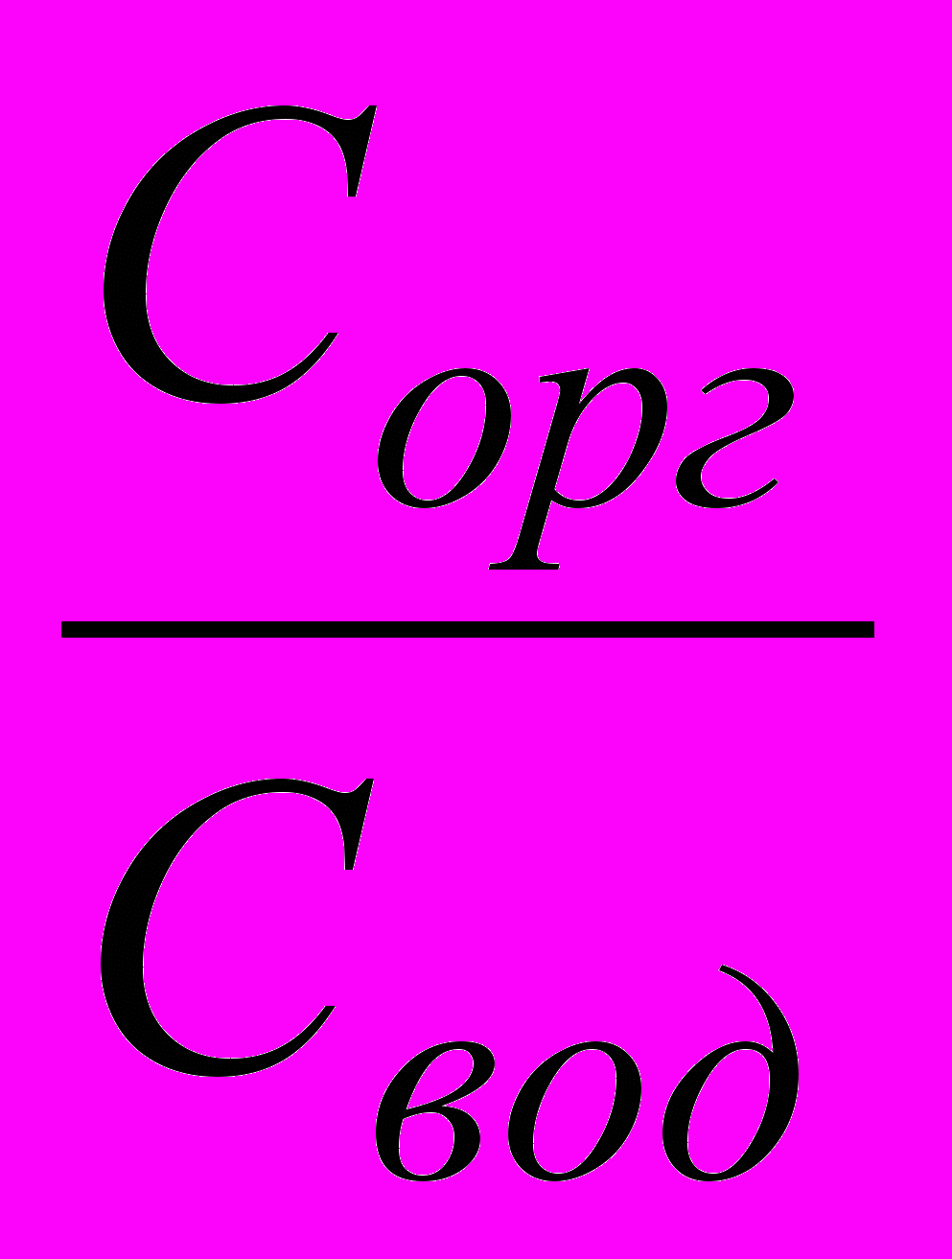где С_орг и С_вод концентрации вещества в органической и водной фазе соответственно

Степень экстракционного извлечения вещества из раствора (Е) находится из формулы

E=

где V_вод и V_орг объемы водной и органической фазы

Из таблицы 2 приложения находим коэффициент распределения брома между фазой и сероуглеродом. При 25°С К_Dброма между сероуглеродом и водой равняется 77.

Находим степень экстракционного извлечения, объем водной фазы 2 л (2000 мл), объем сероуглерода 150 мл

E=

=85,2%

При объеме 50 мл

E=

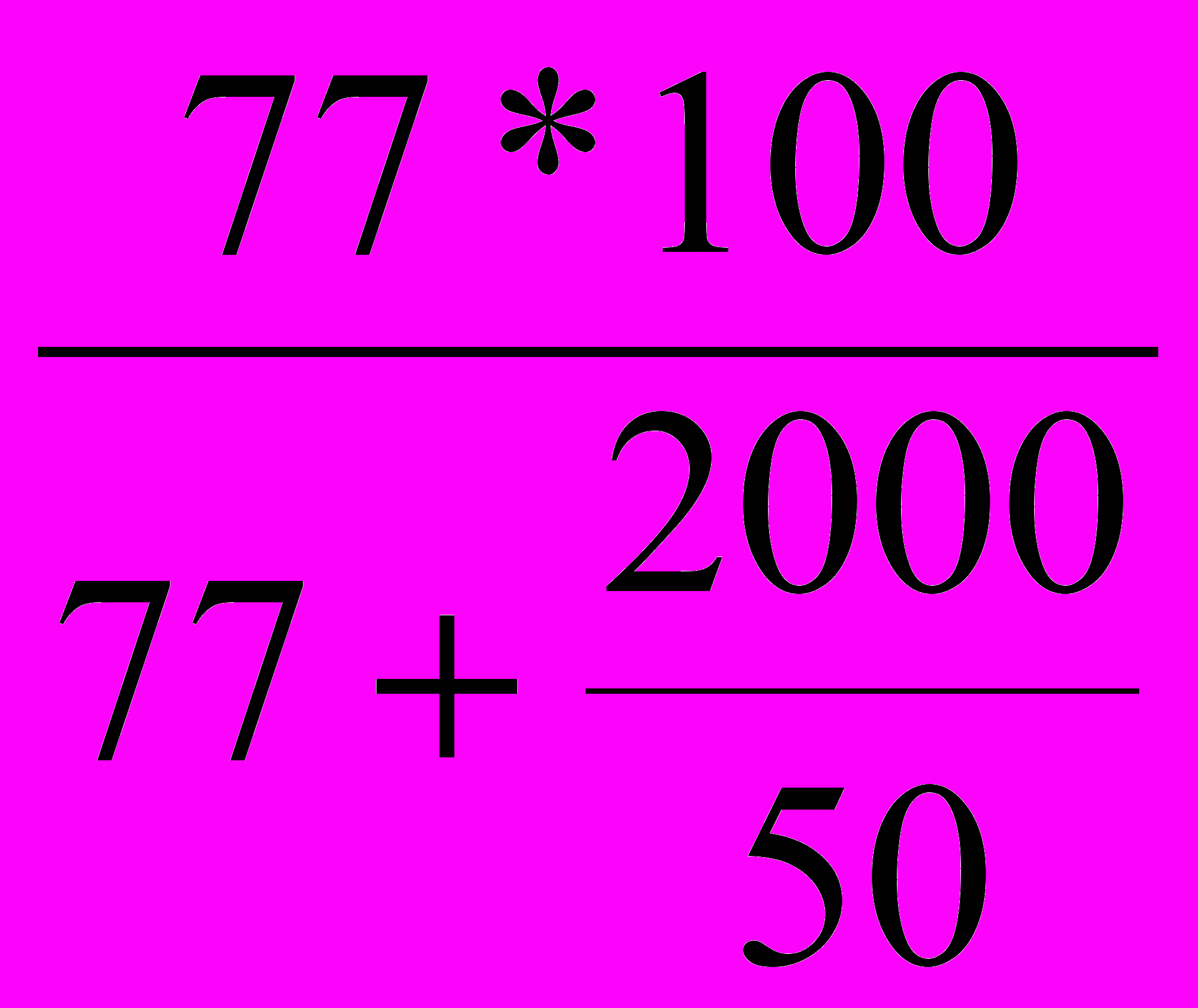=65,8%

Концентрация оставшегося в растворе вещества при повторной экстракции n раз равняется:

С_n=

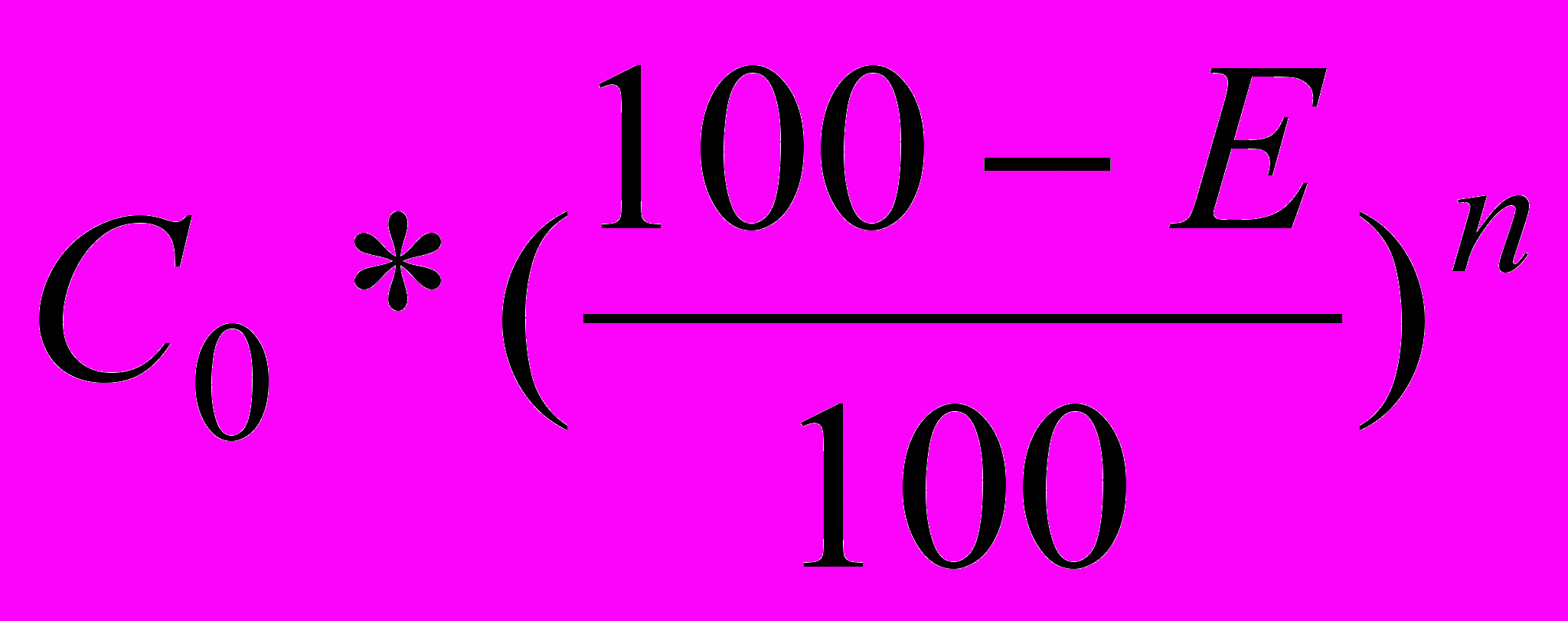
С_n=

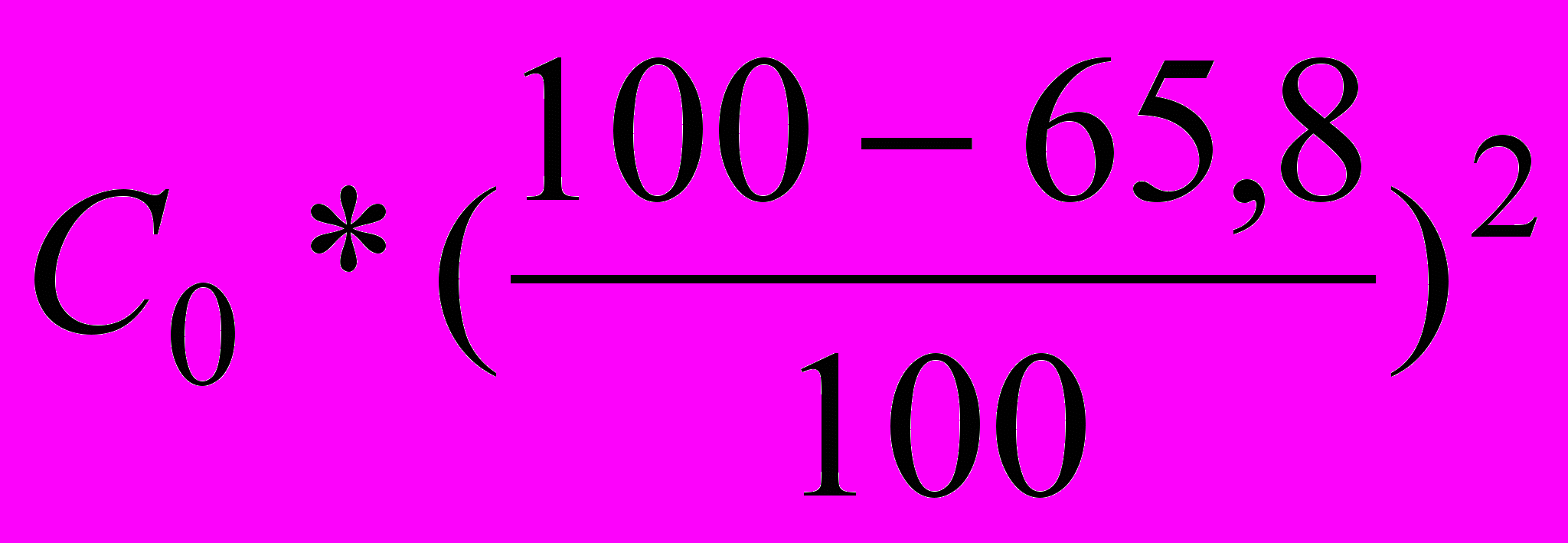=96%

1) Для увеличения степени извлечения нужно проводить многократную экстракцию малыми объемами экстрагента.

2)Наиболее эффективна непрерывная Экстракция, осуществляемая в многоступенчатых аппаратах (экстракторах) при противотоке исходного раствора и экстрагента. В этом случае заданная степень Экстракция достигается при наименьшем расходе экстрагента. Многоступенчатые экстракторы обычно представляют собой вертикальные колонны, разделённые поперечными перфорированными тарелками, вращающимися дисками, мешалками и т. п. на ступени (секции). В каждой ступени происходит перемешивание взаимодействующих фаз и их расслаивание. Т. о., исходный раствор и экстрагент многократно перемешиваются и расслаиваются.

Задача № 49

Строим кондуктограмму

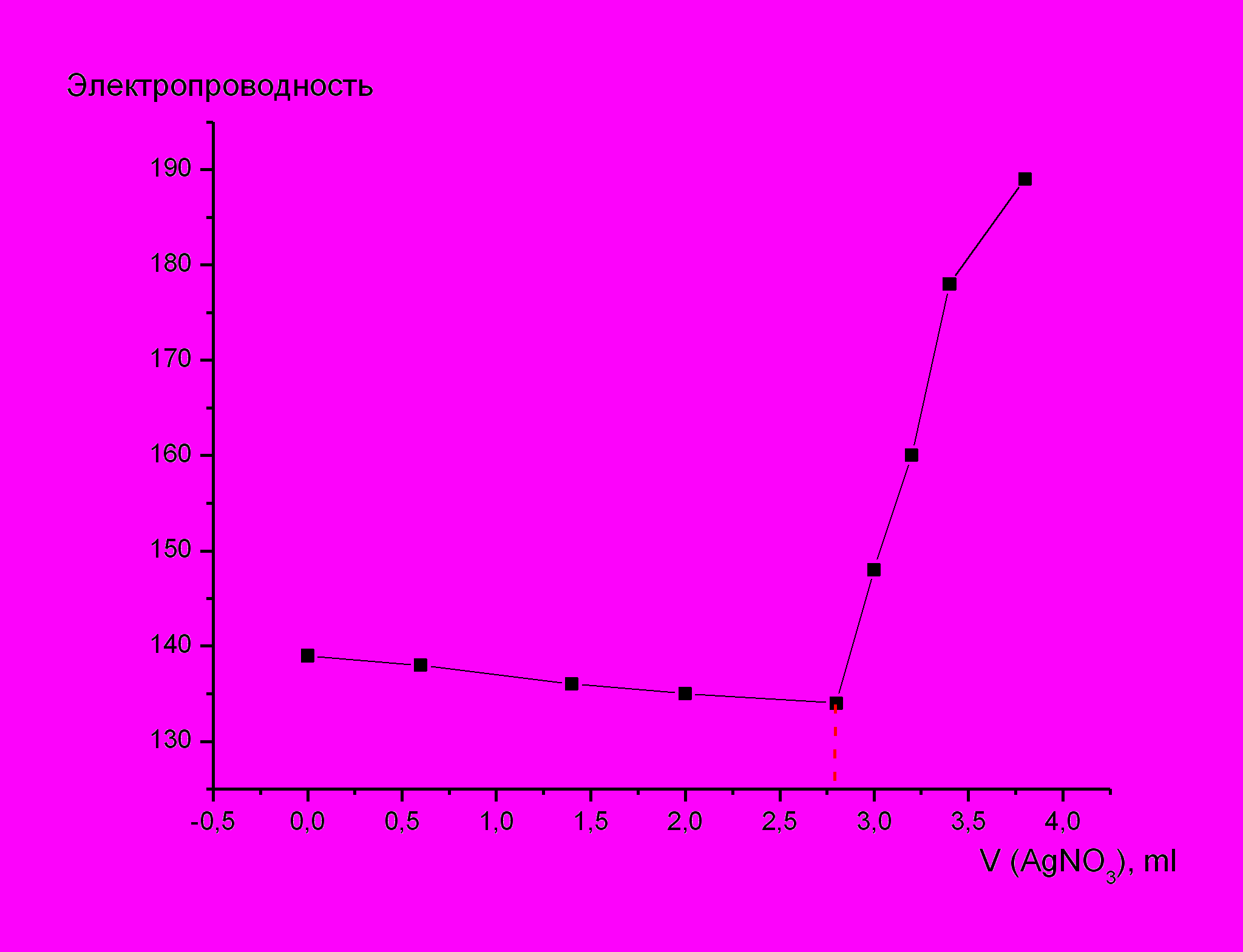
Находим точку эквивалентности. Количество раствора нитрата серебра соответствующее точке эквивалентности находим из кондуктограммы. Объем в точке кондуктограммы где наблюдается резкий изгиб (скачок) элекстросопротивления отвечает точке эквивалентности.

Объем нитрата серебра пошедшего на титрование приблизительно равняется 2,75 мл.

Напишем уравнение химической реакции:

AgNO₃+NaBr=AgBr↓+NaNO₃

Из уравнения реакции можна сделать вывод, что количесво моль нитрата серебра пошедшего на титрование отвечает количеству моль бромида натрия

Находим количество моль AgNO₃

n=C (AgNO₃)*V=0.2*2.75/1000=0.00056 моль

где С(AgNO₃)=0,2моль/л согласно условию задачи

Находим концентрацию раствора бромида натрия учитывая что 0,00056 моль содержится в 50 мл раствора..

C = n /V=0,00056/0,05=0,011 моль/л

Объясним ход кондуктометрической кривой. При добавлении в качестве титранта AgNO₃ в раствор NaBr до точки эквивалентности наблюдается понижение электропроводимости. Это обусловлено уменьшением количества ионов в растворе (ионы обеспечивают проводимость раствора) так как в процессе реакции образуется нерастворимое вещество AgBr. После точки эквивалентности (в этой точке концентрация бромида ничтожно мала) при добавлении нитрата серебра наблюдается повышение электропроводимости. Это обусловлено тем, что новые порции нитрата серебра не вступают в реакцию. Избыток нитрата серебра диссоциирует в растворе, а его ионы повышают проводимость раствора.

Задача № 59

Энергию активации химической реакции можно вычислить по значениям констант скоростей при двух различных температурах по уравнению:

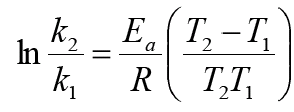
Отсюда, уравнение для расчета энергии активации имеет вид:

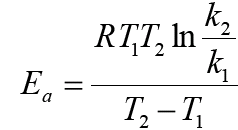
Находим энергию активации:

Е_а=

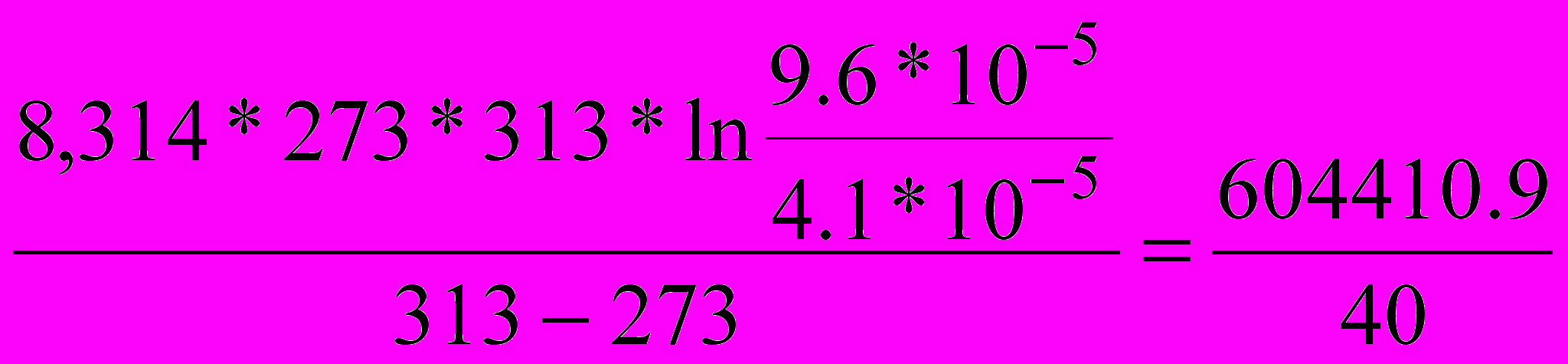=15090 Дж/моль

Задача № 79

Величина адсорбция ПАВ в поверхностном слое связана с его концентрацией уравнением Лэнгмюра:

или Г=Г

*К*С

где Г∞. – предельная адсорбция, С – концентрация адсорбата (ПАВ), К – константа адсорбционного равновесия.

Связь между гиббсовской адсорбцией (Г) растворенного вещества, то есть избытка растворенного вещества в поверхностном слое, и изме-нением поверхностного натяжения раствора устанавливает фундамен-тальное адсорбционное уравнение Гиббса, которое для разбавленных растворов неэлектролитов записывается в виде:

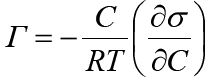
Из адсорбционного уравнения Гиббса следует, что концентрирование вещества в поверхностном слое или переход его в объем-ную фазу определяется знаком производной dζ/dС. Предельное значение этой производной при С→0, взятой со знаком «минус», называется поверхностной активностью g:

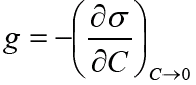
Исследуя поверхностное натяжение водных растворов, Дюкло и Траубе установили зависимость между поверхностной активностью и числом атомов углерода.

Правило Дюкло-Траубе: при уве-личении углеводородного радикала на группу -СН2-, поверхностная актив-ность увеличивается в 3-3,5 раза.

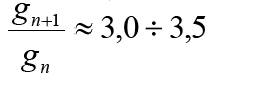
Находим соотношение:

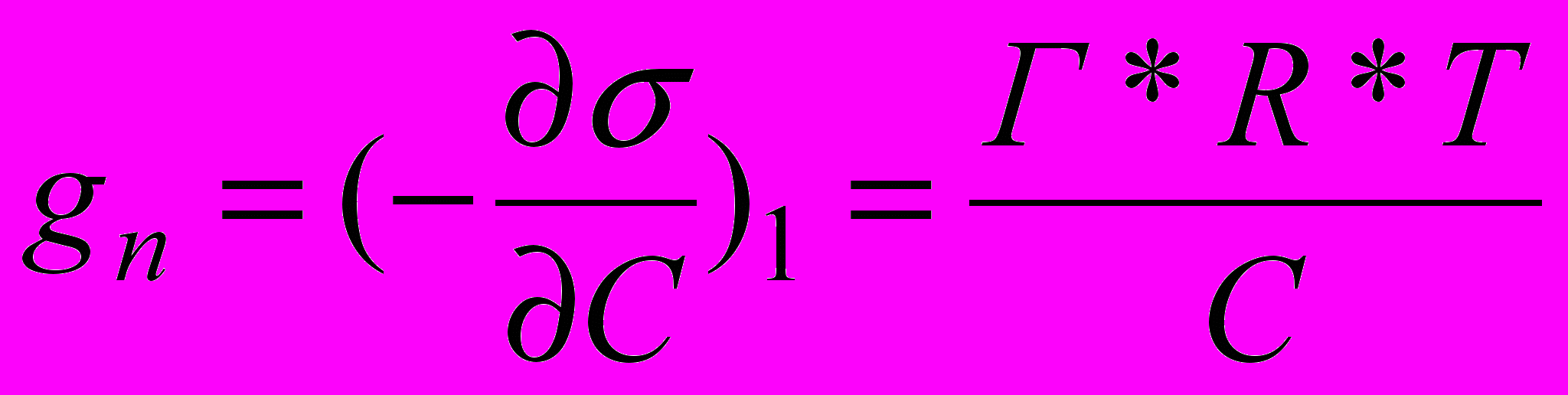для пропионовой кислоты

для масляной кислоты

Тогда:

g_n₊₁/g_n=(Г₁*С₂)/(Г₂*С₁)

Подставляя в полученную формулу данные с таблицы получаем

β=

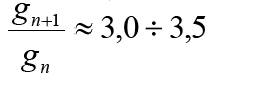
при адсорбции на поверхности графита

При адсорбции на поверхности силикагеля

Задача № 89

1. В избытке SrCI₂

2. SrCI₂+2NaF=SrF₂+2NaCI

3. {m[SrF₂]*n[Sr⁺²]](2n-x)F^-]}⁺^xxF^-

4. Применяют разбавленные растворы для предотвращения коагуляции. Присутствие посторонних ионов может привести к уменьшению толщины двойного электрического слоя (ДЭС).

Избыток одного из реагентов вводят для образования ДЭС, а следовательно и мицелл.

Задача № 99

Порог коагуляции равняется

С_к(KNO₃)=

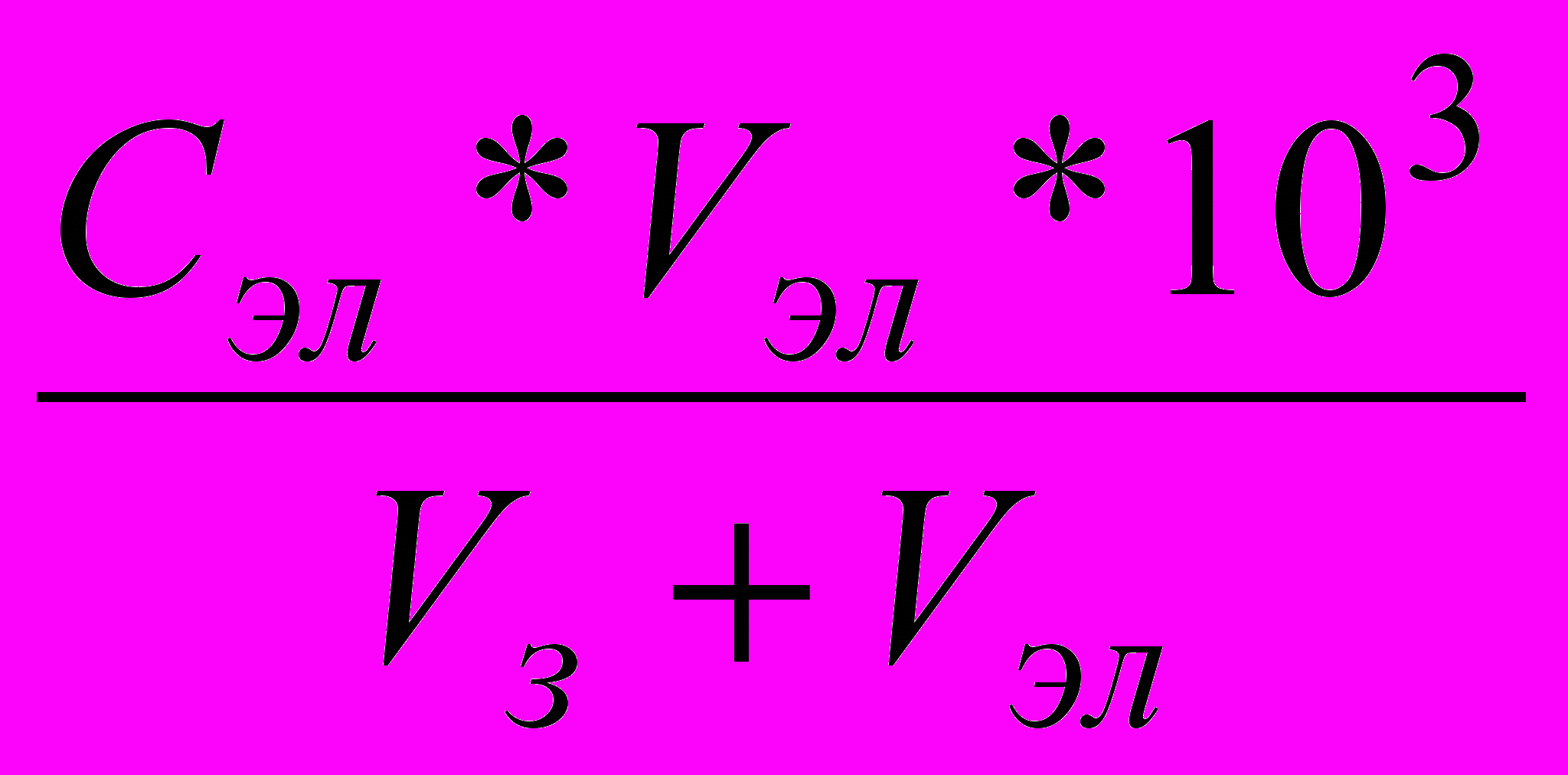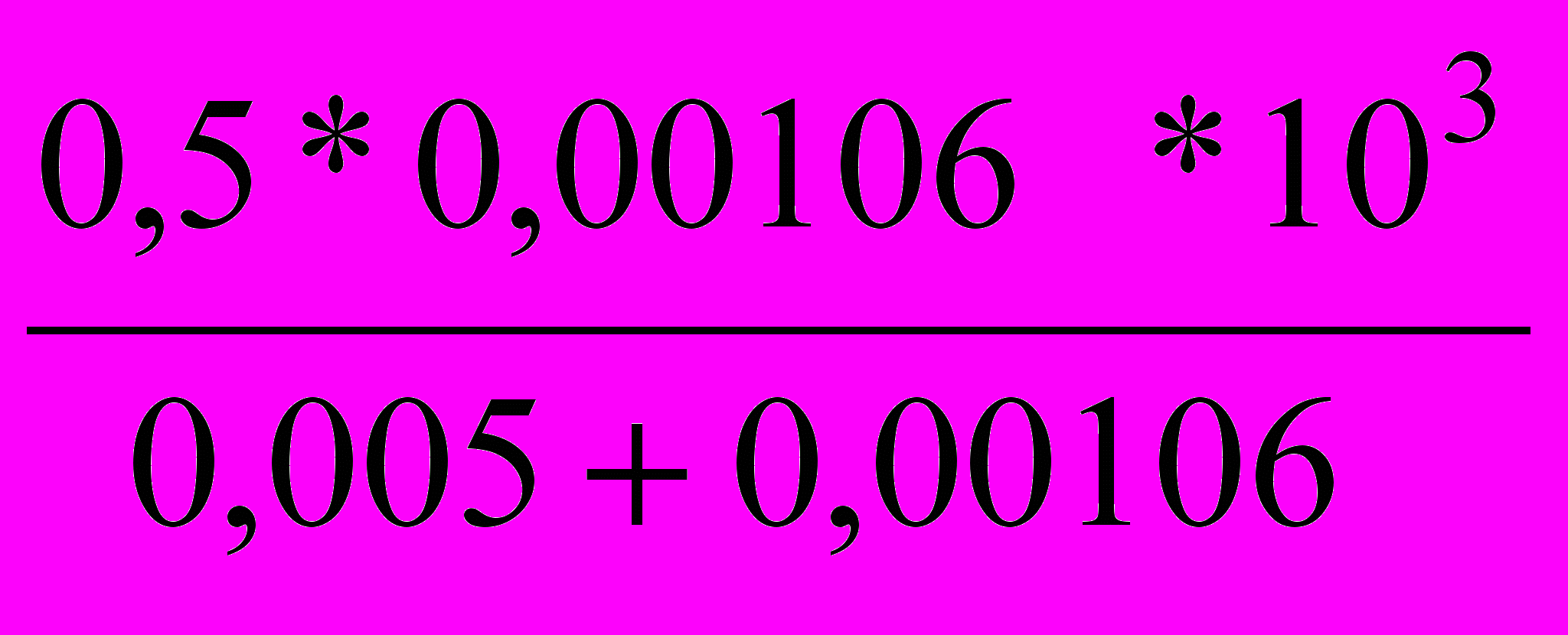=180 ммоль/л

С_к(K₂SO₄)=

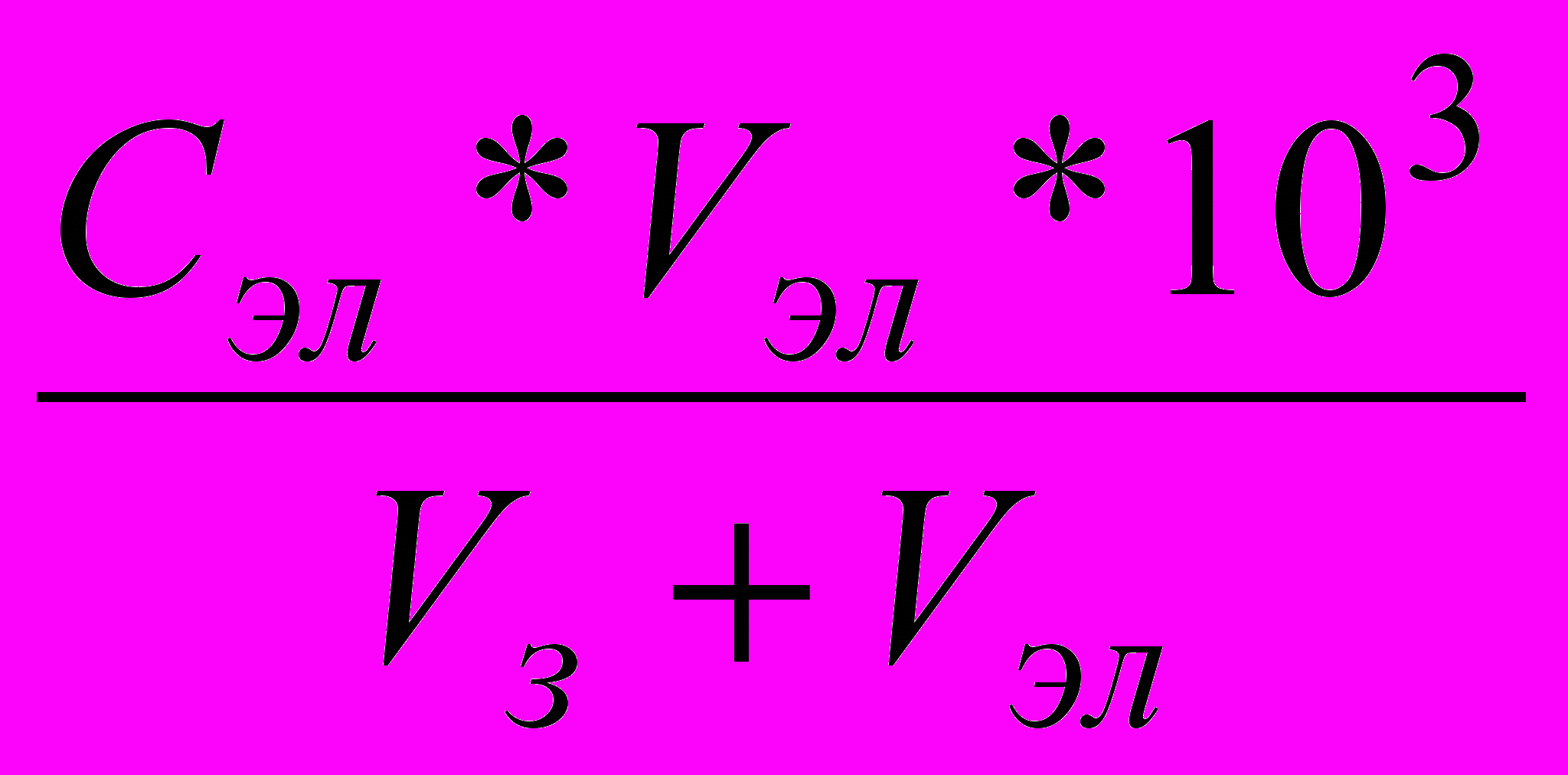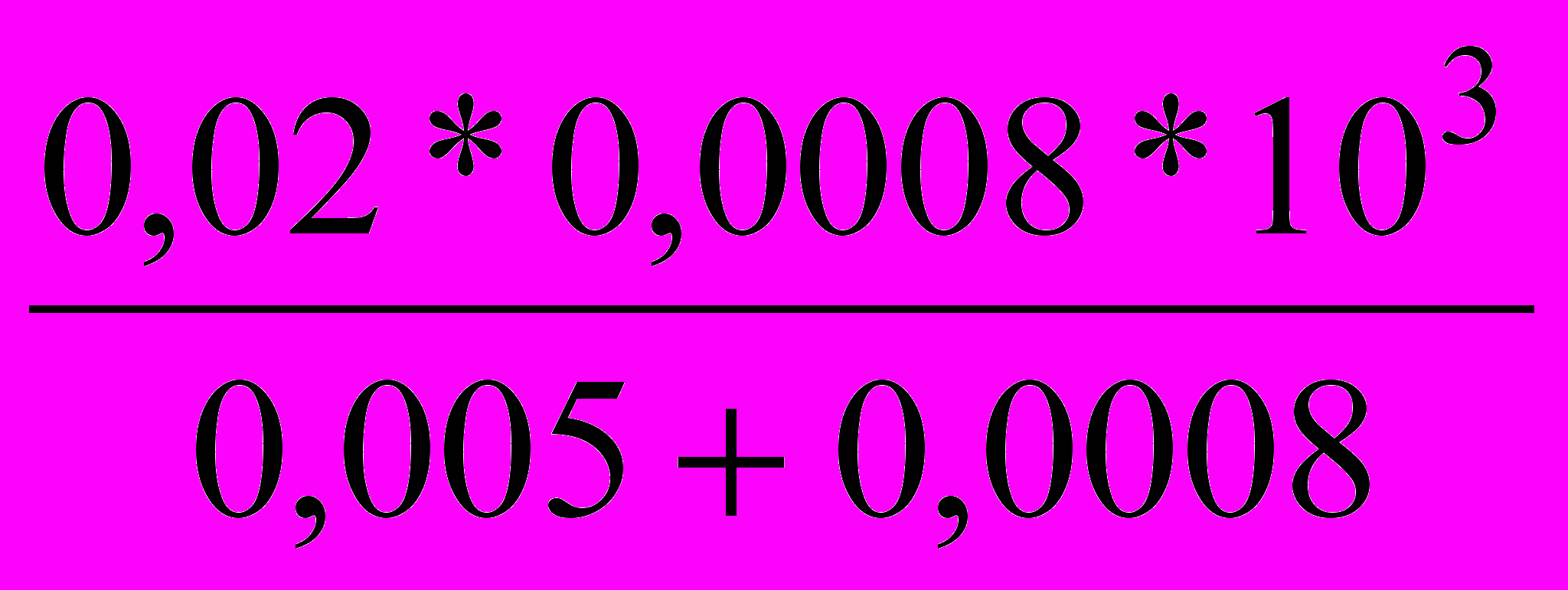=2.76 ммоль/л

С_к(K₃PO₄)=

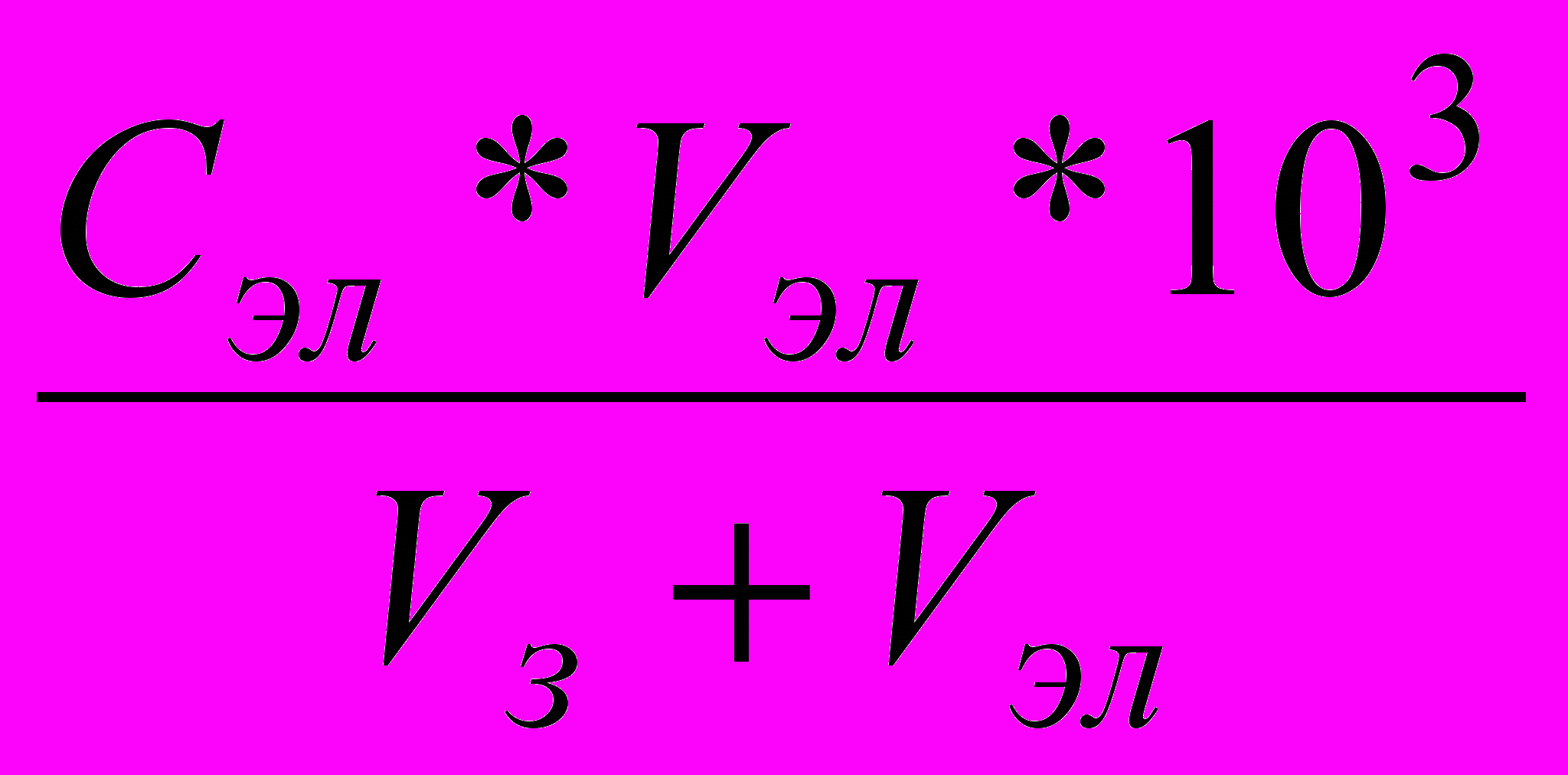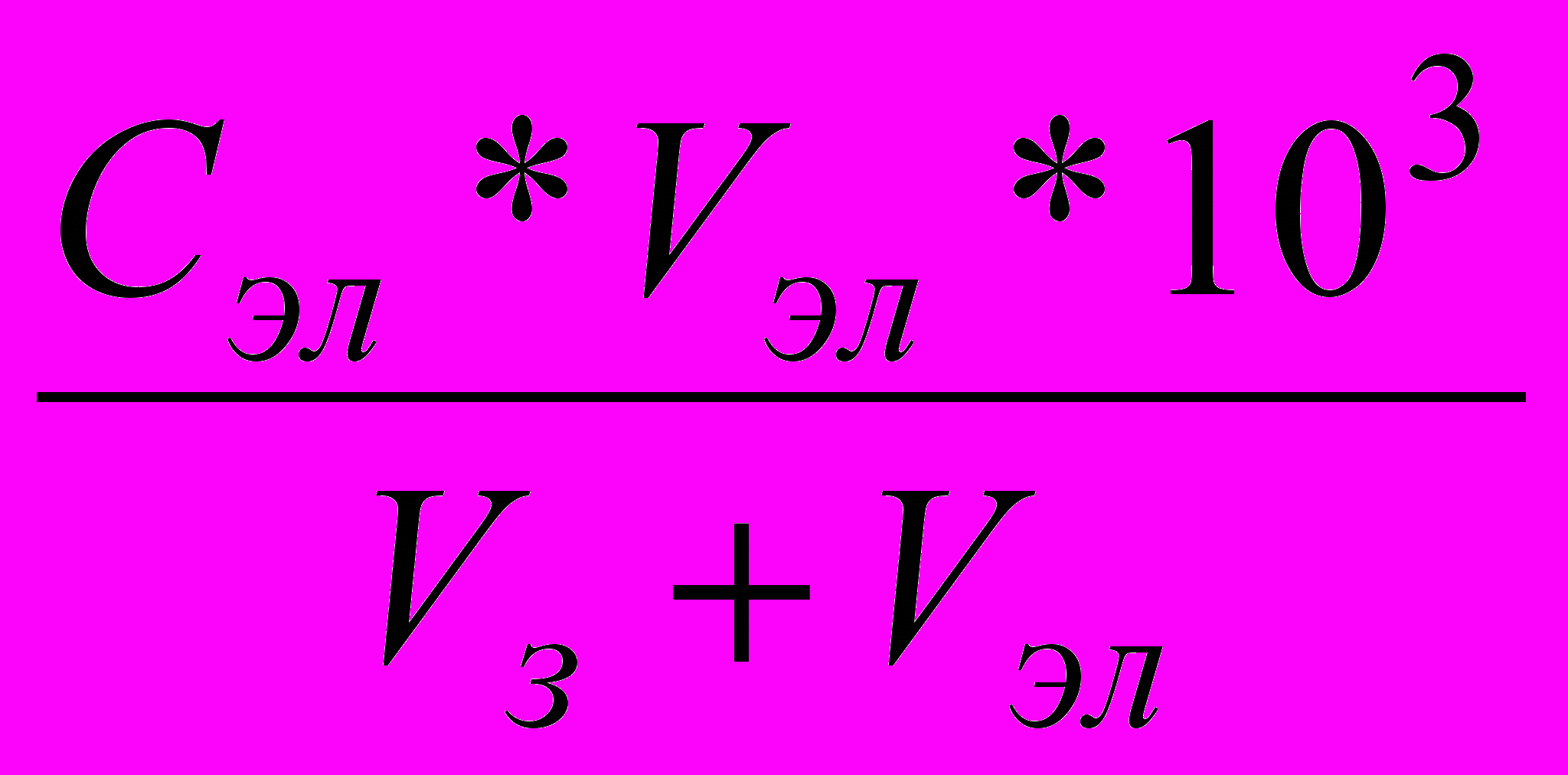=0,27 ммоль/л

где Сэл-концентрация электролита

Vэл-объем электролита

Vз-объем золя

Золь имеет заряд ,,+''

Коагуляция-объединение мелких частиц дисперсных систем в более крупные под влиянием сил сцепления с образованием коагуляционных структур.

Формула исходного золя

{[CdCI₂]Cd²⁺(2n-x)CI^-}^2x⁺2xCI^-

Формула скоагулированного золя

{[CdCI₂]Cd²⁺(2n-y)CI^-}²^y⁺2yCI^-

где x>>у Строение мицелл отличается толщиной ДЭС

Коагуляцию вызывает негативно заряженный ион.

Задача № 109

Согласно уравнению Гельмгольца-Смолуховского

ξ=

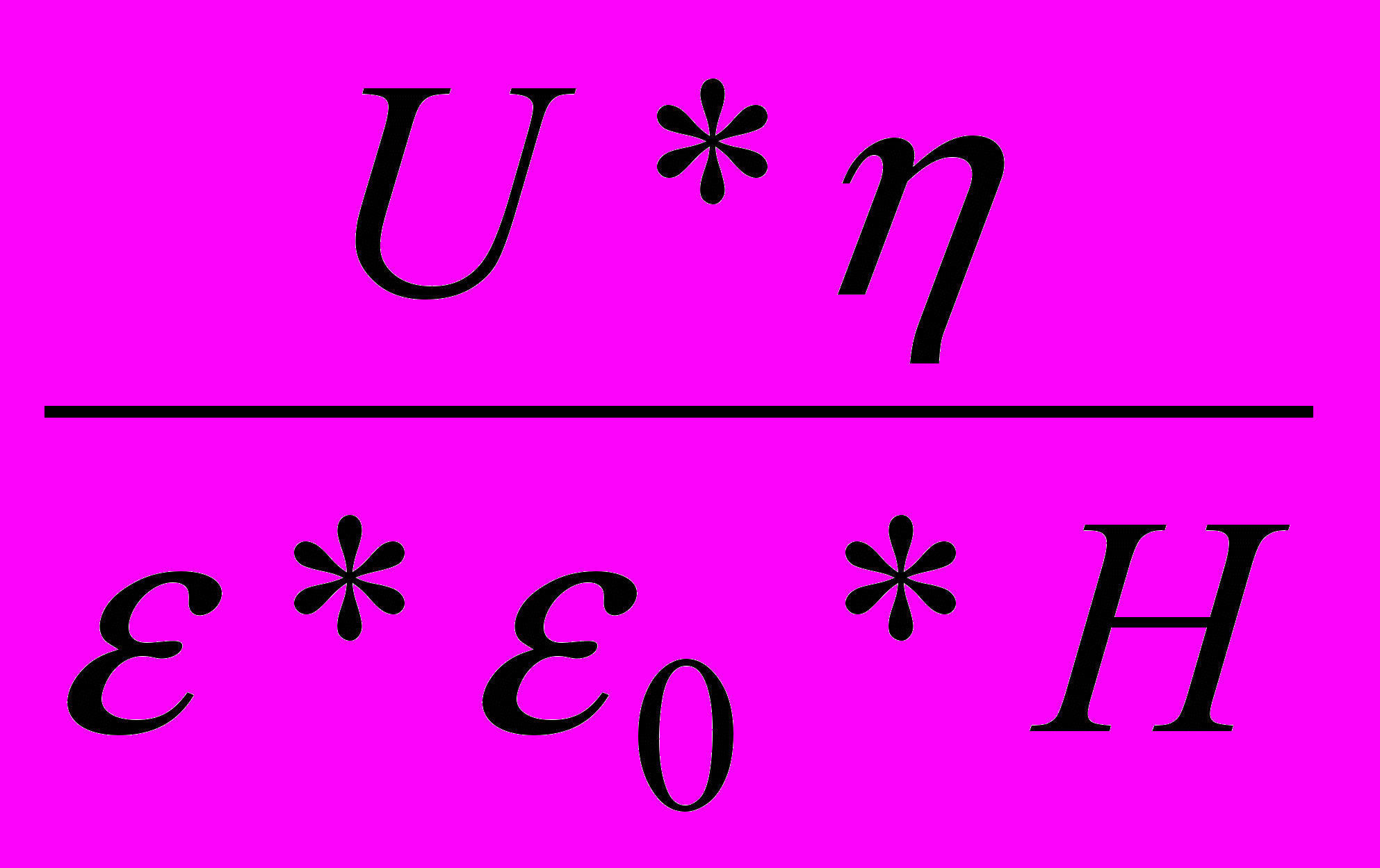
ξ-электрокинетический потенциал

η-вязкость среды Н*с/м²

U-скорость движения золь-боковая жидкость, м/с

Н-напряженность поля В/м

Е-напряженность поля

l-расстояние между электродами

ε* ε₀-диэлектрическая проницаемость

U₁=S/t=0.025/1800=1.389*10^-5 м/c

U₂=S/t=0.011/1800=6,111*10^-6 м/c

ξ1=

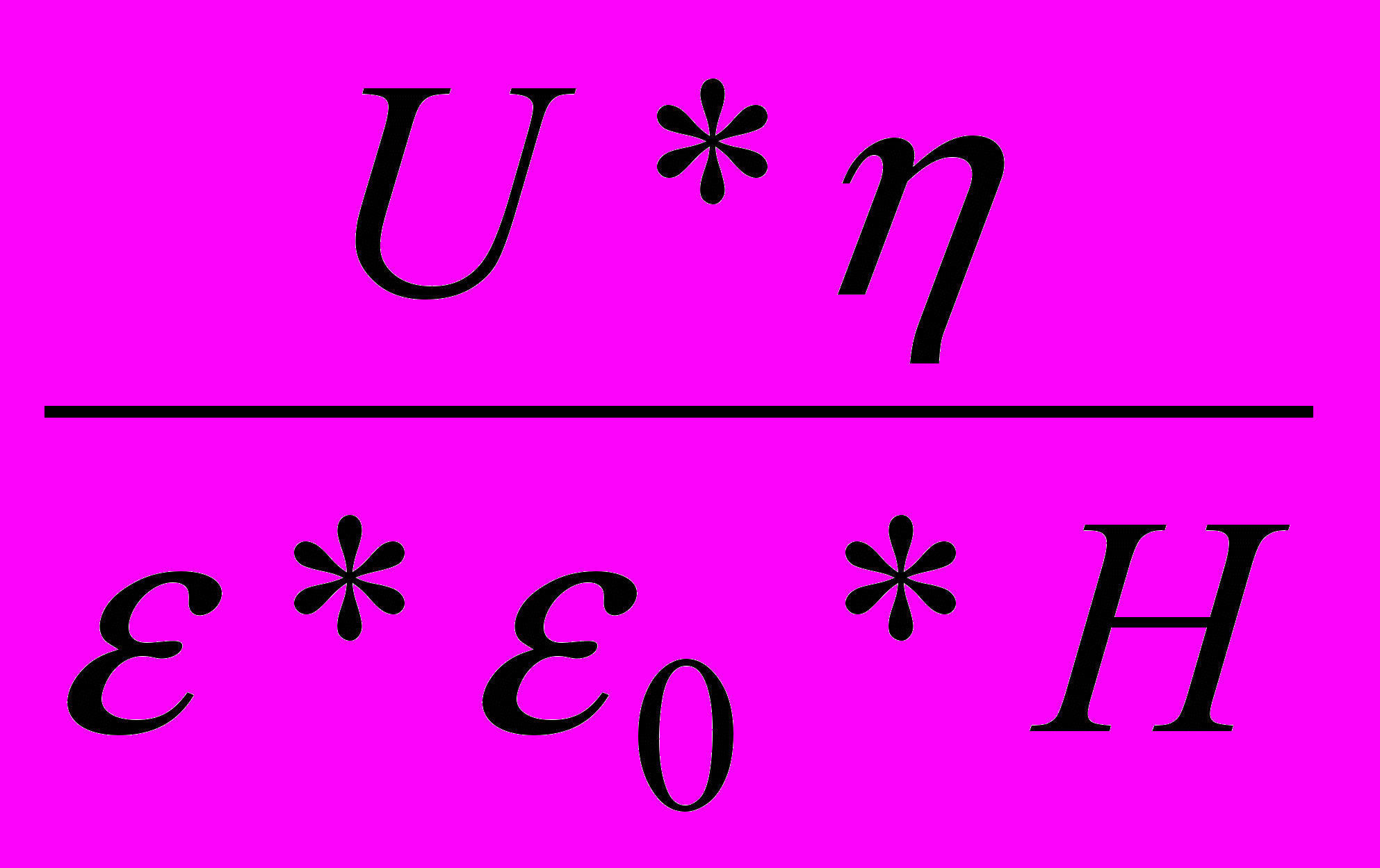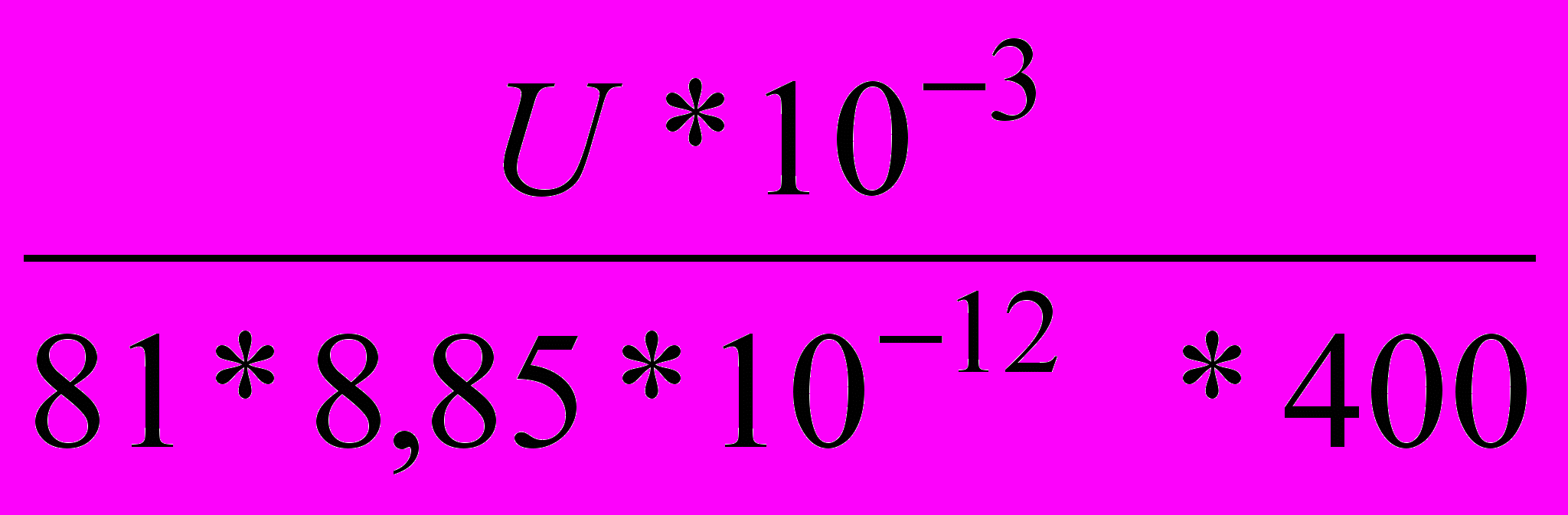=48,44 мВ

ξ2=

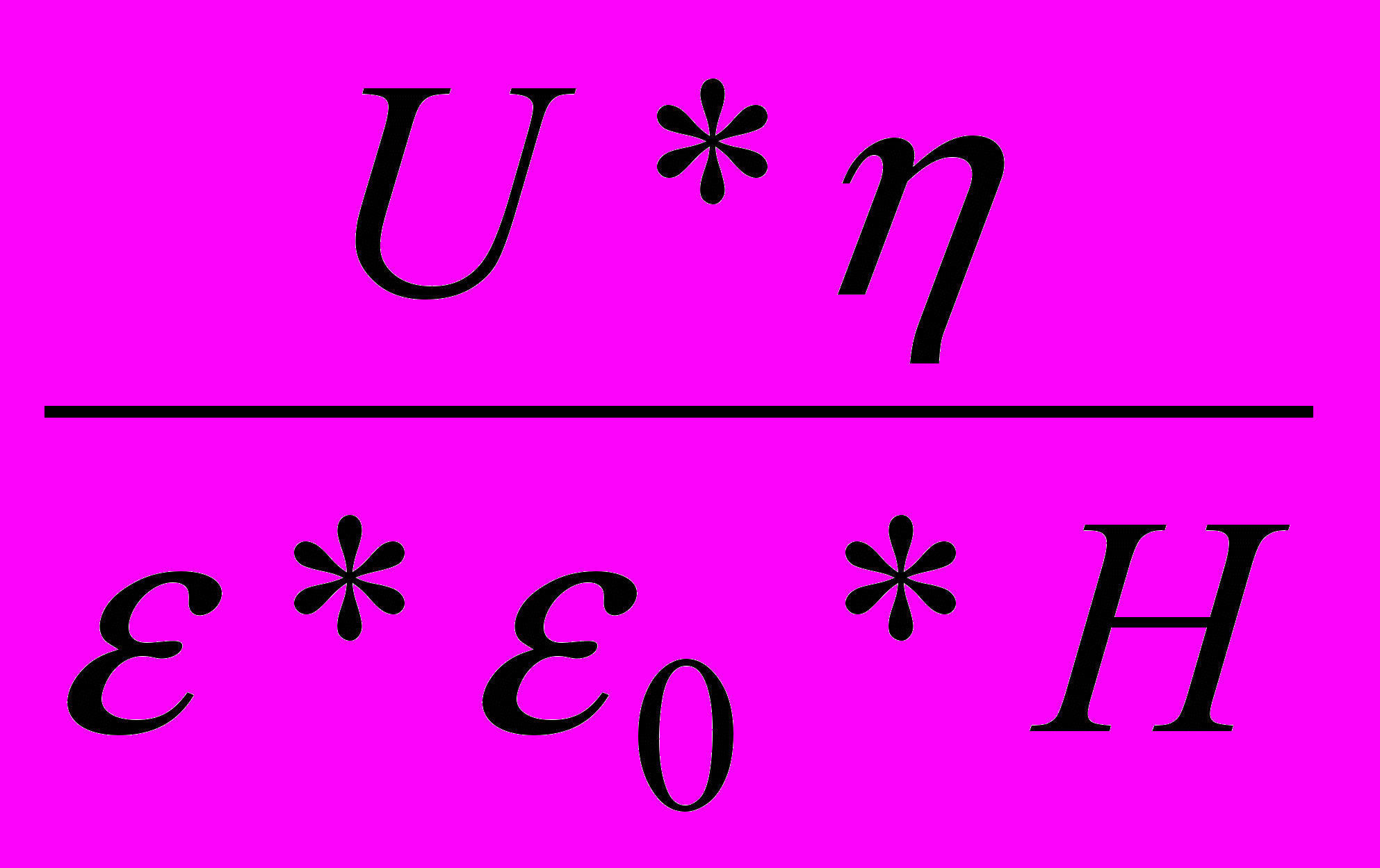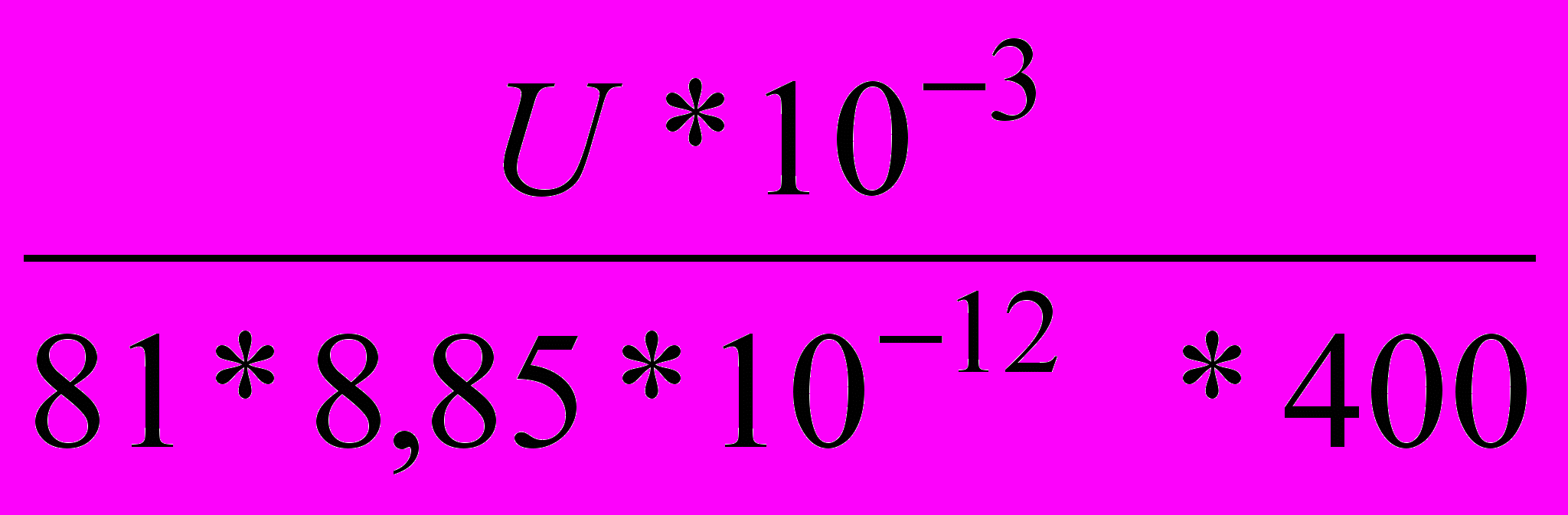=21,31 мВ

1)Формула золя

{[AgI]Ag⁺(n-x) I^-}^x⁺xI^- (до добавления)

{[AgI]Ag⁺(n-у) I^-}^у+уI^- (после добавления) где x>>у

Добавление электролита ведет к уменьшению толщины ДЭС а следовательно и уменьшению ξ-потенциала, что подтвердили расчеты задачи.

Задача № 119

Степень набухания a определяется массой жидкости ( в кг ), которая поглощается на данной стадии набухания и при данной температуре 1 кг высокополимера:

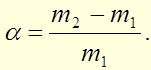
При Т=291 К

Время,с	Масса	Степень набухания
0	1,09	0
50	7,14	5,550459
100	11,55	9,59633
150	14,66	12,44954
200	16,46	14,10092
250	16,9	14,50459

При Т=318 К

Время,с	Масса	Степень набухания
0	2,05	0,880734
50	21,52	18,74312
100	37,43	33,33945
150	19,48	16,87156
200	1,15	0,055046

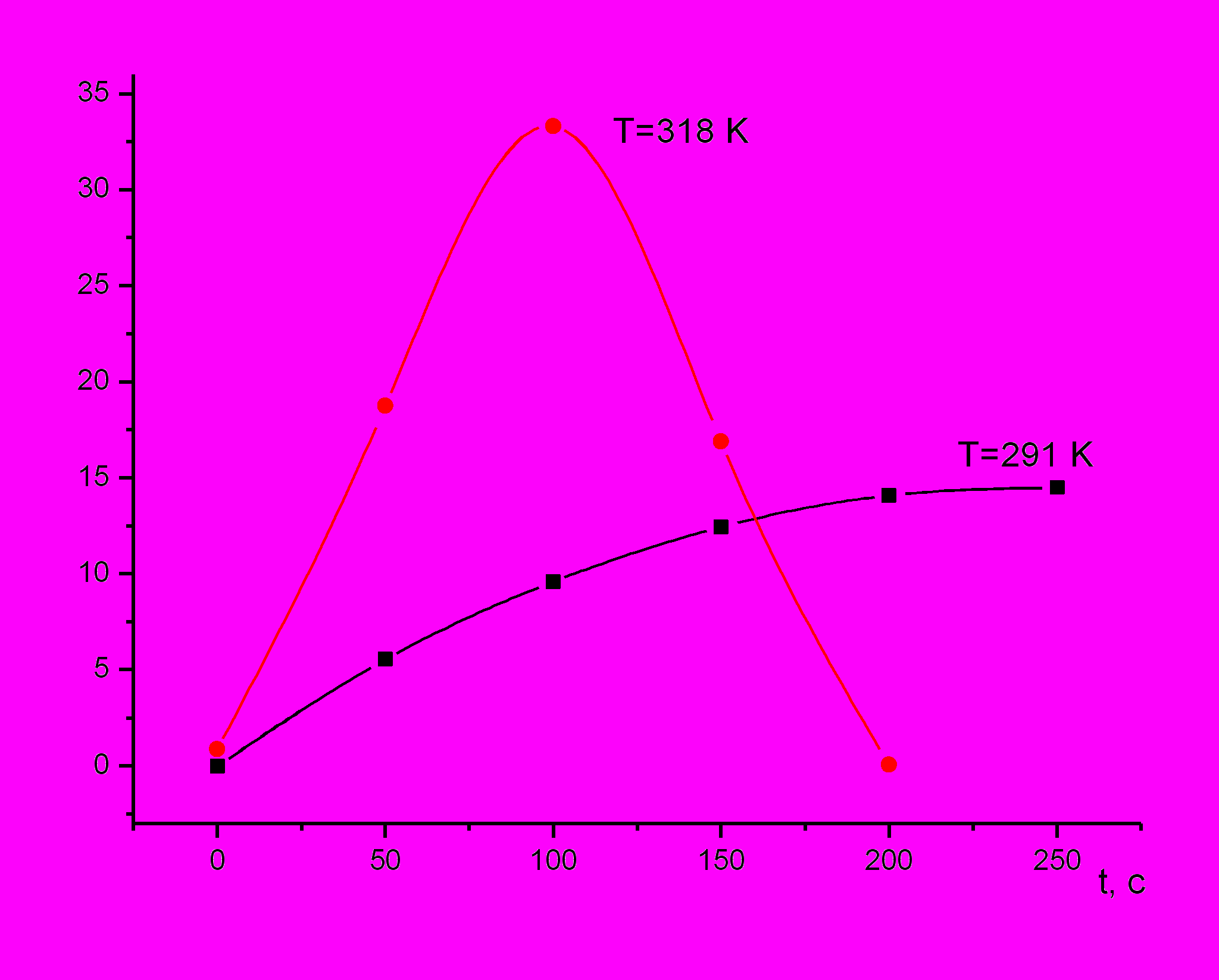
Желатин лиофильный к воде. На степени скорость набухания одного и того же ВМС в одном и томже растворителе влияют такие факторы, как температура, давление, pH среды, присутствие посторонних в – в, в особенности электролитов, степень измельчённости полимера, (возраст) полимера. При повышении температуры скорость набухания увеличивается, а степень предельного набухания уменьшается.

Влияние pH среды хорошо изучено для белков и целлюлозы. Минимум набухания лежит в области изоэлектрической точки (для желатины, например, при pH 4,7 ), по ту и другую сторону от этой точки степень набухания возрастает и, для сильных максимумув (из них большой в кислой зоне при pH 3,2), вновь уменьшается.

На скорость набухания влияет повышение степени измельченности.

Влияние возраста всегда однозначно: чем свежее (моложе) ВМС, тем больше степень набухания и скорость набухания.

Задача № 129

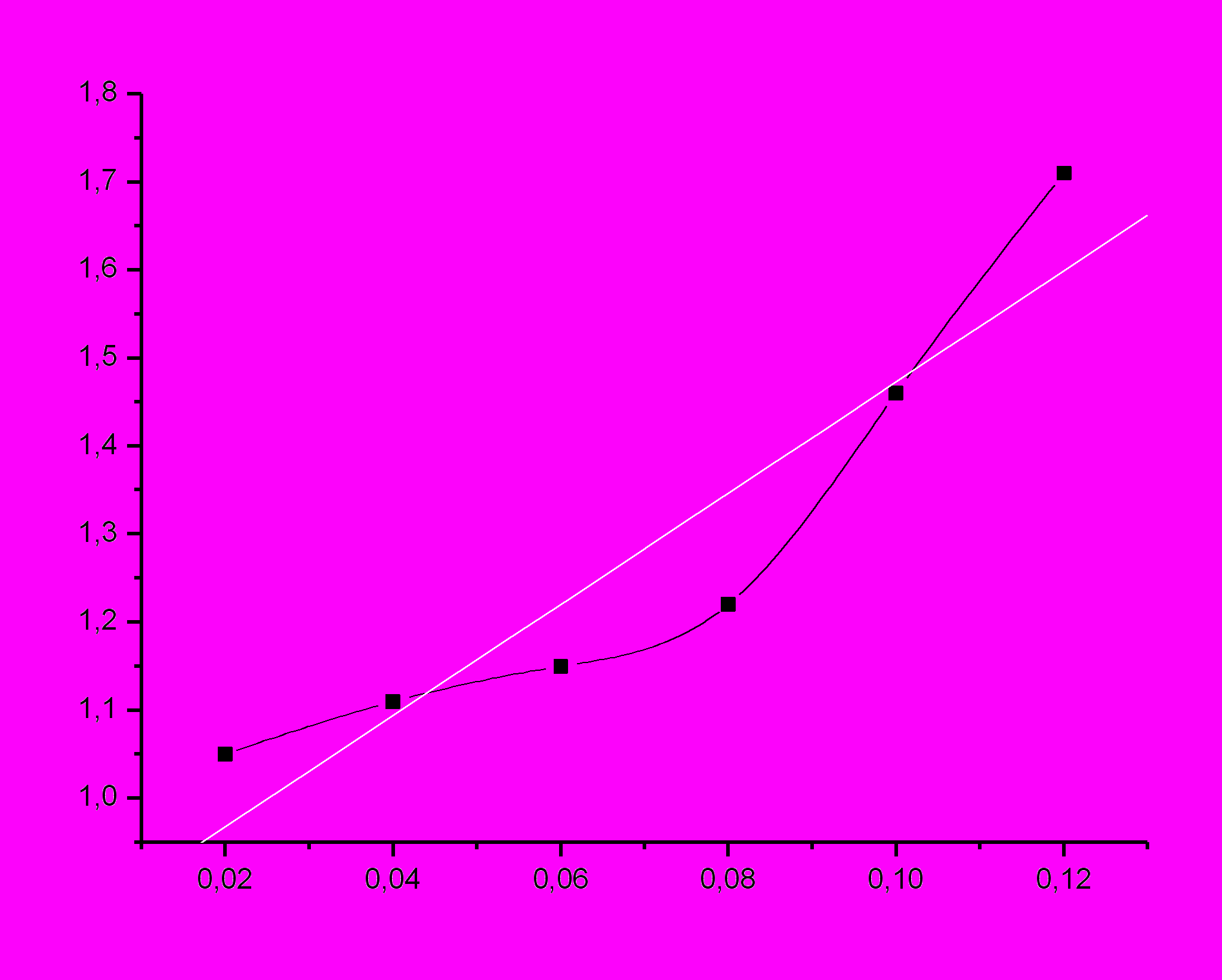
Согласно формуле (уравнение Эйнштейна)

η=η₀(1+α*φ)

где η-вязкость коллоидного раствора

η₀-вязкость растворителя

α-коэффициент формы (для сферических частиц α=2,5)

φ-концентрация коллоидного раствора

Подставляя данные в исходную формулу, получаем

1,05*10^-3=10^-3(1+2,5*0,02), отсюда

φ=19% (объемная концентрация)

Определение графически

1. Уравнение Энштейна для ньютоновских жидкостей. Ньютоновская жидкость - это жидкость, которая продолжает течение (не перестает течь) вне зависимости от внешних сил, действующих на нее (то есть даже если эти силы очень малы, лишь бы они не были строго нулевыми). Например, вода является ньютоновской жидкостью, потому что она продолжает демонстрировать свойства жидкости вне зависимости от скорости перемешивания.

2. Форма частиц влияет на коэффициент формы -α (для сферических частиц α=2,5)

Blog