Азербайджанская Государственная Нефтяная Академия 1 yus fax@yahoo com, 2 rauf1206@rambler ru Защита окружающей среды от загрязнений вредными выбросами нефтегазовой промышленности является глобальной проблемой, решение
| Вид материала | Решение |
СодержаниеU – линейная скорость потока. Граничные и начальные условия для уравнения (1): x |
- Азербайджанская Государственная Нефтяная Академия 4 курс; 124. 5 гр проф. Ахмедов, 89.65kb.
- Проблемы кибернетики и информатики” (pci’2010), 57.04kb.
- Миняев Андрей Олегович Ведущая организация: Московская государственная юридическая, 331.18kb.
- Тема : «Загрязнение и охрана окружающей среды», 38.66kb.
- Г. В. Плеханова (технический университет) М. А. Пашкевич, В. Ф. Шуйский экологический, 1176.09kb.
- Решение 10 сентября 2007 года №36 город Актау, 22.02kb.
- Глобальные последствия загрязнений окружающей среды, 141.96kb.
- Практикум по экологическому мониторингу окружающей среды Учебное пособие, 949.79kb.
- Программа преддипломной практики по специальности 2080202 «Инженерная защита окружающей, 201.67kb.
- Соляная пещера что это? Галотерапия – метод лечения и реабилитации, основанный на использовании, 700.71kb.
Математическое моделирование адсорбционных процессов
Ф.В. Юсубов1, Р.К. Бабаев2, Л.Э.Гулиева
Азербайджанская Государственная Нефтяная Академия
1yus_fax@yahoo.com, 2rauf1206@rambler.ru
Защита окружающей среды от загрязнений вредными выбросами нефтегазовой промышленности является глобальной проблемой, решение которой связано с созданием экологически чистых производств. Перед учеными и инженерами стоит важнейшая задача создания экологически чистых производств. Создание экологически чистых производств обеспечивается не только коренным изменением технологии, но и созданием новых, а также реконструкцией существующих установок [1].
В связи с этим особенную актуальность приобретают математическое .моделирование и оптимизация адсорбционных процессов.
Надо отметить, что адсорбционным методом вредные вещества практически полностью могут быть удалены, если оптимально выбраны как схема и аппаратура процесса, так и его технологический регламент [2].
При этом оптимизация процесса дает также возможность не только обеспечить защиту, но и рационально использовать сырьевые и энергетические ресурсы. С этой точки зрения особую актуальность приобретают исследование процессов жидкофазной адсорбции в неподвижном слое на основе разработанной математической модели.
Стремление к интенсификации промышленных адсорбционных процессов приводит к повышению скорости движения фаз и увеличению локальных и средних градиентов температур и концентраций в неподвижном слое адсорбента аппаратов. Процессы с существенно неоднородными гидродинамическими и концентрационными полями характеризуются различными локальными флуктуациями, что приводит к необходимости
применять новые подходы при математическом описании таких процессов [1].
В частности, адсорбционные процессы, в условиях не стационарности как уже подчеркивалось, являются сложными, существенно нелинейными системами. Для решения задач идентификации нелинейных объектов с использованием экспериментальных данных в процессах целесообразно использовать нелинейных дифференциальных уравнений.
При движении смеси веществ через адсорбер, заполненный пористым сорбентом (неподвижная фаза), образуются фронты концентраций каждого компонента смеси. Разделение веществ осуществляется за счет различия во времени удерживания молекул смеси в неподвижной фазе. Характер движения и размывания фронтов зависит от изотерм сорбции и от факторов не идеальности процесса, т.е.: от конечной скорости установления равновесия между веществом в подвижной фазе и неподвижной (кинетическое торможение); от продольной диффузии вещества в подвижной фазе, обусловленной различными нерегулярностями потока в пористой среде [2].
Дифференциальное уравнение баланса сорбирующего вещества можно составить в виде:
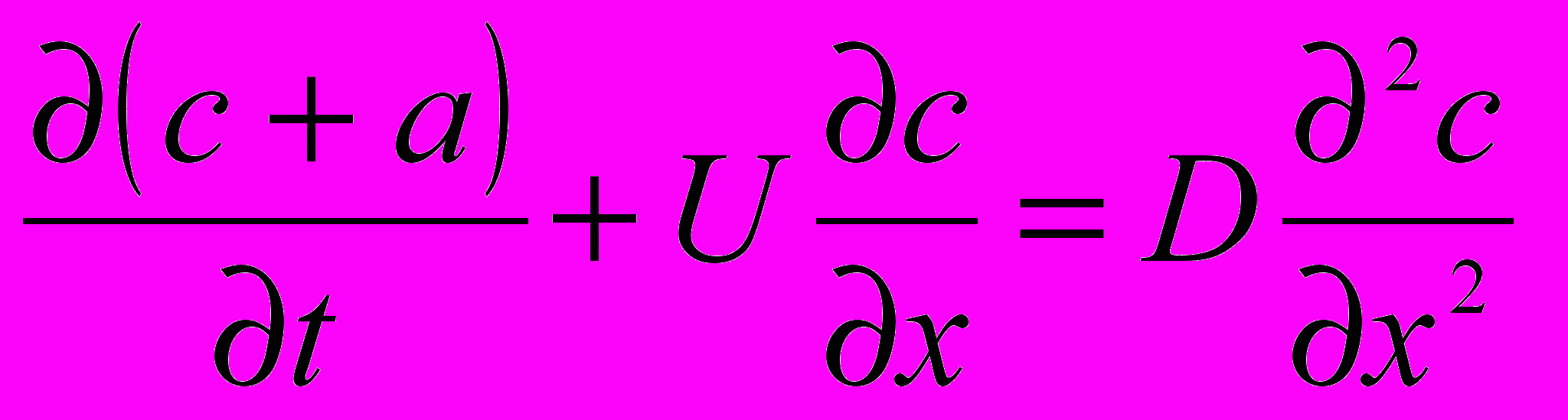 (1)
(1)где, х – расстояние, измеряемое по высоте адсорбера;
t – время;
a – концентрация сорбирующего вещества в твердой фазе;
с – концентрация компонента в подвижной фазе;
D – эффективный коэффициент продольной диффузии, учитывающий продольную диффузию и конвективное перемешивание вдоль колонок
U – линейная скорость потока.
Граничные и начальные условия для уравнения (1):
x=0; c=c0; a=a0;
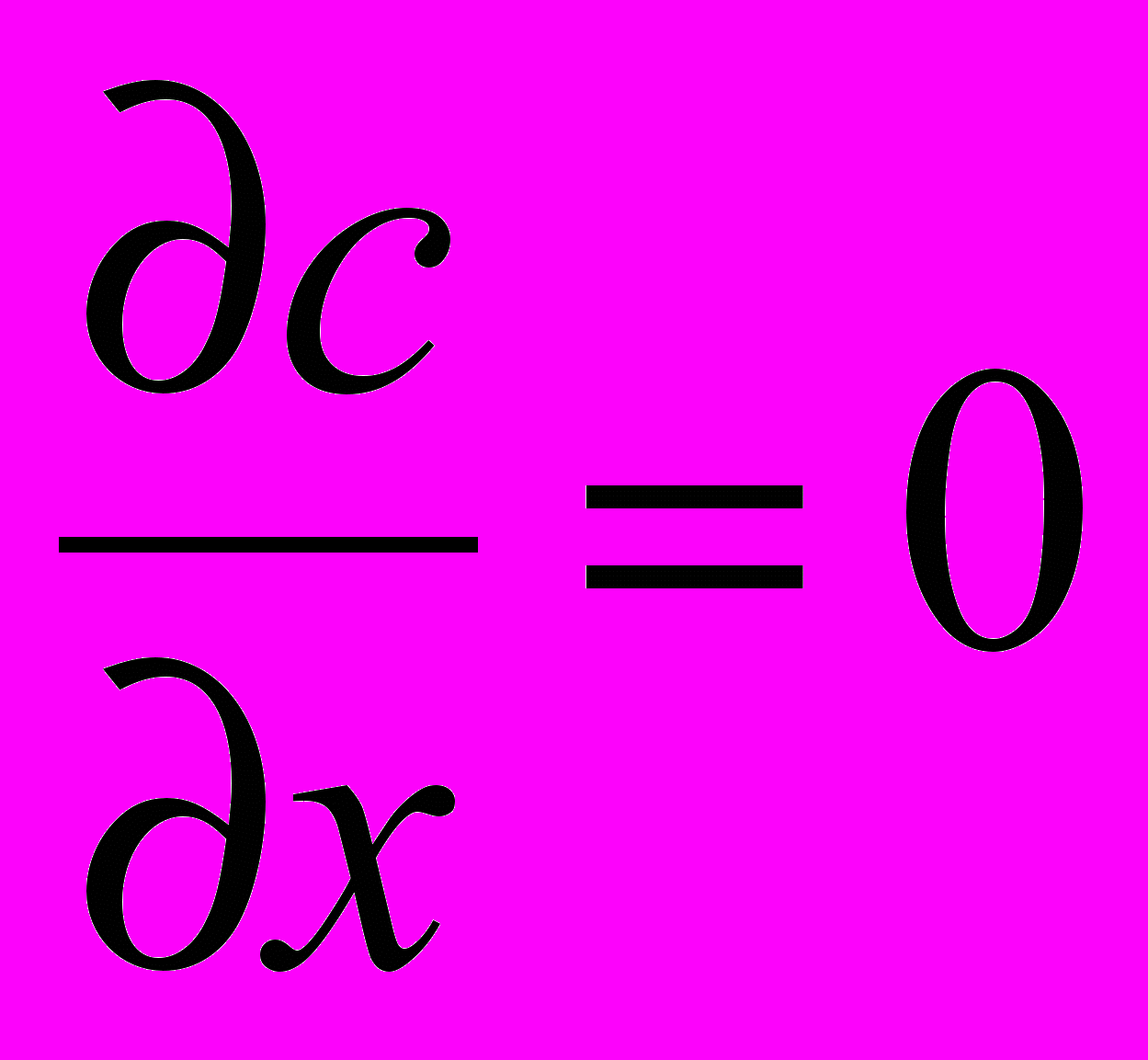 (2)
(2)t=0; c=0; a=0;
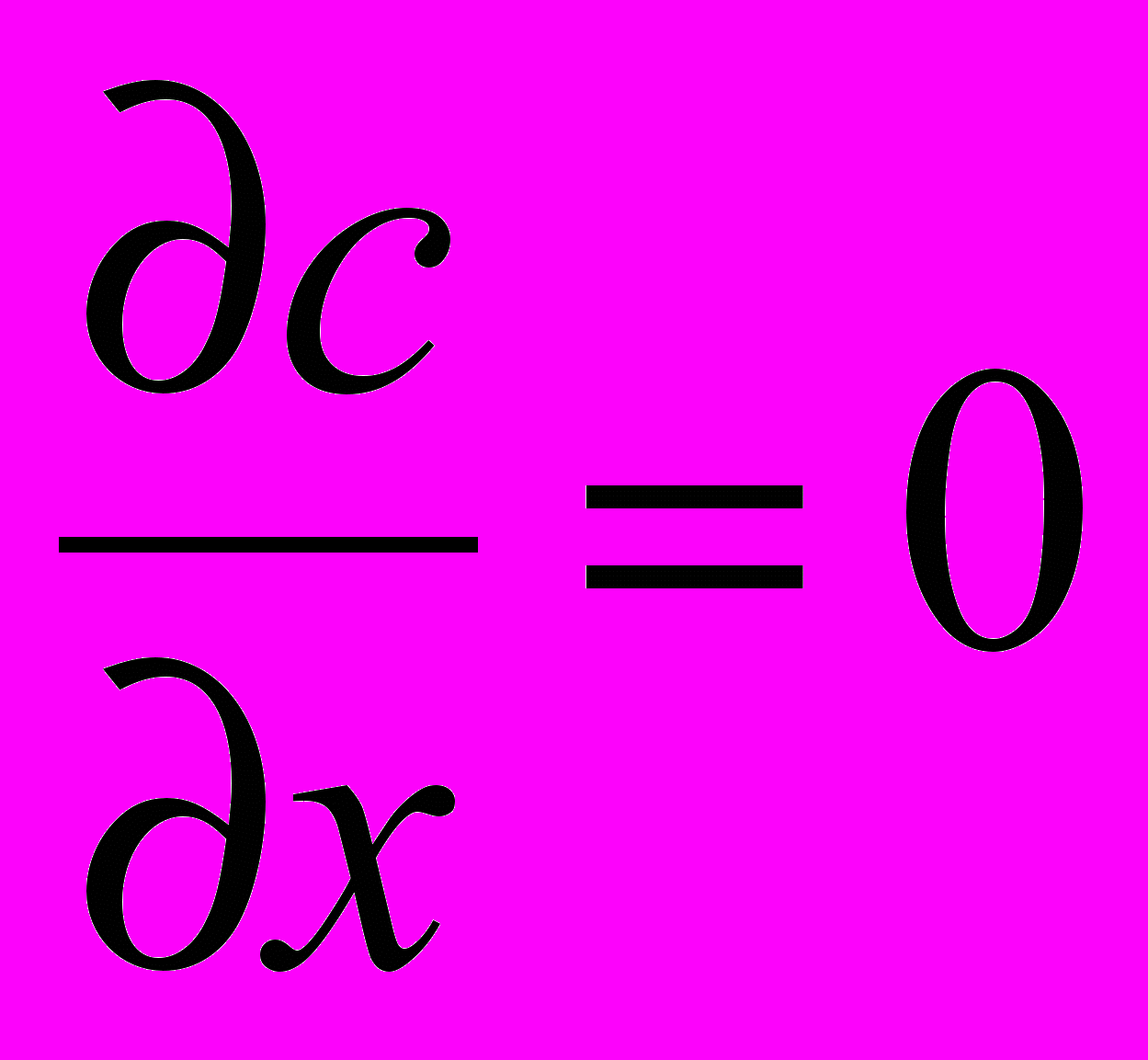 (3)
(3) Уравнение, учитывающее кинетику процесса (предполагается наличие физической адсорбции):
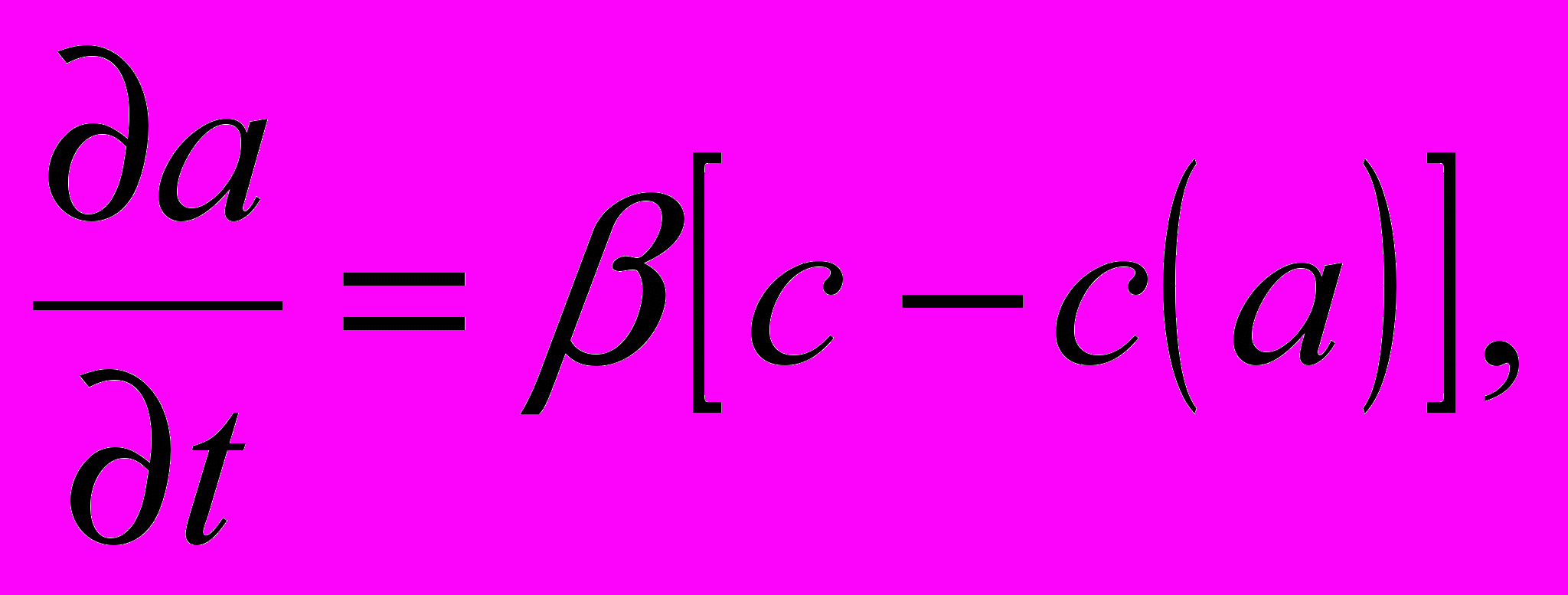 (4)
(4) где, β – суммарная константа скорости внешней и внутренней диффузии сорбирующегося вещества;
с(а) – концентрация вещества у поверхности адсорбции, находящегося в равновесии с концентрацией адсорбирующегося вещества.
- Разработана математическая модель процесса адсорбции в неподвижном слое адсорбента в условиях не стационарности их протекания.
- Экспериментально изучена корреляционные соотношения
Nu=0,288 Re · Eu0,496 · Pr0,415 и функций: (
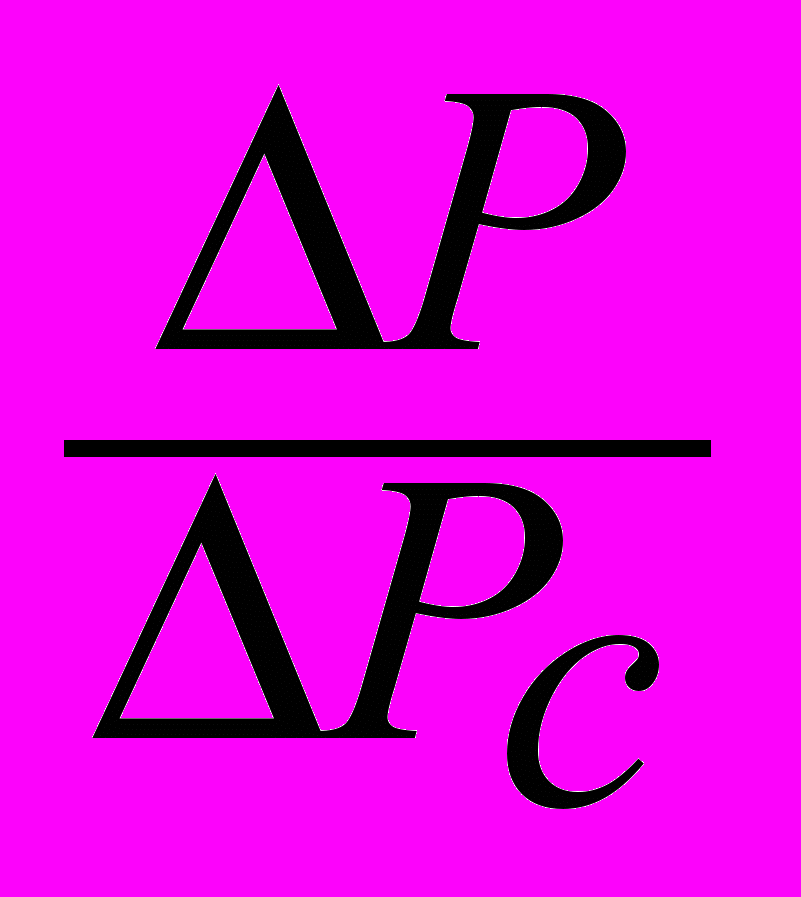 )=f (
)=f (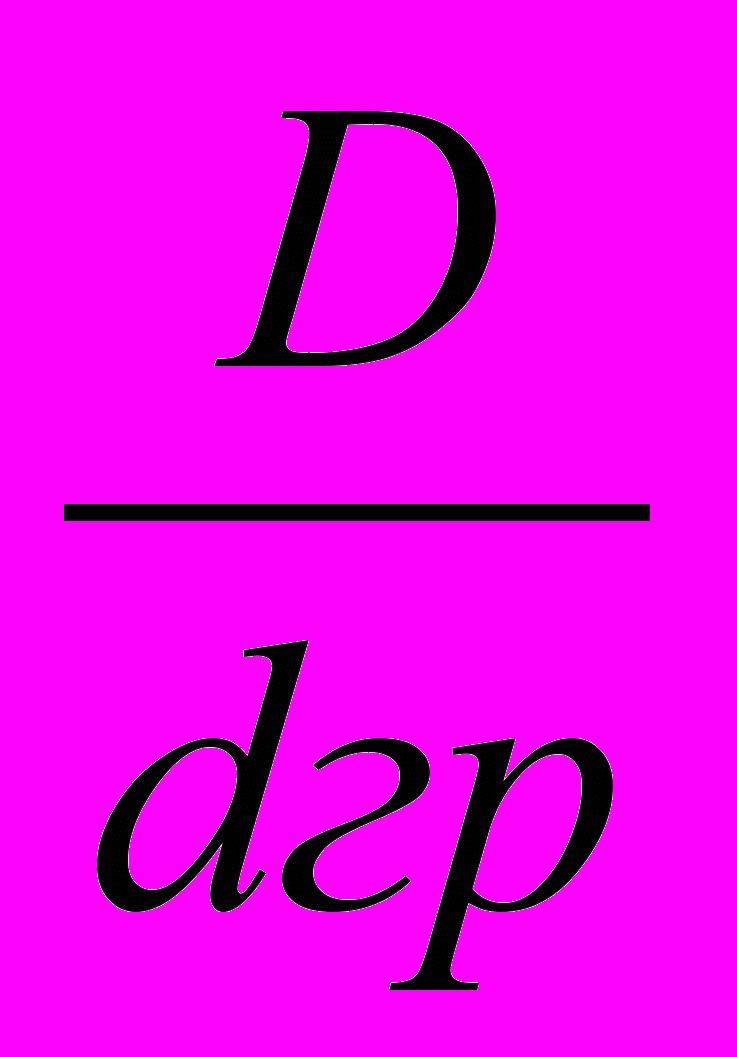 ) , Pe=f(
) , Pe=f(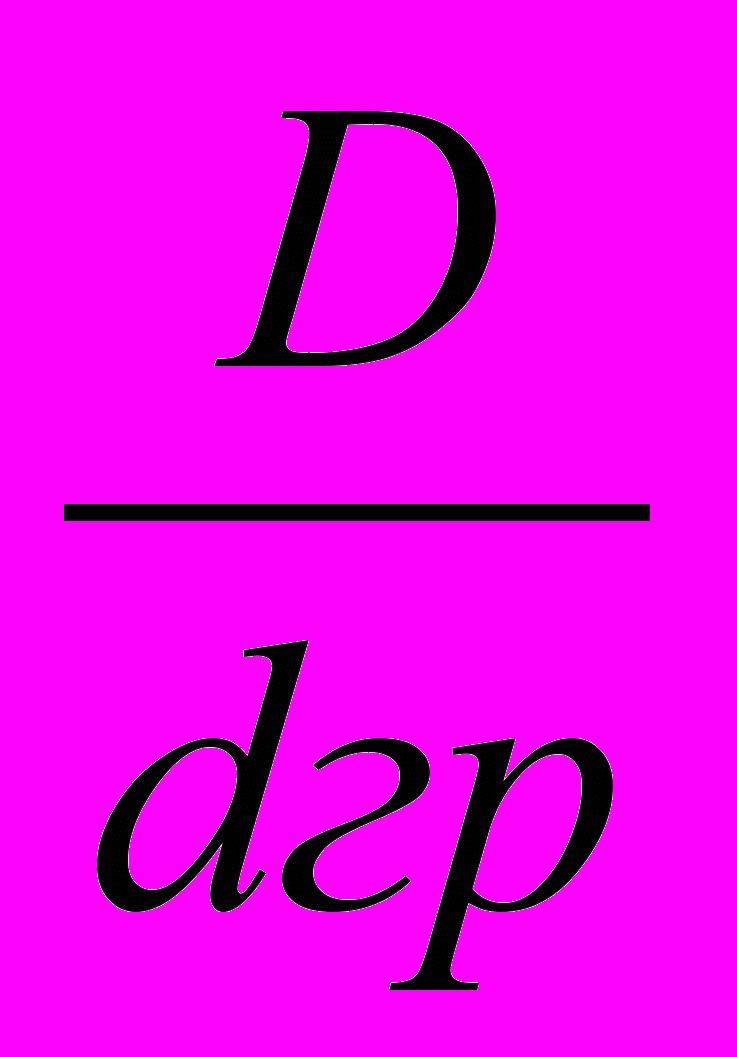 ) и
) и 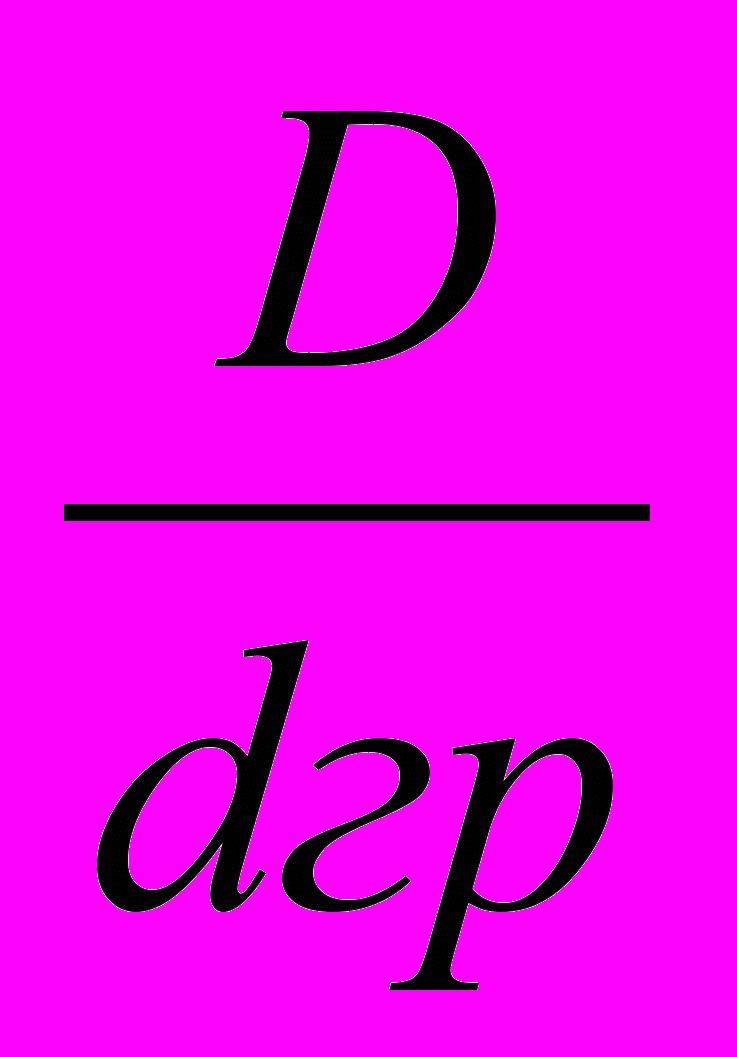 =f(
=f(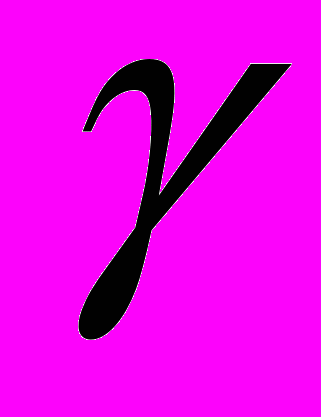 ).
).- Установлено, что при адсорбции многокомпонентной смеси массообмен улучшается в условиях (
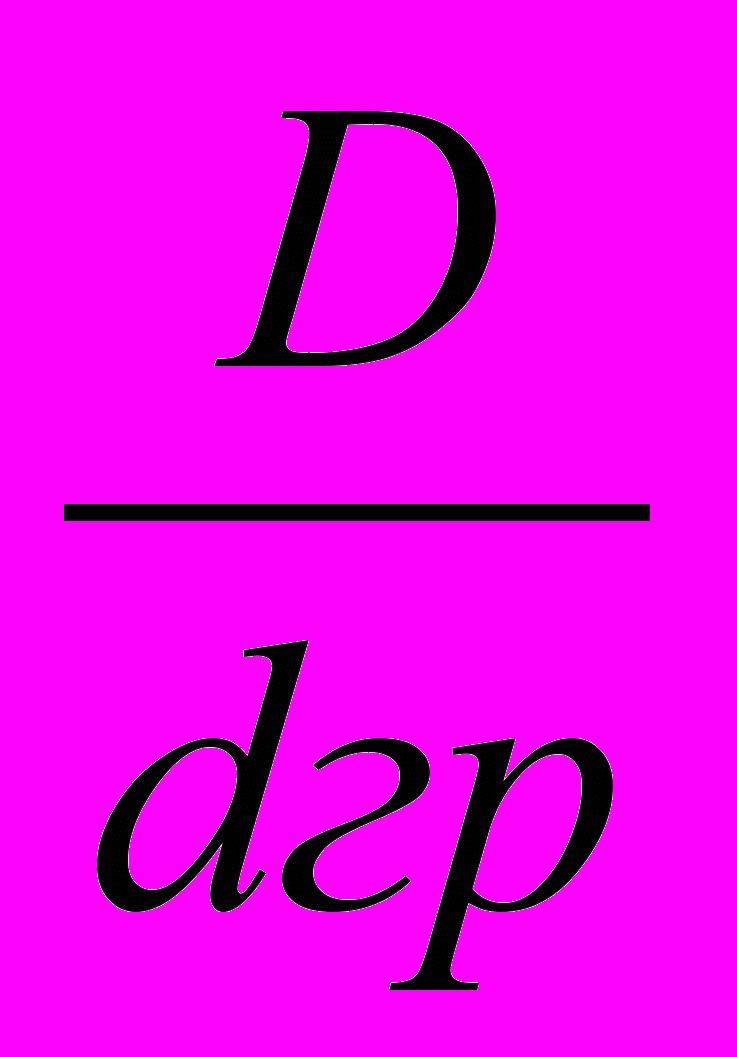 )
)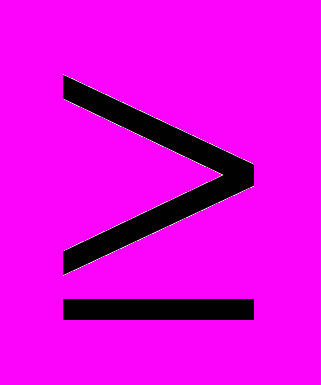 30. Это приводит к устойчивому гидравлическому режиму работы и не возникают застойных зон между распределительными устройствами внутри адсорбера.
30. Это приводит к устойчивому гидравлическому режиму работы и не возникают застойных зон между распределительными устройствами внутри адсорбера.
Литература
- Самойлов Н.А.Моделирование секционированный адсорбционной колонны с неподвижном слоем адсорбента // Журнал прикладной химии. 2000 г., –73. –С.1500-1505.
- Венецианов Е.В., Рубенштейн Р.Н. Динамика сорбции из жидких сред. –М.:Наука, –1983, –237 с.
- Гельперин Н.И., Фролов В.Ф. Основные процессы и аппараты химической технологии, –М.: Химия, –1981. –812 с.
