Blog

На тему: «проблема бернсайда и связанные с ней вопросы»

Вид материала

Документы

Содержание

Учебно–научный семинар «математика. кибернетика. информатика»
Сергея Ивановича Адяна

Подобный материал:

Кафедра Математической теории интеллектуальных систем (МаТИС) механико-математического факультета Московского Государственного Университета им. М. В. Ломоносова Специализированный учебно–научный центр Московского Государственного Университета им М. В. Ломоносова – Школа им. А. Н. Колмогорова УЧЕБНО–НАУЧНЫЙ СЕМИНАР «МАТЕМАТИКА. КИБЕРНЕТИКА. ИНФОРМАТИКА» 24 ноября 2011 года, в четверг, в 17 часов в Актовом зале СУНЦ МГУ состоится доклад действительного члена (академика) Российской Академии Наук (РАН), заведующего отделом математической логики Математического института им. В.А. Стеклова РАН, профессора кафедры математической логики механико-математического факультета МГУ им. М.В. Ломоносова Сергея Ивановича Адяна на тему: «ПРОБЛЕМА БЕРНСАЙДА И СВЯЗАННЫЕ С НЕЙ ВОПРОСЫ»
	Наряду с понятием числа, одним из наиболее важных и распространенных понятий в современной математике является понятие группы. Классическими примерами групп являются известные числовые аддитивные группы: множество целых чисел, множество рациональных чисел, множество действительных чисел (с двуместной операцией сложения +), а также группа всех перестановок на каком-либо множестве, состоящая из множества всех взаимно-однозначных отображений этого множества на себя (с двуместной операцией композиции отображений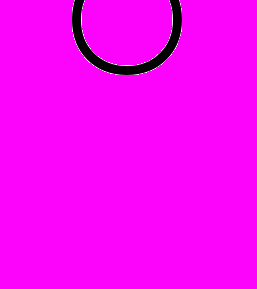 ). Очевидно, всякая конечная группа удовлетворяет тождественному соотношению вида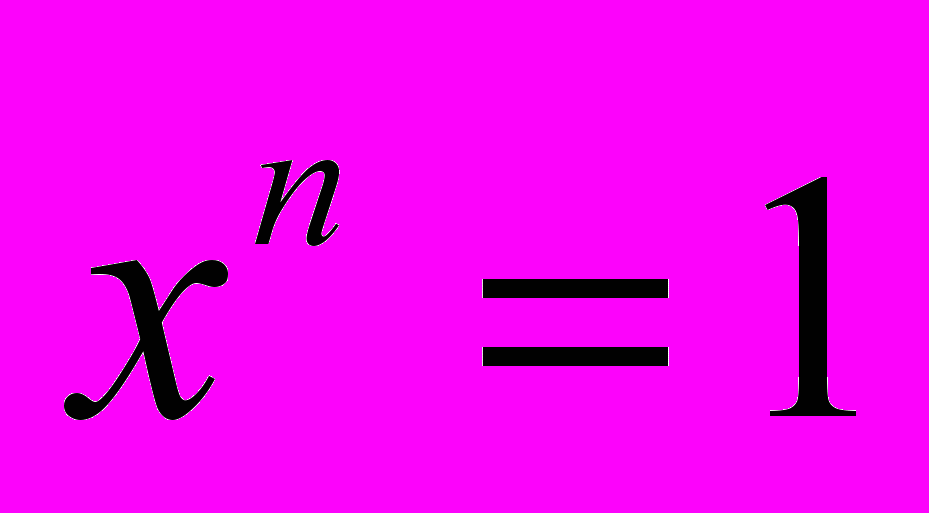 , где в качестве 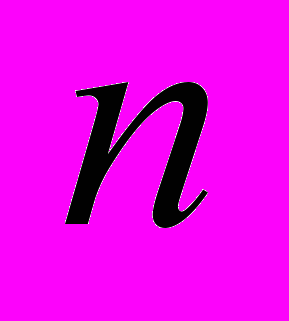можно взять порядок этой группы. Совершенно естественно возникает вопрос о верности обратного утверждения, т.е. будет ли конечной всякая группа, удовлетворяющая такому тождеству и порождаемая конечным числом элементов. Эта проблема была поставлена в 1902 году известным английским учёным У. Бернсайдом в следующей форме: Пусть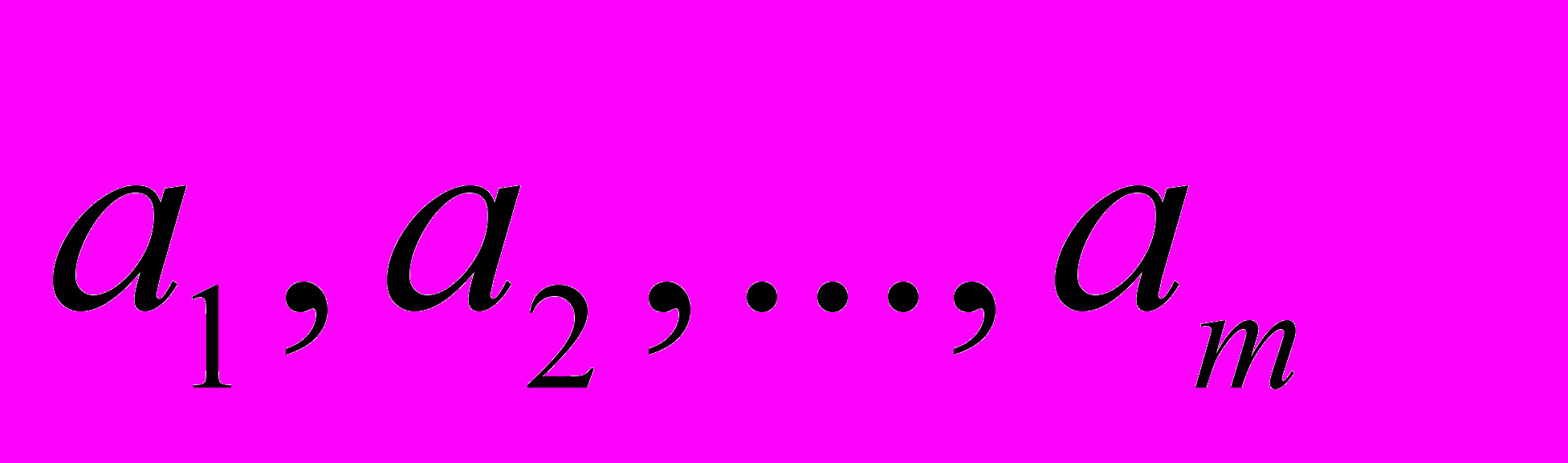 – конечное число независимых элементов, порождающих группу 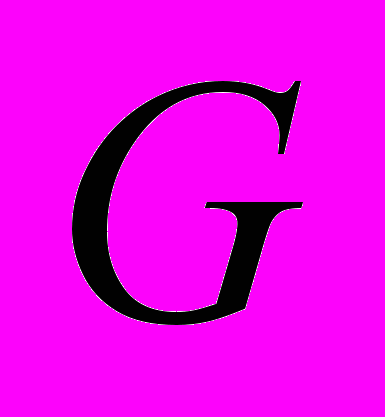, в которой для любого элемента 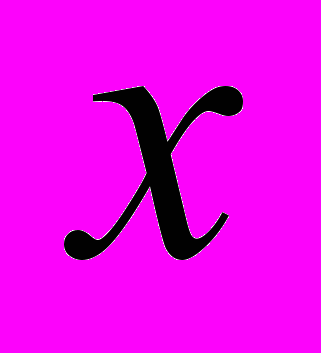выполнено соотношени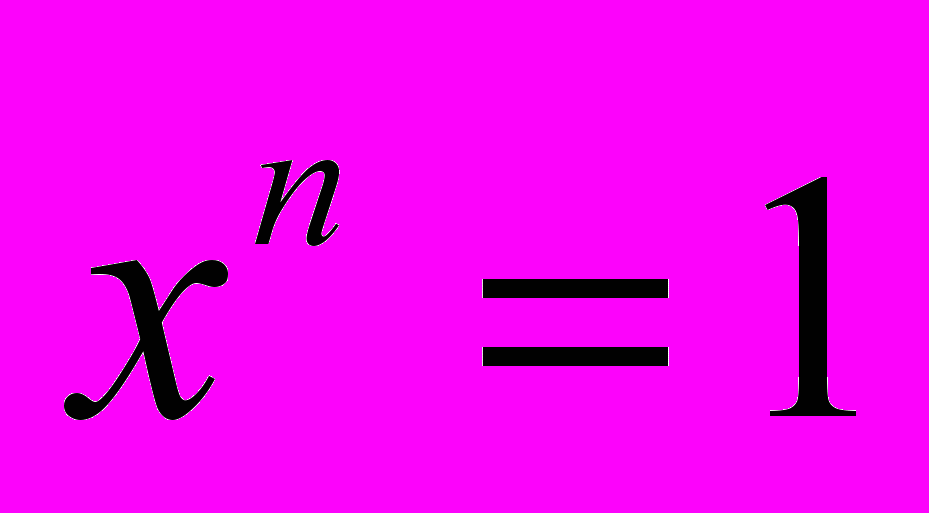е , где 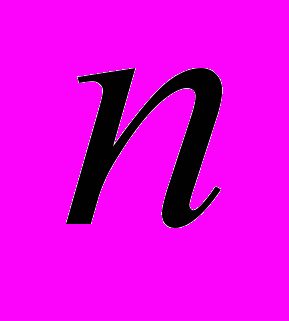– данное целое число. Будет ли определенная таким образом группа 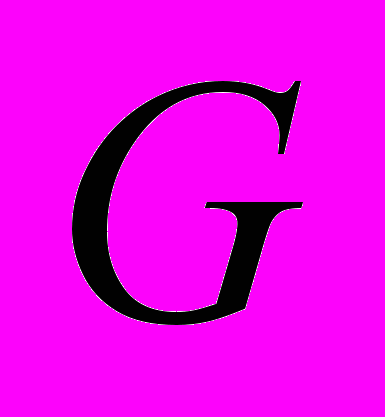конечной и если да, то каков ее порядок? Группы, задаваемые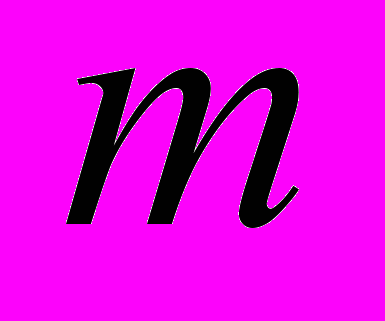 (независимыми) порождающими и тождественным соотношением 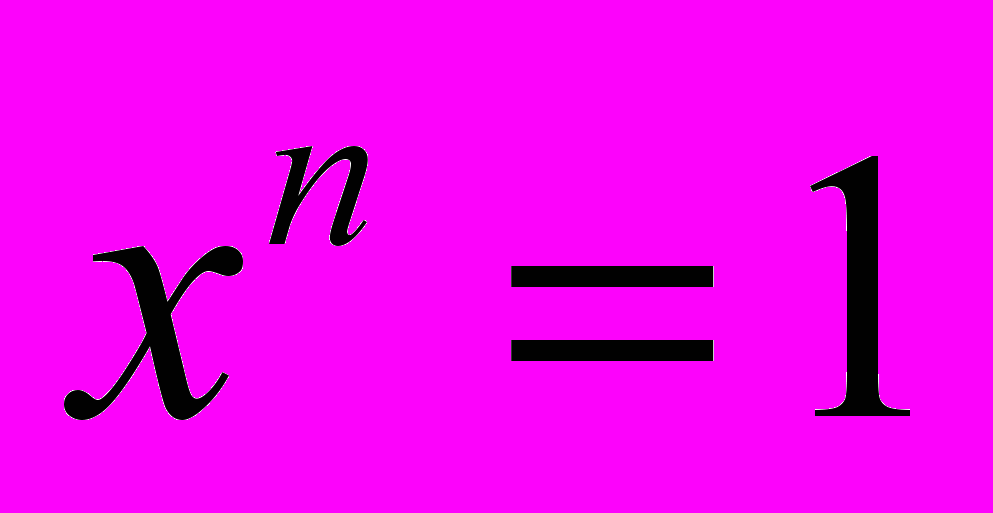, получили название свободные бернсайдовы группы ранга m и экспоненты n (или периода n). Они обозначаются через 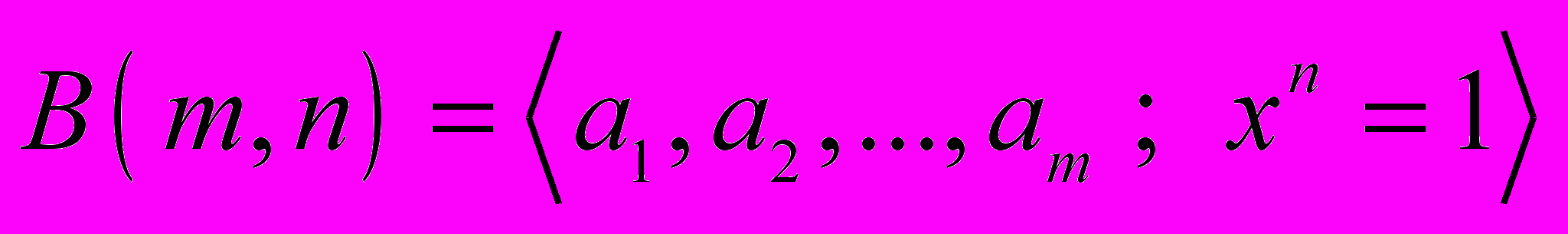. Положительный ответ на основной вопрос Бернсайда до сих пор удалось получить только для очень малых значений экспоненты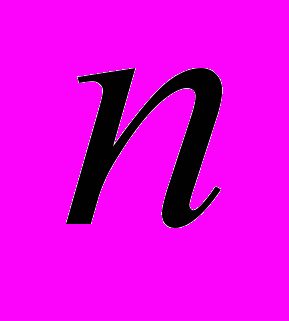 . Сам Бернсайд в 1902 г. доказал конечность групп 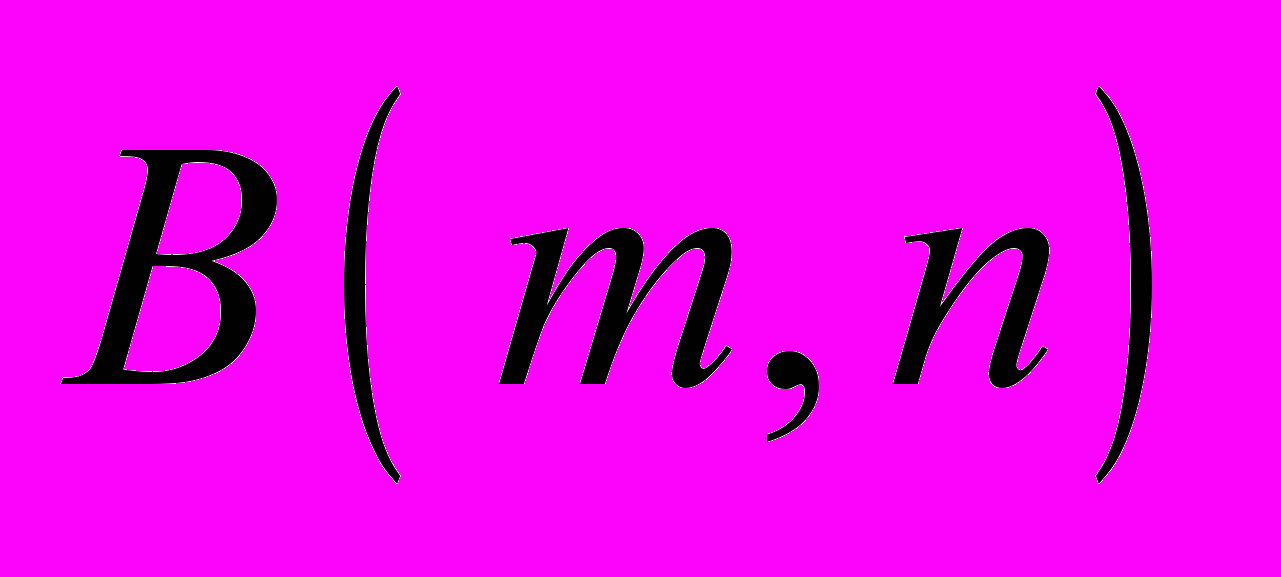для любого числа порождающих 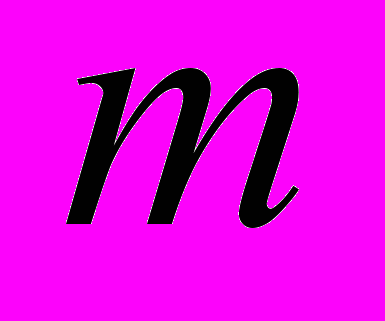и 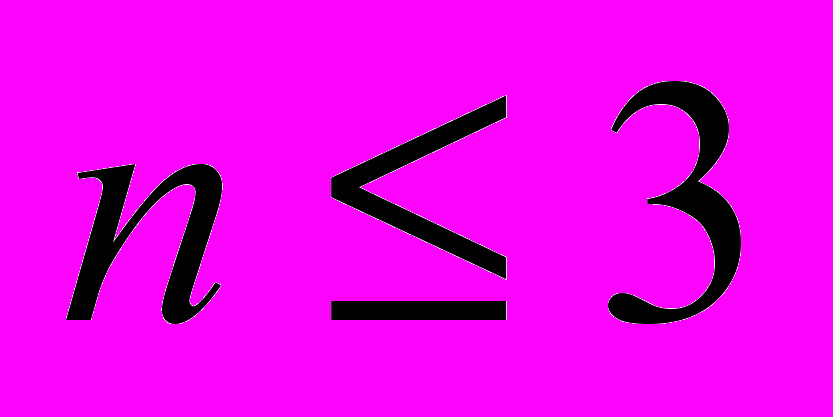, а также конечность 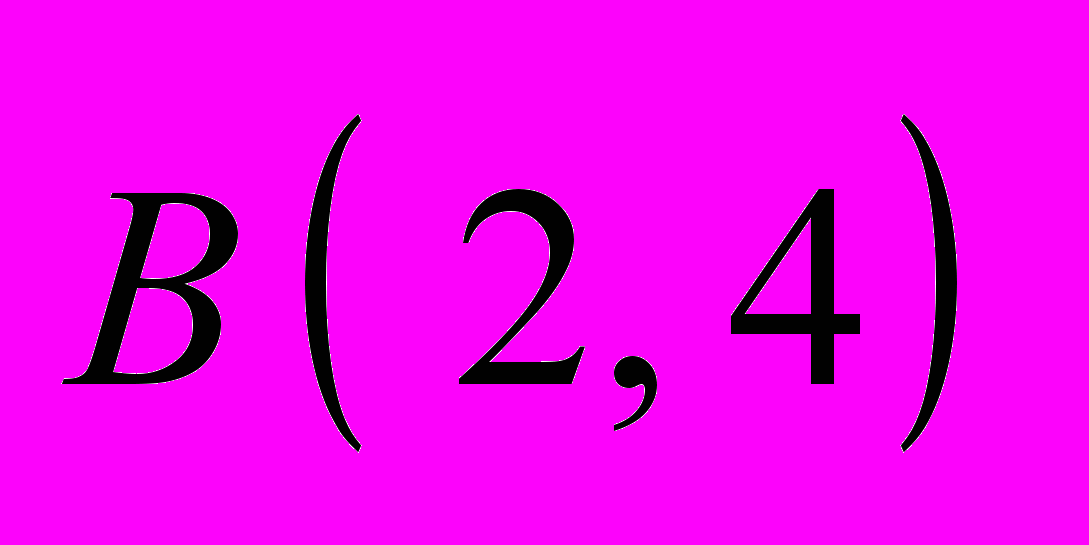. В 1940 г. И.Н. Санов доказал конечность при 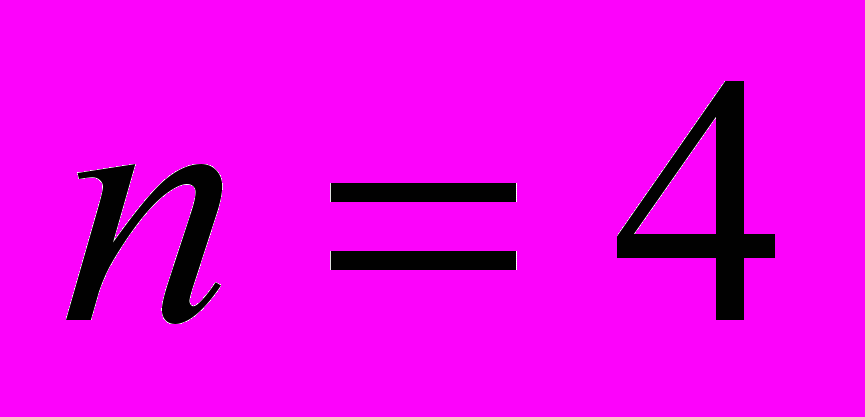для любых 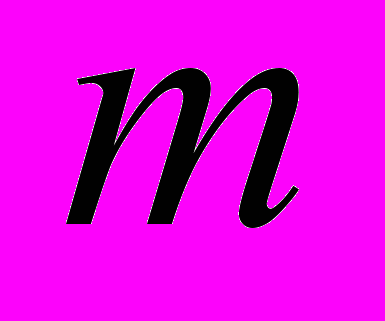. Наконец, в 1958 году Маршалл Холл доказал конечность для 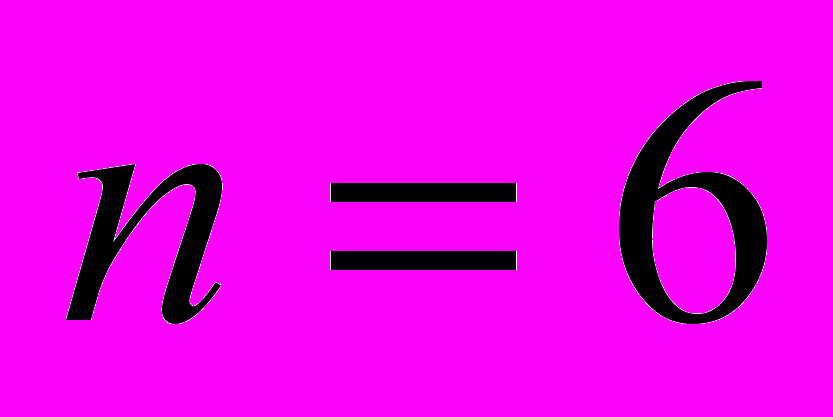и любых .
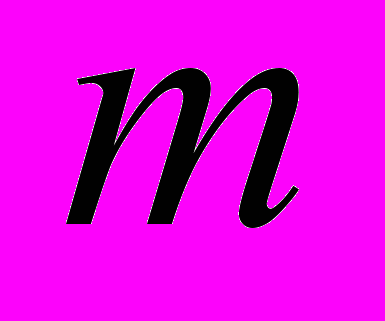До сих пор остаются открытыми интересные вопросы о конечности свободных бернсайдовых групп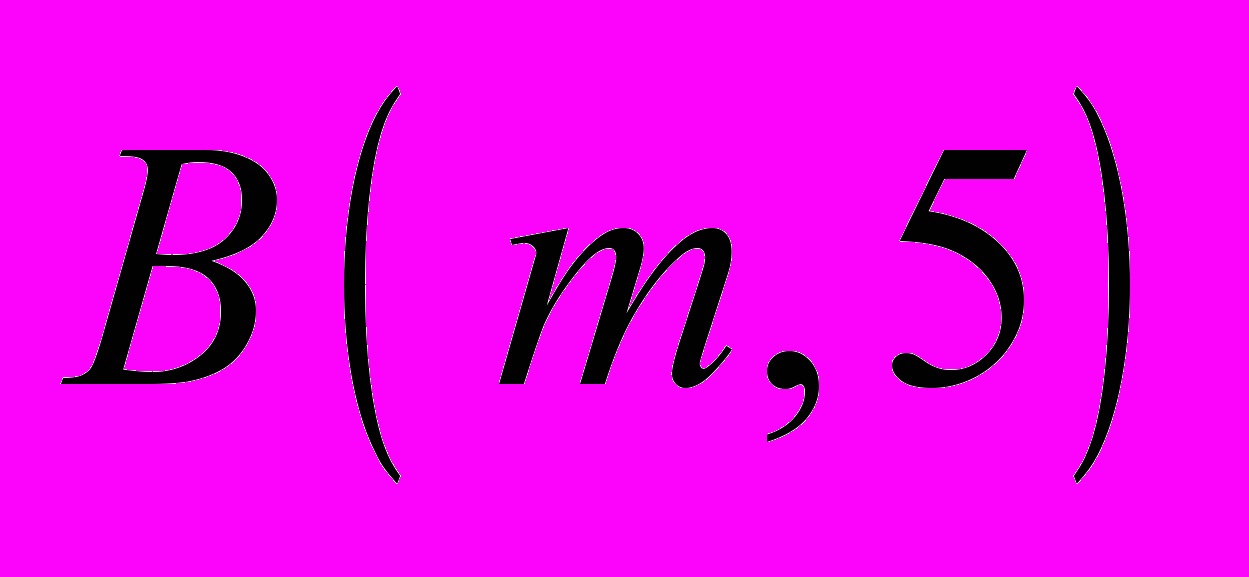 и , даже при 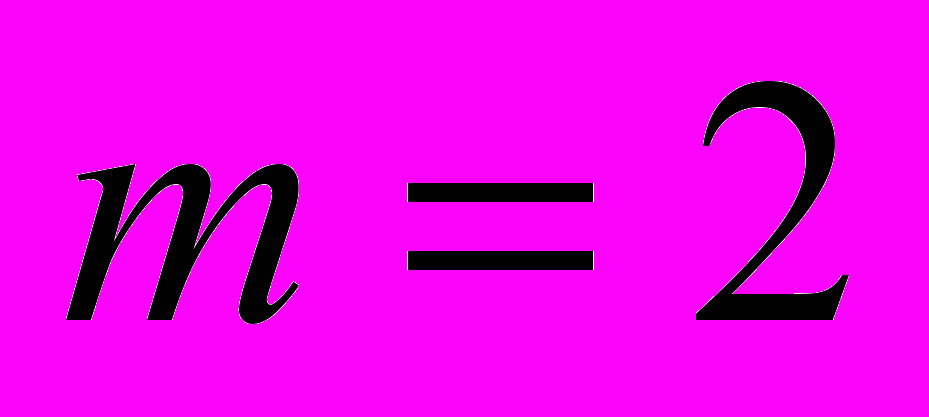. Проблема Бернсайда привлекала внимание выдающихся алгебраистов многих стран в силу естественности и максимальной простоты своей постановки. Возникли различные варианты этой проблемы для разных типов алгебраических систем, а А.Г. Курош ввел в обиход термин «проблема бернсайдовского типа». Однако сама проблема Бернсайда в ее первоначальной формулировке оставалась открытой в течение многих десятилетий. Отрицательный ответ на основной вопрос Бернсайда был впервые получен в совместной работе П.С.Новикова и С.И.Адяна, которая была опубликована в 1968 году в серии совместных статей двух авторов в журнале Известия АН СССР. Cер. матем., Т. 32, № 1, 2, 3. В этих статьях была доказана следующая теорема. Теорема 1. Для любого нечётного периода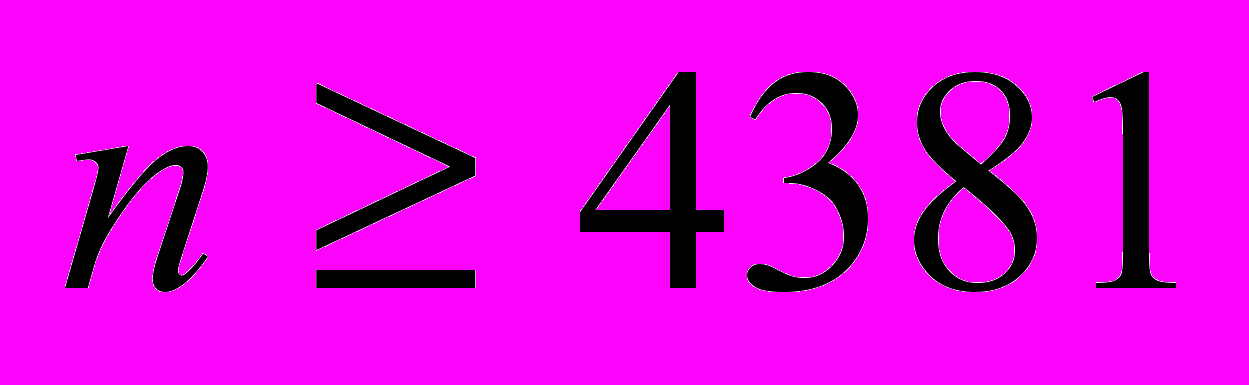 и любого числа порождающих 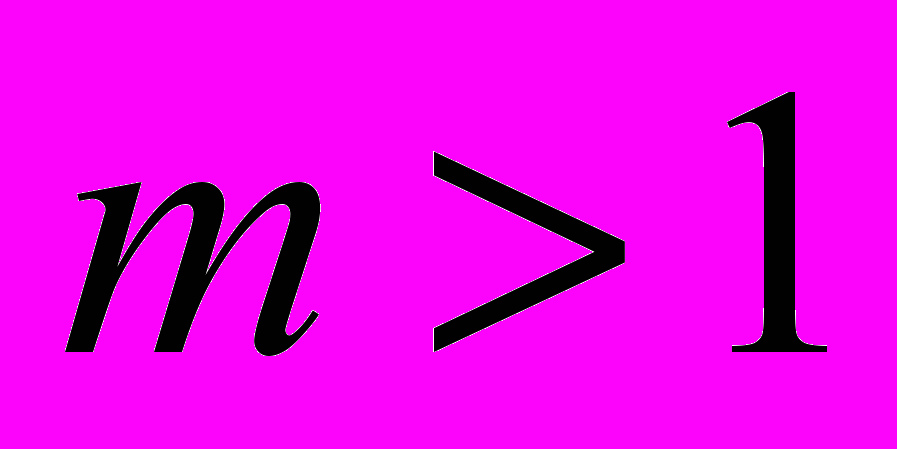свободная периодическая группа 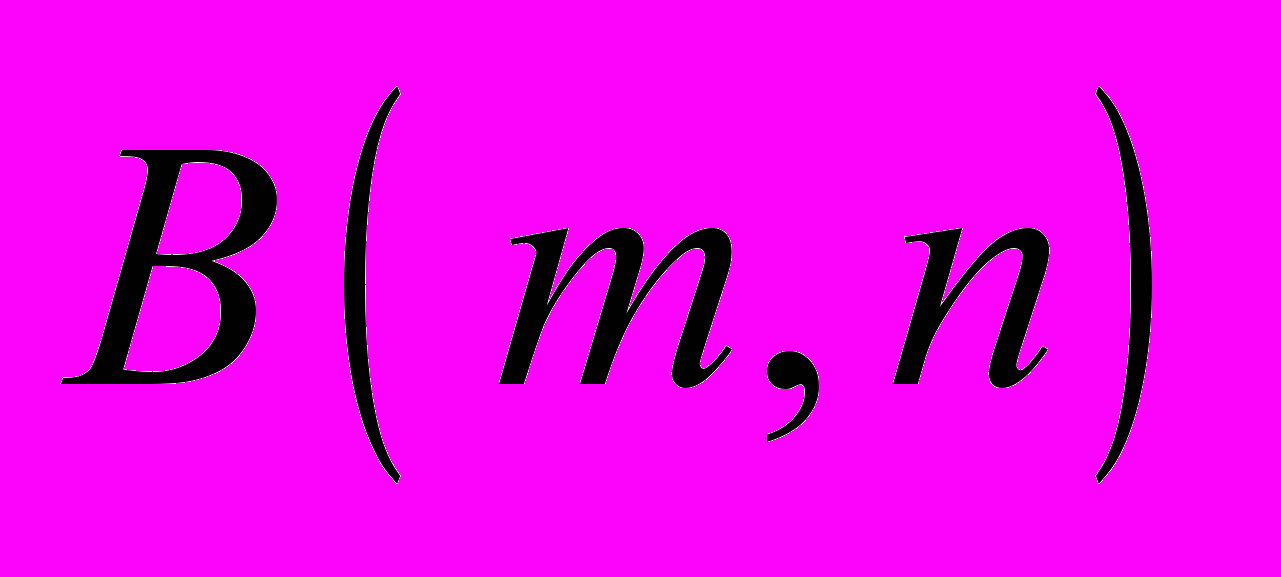бесконечна. Для доказательства этого результата в указанных работах авторами была построена теория преобразований периодических слов, которую можно рассматривать как далеко идущий обобщённый вариант так называемой теории малых сокращений, применимый к системам определяющих соотношений, содержащих достаточно длинные периодические слова. Характерной особенностью теории является то, что в ней большое число взаимосвязанных утверждений доказывается совместной индукцией по натуральному параметру , называемому рангом. В результате индуктивного доказательства получается задание группы 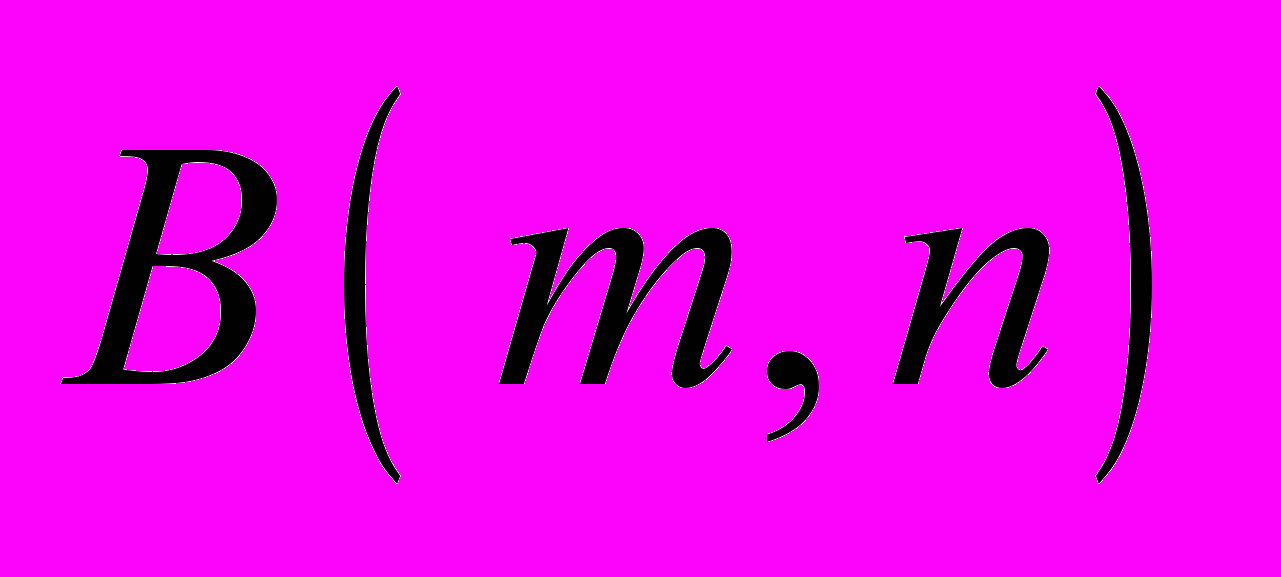с помощью системы определяющих соотношений, классифицированных по рангам. Эта система есть объединение всех соотношений, возникающих в разных рангах. В итоге группа 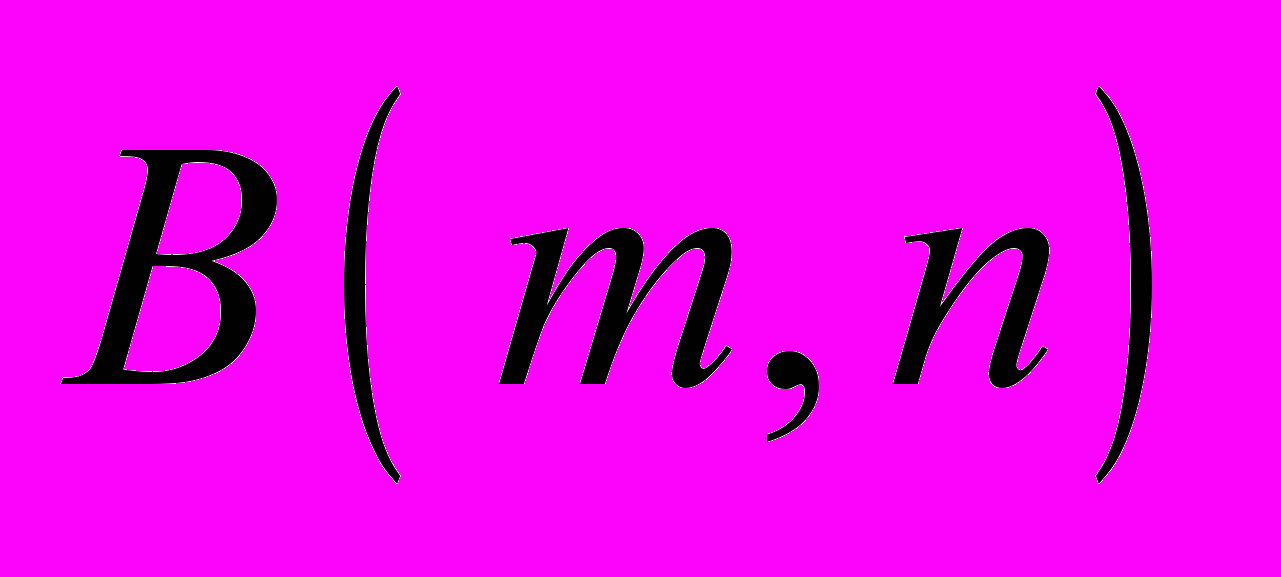получается как предел последовательных аппроксимаций группами 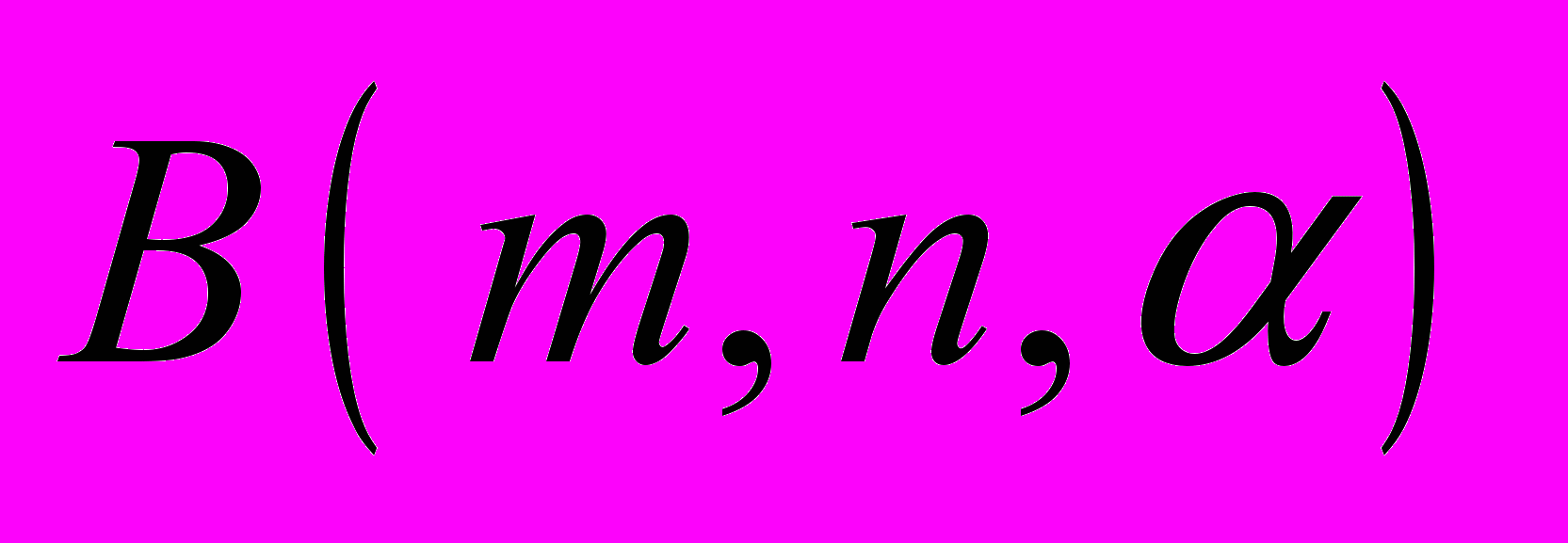, которые задаются соотношениями рангов 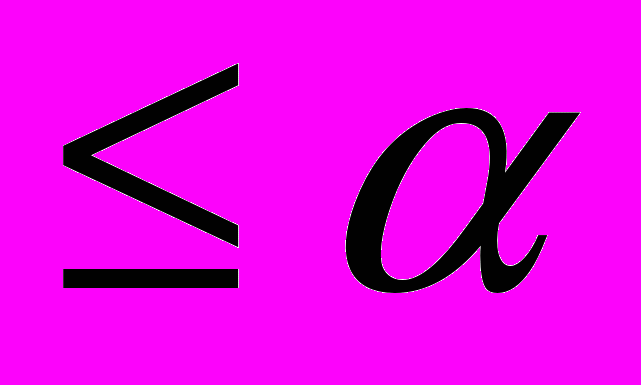. В 1975 году вышла монография автора, в которой было доказано следующее усиление теоремы 1. Теорема 2. Для любого нечётного периода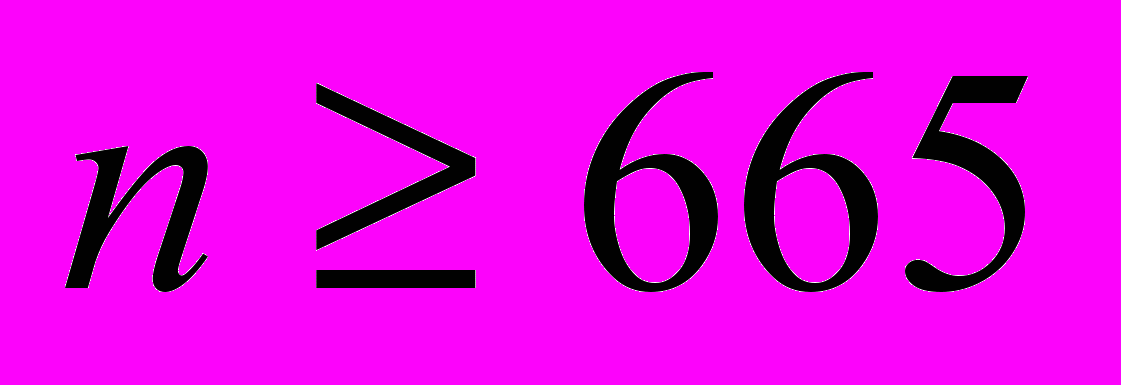 и любого числа порождающих 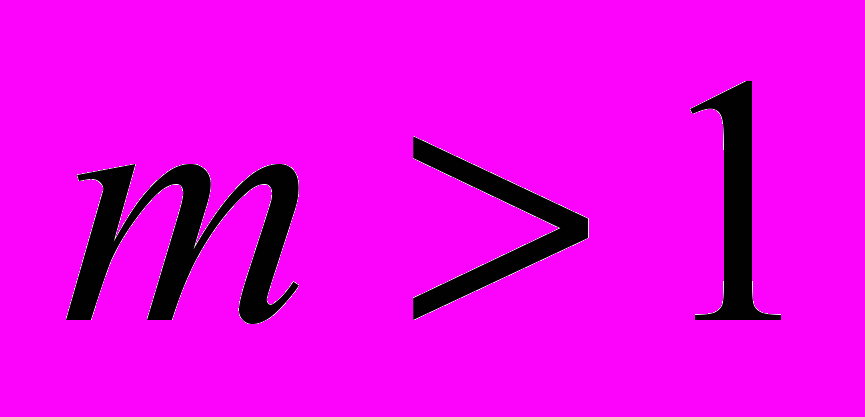свободная периодическая группа 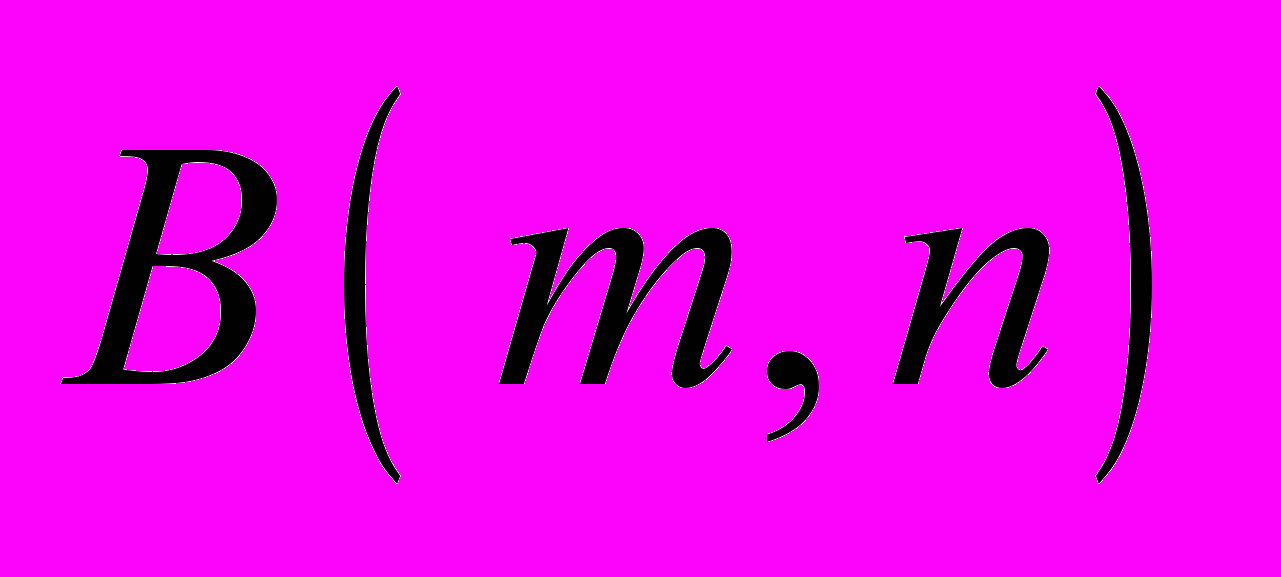бесконечна. Заметим, что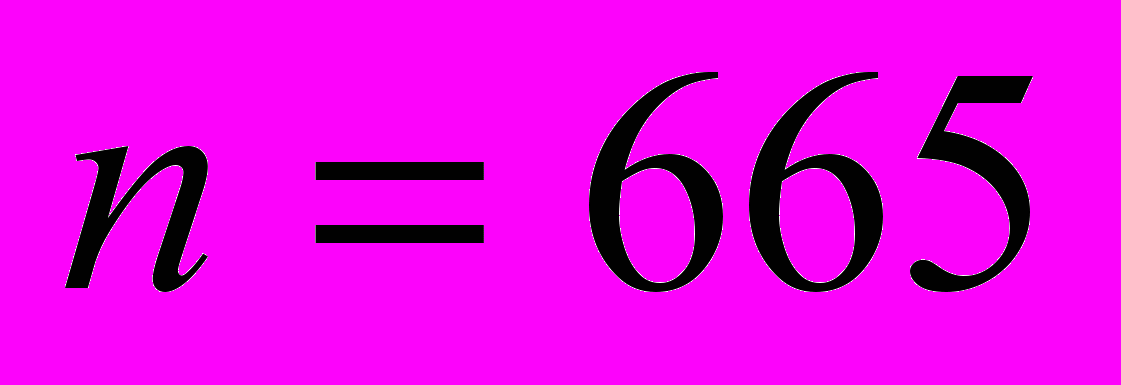 до сих пор остается наименьшим значением периода, для которого удалось доказать бесконечность свободной бернсайдовой группы 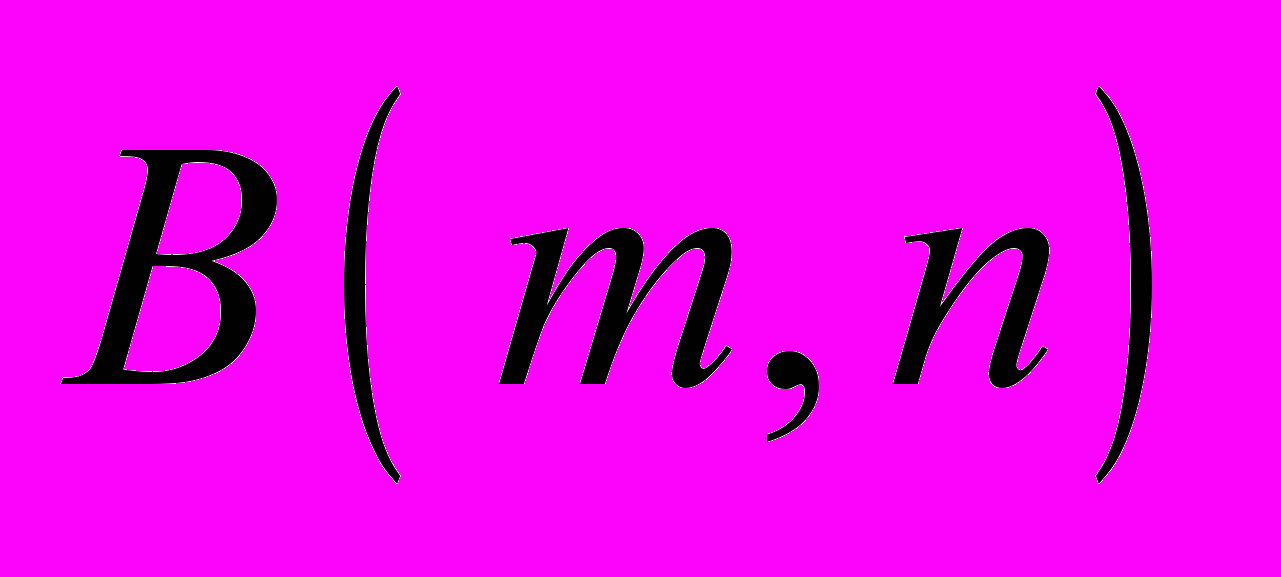. Один из создателей комбинаторной теории групп, выдающийся американский алгебраист В.Магнус в совместной с Б.Чандлером книге 1982г (стр. 57), посвященной истории комбинаторной теории групп, ставит проблему Бернсайда на первое место среди работ по теории абстрактных групп, которые привели к важным достижениям. Авторы отмечают: «Хотя всё ещё остаётся много открытых вопросов, самая трудная часть проблемы Бернсайда была решена: С.И. Адян и П.С. Новиков доказали, что группа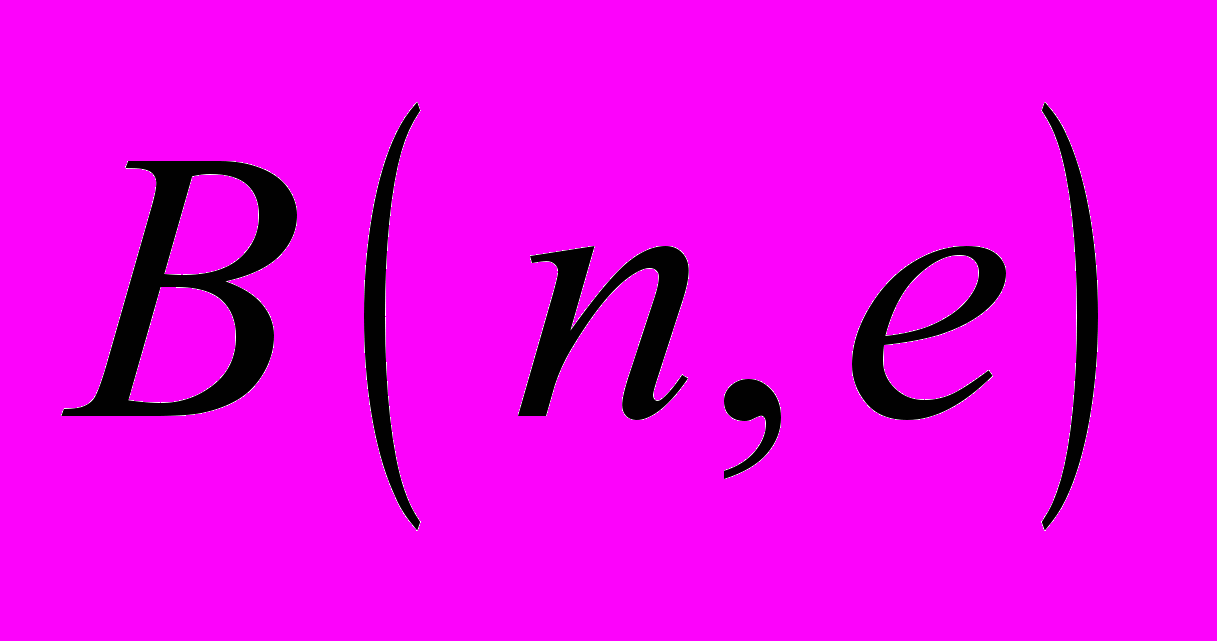 бесконечна для всех 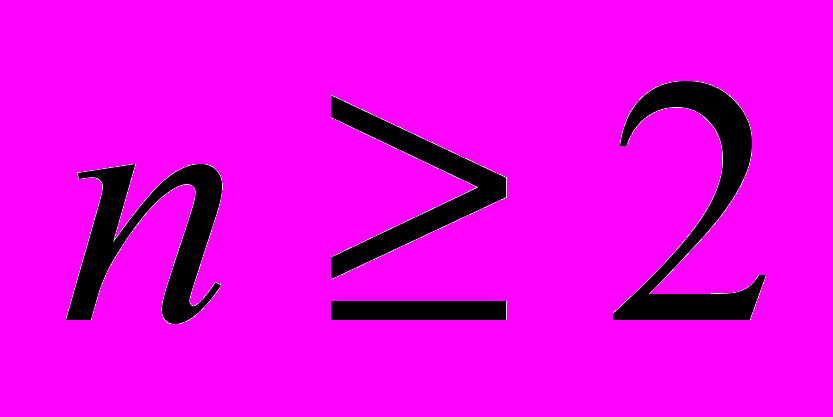и нечётных 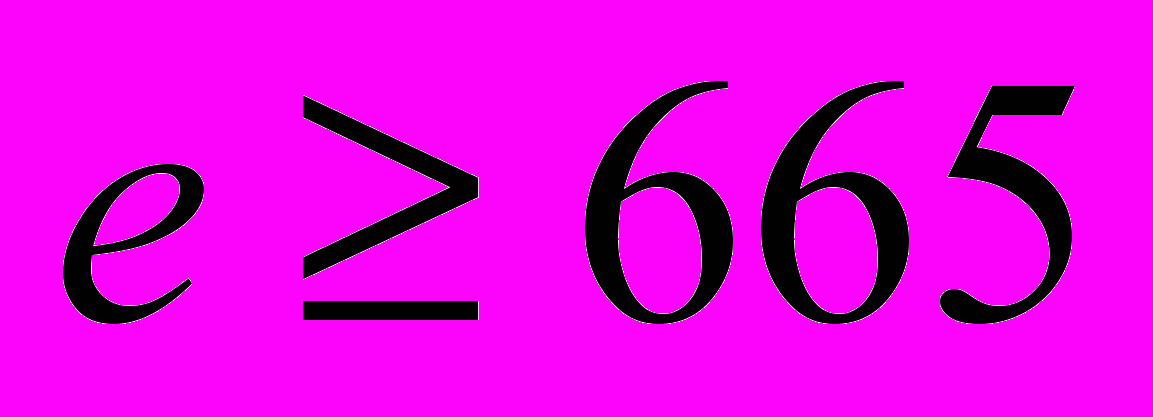». Возвращаясь к этой же теме, на стр. 165 этой книги, авторы добавляют: «Проблема Бернсайда явилась катализатором в исследованиях по теории групп аналогично "Великой теореме Ферма" , в теории чисел. Проблема с весьма простой формулировкой, которая оказывается крайне трудной для решения, таит в себе нечто неотразимо притягательное для разума математика». Здесь Магнус попал в точку. Именно такие ощущения вдохновляли меня, когда я в 60-е годы работал над завершением доказательства нашего результата. Никакие награды не могут сравниться с тем удовлетворением и просто "триумфом", которые ощущает математик, когда при решении достаточно просто формулируемой трудной задачи удается построить цельную теорию, включающую в себя несколько десятков необходимых утверждений, доказываемых сложной совместной индукцией. Необходимость добавления в индуктивное доказательство большинства этих утверждений возникала в процессе работы ввиду того, что без них индуктивное доказательство основных утверждений не удавалось завершить. Можно сказать, что без них создаваемая новая теория преобразований периодических слов оказывалась неполной
1 января 2011 г. исполнилось 80 лет Сергею Ивановичу Адяну. Академик РАН С.И. Адян – выдающийся учёный-математик, специалист в области алгебры, математической логики и теории алгоритмов, автор более 60 научных работ, в том числе 2 монографий. Он является одним из наиболее авторитетных и международно признанных лидеров в этих областях. С.И. Адян является создателем и руководителем одной из ведущих научных школ России по математике. Среди его учеников 3 члена-корреспондента РАН, 8 докторов и более 20 кандидатов наук. С.И. Адян ведёт многогранную научно-организационную работу. Он многие годы был членом Экспертного совета ВАК, Экспертного совета РФФИ по математике, Научной комиссии Отделения математики АН по школьному образованию (в этой комиссии он работает и по настоящее время), председателем Совета ВАК по присуждению докторских степеней при Математическом институте им. В.А. Стеклова РАН. За выдающиеся заслуги в области математики С.И. Адян удостоен ряда престижных премий и почётных званий. С.И. Адян – лауреат Государственной премии РФ, Премии Московского математического общества, Премии им. П.Л. Чебышёва Ан СССР и Международной премии им. Александра фон Гумбольдта (Германия), награждён медалью «За трудовую доблесть» (1975). С 1991 г. С.И. Адян – член-корреспондент Российской Академии Наук (РАН), а с 2000 г. – действительный член (академик) Российской Академии Наук (РАН). С 1973 г. С.И. Адян – заведующий отделом математической логики Математического института им. В.А. Стеклова РАН, с 1965 г. он – профессор кафедры математической логики механико-математического факультета МГУ им. М.В. Ломоносова.
Руководители семинара: –Кудрявцев Валерий Борисович, академик, профессор, заведующий кафедрой МаТИС мехмата МГУ (председатель семинара), –Алёшин Станислав Владимирович, профессор кафедры МаТИС мехмата МГУ, –Часовских Анатолий Александрович, директор СУНЦ МГУ, доцент кафедры МаТИС мехмата МГУ, –Сыркин Геннадий Иосифович, старший преподаватель кафедры математики СУНЦ МГУ (ученый секретарь семинара), Семинар работает в СУНЦ МГУ по четвергам, с 17 час. до 18 час. 30 мин. в ауд. 39 (3-й этаж), либо, в особых случаях (о чём объявляется дополнительно) в Актовом зале СУНЦ МГУ (4-й этаж), возможно, в другое время.