Человек может стать умным тремя путями: путём подражания – это самый лёгкий путь, путём опыта – это самый трудный путь, и путём размышления – это самый благородный путь

Вид материала

Документы

Содержание Математическая лотерея Игра-решение задач, 9 класс Математический турнир 4 этап. Конкурс командиров. 5 этап. Заключительный. Подведение итогов.

Подобный материал:

• "Курс выживания для подростков", 1131.55kb.
• «Расскажите детям сказку!», 24.15kb.
• Тверское библиотечное общество, 19.4kb.
• И. А. Борскивер Рынок и цена категории, обусловленные товарным производством. Причем, 82.6kb.
• Бердяев Н. Спасение и творчество. Два понимания христианства, 322.74kb.
• Конспект урока по теме урока: «Африка. Географическое положение, история исследования», 132.08kb.
• Поморье 2 Историко-культурный потенциал Кемского района, 143.66kb.
• Тема пути в лирике Блока, 40.4kb.
•  Уреаплазмоз, или микоплазмоз это заболевание, передающееся половым путем, и вызывающееся, 58.73kb.
• Норман Уокер Лечение соками, 1243.87kb.

Математическая лотерея

Игра-решение задач, 9 класс

Игроки вытягивают билеты с задачами.

Задачи

№ 1. Река разделяет город на 4 части, соединённые между собой шестью мостами. Один турист решил обойти все мосты, побывав на каждом только один раз. Как это можно сделать, если не требовать обязательного возвращения в тот же район города, из которого начался обход?







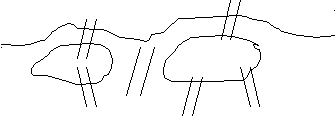
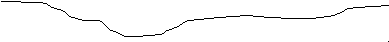
№2.Четвёртые части квадрата и правильного треугольника отрезаны, как показано на рисунке. Каждую из оставшихся фигур разделите на 4 равные части.





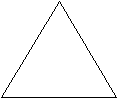
а) б)


№3.Назовите слова, имеющие ось симметрии.


№ 4. Сколько всевозможных фигур можно сложить из 5 квадратиков? Нарисуйте на клетчатой бумаге.


№5. Четыре страны имеют форму треугольников. Как расположены страны одна относительно другой, если у каждой из них есть общие границы с тремя другими?


№.6. Деревянный куб покрасили снаружи краской, каждое его ребро разделили на 5 равных частей, после чего куб распилили так, что получились маленькие кубики., у которых ребро в 5 раз меньше, чем у исходного куба. Сколько получилось маленьких кубиков? У скольких кубиков окрашены три грани? Две грани? Только одна грань? Сколько осталось неокрашенных кубиков?


№7.Разделите правильный треугольник на 3 одинаковые трапеции.


№8. С помощью чертёжного угольника найдите центр данной окружности.


№9.Во сколько раз увеличится объём куба, если его ребро увеличить в 4 раза?


№10. Найдите выход из лабиринта. (Рисунок в книге, откопировать)


Литература. Наглядная геометрия. 5-6 кл. : пособие для общеобразовательных учреждений / И. Ф. Шарыгин, Л. Н. Ерганжиева. – 7-е изд., стереотип. –М. : Дрофа, 2005.

Математический турнир

3-4 кл


Соревнование экипажей по 2 человека.

1 этап – отборочный. Всем детям задаются вопросы; кто правильно отвечает, тот выходит – это командир 1 экипажа. Следующий правильно ответивший – командир 2 экипажа и т. д. До 4 экипажей. Ответивший на 5 вопрос-это член 1 экипажа и т. д. Всего вопросов 8.


Вопросы.

1.Как называется многоугольник, у которого 3 угла?

2.Назовите наибольшее однозначное число.

3. Назовите все числа, на которые делится число 4.

4.Назовите наименьшее двузначное число.

5.Назовите число, состоящее из двух десятков и пяти единиц.

6.Чем отрезок отличается от прямой?

7. Сколько вершин у квадрата?

8.Сколько сантиметров в 1 дециметре?

9. Сколько граммов в 1 килограмме?

10. Что называют периметром прямоугольника?


2 этап. Соревнование экипажей.


Задание 1. Задачи на смекалку.

1. Как число 10 записать пятью одинаковыми цифрами, соединив их знаками действий? (2+2+2+2+2)
   
2. Как число 1 записать тремя различными цифрами, соединив их знаками действий? (По – разному. Например: 0+2-1 и другие)
   
3. Мне навстречу бежали поросята: один впереди двух, один между двух и один позади двух. Сколько поросят всего бежало?(3)
   
4. Кто становится выше, когда садится? (Собака)
   
5. Шестиметровый брусок разрезали на равные части, сделав при этом 5 надрезов. Какой длины получилась каждая часть?(1 м)
   
6. Три мальчика- Миша, Серёжа и Гриша живут на разных этажах-5,7,8. Миша живёт не ниже Гриши, а Серёжа не выше Гриши. Кто где живёт? (Серёжа- на 5, Гриша – на 7, Миша – на 8)
   

Задание 2. Геометрические задания.

1. Нарисуй конверт (показать на доске, какой), не отрывая кончика карандаша от бумаги и не проводя дважды один и тот же отрезок.
   

2. Как, не отрывая карандаша от бумаги, разделить фигуру на шесть равных треугольников? Проводить линии по сторонам квадратов нельзя.
   

3. Раздели равносторонний треугольник на 4 равных треугольника.
   

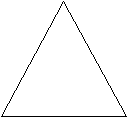
4. Из 5 одинаковых квадратиков составь всевозможные фигуры. Квадратики могут соприкасаться только сторонами. Сколько должно получиться фигур?
   

Пример:




Ответ: 12 фигур

4 этап. Конкурс командиров.


1) Сколько листов между пятым и двенадцатым листами альбома? (6)

2)У брата и сестры было вместе 8 конфет. Когда сестра отдала брату 3 конфеты, конфет у них сталао поровну. Сколько конфет было первоначально у сестры и сколько у брата? ( У брата –1, у сестры –7)


3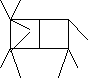)Из шестнадцати спичек выложена корова. Переложи две спички так, чтобы корова смотрела назад.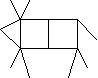




4)Во дворе гуляют куры и поросята. У них всего 5 голов и 14 ног. Сколько кур и сколько поросят? ( 2 поросёнка и 3 курицы).


5 этап. Заключительный.

Вспомните пословицы и поговорки, содержащие числа.

(У семи нянек дитя без глазу. Семеро одного не ждут. Один в поле не воин. Ум хорошо, а два лучше. И другие.)


Подведение итогов.


Литература. С. Акимова. Занимательная математика.. - Санкт-Петербург, «Тригон», 1997