Классификация вещественных функций вещественного аргумента
| Вид материала | Документы |
- Доклад Абсолютная величина, 29.68kb.
- Абрамкина Надежда Юрьевна Студентка 23 группы числовые последовательности реферат, 183.55kb.
- Вопросы к гос экзамену, 90.73kb.
- Краткое описание программы Цель работы состоит в создание двух программ. Первая будет, 46.29kb.
- Курсовая работа по информатике, 20.84kb.
- Модем. Классификация модемов. Устройство модема, 975.51kb.
- Программа междисциплинарного государственного экзамена по специальности 090102 Компьютерная, 116.53kb.
- I. Понятие и классификация функций государства, 287.8kb.
- Превращение энергии гравитационного колебания “элементарных” вещественных частиц, 86.72kb.
- Аннотация программ повышения квалификации Дистанционная форма обучения, 91.62kb.
Классификация вещественных функций
вещественного аргумента
1) Вещественные функции вещественного аргумента делят на два класса: элементарные и не элементарные.
ОПРЕДЕЛЕНИЕ. Элементарной функцией называется функция, которая может быть задана одной формулой
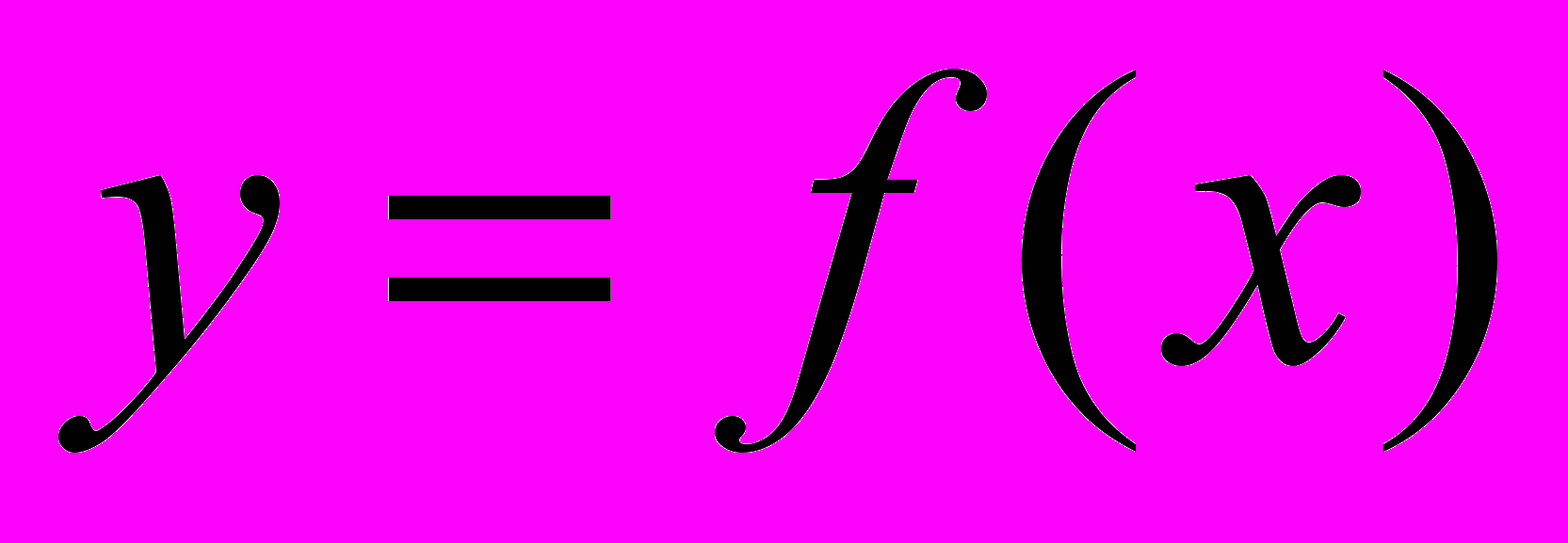 , где
, где 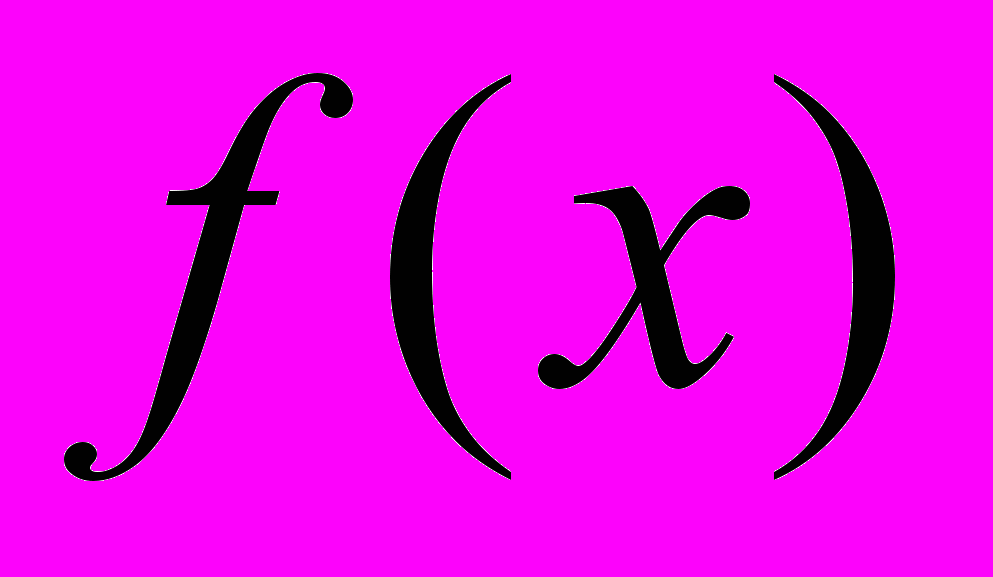 – выражение, составленное из основных элементарных функций и действительных чисел с помощью конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
– выражение, составленное из основных элементарных функций и действительных чисел с помощью конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.Основными элементарными функциями называются следующие функции:
- степенная функция
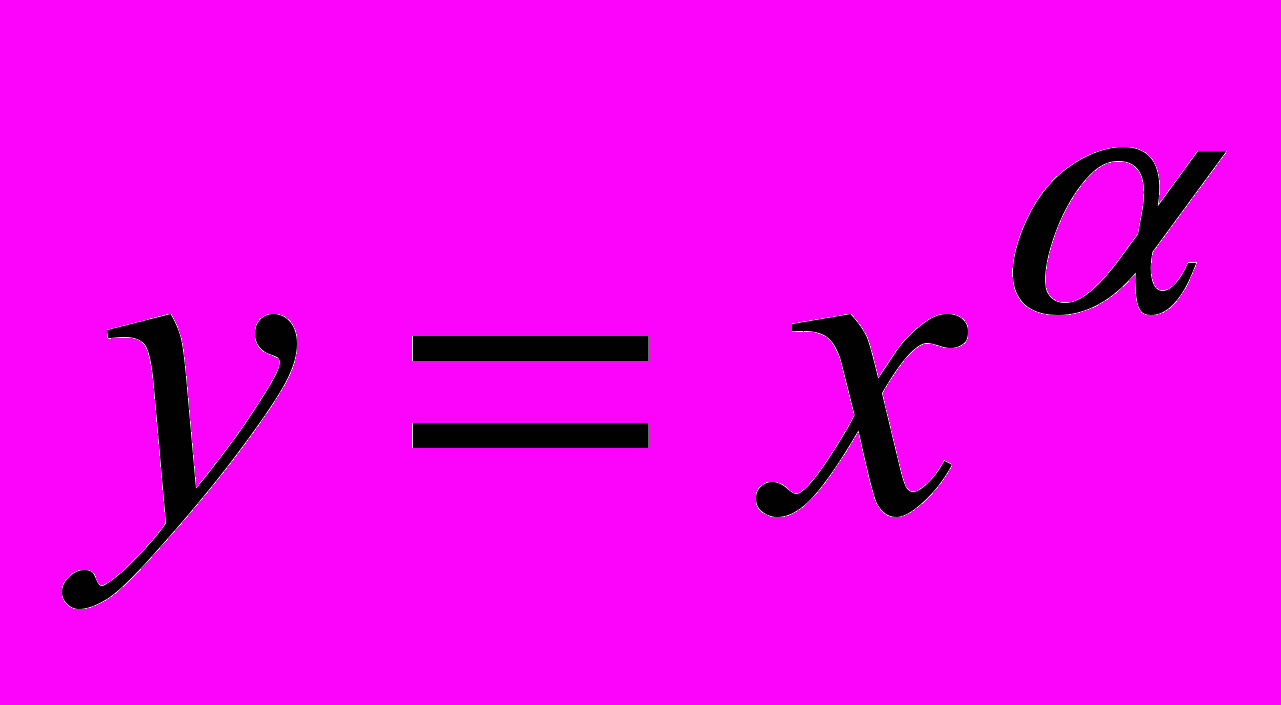 , где
, где 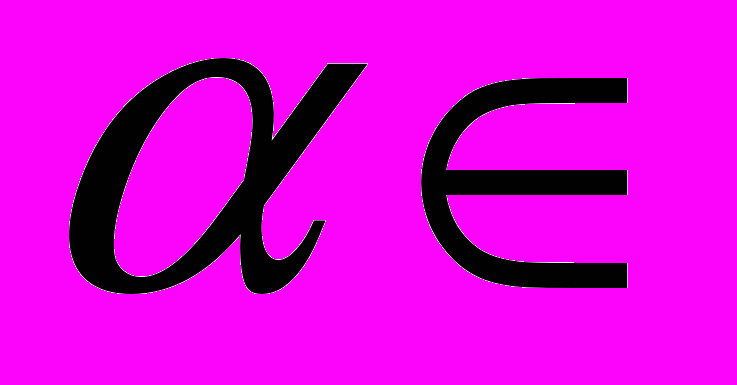 ℝ;
ℝ;
- показательная функция
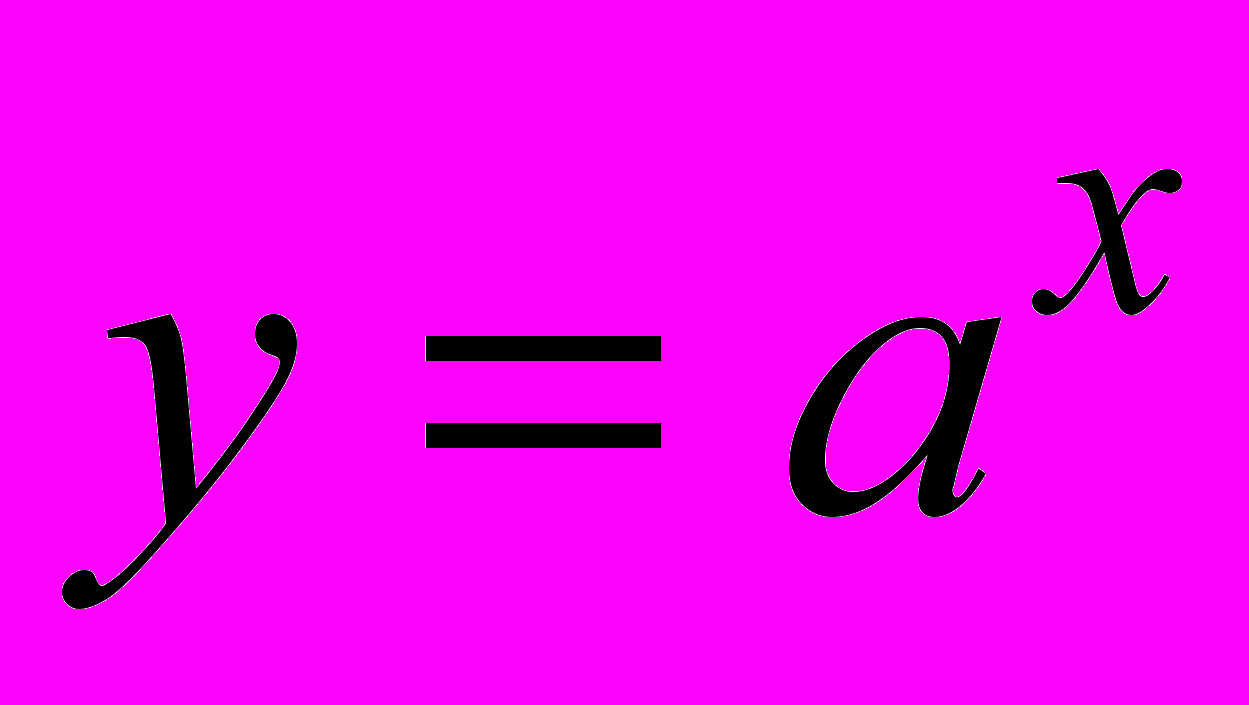 , где
, где 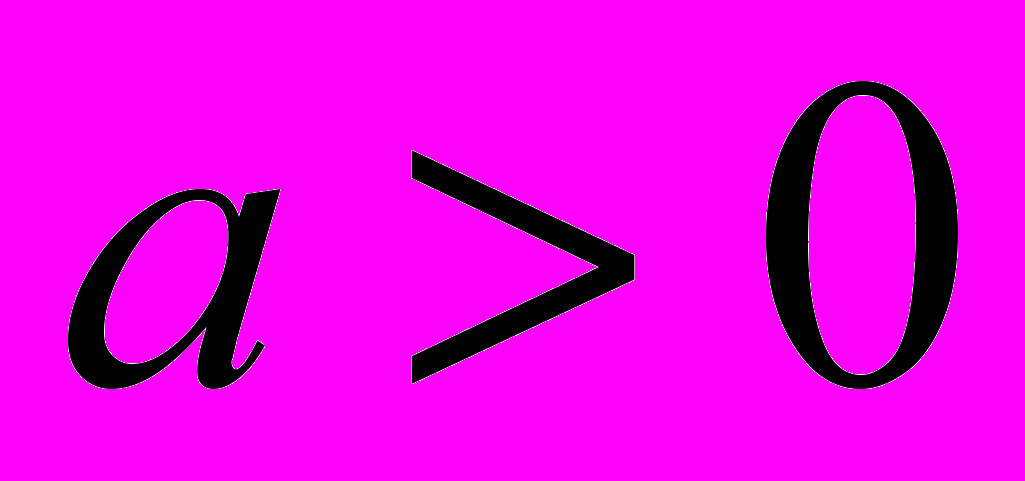 и
и 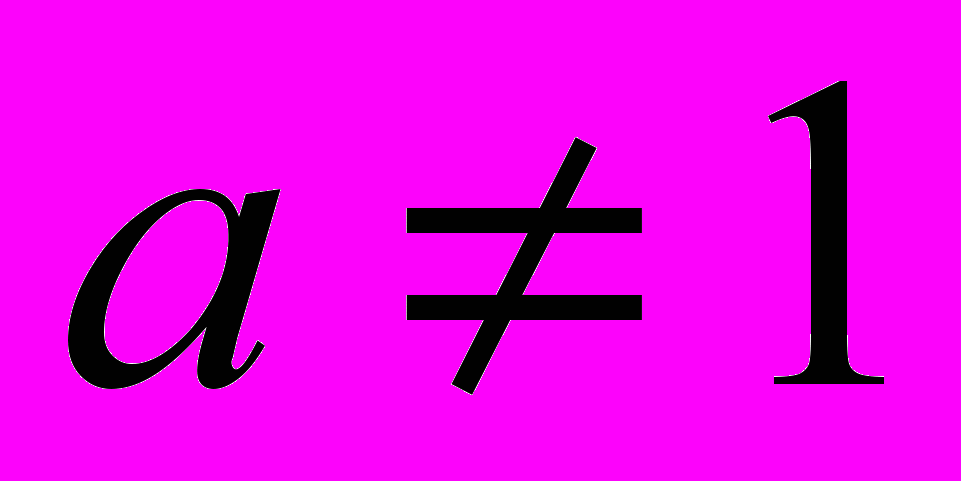 ;
;
- логарифмическая функция
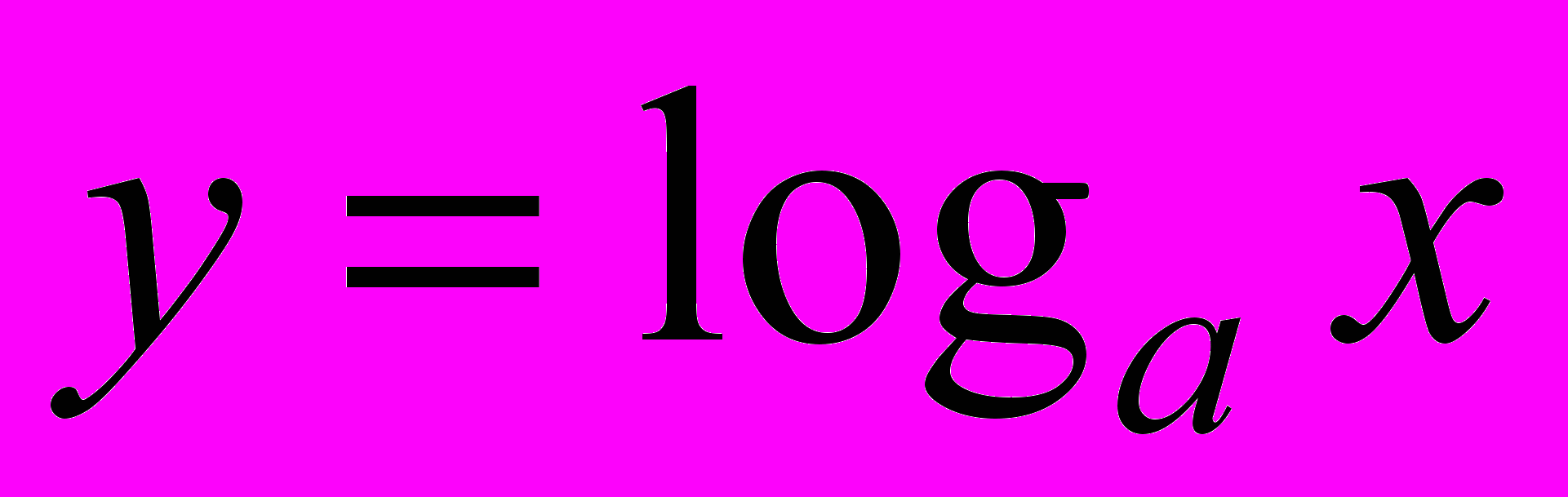 , где
, где 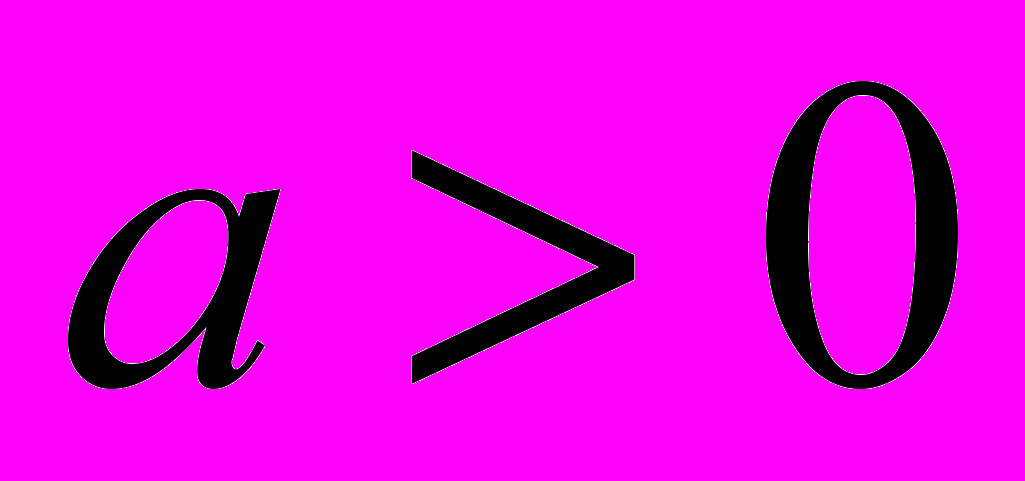 и
и 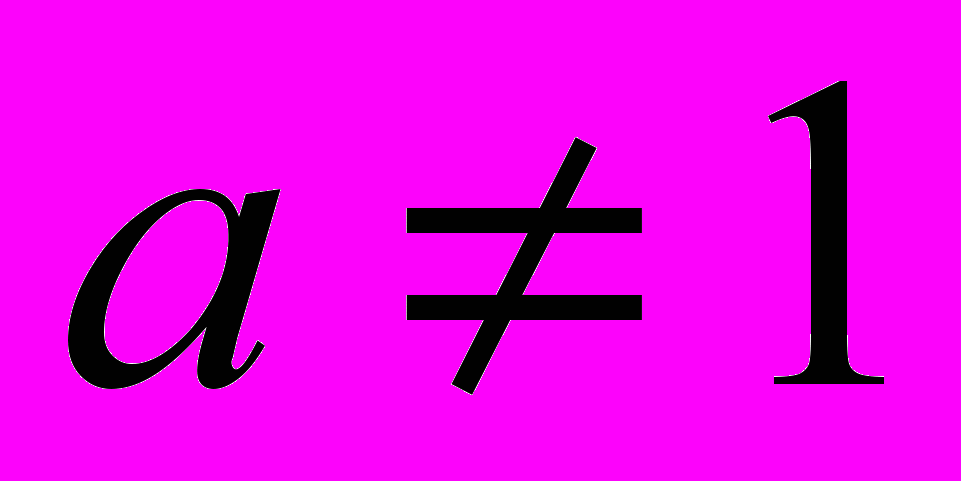 ;
;
- тригонометрические функции
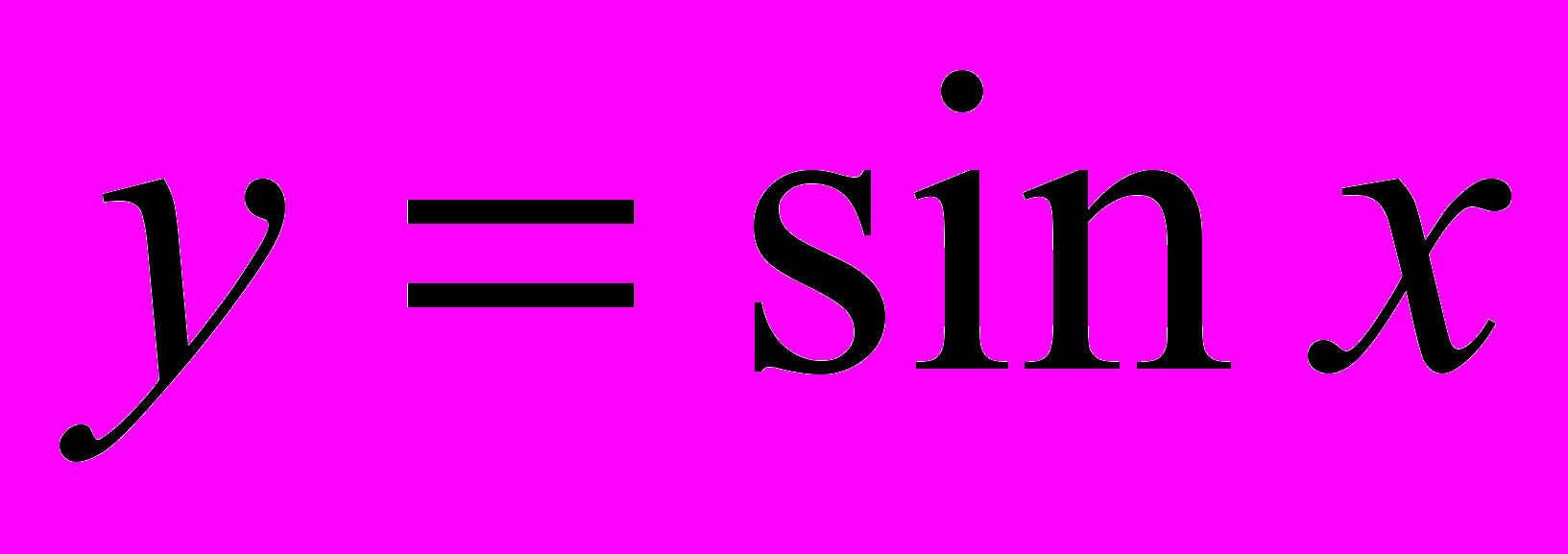 ,
, 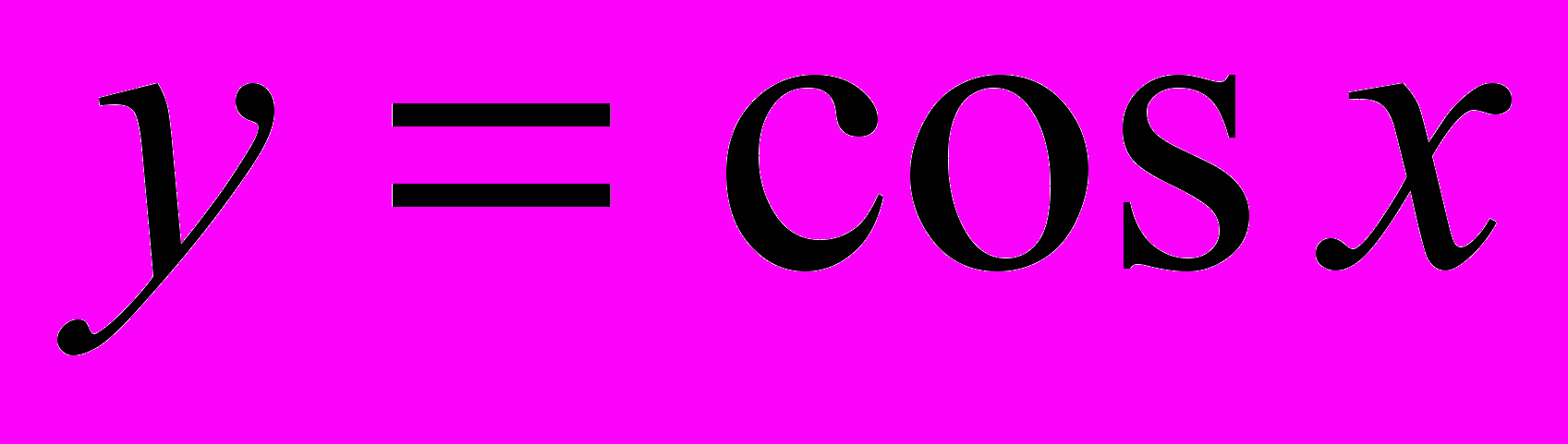 ,
, 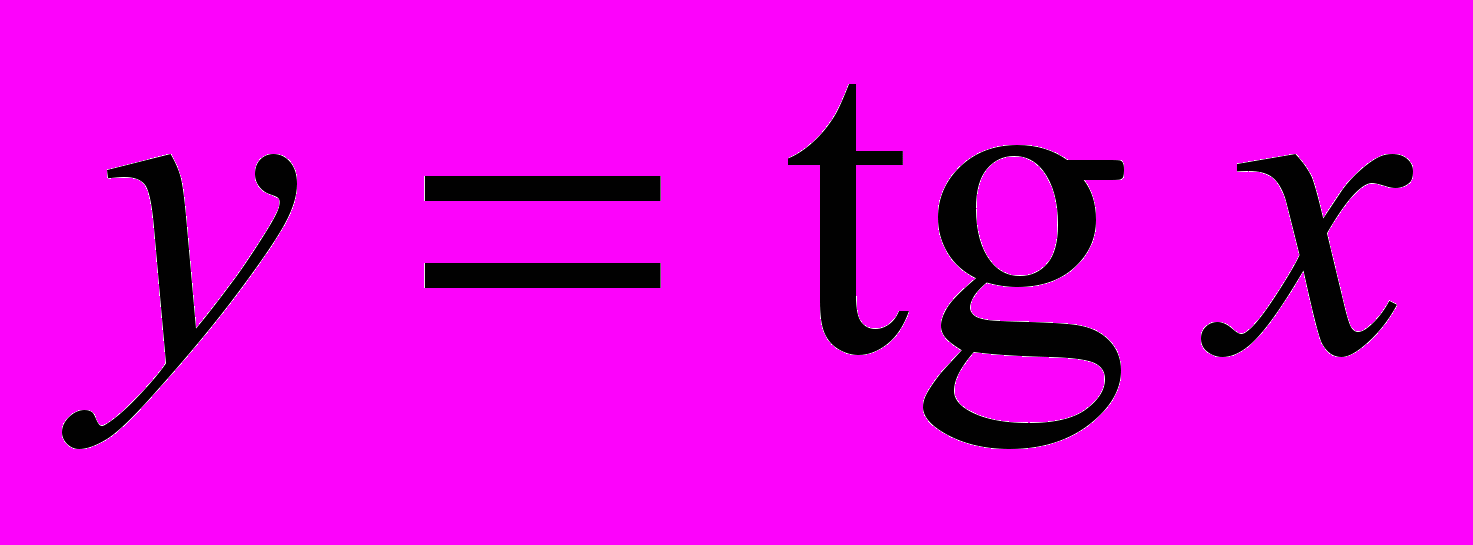 ,
, 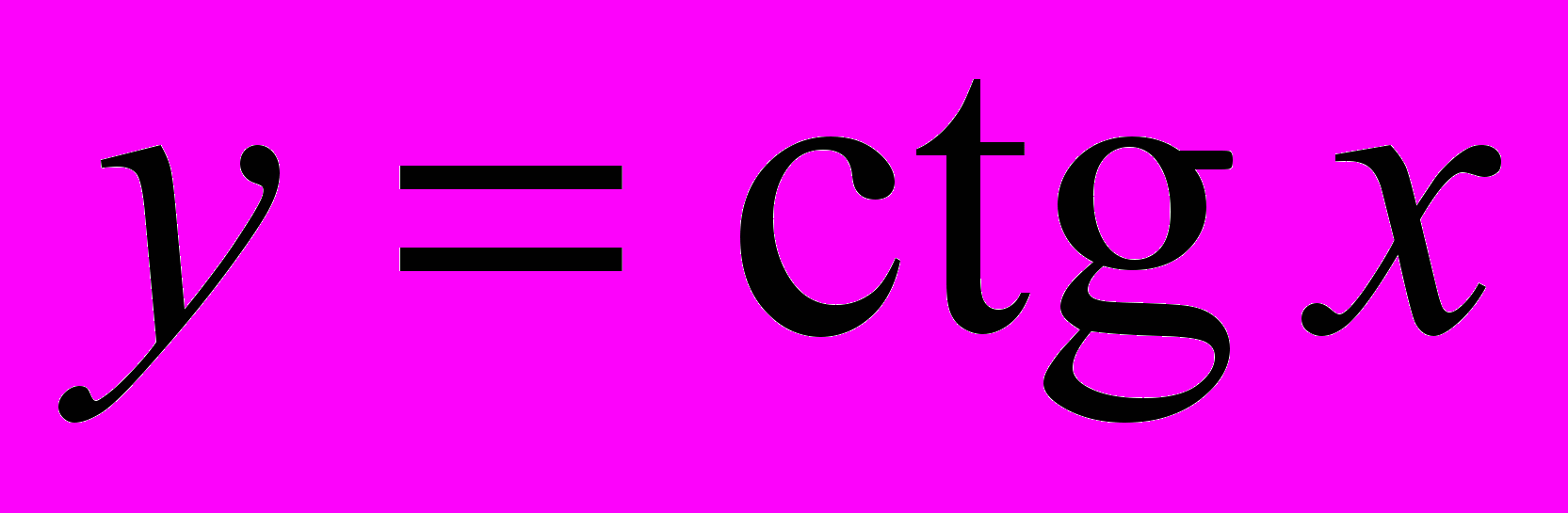 ;
;
- обратные тригонометрические функции
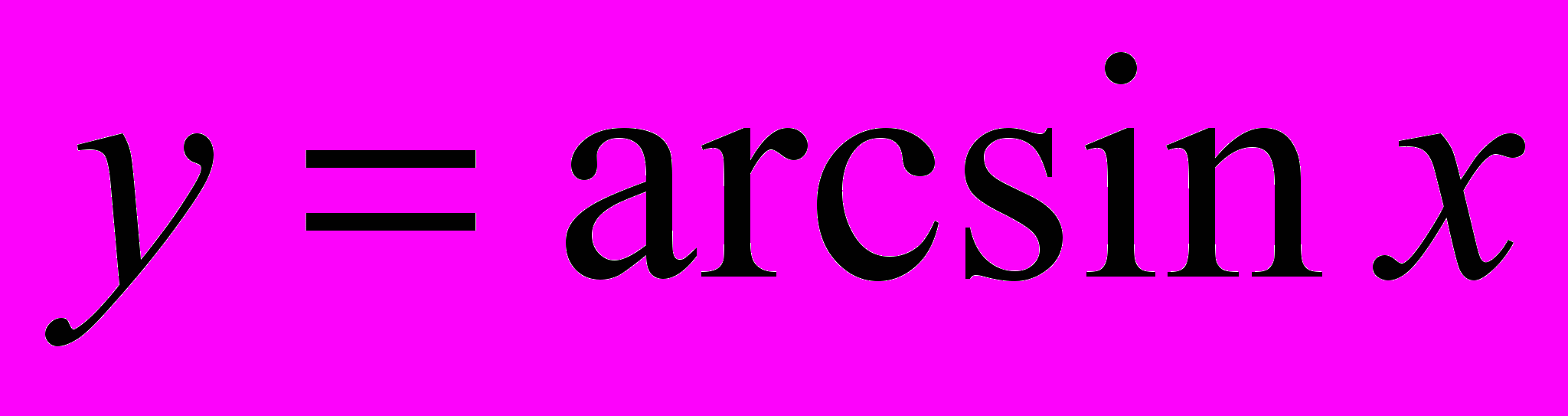 ,
, 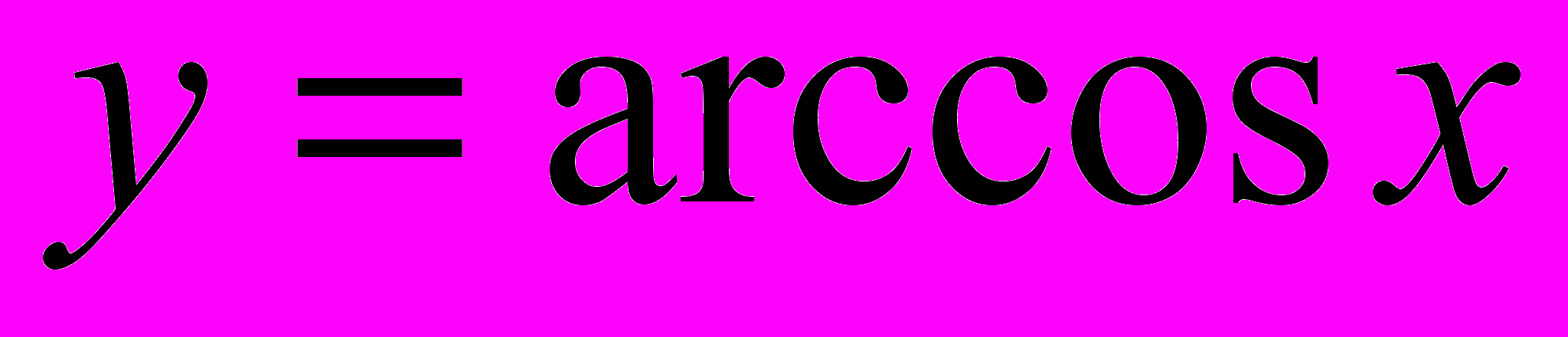 ,
, 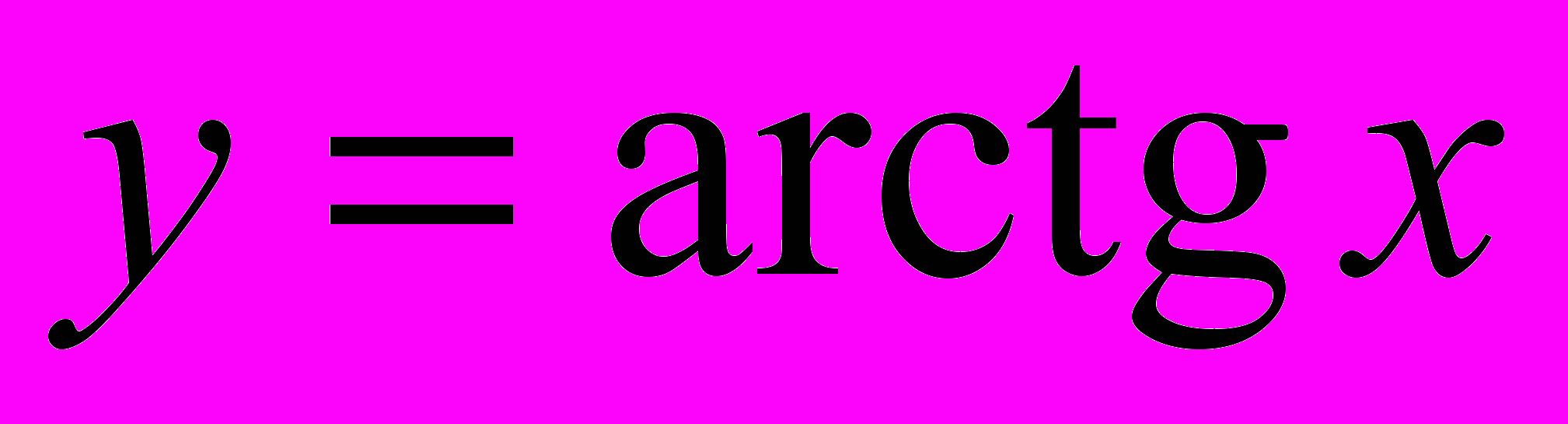 ,
, 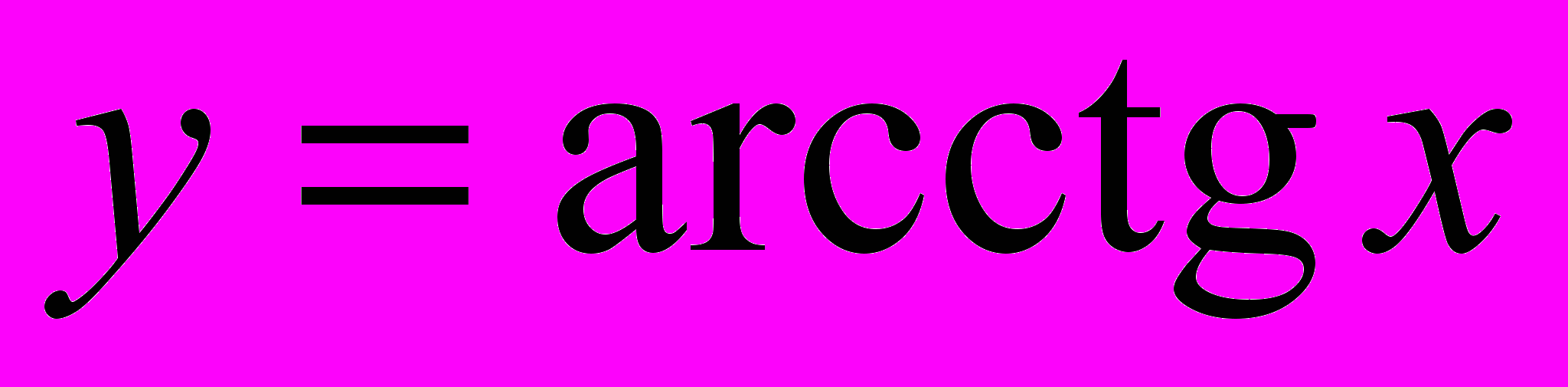 .
.
2) Элементарные функции делят на два класса: алгебраические и трансцендентные.
ОПРЕДЕЛЕНИЕ. Функция называется алгебраической, если ее значение можно получить из аргумента и действительных чисел с помощью конечного числа алгебраических операций (т.е. сложения, вычитания, умножения, деления) и возведения в степень с рациональным показателем. Функция, не являющаяся алгебраической, называется трансцендентной.
3) Алгебраические функции делят на рациональные и иррациональные.
ОПРЕДЕЛЕНИЕ. Алгебраическая функция называется рациональной, если среди действий, которые производятся над независимой переменной, отсутствует извлечение корня. Функция не являющаяся рациональной называется иррациональной.
Рациональные функции бывают двух видов:
- целые рациональные (многочлены)
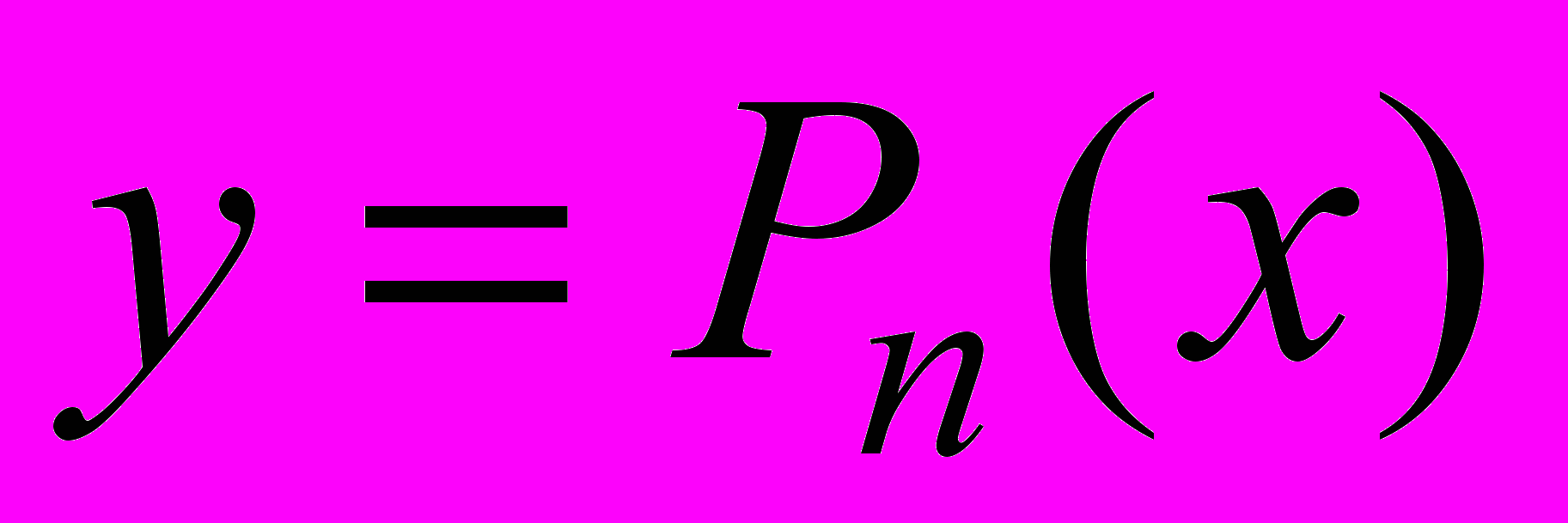 ,
,
где
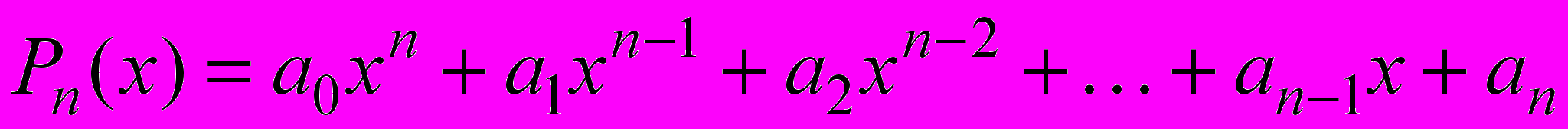 ;
;- дробные рациональные (рациональные дроби)
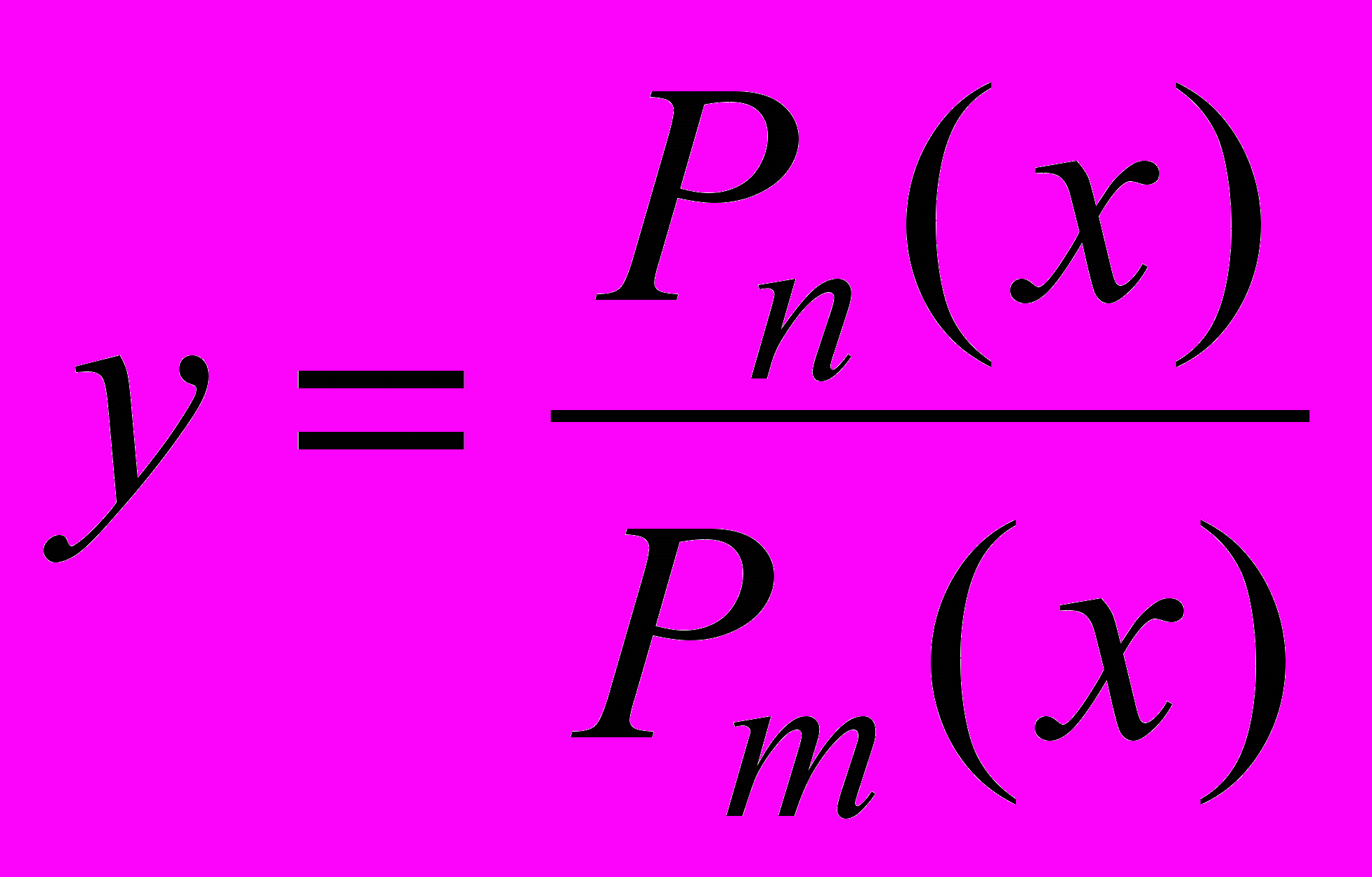 .
.
Основные характеристики поведения функции
Изучить функцию – это значит охарактеризовать ход ее изменения (как говорят «ее поведение») при изменении независимой переменной.
Для характеристики поведения функции используют следующие ее свойства.
1) Четность функции.
ОПРЕДЕЛЕНИЕ. Функция
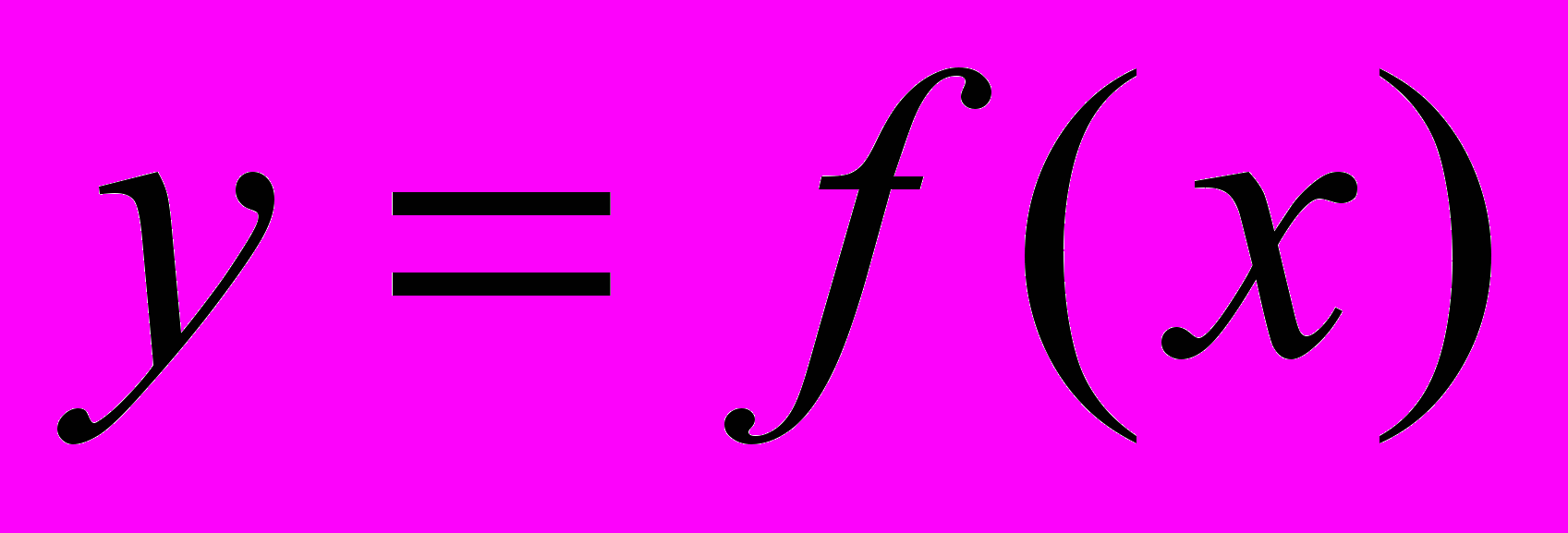 называется четной, если выполняются два условия:
называется четной, если выполняются два условия:а) область определения функции симметрична относительно начала координат;
б) для любого
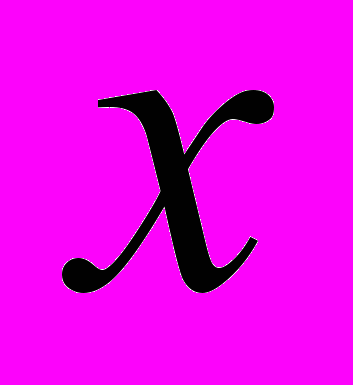 из области определения справедливо равенство
из области определения справедливо равенство 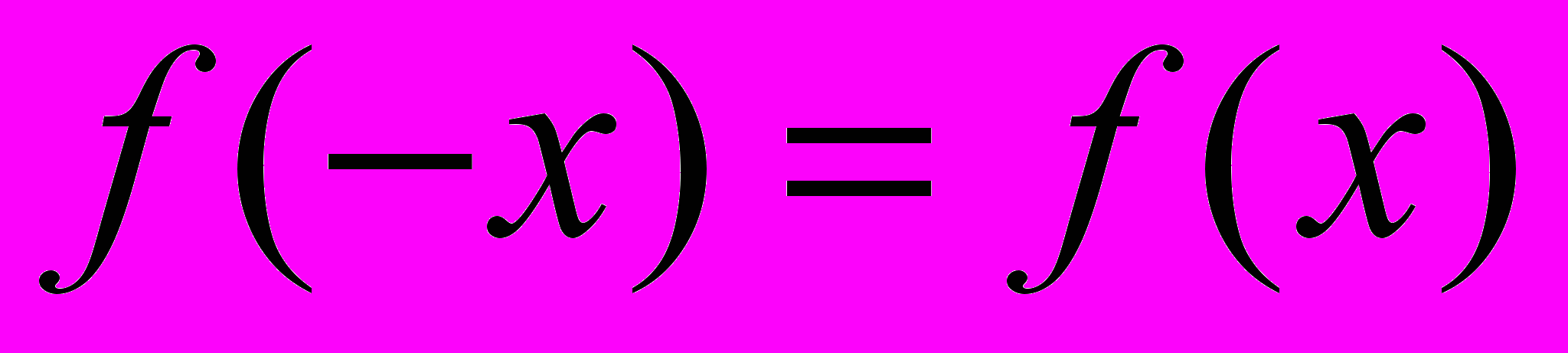 .
.Функция
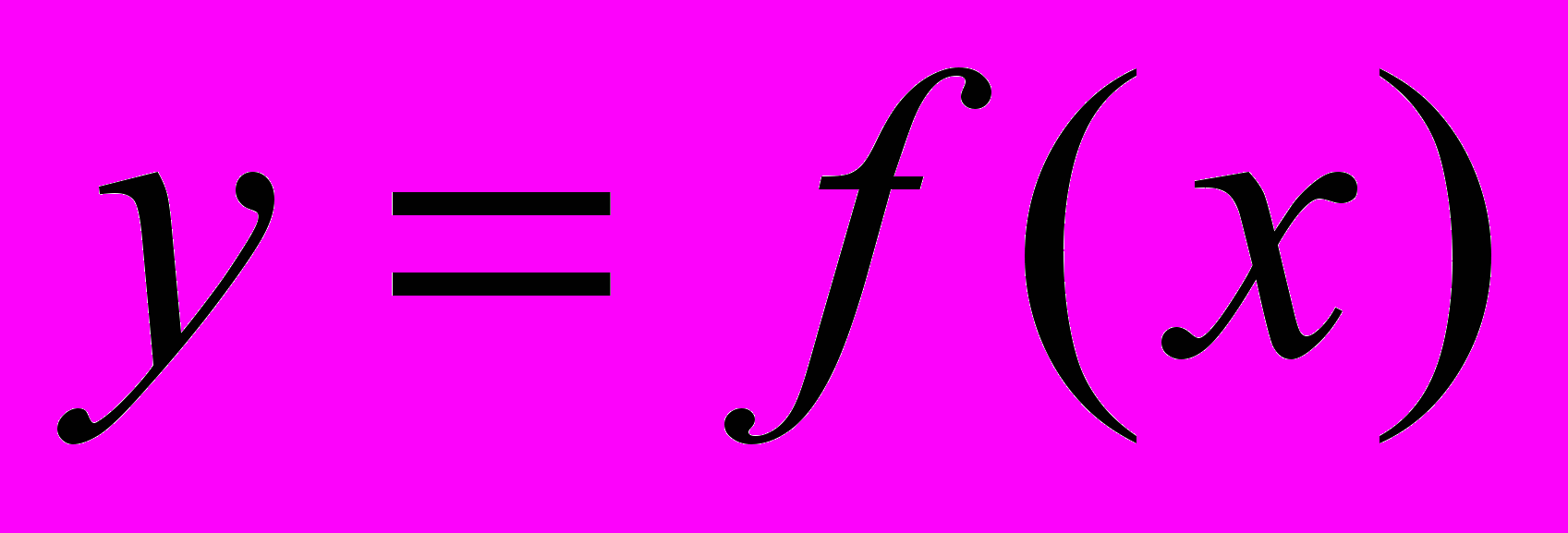 называется нечетной, если выполняются два условия:
называется нечетной, если выполняются два условия:а) область определения функции симметрична относительно начала координат;
б) для любого
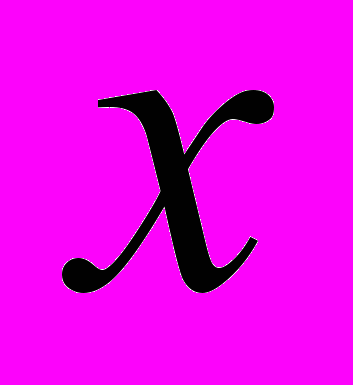 из области определения справедливо равенство
из области определения справедливо равенство 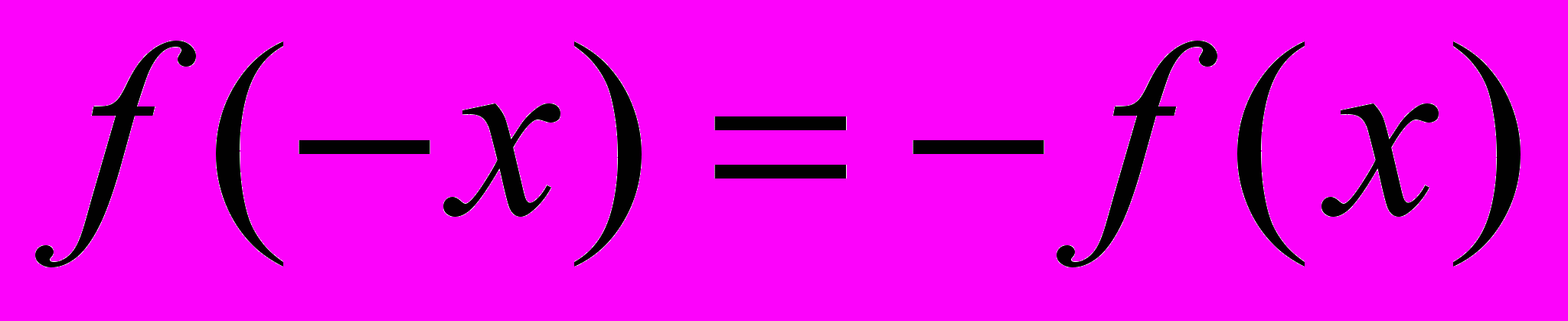 .
.Функция, не являющаяся четной или нечетной, называется функцией общего вида.
Из определения четной и нечетной функции следует, что график четной функции симметричен относительно оси
 , а график нечетной функции симметричен относительно начала координат.
, а график нечетной функции симметричен относительно начала координат.2) Периодичность.
ОПРЕДЕЛЕНИЕ. Функция
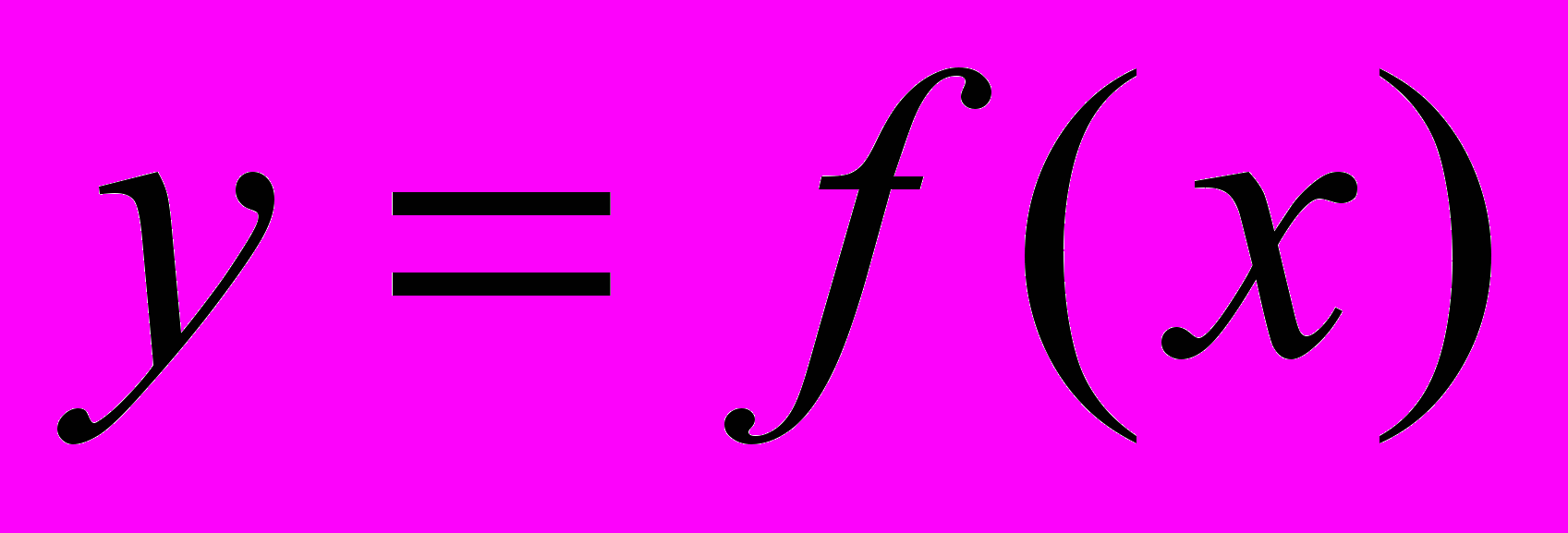 , определенная на множестве
, определенная на множестве 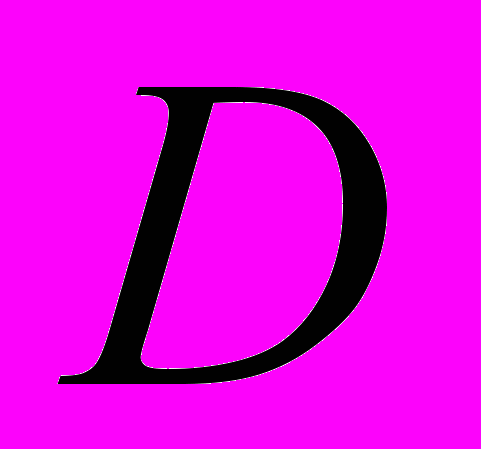 , называется периодической, если существует число
, называется периодической, если существует число 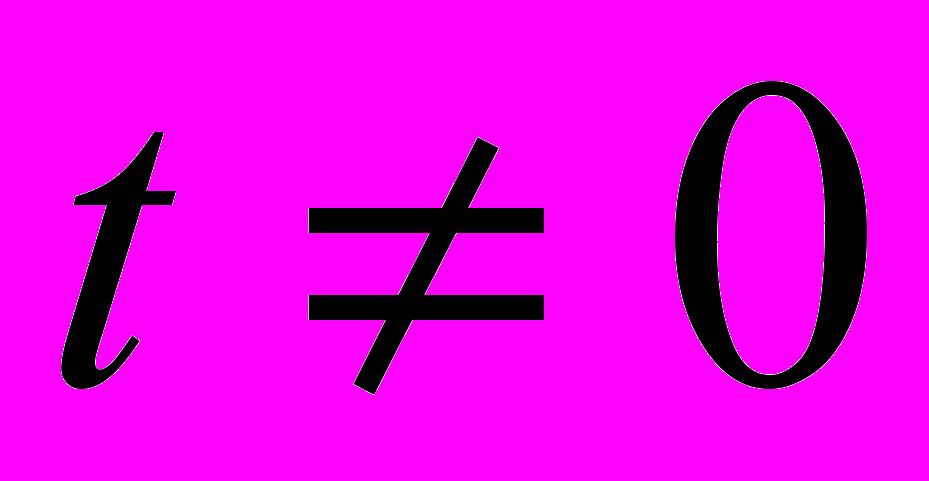 такое, а) что для любого
такое, а) что для любого 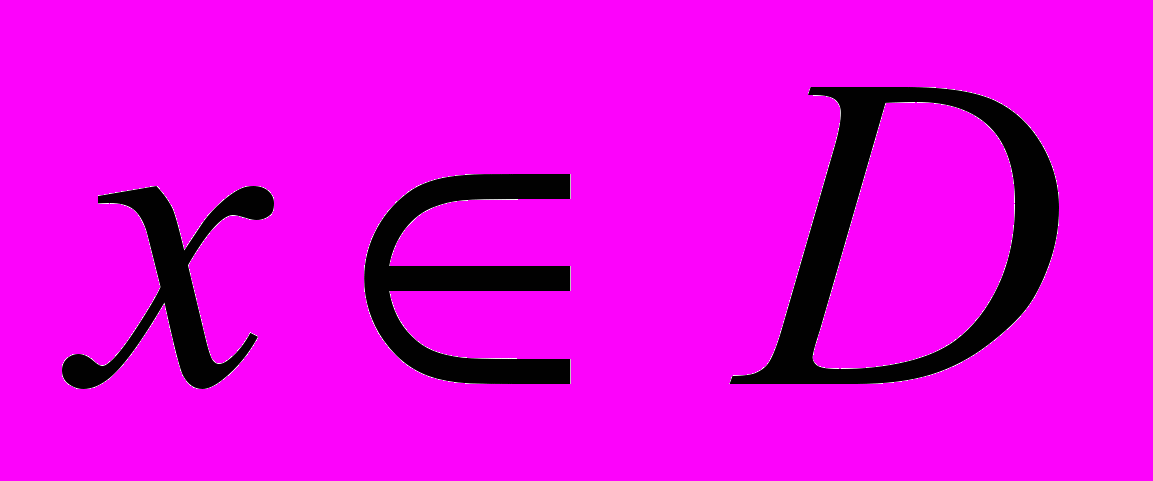 значения
значения 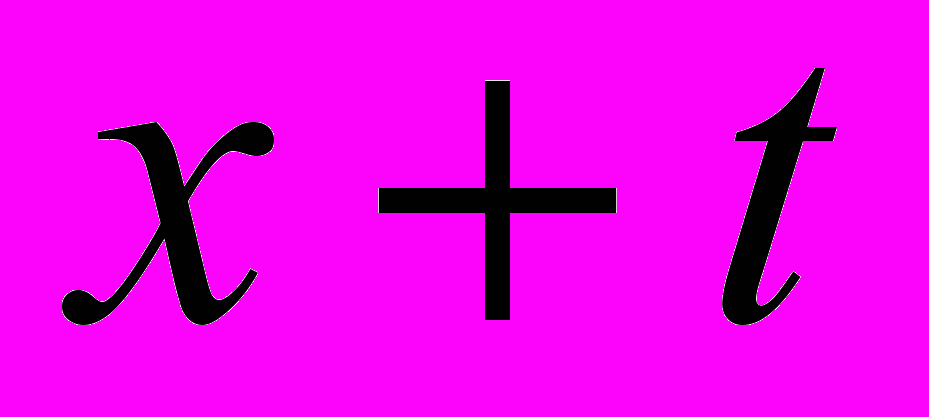 и
и 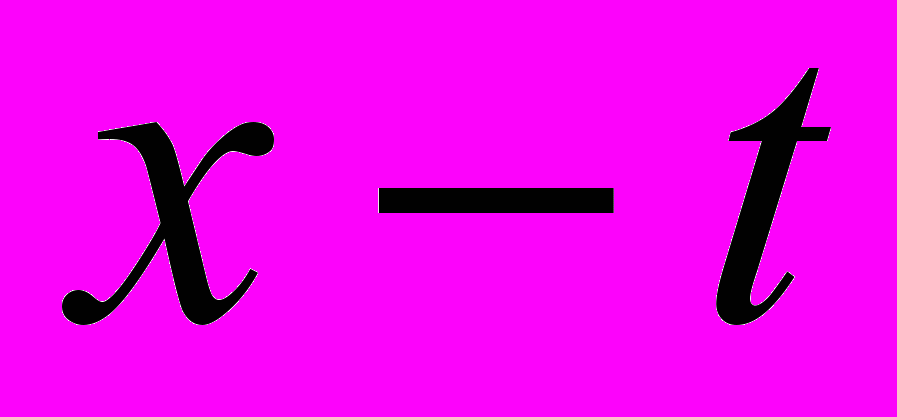 тоже принадлежат
тоже принадлежат 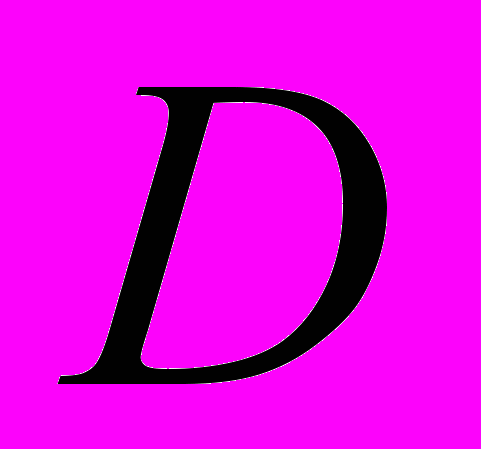 ; б)
; б) 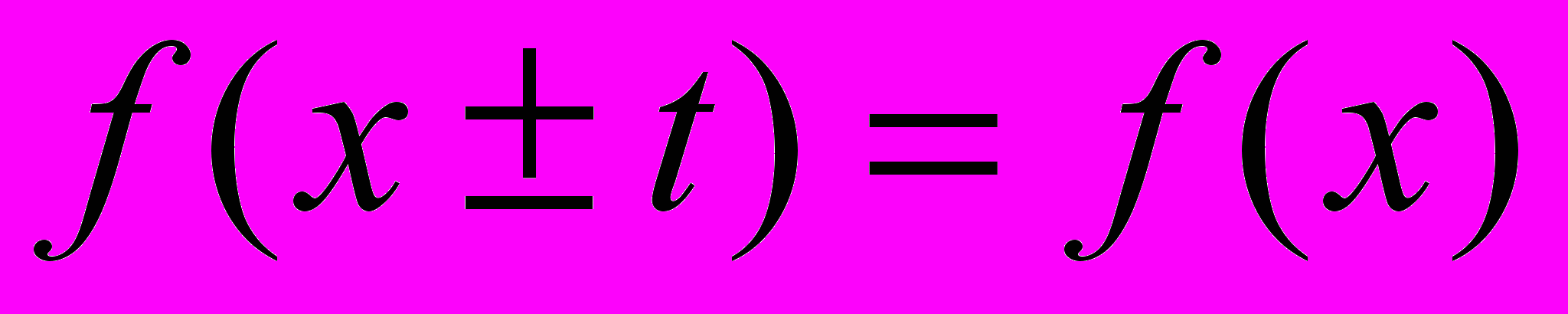 . Число
. Число 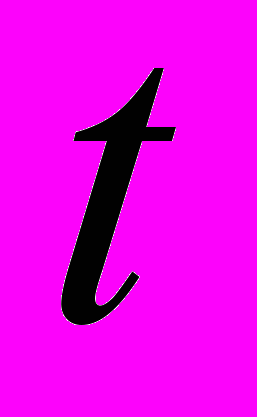 при этом называют периодом функции.
при этом называют периодом функции.Если функция
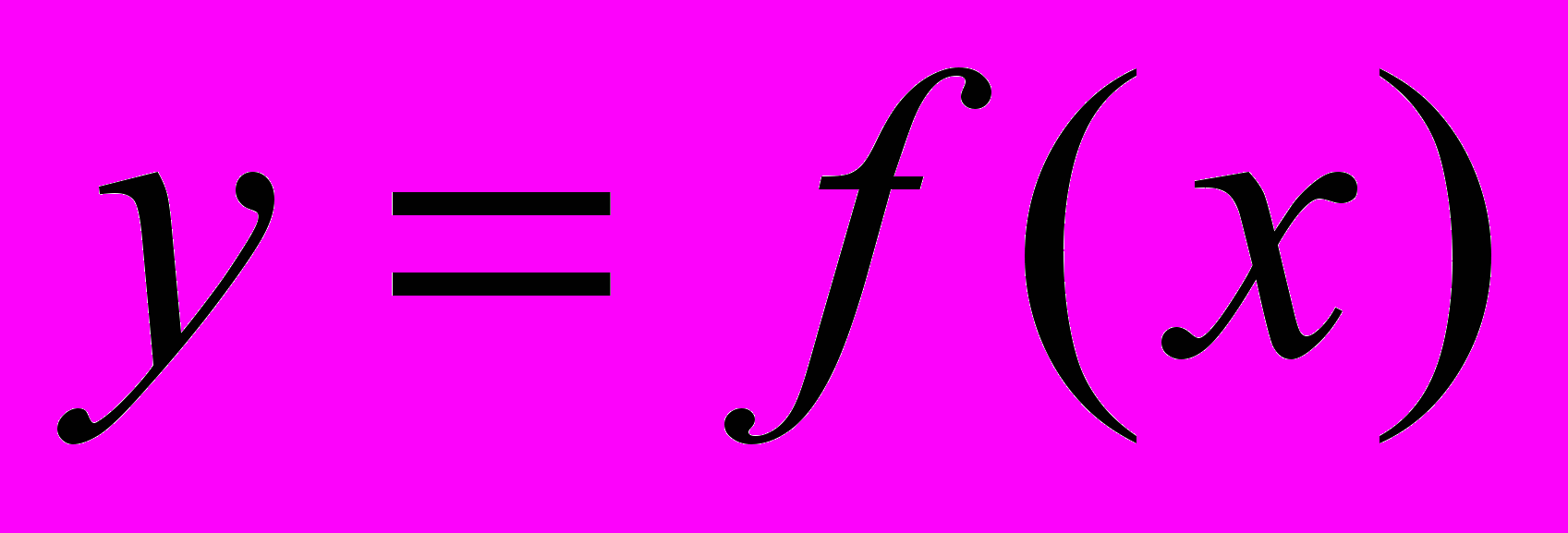 периодическая на множестве
периодическая на множестве 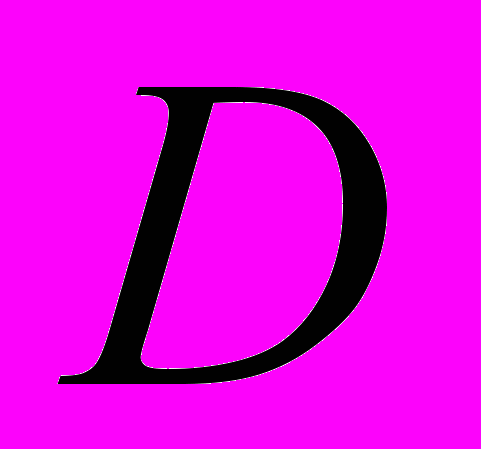 и
и 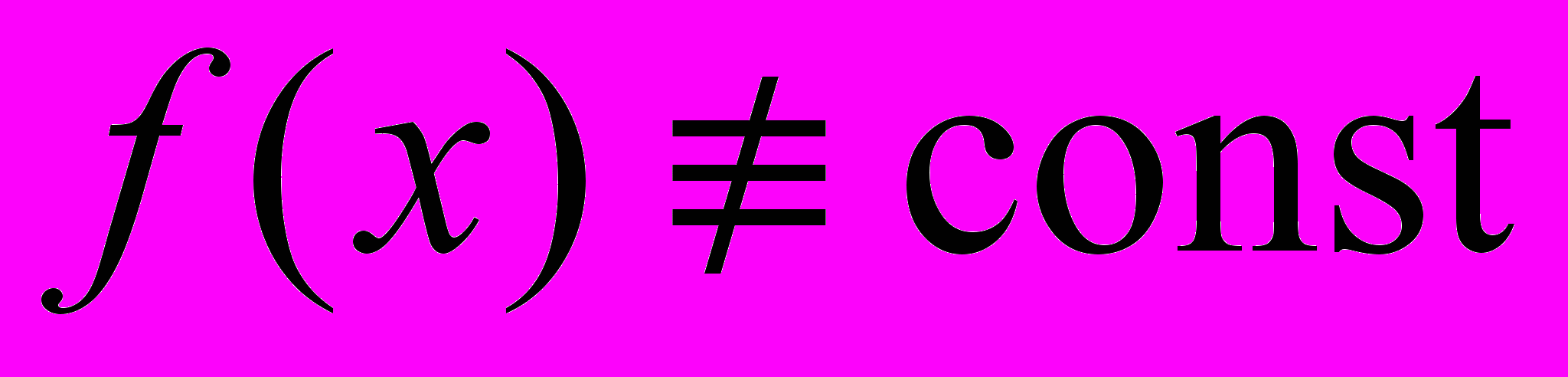 на
на 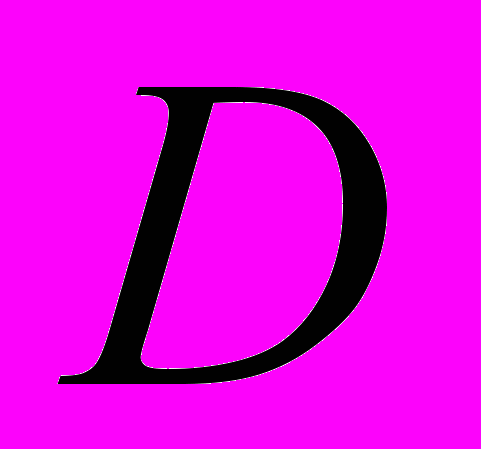 , то для нее существует наименьший положительный период
, то для нее существует наименьший положительный период  и любой период этой функции имеет вид
и любой период этой функции имеет вид 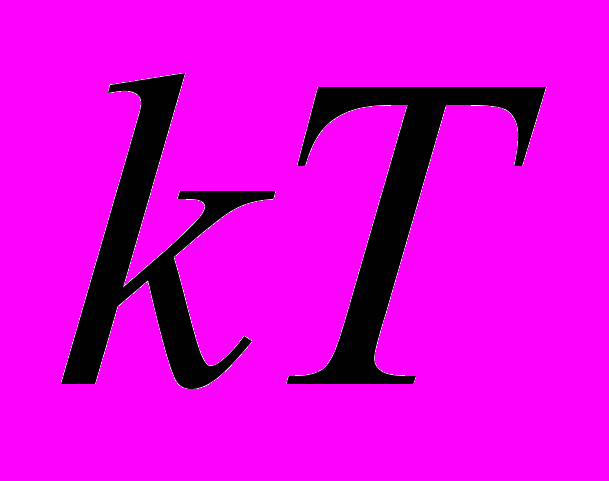 , где
, где 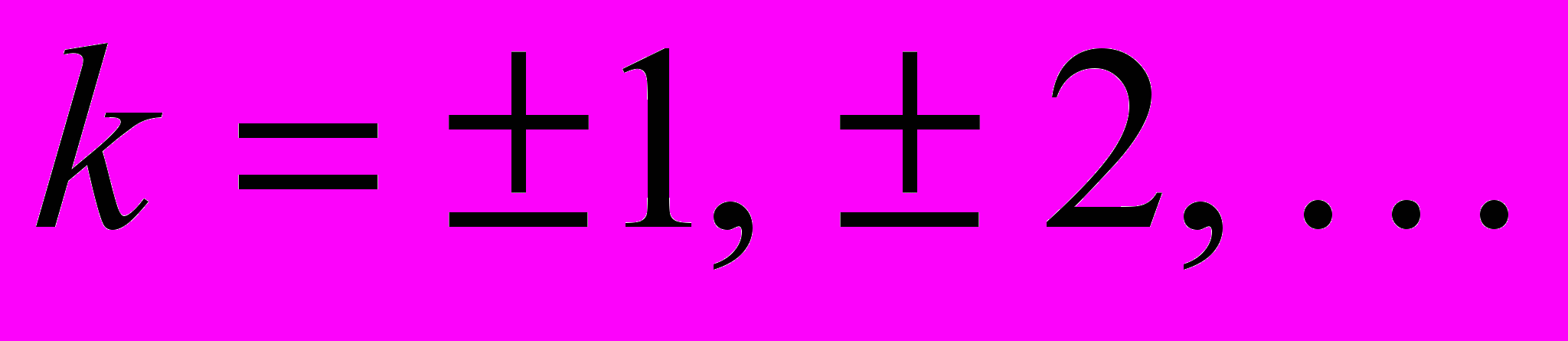 .
.  называют основным периодом функции
называют основным периодом функции 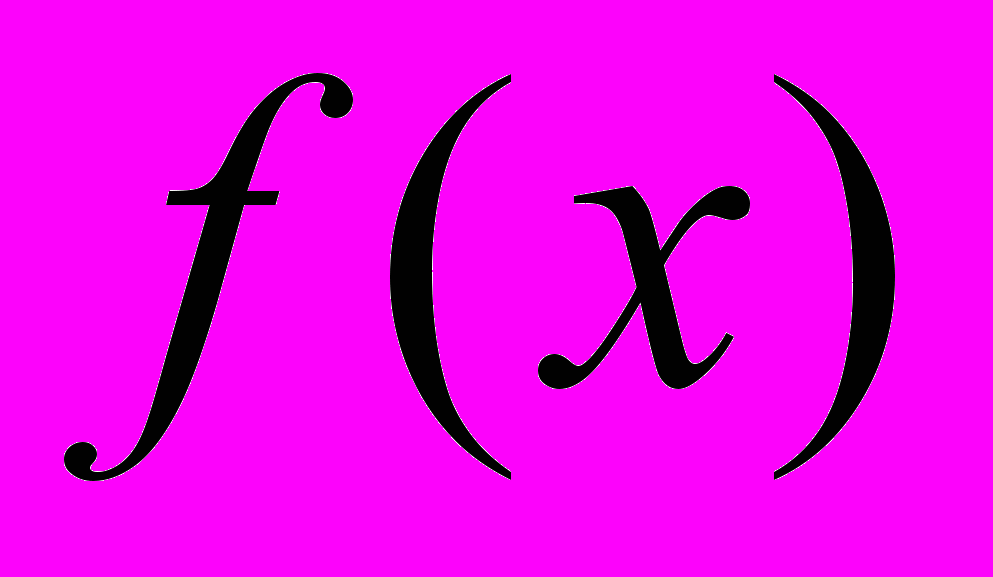 .
.Очевидно, что график периодической функции состоит из повторяющихся фрагментов.
3) Монотонность.
ОПРЕДЕЛЕНИЕ. Функция
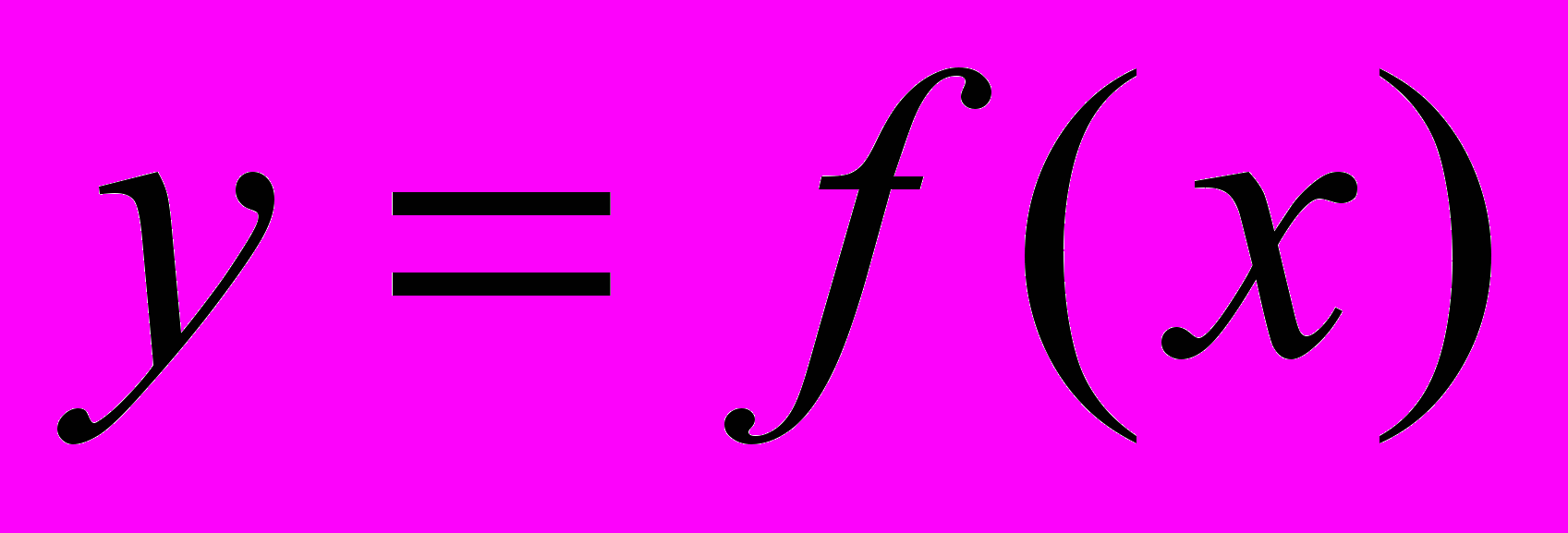 называется возрастающей (неубывающей) на интервале
называется возрастающей (неубывающей) на интервале 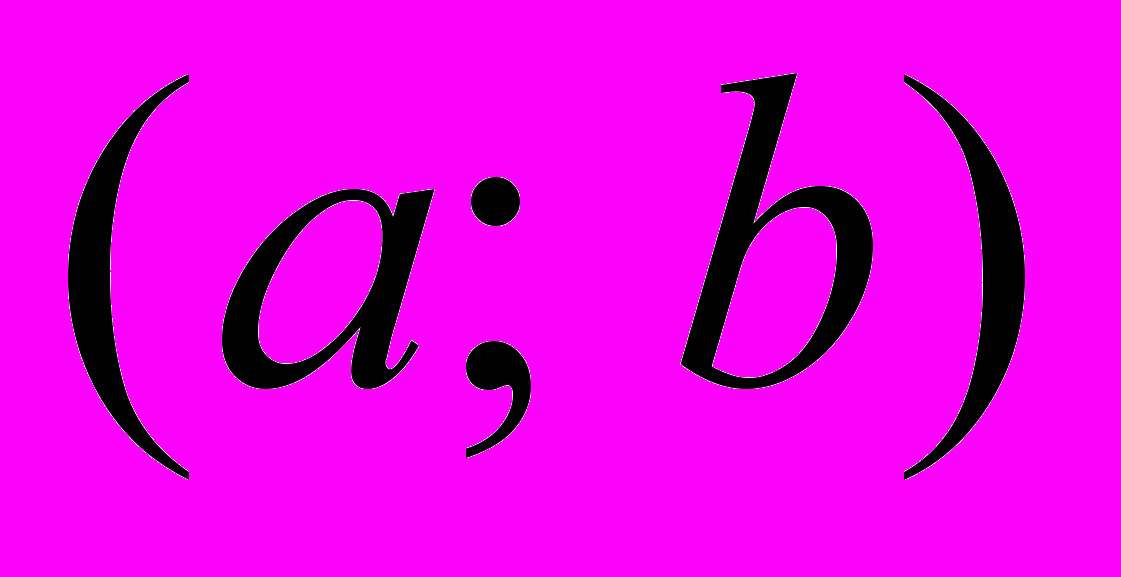 если для любых
если для любых  таких, что
таких, что 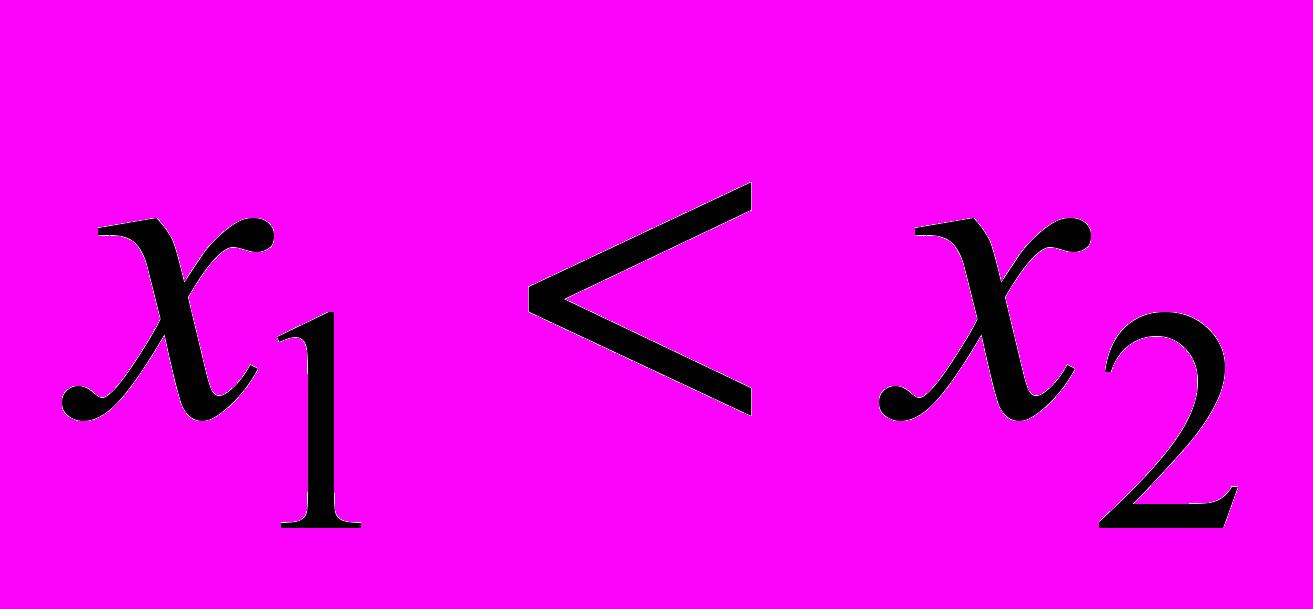 значения функции
значения функции 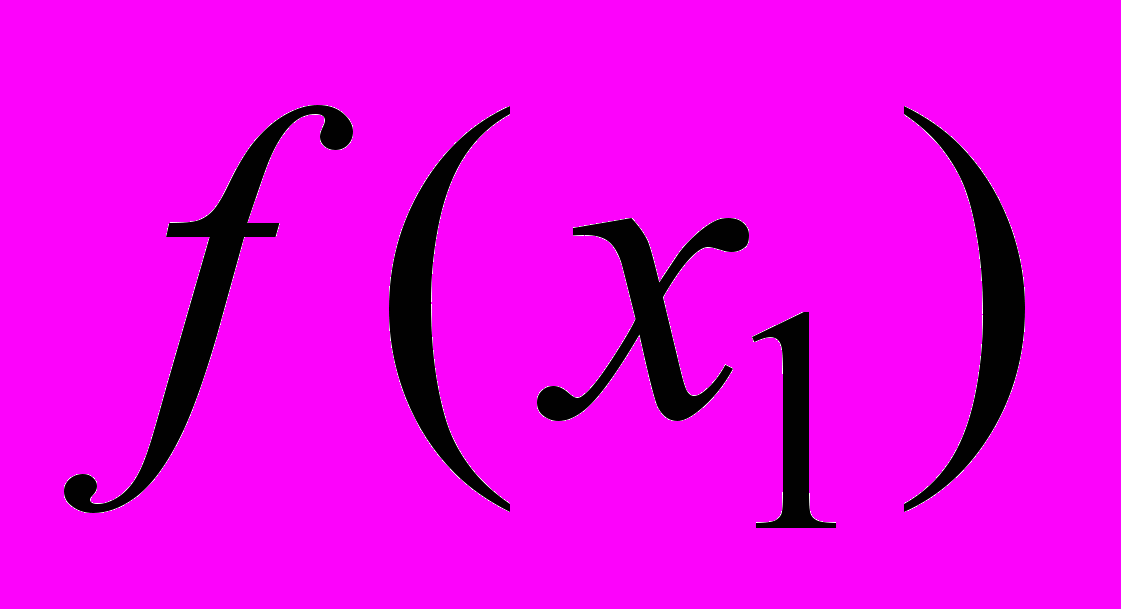 и
и 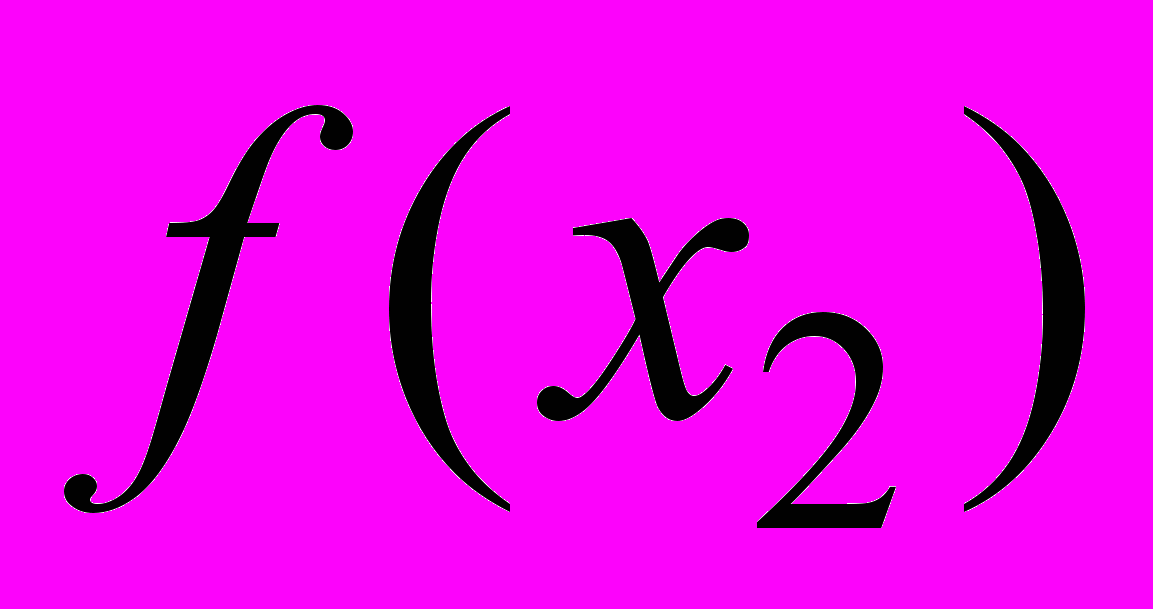 удовлетворяют неравенству
удовлетворяют неравенству 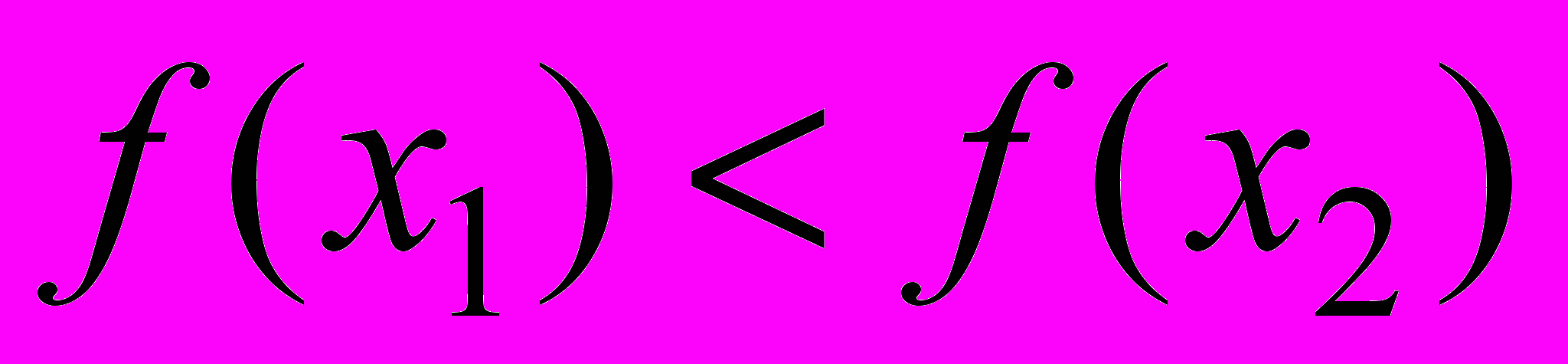 (
(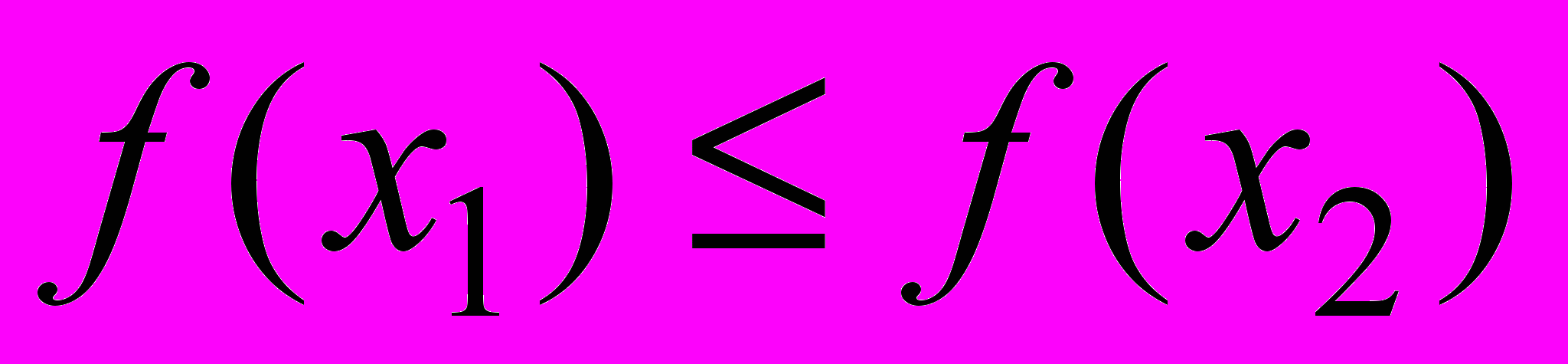 ).
).Функция
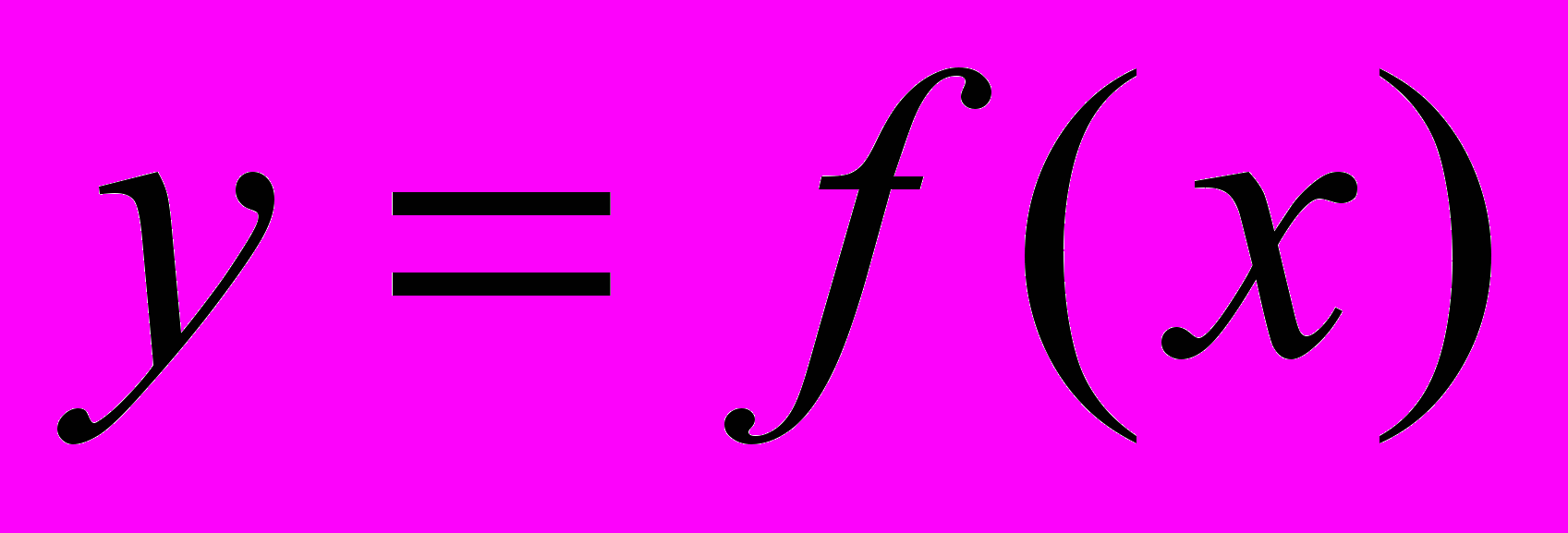 называется убывающей (невозрастающей) на интервале
называется убывающей (невозрастающей) на интервале 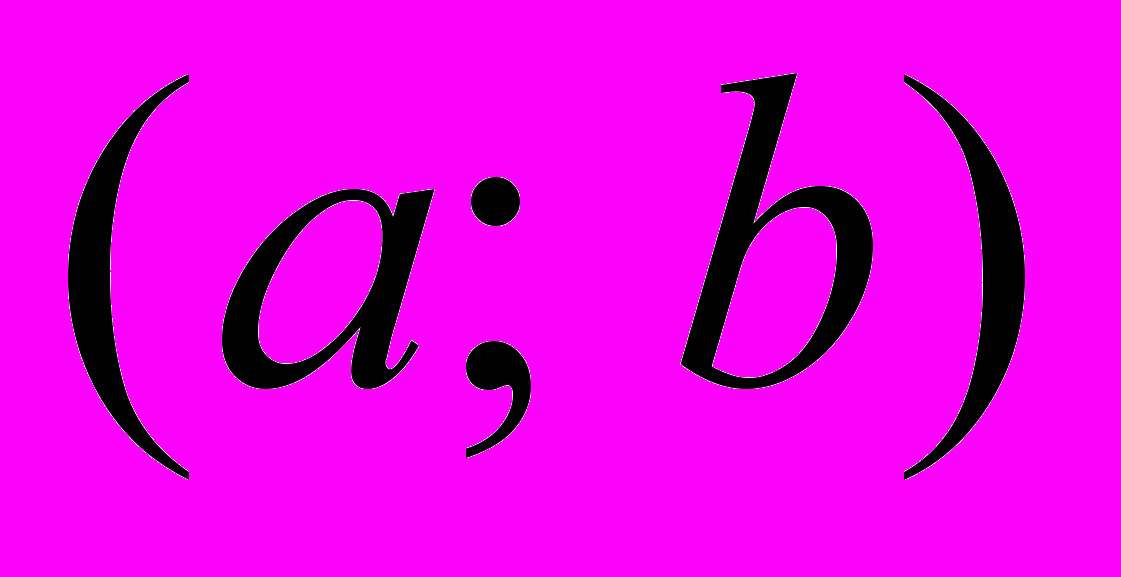 если для любых
если для любых  таких, что
таких, что 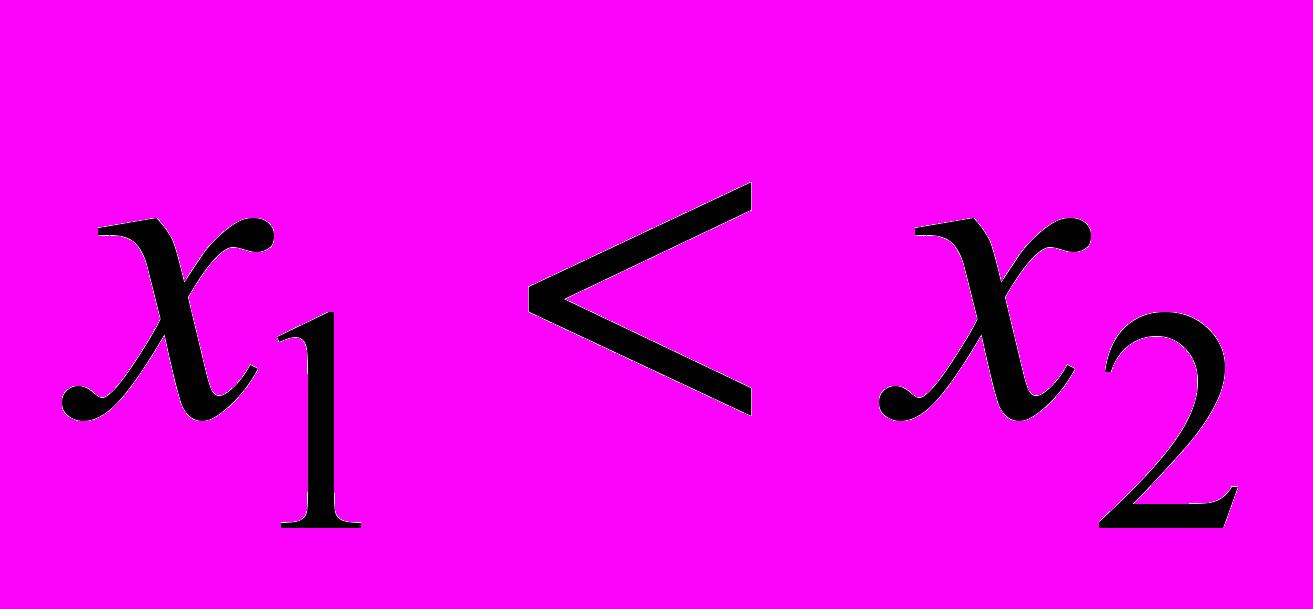 значения функции
значения функции 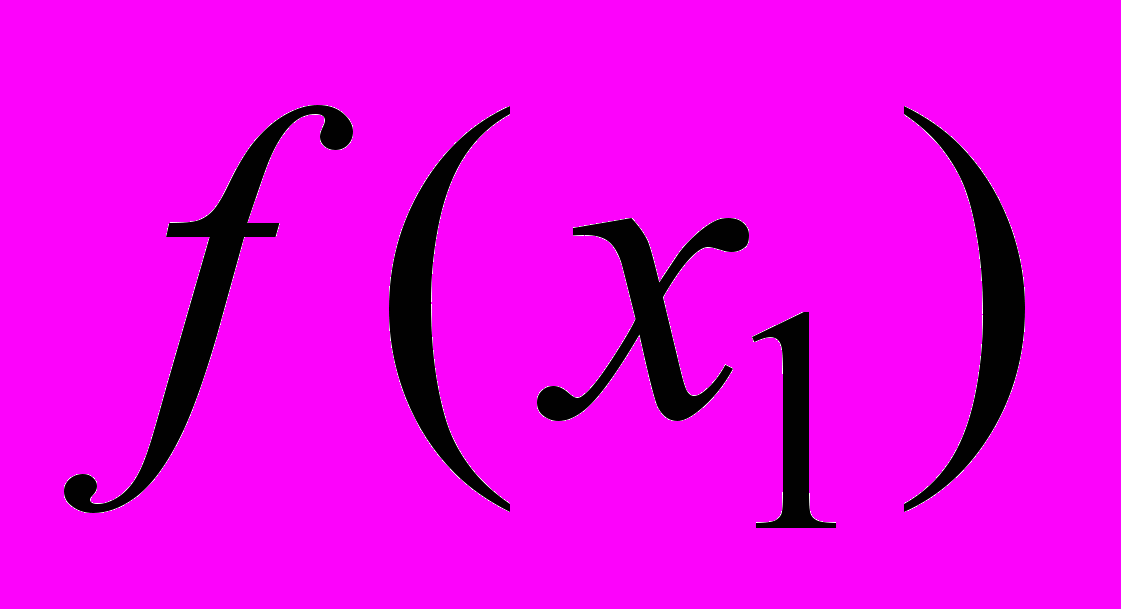 и
и 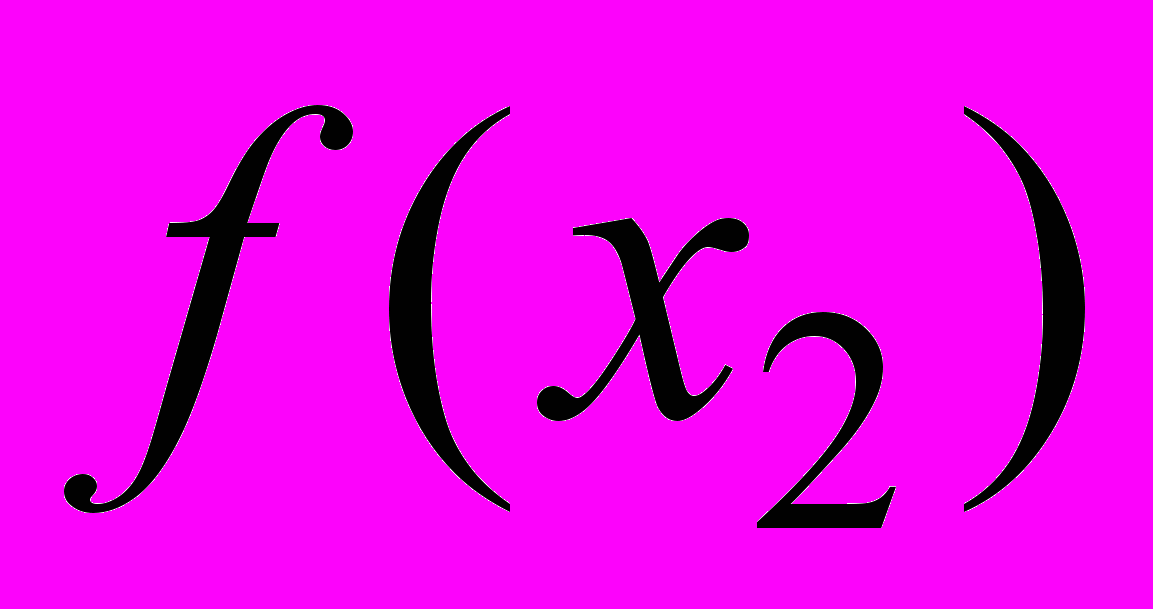 удовлетворяют неравенству
удовлетворяют неравенству 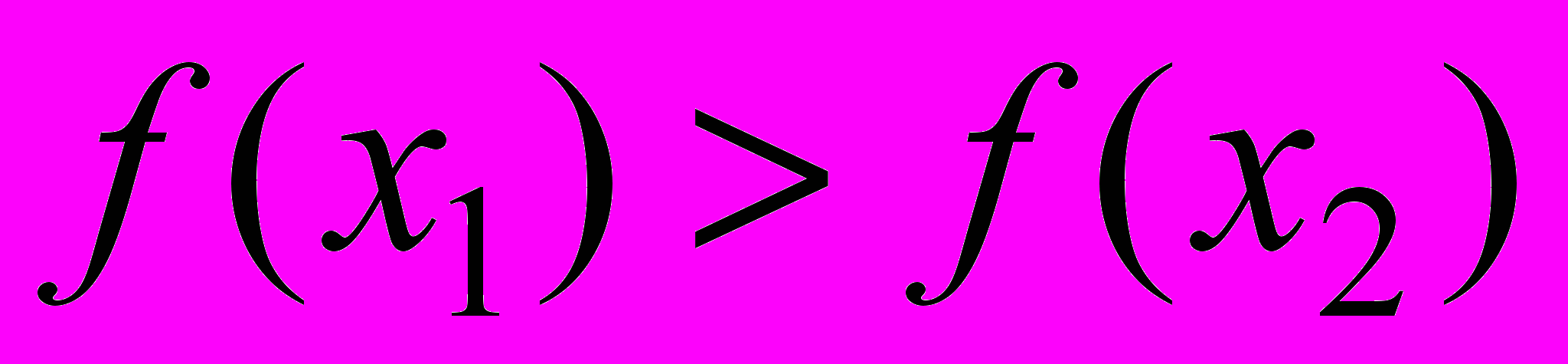 (
(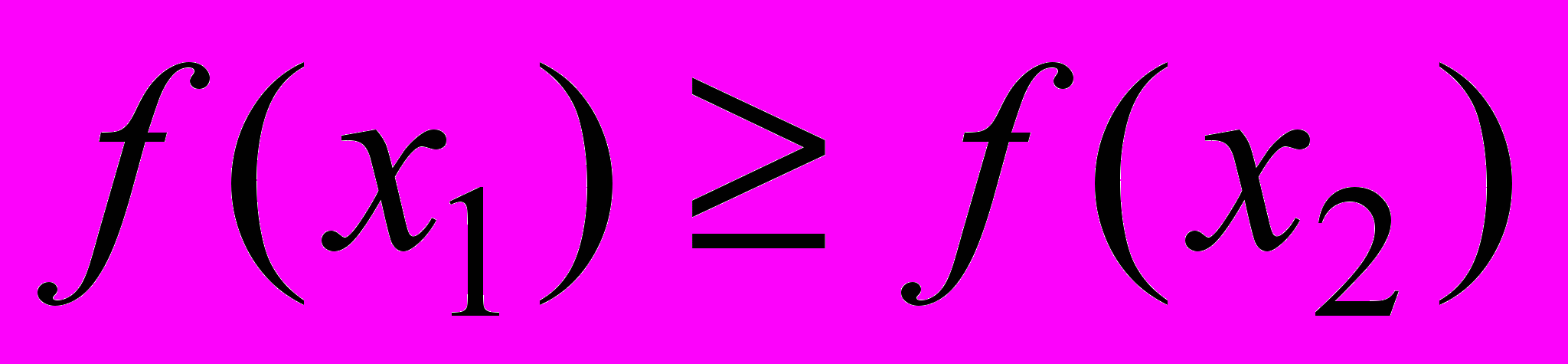 ).
).Возрастающие, убывающие, невозрастающие, неубывающие функции называются монотонными.
4) Ограниченность.
ОПРЕДЕЛЕНИЕ. Функция
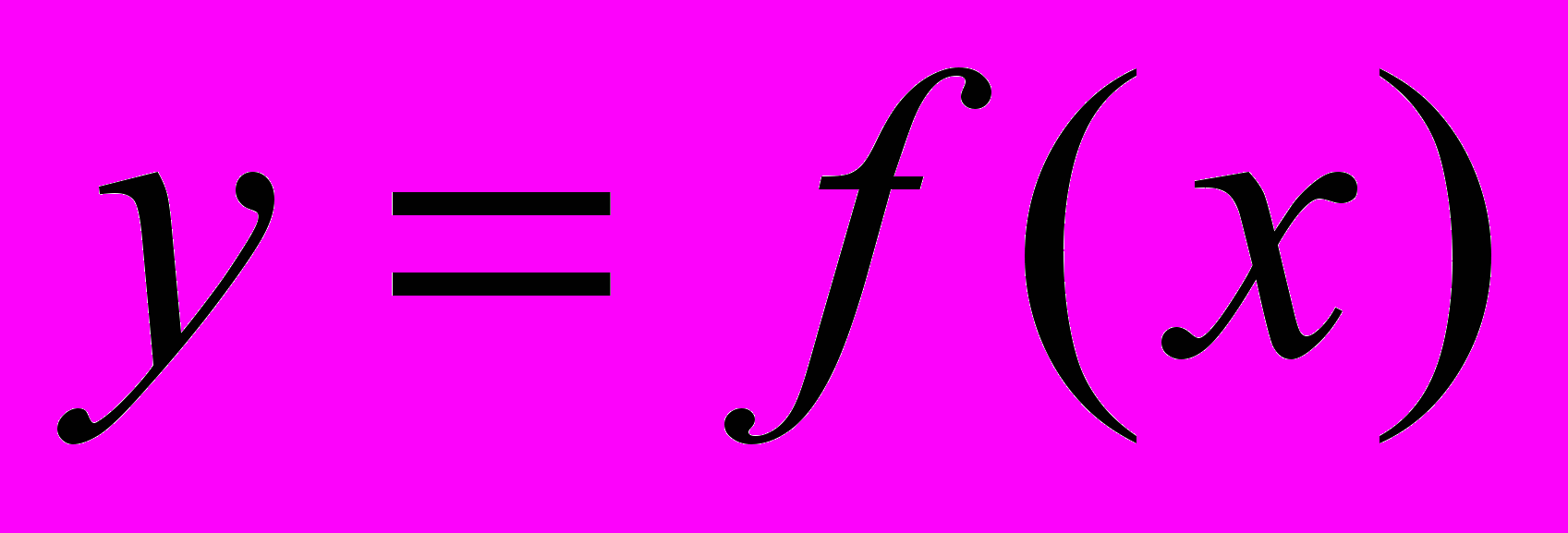 называется ограниченной снизу, если существует
называется ограниченной снизу, если существует 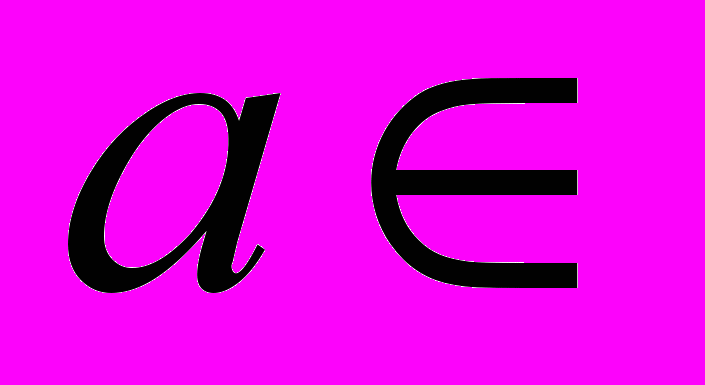 ℝ такое, что
ℝ такое, что 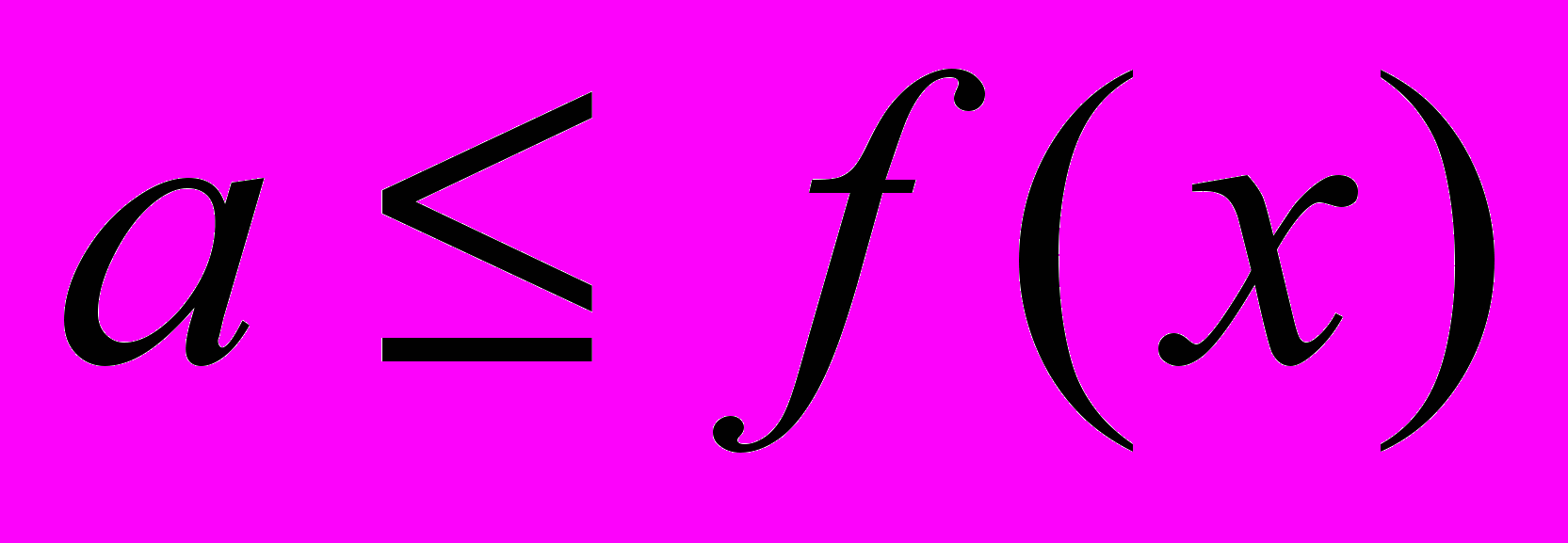 ,
, 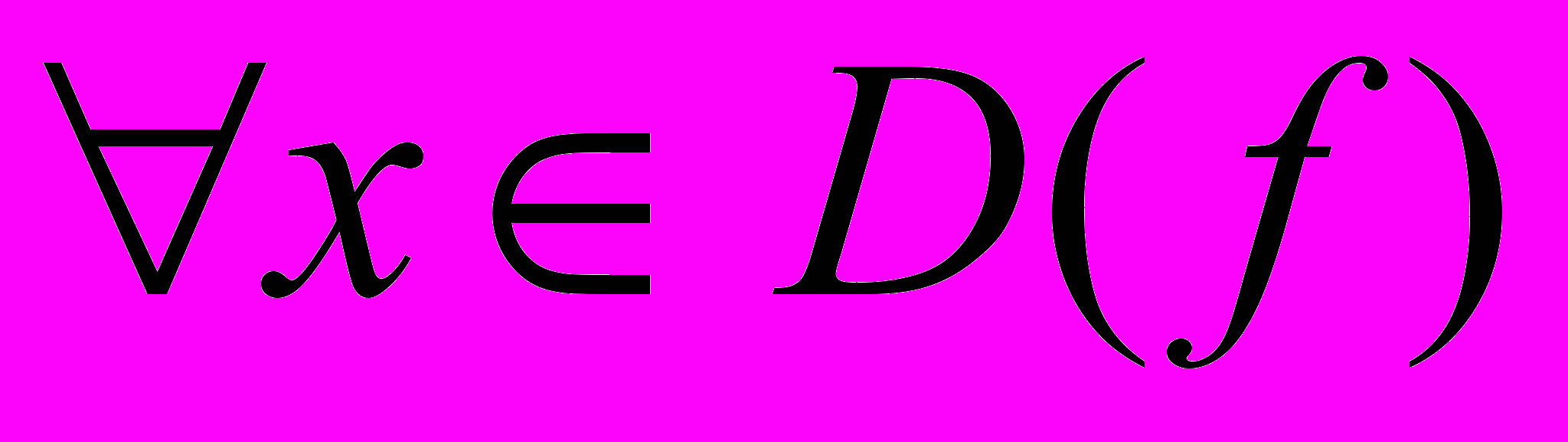 .
.Функция
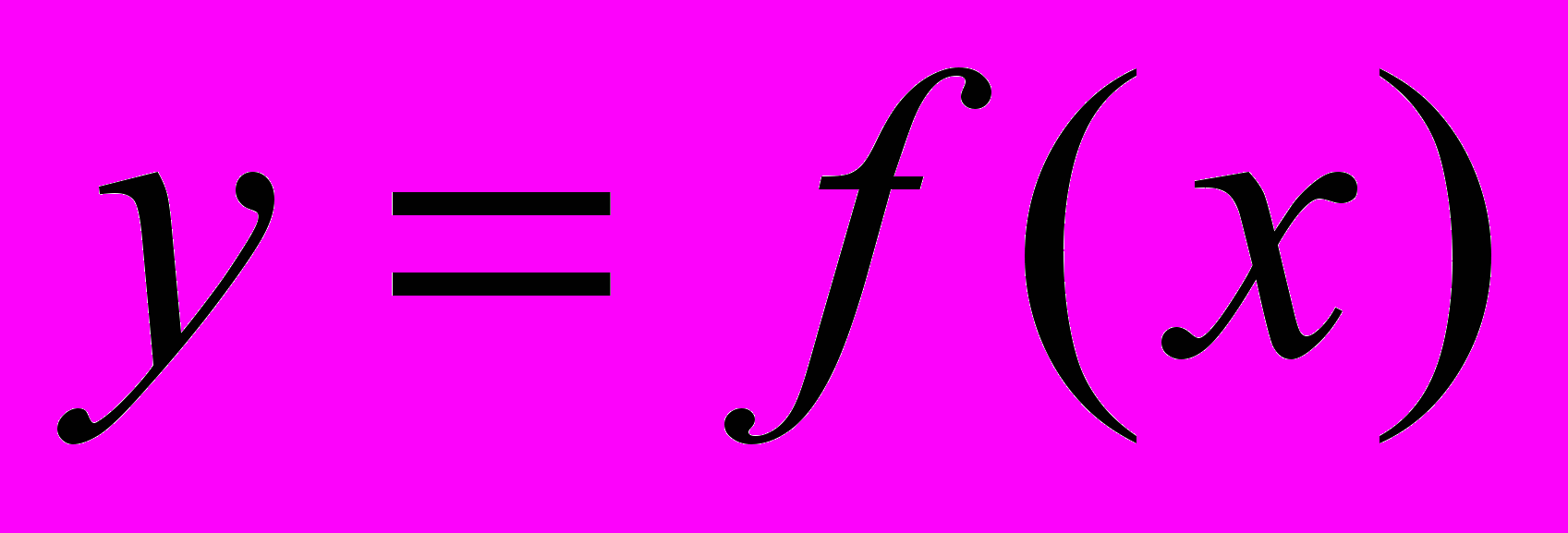 называется ограниченной сверху, если существует
называется ограниченной сверху, если существует 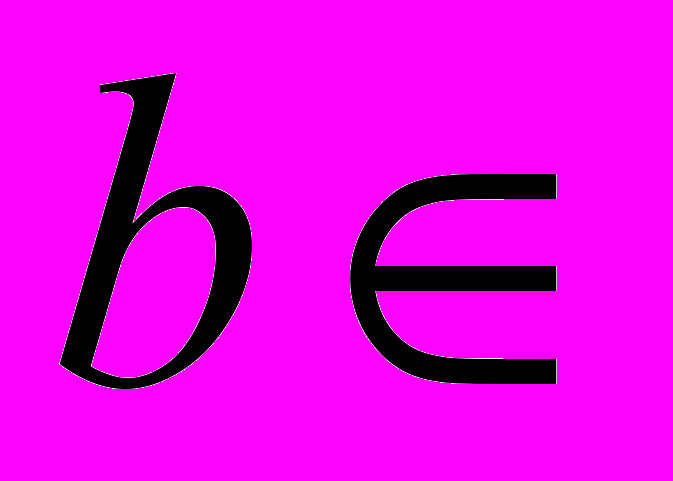 ℝ такое, что
ℝ такое, что 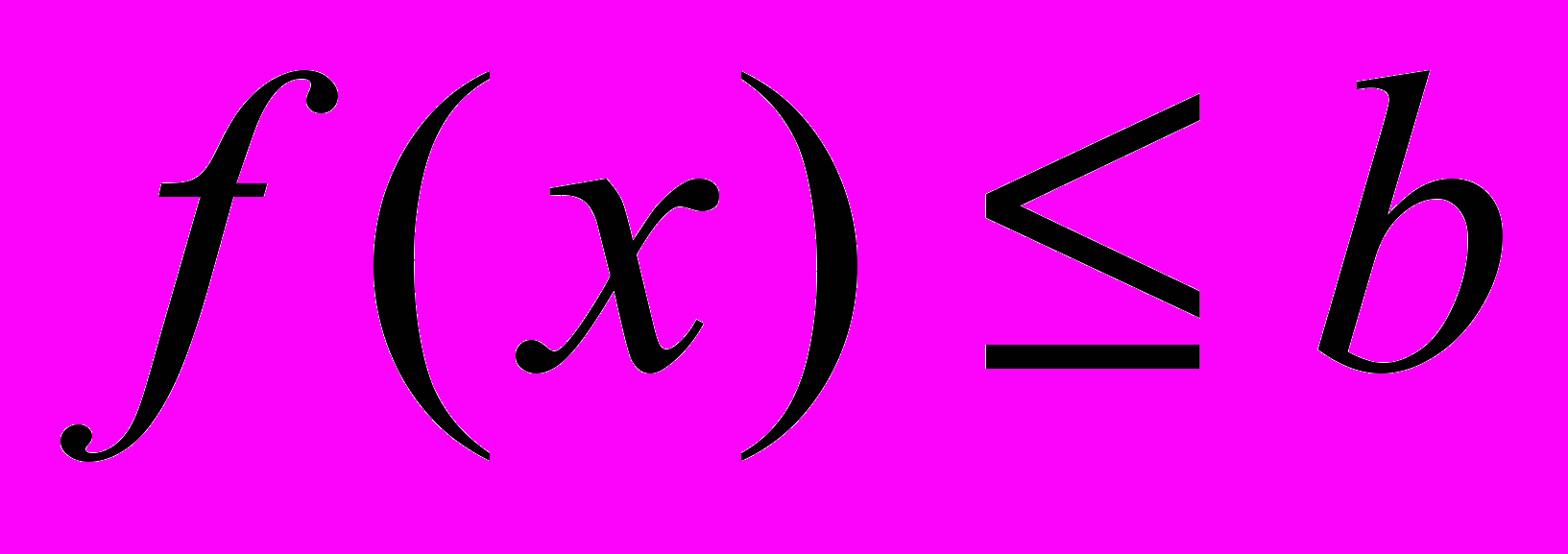 ,
, 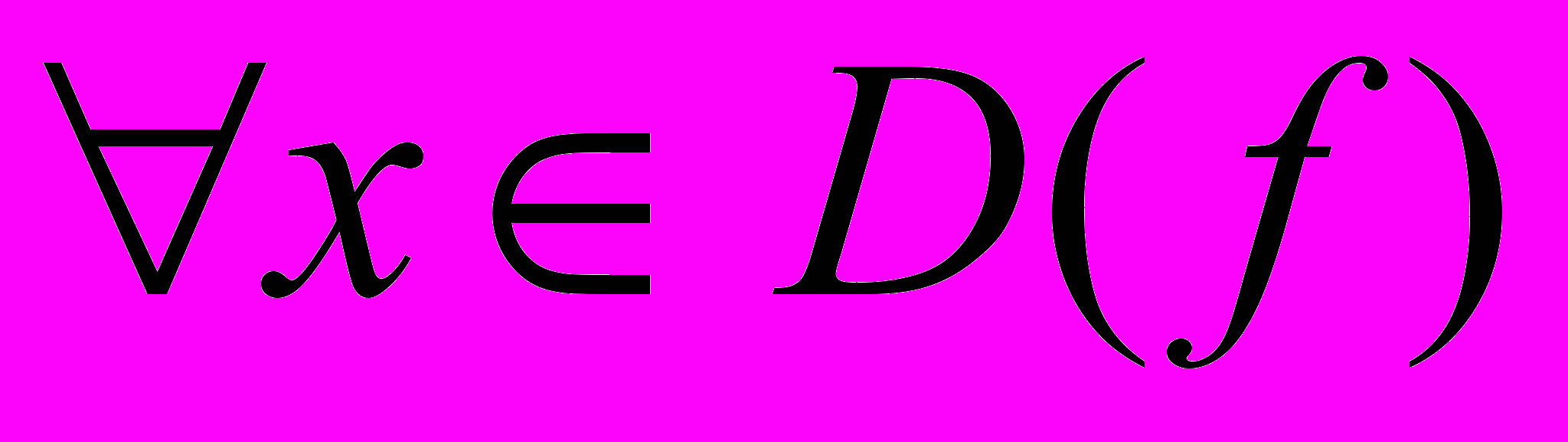 .
.Функция, ограниченная сверху и снизу, называется ограниченной.
Если функция
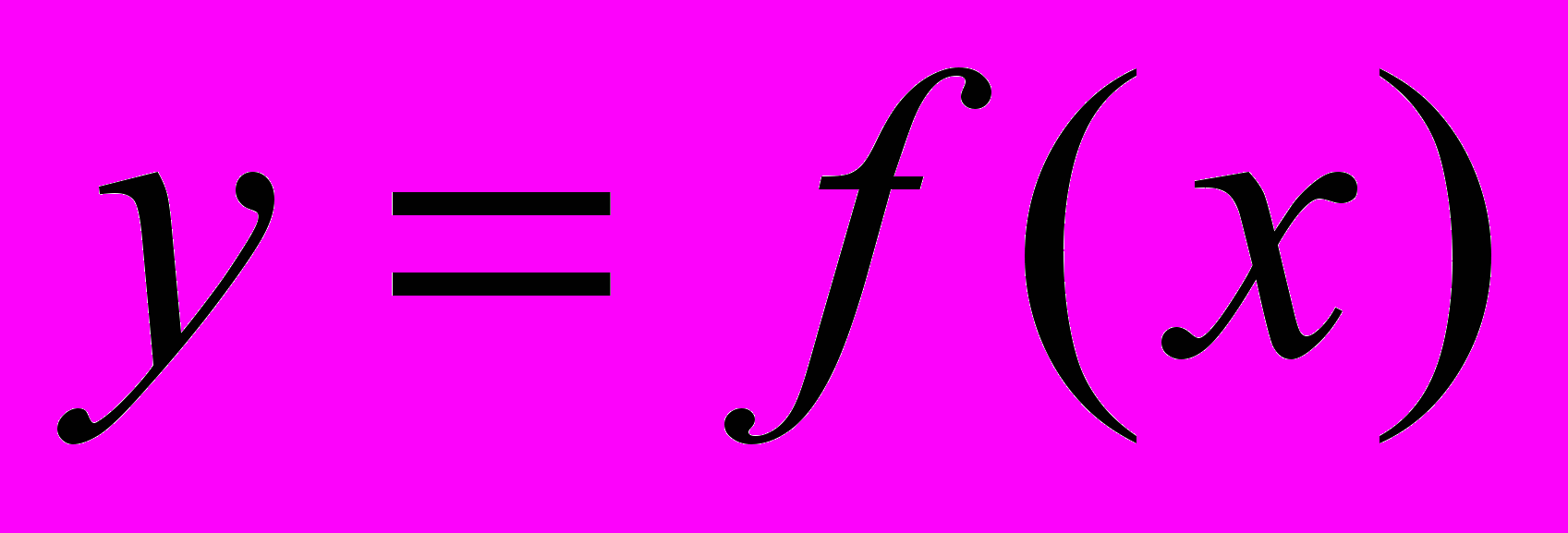 ограничена, то существует
ограничена, то существует 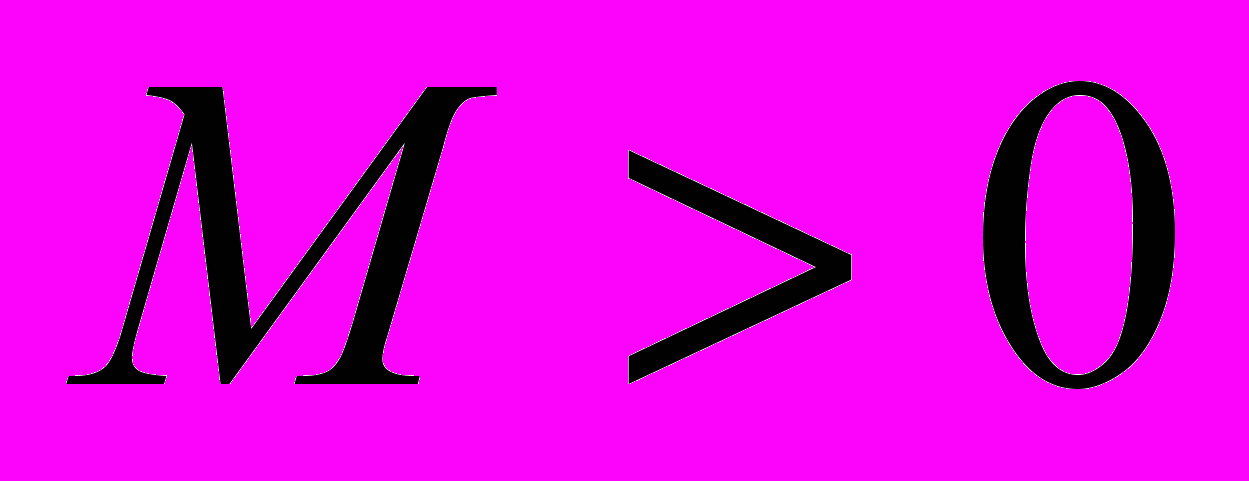 такое, что
такое, что 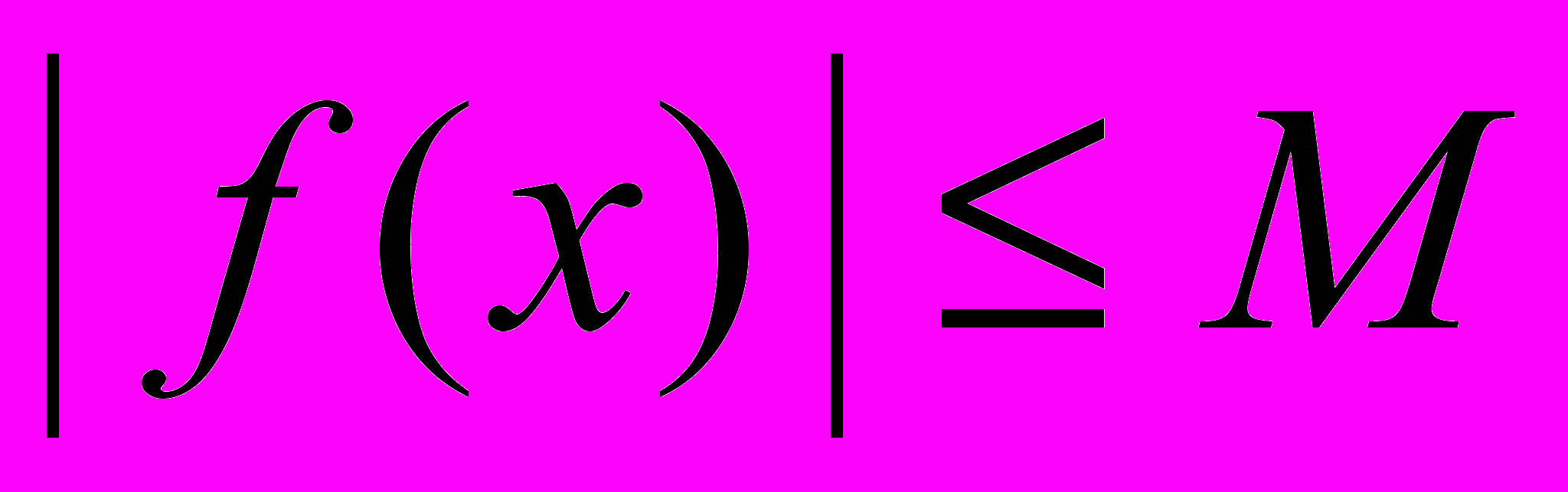 ,
, 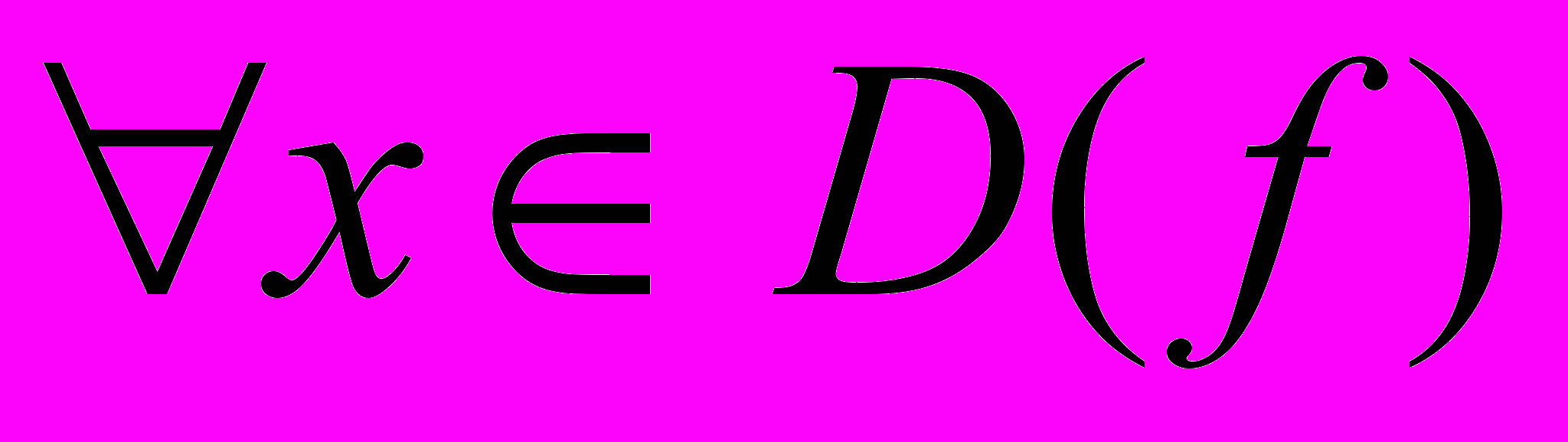 .
. Действительно, если
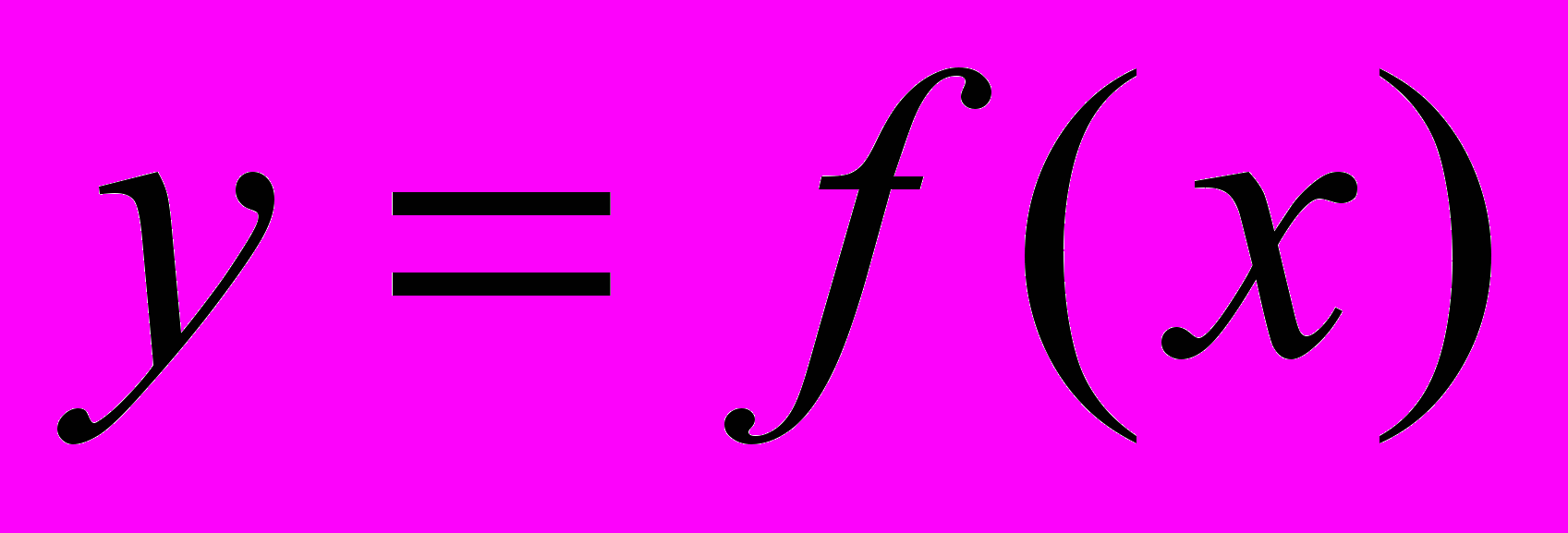 ограничена, то она ограничена сверху и снизу. Значит, существуют
ограничена, то она ограничена сверху и снизу. Значит, существуют 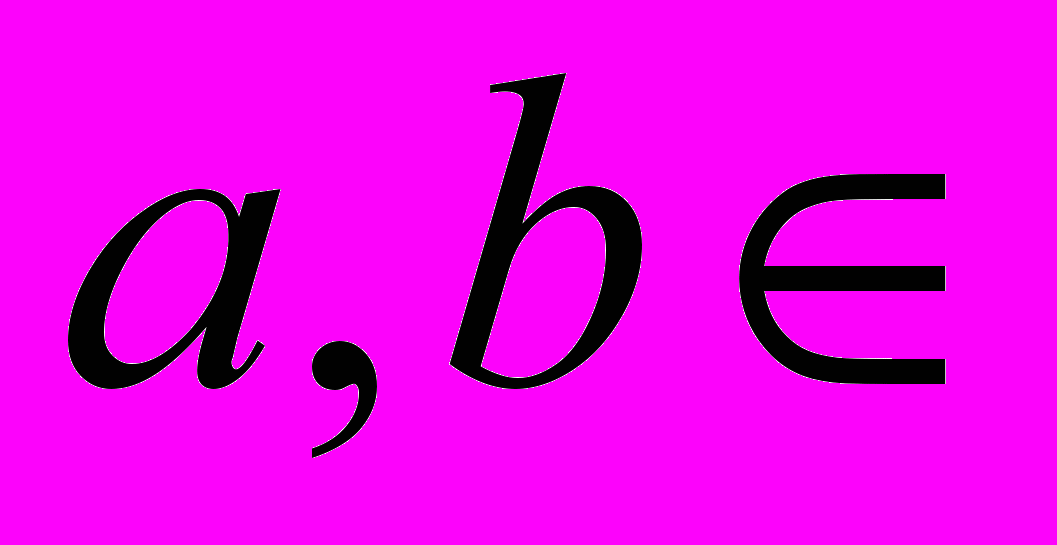 ℝ такие, что
ℝ такие, что 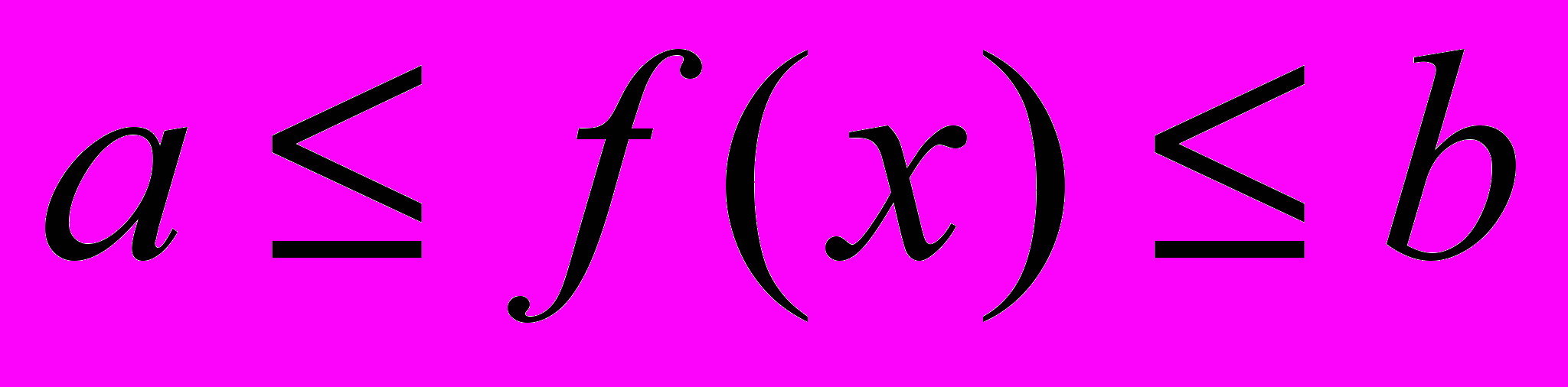 ,
, 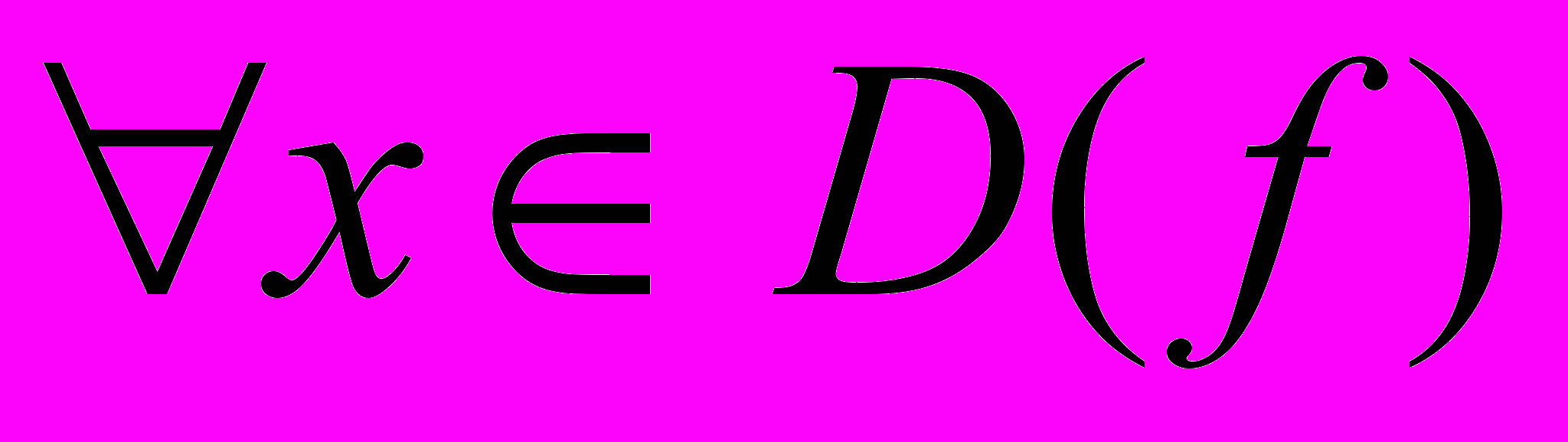 .
.Обозначим через
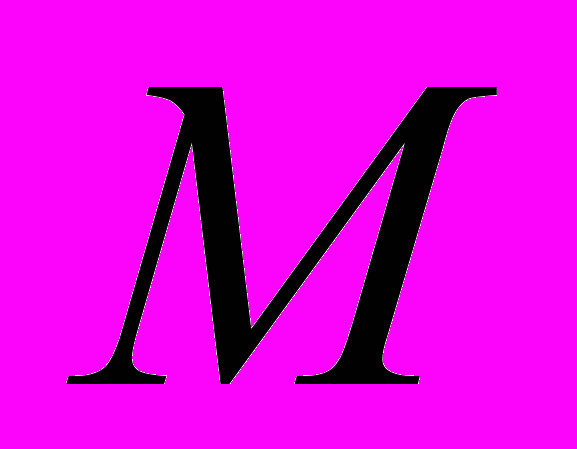
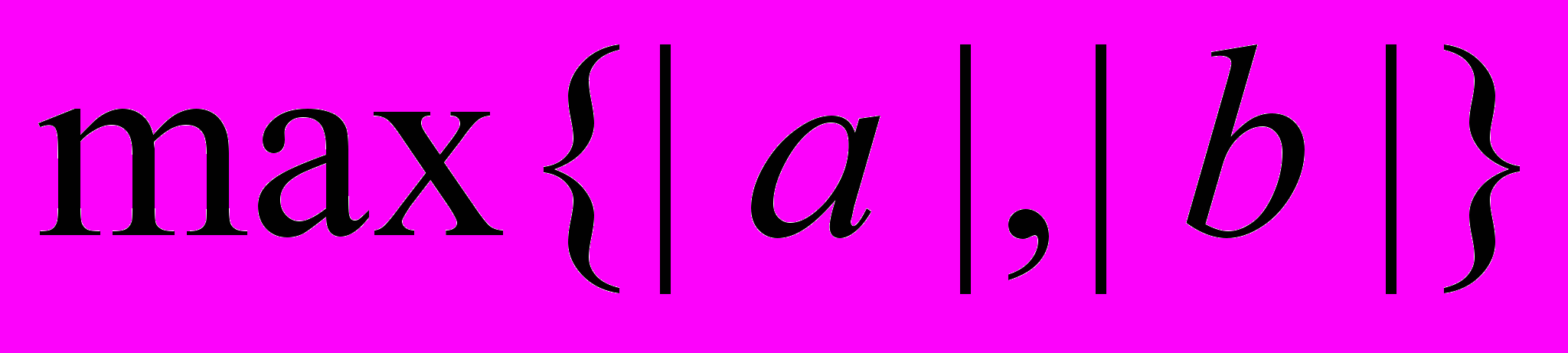 1. Тогда
1. Тогда 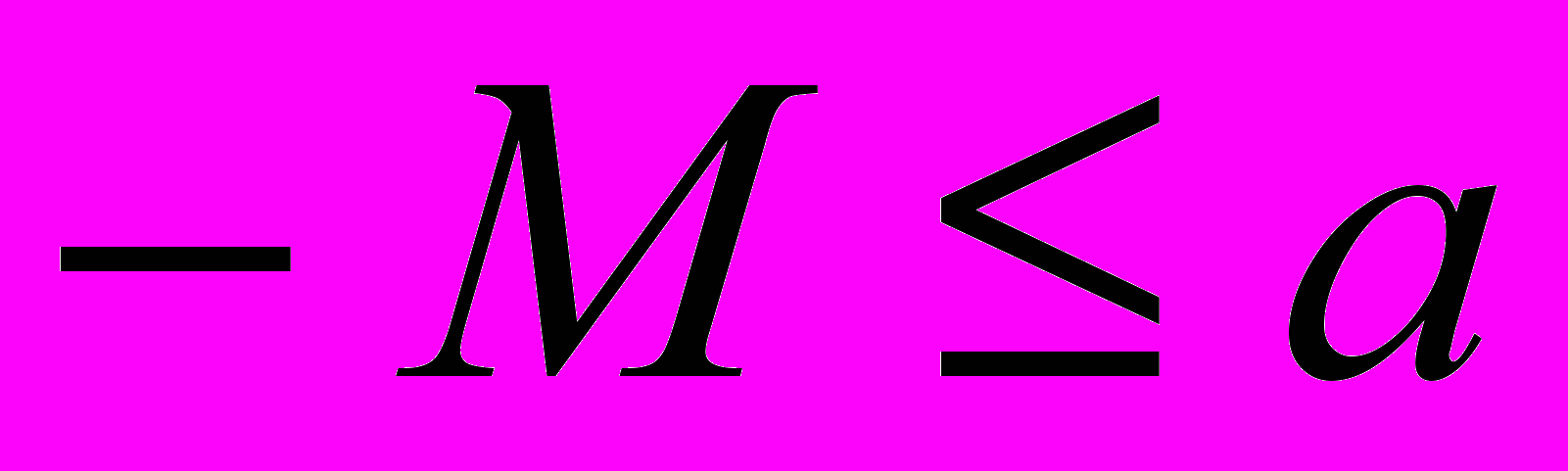 и
и 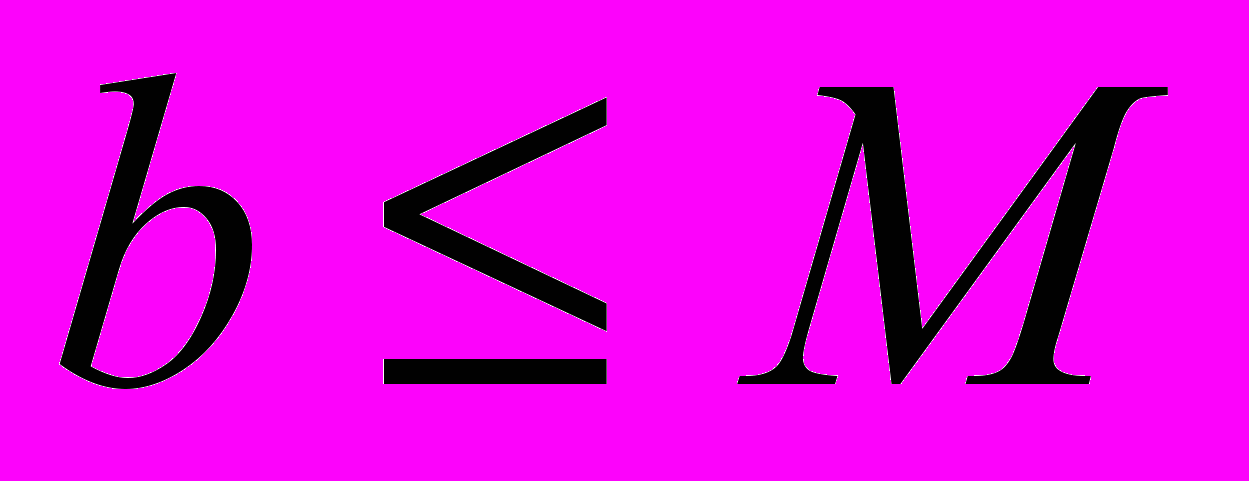 . Следовательно,
. Следовательно, 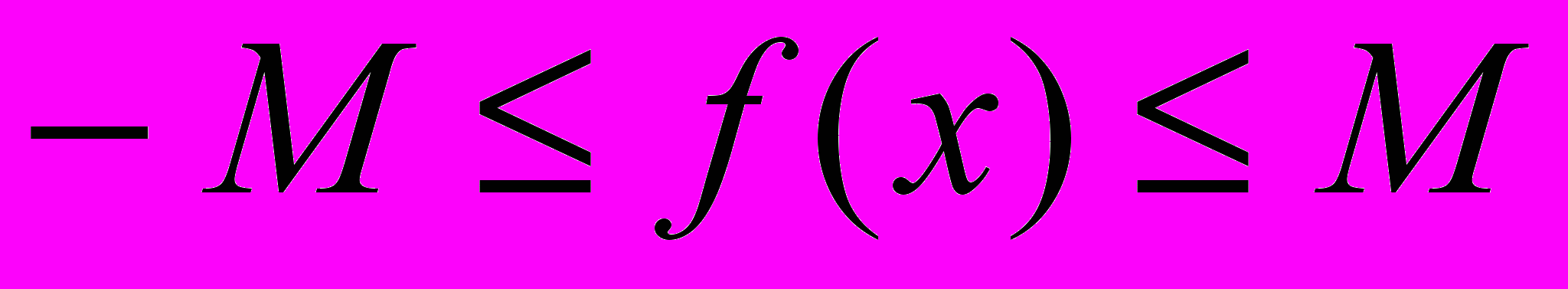 ,
, 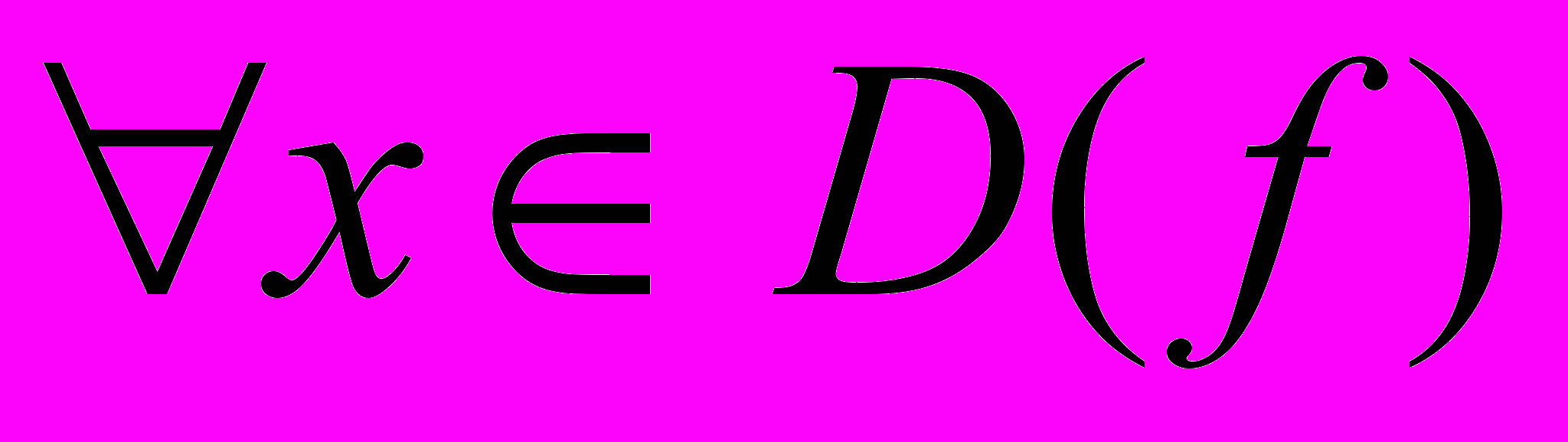 ,
,или
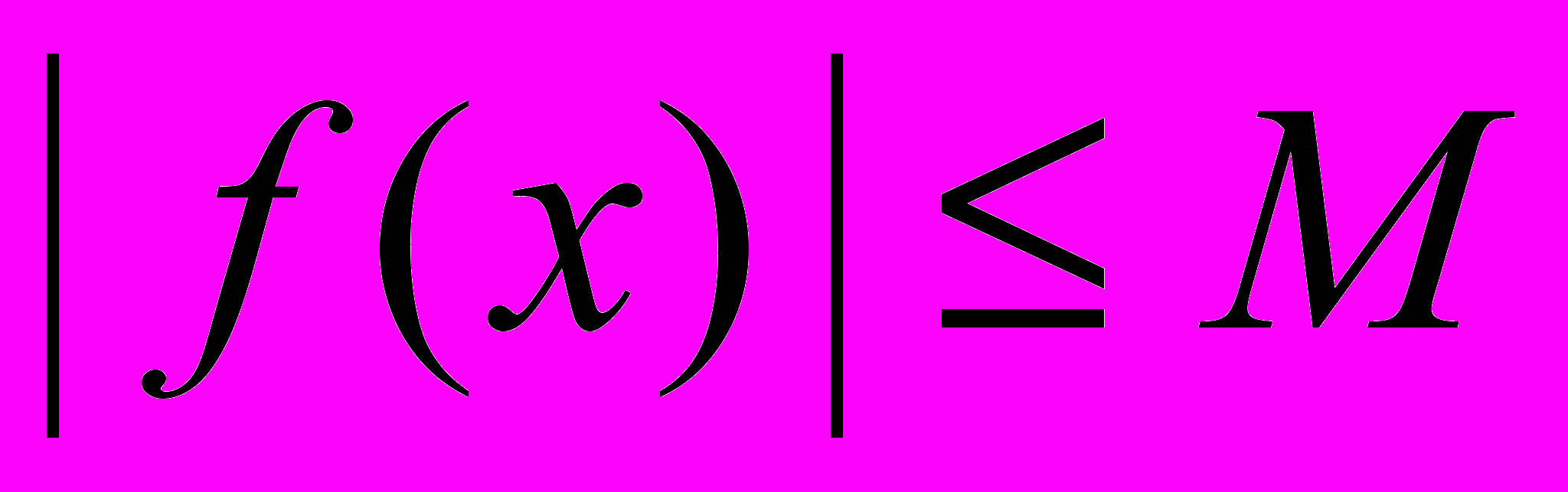 ,
, 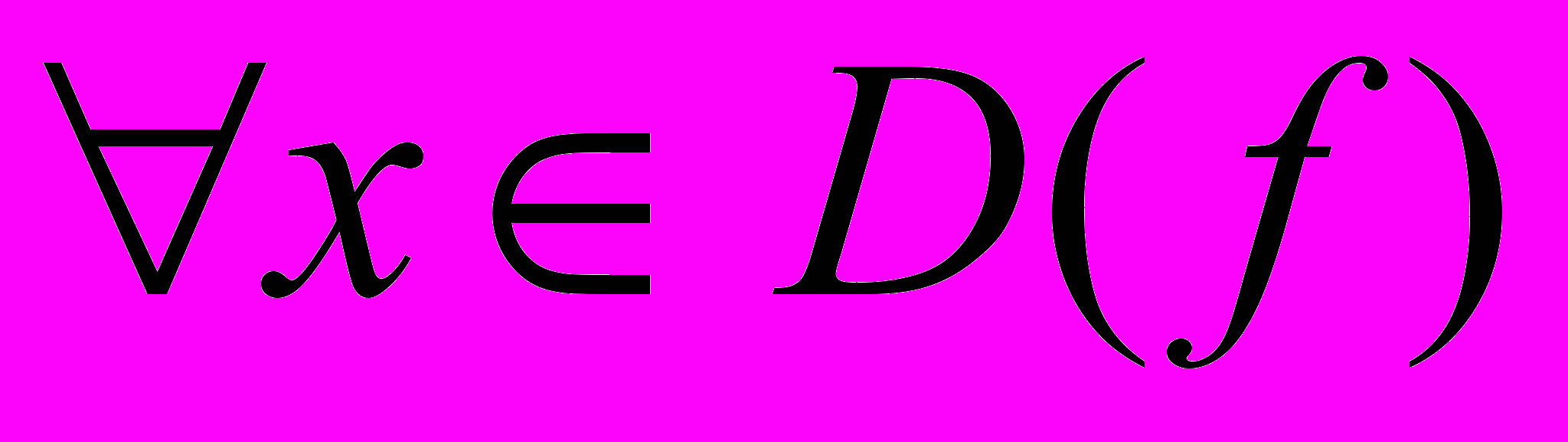 .
.1
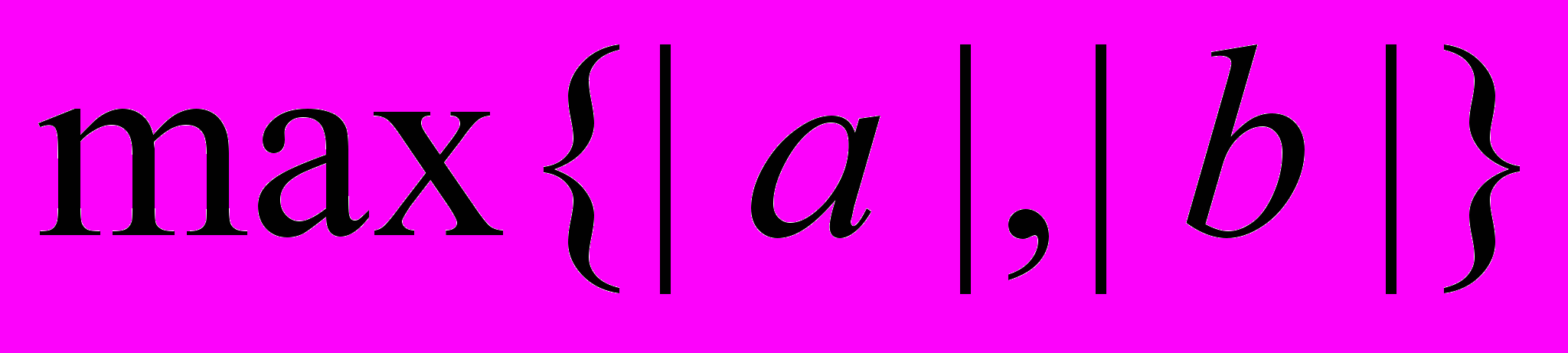 обозначает наибольшее из чисел
обозначает наибольшее из чисел 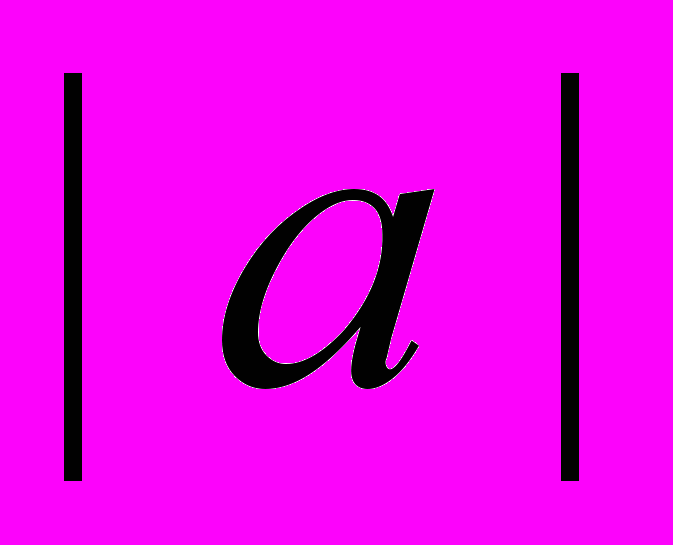 и
и 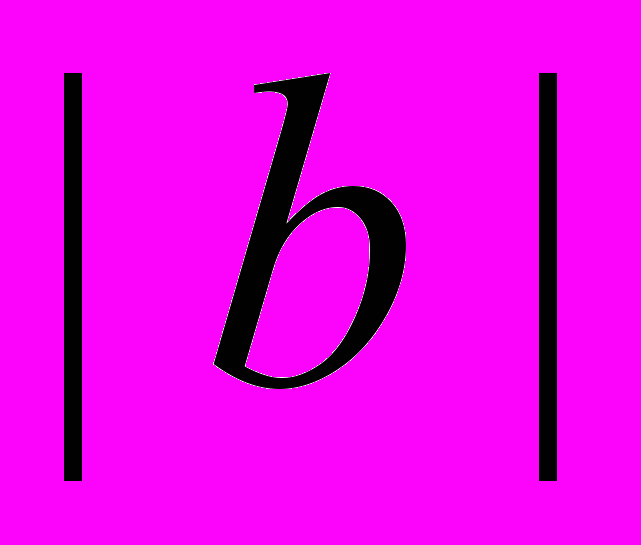 .
.