В. М. Казиев Об арифметических возможностях компьютера и компьютерных возможностях арифметики

Вид материала

Документы

Содержание Задачи и упражнения

Подобный материал:

• Конспект урока литературы в 6-а классе оош №17 г. Славянска Тема: Роман Д. Дефо книга, 86.32kb.
• Здоровье, 1311.39kb.
• Контакты: Руководитель проекта, 157.1kb.
• После трех уже поздно, 1119.32kb.
• Размышления о чужой ностальгии, 87.14kb.
• 1. Новая экономика. Дискуссия о ее возможностях и пределах, 1329.86kb.
• «Социальная адаптация личности школьников», 129.06kb.
• «Социальная адаптация личности школьников», 98.42kb.
• «Таблицы Excel», 75.81kb.
• 1. Стратегия государственной молодежной политики и развитие Российской Федерации, 363.39kb.

Источник - ссылка скрыта

Опубликовано в журнале "Информатика и образование" (N4/2002)

В.М. Казиев

Об арифметических возможностях компьютера
и компьютерных возможностях арифметики

При изучении математики и информатики необходимо акцентировать внимание обучаемых на основные различия действий с числами в обычной, неограниченной ("человеческой") и ограниченной ("машинной") разрядной сетке, арифметике, которые часто остаются "за кадром". Игнорирование этого может приводить к нежелательным последствиям - вплоть до абсолютизации возможностей компьютера и игнорированию адекватных описаний структур данных и операций с ними (например, проверки чётности числа x условием вида int(x/2)=x/2 и т.д.).

Множество чисел ограниченной разрядности является моделью расширенной числовой прямой, т.е. числовой прямой с тремя абстракциями (потенциальной осуществимости): нуль, положительная бесконечность, отрицательная бесконечность.

Целые числа (в математике) и их аналоги в n - разрядных арифметиках тождественны (по отражаемым им количествам) в рамках их представления в этой разрядности. При этом можно отметить основные отличия представления чисел в поле памяти человека и в поле памяти n - разрядной арифметики (компьютера):

 бесконечное и счётное (нумеруемое) множество целых чисел Z представляется отрезком [-N;+N], где N - максимальное число, представимое в этой арифметике (многоточие - общее число единиц равное n): N = 111...1₂;

 бесконечное и несчётное множество действительных чисел, располагающееся на числовой оси от "минус бесконечности" до "плюс бесконечности" равномерно и плотно, представляется в n-разрядной арифметике множеством с неравномерной плотностью (сгущение у нуля и сжатость со стороны меньших чисел);

 нуль во множестве действительных чисел R в любой своей окрестности имеет множество чисел, а нуль в n-разрядной арифметике представлен изолированно: в окрестности с радиусом, равным наименьшему представимому в этой арифметике числу, нет других чисел.

С точки зрения обычной арифметики, например, в интервале (-1;1) имеется бесконечное множество "плотно" расположенных точек, причем в любой окрестности каждой такой точки имеется хотя бы одна точка из этого множества. Такую арифметику называют часто регулярной арифметикой.

Машинная же арифметика нерегулярна - точки интервала сгущаются около нуля. Кроме того, в этом интервале точка х "изолирована" - если взять её любую окрестность (х-а; х+а), где а - число, которое не превосходит машинного нуля (наименьшего представимого в машине числа), то в этом интервале нет других точек (отличных от х). Говоря языком теории вероятностей, плотности распределения чисел в регулярной и нерегулярной арифметике - различны, как, впрочем, плотности распределения целых и вещественных чисел в одной и той же арифметике. Множество вещественных чисел в машинной арифметике представляется как подмножество множества рациональных чисел, определяемое разрядностью арифметики.

Есть и другие особенности этих множеств (связанные, например, с выполнением операций), но указанные выше особенности - основные.

Различия в представлении чисел в обычной и в машинной (n-разрядной) арифметике ограничивают как "арифметические возможности" компьютера, так и "компьютерные возможности" арифметики, математики, использование математических методов, алгоритмов в компьютерах.

Нужно всегда иметь в виду, что точность в теоретической математике - понятие абстрактное и в практической математике может возникать иллюзия точности там, где её на самом деле нет, - если не произведена достаточно корректная интерпретация научно-практической точности т.е. нет корректной договорённости о пределах возможных значений неизбежных погрешностей в рамках рассматриваемых вычислительных ресурсов, например, трудоёмкости и времени, а также не оговорена стратегия и тактика управления этой погрешностью.

Так как диапазон n-разрядных чисел системы счисления с основанием p находится в пределах



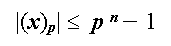
то для представления дробных чисел этот диапазон ещё уменьшается, так как часть разрядов необходимо отвести под изображение мантиссы. Таким образом, имеются так называемые "зоны нечувствительности" форм представления чисел в n-разрядных арифметиках.

В 1937 году немецким учёным Конрадом Цузе (разработавшим, кстати говоря, не только ряд положений арифметических основ цифровых машин, но и прототипы ЦВМ - машины "Ц-1", "Ц-2") для увеличения диапазона чисел, представимых в арифметике двоичных чисел, а также для повышения точности этого представления чисел, было предложено представление чисел в плавающей, нормализованной форме.

Число x представляется в нормализованном виде:



где m - мантисса числа, k - целый порядок числа,



Пусть даны два числа



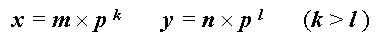
Тогда можно проверить, что результаты выполнения операций будут равны:



Если из n разрядов, отводимых под изображение чисел, m двоичных разрядов отвести под мантиссу, k - под порядок, один разряд - под знак числа и один разряд - под знак порядка (например, 0 - плюс, 1 - минус), то диапазон представимых в форме с плавающей запятой чисел резко увеличивается (m + k + 2 = n):



(многоточие соответствует k единицам).

Числа, меньшие нижней границы положительных чисел и большие верхней границы отрицательных чисел, считаются равными нулю, не различаются между собой. Числа, большие верхней границы положительных чисел, полагаются равными положительной бесконечности, а меньшие нижней границы отрицательных - отрицательной бесконечности. Сравнение двух разных по величине чисел в арифметике с ограниченной разрядностью может приводить поэтому к неверному результату, как и сравнение двух равных в таких системах чисел с точки зрения математической.

Такое представление очень удобно для хранения в ЭВМ, так как на самом деле необходимо хранить не само число, а его знак, мантиссу, порядок и знак порядка и все операции с числами сводятся к операциям с этими, более "компактными", объектами. Операции с этими объектами достаточно просты: сравнение знаков, увеличение, уменьшение порядка, сложение мантисс, нормализация, т.е. в конечном итоге сводятся к достаточно просто реализуемым операциям сдвига, выравнивания, сравнения разрядов. Это упрощает аппаратную их реализацию и является основой для различных архитектур - микропрограммных, RISC и др.

Пример. В 16-разрядной арифметике двоичных чисел можно представить диапазон целых чисел х:



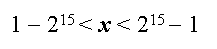
(старший разряд отвели под знак числа). Если в этой арифметике (не меняя её разрядность) отвести 7 разрядов под мантиссу, а 7 разрядов - под порядок, то уже представим диапазон чисел:



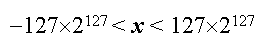
(два разряда - под знак числа и знак порядка; несколько упрощена и общая картина представления - для наглядности).

К "неудобствам" этой формы представления чисел можно отнести возможность возникновения следующих "особо опасных" ситуаций:

а) если число достаточно мало, например, а=0.12Е+00, то оно может быть представлено любым числом из наименьшего интервала включающего а, в частности, числом 0.120000001 или 0.199999999 и в этом случае сравнивать на равенство "в лоб" нельзя (вещественные числа в форме с плавающей запятой на совпадение опасно сравнивать);

б) порядок выполнения операций может влиять на результат, например, в 4-разрядной арифметике с фиксированной запятой 20.0000+0.0001=20.0001, но при этом 0.2000Е+02+0.1000Е-05=0.2000Е+02;

в) может возникнуть так называемая ситуация "переполнения порядка" при сложении (умножении) "очень больших чисел" или "исчезновения порядка" при сложении (умножении) "очень малых чисел", например, результат 0.6000Е+39*0.1200Е+64 равен 0.9999Е+99 (или не определен) и результат 0.6000Е-35*0.0200Е-65 равен 0.9999Е-99 (или не определен) при соответствующим образом определенной разрядности десятичной арифметики;

г) при сложении чисел с плавающей запятой (а в конечном счёте, все операции выполняются, как известно, через сложение, точнее, - через поразрядное сравнение и сдвиги) происходит выравнивание порядков для последующего сложения мантисс, а при выравнивании степеней может происходить потеря (усечение) младших разрядов, например, такая ситуация может возникнуть при сложении одного "очень большого числа" с одним "очень малым числом" (почему?).

Реализация операций в арифметике с плавающей запятой требует необходимости выравнивания порядков при сложении и вычитании и нормализации результатов. Если диапазоны чисел, представимых в арифметике с фиксированной запятой и с плавающей запятой, соизмеримы, то числа с фиксированной запятой могут более точно представлять (кодировать) величины, так как свободны от часто необходимой для чисел с плавающей запятой операции округления. При машинной реализации такая операция обычно выполняется в устройстве-предшественнике (например, сумматор) с высокой точностью (большой разрядностью), а затем отсылается в устройство-преемник (например, регистр) с учётом заданной (например, декларированной в описаниях типов и структур данных) точности или с сохранением всех значащих разрядов. Таким образом, копирование непосредственного результата операции происходит либо с помощью операции округления, либо с помощью операции усечения.

Эти две основные операции (кроме арифметических операций) вводятся следующим образом:

 усечение, отбрасывание цифр числа до определённого разряда, например, до ближайшего, меньшего целого числа и т.п.;

 округление, усечение с коррекцией числа по определённым правилам, например, до числа кратного заданному числу, до ближайшего целого и т.п.

Пример. Операция взятия целой части числа x (функция Антье - [x] или int(x)) - операция усечения, [2.65]=2, [-1.999]=-2. Операция взятия целой части числа x + 0.5 вместо значения числа х есть округление {x} до ближайшего целого, {1.05}={0.91}=1, {2.61}=[2.6+0.5]=3.

Задачи и упражнения

1. Задайте 20-ую систему счисления и выполните операции над числами в этой системе.
   
2. В саду 1000 деревьев - 140 яблонь и 420 груши. В какой системе счисления посчитаны эти деревья? Найдите общее число деревьев в саду в шестнадцатеричной системе.
   
3. Имеются ящики: 4 черных, 3 красных, 2 желтых и 1 зеленый (ящики посчитаны в десятичной системе). В каждом черном ящике - 21_p шара, красном - 23_p шара, жёлтом - 23_p шара, зелёном - 111_p шара. Определить основание p системы счисления, в которой были посчитаны шары, если всего было 244_p шаров. Чему равно общее число шаров в восьмеричной системе?
   
4. Число х = 176_p (рассматриваемая в системе счисления с основанием р, 1<р<20) делится нацело на 7. Найти р (не перебирая все указанные р). Вычислить х в восьмеричной системе.
   
5. Найти основание системы р (в которой было выполнено сложение) и неизвестные цифры (обозначены ?), если 24??1 + ?235? = 116678.
   
6. Какова разрядность двоичной системы счисления, в которой представим лишь диапазон чисел из интервала (-255; 255)?
   
7. Найти числа, соответствующие понятиям "нуль" и "бесконечность" в 10-разрядной десятичной системе счисления и сравнить их. Указать эти числа для двоичной, восьмеричной и шестнадцатеричной систем.
   
8. Сформулировать какие-то признаки делимости на 8 (на 11) числа x записанного в системе счисления с основанием p=12, не переводя эти числа в десятичную систему. Рассмотреть другое значение р.
   
9. Найти число х, записанное в системе счисления с основанием р, если оно совпадает со своим дополнительным кодом. При каких р это возможно?
   
10. Найти все ошибки в следующих утверждениях и объяснить все причины их появления:
    

а) 1111111111=2¹⁰ -1,

б) 7777777777=7*1111111111=7*(2¹⁰-1),

в) 7777777777=8¹⁰-1,

г) из б) и в) следует, что 7*2¹⁰- 6=8¹⁰ или 2³⁰=7168 (!).

11. Запишите числа 0, 42, 1000, 1, -25, -100 в формате целых чисел в шестнадцатеричную ячейку памяти, изобразив ее схематически.
    
12. Запишите числа 99, 12.5, 0.025, -4.18, -0.01 в формате вещественных чисел с фиксированной запятой (ячейка памяти- 16-разрядна, разряды 1-8 отводятся под целую часть, разряды 9-15 - под мантиссу, 0 - знак). Оцените погрешность такого представления чисел.
    
13. Какое максимально положительное и минимально отрицательное число можно записать в указанную для задачи 12 ячейку памяти?
    
14. Запишите числа 99, 9999, 12.7, 0.005, -64.5, -0.002, 0 в формате чисел с плавающей запятой в ячейку памяти разрядности 16 (нулевой разряд - знак числа, первый разряд - знак порядка, 2-12 разряды - мантисса, 13-15 разряды - порядок). Оцените погрешность такого представления чисел.
    
15. Какое максимально положительное и минимально отрицательное число можно записать в ячейку памяти, указанную в задаче 14?
    
16. Какой минимальной разрядности должна быть ячейка памяти у условной трехадресной ЭВМ с однородной памятью, если она имеет набор из 50 различных команд и 2 мегабайта адресуемой памяти, а адресуется каждый байт.