Два вида зарядов в электродинамике
| Вид материала | Документы |
- Электризация тел. Два рода зарядов. Взаимодействие зарядов. Электроскоп, 63.08kb.
- Программа dymas позволяет рассчитывать как траектории отдельных зарядов, так и все, 22.32kb.
- Электрические и магнитные явления, 37.61kb.
- А. В. Чернетский процессы в плазменных системах, связанные с разделением электрических, 299.03kb.
- Специальная теория относительности (сто) покоится на двух китах: оптике и механике,, 544.46kb.
- Рекомендации по анализу внеклассных воспитательных мероприятий Известны два полхода, 797.09kb.
- Рекомендации по анализу внеклассных воспитательных мероприятий Известны два полхода, 806.43kb.
- Рекомендации по анализу внеклассных воспитательных мероприятий Известны два полхода, 855.03kb.
- Его причины и особенности, силовые связи между частицами среды, перенос энергии без, 14.74kb.
- В классификации рыночных структур Штакельберга они вообще не разделяются на два отдельных, 211.98kb.
Проблемы, заблуждения и ошибки в электродинамике. Часть 3
Часть 3. Два вида зарядов в электродинамике.
Корнева М.В., Кулигин В.А., Кулигин Г.А. (Исследовательская группа «Анализ»)
Аннотация. Доказано, что заряды в уравнениях Максвелла существуют два вида зарядов. Показано, что учет этих зарядов ведет к разделению уравнений на две независимых группы: уравнения для волн и уравнения для полей зарядов. Показано, что только такой подход избавляет электродинамику от многих противоречий, заблуждений и предрассудков.
Введение
«Группа «Анализ» не ставит своей специальной задачей выдвижение каких-либо гипотез. Она четко понимает, что строить новую науку на гнилом основании – авантюризм и безответственность. Главная цель – очистить физические теории от внутренних противоречий, математических, физических и гносеологических ошибок, чтобы создать платформу для новых исследований.» [1].
Теперь мы перейдем к анализу формальных «доказательств», из которых следуют ошибочные или некорректные выводы. В настоящее время эти выводы превратились в предрассудки. В этой части речь будет идти о калибровках и единственности решений уравнений Максвелла. Она является логическим продолжением Второй части обзора «Проблемы, заблуждения и ошибки в электродинамике».
Как известно, что для волнового уравнения доказана теорема существования и единственности решения при заданных начальных и граничных условиях. Уравнения для полей Е и Н можно представить в виде волновых уравнений и использовать теорему о существовании и единственности решения.
Однако сейчас мы будем говорить не о математической, а о физической единственности решения. Причина в том, что решения одной и той же физической задачи может иметь различные функциональные выражения, интерпретация которых может оказаться взаимоисключающей. Результат зависит как от начальных и граничных условий, так и от выбора калибровки уравнений Максвелла.
В одних случаях в решении могут появиться продольные волны, существование которых противоречит эксперименту. В других случаях появляется мгновенное действие на расстоянии, которое противоречит современной концепции о существовании «предельной скорости распространения взаимодействий».
Эти вопросы достаточно широко обсуждаются в зарубежной литературе [2] (см. библиографию в этой работе). В российских «толстых» научных журналах обсуждение подобных проблем не допускается. «Толстые журналы» это шаг в прошлое, т.е. схоластика и тиражирование закоренелых ошибок. Согласно критерию Гинзбурга-Круглякова [3]: “ЕСТЬ МИРОВАЯ НАУКА, А ВСЕ, ЧТО НЕ ВПИСЫВАЕТСЯ В ЕЕ КРИТЕРИИ – ЭТО ЛЖЕНАУКА”. Этот критерий обрекает российскую науку на глубокий застой и ошибки.
-
Продольные волны
Рассмотрим проблему продольных волн в калибровке Лоренца. Продольные волны могут образоваться как скалярным потенциалом, так и безвихревой частью векторного потенциала. В [4] относительно преобразования потенциалов в калибровках пишется: «Описанная неоднозначность потенциалов всегда дает возможность выбрать их так, чтобы они удовлетворяли одному произвольному, дополнительному условию, - одному, так как мы можем произвольно выбрать только одну функцию ψ в (18.12). В частности, всегда можно выбрать потенциалы так, чтобы скалярный потенциал был бы равен нулю».
Попробуем реализовать такую возможность, опираясь на уравнения Максвелла в калибровке Лоренца. Для удобства мы представили векторный потенциал и ток как сумму вихревой и безвихревой компонент:
A = A1 + A2; (div A 1 = 0; rot A2= 0); j = j1 + j2; (div j1 = 0; rot j2 = 0)
Применим операцию div к волновому уравнению для векторного потенциала A2 и продифференцируем по времени волновое уравнение для скалярного потенциала. Сложив результаты, получим

или
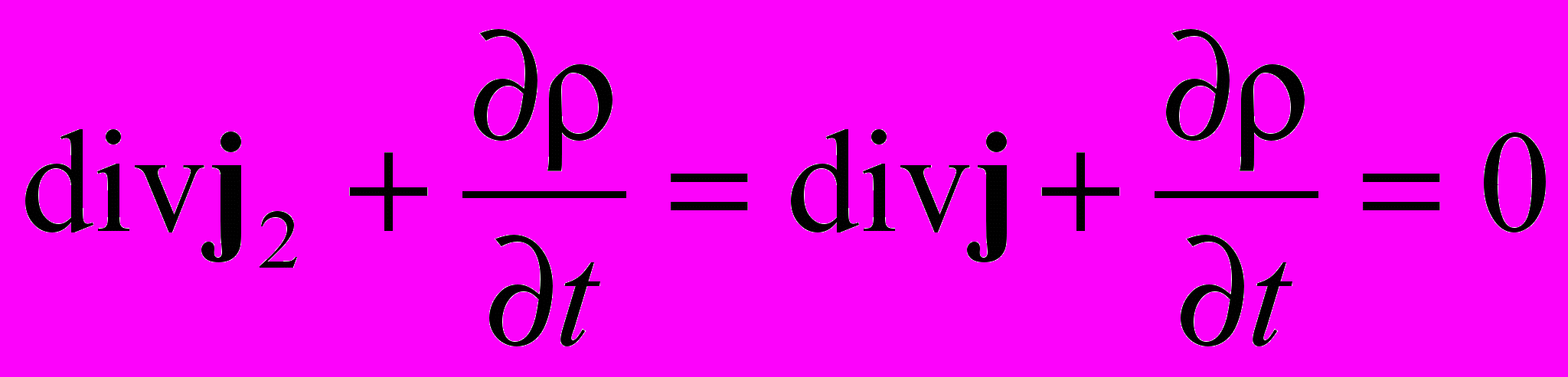
Итак, мы получили уравнение непрерывности для тока.
С другой стороны, мы должны потребовать отсутствия продольных волн скалярного и векторного потенциала, как об этом пишется в работе [5] (Глава 7). Это будет возможно, когда поле скалярного потенциала будет «подавлено» безвихревой частью поля векторного потенциала ЕL = 0. Запишем это условие, присоединив к нему уравнение непрерывности для векторного потенциала
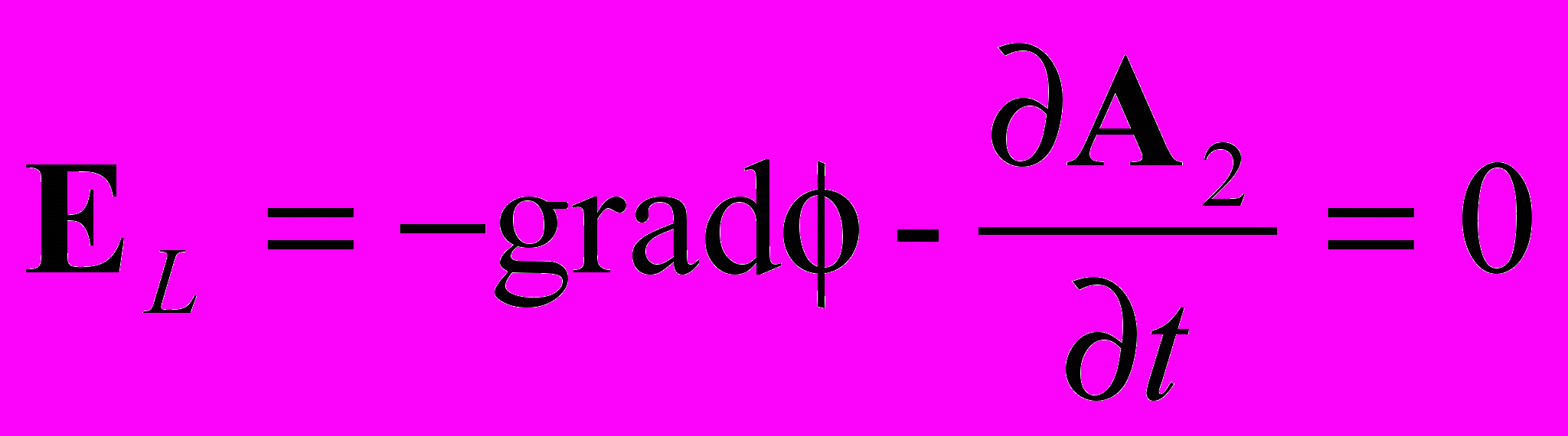
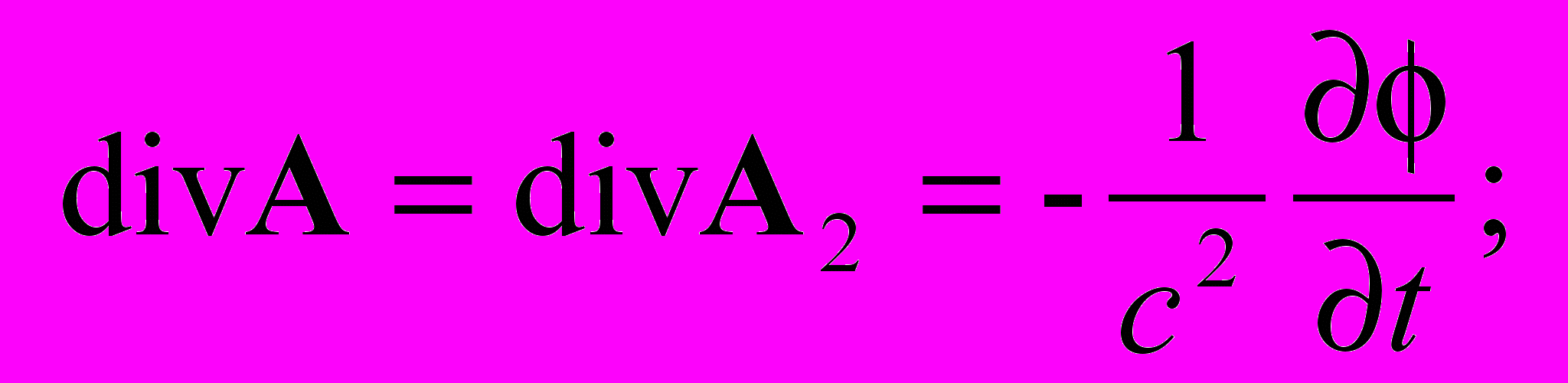
Если теперь мы применим к этим уравнениям оператор , то получим

Исключая плотность тока ток или плотность пространственного заряда, получим

Как мы видим, плотность тока и плотность пространственного заряда должны удовлетворять волновым уравнениям. Следовательно, плотность пространственного заряда имеет запаздывающий характер (r - ct), соответственно, плотность тока будет равна j = (r - ct)c . А это и есть безынерциальная плотность тока, и заряда. Таким образом, в уравнениях Максвелла фигурируют два вида проводимостей: проводимость, обусловленная инерциальными носителями, и проводимость безынерциальных носителей (положительных и отрицательных). Тем самым мы другим способом подтвердили выводы Второй части нашей работы [6].
-
Калибровка уравнений электродинамики
Теперь мы можем, опираясь на принцип суперпозиции, представить заряды и токи в уравнениях Максвелла в виде суммы и разделить эти уравнения на две группы (для безынерциальных зарядов и для инерциальных зарядов). Уравнения для разных видов зарядов должны быть различными. Инерциальные заряды не могут описываться волновыми уравнениями.
В то же время, мы не можем выходить за рамки уравнений Максвелла, поскольку здесь пришлось бы вводить и обосновывать какие-то гипотезы, которых мы в нашем анализе стараемся избегать. Как и во Второй части положим, что

Результаты сведены в Таблицу 1 и Таблицу 2.
Таблица 1.
| Уравнения для безынерциальных зарядов и токов | |
| Калибровка Лоренца | Кулоновская калибровка |
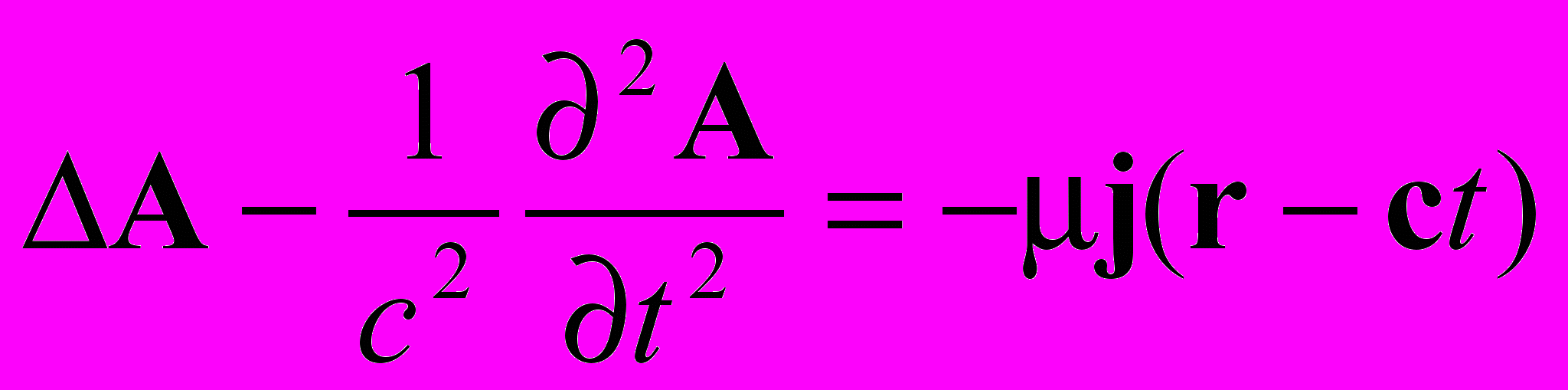 |   |
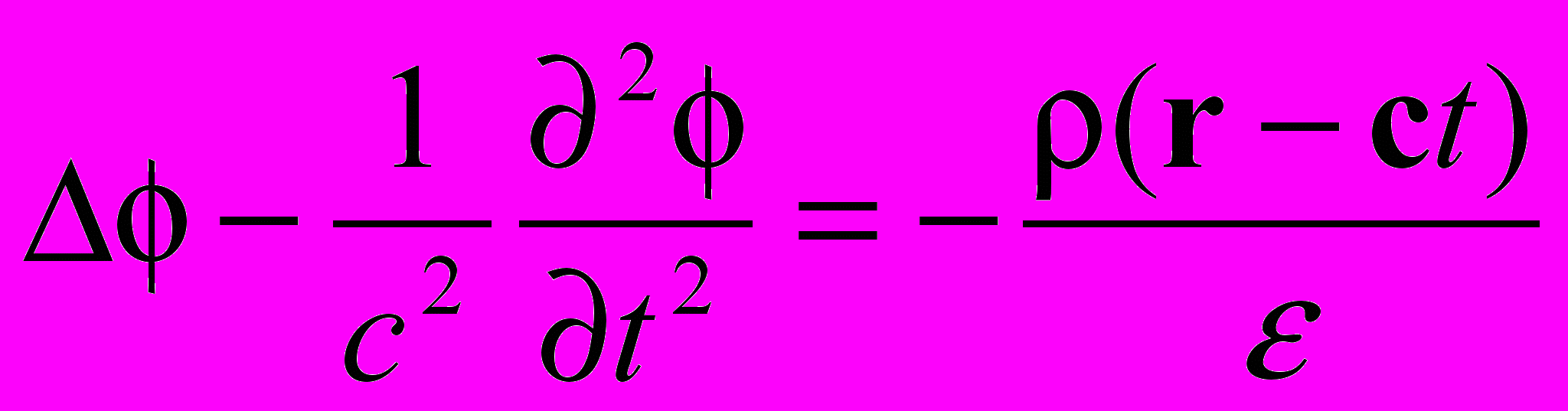 | Уравнение для скалярного потенциала исчезло, поскольку оно скомпенсировано полем векторного потенциала А2 Уравнение для векторного потенциала А2 исчезло по той же причине уравнение для скалярного потенциала |
 ; ; 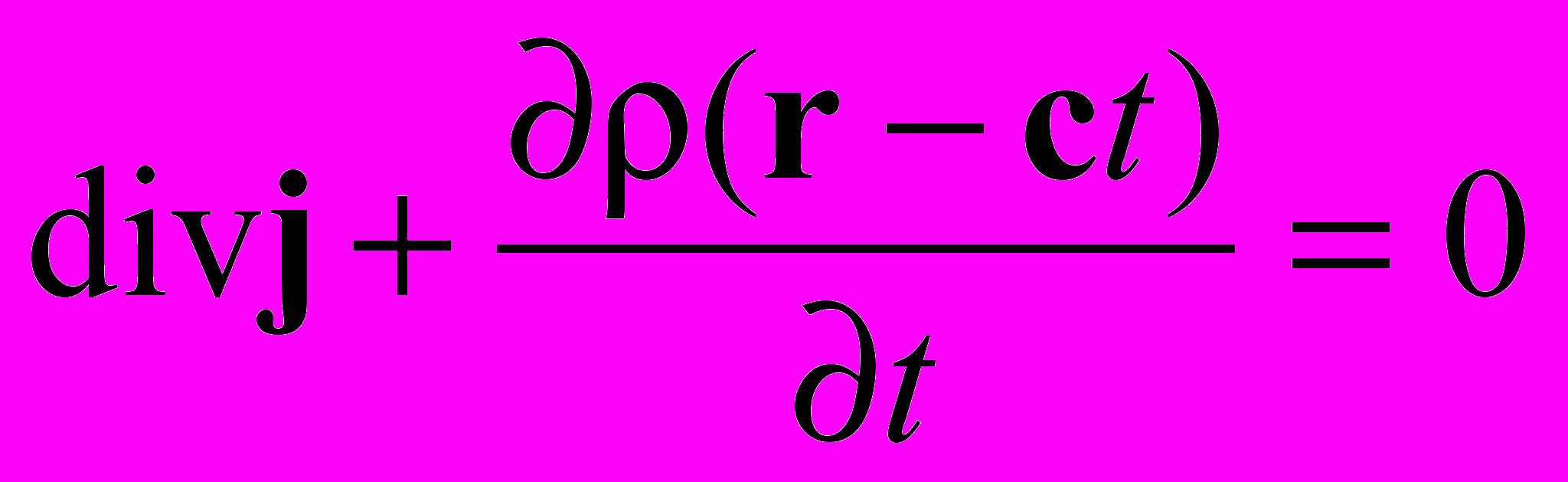 | |
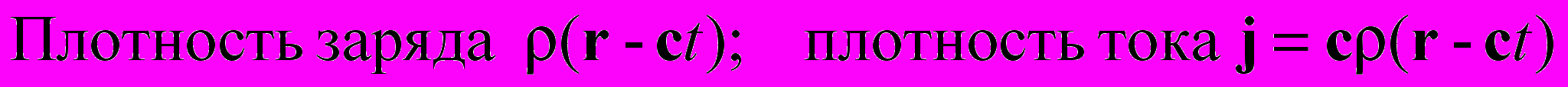 | |
Первая группа описывает запаздывающие потенциалы, отвечающие за излучение и прием электромагнитных волн. Вторая группа описывает поля инерциальных зарядов. Для ясности мы будем обозначать индексом «0» потенциалы инерциальных зарядов.
Обе группы уравнений независимы друг от друга. Теперь векторный потенциал поля заряда обретает четкий физический смысл. Становится более ясным подход к эффекту Аронова-Бома.
Таблица 2.
| Уравнения для инерциальных зарядов и токов | |
| Уравнение для векторного потенциала |  |
| Уравнение для скалярного потенциала |  |
| Связь потенциалов | 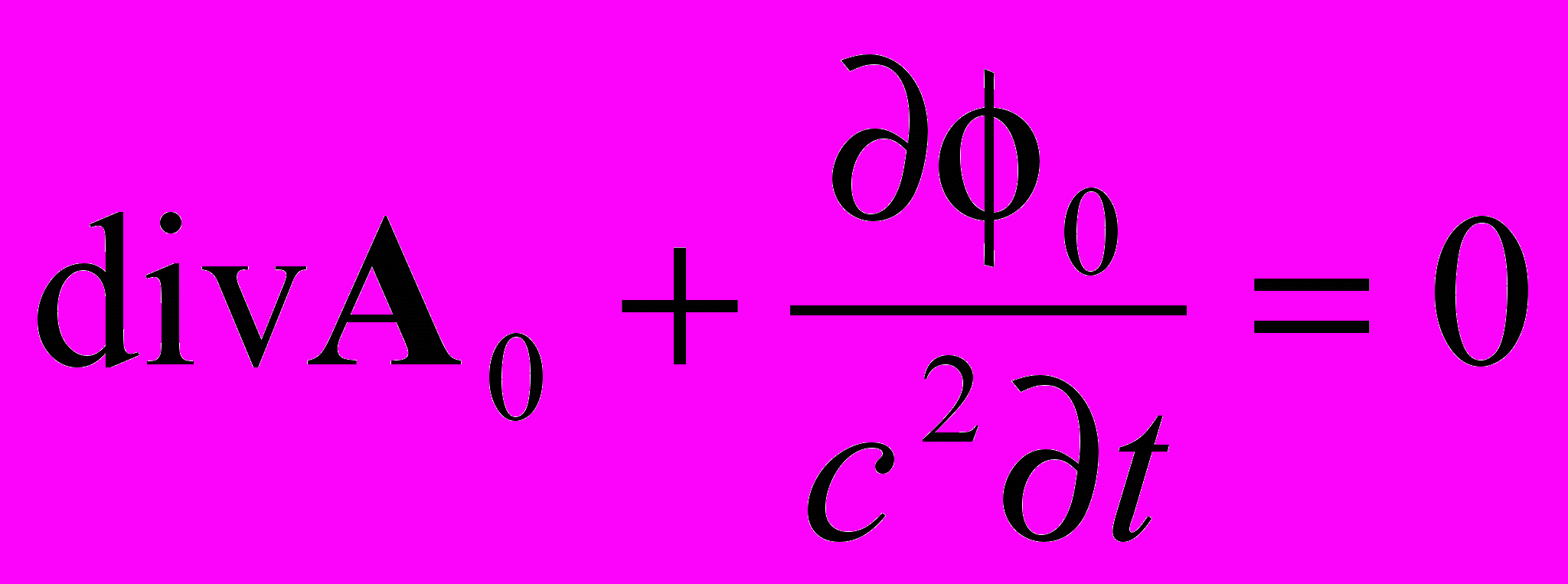 ; A0 = 0 v/c2 ; A0 = 0 v/c2 |
| Плотность заряда и плотность тока | j0 = 0v; 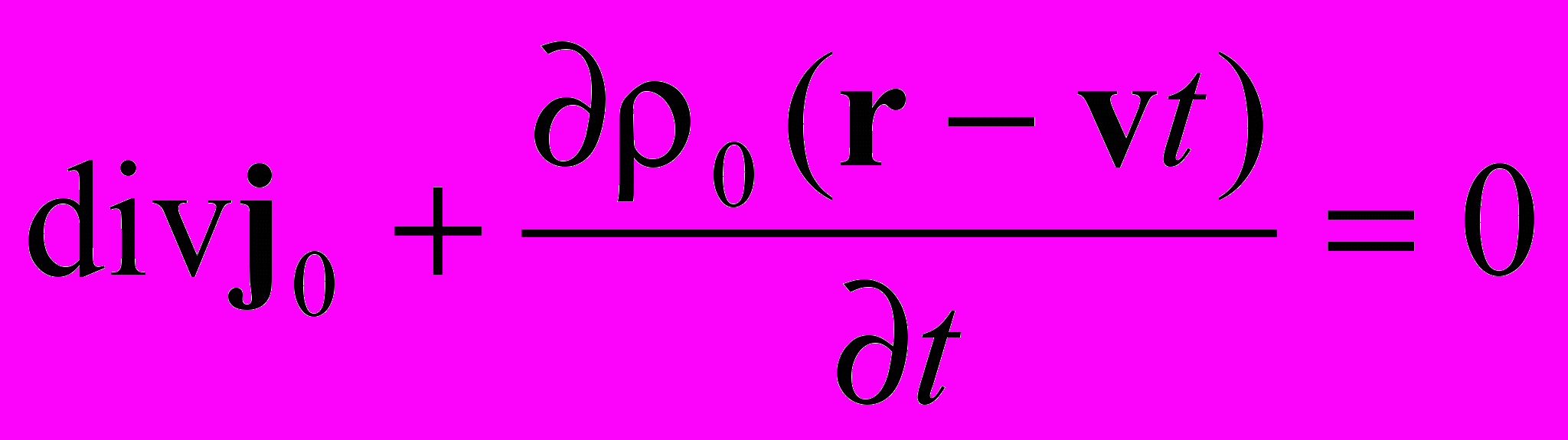 |
| | |
Пожалуй, основная ошибка исследователей заключалась в том, что они не проанализировали до конца свойства решений волновых уравнений при наличии уравнений связи (уравнение непрерывности потенциалов) и свойства уравнений Максвелла. Это «потянуло» за собой цепь последующих ошибок и предрассудков. Обоснование уравнений для инерциальных зарядов дано в Приложении 1.
Появление мгновенно действующих потенциалов в уравнениях Максвелла неизбежно. Это не согласуется со СТО и требованием Лоренц-ковариантности уравнений. Заметим, что СТО была создана на основе электродинамики. Следовательно, изменение уравнений Максвелла повлечет за собой и изменение эйнштейновской теории. Этот вопрос мы обсудим в Четвертой части. А сейчас мы покажем результаты мгновенного действия на расстоянии применительно к квазистатическим явлениям.
-
Скорость распространения взаимодействий
Прежде, чем переходить к дальнейшему анализу, нам необходимо определить свое отношение к мгновенному действию на расстоянии. В настоящее время существует термин «скорость распространения взаимодействий». Причиной его появления послужил предрассудок: для передачи характеристик взаимодействия необходим некий «посредник». Процитируем БСЭ:
«ВЗАИМОДЕЙСТВИЕ в физике, воздействие тел или частиц друг на друга, приводящее к изменению состояния их движения. В механике Ньютона взаимное действие тел друг на друга количественно характеризуется силой. Более общей характеристикой В. является потенциальная энергия. Первоначально в физике утвердилось представление о том, что В. между телами может осуществляться непосредственно через пустое пространство, к-рое не принимает никакого участия в передаче В.; при этом В. перемещается мгновенно…. В этом состояла т.н. концепция дальнодействия….
…Было доказано, что В. электрически заряженных тел осуществляется не мгновенно и перемещение одной заряженной частицы приводит к изменению сил, действующих на др. частицы, не в тот же момент, а лишь спустя конечное время. … Соответственно имеется «посредник», осуществляющий В. между заряженными частицами. Этот посредник был назван электромагнитным полем. …. Возникла новая концепция – концепция близкодействия, к-рая затем была распространена на любые другие В.»
«Доказательство», о котором говорится, опирается на факт, что уравнения Максвелла в калибровке Лоренца сводятся к волновым уравнениям. Само определение «взаимодействия», приведенное в БСЭ, не корректно.
На самом деле взаимодействие есть процесс, который характеризуется взаимным изменением характеристик состояний взаимодействующих материальных объектов (переход видов энергии из одного вида в другой и обратно, от одного материального объекта к другому, изменение движения самих материальных объектов и т.д.). Взаимодействие локализовано в пространстве и может иметь определенную продолжительность во времени. Его нельзя отрывать от взаимодействующих объектов.
Но взаимодействие не материальный объект, а взаимный процесс. Оно не имеет своих параметров таких, как, например, «масса», и т. п. Это не волейбольный мяч, который «прыгает» через сетку от одной команды к другой. По этой причине говорить о «скорости распространения взаимодействия», беспредметно. «Скорость распространения взаимодействия» - бессодержательное понятие. Можно говорить об интенсивности взаимодействия, о скорости течения процесса во времени, но не о «скорости его распространения».
Приведем пример. Пусть имеются два заряда. Один из зарядов начал двигаться. От него распространяется возмущение (волна). Второй заряд «почувствует» это возмущение только тогда, когда возмущение его достигнет. Существует ли взаимодействие второго заряда с этим возмущением, если это возмущение еще только распространяется и не достигло второго заряда? О какой «скорости распространения взаимодействий» можно говорить, если взаимодействие еще не наступило? Взаимодействие с волной наступит только тогда, когда возмущение достигнет второго заряда.
Отождествление процесса распространения волны и «распространения взаимодействия» есть следствие философской несостоятельности (философского невежества) человека, придерживающегося такой терминологии.
Как показано в [7] существуют две модели причинности, связанные между собой: эволюционная и диалектическая. Как правило, физики под причинностью понимают эволюционную модель: «сначала он меня в нос, потом я ему по носу»! Это однобокое понимание причинности послужило основой для многих предрассудков. Мгновенное действие на расстоянии опирается на диалектическую модель причинности и не противоречит этой модели причинности. На диалектическую модель опираются все парные взаимодействия в природе.
Помимо «волновых» взаимодействий (взаимодействие заряда и волны) в физике существуют «контактные» взаимодействия. Примером может служить столкновение биллиардных шаров. При таком взаимодействии (соударении) имеет место «точечный» контакт. Нам представляется, что взаимодействия мгновенного характера тоже можно отнести к контактному типу.
Представьте себе, что с горки спускается платформа, и после разгона упруго ударяет другую, стоящую на ее пути. Такое соударение относится к «точечному» контактному типу. Теперь поместим между тележками упругую пружину. Если пружина обладает массой, то при ударе движущейся тележки по пружине вдоль пружины будет распространяться волна сжатия. Скорость этой волны будет зависеть от жесткости и массы пружины.
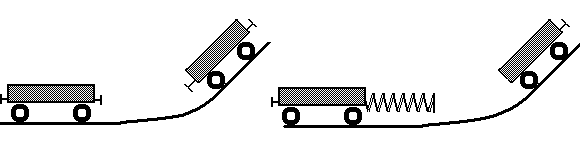
Рис. 1. Столкновение тележек
Допустим теперь, что масса пружины равна нулю. В пределе скорость распространения волны от движущейся тележки к неподвижной и обратно будет бесконечной. Такое соударение уже не будет «точечным», поскольку тележки разделены пружиной. Однако взаимодействие сохранит свой контактный характер. Такое взаимодействие мы назвали контактным взаимодействием объемного типа.
Теперь можно рассмотреть случай взаимодействия электрических или гравитационных зарядов. Здесь возможны два варианта объяснения. Они зависят от того, где по нашему предположению сосредоточена электромагнитная масса. Электромагнитная масса определяется двояко:
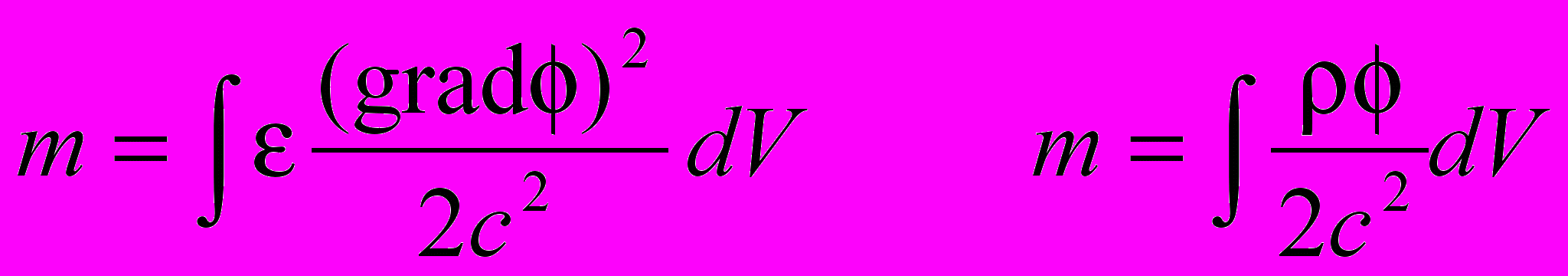
Согласно первому подходу энергия и электромагнитная масса распределены в поле, окружающем заряд. Плотность энергии взаимодействия двух зарядов равна w = ε(gradφ1dradφ2). Это означает, что взаимодействие зарядов выражается через контактное взаимодействие полей этих зарядов в каждой точке пространства. В каждой такой точке имеет место точечное взаимодействие. Совокупность всех взаимодействий образует объемное взаимодействие контактного типа.
Согласно второму подходу, который поддерживается нами, электромагнитная масса сосредоточена в самом заряде. Как следствие, электрическое поле, окружающее заряд, не имеет инерциальных свойств подобно безынерциальной пружине, рассмотренной ранее. Аналог этого поля – силовые линии, которые обладают упругими свойствами. Они определяют контактный характер взаимодействия.
-
Электромагнитная масса
Итак, исходя из математического анализа уравнений Максвелла и опытных данных, мы можем достоверно утверждать, что существует два вида проводимости. Соответственно, каждый вид проводимости описывается своими независимыми системами уравнений, своими полями и потенциалами. Положение о том, что поля инерциальных зарядов и поля электромагнитных волн – есть единое поле – оказалось предрассудком. Как следствие, предрассудком, породившим тупиковые направления исследований, является требование от всех уравнений Лоренц-ковариантной формы.
Теперь, опираясь на уравнения для полей зарядов, мы можем привести строгое решение проблемы электромагнитной массы инерциального заряда. Это решение было получено в дифференциальной форме еще в 1974 году. Была подана заявка на открытие (Заявка на открытие 32-ОТ-84-57, 1974), но она была отклонена с формулировкой: «Решение не имеет Лоренц-ковариантную форму» (!). Позже было получено доказательство в интегральной форме [5] (Глава 3), [8] (Часть 5).
Заявка имеет следующую формулировку:
«Электромагнитная масса инерциальной частицы обладает всеми свойствами обычной механической инерциальной массы. Плотность электромагнитной массы не зависит от формы и структуры электрического заряда, а определяется плотностью энергии электрического поля в соответствии с формулой Е = mc2».
Для электромагнитной массы mе справедливы ньютоновские соотношения для импульса и кинетической энергии:

Доказательство опирается на два закона сохранения: закон Умова и закон Ленца [5] (Глава 3), [8] (Часть 5). Опишем их.
Закон Умова. Этот закон имеет стандартную форму уравнения непрерывности для равномерно движущегося заряда
 , где
, где 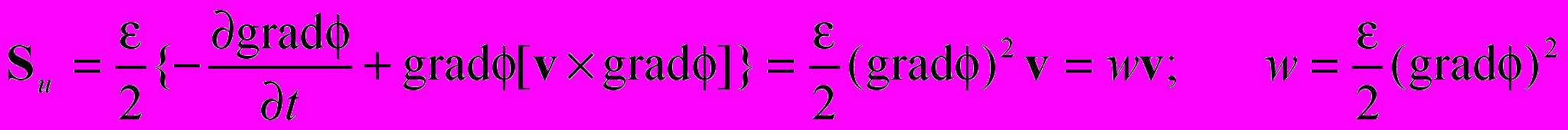
Вектор Умова описывает конвективный перенос энергии поля заряда со скоростью v и принципиально отличается от вектора Пойнтинга. Вектор Пойнтинга описывает перенос энергии электромагнитной волны со скоростью света.
Закон Ленца (закон баланса кинетической энергии).
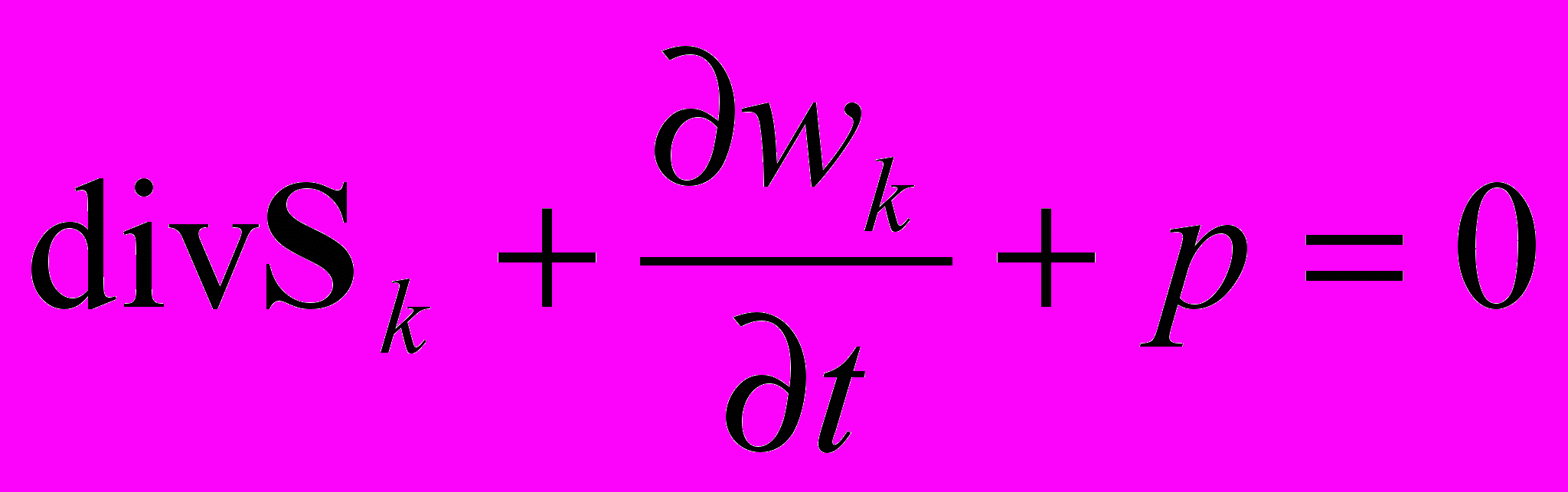 , где
, где
где: Sk - плотность потока Ленца; wk – плотность кинетической энергии; p – плотность работы тока.
Заметим еще раз, что старые интерпретации, опирающиеся на вектор Пойнтинга, неприменимы к полям зарядов. Проиллюстрируем закон Ленца для элемента тока, величина которого зависит от времени.
Векторный потенциал элемента тока

Плотность кинетической энергии

Плотность потока кинетической энергии (вектор Ленца)
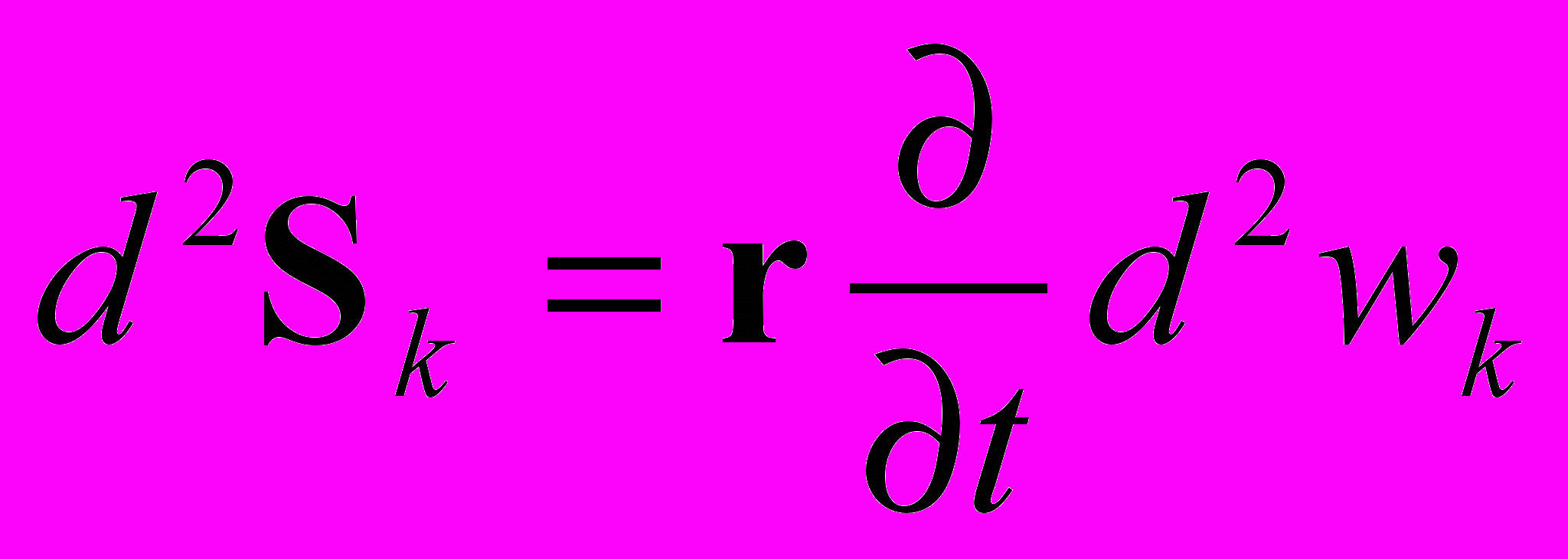
Изменение плотности кинетической энергии d2wk, окружающей элемент тока, связано с плотностью потока кинетической энергии d2Sk. Плотность потока d2Sk, в свою очередь, зависит от изменения квадрата силы тока I во времени. Если величина тока (независимо от его направления) увеличивается, плотность потока кинетической энергии d2Sk положительна и d2Sk направлена вдоль радиуса. Она увеличивает энергию поля векторного потенциала, окружающего элемент тока.
Если же ток уменьшается, тогда поток направлен к этому элементу тока. Он стремится поддержать и сохранить величину тока в этом элементе. При любом изменении величины тока потери на излучение отсутствуют. Заметим, что плотность потока d2Sk уменьшается в пространстве по мере удаления от элемента тока как 1/r3.
Когда изменение тока имеет место, плотность потока кинетической энергии возникает одновременно во всех точках пространства безо всякого запаздывания, т.е. мгновенно. Все это принципиально отличает вектор Ленца от вектора Пойнтинга, который не в состоянии описать возвращение энергии к источнику при уменьшении величины тока источника.
-
Взаимодействие инерциальных зарядов
В работе [9] мы уже говорили о некорректном поучении классической функции Лагранжа для взаимодействующих зарядов из релятивистской функции. В результате этого релятивисты пытались «доказать», что классическая электродинамика не способна объяснить магнитные явления. Решение проблемы электромагнитной массы показало, что при движении заряда образуется векторный потенциал А, образованный движением скалярного потенциала . Это известное соотношение для поля заряда
 . Здесь индекс «0» мы опускаем, чтобы не загромождать формулы.
. Здесь индекс «0» мы опускаем, чтобы не загромождать формулы.В силу этого [5] (Главы 3, 4, 5, 6), скорость относительного движения зарядов должна входить в функцию Лагранжа
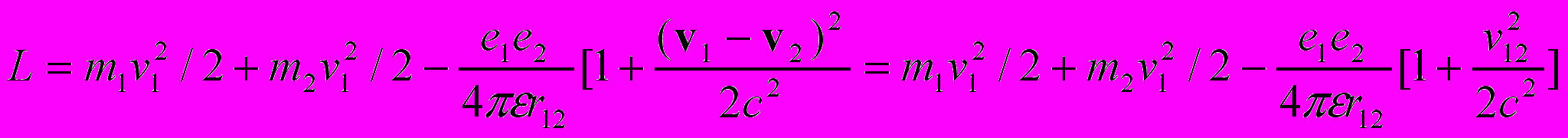 или
или 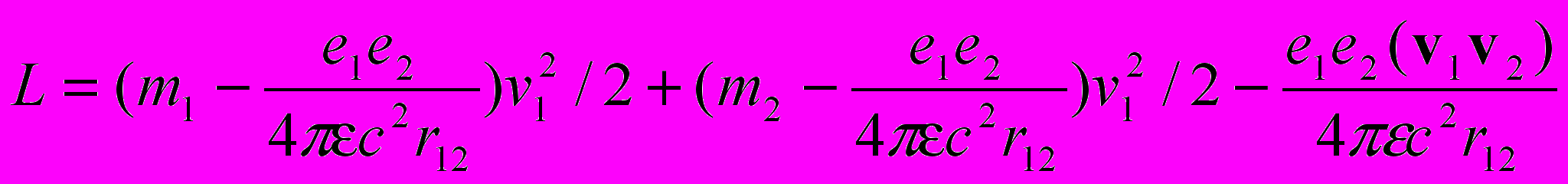 .
. Записанная функция Лагранжа инвариантна относительно преобразования Галилея. Вообще говоря, зависимость взаимодействия от относительной скорости движения зарядов при больших относительных скоростях может иметь более сложный вид, например,
 (5.1)
(5.1)Этот вопрос должен решаться экспериментами. Опираясь на открывшуюся аналогию между явлениями тяготения и квазистатическими явлениями электродинамики, выражение, аналогичное (5.1), можно использовать для описания взаимодействия гравитационных масс.
Остановимся еще на одной фальсификации. В современной классической электродинамике малых скоростей (v << c) функция Лагранжа для заряда в электромагнитном поле равна:
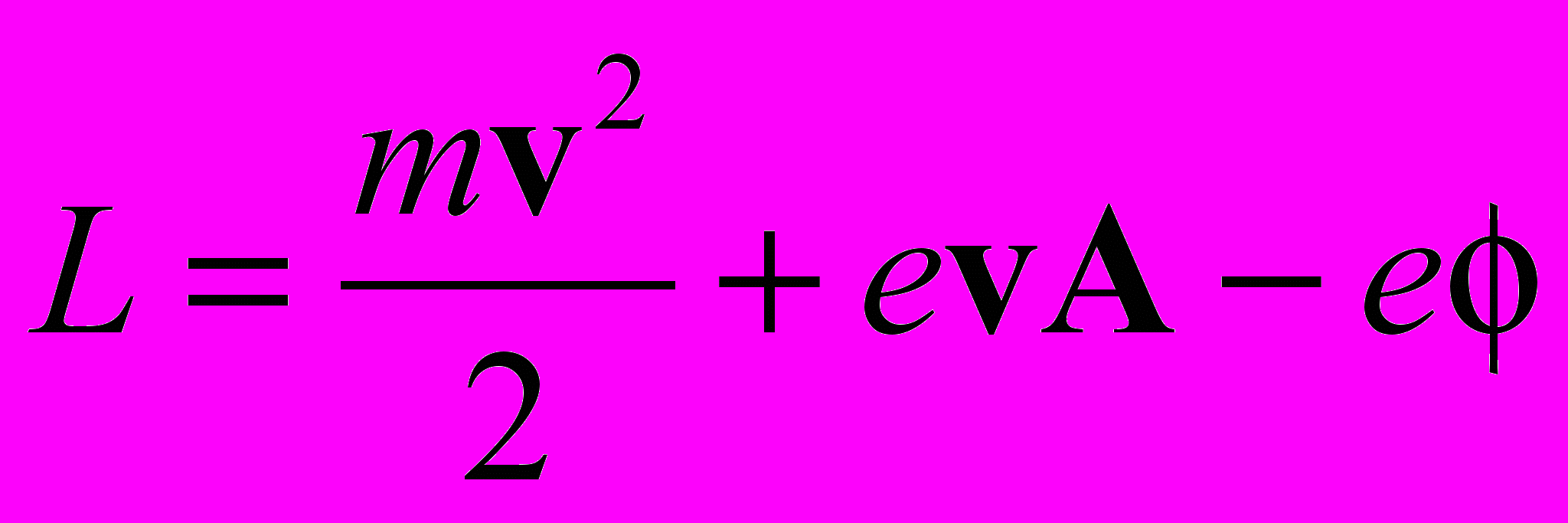
В этом приближении вводится обобщенный импульс частицы. Он равен
 . Функцию Гамильтона записывают в следующей форме
. Функцию Гамильтона записывают в следующей форме
Само введение обобщенного импульса явление нормальное для математики, механики и физики. Фальсификация начинается дальше, когда обобщенный импульс интерпретируют как механический импульс. Релятивисты как бы забывают, что в него входит векторный потенциал А. Эту фальсификацию можно было избежать, если (как уже говорилось) была бы правильно вычислена нерелятивистская функция Лагранжа из релятивистской [9].
-
Взаимодействие токов
Некорректная функция Лагранжа для взаимодействия зарядов «потянула» за собой много противоречий и ошибок в объяснении магнитных явлений. Среди них можно упомянуть «конвективный потенциал», пример Тамма о нарушении принципа равенства действия противодействию и другие проблемы.
Новый подход позволяет разрешить эти противоречия. Например, функция Лагранжа, описывающая взаимодействие для двух элементов тока (взаимодействие двух проводников с токами), имеет следующий вид [5] (Глава 4, 5, 6), [8] (Часть 6)
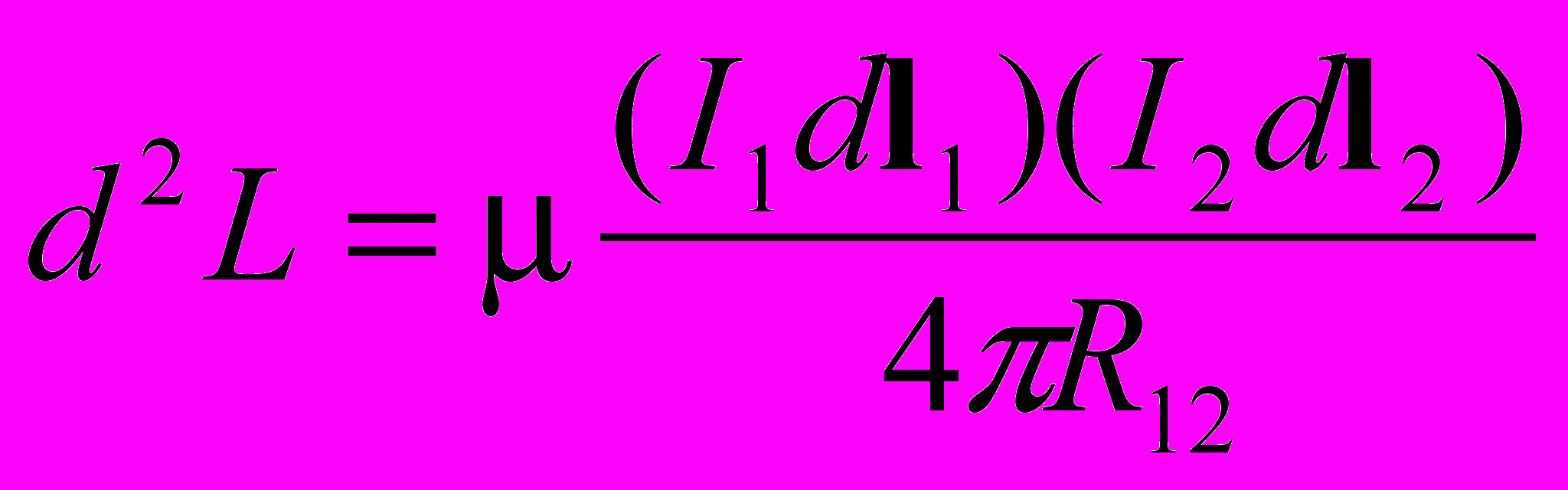
Эта функция получена с использованием функции Лагранжа (5.1) и условия квазинейтральности проводников. Она инвариантна относительно преобразования Галилея. Из лагранжиана следуют выражения для сил и момента сил, действующих на эти элементы токов:
Сила Ампера
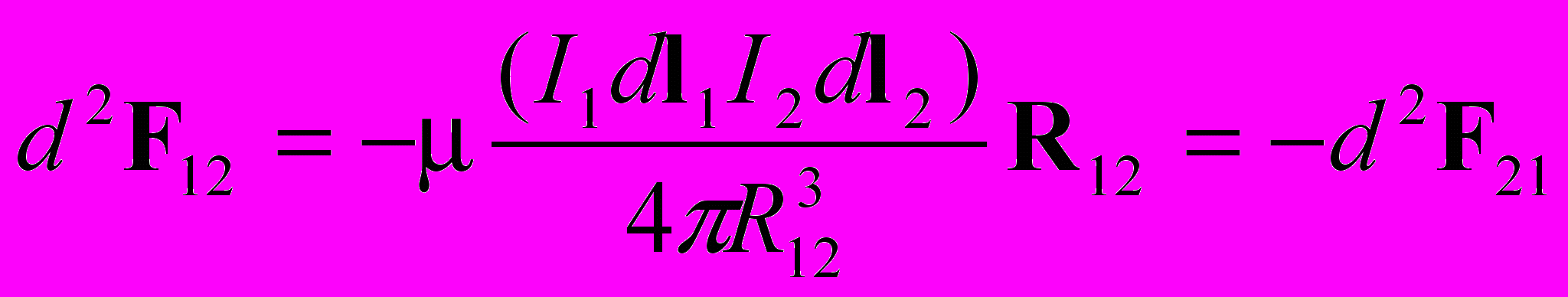
Вращающий момент сил
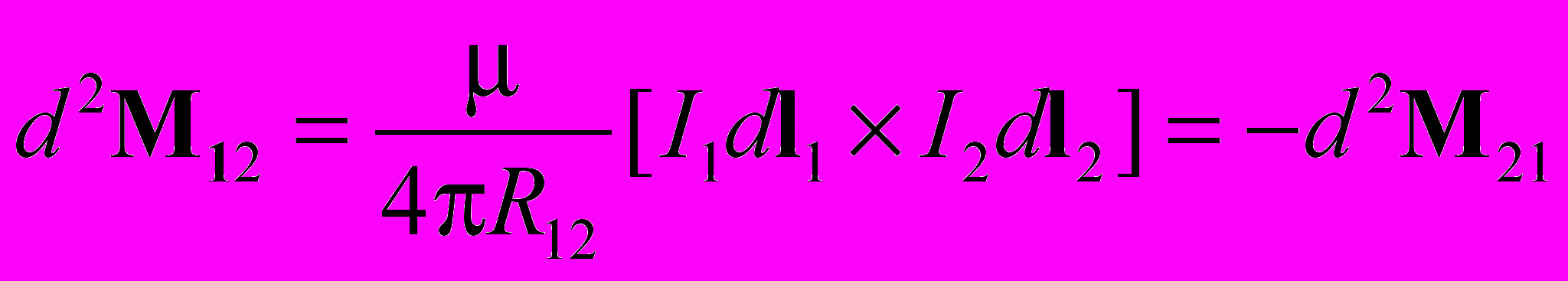
Как мы видим, принцип равенства действия противодействию соблюдается.
Эти выражения инвариантны относительно преобразования Галилея, т.е. силы и моменты сил не зависят от выбора инерциальной системы отсчета.
-
Взаимодействие заряда и электромагнитной волны
Разделение уравнений для полей зарядов и электромагнитных волн отвергает многие прежние представления и ставит перед классической электродинамикой новые задачи. Среди них:
- Проблема взаимодействия инерциального заряда и электромагнитной волны.
- Проблема взаимодействия инерциального и безынерциального зарядов.
- Проблема взаимодействия между собой безынерциальных зарядов и другие.
Мы здесь рассмотрим подход к решению первой проблемы. Проблема взаимодействия волны с инерциальным зарядом напоминает задачу дифракции волны на проводящем теле.
Имеется волна, падающая на это тело. В результате часть энергии поглощается телом, другая часть рассеивается в пространстве в форме вторичных (отраженных, переизлученных) волн.
Аналогичная ситуация возникает и при воздействии электромагнитной волны на инерциальный заряд. Отличие в том, что часть энергии электромагнитной волны превращается в кинетическую энергию заряда или же имеет место обратный процесс. Часть кинетической энергии превращается в энергию электромагнитной волны. Помимо этого (в отличие от дифракционный задач) положение и скорость инерциального заряда меняются. Такой процесс носит диссипативный характер и для его описания необходимы специальные методы. Приведем пример из механики [10].
Рассмотрим маленький шарик массой m (материальная точка), который закреплен на бесконечной натянутой струне. Этому шарику с помощью молоточка сообщается импульс p. Начальная скорость шарика равна V0. От удара шарик начнет движение, и вместе с ним будут распространяться две поперечные волны, бегущие по оси x в разные стороны от шарика, как показано на рис. 2.
Для смещения струны от положения равновесия необходима энергия. Кинетическая энергия шарика постепенно расходуется на изменение положения элементов струны, скорость шарика уменьшается, и он постепенно останавливается. При этом струна стремится к своему асимптотическому пределу. Запишем процесс математически.
- Уравнение движения шарика:
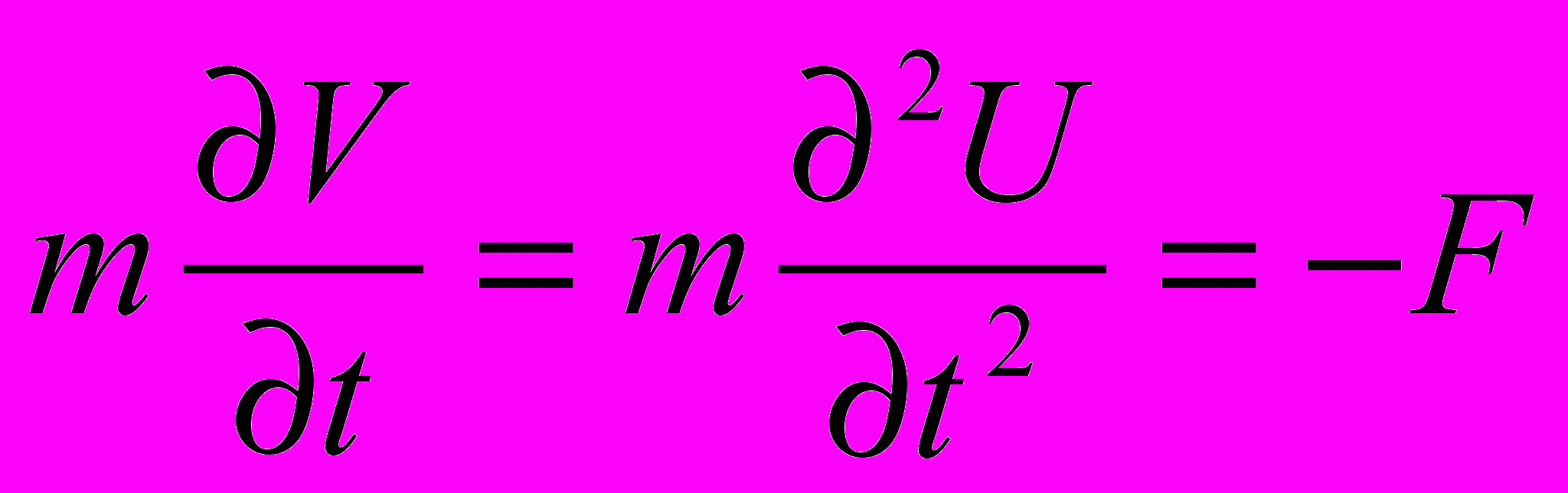 , где U – вертикальное смещение шарика;
, где U – вертикальное смещение шарика; 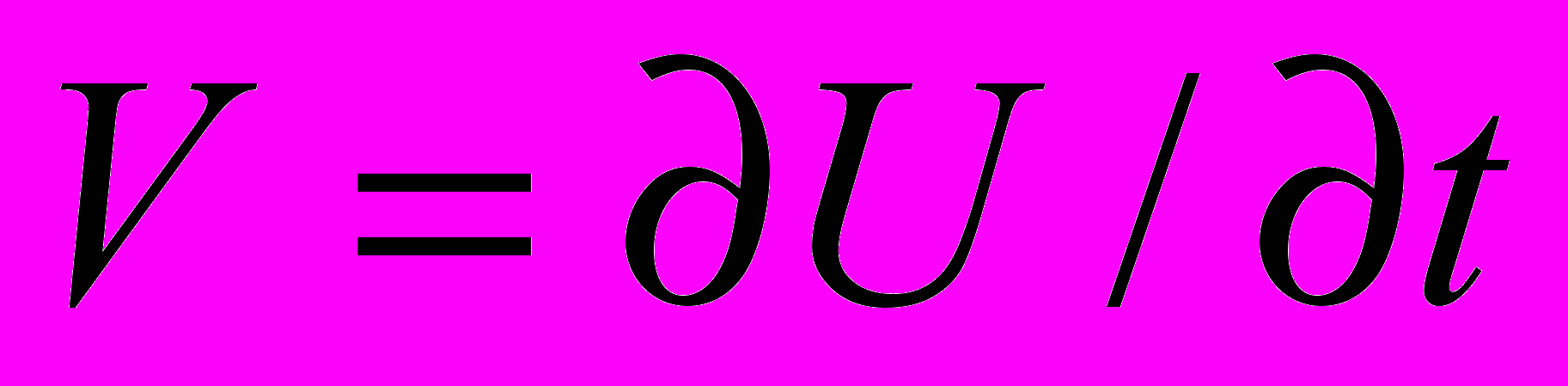 – скорость шарика; F – сила, действующая на шарик со стороны струны.
– скорость шарика; F – сила, действующая на шарик со стороны струны.
- В силу того, что заряд точечный, нет необходимости использовать полную производную, которая совпадает с частной производной.
Уравнение движения струны [11]:
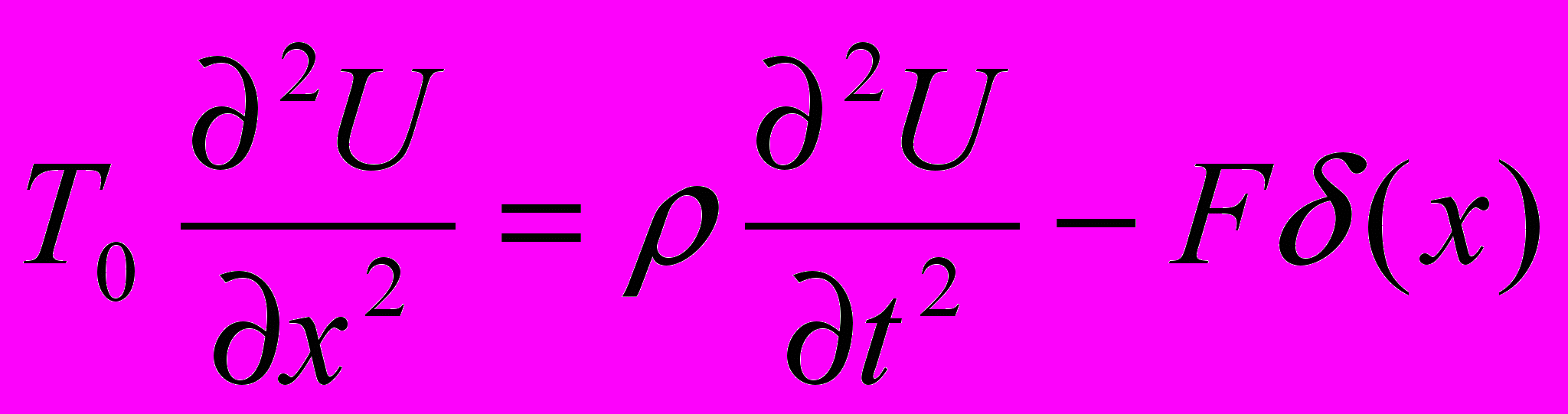 , где: Т0 – натяжение струны; ρ – линейная плотность массы струны.
, где: Т0 – натяжение струны; ρ – линейная плотность массы струны. Уравнение движения струны можно привести к виду
 ,
, где: c2 = T0 / ρ - квадрат скорости распространения волны; f = F / ρ – плотность силы, отнесенная к плотности массы струны.
По аналогии с теорией длинных линий параметр (T0 ρ) - ½ можно назвать «волновым сопротивлением» струны.

Рис 2. Распространение волн при движении шарика.
Можно решить эти уравнения «в лоб» (см. [11], Задача № 9, стр. 80). Мы будем исходить из закона сохранения энергии, поскольку это нагляднее.
1. Шарик. Изменение скорости шарика происходит по экспоненциальному закону, поэтому можно предположить, что сила F , которая противодействует движению заряда (диссипативная сила) пропорциональна скорости движения заряда.
 , где λ – некоторая постоянная (констата диссипации).
, где λ – некоторая постоянная (констата диссипации).Решение для вертикальной координаты шарика имеет вид
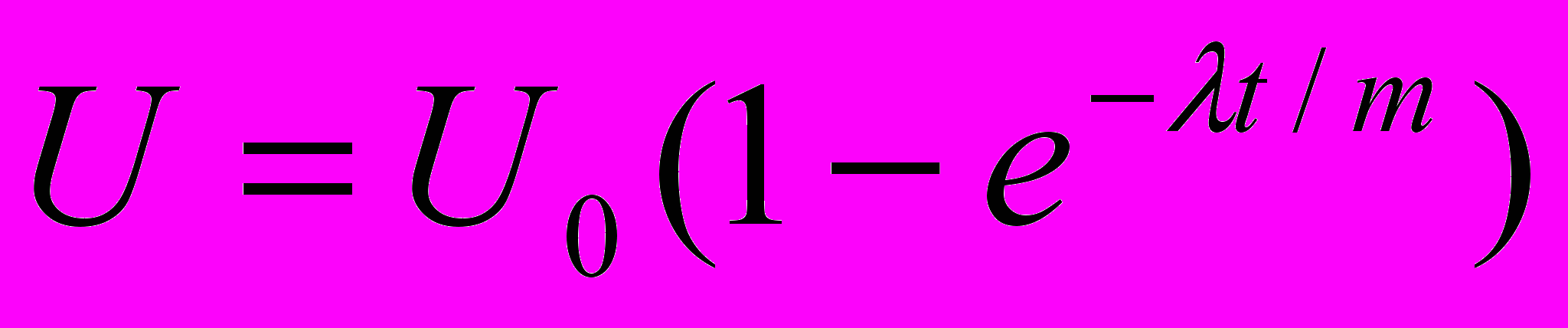 (7.1).
(7.1).Начальная скорость, импульс и кинетическая энергия шарика соответственно равны
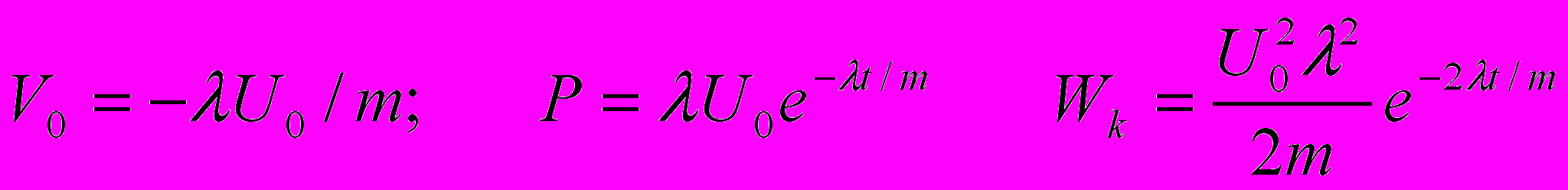
2. Струна. Рассмотрим теперь энергетические соотношения для струны и определим параметр λ. Мы будем исходить из того, что точка соприкосновения шарика со струной изменяет свое положение U в соответствии с выражением (7.1). Соответственно, соседние точки (х ≠ 0) будут определяться следующими выражениями

Подсчитаем энергию струны, учитывая симметричность ее распределения
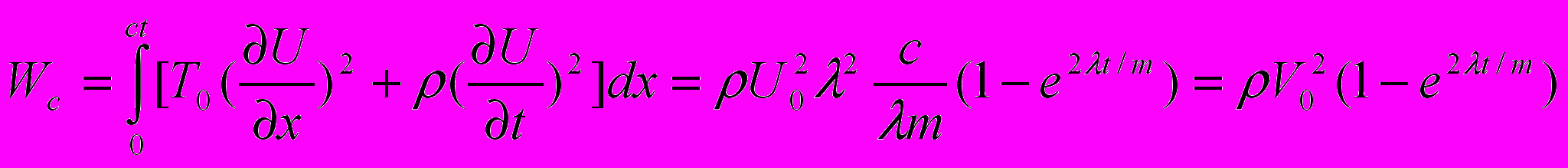
Сложим энергии струны и шарика. Учитывая закон сохранения энергии, найдем величину параметра λ.

Здесь мы подобрали λ так, чтобы суммарная энергия не зависела от времени. Проверим теперь закон сохранения импульса. Суммарный импульс шарика и возбужденных элементов струны не должен зависеть от времени. Действительно
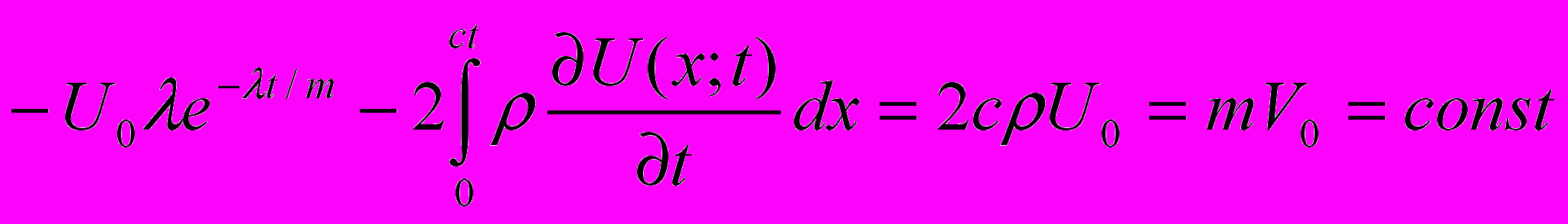
Величина силы зависит только от параметров струны и скорости шарика

Итак, кинетическая энергия механического движения шарика преобразуется в волновую энергию струны, распространяющуюся от шарика. Еще раз отметим, что взаимодействие шарика и неограниченной струны носит диссипативный характер.
- Взаимодействие частиц с волной носит диссипативный характер и требует введение параметра диссипации. В свое время Релей вынужден был ввести в функцию Лагранжа диссипативный член для описания потерь в системах.
- Величина параметра диссипации λ не зависит от амплитуды колебаний струны.
- Поток энергии распространяется по оси х в обе стороны, а механический импульс шарика р = mv как бы «пропадает», преобразуясь в поток волны.
- Аналогичные явления должны иметь место при взаимодействии заряда с электромагнитной волной, например, в ускорителях элементарных частиц бегущей волны, в приборах вакуумной электроники СВЧ (генераторы, усилители) и т.д.
Результаты исследований опубликованы в работах [5], [12], [13], [14] и других.
-
Подведем итоги
Теперь можно подвести некоторые итоги.
Во-первых, теоретически установлено и экспериментально установлено, что проводимость, обусловленная токами и зарядами, определяется безынерциальными и инерциальными носителями электричества. Соответственно, правая часть уравнений Максвелла должна содержать не только поля инерционных зарядов, но и безынерциальных зарядов.
Во вторых, уравнения Максвелла разделяются на две группы независимых уравнений. Первая группа описывает электромагнитные волны, излучаемые безынерциальными зарядами. Вторая группа уравнений описывает квазистатические поля, носителями которых являются инерциальные заряды и токи. Игнорирование этого факта стало одним из важных источников ошибок и предрассудков. Поле заряда и поле электромагнитной волны это разные виды полей.
В третьих, каждой группе уравнений соответствуют свои электромагнитные потенциалы, которые обретают четкий физический смысл, позволяя устранить трудности и противоречия в интерпретации явлений электродинамики.
В четвертых, необходимо дальнейшее переосмысление взаимодействий в классической электродинамике.
Все это неизбежно должно изменить многие положения и выводы КЭД. Как писал в свое время один из специалистов по КЭД, бурное развитие квантовой электродинамики породило надежды, что с развитием КЭД будут устранены трудности классических теорий. Со временем физики все яснее начали осознавать, что трудности самой КЭД имеют классические корни. Этот вопрос требует специального анализа и отдельного изложения.
Полученные результаты не совместимы с положениями специальной теории относительности. В частности, наличие мгновенного действия на расстоянии не совместимо со СТО. Как известно, СТО была порождена электродинамикой. Коль скоро классическая электродинамика и интерпретация многих явлений в ней меняется, должны измениться положения СТО и физическая интерпретация преобразований Лоренца. Этому вопросу будет посвящена Часть 5 настоящего обзора проблем, заблуждений и ошибок в современной электродинамике.
В настоящее время в МГУ планируется строительство супер-коллайдера. Само по себе столь дорогостоящее строительство могло бы иметь оправдание. Но с точки зрения приведенного анализа это строительство может оказаться авантюрой, предметом насмешек. Нельзя опрометчиво тратить столь крупные суммы для подобных «экспериментов», особенно если фундамент науки содержит принципиальные ошибки и противоречия.
Так кто же отвечает за Российскую Науку?
Ошибки и предрассудки, тиражируясь в лекциях, учебниках и исследованиях, не способствуют нормальному развитию науки и воспитанию будущих ученых. Эти «погрешности науки» необходимо искоренять. Есть много организаций, которые имеют отношение к высшему образованию и науке.
Минобрнауки, возглавляемое Фурсенко. Можно обратиться туда. Но какой смысл? Судя по реформам образования, в этом министерстве нет специалистов ни по науке, ни педагогике («кухарки»!). Недавно Чубайс назвал Фурсенко крупным реформатором. Сколько же нужно сделать нехорошего для России, чтобы заслужить такую похвалу?
Есть РАН с Президентом Ю.Осиповым. Многочисленные обращения профессоров по поводу современного состояния физики (без ответов от РАН) не оставляют сомнения, что Осипов мирно дремлет в Президентском кресле. Вместе с ним богатырским сном спит Отделение Физических Наук. Их мирный сон охраняет Комиссия по борьбе с лженаукой и фальсификацией научных исследований.
Обращение в Комиссию по борьбе с лженаукой и фальсификацией научных исследований тоже не имеет перспектив. Уж больно «топорным» критерием научности пользуется эта Комиссия: « ЕСТЬ МИРОВАЯ НАУКА, А ВСЕ, ЧТО НЕ ВПИСЫВАЕТСЯ В ЕЕ КРИТЕРИИ – ЭТО ЛЖЕНАУКА». Мы обнаружили ошибки в научных теориях современной физики. Выводы «противоречат твердо установленным научным фактам» (по Гинзбургу), т.е. «не вписываются в кругляковские критерии научности». Нам заранее уготовлена участь быть обвиненными в «невежестве», «некомпетентности», «шарлатанстве» и т.д. [15]. Однако сейчас кличка «альтернативщик» уже утратила свой оскорбительный смысл. Напротив, она отражает нетерпимость исследователя-альтернативщика к ошибкам и предрассудкам в современной физике. Не без оснований Грызлов назвал эту Комиссию «гнездом мракобесия». Быть может Единая Россия здесь поможет?
Обратились в Приемную Грызлова. Нам обещали дать ответ через месяц. Год ждем. Как при игре «домино» и здесь выпадает фишка «пусто-пусто». Уж очень странная эта Партия «Единая Россия», много обещающая.
Есть пословица: «У семи нянек дитя без глазу». Это верно, если нянек интересует не «дитя», а ученые степени, научные звания, хорошие зарплаты и высокие должности. Им ли до «дитяти»? Все как в сказке: Докторов наук тьма, а Ученых нема!
Так и остался наш вопрос без ответа: Кто же все-таки отвечает за Российскую Науку?
В последующих Частях мы продолжим публикацию анализа ошибок и предрассудков в электродинамике. Мы рассмотрим вопросы, касающиеся явлений Специальной теории относительности.
Приложение 1
Для обоснования системы уравнений мы будем исходить из известных соотношений для связи потенциалов
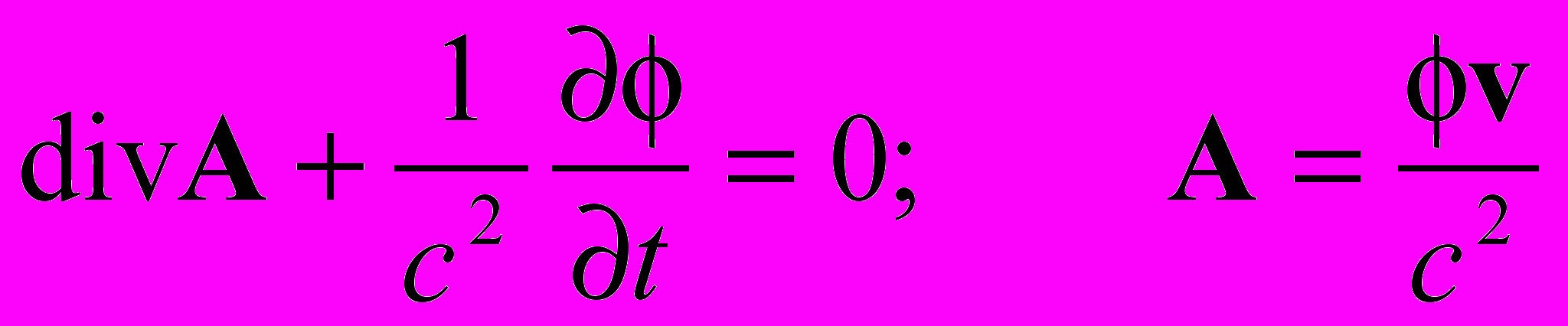 ,
,которые аналогичны соотношениям

Из уравнения
 (П.1) следует, что
(П.1) следует, что 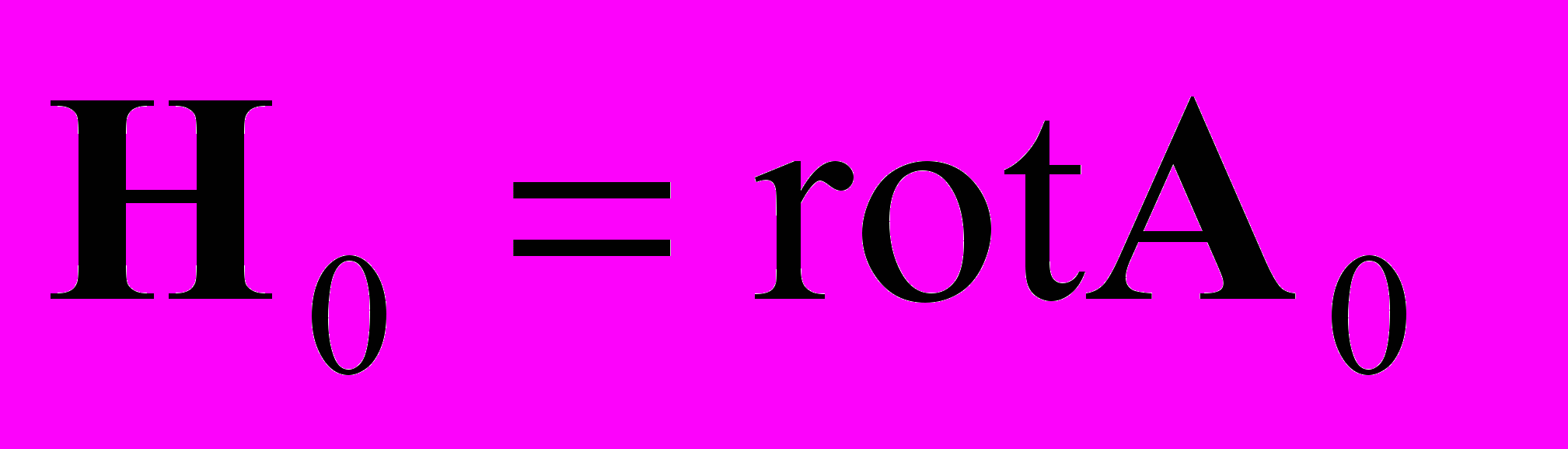 (П.2).
(П.2).Из уравнения
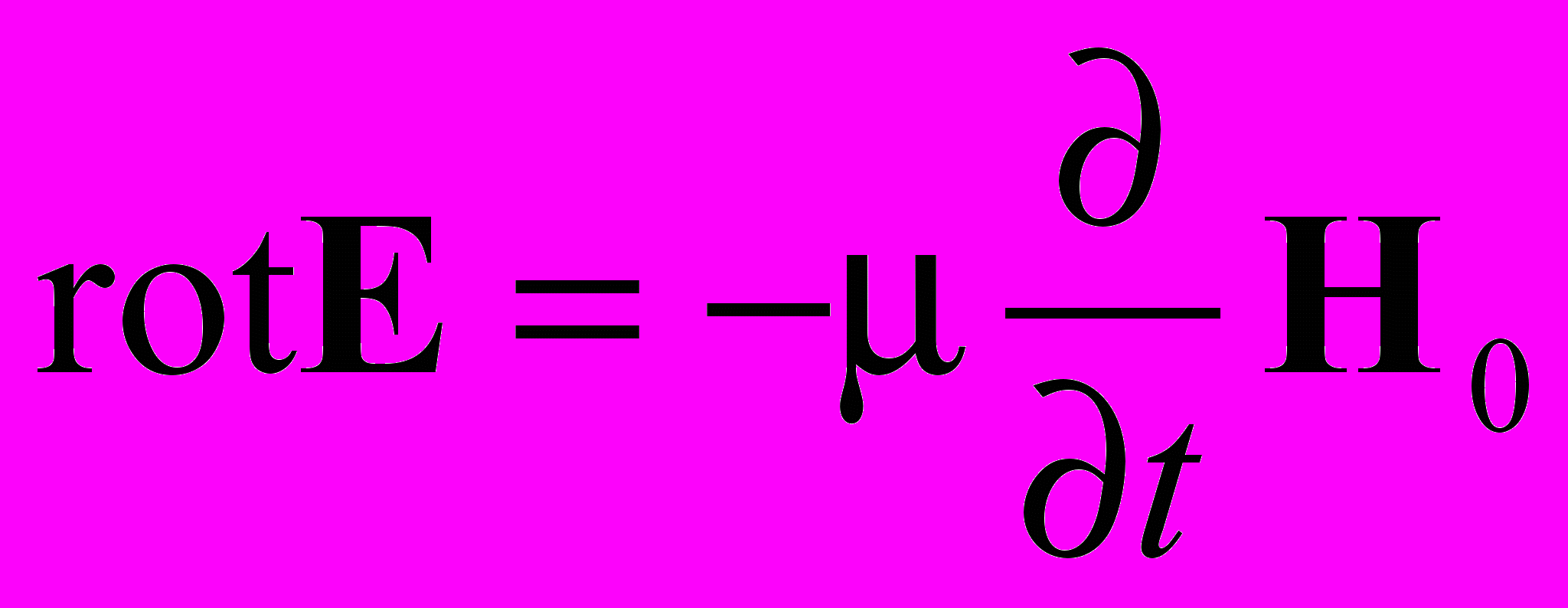 (П.3) вытекает
(П.3) вытекает 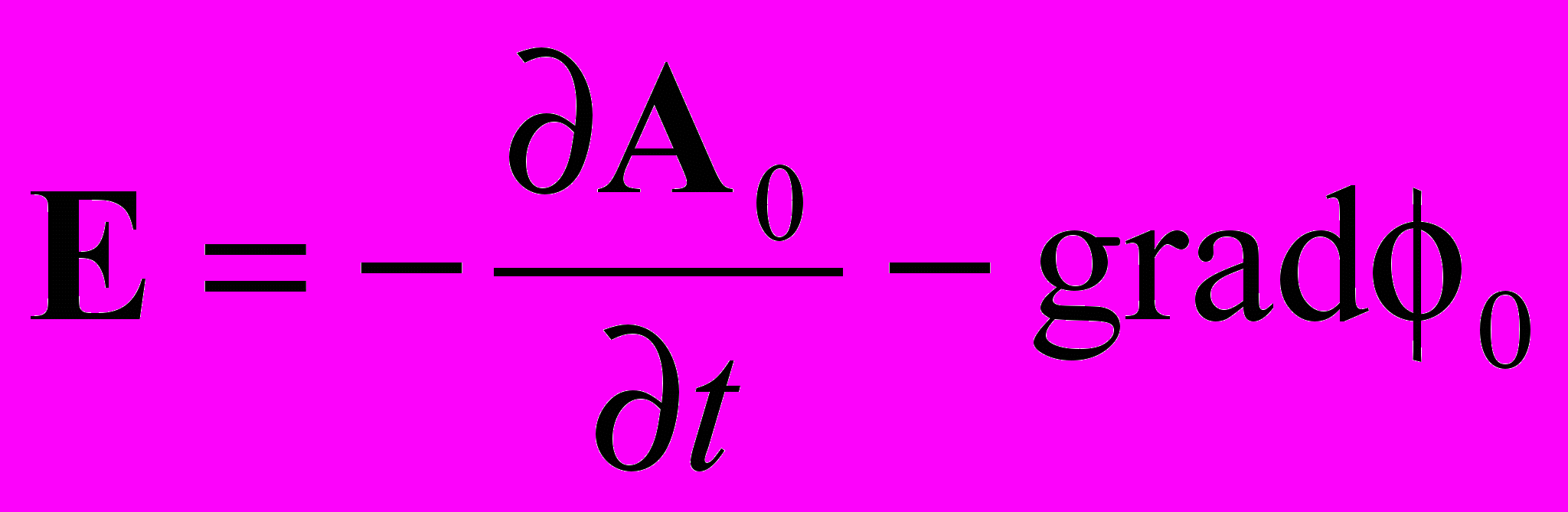 (П.4)
(П.4)Из уравнения
 (П.5) , используя (П.4) можно найти
(П.5) , используя (П.4) можно найти  (П.6)
(П.6)Из теоремы Гаусса известно, что интеграл по поверхности , окружающей объем V от напряженности электрического поля, равен сумме зарядов внутри этого объема.
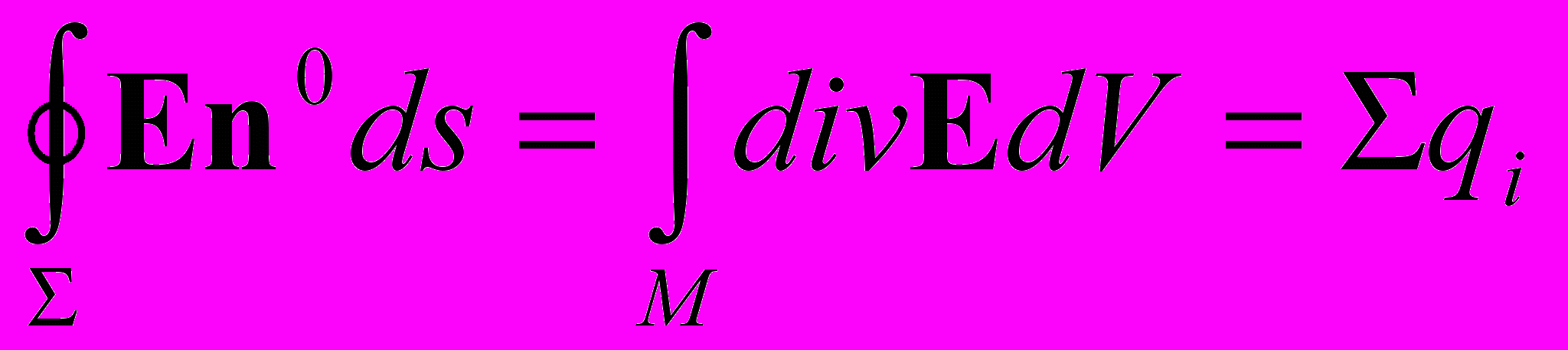
Обратимся к (П.6). Если заряды внутри объема неподвижны, то их величина определяется градиентом скалярного потенциала. Та же самая величина заряда должна сохраниться, если заряды движутся внутри объема, не покидая его. Следовательно, член
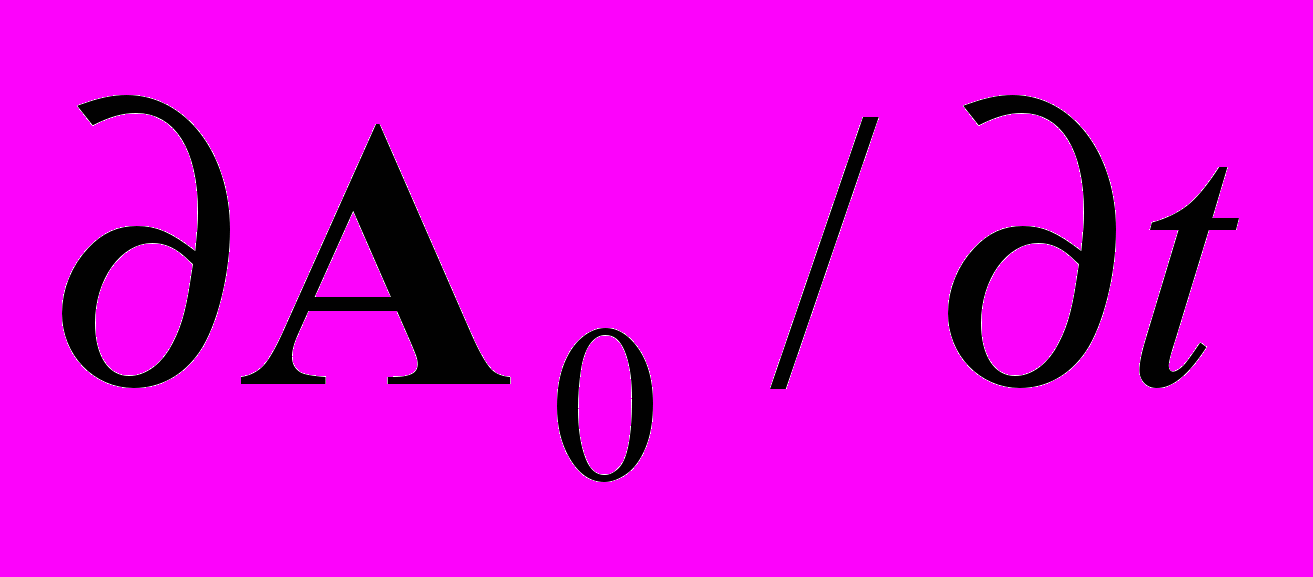 в выражении (П.6) является лишним. Этот член обусловлен не зарядами непосредственно, а движением скалярного потенциала. Поэтому он не может и не должен давать вклад в величину заряда.
в выражении (П.6) является лишним. Этот член обусловлен не зарядами непосредственно, а движением скалярного потенциала. Поэтому он не может и не должен давать вклад в величину заряда.С учетом сказанного уравнение для скалярного потенциала (П.6) примет вид
 (П.7)
(П.7) Электрическое поле будет определяться градиентом этого потенциала
 (П.8)
(П.8)Теперь рассмотрим уравнение
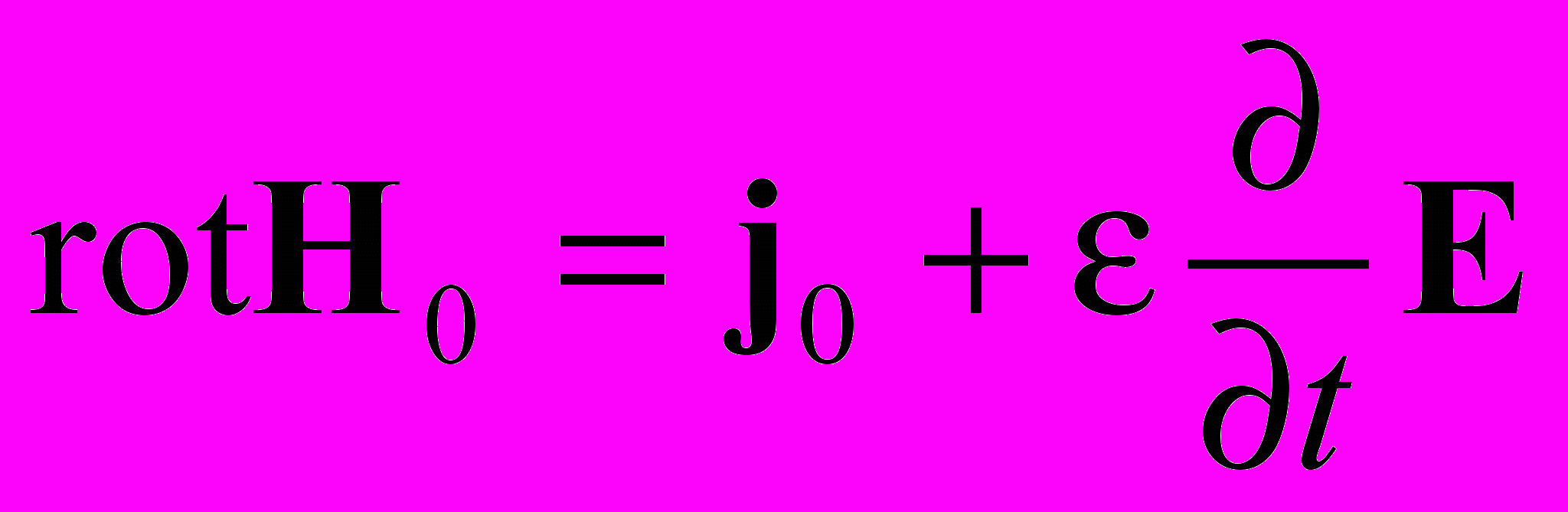 (П.9)
(П.9) Здесь так же как в предыдущем случае, мы должны в правой части использовать вектор Е0 . Действительно, если мы возьмем дивергенцию от членов (П.9), то получим
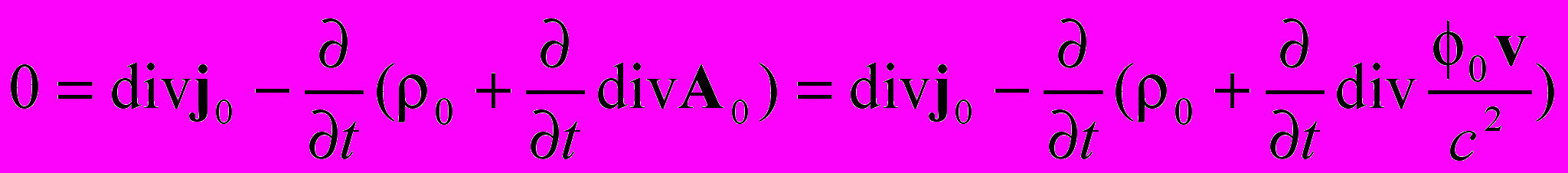 (П.10)
(П.10)Очевидно, что, поскольку дивергенция векторного потенциала А0 не связана с самостоятельными зарядами, как мы выяснили выше, производная от него по времени не может создавать ток смещения. По этой причине, сохраняя стандартный вид уравнения непрерывности для тока, мы должны считать, что ток смещения создается только градиентом скалярного потенциала. Иными словами
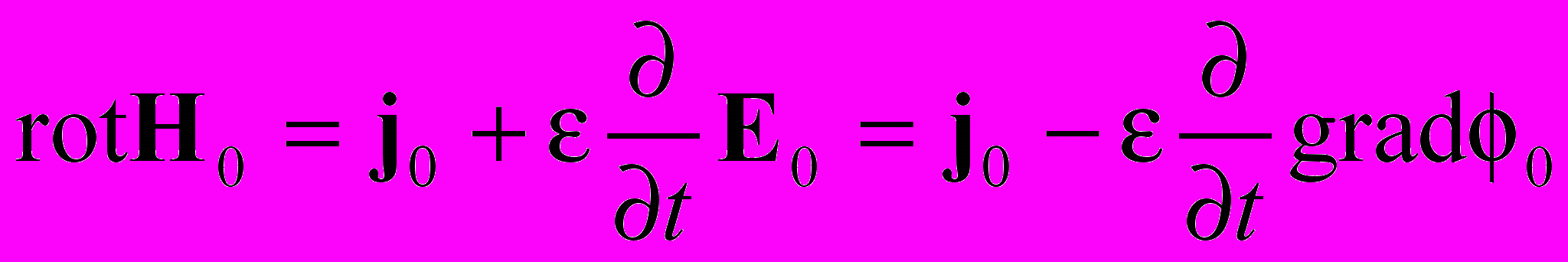 (П.11) или
(П.11) или  (П.12)
(П.12)Таким образом, мы можем записать полную систему уравнений Максвелла для инерциальных зарядов, выразив ее через потенциалы (Таблица 2).
Выражения для полей стандартные
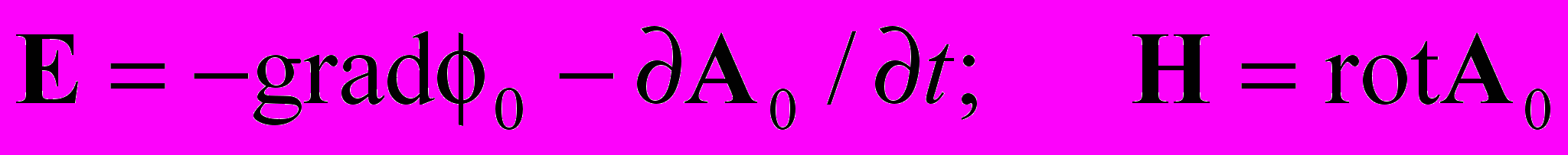
Источники информации
- Исследовательская группа АНАЛИЗ ссылка скрыта
- A Chubykalo, A Espinoza and R Alvarado Flores. Electromagnetic potentials without gauge transformations. Phys. Scr. 84 (2011)
- Кулигин В.А. Одноглазый циклоп в физике. ссылка скрыта
- Ландау Л.Д., Лифшиц Е.М. Теория поля. Физматгиз., М. 1961.
- Кулигин В.А., Корнева М.В., Кулигина Г.А. Анализ классической электродинамики и теории относительности ссылка скрыта
- Корнева М.В., Кулигин В.А., Кулигина Г.А Проблемы, заблуждения и ошибки в электродинамике. Часть 2. ссылка скрыта
- Кулигин В.А. Причинность и взаимодействие в физике. ссылка скрыта
- Кулигин В.А., Корнева М.В., Кулигина Г.А. Кризис релятивистских теорий. ссылка скрыта
- Корнева М.В., Кулигин В.А., Кулигина Г.А. Проблемы, заблуждения и ошибки в электродинамике (Часть 1. Явные ошибки) ссылка скрыта
- Корнева М.В., Кулигин В.А., Кулигина Г.А Взаимодействие с волной как диссипативный процесс ссылка скрыта
- Тихонов А.Н., Самарский А.А. Уравнения математической физики. ГИТТЛ, М., 1953.
- Корнева М.В., Кулигин В.А., Кулигина Г.А. Физика и философия парных взаимодействий (начало) narod.ru/kuligin-1.php
- Корнева М.В., Кулигин В.А., Кулигина Г.А. Физика и философия парных взаимодействий (окончание) ссылка скрыта
- Кулигин В.А., Корнева М.В., Кулигина Г.А Три модели взаимодействия. /kuligin/kuligin5.htm
- Перова О.И.. Темные игры в физике bai.kz/articles/dark-games.htm
Примечание.
Первая часть исследования «Проблемы, заблуждения и ошибки в электродинамике» (Часть 1.) опубликована на сайте ссылка скрыта
Вторая часть исследования «Проблемы, заблуждения и ошибки в электродинамике» (Часть 2.) опубликована на сайте clibrary.ru/rus/catalog/pages/11208.php
