О единицах и размерностях основных характеристик электромагнитного поля

Вид материала

Документы

Содержание Е и магнитной индукции В В и напряженности магнитного поля Н Е и поляризованность Р Таблица 3 Формулы размерности и соотношения между электромагнитными единицами СИ и СТ Физическая величина E и электрическим смещением D Р и электрическое смещение D D = E , т.к. в вакууме Р E, электрическое смещение D H связана с индукцией магнитного поля В В и напряженностью магнитного поля Н М и напряженность магнитного поля Н Н = В , т.к. в вакууме М B – индукция магнитного поля, а величина H

Подобный материал:

• Исследование электрических свойств подстилающей среды и пространственно-временных характеристик, 349.6kb.
• Единая теория электродинамики и гравитации  Абрамов А. П., 2006, 103.9kb.
• «Становление электромагнитного поля над наклонными геоэлектрическими границами и поляризующимися, 358.12kb.
• Элементы теории электромагнитного поля, 81.12kb.
• Книга Дж. Дж. Томсона "Электричество и материя", появившаяся в 1903 году, сохраняет, 527.71kb.
• 1. Основные понятия и законы электромагнитного поля и теории электрических и магнитных, 87.26kb.
• 1. Основные законы электрического поля, 316.07kb.
• Задачи: Исследовать литературу содержащую, необходимую информацию для проекта. Исследовать, 165.52kb.
• Аннотация дисциплины, 786.67kb.
• «влияние электромагнитных волн на здоровье человека», 452.98kb.

О ЕДИНИЦАХ И РАЗМЕРНОСТЯХ ОСНОВНЫХ ХАРАКТЕРИСТИК
ЭЛЕКТРОМАГНИТНОГО ПОЛЯ


Г.М.Трунов


Приведем в качестве вступления цитату из фундаментального труда К.М. Поливанова, изданного в 1969 г. [1, с.81]: «При рассмотрении поля в поляризуемых вещественных средах в уравнениях Максвелла вводятся новые векторы D = ₀E + P и
Н = В/₀ – M. При этом векторы D и Н часто определяются так невнятно, как, пожалуй, ни одна другая физическая величина». Можно добавить, что разные авторы учебников приводят различные определения основных характеристик электромагнитного поля:
в частности, в обзоре [2], приведены 5 (пять !) определений индукции магнитного
поля В, которые используются в различных учебниках:

– в системе СГС и в системе Хевисайда – Лоренца:

В = Н + 4М [3, с.26], В = Н + М [4, с.76],

(1а)

– в СИ

В =0 (Н + M) [5, с.269], В = Н + 0M [6, с.142], В = 0 Н + M [7, с.260].

(1б)

В соответствии с ГОСТ 8.417–81. ГСИ. «Единицы физических величин» [8]
в учебном процессе во всех учебных заведениях рекомендована к обязательному
использованию Международная система единиц (СИ). Тем не менее, в последние годы появилась тенденция [9, 10] при изложении курса «Электромагнетизм» использовать только систему СГС, хотя эта система единиц даже не значится в числе допускаемых
к применению в учебном процессе. Можно также констатировать, что в учебниках
физики прошлого времени наиболее авторитетных авторов (Л.Д. Ландау, И.Е. Тамм,
Д.В. Сивухин) [11 – 13] и в фундаментальном Берклеевском курсе физики [14] использовалась система СГС, а не система МКСА.

В табл.1 представлены некоторые уравнения электромагнетизма, имеющие различный вид в СИ и системе СГС.


Таблица 1

Некоторые уравнения электромагнетизма, записанные в СИ и системе СГС

ВЕЛИЧИНА	ОПРЕДЕЛЕНИЕ		ФОРМУЛА РАЗМЕРНОСТИ
	СИ	СГС	СИ	СГС
Напряженность электрического поля Е	Е = F/Q		LMT–3I–1	L–1/2M1/2T–1
Электрическое смещение D	D = 0E +P	D = E +4P	L–2TI	L–1/2M1/2T–1
Поляризованность Р	Р =  pi / V		L–2TI	L–1/2M1/2T–1
Связь между Р и Е D и Е	Р = 0E D = 0E	Р = E D = E
Магнитная индукция В	F = Q [v  B]	F = Q [ 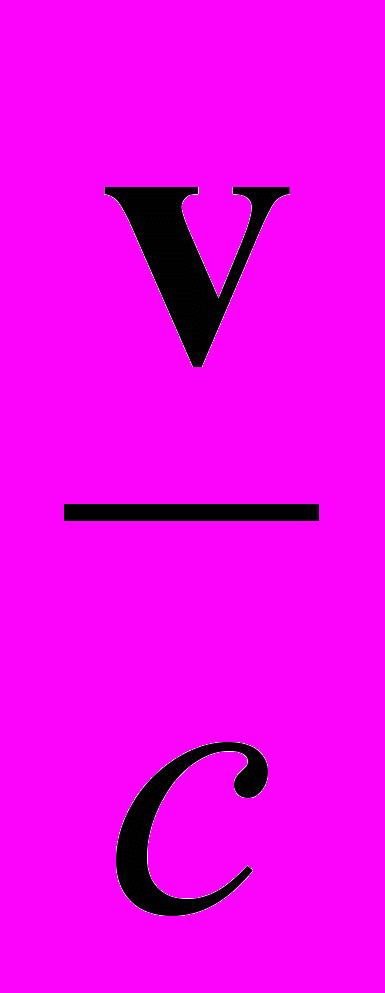 B]	MT–2I–1	L–1/2M1/2T–1
Напряженность магнитного поля Н	Н = B/0 – M	Н = В – 4M	L–1I	L–1/2M1/2T–1
Намагниченность М	М =  pmi / V		L–1I	L–1/2M1/2T–1
Связь между М и Н	М = Н
Связь между Н и В	Н = В/(0),	Н = В/,

Причины различия математической формы записи некоторых уравнений электромагнетизма в СИ и системе СГС подробно рассмотрены в [15], поэтому отметим только тот факт, что все электромагнитные единицы СИ были заимствованы из системы единиц МКСА. Эта система (основные единицы: метр, килограмм, секунда, ампер) была основана на уравнениях, соответствующих научным воззрениям на электромагнитное поле середины XIX века, согласно которым вакуум («светоносный эфир» по терминологии того времени) по своим свойствам принципиально не отличается от обычных сред и, следовательно, должен обладать диэлектрической ₀ и магнитной ₀ проницаемостями вакуума. Величины ₀ и ₀ , называемые в настоящее время, соответственно, электрической и магнитной постоянной, не имеют никакого физического смысла и лишь их комбинация 1/ 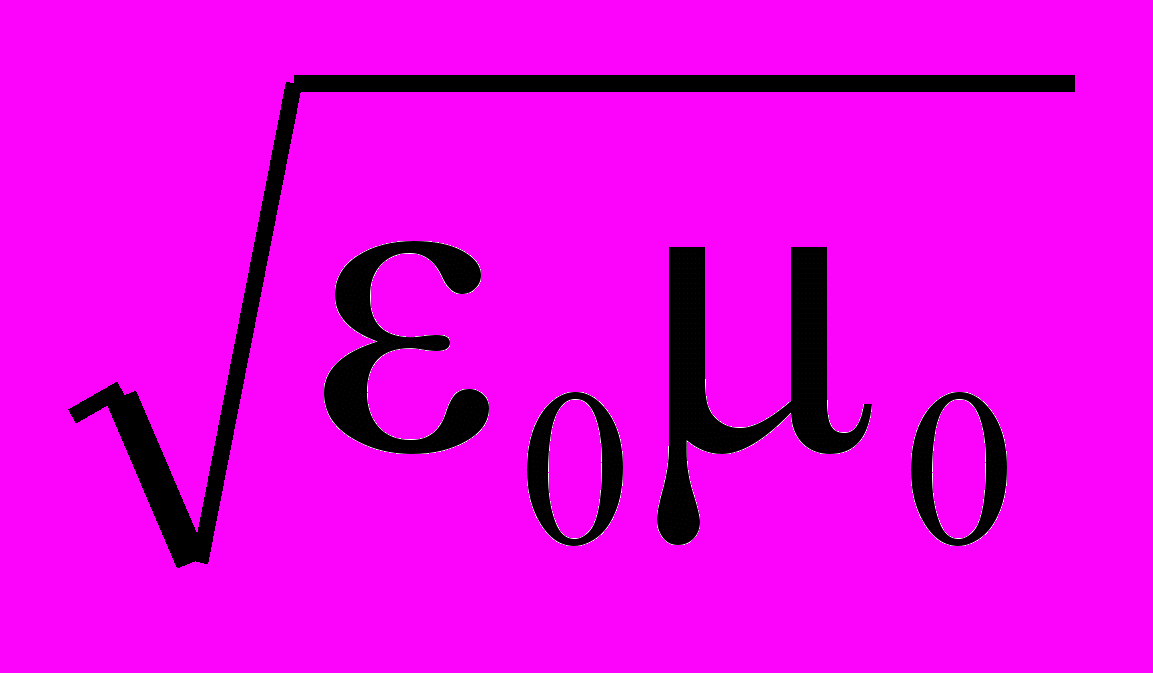= с представляет собой скорость света в вакууме.

Для описания электромагнитного поля в веществе в СИ, кроме силовых характеристик – напряженности электрического поля Е и магнитной индукции В – используют вспомогательные величины: электрическое смещение D и напряженность магнитного поля Н, которые связаны между собой, соответственно, уравнениями D = ₀E и
Н = В/(₀). В вакууме электромагнитное поле также характеризуется четырьмя векторами Е и D (D = ₀Е), В и Н (Н = В/₀). Следовательно, величины D и E, Н и В имеют в СИ, соответственно, разные формулы размерности (см. табл. 1).

Особо отметим, что в СИ одинаковые размерности имеют величины разного физического смысла: соответственно, электрическое смещение D и поляризованность Р, напряженность магнитного поля Н и намагниченность М

Согласно современным научным представлениям [16]:

1) деление единого электромагнитного поля на электрическое и магнитное поле относительно, т.е. зависит от выбранной системы отчета, и поэтому силовые характеристики электромагнитного поля (напряженность электрического поля Е и магнитная индукция В) должны быть однородными величинами и иметь одинаковую размерность: dim E = dim B;

2) для описания электрического и магнитного полей в вакууме достаточно двух векторов Е и В, т.к. в вакууме должны выполняться равенства: D = E и H = B.

Из табл.1 видно, что некоторые уравнения электромагнетизма, записанные в СИ, не соответствуют современным научным представлениям. Поэтому преподавание курса физики с использованием электромагнитных единиц СИ дает «повод для введения неправильных представлений о сущности электрических и магнитных полей [13]».

В системе СГС однородные величины Е и В имеют одинаковую формулу размерности, а уравнения электромагнетизма «отличаются той неповторимой простотой и стройностью, за которые не жаль заплатить переводом электромагнитных единиц из СГС в СИ и обратно [17]».

Но возврат к системе СГС, на наш взгляд, является регрессивным шагом,
т.к. электромагнитные единицы этой системы обладают многими принципиальными недостатками:

1) большинство единиц имеет дробные показатели размерности (по выражению
А. Зоммерфельда – «противоестественные» размерности);

2) некоторые электромагнитные величины имеют размерности механических
величин, например, индуктивность и емкость имеют размерность длины;

3) многие электромагнитные единицы СГС не имеют собственных названий;

4) единицы магнитной индукции В и напряженности магнитного поля Н имеют разные названия (соответственно, «гаусс» и «эрстед»), хотя в вакууме эти величины, как было сказано выше, должны быть неразличимы;

5) одинаковые размерности имеют величины разного физического смысла, соответственно, напряженность электрического поля Е и поляризованность Р, магнитная индукция В и намагниченность М.

Напомним, что напряженность электрического поля Е – это сила, действующая со стороны поля на положительный единичный заряд, отнесенная к величине этого заряда, а поляризованность P – это суммарный электрический момент объема диэлектрика, отнесенный к величине этого объема (P =  p_i / V); индукция магнитного поля В – это сила, действующая со стороны магнитного поля на единичный заряд, движущийся со скоростью v, а намагниченность М – это суммарный магнитный момент объема магнетика, отнесенный к величине этого объема (М =  p_mi / V).

Таким образом, преподавание курса физики «Электромагнетизм» с использованием системы СГС или СИ, вызывает те или иные трудности.

В работах [15, 18, 19] было показано, что для разрешения этого противоречия
необходимо записать уравнения электромагнетизма в таком же виде, что и в системе СГС, т.е. без размерных коэффициентов ₀ и ₀, но с привлечением фундаментальной постоянной с = 310⁸ м/с– скорости света в вакууме и размерного коэффициента
k₀ = 910⁹ Нм²/Кл² , и на их основе разработать новую четырехразмерную систему электромагнитных единиц, которая не имеет недостатков электромагнитных единиц СИ и системы СГС и предназначена для преподавания курса физики «Электромагнетизм».

В табл. 2 представлены некоторые уравнения электромагнетизма, которые соответствуют современным научным взглядам на электромагнитное поле.

При обсуждении новой системы электромагнитных единиц на VIII Международной конференции «Физика в системе современного образования (ФССО-2005)» [20], состоявшейся в г. Санкт-Петербурге в 2005 г., было рекомендовано назвать эту систему Теоретической системой электромагнитных единиц, сокращенно: СТ.

В СТ основные единицы совпадают с основными единицами СИ (т.е. используются метр, килограмм, секунда и ампер). Производные единицы СТ определяются в соответствии с уравнениями, представленными в табл. 2; при этом названия всех единиц электрических величин (кроме электрического смещения и потока электрического смещения) совпадают с названиями соответствующих единиц СИ.


Таблица 2

Уравнения электромагнетизма, записанные в СТ

и единицы некоторых электромагнитных величин

ЗАКОН или ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ	СТ
	k0 = 9109 Нм2/Кл2 с  3108 м/с	НАЗВАНИЕ ЕДИНИЦЫ
Закон Кулона	F = k0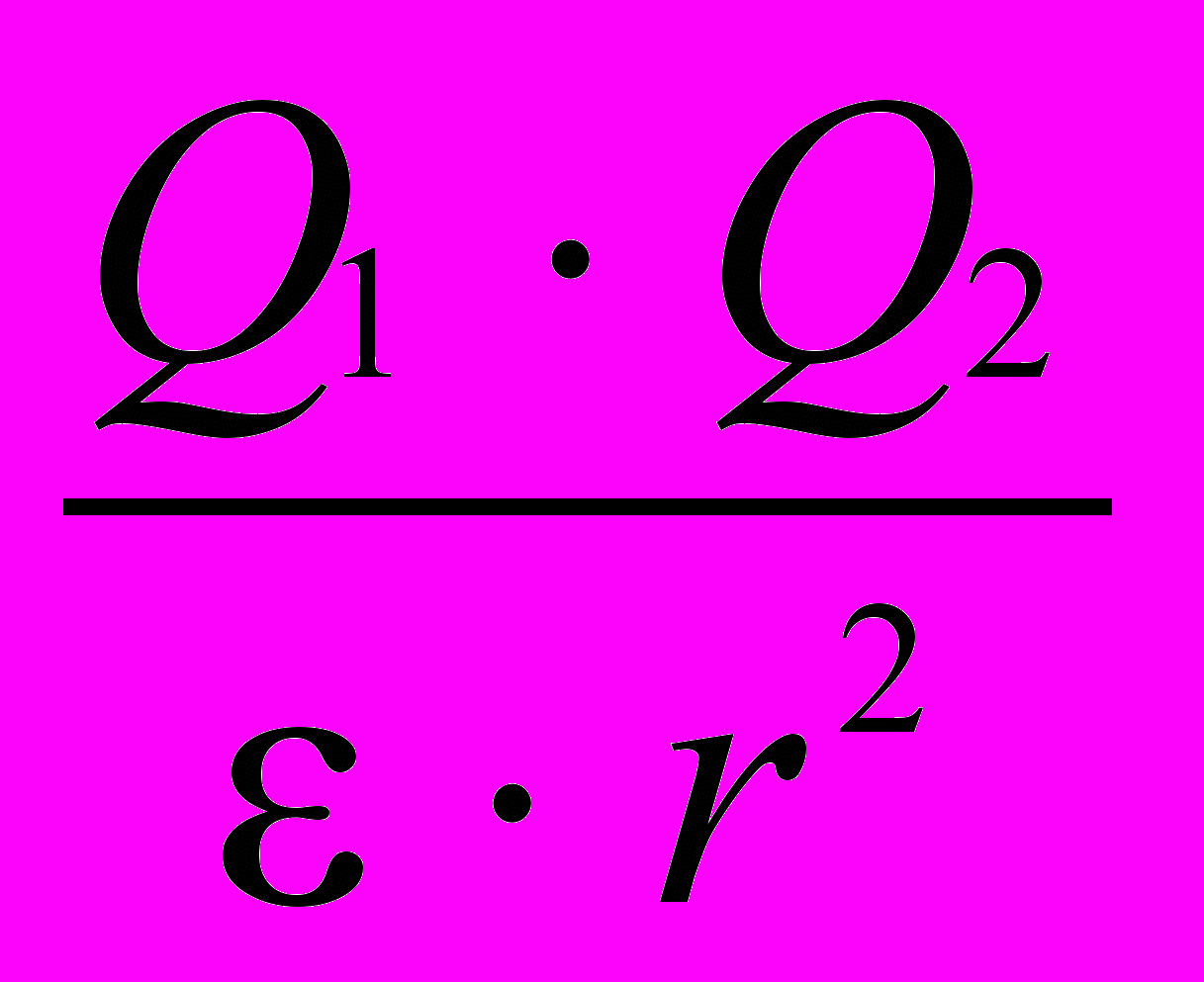
Закон Ампера для параллельных токов	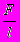= k0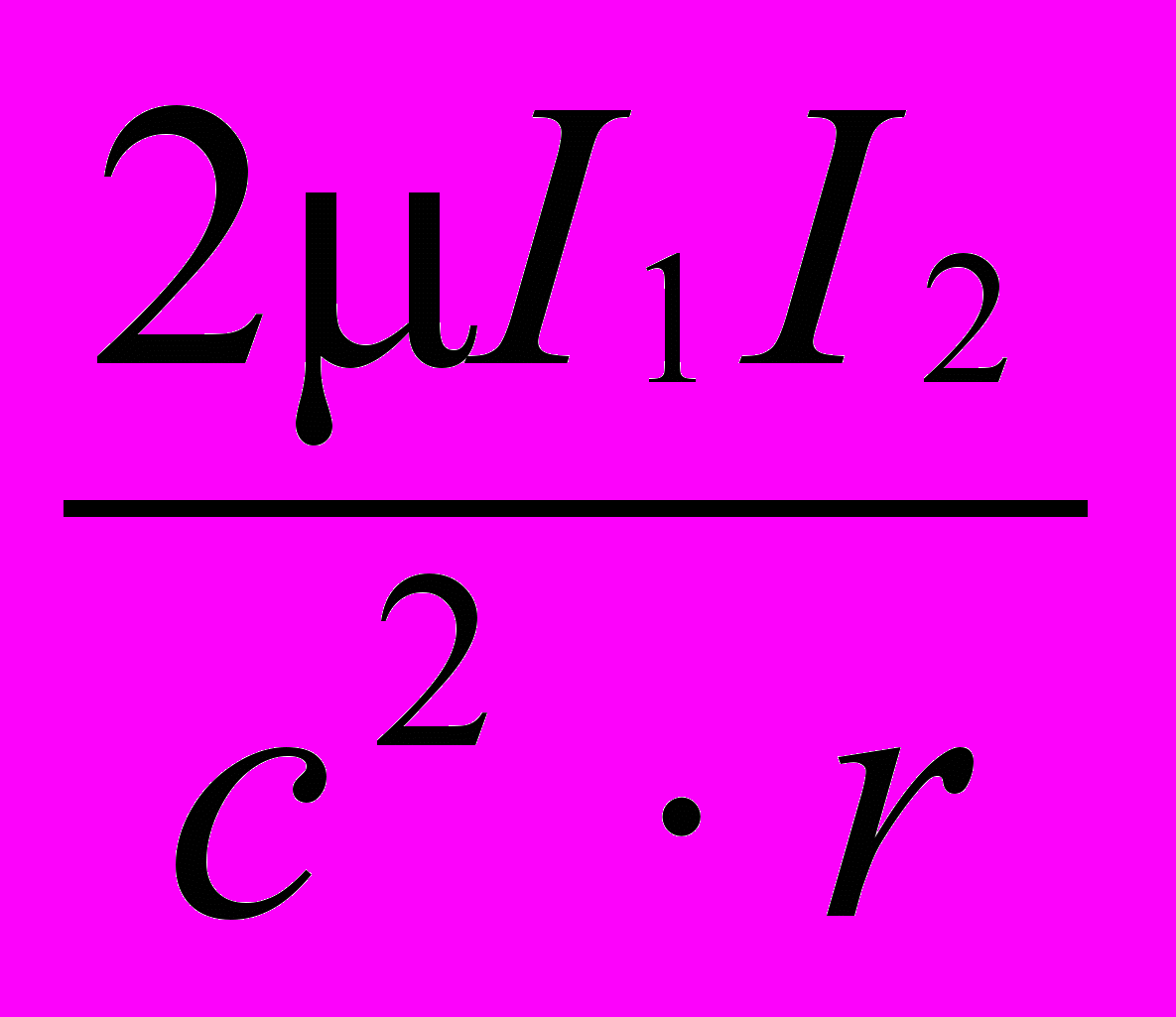
Закон Био–Савара– Лапласа	dВ = k0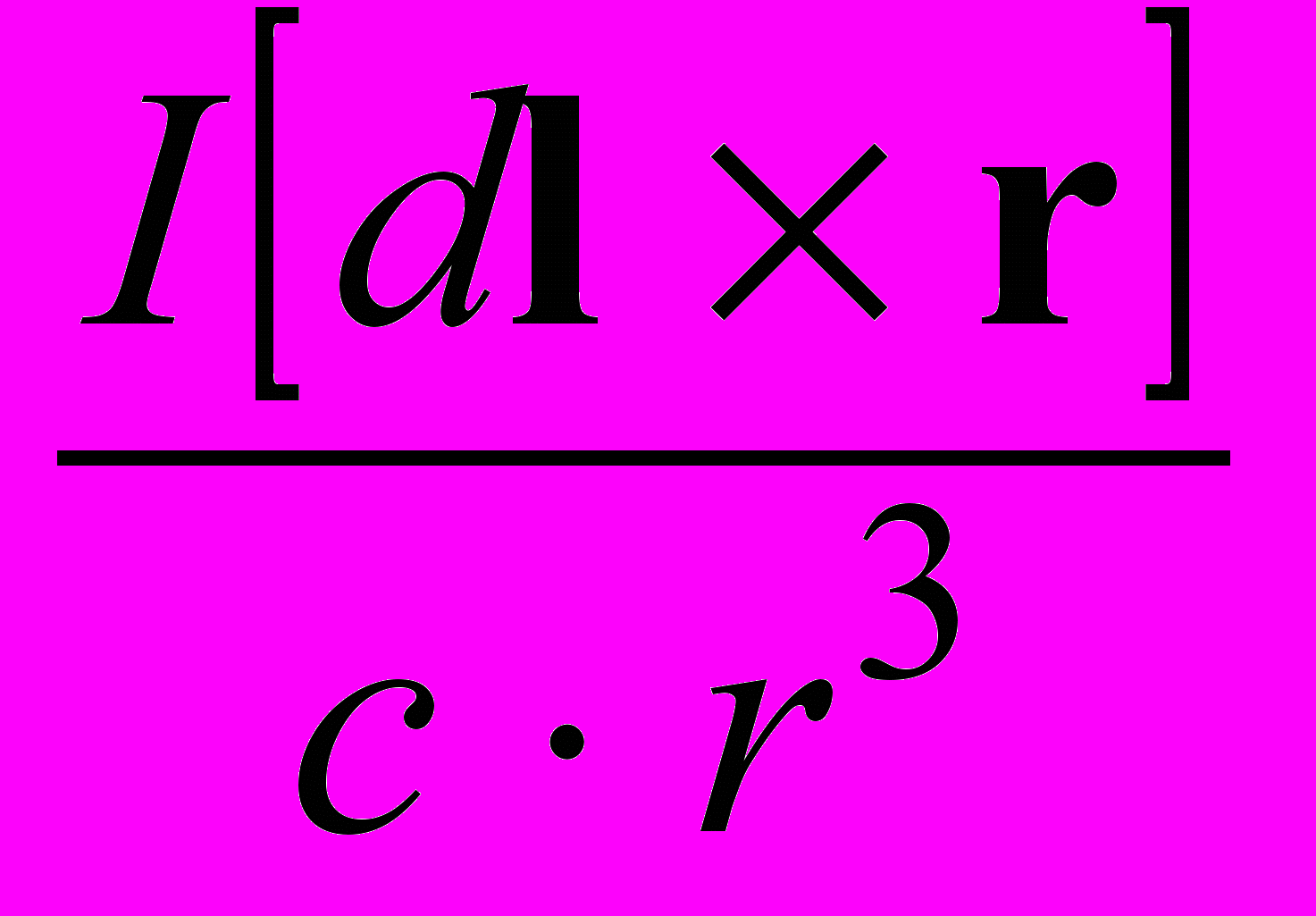
Напряженность электрического поля Е	Е = F/Q	1 В/м вольт на метр
Электрическое смещение D	D = E + 4k0P	1 В/м вольт на метр
Электрический момент диполя р	p =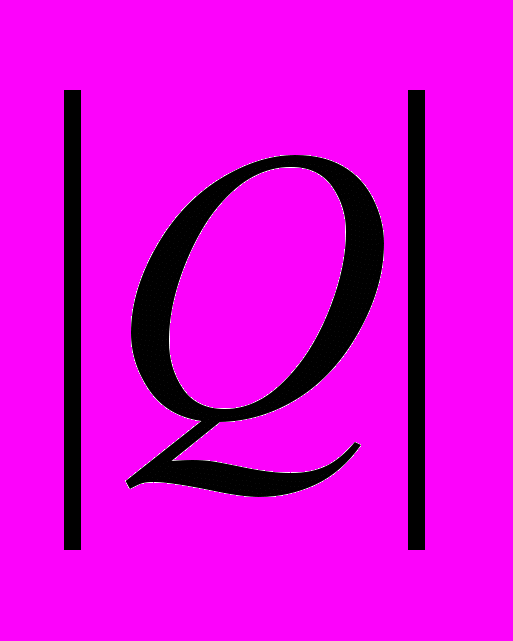 l	1 Клм Кулон-метр
Поляризованность Р	Р =  pi / V	1 Кл/м2 кулон на кв. метр
Связь между Р и Е D и E	Р = Е/k0 D = E
Магнитная индукция В	F = Q [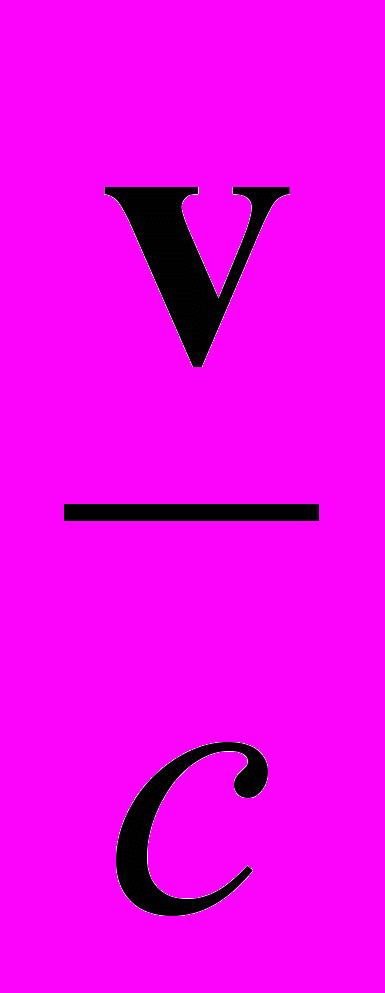  B]	1 Тл(Т) теоретическая тесла
Напряженность магнитного поля Н	Н = В – 4k0M	1 Тл(Т) теоретическая тесла
Магнитный момент рm	pm =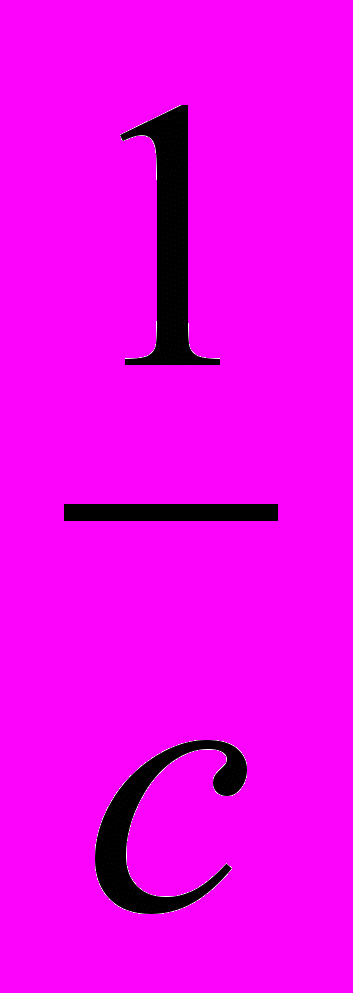 IS n	1 Тм тамм
Намагниченность М	М =  pmi / V	1 Тм/м3 тамм на куб. м
Связь между М и Н	М = Н/k0
Связь между Н и В	Н = В/

Числовое значение размерного коэффициента k₀ определяется из закона Ампера для параллельных токов: k₀ = 10^–7²  9·10⁹ Нм²/Кл², где  = 2, 9979245810⁸ – числовое значение скорости света в вакууме.

Названия некоторых магнитных единиц СТ образованы от названий соответствующих магнитных единиц СИ с добавлением прилагательного «теоретический (ая)», которое позволяет отличить единицу СТ от соответствующей единицы СИ. В частности, в СТ единица магнитной индукции В имеет название «тесла теоретическая», при написании: 1 Тл(Т). Единица магнитного момента в СТ получила название «тамм»
(1 Тм) в честь лауреата Нобелевской премии И.Е. Тамма.

Формулы размерности и соотношения между единицами некоторых электромагнитных величин в СТ и СИ представлены в табл. 3.

Таблица 3

Формулы размерности и соотношения между электромагнитными единицами СИ и СТ

ФИЗИЧЕСКАЯ ВЕЛИЧИНА	ФОРМУЛА РАЗМЕРНОСТИ		СООТНОШЕНИЯ МЕЖДУ ЕДИНИЦАМИ СИ И СТ
	СИ	СТ
Электрический заряд Q	TI		1 Кл
Сила электрического тока I	I		1 A
Потенциал  Напряжение U	L2MT-3I–1		1 В
Электрический момент диполя p	LTI		1 Клм
Поляризованность P	L–2TI		1 Кл/м2
Напряженность электрического поля E	LMT–3I–1		1 В/м
Электрическое смещение D	L–2TI	LMT–3I–1	1Кл/м2 = 36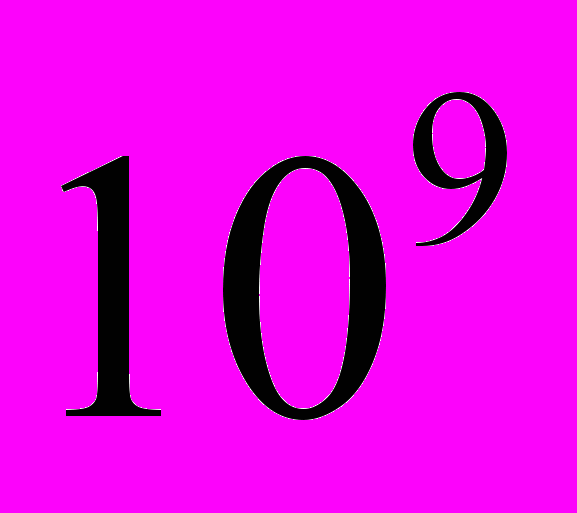 В/м
Магнитная индукция B	MT–2I–1	LMT–3I–1	1Tл = 3108 Tл(Т)
Напряженность магнитного поля H	L–1I	LMT–3I–1	1А/м = 120 Tл(Т)
Магнитный момент pm	L2I	LTI	1Aм2 = Тм
Намагниченность M	L–1I	L–2TI	1А/м = Тм/м3

Полная сводка формул размерности и соотношений между единицами электромагнитных величин в СТ и СИ представлены в работах [18, 19].

Проведем анализ размерностей основных характеристик электромагнитного поля.

Силовые характеристики Е и В имеют в СТ одинаковые размерности (LMT^–3I^–1), представляющие собой отношение dim F / dim Q.

В СТ электрическое смещение D связано с напряженностью электрического
поля Е уравнением D = Е (в вакууме D = Е), поэтому в СТ электрическое смещение D имеет такую же размерность (LMT^–3I^–1) и измеряется в тех же единицах, что и напряженность электрического поля (1 В/м).

Рассмотрим подробнее в связь между напряженностью электрического поля E и электрическим смещением D на примере плоского конденсатора, пластины которого находятся в сосуде с высоким вакуумом (воздушный конденсатор). Предположим, что на пластинах имеются заряды + Q и – Q , которые создают внутри конденсатора однородное электрическое поле (краевыми эффектами пренебрегаем) с напряженностью E₀.

Заполним частично пространство между пластинами двумя слоями однородных диэлектриков с проницаемостью ₁ = 3 и ₂ = 2 (см. рис.1).





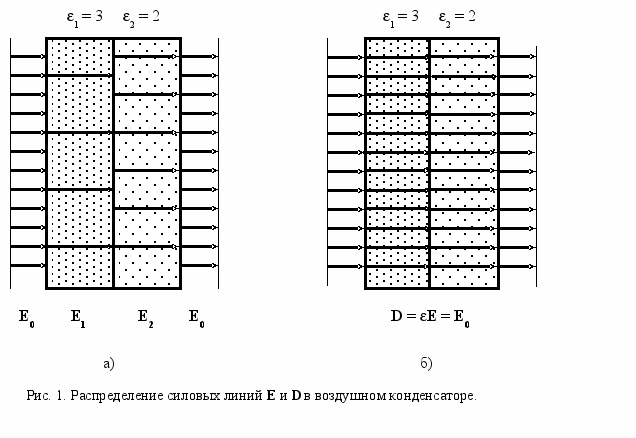
В этом случае диэлектрики поляризуются, на их границах появляются связанные заряды, которые создают электрическое поле связанных зарядов, направленное в противоположную сторону от направления поля, созданного зарядами на пластинах конденсатора. При этом значения напряженности электрического поля в точках, расположенных внутри диэлектриков, уменьшатся: E₁ = E₀/₁ в первом диэлектрике и E₂ = E₀/₂ во втором.

В той части пространства конденсатора, в которой нет диэлектриков, напряженность поля равна E₀. Это означает, что напряженность электрического поля на границе раздела двух диэлектриков скачкообразно меняет свое значение. Распределение силовых линий электрического поля в этом случае показано на рис. 1, а.

С другой стороны, электрическое поле в диэлектрике мы можем описать с помощью вспомогательной величины – электрического смещения D, которое в СТ определяется по уравнению

D = E + 4k0P.

(2)

Необходимо особо отметить, что из уравнения (2) следует, что

1) поляризованность Р и электрическое смещение D имеют разные формулы размерности, т.к. эти величины качественно отличаются друг от друга (в СИ величины Р
и D имеют равную размерность);

2) в вакууме выполняется равенство D = E , т.к. в вакууме Р  0 (в СИ величины
D и E являются неоднородными величинами, т.к. D = ₀E).

В отличие от напряженности электрического поля E, электрическое смещение D не меняет своего значения на границе раздела двух диэлектриков, следовательно, в рассмотренном выше примере с воздушным конденсатором с двумя слоями диэлектриков значение D в любой точке между пластинами равно постоянной величине, равной E₀. Действительно, в пространстве, незаполненном диэлектриком, поляризованность Р равна нулю, поэтому из уравнения (2) следует, что D = E₀ . В каждом слое диэлектрика выполняются равенства D = ₁ E₁ = ₁ E₀ /₁ = E₀ и D = ₂ E₂ = ₂ E₀ /₂ = E₀ . Распределение силовых линий электрического смещения в диэлектрикe показано на рис. 1, б.

В СТ магнитная индукция B определяется из уравнения для силы Лоренца
dF = 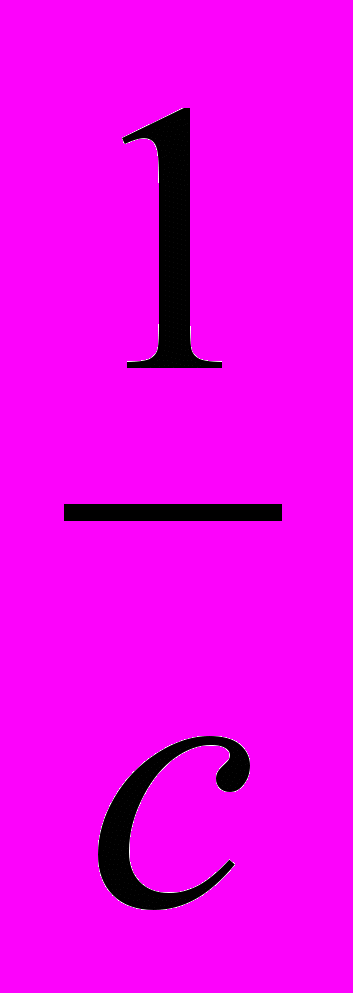I[dl  B], из которого следует размерность магнитной индукции (LMT^–3I^–1) и ее единица, имеющая название «теоретическая тесла», при написании – 1 Тл(Т)

В СТ напряженность магнитного поля H связана с индукцией магнитного поля В уравнением Н = В/ (в вакууме Н = В), поэтому напряженность магнитного поля H
в СТ имеет такую же размерность (LMT^–3I^–1) и единицу, что и магнитная индукция B
(теоретическая тесла, 1 Тл(Т)).

Рассмотрим подробнее связь между индукцией магнитного поля В и напряженностью магнитного поля Н. Пусть в однородном магнитном поле с индукцией В находится магнетик, состояние которого характеризуется намагниченностью М (М =  p_mi / V ).

Величины B и М характеризуют магнитное состояние вещества, но «ради удобства вычислений имеет смысл ввести комбинацию этих величин [16]», вспомогательный вектор – напряженность магнитного поля Н:

H = B – 4k0М.

(3)

Необходимо особо отметить, что уравнения (3) качественно отличается от уравнений (1а) и (1б), т.к. из уравнения (3) следует, что

1) намагниченность М и напряженность магнитного поля Н имеют разные формулы размерности, т.к. эти величины качественно отличаются друг от друга (в СИ величины М и Н имеют равную размерность);

2) в вакууме выполняется равенство Н = В , т.к. в вакууме М  0 (в СИ величины Н и В являются неоднородными величинами, т.к. Н = В/₀).

Величина H часто понимается как некоторое реальное магнитное поле. Это связано с тем, что первоначально источниками магнитного поля считались магнитные заряды. Именно тогда и была введена напряженность магнитного поля H как характеристика реального физического поля, а величина B – как комбинация величин H и М по аналогии с определением величины D по уравнению (2) была названа индукцией магнитного поля.

На самом деле, магнитных зарядов не существует и согласно современным представлениям об электромагнитном поле, реальной характеристикой магнитного поля
является величина B – индукция магнитного поля, а величина H, сохранив свое историческое название – напряженность магнитного поля, является вспомогательной величиной, определяемой в системе СТ по уравнению (3). Следовательно, «H – не физическое поле, а сконструированный очень удачно комплекс из двух величин разной физической природы [16]».

В отличие от диэлектрической проницаемости  , магнитная проницаемость  не является постоянной величиной, а зависит от индукции магнитного поля, т.е.  =  (В), поэтому зависимость Н = f (В) носит нелинейный характер. На рис. 2 представлен вид зависимости В = f (Н) для некоторого сорта железа в СТ и СИ.



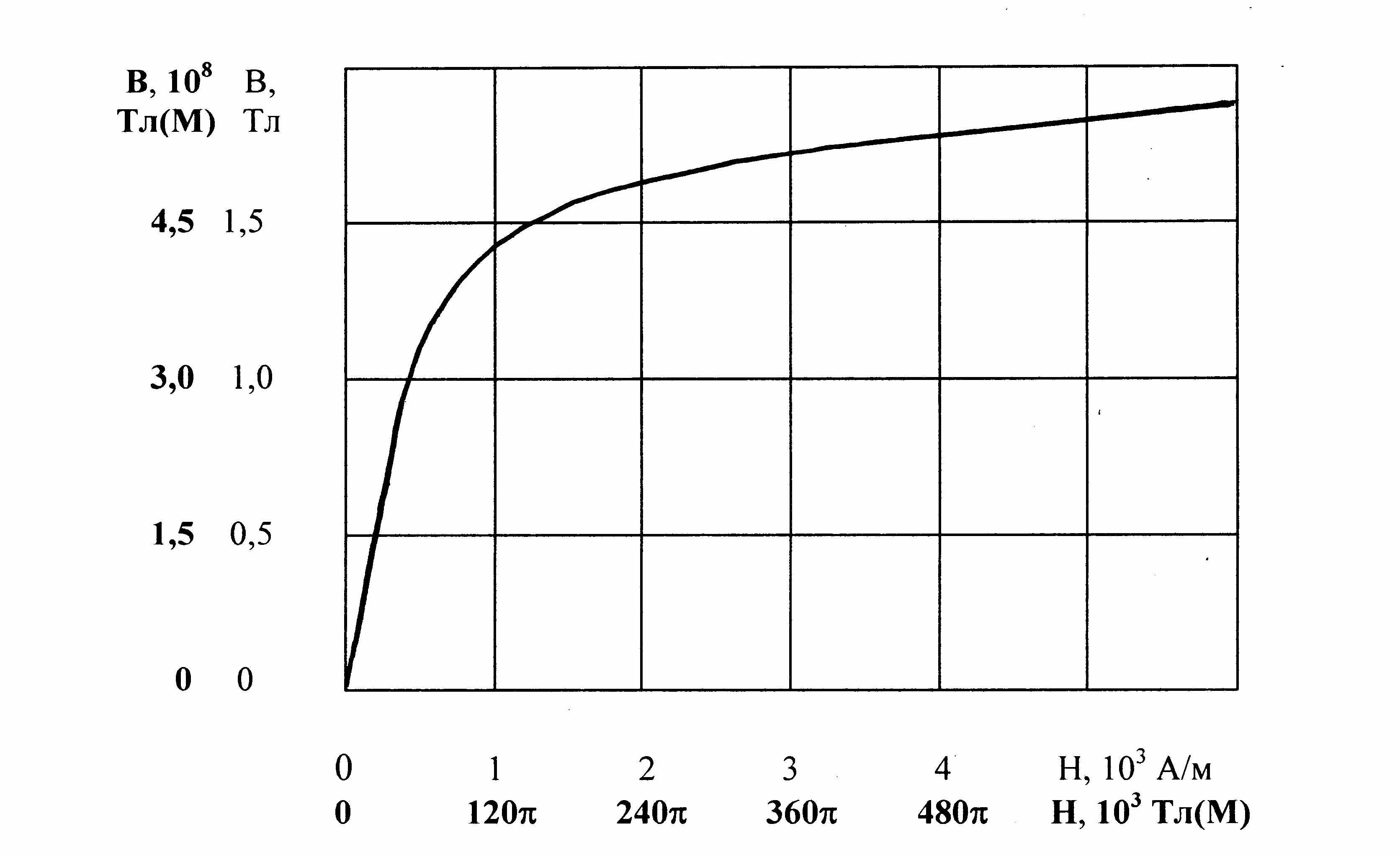
Рис. 2. График зависимости магнитной индукции от напряженности

магнитного поля для некоторого сорта железа.


Из табл.3 и рис 2. видно, что магнитная индукция В и напряженность магнитного поля Н имеют в СТ одну и туже единицу. Это обстоятельство является своеобразным подтверждением следующих высказываний: «Между гауссом и эрстедом абсолютно нет никакой разницы. Это – разные названия одной и той же единицы. Следовало бы сохранить только одно из этих названий – либо гаусс, либо эрстед [13]» и «Нет никакой необходимости в другом названии единицы Н. Тем не менее люди, которые любят
давать названия вещам, дали единице Н собственное название – эрстед [14]».

В СИ величины В и Н имеют не только разные единицы (соответственно, «тесла» и «ампер на метр»), но и разные формулы размерности: dim B = MT^–2I^–1 и dim Н = L^–1I, хотя, как было сказано выше, величины В и Н должны быть однородными величинами.

Таким образом, проведенный анализ единиц СТ и их размерностей показал, что Теоретическая система электромагнитных единиц (СТ) не имеет недостатков системы СГС и электромагнитных единиц СИ, и поэтому использование СТ при изложении раздела физики «Электромагнетизм» дает возможность формировать у студентов знания, которые соответствуют современным научным взглядам на электромагнитное поле.


ЛИТЕРАТУРА

1. Поливанов К.М. Теоретические основы электротехники. Ч. 3. Теория электромагнитного поля. М.: Энергия, 1969.
   
2. Антонов Л.И. Макроскопическое представление поля вектора намагниченности магнетика // УФН – 2003. – Т. 173. – № 11. – С. 1241 – 1245.
   
3. Терлецкий Я.П., Рыбаков Ю.П. Электродинамика. М.: Высшая школа, 1990.
   
4. Можен Ж. Механика электромагнитных сплошных сред. М.: Мир, 1991.
   
5. Матвеев А.Н. Электричество и магнетизм. М.: Высшая школа, 1983.
   
6. Фейнман Р. , Лэйтон Р., Сэндс М. Фейнмановские лекции по физике. Т.7 . Физика сплошных сред. М.:Мир, 1977.
   
7. Телесин Р.В., Яковлев В.Ф. Курс физики. Электричество. М.: просвещение, 1969.
   
8. ГОСТ 8.417–81. ГСИ. «Единицы физических величин». – М.: Изд-во стандартов, 1891. – 40 с.
   
9. Ипатова И.П., Мастеров В.Ф., Уханов Ю.И. Курс физики в 2 т. Т. II. Электромагнитные явления. – СПб.: Изд-во СПбГПУ, 2003. – 323 с.
   
10. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика: Учебное пособие.– СПб.: Изд-во «Лань», 2003. – 400 с.
    
11. Тамм И.Е. Основы теории электричества: Учеб. пособие для вузов. – 10-е изд., испр. – М.: Наука, 1989. – 430 с.
    
12. Ландау Л.Д., Лившиц Е.М. Теория поля. 7-е изд., испр.– М.: Наука, 1988. – 510 с.
    
13. Сивухин Д.В. Общий курс физики. Т. 3. Электричество, 2-изд. – М.: Наука, 1983. – 688 с.
    
14. Парселл Э. Электричество и магнетизм. Берклеевский курс физики. Т.2. – М.: Наука, 1971. – 448 с.
    
15. Трунов Г.М. Приведение единиц электрических и магнитных величин системы СИ в
    соответствие с современным представлением об электромагнитном поле // Физическое образование в вузах. – 2001. – Т.7. – № 4. – С. 12 – 21.
    
16. Халилеев П.А. Основные понятия электродинамики сплошных сред: Методические заметки. – Свердловск: УрО АН СССР, 1989. – 226 с.
    
17. Кобзарев Ю.Б., Незлин М.В. Физическая книга о единицах и размерностях // УФН.– 1979. – Т. 129. – С. 351 – 352.
    
18. Трунов Г.М. О возможности изменения некоторых электромагнитных единиц СИ // Метрология. – 2003. – №3. – С. 28 – 36.
    
19. Трунов Г.М. Коррекция электромагнитных единиц СИ // Законодательная и прикладная метрология. – 2003. – № 6. – С. 45 – 50.
    
20. Трунов Г.М. О необходимости изменения математической формы записи некоторых уравнения электромагнетизма в СИ // Физика в системе современного образования (ФССО-2005). Материалы VIII Межд. конф. – СПб.: Изд-во РГПУ им. А.И.Герцена, 2005. – С. 126 – 129.
    

Законодательная и прикладная метрология. – 2005. – № 6. – С. 45 – 50.