Geum.ru

Пеги Феникс Дабро Элегантное обретение силы. Эволюция сознания

Вид материалаДокументы
Рисунок 3а Рисунок 3б
В: эволюционный компонент биополя
Подобный материал:
1   ...   15   16   17   18   19   20   21   22   23

Рисунок 2


(Детела)


бе эти проблемы могут быть решены с помощью слегка измененной полевой структуры. Давайте представим, что вышеописанная веревка в поле имеет конечную длину (тогда мы имеем сегмент веревки) и скручена в виде замкнутой петли (рис. 2). В этом случае мы можем сразу же избежать первой проблемы. А как насчет второй? Несмотря на то, что благодаря новой модификации, в середине веревки поле меняется незначительно, оно может значительно измениться в области, удаленной от центра петли. Следовательно, можно ожидать абсолютно новых решений – возможно с конечной магнитной энергией.

Когда уравнение (1) анализируется в тороидальной системе координат4, 5, могут быть найдены характеристики новых решений. Исчисления здесь очень сложные. Решения (тороидальные решения) не могут выражаться обычными аналитическими функциями. Но визуально, такие решения очень привлекательны. Они похожи на вышеупомянутые замкнутые петли, сделанные из спирально закрученных веревок. Таким образом, линии поля обладают той же самой структурой, что и нити тороидальных узлов6. Тороидальные узлы можно визуализировать как нить, намотанную на поверхность тора. Самый простой тороидальный узел показан на рисунке 3 (см. следующую страницу).

В

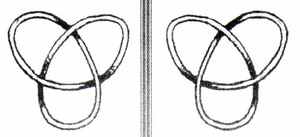
Рисунок 3а Рисунок 3б


(Детела) (Детела)


се тороидальные узлы киральны, то есть, имеют левосторонний и право-сторонний вариант. Киральные струк-туры – это такие структуры, у кото-рых отсутствует центр инверсии, это означает, что их зеркальное отраже-ние не идентично оригиналу. Таким образом, все киральные структуры яв-ляются двусимметричными формами, например, левая рука и правая рука (греческое слово kiros = рука), левосторонний и правосторонний шуруп, левосторонний и правосторонний узел (рисунки 3а и 3б), и так далее. Легко показать, что все математические решения уравнения (1) должны быть киральными: Дифференциальный оператор rot (= ротору) преобразовывает полярный вектор в аксиальный (осевой) (или наоборот), таким образом, k - это, фактически, не обычная скалярная константа – это псевдоскаляр7. Каждый псевдоскаляр обладает киральными свойствами. Когда константа k используется с противоположным знаком, мы получаем полностью эквивалентные решения, хотя и не идентичные – они являются зеркальным отражением оригинала.

Можно показать, что для тороидальных решений, вышеописанная область интеграла сходится. Тороидальные решения – хорошие решения для уравнения (1), ибо представляют собой нефиктивные полевые паутины, паутины с конечной энергией и нечувствительные к отдаленным пограничным условиям.

Здесь наблюдались только самые простые хорошие решения (тороидальные узлы), ибо они могут быть установлены умеренно простыми математическими инструментами. Также, для уравнения (1) могут существовать более сложные решения, например, заузленные структуры, не тороидальные и намного более сложные. Мы будем называть все эти заузленные структуры полевыми паутинами.

Легко видеть, что информационные паутины не излучают энергию. Вектор Направления8 выражается произведением векторов электрического и магнитного полей, но внутри информационной паутины, согласно уравнению (2), эти два поля полностью коллинеарны, и произведение их векторов обращается в нуль. Таким образом, в и вне этой паутины излучения не существует. В этом случае паутина временно устойчива.

Являются ли такие структуры устойчивыми к внешним возмущениям? Могут ли такие возмущения медленно искажать и разрушать наши паутины? Ответ на эти вопросы не прямой. Давайте оговорим две подсказки:

(1) Информационные паутины связаны с эволюционными паутинами (подробнее об этом позже). Синтропические процессы в эволюционных паутинах обеспечивают их устойчивость, и, в результате, также стабилизируют информационные паутины.

(2) Мы изучили уравнения Максвелла в классическом пределе, но в действительности, магнитный поток в паутинах квантованный. Если петли заузленной структуры очень крошечные и если плотность магнитного потока маленькая, то через каждую петлю проходит только очень ограниченное количество магнитного квантового потока (флюксонов). Паутина может излучать только тогда, когда значительное возмущение изменило бы поток, по крайней мере, на один флюксон.

Фактически, оба объяснения в основном означают одно и то же. Синтропическая природа материи – основа всех квантовых явлений. Сегодня мы все еще не можем говорить о детально разработанной теории квантовых процессов, интерпретированных посредством синтропической активности на субквантовом уровне (в субквантовом вакууме или, по другой терминологии, в эфире). Но некоторые, уже появившиеся предварительные концепции многообещающи. Такая интерпретация намного ближе к некоторым альтернативным интерпретациям квантовой физики (например, в современные времена к школе Бома), чем к уже существующей “классической” копенгагенской интерпретации.

Мы видели, что уравнение (1) приводит к крайне интересным решениям и ситуациям. Как иллюстрацию, позвольте упомянуть о другом интересном приложении того же самого уравнения. Если мы монтируем тороидальную катушку, следуя линиям, являющимся решениями уравнения (1), то электрический ток в такой катушке полностью коллинеарен вектору магнитного поля, генерируемого этой же катушкой. Такая катушка свободна от сил Лоренца, то есть, механически очень устойчива. Катушки такого типа иногда используются для генерирования очень сильных магнитных полей, если бы ограничивающим фактором9 могла быть механическая сила самой катушки.

В: ЭВОЛЮЦИОННЫЙ КОМПОНЕНТ БИОПОЛЯ

Здесь, ЭМ поле обладает структурой, похожей на информационные паутины (киральные узлы – по крайней мере, частично тороидальные узлы). При некоторых условиях, эволюционная паутина может перерастать информационную. Основное условие для этого – наличие в области паутины электрического заряда. До настоящего момента, мы обсуждали ЭМ поле в пустоте. Изотропная однородная субстанция не могла бы изменить наши уравнения (потребовалось бы только прибавить диэлектрическую константу с). Это было бы даже более реальным, ибо биополе редко обнаруживается отделенным от биологической материи. Однако, наличие электрического заряда высокой подвижности вносит критическую новизну в наши уравнения: этот заряд рассеивается преимущественно только в ЭМ поле паутинообразной структуры.

Если в паутине соблюдаются условия для синтропических процессов (см. ниже), в биополе начинается синтропическая самоорганизация. Это нечто большее, чем просто обычная самоорганизация протеиновых структур (autopoiesis10) или самоорганизация в рассеивающихся структурах11 Пригожина. Все три установленных явления (autopoiesis, самоорганизация Пригожина и синтропическая самоорганизация) происходят, когда материя далека от термодинамического равновесия. Это очевидно для всех трех процессов самоорганизации. Разница в том, что синтропические процессы (в отличии от двух других) сами создают состояние, далекое от термодинамического равновесия12. Первичное нарушение равновесия может вноситься колебанием, превышающим определенный порог. С этого момента, нарушение равновесия продолжается без какого-либо внешнего вмешательства.

Синтропические процессы, создающие новые эволюционные паутинообразные структуры, происходят при следующих условиях:

• наличие электрического заряда высокой подвижности

• низкая масса несущих заряд частиц

• киральная симметрия с паутинообразной структурой

• ориентированный во времени паттерн ЭМ вибрации (стрела времени в

паутинообразной структуре)

• квантовая связанность в состояниях заряженных частиц (длина

связанности превышает период заузленной структуры)

• адекватная амплитуда плотности магнитного поля.

Третье условие выполняется с самого начала, ибо структура информационного компонента уже киральная. И все же, четвертое условие (стрела времени) выполняется не автоматически. Однако, адекватное первичное колебание создает стрелу времени, и с этого момента, становятся возможными все последующие синтропические процессы самоорганизации. Немного позже мы будем описывать это колебание более детально. Наше описание будет основываться на современной теории хаоса.

Третье и четвертое условия представляют собой требуемые свойства пространственно-временной симметрии паутинообразной структуры. Они предписываются некоторыми основными физическими законами (неизменность единичных преобразований пространства и времени). В совершенном квантовом состоянии заряженной частицы должны быть отражены паттерны структуры с требуемой симметрией пространства-времени, но это возможно только тогда, когда длина связанности квантового состояния превышает, по крайней мере, размер отдельных узлов, а связанность времени – по крайней мере, один период ЭМ колебания. Этот факт приводит к пятому условию. Несомненно, квантовая связанность – чисто квантовый эффект и не обладает никакой классической аналогией13. Причина этому - особая информационная взаимосвязь в квантовых состояних; такая взаимосвязь не имеет места в классическом мире. Квантовая связанность вносит в физику совершенно новые понимания – давайте вспомним Аспекта и другие экперименты14, относящиеся к Восприятию Удаленных Электрических волн.

Второе и шестое условия взаимосвязаны: Необходимая амплитуда магнитного поля обладает некоей связанностью с массой заряженных частиц и с размером петель заузленной структуры. Чем больше масса и меньше размер петель, тем больше результирующее критическое поле (больше о критическом поле позже). Все это работало бы только с электронами, если бы петли были очень большими, но, как следствие, длина связанности тоже должна была быть большой. Такого рода эффект мог быть возможен в сверхпроводящих материалах. Температурное группирование сверхпроводящих пар Купера и атомов материи незначительно; следовательно, в этом случае происходила бы только самоорганизация электронного газа (без группирования с сетью). Несмотря на это, такой гипотетический процесс в сверхпроводниках предлагает невероятные возможности для обработки информации. Совсем не глупо предположить, что нечто похожее происходит в меланиновых белковых структурах нервной ткани (Коуп). Также мы можем себе представить многие другие виды квантовых компьютеров15 на том же самом уровне.

В этой статье, я буду обсуждать другой вариант процессов самоорганизации. Давайте представим существование электрически заряженных частиц с очень маленькой остаточной массой. Числовые прикидки подсказывают, что в этом случае синтропические условия легко выполнимы, даже если магнитное поле очень слабое и длина связанности относительно мала. Такие частицы ускользают от наших обычных наблюдений и измерений. Почему? Как я уже указывал в своих последних работах, такие частицы не могут существовать независимо, а только вместе с завершенной паутинообразной структурой. Их дом – паутина, возможно, она, также, и их тело – паутинообразная структура может определять их проявленные свойства (а вместе в этими свойствами и сами частицы). Также, паутинообразная структура препятствует аннигиляции (уничтожению) сверхлегких частиц и античастиц, храня каждый из этих видов в отдельных областях.

Таким образом, обнаружение сверхлегких частиц будет невозможно до тех пор, пока мы не научимся обнаруживать биополе (обнаружение научным методом). Паутины остаются в связанном самосохраняющем и самоорганизующем состоянии без внутреннего переноса энергии (вектор Направления для информационной компоненты равен нулю). Но, несмотря на это, существует некая внутренняя информационная взаимосвязь. Перенос энергии – не то же самое, что перенос информации (информация и энергия – не одно и то же)! Как только растворяется биополе, растворяются также и сверхлегкие частицы. Посредством аннигиляции и других реакций, они преобразуются в фотоны и другие известные частицы. Сверхлегкие заряженные частицы находятся в тесной связи с биополем; они создаются и уничтожаются вместе с ним. И, вместе с полем, они – паутина.

Следовательно, для полного понимания, существенно знать, что паутины одушевлены. С другой стороны, традиционная физика основана на передаче информации только в связи с передачей энергии (например, гамильтонианское представление влияний в квантовой механике). Она трактует материю как нечто мертвое, измеряет только мертвые частицы и, следовательно, сначала убивает паутины, а потом теряется возможность узнать о них нечто новое16.

Синтропический процесс, хранящий живую эволюционную паутину, - выразительно нелинейное явление. Эволюционная паутина (основанная на нелинейном синтропическом процессе) контролирует линейную информационную паутину. Как мы вскоре увидим, страведливо также и обратное: Линейная информационная паутина контролирует нелинейную эволюционную паутину. Эволюционный компонент биополя является той прибавкой к информационному компоненту, которая ведет к его эволюции. И в противоложном смысле, информационный компонент является первичной информацией (как первичное семя) для эволюционного компонента. Синтропический (эволюционный) процесс отличается только определенными пространственно-временными паттернами (топологиями) паутинообразной структуры. В таких синтропических областях мы не обнаруживаем никакой синтропической самоорганизации (например, если поле не превышает некоего критического поля). Следовательно, синтропический паттерн является аттрактором (точкой притяжения) (известным из теории динамики нелинейных систем), создающим себя в эволюционной паутине. Если паутинообразная структура очень проста (самые простые синтропические узлы, которые могут выжить), то аттрактор может быть периодическим, но в более сложных паутинообразных структурах мы обнаруживаем аттракторы, обладающие большим сходством с хаотическими аттракторами. Однако, такая “хаотичная” природа проявляет особые черты, характерные только для синтропического поведения. (Например, аттракторы в рассеивающихся структурах Пригожина совсем другие.) Эволюционная паутина вибрирует и постоянно преобразовывает себя, согласно своим собственным природным законам. Следовательно, аттракторы такого вида можно отнести к особому классу: синтропическим аттракторам.

Почему информационная и эволюционная паутины так тесно связаны? Потому что киральная полевая структура эволюционных паутин очень похожа на киральную полевую структуру информационных паутин. Главная причина такого сходства в том, что обе паутины могут описываться одними и теми же дифференциальными уравнениями17. В следующих параграфах я буду представлять довод (хотя очень неточный), что уравнение (1), описывающее структуру информационной паутины, справедливо и для эволюционной паутины на ранних стадиях ее развития:

Траектории заряженных частиц внутри эволюционной паутины (взятые как среднее многих заряженных частиц) выравниваются вдоль линий магнитного поля этой же самой паутины:

j = f (B) (4)

где, j – вектор плотности электрического потока. Векторная функция f (B) нелинейна, плотность потока j может быть выражена экстремумами в определенных плотностях магнитного поля В. В таких случаях мы можем ожидать синтропическую ориентацию (направление) заряженных частиц.

Сейчас, давайте рассмотрим, что происходит, если функция (4) была бы линейной. Несомненно, такое допущение не имеет места в синтропической области параметров (когда плотность поля больше, чем критическая величина – как мы увидим это вскоре). Однако, мы заинтересованы в знании, где находится источник нелинейности (и синтропического направления). Мы начинаем с наблюдения ранней эволюционной стадии, когда поле В еще слабое (ниже критической величины), но уравнение (4) все еще справедливо. На этой стадии, линейный термин уравнения (4) предписывает:

j = p • B , где р – скалярная константа (снова псевдоскаляр). (5)

Когда j вставляется в первое уравнение Максвелла (сейчас, мы также имеем влияние материи и электрические потоки заряженных частиц), мы получаем:

rot B = εεоμμо • ∂Е/∂t + μμо • В (6)

Давайте снова допустим, что вибрация гармонична и что векторные поля Е и В коллинеарны (что истинно для простых информационных паутин), тогда мы получаем уже известное уравнение

rot B = k' • B (7)

подтверждающее наше допущение о коллинеарности полей Е и В. Если бы два оставшихся допущения тоже были истинными (что функция f линейна и вибрация гармонична), то эволюционная паутина и соответствующая информационная паутина демонстрировали бы одну и ту же пространственно-временную структуру ЭМ поля ( другим был бы только размер, а именно k ≠ k'). Но в синтропической области параметров не могут быть выполнены ни первое, ни второе условия. Функция j = f (B) должна прерываться, чтобы быть линейной выше критической точки, и вибрация больше не гармонична, если прибавляется временно-ориентированная эволюция. (Но она все еще может выражаться суммой гармонических вибраций формы Фурье.)

Эти две сложности (нелинейность и негармоничность) деформируют паутинообразную структуру и делают ее более запутанной. Как мы могли бы описать такую деформацию?

Во-первых, давайте рассмотрим негармоничность. Каждая периодическая вибрация (даже негармоничная) может быть выражена гармоническими компонентами Фурье. Уже существующие уравнения (по определению) линейны, таким образом, можно обнаружить отдельные решения для каждого гармонического компонента отдельно (как мы знаем, самые простые решения – киральные структуры в форме тороидальных узлов), затем, мы можем суммировать эти решения для отдельных гармонических компонентов. Следовательно, совокупное решение должно быть суммой, представленной различными узлами (разное k' для разных гармонических компонентов). Отношение между частотами гармоничных компонентов очень регулярно (отношение между разными числами), тогда уравнение (3) (вместе с допущением линейности) тоже создает регулярное отношение между параметрами k'. Это означает, что структура совокупного узла (сочетание всех гармоничных компонентов) тоже будет регулярной. Естественно, совокупный узел теперь намного более запутанный, чем тороидальный, и, более того, его совокупная топология меняется в течение одного периода (чего не происходит с узлом одного чистого гармонического компонента).

Но теперь, мы все еще имеем нелинейность функции (4). Это условие изменяет структуру узла еще более радикально. Чтобы упростить анализ, давайте начнем с паутины, состоящей из одного чистого гармонического компонента.

Нелинейная зависимость (4) может быть записана в форме потенциального ряда степеней (но без условия, что n = 0, ибо когда В = 0, j = 0 тоже; нет синтропического направления частиц).

j = ∑ рn • Bn (8)

n = 1,2,3…

Давайте понаблюдаем за условиями, когда В увеличивается от В = 0. Сначала В маленькое (например, в тороидальном узле). В более высоких полях линейная структура страдает от непрерывной деформации. Позже, в критическом поле Вk создается неустойчивость18, и узловая струк-тура страдает от резкого изменения (фазового превращения). При еще более высоком поле В, в дополнительную структурную разновидность вносится бифуркация. Хотя такие бифуркации тоже являются видом фазового превращения, они обладают особым свойством; из первоначальной фазы не всегда развивается такая же новая фаза – существует несколько возможностей. Линия фазовых возможностей расщепляется с каждой бифуркацией. Магнитный узел еще больше усложняется, хотя внутренне упорядочен не меньше (рисунок 4). Подобные явления известны из неравновесной т