Вобщем среднем образовании за последнее время произошли существенные перемены, ориентированные на улучшение результатов работы школы
| Вид материала | Документы |
- В последнее время в России произошли существенные изменения в структуре, клинике, 48.44kb.
- Вистории России на протяжении ХVII века произошли большие перемены. Вначале столетия, 359.96kb.
- Основы вероучения неосалафитской (ваххабитской) школы в исламе Айдын Ализаде в последнее, 273.62kb.
- Соглашение о взаимном признании и эквивалентности документов о среднем (общем) образовании,, 66.64kb.
- Исследовательский проект, 109.04kb.
- Выступление, 117.29kb.
- Выступление, 126.34kb.
- Педагогические условия адаптации, 79.05kb.
- Методические рекомендации для родителей, будущих первоклассников. Муниципальное дошкольное, 189.94kb.
- Приказ № от Документ о предшествующем образовании, дата выдачи и наименовании учреждения, 192.96kb.
Введение
В общем среднем образовании за последнее время произошли существенные перемены, ориентированные на улучшение результатов работы школы. Одним из направлений является мониторинг оценки качества предметных достижений обучающихся 4 - ых классов общеобразовательных учреждений области и по математике тоже.
Актуальность. «Низкие результаты у обучающихся городов Тайга, Осинники, Полысаево … Хуже всего справились с заданием, в котором необходимо осуществить самостоятельную конструкторскую деятельность с учётом возможностей применения разных геометрических фигур ( процент выполнения – 34,57% ).» ( из газеты «Педагогический поиск», № 4 (184), август,2009 год. Стр.10,11. Приложение № 1 и тест из мониторинга. Приложение 2
Итак : проблема уже у пятиклассников Тайги выявлена – низкая оценка уровня математической грамотности и, в том числе, низкий уровень геометрической подготовки учащихся. Так почему трудно решать геометрические задачи ? Да, ряд требований можно предъявить и учителю начальной школы, но повышать уровень математической грамотности обучающихся в четвёртых классах г. Тайги придётся учителям пятых классов этого же города. В своей работе мы остановимся на поиске ответа на вопрос : «Почему трудно решать геометрические задачи ?» На наш взгляд , введение в курс 5 класса дополнительных занятий со специально подобранными упражнениями направленные на развитие творческого мышления, обновления методов и средств обучения, будет способствовать повышению качества не только геометрических знаний и умений, а вообще повышению математического уровня и более интенсивному развитию школьников. Целью написания работы является выявление трудностей, возникающие при решении геометрических задач и разработка методических рекомендаций при формировании пространственных представлений обучающихся при решении геометрических задач.
Для достижения поставленной цели необходимо решить следующие задачи, которые определили содержание и структуру нашей работы в её теоретической и практической частях :
1. Изучить и учесть психологические особенности подростка.
2. Рассмотреть психолого-педагогические основы методики формирования у учащихся пространственных представлений.
3. Выявить у учащихся основные трудности, возникшие при решении геометрических задач.
4. Охарактеризовать роль геометрии в школьном курсе математики.
5. Показать преимущество методических рекомендаций при формировании пространственных представлений обучающихся при решении геометрических задач.
Глава 1. Психолого-педагогические основы методики формирования у подростка пространственных представлений.
1.1. Психологические особенности подростка.
Успех учебно-воспитательной работы со школьниками зависит от знания и учета их возрастных особенностей. Это положение ещё в большей степени относится к подростковому возрасту (от 10 и 15 лет), который считают переломным. Подростковый возраст связан с перестройкой психических процессов, деятельности личности школьника и поэтому требует решительных, но постепенных изменений в формах взаимоотношений, организации деятельности, руководства со стороны взрослых, в частности учителей.
Трудности, встречающиеся порой в учебной работе со школьниками-подростками, объясняются иногда недостаточным знанием или игнорированием особенностей и закономерностей психологического развития в этом возрасте. Подростковый возраст считается более трудным для обучения, чем младший и старший возрасты. Сам процесс превращения ребенка во взрослого труден, так как связан с серьезной перестройкой психики и ломкой старых, сложившихся форм отношений с людьми, изменением условий жизни и деятельности. В самом деле, старые формы и методы объяснения нового материала постепенно становятся непригодными. Если школьник еще недавно слушал подробные объяснения учителя, то теперь подобная форма знакомства с новым материалом часто вызывает у ученика скуку, равнодушие, явно тяготит его. Склонный ранее к дословному воспроизведению учебного материала, учащийся стремиться теперь излагать материал «своими словами» и протестует, когда учитель требует от него точного воспроизведения формулы, закона, определения.
Основной особенностью мыслительной деятельностью подростка является нарастающие с каждым годом способность к абстрактному мышлению, изменение соотношения между конкретно-образным и абстрактным мышлением в пользу последнего. При этом наглядные компоненты мышления не регрессируют, не исчезают, а сохраняются и развиваются, продолжая играть существенную роль в общей структуре мышления. Например: развивается способность к конкретизации, иллюстрации, раскрытию содержания понятий в конкретных образах и представлениях. Игнорирование особенностей наглядно-действенного мышления подростков приводит к известным фактам: тормозится вычленение абстрактных существенных признаков объекта.
Традиционные требования школьного обучения обращены к развитию дискурсивного мышления, предполагающего доминирование фактора вербального понимания. Преобразование же вербального понимания тормозит развитию наглядно-образного компонента интеллектуальной активности.
Школа переоценивает роль левого полушария, ориентируясь на логику, порядок, технологичность, и непроизвольно помещает в невыгодные условия учащегося с доминирующим правым полушарием, зависимых от контекста.
Следовательно, подобрав стиль обучения с учетом психологических особенностей, можно избежать определенных трудностей в усвоении знаний, ориентировать учащихся на успех, не допускать появления школьных неврозов.
1.2. Педагогические основы методики формирования у подростков пространственных представлений
Целевые установки на преподавание геометрии в средней общеобразовательной школе в программе по математике выражены следующим образом:
- формировать у учащихся диалектико – материалистическое мировоззрение, ознакомить их с ролью геометрии в формировании целостной научной картины мира, с соотношениями математических абстракций и реальной действительности;
- формировать у учащихся систему геометрических знаний и умений, обеспечить прочное и сознательное овладение методами их получения:
- развивать пространственное воображение и логическое мышление учащихся;
- вооружить школьника геометрическими знаниями, умениями и навыками, необходимыми в повседневное жизни и в работе, достаточными для изучения в школе других наук, для продолжения образования после учебы в школе.
Структуру умственной деятельности школьников в области геометрии, следуя Г. Д. Глейзеру, можно представить в виде следующих взаимосвязанных составляющих: интуитивный, пространственный, метрический, логический, конструктивный, символический компоненты.
Одной из главных целей преподавание геометрией считают формирование у учащихся пространственных представлений. И это не столько внутренняя задача курса геометрии, сколько внешняя, связанная с подготовкой школьников к жизни, к труду, способность создавать и оперировать пространственными образами характеризует уровень общего развития человека. Ориентация человека в пространстве является тем фундаментом, который необходим для практической деятельности по многим специальностям: архитектор, инженер, строитель, геодезист, чертежник, оператор, диспетчер, космонавт, кристаллограф и т. д. Пространственные представления необходимы учащимся и для восприятия учебного материала курса геометрии и для решения различного рода задач.
Не смотря на столь большую роль, которую играют пространственные представления, они сформированы у учащихся на низком уровне. Об этом свидетельствует такой показатель как, экзамен, мониторинг. Приложение 1 Приведенные результаты показывают на сколько остро в школе стоит проблема формирования о учащихся и в пространственных представлениях. Заметим, что пространственные представления формируются не только в процессе обучения математики, но и рисованию, географии, черчению, физике, труду и т. д.
1.3. Психологические основы методики формирования у подростков пространственных представлений.
Говоря о пространственных представлениях, следует учитывать, что в психологии различают два их вида - представление памяти и воображения. Под представлениями памяти понимают образы, возникшие в сознании на основе прошлого опыта, в результате отражения пространственных свойств и отношений ранее воспринятых предметов. Под представлениями воображения понимают новые образцы, формируемые в результате трансформаций представлений памяти.
Пространственный образ возникает под воздействием наглядной основы и требований деятельности, обусловленный конкретными условиями задачи, образ опостредствуется деятельностью.
Пространственными характеристиками объекта, лежащими в основе возникновения образа, являются: форма, величина, взаимоположение составляющих его элементов, расположение их на плоскости, в пространстве относительно любой заданной точки отсчета.
Подчеркнем, что в пространственных представлениях следует различать две их стороны: создание пространственных образов и оперировании ими. Заметим, что учащиеся испытывают большие трудности в оперировании образами, нежели в их создании. Геометрия наиболее значимо оперирование образами геометрических фигур. Как показали психологи , оперирование образами есть основное содержание пространственных представлений и является критерием уровня их развития. Вот почему учитель должен обратить самое пристальное внимание на формирование у учащихся умениям оперировать образами.
Процесс формирования пространственных представлений проходит следующие этапы :
- Создание целостного образа на наглядной или абстрактно-логической основе путем опоры на ранее сформированные пространственные представления.
- Оперирование образом в односложных связях и несколько измененных условиях и закрепление его существенных признаков путем варьирования несущественных.
- Оперирование образом в сильно измененных условиях.
- Активное оперирование образом в существенно измененных условиях
внутрипредметных и межпредметных связей и отношениях.
- На базе сформированных ранее образах творческое конструироваие новых образов и отношений между ними.
Заметим, что в результате оперирования пространственными образами происходит их воссоздание,перестройка,видоизменение в требуемом направлении, при этом ученик овладевает способами пространственного преобразования объектов с учетом их функций в деятельности.
Глава 2 Трудности при решении геометрических задач.
2.1. Основные трудности, возникающие у учащихся при решении геометрических задач.
Прежде хотим вернуть вас к философскому основанию мотивации – к процессу познания. Процесс познания происходит по трём этапам :
от чувственного созерцания к → абстрактному мышлению и к → практике.
Т.е. в начале явление наблюдаем, созерцаем, потом делаем выводы, правила, законы, формулы записываем, а уж далее решаем. Проблема будет, если этапность при решении задачи нарушается. Рассмотрим задание геометрического характера взятые из мониторинга в четвёртых классах 2009 года.
Приложение 2. Во всех трёх задачах был текст, рисунок , т.е. процесс познания казалось бы сработал по схеме : От текста к чувственному образу - рисунку это первый этап познания. По нему заставили пройти каждого ученика. Ко второму этапу – абстрактному мышлению - восстановлению правила их тоже подвели. Осталось вспомнить понятие, правило и вычислять, но увы , 2 и 3 этапы прошли 65,43% учащихся. На каком этапе 34,57% детей не восстановили знания, совершили ошибки ? Или не знают понятий связанных с геометрическими фигурами, с соразмерностью «больше на», «меньше на», не знают формул для вычисления площади, периметра фигур, не умеют выполнять арифметические расчёты или допускают их. На эти вопросы надо ответить учителю. Так почему трудно решать геометрическую задачу? Давайте вспомним трудности, возникающие у учащегося при решении геометрических задач :
Первая трудность в знакомстве с задачей через текст, вторая – получение рисунка, схемы по тексту, третья – понимание рисунка, схемы, если они есть. Четвёртая – выполнение дополнительных линий, изображений, построение фигур. Пятая – трудность выбора правил, формулы, свойства. Шестая трудность - арифметические вычисления.
2.2 Анализ трудностей, возникающих у учащихся при решении геометрических задач.
Представьте себе ученика, у которого проблемы с геометрическими задачами. Первое – заставьте его самого прочитать текст этой задачи. Язык задачи должен быть приспособлен к детям, к 11-му классу язык постепенно осложняется. Второе – особое внимание надо обратить на рисунки, если они есть. Если нет, то выполнить. Рисунок плоской фигуры или объёмной надо
чертить с правильным соотношением данных в условии задачи размеров величин и правильно его читать, использовать. Третье – изготовить модель, если рисунок не помогает ученику, но она не должна заменять, а только дополнять рисунок.
А теперь проанализируем трудности: во-первых, пока ученик читает словесный текст, он мало интересуется тем, что даётся вне текста. Это как при решении арифметических задач – он ищет зависимость, выраженную в явной форме в самой задаче, которая помогла бы ему решить задачу.
Здесь помимо текста задачи ученик должен быть хорошо знаком с целым рядом геометрических понятий, различных утверждений и фактов. И ученик принуждён те зависимости, которые необходимы ему для решения геометрической задачи, искать не только в самом тексте её, но и выбирать эти зависимости из целого ряда понятий, утверждений, фактов, не имеющихся в тексте задачи. А это – чрезвычайно сложная задача для ученика. Первая особенность геометрической задачи в значительной мере усложняет ученику процесс решения. И лучше, содержание текста задачи изобразить, визуально представить. И тогда появится вторая характерная особенность геометрической задачи – это рисунок.
Рисунок геометрической задачи играет две роли : с одной стороны, этот рисунок конкретизирует те величины, о которых идёт речь в условии задачи и с которыми ученику надо оперировать; с другой стороны – этот геометрический рисунок должен помочь ученику найти из целого ряда зависимостей ту зависимость, которая свяжет между собой величины, данные в тексте задачи. И, наконец, третья группа трудностей – это трудность арифметического характера задачи. Вот эти особенности геометрической задачи и являются источником тех трудностей, с которыми ученик встречается на пути решения геометрической задачи на вычисление. А наших учеников порой затрудняет самая элементарная техника рисования. Тем более будут затруднять рисунки, в которых надо выполнить дополнительные построения или восстановить фигуру по некоторым данным точками.
Глава 3.Упражнения для формирования пространственных представлений.
3.1. Упражнения на распознавание чертежей и моделей.
Разрешите несколько подробней остановиться на каждой из этих групп трудностей. Начнём с рисунка. Первое, что надо сделать ученику, это чётко представить себе те пространственные формы, о которых идёт речь в задаче. И вот, часто ученику трудно представить ту или иную форму, о которой едёт речь. Школьников 5-6 классов следует учить распознавать не только плоские фигуры, но и объёмные фигуры, сравнивать друг с другом, выполнять простейшие измерения и при этом самое пристальное внимание должно быть уделено формулировке выводов из наблюдений.
Пример 1. Из предложенных моделей ( рис.1 Приложение 3 ) отображать те, с помощью которых можно составить указанную фигуру (и).
Пример 2. Стороны шестиугольника равны между собой. Сколько равнобедренных треугольников изображено на рисунке?
А. Б. В. Г.
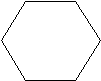







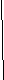











Пример 3. Сколько треугольников, прямоугольников, квадратов, равнобедренных треугольников изображено на рисунке, если длина прямоугольника АСЕО в два раза больше ширины?

Д



 С Е
С Е B F
B FA K O
Пример 4. ( на распознавание моделей)
Демонстрируется набор моделей и учащимся предлагается найти среди них:
а) пирамиду;
б) конус;
в) цилиндр;
г) шар;
Приложение 4
Пример 5.
 Сколько треугольников на рисунке А., сколько четырехугольников на рисунке Б..
Сколько треугольников на рисунке А., сколько четырехугольников на рисунке Б..А. Б.

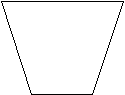


Пример 6. Сколько ребер у многогранника?
А. 5 Б. 7 В. 8




Итак, при решении геометрической задачи самое трудное – это умение выделять из рисунка часть и рассматривать её под определенным углом зрения. Переключить своё внимание на другую плоскую фигуру и глубоко анализировать – вот это и есть конструктивная способность ученика.
Пример 7. Стороны прямоугольника АВСД равны 6 см, 8 см, от него отрезали квадрат. Найти периметр закрашенного прямоугольника.
А В





Д С
(Приложение 2, задачи 7 в каждом варианте)
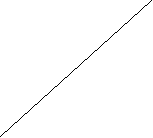
Пример 8. Развертка какой поверхности изображена?
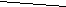

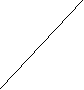
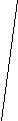
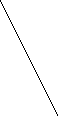
 А. Четырехугольной призмы
А. Четырехугольной призмыБ. Четырехугольной пирамиды
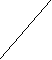
 В.Пятиугольной пирамиды
В.Пятиугольной пирамиды

Пример 9. Какого слова нет в списке названий плоских геометрических фигур?
А. Квадрат
Б. Треугольник
В. Пирамида
Пример 10. Какого слова нет в списке названий пространственных геометрических фигур?
А. Куб
Б. Круг
В. Шар
3.2. Упражнения на одновременную работу с моделью, чертежом и рисунком.
Пример 1. Разрезать прямоугольник со сторонами 4 см и 9 см на две части так, чтобы затем, сложив их, получить квадрат. (Приложение 4)
Пример 2. Квадратный лист сложили вдвое по диагонали, затем ещё раз вдвое так, что получился равнобедренный треугольник. Какая образуется фигура, если каждую вершину последнего треугольника отрезать по линии одинаковой длины, как показано на рисунке, и развернуть лист?






Пример 3. Разрезать фигуру, изображённую на рисунке, на три части так, чтобы из них можно было сложить квадрат.






Пример 4. Вырежьте из листа бумаги квадрат. разрежьте его так, как показано на рисунке. Из полученных семи частей составьте 13 различных многоугольников.




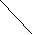
Пример 5. На рисунках даны развёртки прямоугольных параллелепипедов и на них отмечены кружок и крестик. Перенесите их имеющиеся модели этих фигур.
А

 . Б.
. Б.










Пример 6. На модели прямоугольного параллелепипеда отмечены кружок и крестик. Перенесите их на развёртку этой же модели.
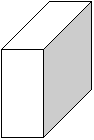








3.3. Упражнения, требующие проверки и доказательств .
На уровне 5 и 6 классов следует проводить работу, которая показала бы учащимся , что мы не можем безраздельно доверять нашим органа чувств при обосновании утверждений, получаемые в результате наблюдения выводы, необходимо проверять путём логических умозаключений . Готовить школьников к пониманию необходимости доказательств можно на основе иллюстраций зрительных иллюзий. Приведём примеры таких иллюзий.
Пример 1 На рисунках а, б, в прямые АВ и СД параллельны?




 А С
А С











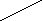













а)
В Д
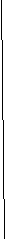



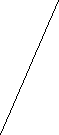
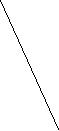

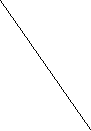

 А С в). А С
А С в). А Сб).
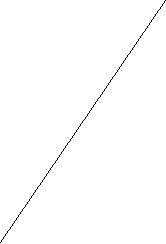






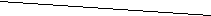
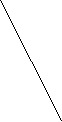
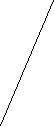

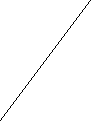


В Д В Д
Пример 2 На рисунке отрезки равны.


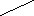
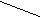
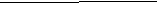

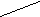
Пример 3 Могут ли существовать тела?













Последняя задача иллюстрируют мысль о том, что нарисовать можно любую фигуру, даже ту, которой нет в действительности, вот почему надо внимательно относится к рисункам проверяя всякий раз их правильность либо на моделях, либо путем логических рассуждений.
3.4. Упражнения на восстановление фигур.
Задачи на восстановление фигур, вообще говоря, являются задачами на построение .Заслуживают внимание некоторые особенности. Прежде всего следует отметить, что эти задачи имеют большое практическое значение, чем традиционные задачи на построение.
В теоретическом отношении решение задач на восстановление фигур опирается на свойстве фигур и не нуждается в каких-либо особых приёмах решения.
Пример 1 Земельный участок, имеющий форму квадрата, был обнесен забором. Со временем забор разрушился.
От него остались:
а) два столба, расположенные на параллельных сторонах квадрата. Кроме того, сохранился ещё один столб в центре квадрата ;
б) два столба сохранились на смежных сторонах квадрата;
в) два столба сохранились на одной стороне квадрата;
г) один столб – в одной из вершин;
д) один столб – в середине одной из сторон и т.д.
Требуется восстановить границу участка .
Пример 2 На листе бумаге были начерчены прямая линия, ломаная и кривая, но по неосторожности чертеж залили тушью. Остались видны только окончания этих линий. Можно ли восстановить линии?
Пример 3 Можно ли и каким образом восстановить отрезок:
а) по двум точкам, являющимися концами его;
б) по двум промежуточным точкам;
в) по середине и одному концу;
г) по одной середине?
Пример 4 По каким точкам может быть восстановлен угол?
Пример 5 Восстанови четырехугольник по серединам его сторон.
Пример 6 Восстанови квадрат по четырем точкам лежащим на его сторонах ( по одной точке на каждой стороне ).
В методическом отношении существенно также то, что задачи на восстановление фигур возбуждают у учащихся значительный интерес, во всяком случае больший, чем традиционные задачи на построение, и было бы неблагоразумно не использовать этот интерес в целях более успешного изучения учащимися геометрии.
Задачи на восстановление фигур могут быть составлены и по другим задачам курса планиметрии.
3.5. Упражнения на представление количественных характеристик единиц измерения.
Нами было замечено на практике, что школьники не владеют интуитивным представлением о количественной характеристики единиц измерения, то есть не развит глазомер.
Пример 1 Задача №10 из мониторинга четвертых классов 2009г.
Приложение 2.
Пример 2 Периметр какой фигуры равен периметру прямоугольника АВСД?
А 9 см В 6см
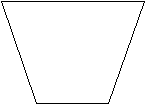 А.
А. 2 см
5см 5см
Д С
6см 2см
Б

 . В.
. В.3 см
7см 7см
8см
Пример 3 Какая из данных величин выражает длину авторучки?
А. 16мм
Б. 16см
В. 16дм
Пример 4 Какая из данных величин выражает площадь комнаты?
А. 17 кв.см
Б. 17 кв.дм
В. 17 кв.м
П



 ример 5 Площадь заштрихованного треугольника равна 20кв.см. Определите площадь квадрата?
ример 5 Площадь заштрихованного треугольника равна 20кв.см. Определите площадь квадрата?А. 5кв.см
Б. 40 кв.см
В. 80кв.см
Пример 6 Площадь заштрихованного квадрата равна 50кв.см, а площадь треугольника равна 20 кв.см. Определите площадь заштрихованной части квадрата.

Пример 7 Изобразить на плоскости фигуру, площадь которой была бы примерно равна 15кв.см.
Анализ выполнения последнего задания показал значительный разброс изображенных фигур : от 5 кв.см до 40 кв.см. Тоже самое наблюдается и при изображении отрезков, указанной длины и в этом плане полезны рекомендуемые упражнения.
Заключение
В соответствии с целями и задачами работы нами рассмотрены : такие вопросы: психологические особенности подростка, педагогические основы методики формирования у подростка пространственных представлений, типы трудностей при решении геометрических задач, выявлена роль активных методов обучения при решении геометрических задач, даны упражнения и методические рекомендации по формированию у учащихся пространственных представлений.
В ходе работы были сделаны следующие выводы: сложность задачи – это объективная характеристика ,зависящая не от субъекта, а от внутренней структуры задачи. И при решении задач геометрического характера надо использовать такого типа задач, как диагностические, конструктивные, графические, интегрирующие .
Любой учитель постоянно накапливает фонд «типичных» ошибок учащихся. Исправлять уже «сформированные ошибки» намного труднее, чем предупреждать их. Умелая организация учебного процесса помогает глубже познать возможности каждого ученика. Использование разнообразных методов и форм обучения на уроках математики и в неурочное время повысит качество обучения. Таким образом цель работы достигнута и определила педагогические условия в поиске ответа на вопрос «Почему так трудно решать геометрические задачи».
Список литературы
- Астряб,А. М.Почему трудно решать геометрические задачи на вычисления [ Текст ] / А. М. Астряб //Математика в школе.-2009.-№5,С.76-79.
- Верченко, С. Б. Задачи на наблюдения для развития пространственных представлений [ Текст ] / С. Б. Верченко//Математика в школе.-1992.-С.34-39.
- Глейзер, Г. Д. Психолого-математические основы развития пространственных представлений при обучении геометрии [ Текст ] / Г. Д. Глейзер// Преподавание геометрии- М.: Просвещение,1980.-С.253-269
- Глейзер, Г. Д. Развитие пространственных представлений школьников при изучении геометрии [ Текст ] – М. : Педагогика,1972.-423c.
- Гусев, В. А., Комбаров, А. П. Математическая разминка [ Текст ] -М.: Просвещение, 2005.-94с.
- Далингер, В. А.Методика формирования пространственных представлений у учащихся при обучении геометрии [ Текст ]: учеб.пособие / В. А. Далингер,-Омск: ОГПИ,1992,96c.
- Каплунович, И. Я. О структуре пространственного мышления при решении математических задач [ Текст ]/ И. Я. Каплунович// Вопросы психологии .-1978.-№3.-С.79-84.
- Крутетский, В. А. Психология математических способностей школьника [ Текст ]-М.: Просвещние,1968.-432с.
- Нагибин, Ф. Ф. Задачи на восстановление фигур[ Текст ] /Ф. Ф. Нагибин//Математика в школе.-2009.-№3, с.76-79.
- Рослова , Л. Методика преподавания наглядной геометрии учащимся 5-6классов [ Текст]/Л. Рослова// Математика в школе-2009.-№17, с.39-42.
