Методическое пособие по курсу " Передача информации" для студентов, обучающихся по направлению "Информатика и вычислительная техника" и по специальности

Вид материала

Методическое пособие

Содержание Методы кодирования информации в каналах связи Построение и реализация эффективных кодов 1.1. Указания к построению кодов 1.2. Программные и технические средства реализации 1.3. Описание программного обеспечения и технической ЗАДАНИЕВыполняется при домашней подготовке Построение и реализация групповых кодов 2.1. Определение числа избыточных символов К-разрядного кода нам необходимо поставить в соответствие комбинацию из n 2.2. Составление таблицы опознавателей Таблица 2.3 Опознаватели одиночных ошибок для кода, исправляющий двойные независимые ошибки Таблица 2.5 Опознаватели одиночных ошибок для кода, исправляющего пачки ошибок в трех и менее разрядах 2.3. Определение проверочных равенств 2.4. Мажоритарное декодирование групповых кодов 2.5. Описание программного обеспечения Построение и реализация циклических кодов Указания к построению кодов. 3.1. Выбор образующего многочлена G =При описании циклических кодов n 3.2. Метод и средства кодирования ... Полное содержание

Подобный материал:

• «Информатика и вычислительная техника», 723.11kb.
• Методическое пособие по курсу "Моделирование" для студентов, обучающихся по направлению, 512.51kb.
• Рабочая программа дисциплины «Теория систем» по направлению подготовки дипломированного, 142.63kb.
• Рабочая программа дисциплины «Компьютерная графика» по направлению подготовки дипломированного, 108.6kb.
• Рабочая программа дисциплины «Методы оптимизации» по направлению подготовки дипломированного, 132.79kb.
• Рабочая программа дисциплины «Параллельные вычислительные процессы» по направлению, 108.72kb.
• Рабочая программа дисциплины «Теория принятия решений» по направлению подготовки дипломированного, 176.95kb.
• Рабочая программа дисциплины «Инструментальные средства 3D графики» по направлению, 112.55kb.
• Рабочая программа дисциплины «Системный анализ и исследование операций» по направлению, 161.5kb.
• Рабочая программа дисциплины «Проектирование интеллектуальных автоматизированных систем», 126.15kb.

621.398

M 545


МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

_________________


МОСКОВСКИЙ ЭНЕРГЕТИЧЕСКИЙ ИНСТИТУТ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

__________________________________




Ю.Н. Кушелев , Г.В. Рыженков, П.М. Сорокин, Н.В. Якушин


МЕТОДЫ КОДИРОВАНИЯ ИНФОРМАЦИИ В КАНАЛАХ СВЯЗИ


ЛАБОРАТОРНЫЕ РАБОТЫ № 101 – 104


Методическое пособие


по курсу

“Передача информации”


для студентов, обучающихся по направлению

“Информатика и вычислительная техника”

и по специальности

“Вычислительные машины, комплексы, системы и сети”


621.398

M 545

УДК: 621.398.725.3 (076.5)


Москва Издательство МЭИ 2001

Утверждено учебным управлением МЭИ

Подготовлено на кафедре вычислительных машин, систем и сетей


Рецензент д-р техн. Наук, проф. А.Б. Фролов


Кушелев Ю.Н. , Рыженков Г.В., Сорокин П.М., Якушин Н.В.

Методы кодирования информации в каналах связи: лабораторные работы 101–104. – М.: Издательство МЭИ, 2001.– 41 с.

Цикл рабораторных работ включает четыре работы: построение и реализация эффективных кодов, построение и реализация групповых кодов, построение и реализация циклических кодов, построение и реализация рекуррентных кодов.

Для студентов специальности “Вычислительные машины, комплексы, системы и сети”, изучающих курс “Передача информации”.

­­­­­­­­­­­­­­­­­­­­­­––––––––––––––––––––––––––––––––––––––

Учебное издание


Кушелев Юрий Николаевич , Рыженков Геннадий Васильевич,

Сорокин Павел Михайлович, Якушин Николай Владимирович


МЕТОДЫ КОДИРОВАНИЯ ИНФОРМАЦИИ В КАНАЛАХ СВЯЗИ

ЛАБОРАТОРНЫЕ РАБОТЫ № 101 – 104

Методическое пособие


по курсу

“Передача информации”


Редактор А.И. Евсеев

Редактор издательства




Темплан издания МЭИ 2001г., метод. Подписано к печати

Формат 60x84/16 физ. леч. л. 2,5

Тираж 300 Изд. # Заказ




Издательство МЭИ, 111250, Москва, ул. Красноказарменная, д.14


 Московский энергетический институт, 2001


Лабораторная работа № 101


ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ ЭФФЕКТИВНЫХ КОДОВ


Целью работы является усвоение принципов построения и технической реа­лиза­ции кодирующих и декодирующих устройств эффективных кодов.


1.1. Указания к построению кодов


Учитывая статистические свойства источника сообщений, можно миними­зиро­вать среднее число двоичных символов, требующихся для выражения од­ной буквы сообщений, что при отсутствии шума позволяет уменьшить время передачи или емкость запоминающего устройства. Такое эффективное кодиро­вание базируется на основной теореме Шеннона для каналов без шума.

К. Шеннон доказал, что сообщения, составленные из букв некоторого алфа­вита, можно закодировать так, что среднее число двоичных символов на бу­кву будет сколь угодно близко к энтропии источника этих сообщений, но не менее этой вели­чины.

Теорема не указывает конкретного способа кодирования, но из нее сле­дует, что при выборе каждого символа кодовой комбинации необходимо ста­раться, чтобы он нес максимальную информацию. Следовательно, каждый сим­вол должен принимать значения 0 или 1 по возможности с равными вероятно­стями, и каждый выбор должен быть независим от значений предыдущих сим­волов.

Для случая отсутствия статистической взаимосвязи между буквами кон­струк­тивные методы построения эффективных кодов были даны впервые Шен­ноном и Фено. Их методики существенно не отличаются, и поэтому соответст­вующий код по­лучил название кода Шеннона - Фено.

Код строится следующим образом: буквы алфавита сообщений выписыва­ются в таблицу в порядке убывания вероятностей их встречаемости. Затем их разделяют на две группы так, чтобы суммы вероятностей встречаемости букв в каждой из групп были бы по воз­можности одинаковыми. Всем буквам верхней половины в качестве первого сим­вола записывается ­– 1, а всем нижним – 0. Каждая из полученных групп, в свою очередь, разбивается на две под­группы с одинаковыми суммарными веро­ятностями и т.д. Процесс повторяется до тех пор, пока в каждой подгруппе не останется по одной букве.

Все буквы будут закодированы различными последовательностями символов из “0” и ”1” так, что ни одна более длинная кодовая комбинация не будет начинаться с более короткой, соответствующей другой букве. Код, обладающий этим свойством, называется индексным. Это позволяет вести запись текста без разделительных символов и обеспечивает однозначность декодирования.

Рассмотрим алфавит из 8 букв. Ясно, что при обычном (не учитывающем вероятностей встречаемости их в сообщениях) кодировании для представления каждой бу­квы требу­ется 3 символа (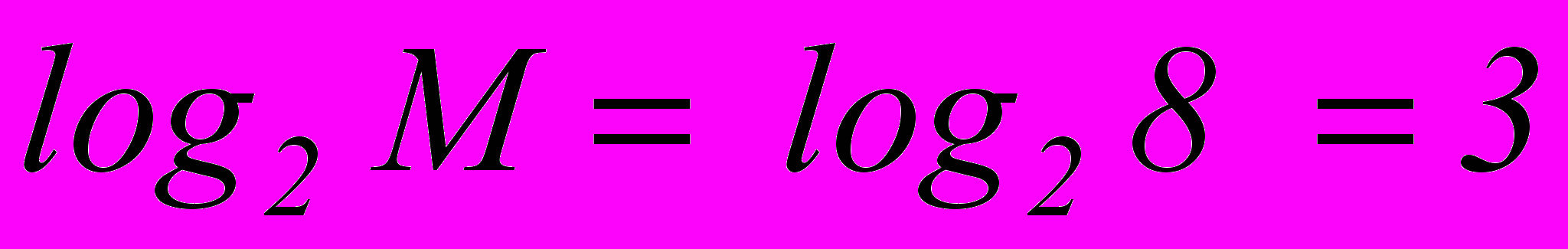), где M – количество букв в алфавите.

Наибольший эффект "сжатия" получается в случае, когда вероятности встречаемости букв представляют собой целочисленные отрицательные степени двойки. Среднее число символов на букву в этом случае точно равно энтропии. В более общем слу­чае для алфавита из 8 букв среднее число символов на букву будет меньше трех, но больше энтропии алфавита H(M).



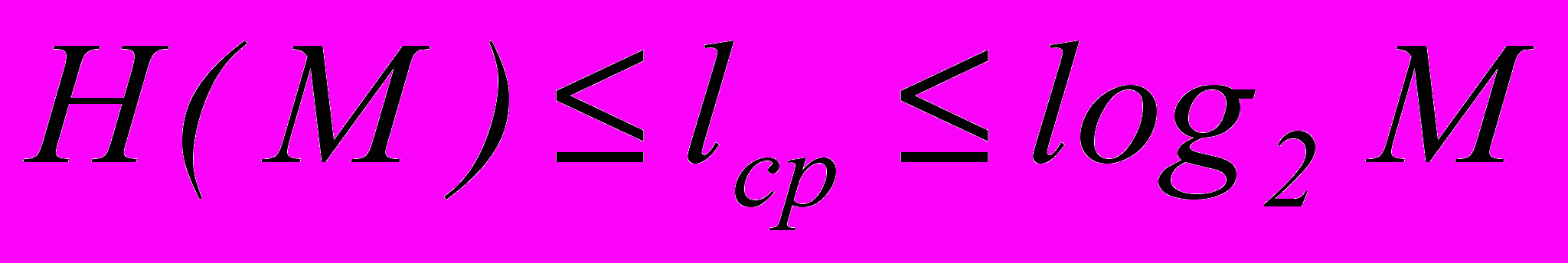
Для алфавита, приведенного в табл.1.1, энтропия H(M) равна 2.76, а среднее число символов на букву:

,

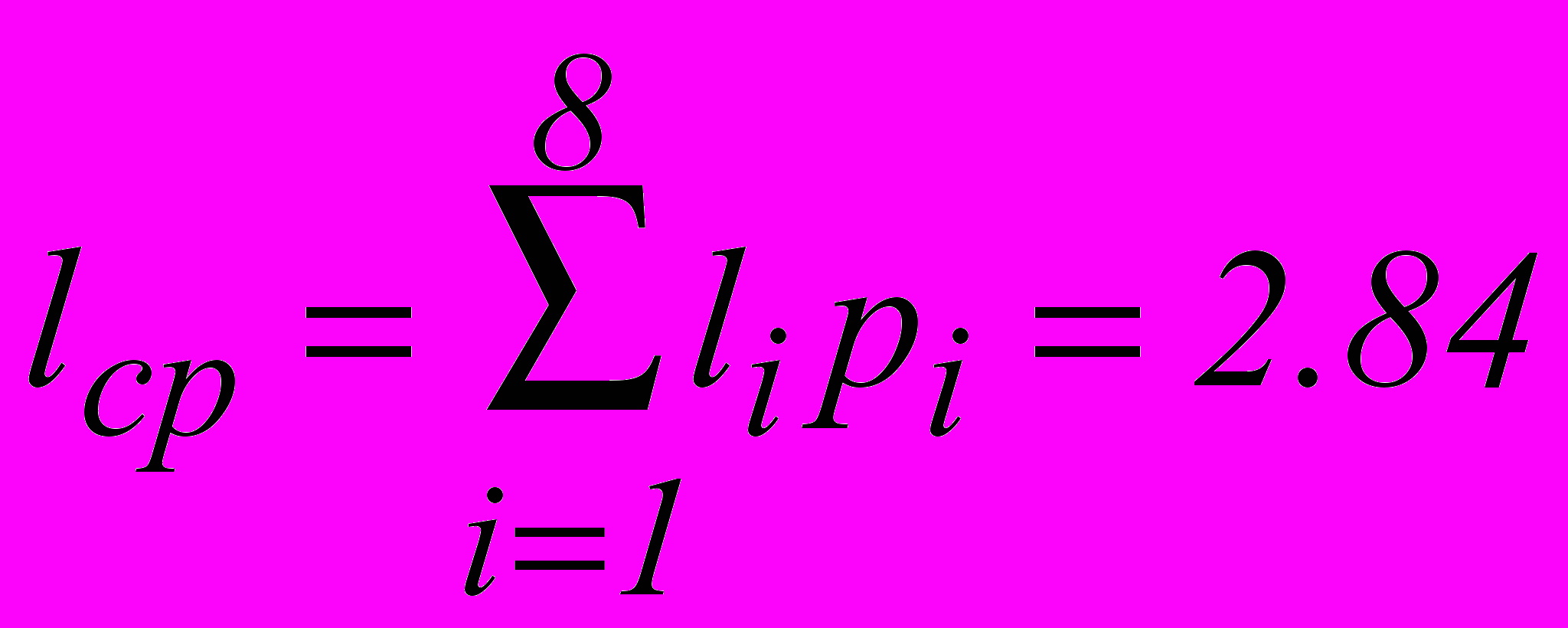где l_i – количество символов для обозначения i-ой буквы.

Таблица 1.1

Буква	Вероятности	Кодовая ком­бинация	№ деления
A1 A2 A3 A4 A5 A6 A7 A8	0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02	11 101 100 01 001 0001 00001 00000	II III I IV V VI VII

Следовательно, некоторая избыточность в кодировании букв осталась. Из теоремы Шеннона следует, что эту избыточность можно устранить, если перейти к кодированию блоками.

Рассмотрим сообщения, образованные с помощью алфавита, состоящего всего из двух букв А₁ и А₂ с вероятностями появления соответственно

Р₁ (А₁)=0,9 и Р₂(А₂)=0,1.

Поскольку вероятности не равны, то последовательность из таких букв бу­дет обладать избыточностью. Однако, при побуквенном кодировании мы ни­какого эффекта не получим.

Действительно, на передачу каждой буквы требуется символ либо 1, либо 0, в то время как энтропия равна 0,47. При кодировании блоками, вклю­чающими по две буквы, получим табл. 1.2. Так как буквы статистически не свя­заны, вероятности встречаемости бло­ков определяют как произведение вероятностей состав­ляющих их букв.


Таблица 1.2

Буква	Вероятности	Кодовая ком­би­нация	№ деления
А1А1 А1А2 А2А1 А2А2	0.81 0.09 0.09 0.01	1 01 001 000	I II III

Среднее число символов на блок получается равным 1.29, а на букву – 0.645.

Кодирование блоков, включающих по три буквы, дает еще больший эф­фект. Среднее число символов на блок в этом cлучае равно 1,59, а на букву – 0,53, что всего на 12% больше энтропии. Теоретический минимум Н(M)=0,47 может быть достигнут при кодировании блоков, включающих бесконечное число букв:




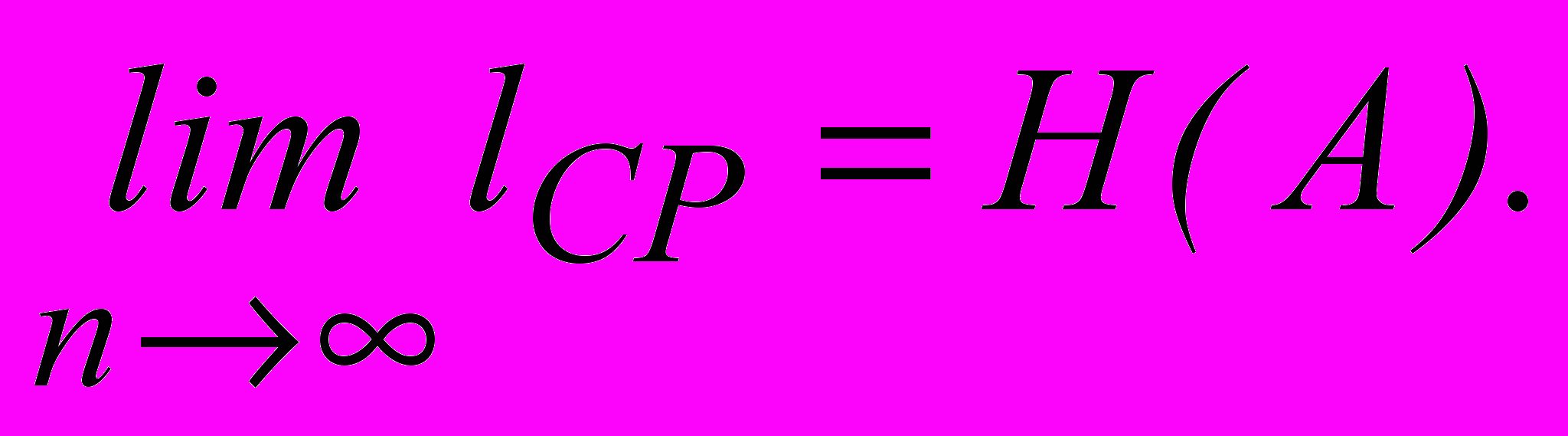
Следует подчеркнуть, что уменьшение l_ср при увеличении числа букв в блоке не связано с учетом статистических связей между соседними буквами, так как нами рассматривались алфавиты с некоррелированными буквами. По­вышение эффективности определяется лишь тем, что набор вероятностей, по­лучающийся при укрупнении блоков, можно делить на более близкие по сум­марным вероятностям подгруппы.

Для учета взаимосвязи между буквами текста, кодирование очередной буквы необходимо вести с учетом предыдущей последовательности букв в зависимости от глубины этой связи. При таком кодировании энтропия на одну букву уменьшается, но существенно усложняется система кодирования, поскольку приходится учитывать не один столбец вероятностей, а M^m столбцов, где m – глубина взаимосвязи между соседними буквами.

Рассмотренная нами методика Шеннона - Фено не всегда приводит к одно­значному построению кода, так как, разбивая на подгруппы, большей по сум­марной вероятности можно сделать как верхнюю, так и нижнюю подгруппы.

Вероятности, приведенные в табл.1.1, можно было бы разбить иначе (табл. 1.3):

Таблица 1.3

Буква	Вероятности	Кодовая ком­бинация	№ разбиения
A1 A2 A3 A4 A5 A6 A7 A8	0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02	11 10 011 010 001 0001 00001 00000	II I IV III V VI VII

При этом среднее число символов на букву оказывается равным 2.80. Таким образом, построенный код может оказаться не самым лучшим. При по­строении эф­фективных кодов с основанием m>2 неопределенность становится еще больше. От указанного недостатка свободна методика Хаффмена. Она га­рантирует однозначное построение кода с наименьшим для данного распреде­ления вероятностей средним числом символов на букву. Для двоичного кода методика сводится к следующему.

Буквы алфавита сообщений выписываются в первый столбец в порядке убывания вероятностей. Две последние вероятности объединяются в одну вспомога­тельную, которой приписывается суммарная вероятность. Вероятности букв, не участ­вующих в объединении, и полученная суммарная вероятность снова располагаются в порядке убывания вероятностей в дополнительном столбце, а две последние вероятности снова объе­диняются. Процесс продолжается до тех пор, пока не получим единственную вспо­могательную вероятность равную единице. Поясним методику на примере (табл. 1.4). Значения вероятностей примем те же, что и в табл. 1.1.

Для получения кодовой комбинации, соответствующей данной букве, необходимо проследить путь перехода ее вероятности по строкам и столбцам табл. 1.4. Для наглядности построим кодовое дерево. Из точки, соответствую­щей вероятно­сти 1, направим две ветви, причем ветви с большей вероят­ностью присвоим символ 1, а с меньшей – 0. Такое последовательное ветвление продолжим до тех пор, пока не дойдем до вероятности каждой буквы. Кодовое дерево для алфа­вита букв, рассматриваемого в нашем примере, приведено на рис. 1.1.

Таблица 1.4

Буква	Вероятности	Вспомогательные столбцы
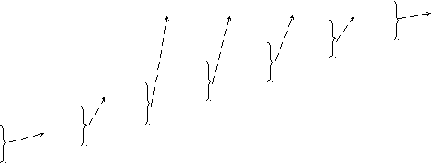A1 A2 A3 A4 A5 A6 A7 A8	0.22 0.20 0.16 0.16 0.10 0.10 0.04 0.02	1	2	3	4	5	6	7
		0.22 0.20 0.16 0.16 0.10 0.10 0.06	0.22 0.20 0.16 0.16 0.16 0.10	0.26 0.22 0.10 0.16 0.16	0.32 0.26 0.22 0.20	0.42 0.32 0.26	0.58 0.42	1

Теперь, двигаясь по кодовому дереву от единицы через промежуточные вероятности к вероятностям каждой буквы, можно записать соответствующую ей кодовую комбинацию: А₁ - 01, А₂ - 00, А₃ - 111, А₄ - 110, А₅ - 100, А₆-1011, А₇ - 10101, А₈ - 10100. При этом получим l_ср =2,80 символа на букву.







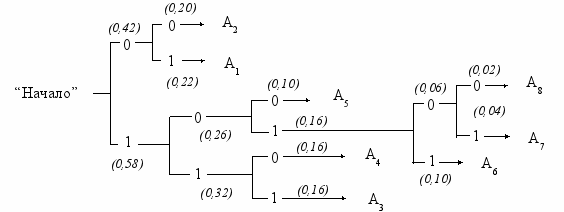
Рис. 1.1. Кодовое дерево

Отметим в заключение особенности систем эффективного кодирования.

Одна из особенностей обусловлена различием в длине кодовых комбина­ций для разных букв. Если буквы выдаются через равные промежутки времени, то коди­рующее устройство через равные промежутки времени выдает комбинации раз­личной длины. Поскольку линия связи используется эффективно только в том случае, когда символы посту­пают в нее с постоянной скоростью, то на выходе кодирующего устройства должно быть предусмотрено буферное устройство ("упругая" задержка). Оно запасает сим­волы по мере их поступления и выдает их в линию связи с постоянной скоростью. Ана­логичное устройство необходимо и на приемной стороне.

Вторая особенность связана с возникновением задержки в передаче ин­форма­ции. Наибольший эффект достигается при кодировании длинными бло­ками, а это приводит к необходимости накапливать буквы, прежде чем сопос­тавить им опреде­ленную последовательность символов. При декодировании задержка возникает снова. Общее время задержки может быть велико, особенно при появлении блока, ве­роятность которого мала. Это следует учитывать при выборе длины кодируемого блока.

Еще одна особенность заключается в специфическом влиянии помех на дос­товерность приема. Одиночная ошибка может перевести передаваемую ко­довую ком­бинацию в другую, не равную ей по длительности. Это повлечет за собой неправиль­ное декодирование целого ряда последующих комбинаций, ко­торый называют треком ошибки. Специальными методами построения эффек­тивного кода трек ошибки стараются свести к минимуму.


1.2. Программные и технические средства реализации


Лабораторная работа выполняется на ПЭВМ, подключенных к локальной сети кафедры. При проведении занятий на кафедре ВМСС необходимо при по­мощи опре­деленных команд войти в кафедральную сеть. Затем запустить на выполнение про­грамму effect.exe, состоящую из трёх частей. В первой части строится кодирующее устройство по методу Шеннона-Фено, во второй – по ме­тоду Хаффмена. Третья часть представляет собой пример построения дерева Хаффмена. Для случая, когда корре­ляционные связи между буквами отсутст­вуют и имеется возможность управлять мо­ментами считывания информации с источника.


1.3. Описание программного обеспечения и технической

реализации эффективных кодов


Управление программой осуществляется через главное меню. Работу ре­ко­мендуется начать со сборки кодирующего устройства – кодера (рис.1.2).




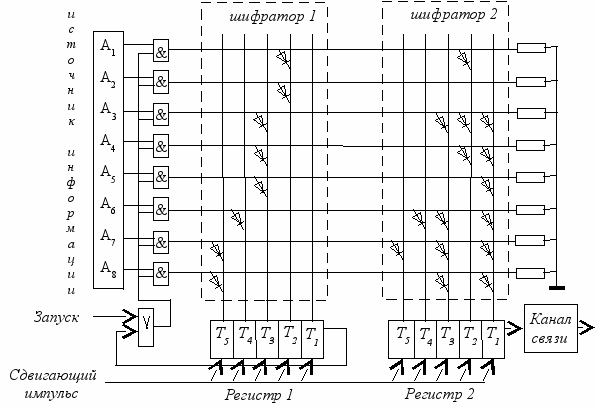
Рис. 1.2. Пример схемы кодирующего устройства для

технической реализации эффективных кодов


Устройство включает схему поучения моментов считывания очередной буквы (матричный шифратор 1 с регистром сдвига 1) и шифратор букв (матрич­ный шифратор 2 с регистром сдвига 2). Число горизонтальных шин шифраторов равно числу кодируемых букв, а число вертикальных шин в каждом из них равно числу символов в самой длинной комбинации исполь­зуемого кода. Схема рассчитана на использование алфавита из 8 букв (сооб­щений). Источник информации удовлетворяет требованиям идеального источ­ника по Хартли, т.е. в каждый данный момент он воз­буждает шину только од­ной буквы, выставляя на нее сигнал "1". В регистре 1 появля­ется сигнал "1" в разряде соответствующем длине кодовой комбинации буквы, что обеспечивается диодным переходом. В регистре 2 появляется код со­ответствующий букве, шина которой возбуждена. Что тоже обеспечивается соответ­ствующими диодными переходами с возбужденной шины на триггеры регистра 2. Сдвигающими импульсами код буквы последовательно выталкивается в канал связи, а единица "вы­толкнутая" из регистра 1 разрешает источнику выдать очередную букву.

При выполнении домашней подготовки студент должен построить эффектив­ный код, используя методики Шеннона - Фено и Хаффмена. В первой части лабо­раторной работы применяется кодирование по Шеннону - Фено. На экране представ­лена заготовка схемы кодера. Необходимо правильно расставить диоды шифраторов. Теку­щее соединение отображается красной пунктирной линией, которую можно переме­щать клавишами управления курсором. Фиксируется соединение клавишами <Про­бел> или . В случае ошибки снять соединения можно с помощью все тех же клавиш.

Закончив сборку схемы, нажмите . Протестируйте схему для каждой буквы. Исправьте допущенные ошибки.

Сборка декодирующего устройства – декодера производится аналогично сборке кодера рис 1.3.

Информация поступает из канала связи в приемный регистр 3. Регистр 3 состоит из триггеров, количество которых на один больше, чем самая длинная кодовая комбинация одной из букв алфавита. В начальном состоянии в регистре 3 в триггере T₆ записана “1”. Перемещаясь по регистру сдвигающими импульсами по мере приема информации из линии связи, она информирует о приеме очередной буквы. Когда кодовая комби­нация буквы разместится в регистре 3 полностью, в этот момент должна схема совпадения “И”, соответствующая принятой букве.

Для этого на все входы схемы "И" этой буквы должны быть поданы сигналы "1" через диоды подключеные к триггерам регистра 3, состояния которых соответствуют кодовой комбинации принятой буквы. Если триггер находится в состоянии "1", то диод подключается к правому или единичному выходу, а если в состоянии "0", то к левому или нулевому вы­ходу. Срабатывание схемы "И" принятой буквы индицирует ее и через схему “ИЛИ” сбрасывает в ноль все разряды ре­гистра 3, кроме первого, в котором снова выставляется "1". После этого схема декодера готова к приему очередной буквы.

После завершения сборки производится тестирование декодера для каждой буквы.

После проверки работы кодера и декодера в отдельности проверим их совместную работу. В начале предлагается выбрать последовательность кодируемых букв. Это осуществляется с помощью клавиш управления курсором и . Ошибки исправляются через . Выбрав нужную последовательность, переведите курсор на <кодировать>. Схема кодера ра­ботает потактно. Причем процессы кодирования и передачи сигналов разделены, что позволяет четко проследить прохождение каждого сигнала по схеме. Переданные сигналы высвечиваются темно-зеленым цветом, полученные – ярко-зеленым. Номер такта отображается в правом верхнем углу. Закодированная последовательность вы­ходит из схемы в "перевернутом" виде (справа-налево). Для выполнения схемой сле­дующего такта нажмите любую клавишу.

После того, как будут закодированы все заданные буквы, для продолжения процесса передачи букв также нажмите любую клавишу.

Затем производим проверку работы декодера. Управление схемой декодирования аналогично управлению схемой кодирования. После завершения процесса декодирования проверьте соответ­ствие закодированных и декодированных букв. Далее рекомендуется запустить деко­дер с изменением в одном разряде и выяснить как это отразится на декодировании.


регистр 3



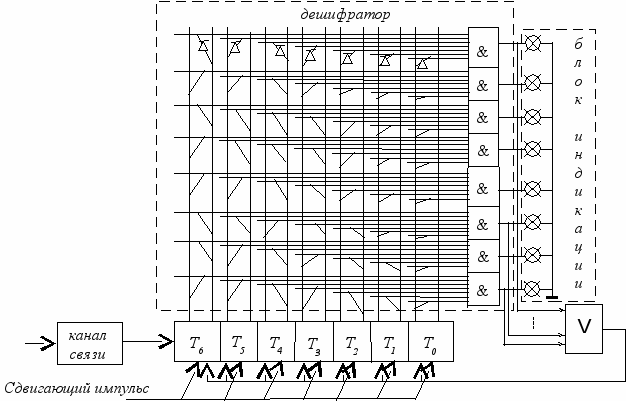
Рис. 1.3. Пример декодирующего устройства для

технической реализации эффективных кодов


С помощью главного меню можно получить информацию о способах эффек­тивного кодирования и как работать с данной программой.

Во второй части лабораторной работы применяется кодирование по Хаф­фмену. Порядок действий аналогичен выполнению первой части лабораторной работы.

Заключительной частью лабораторной работы является построение дерева Хаффмена для кодирования небольшого текста. Эта часть является чисто демонстрационной. В ней шаг за шагом рассматривается процесс кодирования и построения дерева Хаффмена.

В окно с надписью "Текст для кодирования" вводится подготовленный текст. Во всех случаях для продолжения работы нажимается F10, для возврата назад – F9, подсказка – F1. Рядом в окне показывается частота появления букв в тексте. Для удобства можно передвигаться по тексту и выбрав любую букву клавишей , наглядно посмотреть эту букву в тексте. Она будет выделена другим цве­том.

На следующем этапе строится дерево Хаффмена. Дерево расшифровывается следующим образом. Красный прямоугольник – узел дерева, соответствующий букве. В нижней половине прямоугольника выводится сама буква, а в верхней – количество вхожде­ний этой буквы в текст. Серые узлы дерева – узлы, которые получились в про­цессе свертки. Число внутри такого узла показывает общую сумму вхождений. Ка­ждому ребру дерева присваивается “0” или “1”. Чтобы определить код конкретной буквы, входящей в текст, необходимо пройти путь от начала дерева до этой буквы в его конце, накапливая символы (“0” или “1”) при перемещении по ребрам дерева.


ЗАДАНИЕ


Выполняется при домашней подготовке

1. Изучить описание и рекомендованную литературу, изучить методы построения и технической реализации эффективных кодов.

2. По конкретным значениям вероятностей встречаемости букв, заданных студенту препо­давателем или выбранно самостоятельно (отличающихся от рассмотренного в описании, не более 8 букв и нетривиальный случай), построить эффективный код, используя методики Шеннона-Фено и Хаф­фмена.

3. Вычислить энтропию источника и среднюю длину комбинации полученного кода.

4. Подготовить небольшой текст на 150–200 букв для построения дерева кодирования демонстраци­онной программой.


Выполняется в лаборатории

1. Используя построенный код по методу Шеннона-Фено и Хаффмена пра­вильно расставить диоды в схемах кодирующего и декодирующего устройства.

2. Проверить работоспособность системы передачи.

3. Ввести текст для построения дерева кодирования.

4. Зарисовать таблицу и дерево Хаффмена.
   
5. Подсчитать выигрыш от записи текста эффективным кодом.
   

Требования к отчету


Отчет должен включать:

1. таблицу построения эффективного кода по методике Шеннона-Фено;
   
2. схемы шифратора и дешифратора для построенного кода;
   
3. таблицу и кодовое дерево, иллюстрирующие построение эффективного кода по методике Хаффмена.
   
4. Результаты расчетов энтропии источника и среднюю длину кода для буквы, отдельно для заданного Вами алфавита из 8 букв и текста.
   

Контрольные вопросы

1. Когда целесообразно использовать эффективное кодирование?
   
2. Каковы сложности в реализации систем передачи с применением эффективных кодов?
   

3. До какого предела может быть сокращена средняя длина кодовой комбинации?

4. Каковы преимущества методики Хаффмена?

5. Какой код называется префиксным?
   
6. Как учесть взаимосвязь букв в тексте ? Что произойдет с энтропией, если учесть взаимосвязь букв ?
   

ЛИТЕРАТУРА

1. Дмитриев В.И. Прикладная теория информации. – M.: Высш. шк., 1989. – 320 с. (С. 184–196).
   
2. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники. М.: Энергия, 1979.– 512с. (С. 119-131).
   

Лабораторная работа N 102


ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ ГРУППОВЫХ КОДОВ


Целью работы является усвоение принципов построения и технической реали­зации кодирующих и декодирующих устройств групповых корректирующих кодов.

2 Указания к построению кодов

2.1. Определение числа избыточных символов


Групповой код относится к блоковым кодам, в которых формируемая кодовая комбинация содержит n разрядов, из которых k–информационных и m– проверочных (m=n-k). Взаимосвязь между блоками отсутствует , то есть передача и исправление ошибок в разных блоках происходят независимо друг от друга. Математической основой группового кода является теория групп (отсюда и название кода) [1]. В качестве основной операции в групповых кодах используется операция сложения по модулю два.

Построение конкретного корректирующего кода производится исходя из числа передаваемых букв (команд) или дискретных значений измеряемой величины, то есть алфавита из N элементов и статистических данных о наиболее вероятных векторах ошибок в используемом канале связи. Вектором ошибки будем называть кодовую комбинацию, имеющую единицу в разрядах, подвергающихся искажению, и нули во всех остальных разрядах. Любую искаженную кодовую комбинацию можно рассматривать теперь как сумму по модулю два разрешенной кодовой комбинации и вектора ошибки.

Будем рассматривать как независимые ошибки, так и пачки ошибок. Независимые ошибки, это когда по одной из них ничего нельзя сказать о других. В пачках ошибки расположены рядом. Длиной пачки ошибки называется дистанция между первым и последним искаженным символом. Внутри пачки могут оказаться и неискаженные символы.

Исходя из неравенства 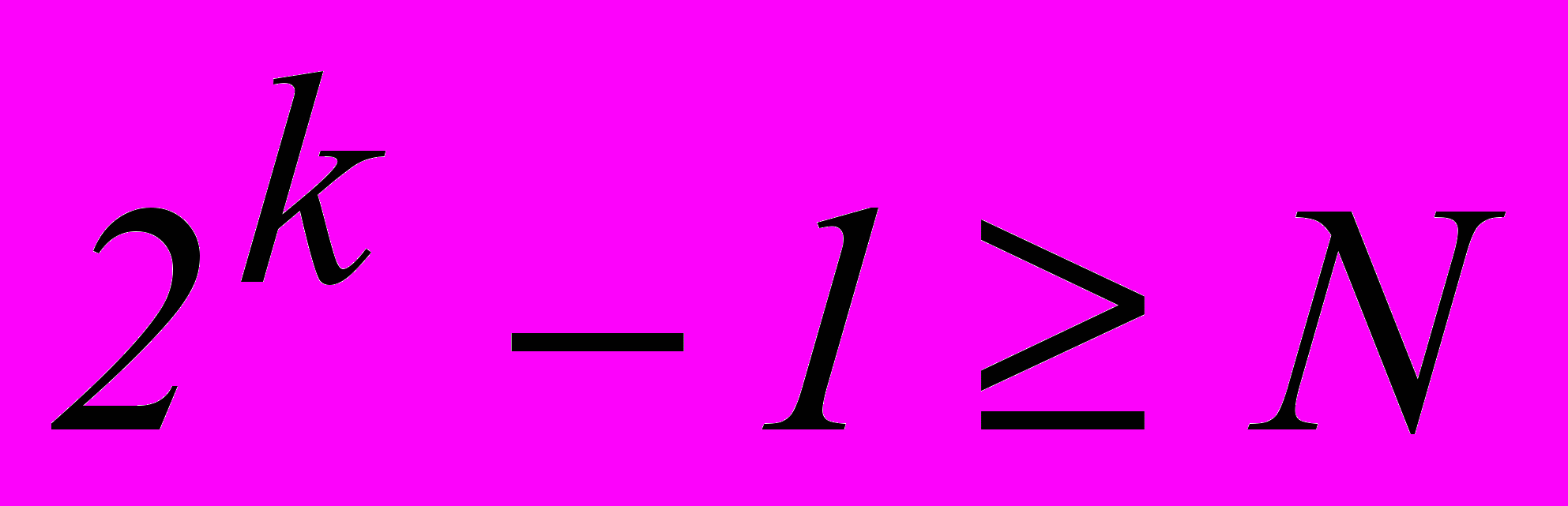, определяем число информационных разрядов k, необходимое для передачи заданного числа команд обычным двоичным кодом.

Каждой из 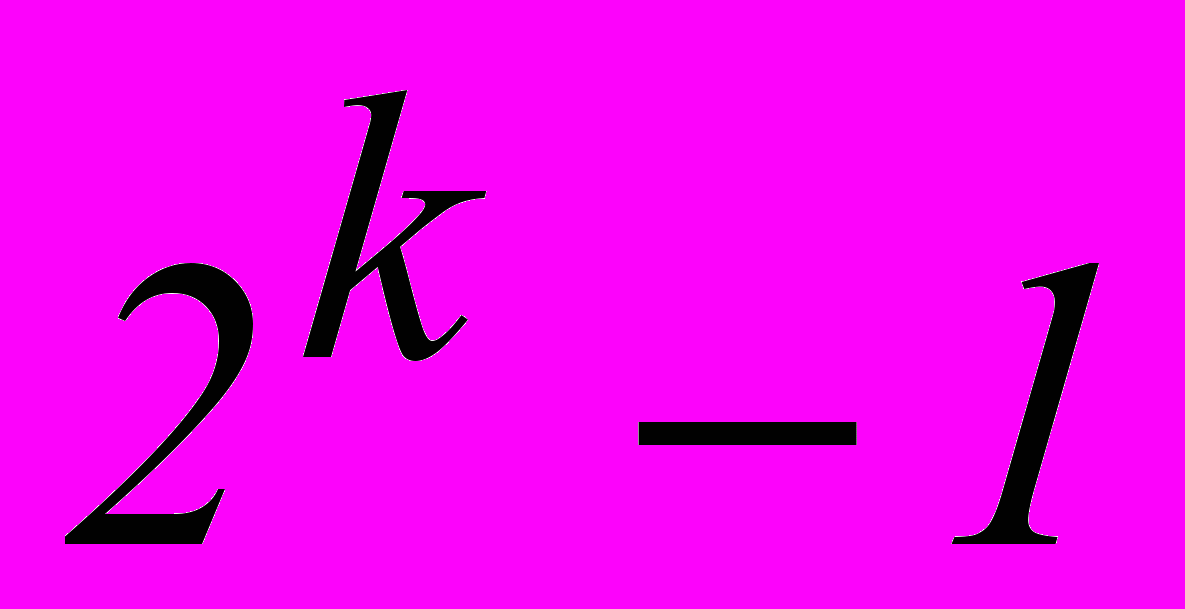ненулевых комбинаций К-разрядного кода нам необходимо поставить в соответствие комбинацию из n разрядов. Значения символов в n–к проверочных разрядах такой комбинации устанавливаются в результате суммирования по модулю два значений символов в определенных информационных разрядах.

Нам надлежит определить число проверочных разрядов, их значение и местоположение в n-разрядной кодовой комбинации.

Из общего числа 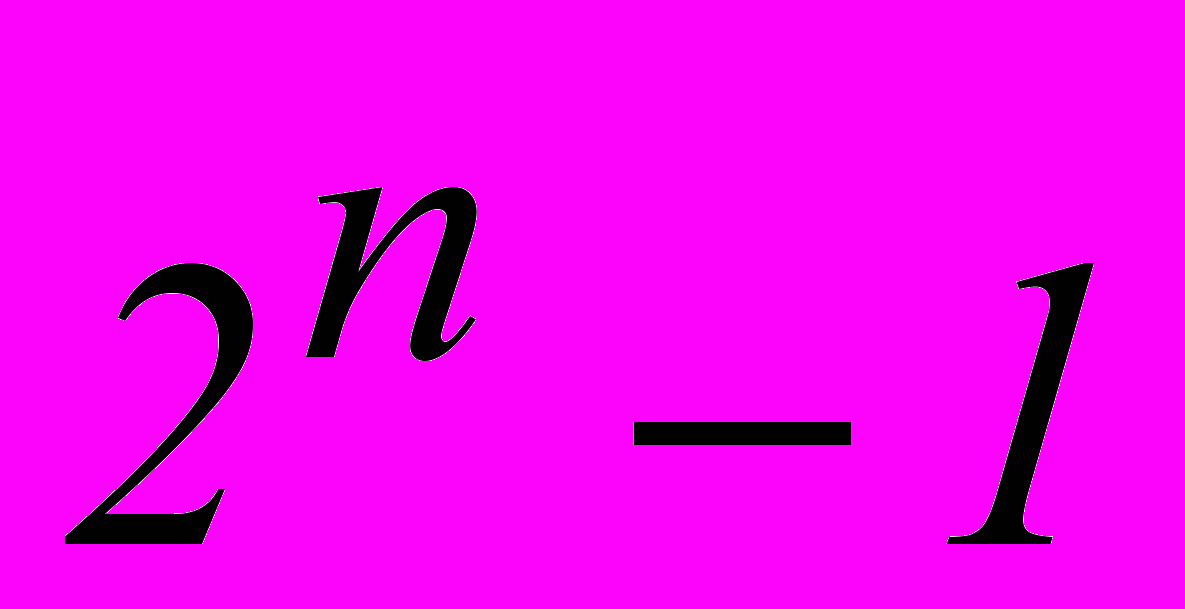возможных ошибок, групповой код может исправить всего 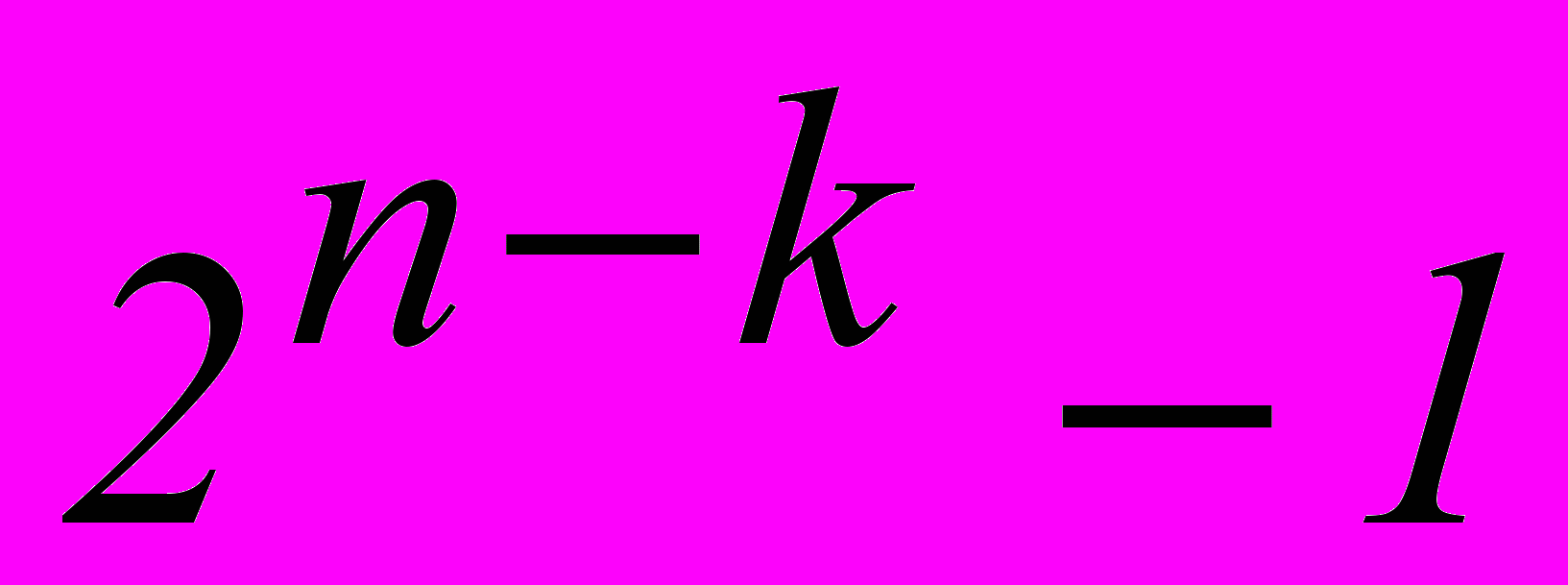разновидностей ошибок [1].

Чтобы иметь возможность получить информацию о векторе ошибки, воздействию которого подверглась полученная кодовая комбинация, каждому вектору ошибки, подлежащей устранению, должна быть сопоставлена некоторая контрольная последовательность символов, называемая опознавателем.

Каждый символ опознавателя будет определяться в результате проверки одного из равенств на приемной стороне. Эти равенства мы составим для определения значений проверочных символов при кодировании на передающей стороне.

В групповом коде значения проверочных символов подбираются так, чтобы сумма по модулю два всех символов (включая проверочный), входящих в каждое из равенств, равнялась нулю. В таком случае число единиц среди этих символов при отсутствии ошибок четное. Поэтому операции определения символов опознавателя называют проверками на четность. При отсутствии ошибок в результате всех проверок на четность образуется опознаватель, состоящий из одних нулей. Если проверочное равенство не удовлетворяется, то в соответствующем разряде опознавателя появляется единица. Исправление ошибок возможно лишь при наличии взаимно однозначного соответствия между множеством опознавателей и множеством подлежащих исправлению разновидностей ошибок.

Таким образом, количество подлежащих исправлению ошибок является определяющим для выбора числа избыточных разрядов n-к. Последних должно быть достаточно для того, чтобы обеспечить необходимое число опознавателей.

Если, например, мы желаем исправлять все одиночные ошибки, то исправлению подлежит n ошибок. Вектора ошибок имеют в этом случае следующий вид :

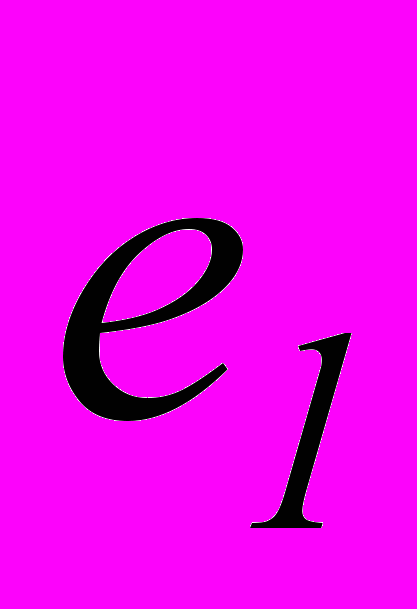=(000...01)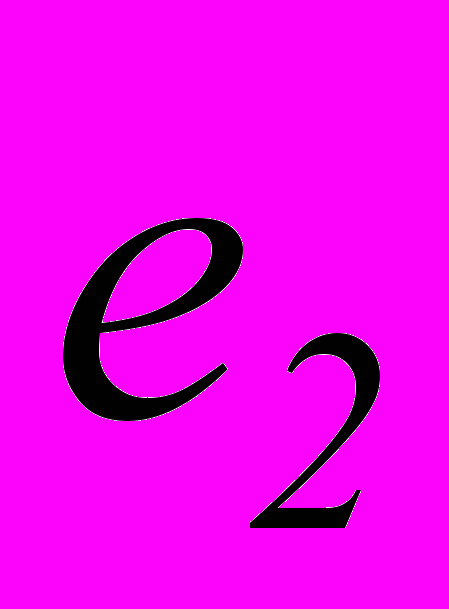=(000...10) ........ 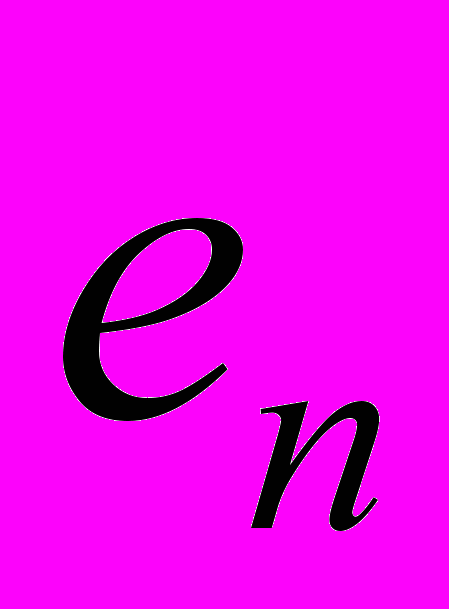=(100...00)

Различных ненулевых опознавателей должно быть не менее n.

Необходимое число проверочных разрядов, следовательно, должно определяться из соотношения :

.

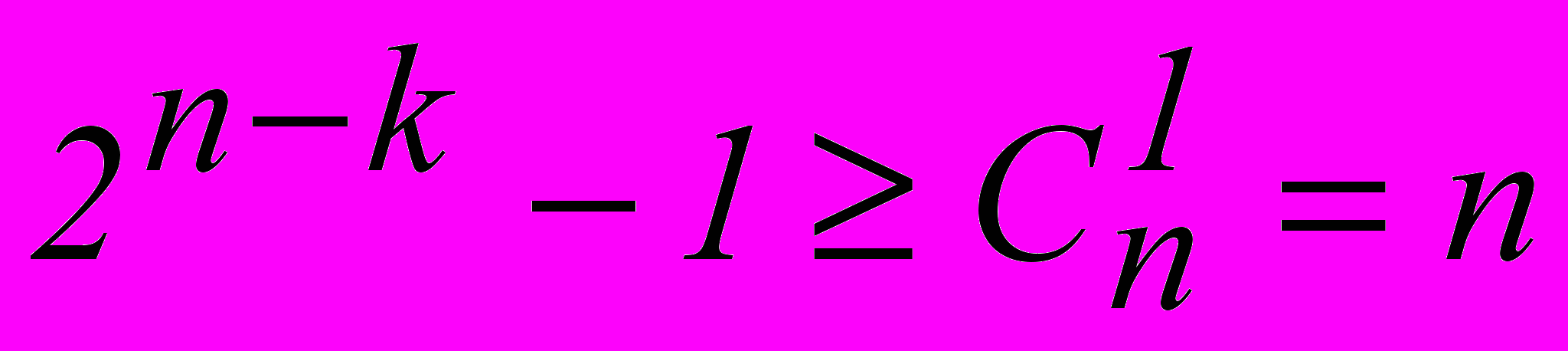В общем случае для исправления всех независимых ошибок кратности до t включительно получаем :

.

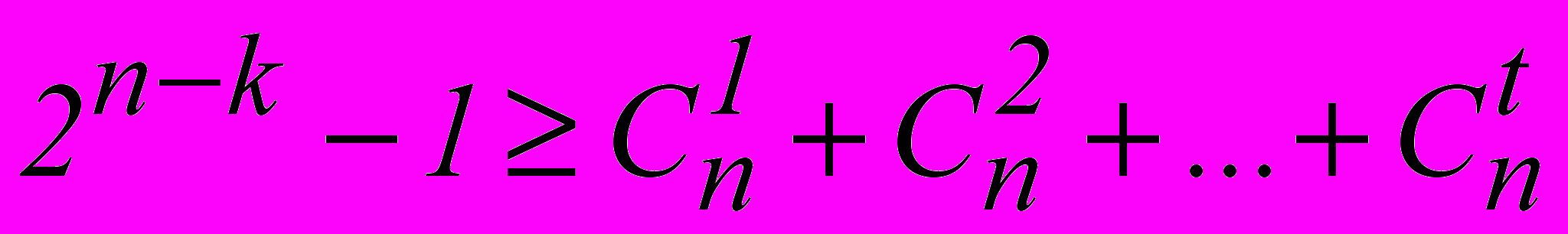В общем случае это неравенство записывается следующим образом: 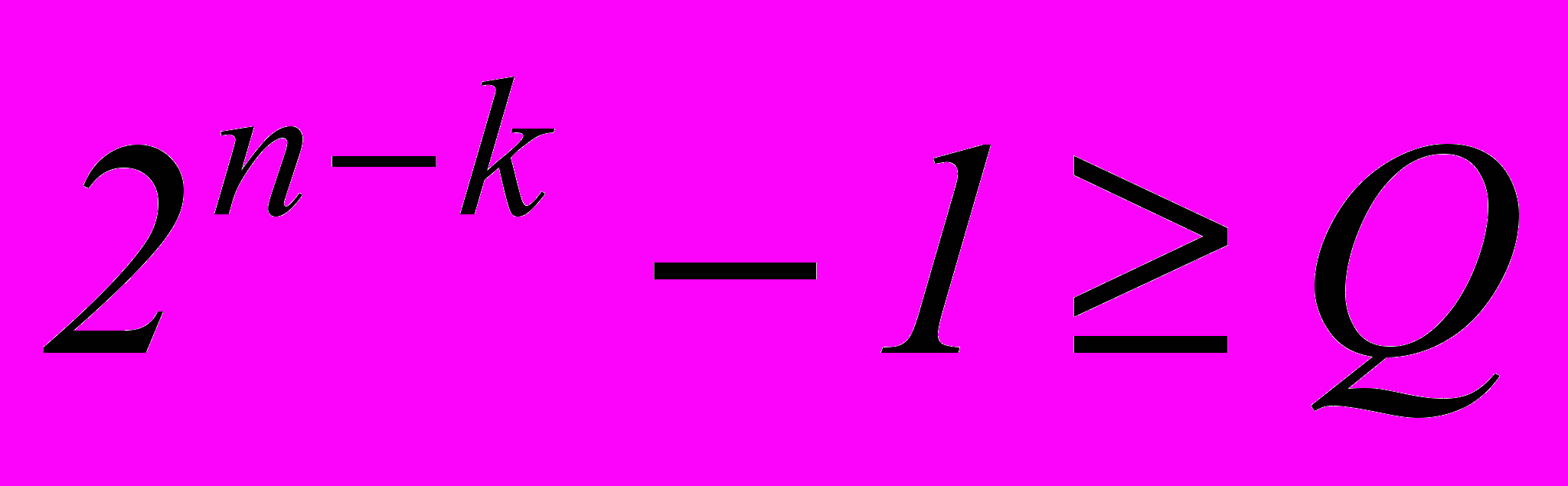, где Q число ошибок, кеоторые необходимо исправить. Например, для исправления пачек в 3 и менее символов

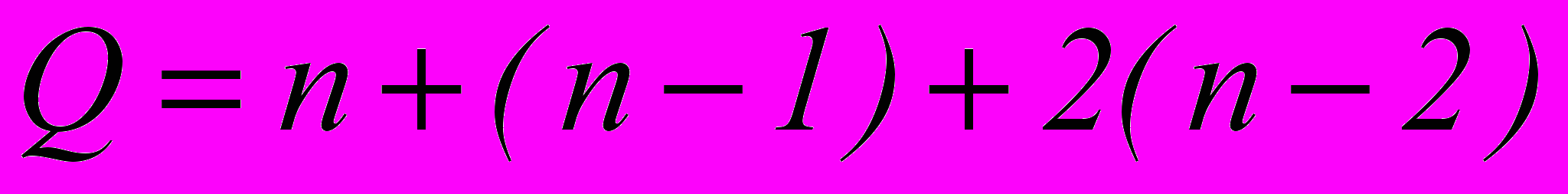, где

n – одиночные ошибки,

(n-1) – пачки в 2 соседних символа (… 0110…)

2(n-2) – пачки в 3 соседних символа (…01110…) и в два символа через один (…01010…).

Стоит подчеркнуть, что в приведенных соотношениях указывается теоретический предел минимально возможного числа проверочных разрядов, который далеко не во всех случаях можно реализовать практически.


2.2. Составление таблицы опознавателей


Начнем для простоты с установления опознавателей для случая исправления одиночных ошибок. Допустим, необходимо закодировать 15 команд (букв).


Таблица 2.1

N разряда	Вектор ошибки	Опознаватель
1 2 3 4 5 6 7	0000001 0000010 0000100 0001000 0010000 0100000 1000000	001 010 011 100 101 110 111

Тогда к=4, n=7. Три избыточных разряда позволяют использовать в качестве опознавателей трехразрядные двоичные последовательности. В принципе они могут быть сопоставлены подлежащим исправлению ошибкам в любом порядке. Однако, более целесообразно опознаватели сопоставлять с номерами разрядов, в которых произошли ошибки (табл. 2.1).

Коды, в которых опознаватели устанавливаются по указанному принципу, известны как коды Хэмминга.

Возьмем теперь более сложный случай исправления всех одиночных и двойных независимых ошибок, то есть две ошибки в любых разрядах. В качестве опознавателей одиночных ошибок в первом и втором разрядах можно принять, как и ранее две комбинации 0...001 и 0...010 (табл. 2.2).

Подлежащий исправлению вектор ошибки 0...011 может рассматриваться как результат суммарного воздействия двух векторов ошибок 0...010 и 0...001 и, следовательно, ему должен быть сопоставлен опознаватель, представляющий собой сумму по модулю два опознавателей этих ошибок, т.е. 0...011.

Вектору ошибки 0...0100 сопоставляем опознаватель 0...0100 и т.д. Выбирая в качестве опознавателя единичной ошибки в i-м разряде комбинацию с числом разрядов меньшим i, необходимо убедиться в том, что для всех остальных подлежащих исправлению векторов ошибок, имеющих единицы в i-м и более младших разрядах, получаются опознаватели, отличные от уже использованных. В результате имеем:


Таблица 2.2

Вектор ошибки	Опознаватель	Вектор ошибки	Опознаватель
00000001 00000010 00000011 00000100 00000101 00000110 00001000 00001001	000001 000010 000011 000100 000101 000110 001000 001001	00001010 00001100 00010000 00010001 00010010 00010100 00011000 00100000	001010 001100 001111 001110 001101 001011 000111 010000

Таким путем можно получить таблицу опознавателей для векторов ошибок в любом числе разрядов.

Если опознаватели векторов ошибок с единицами в нескольких разрядах устанавливаются как суммы по модулю два опознавателей одиночных ошибок в этих разрядах, то для определения проверочных равенств достаточно знать только опознаватели одиночных ошибок в каждом из разрядов.

Для построения кодов, исправляющих двойные независимые ошибки, пачки ошибок в двух и трех разрядах опознаватели одиночных ошибок в каждом из разрядов сведены в табл. 2.3, 2.4, 2.5, которые составлены с помощью ЭВМ.

Таблица 2.3 Опознаватели одиночных ошибок для кода, исправляющий двойные независимые ошибки

Таблица 2.4 Опознаватели одиночных ошибок для кода, исправляющего пачки ошибок в двух и менее разрядов

N разряда	Опознаватель		N разряда	Опознаватель
1 2 3 4 5 6 7 8 9	0000001 0000010 0000100 0001000 0001111 0010000 0100000 0110011 1000000		1 2 3 4 5 6 7 8	00001 00010 00100 01000 01101 00111 01110 10000

Таблица 2.5 Опознаватели одиночных ошибок для кода, исправляющего пачки ошибок в трех и менее разрядах

N разряда	Опознаватель
1 2 3 4 5 6 7 8 9 10	0000001 0000010 0000100 0001000 0010000 0100000 0001001 0010010 0100100 1000000

2.3. Определение проверочных равенств


Пользуясь таблицей опознавателей одиночных ошибок в каждом из разрядов, нетрудно определить, символы каких разрядов должны входить в каждую из проверок на четность.

Возьмем в качестве примера табл. 2.1 опознавателей для кодов, предназначенных исправлять одиночные ошибки. В принципе можно построить код, усекая эту таблицу на любом уровне. Однако оптимальными будут коды, которые среди кодов, имеющих одно и то же число проверочных символов, допускают наибольшее число информационных символов, например код (7,4) n=7, к=4.

То есть при трех проверочных разрядах опознавателя мы можем передавать четыре информационных символ. Найдем места и значения проверочных разрядов.

Предположим, что в результате первой проверки на четность для младшего разряда опознавателя будет получена единица. Очевидно, это может быть следствием ошибки в одном из разрядов, опознаватели которых в младшем разряде имеют единицу. Следовательно, первое проверочное равенство должно включать символы 1-го, 3-го, 5-го и 7-го разрядов :

.

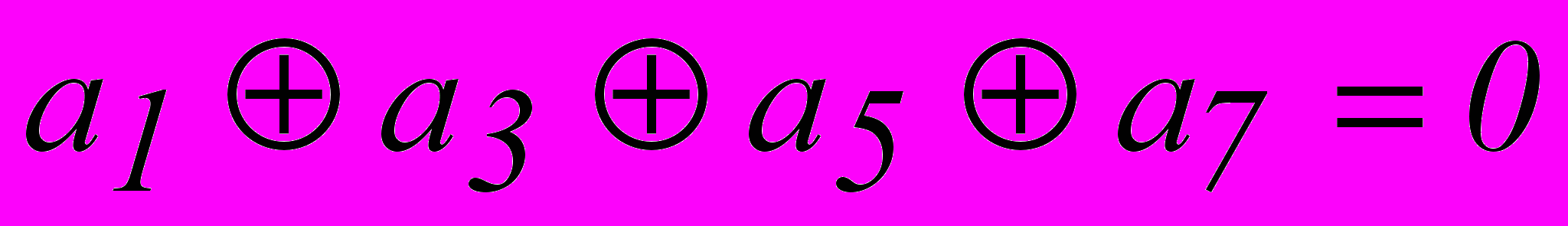Единица во втором разряде опознавателя может быть следствием ошибки в разрядах, опознаватели которых имеют единицу во втором разряде. Отсюда, второе проверочное равенство должно иметь вид :

.

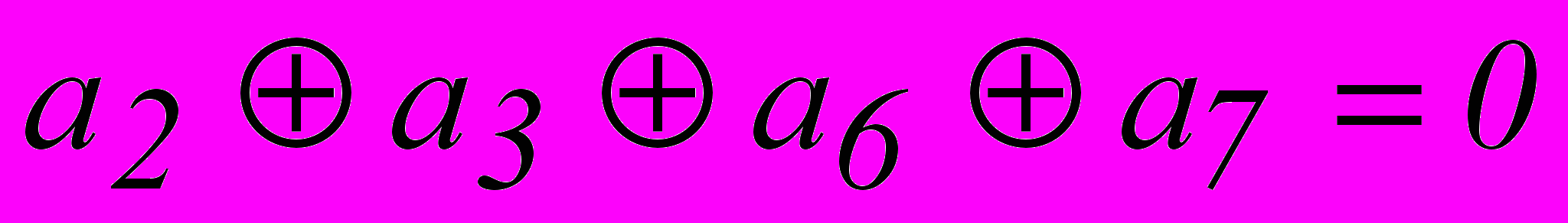Аналогично находим и третье равенство :

.

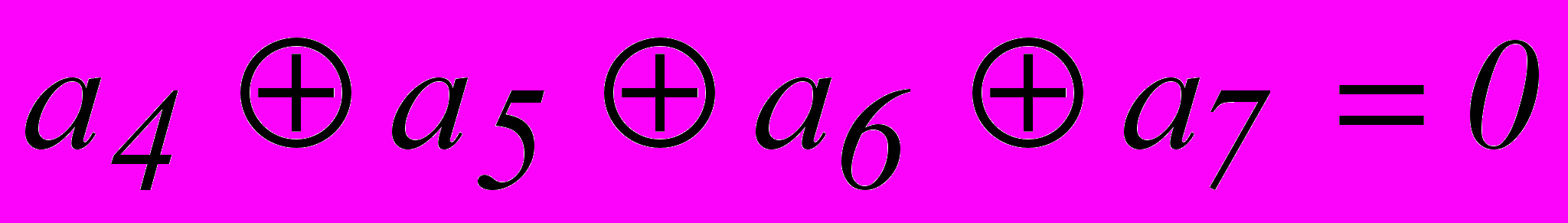Чтобы эти равенства при отсутствии ошибок удовлетворялись при любых значениях информационных символов в кодовой комбинации, в нашем распоряжении имеется три проверочных разряда. Мы должны так выбрать номера этих разрядов, чтобы каждый из них входил только в одно из равенств. Это обеспечит однозначное определение значений символов в проверочных разрядах при кодировании. Указанному условию удовлетворяют разряды, по одному разу входящие в полученные уравнения. В нашем случае это будут первый, второй и четвертый разряды.

Таким образом, для кода (7,4), исправляющего одиночные ошибки, искомые правила построения кода, т.е. соотношения, реализуемые в процессе кодирования, принимают вид :







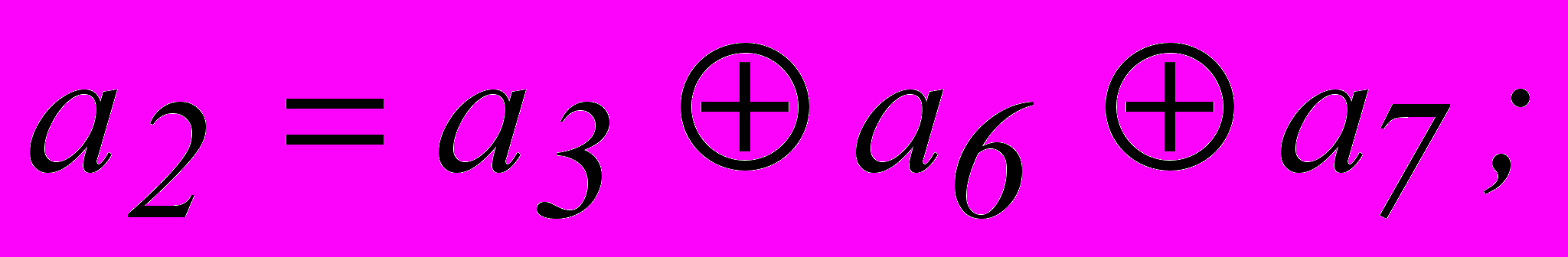
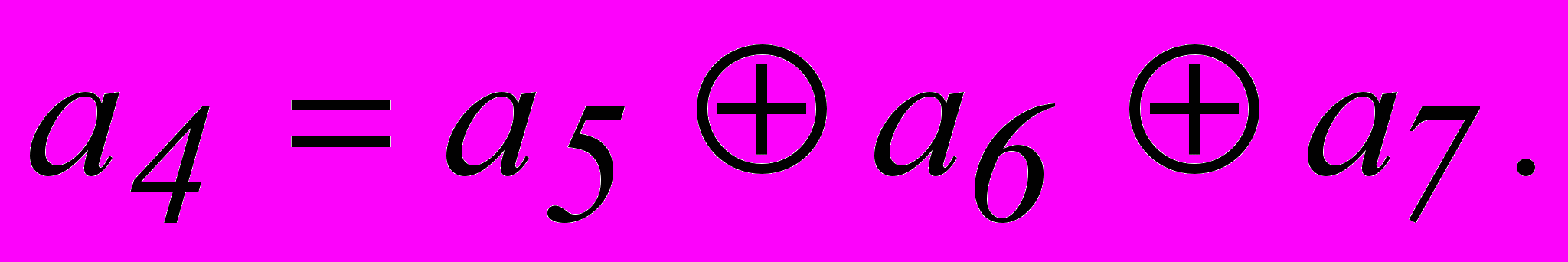
Введение проверочного разряда, обеспечивающего четность числа единиц во всей кодовой комбинации, 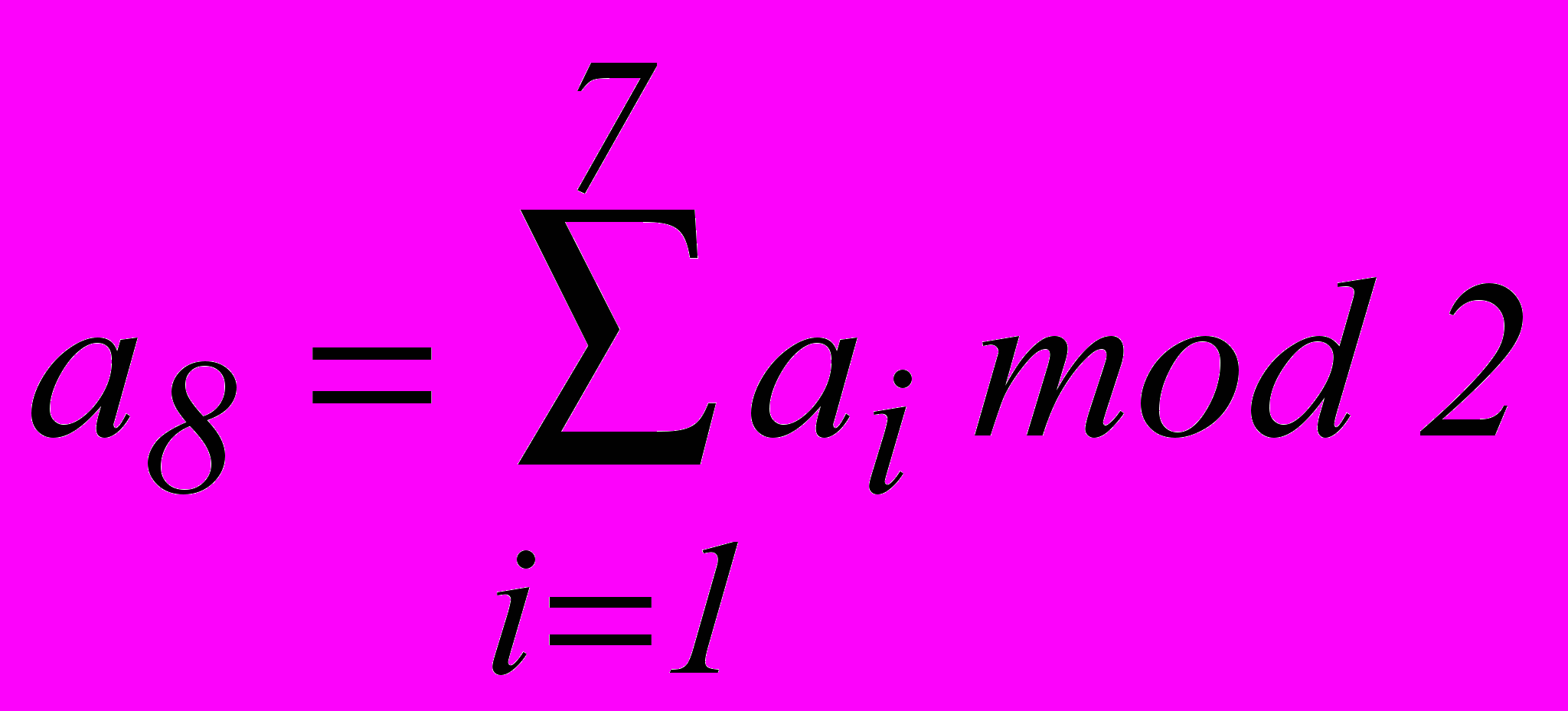позволяет построить код (8,4), способный одновременно исправлять одиночные ошибки и обнаруживать двойные.

Используя таблицу опознавателей (табл.2.3) и рассуждая аналогичным образом, можно составить проверочные равенства для любого кода, исправляющего одиночные и двойные независимые ошибки. Например, для кода (8,2). Минимальное число разрядов в кодовой комбинации должно быть менее 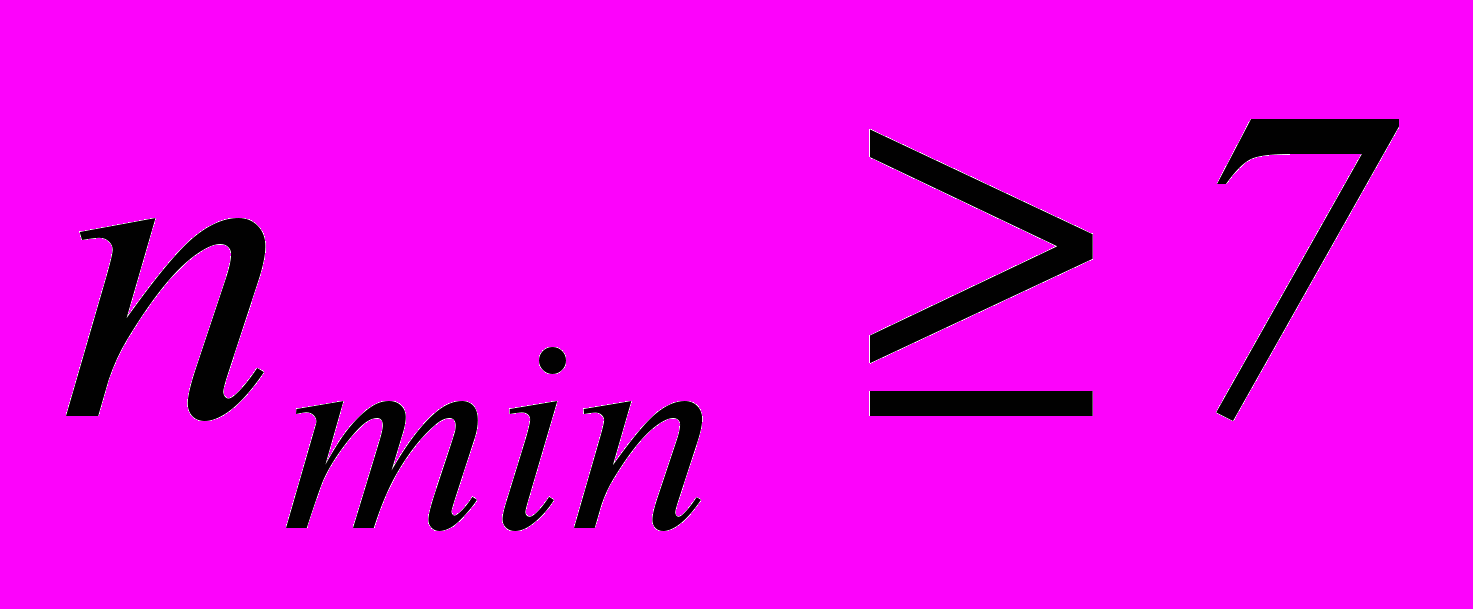. Находятся из уравнения 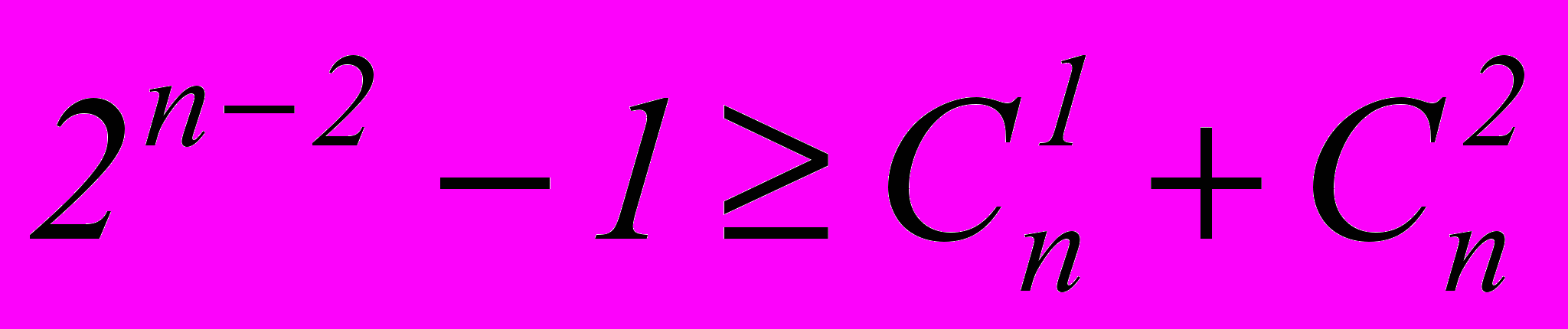. При n = 7 имеем 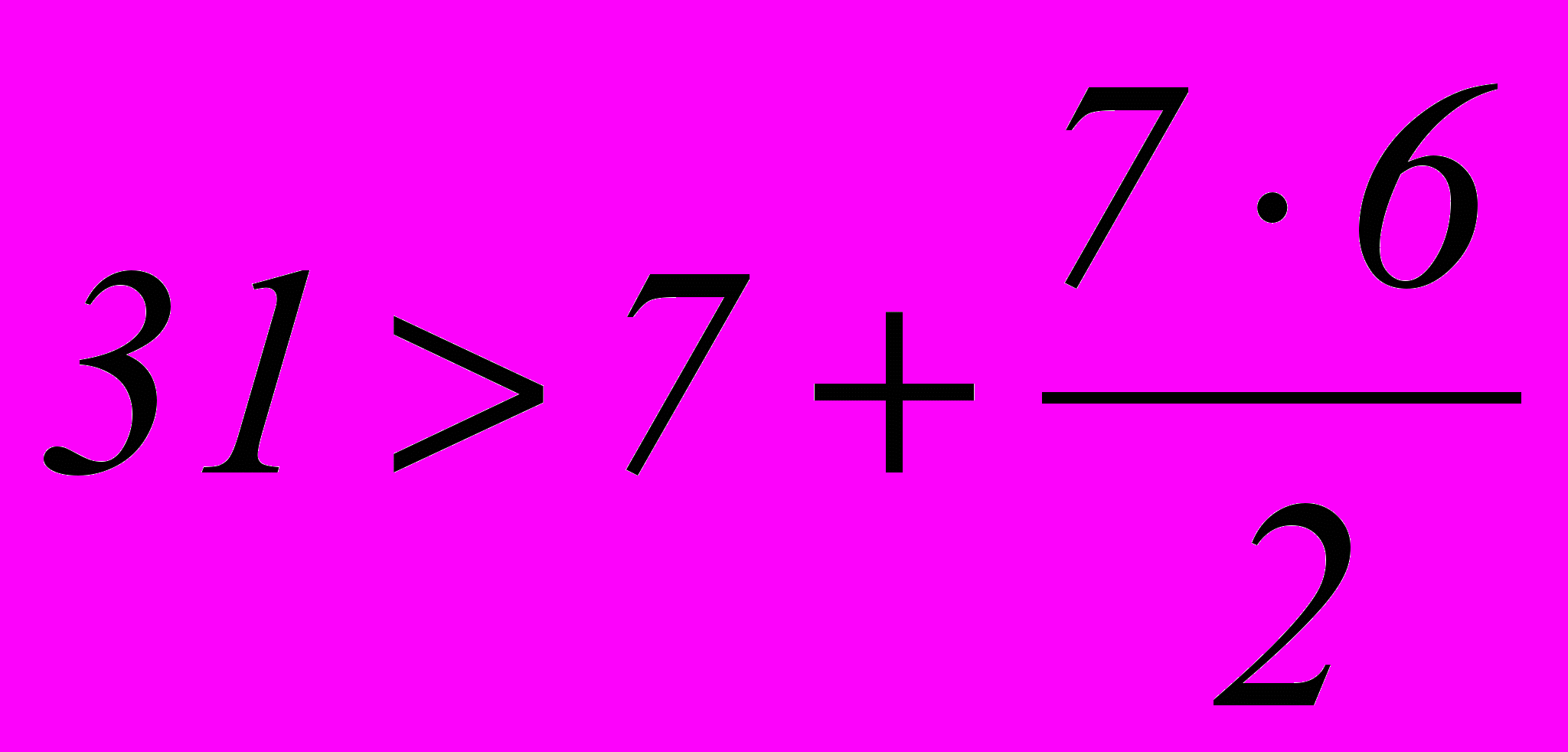. Однако, из табл. 2.3 для опознавателя кодовой комбинации из 7 разрядов требуется 6 разрядов. Поэтому приходится применить код (8,2). Соотношения, которые необходимо реализовать в процессе кодирования и декодирования этого кода:

1.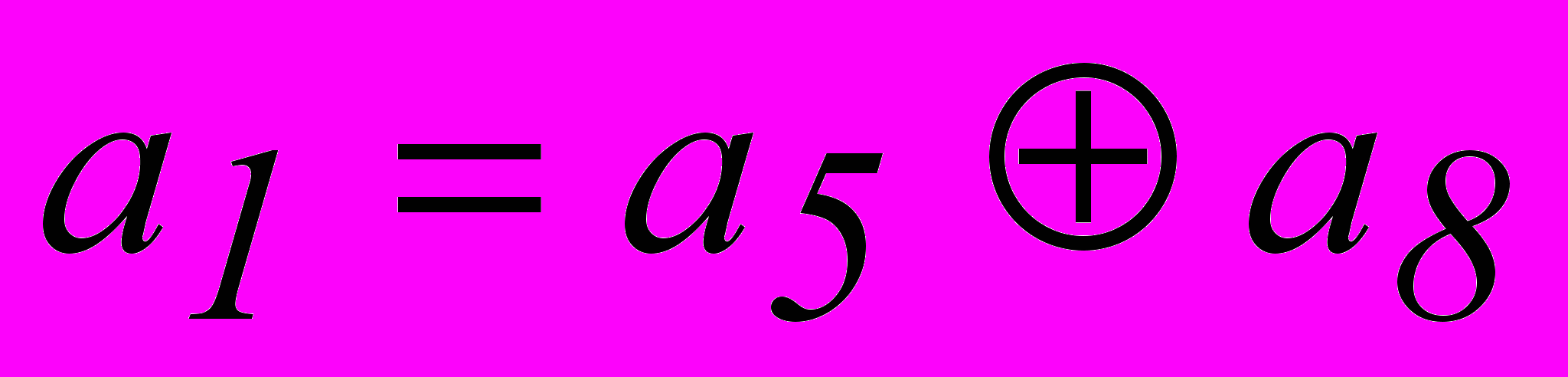
2.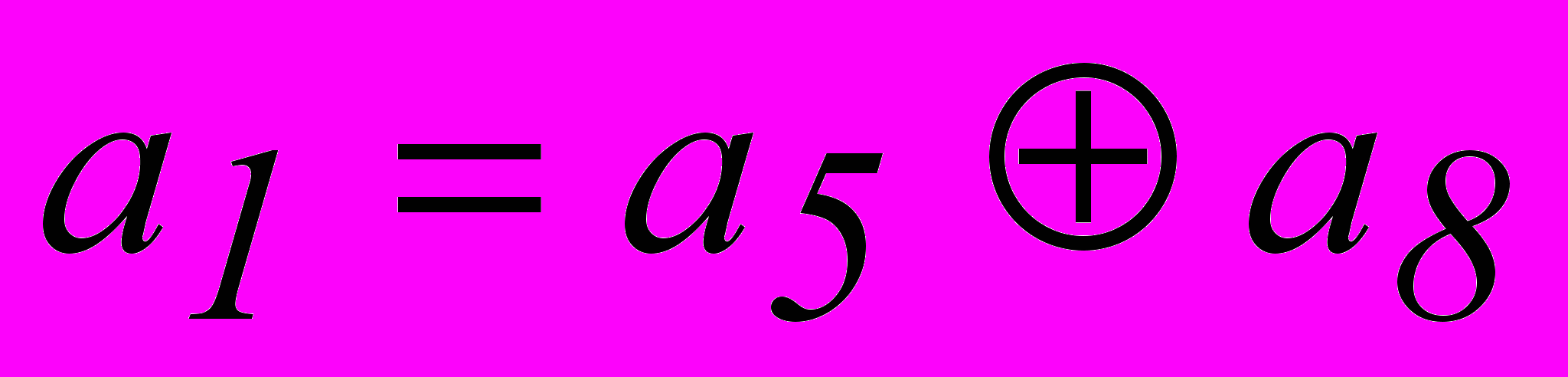
3.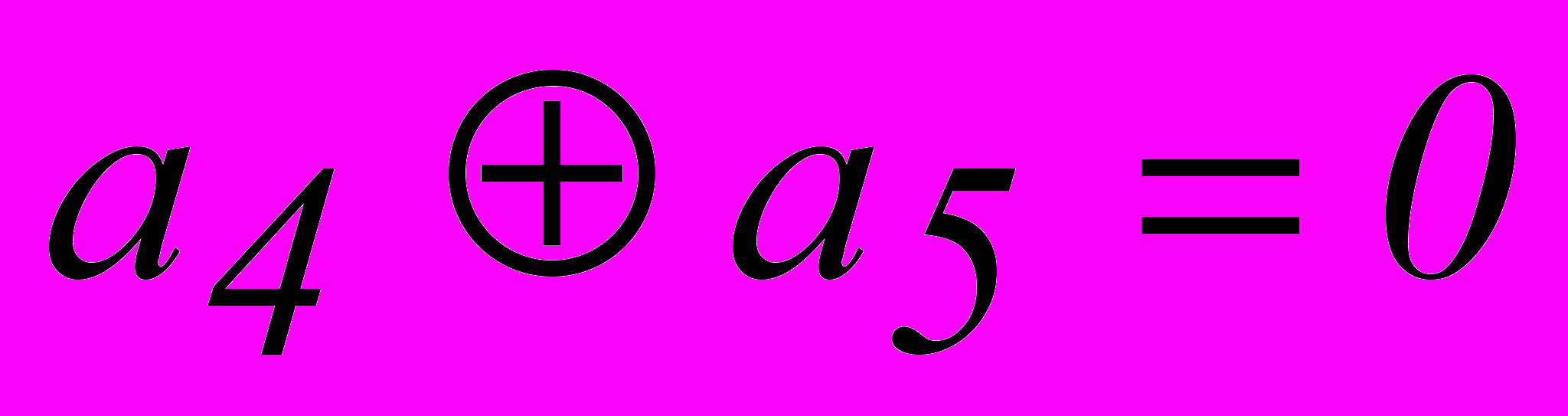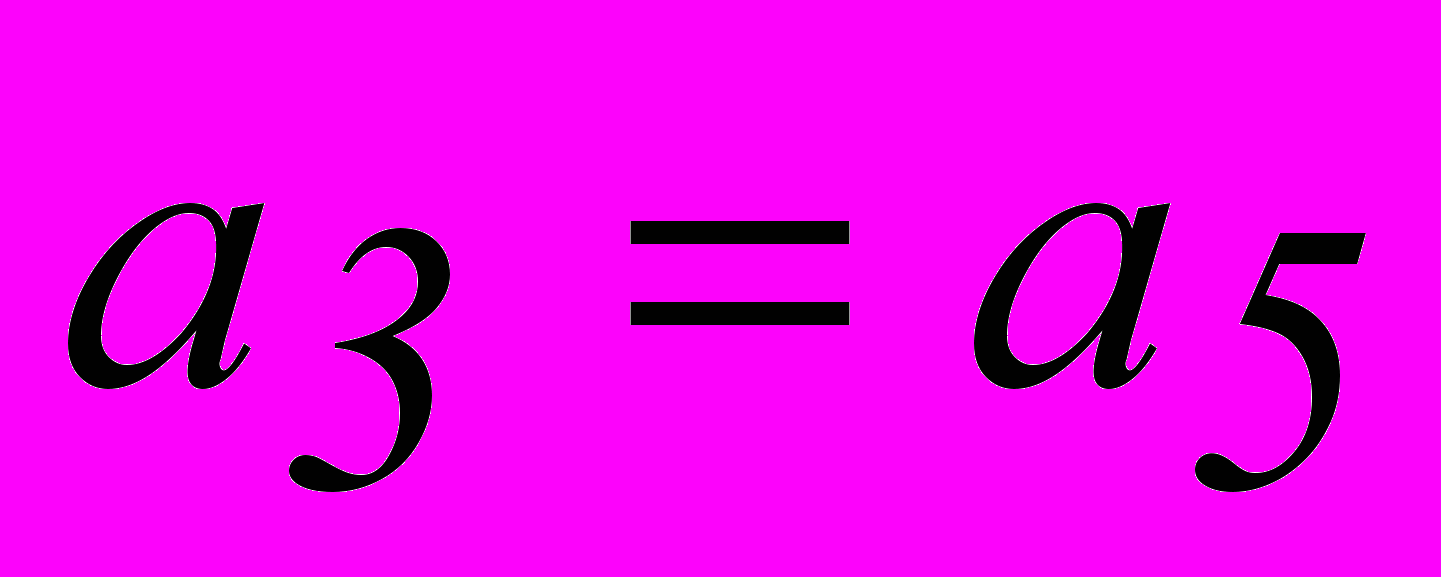
4.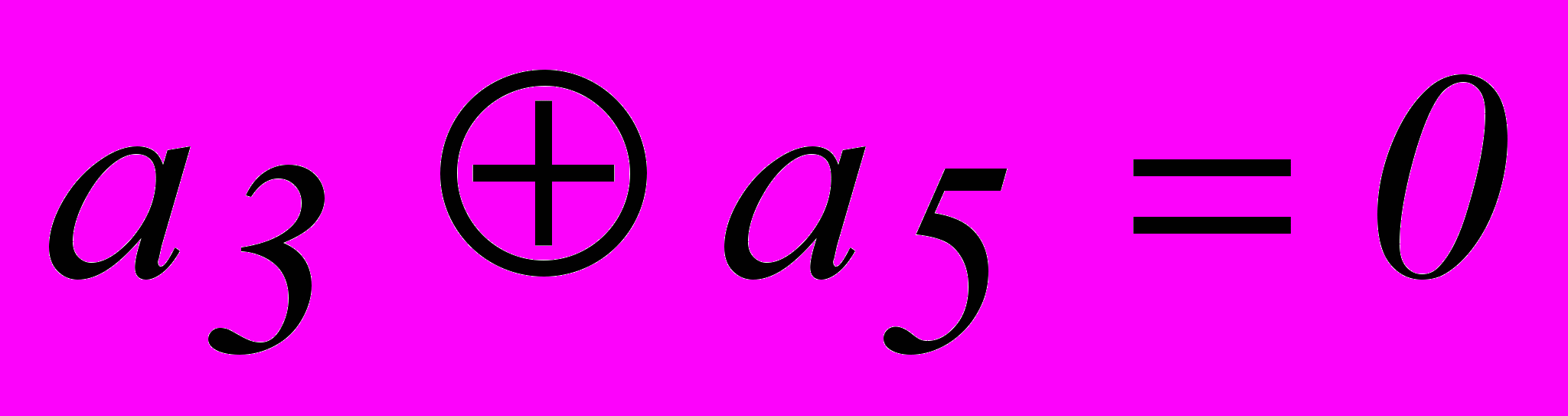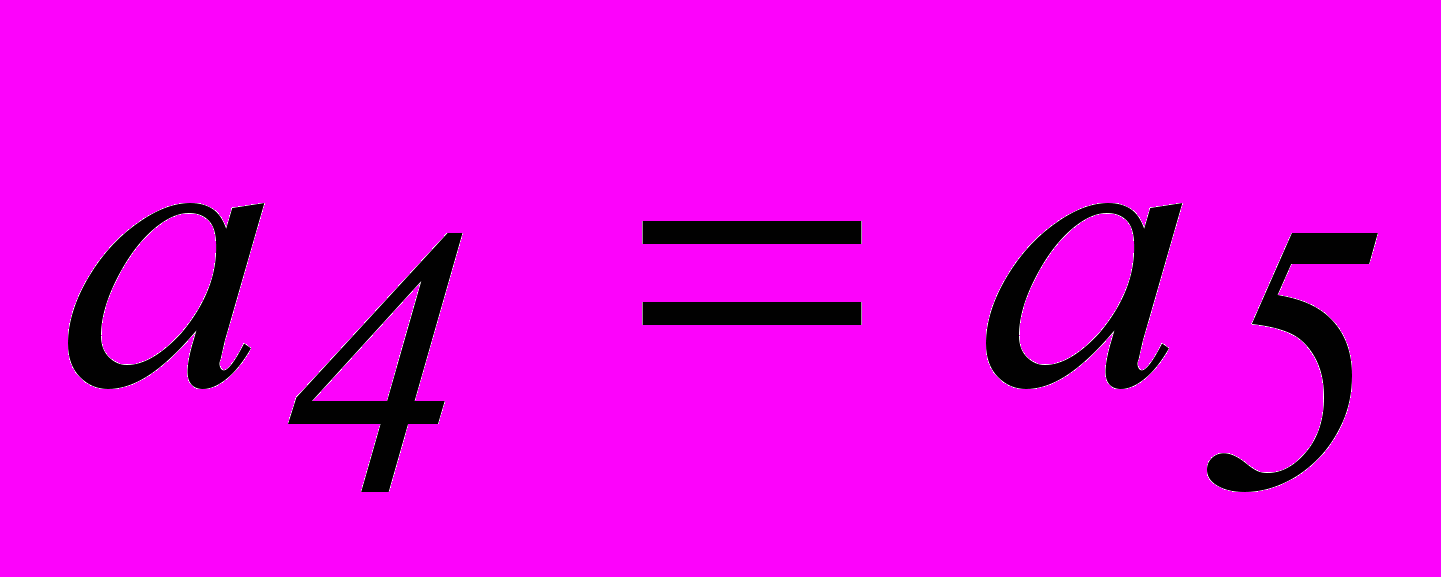
5.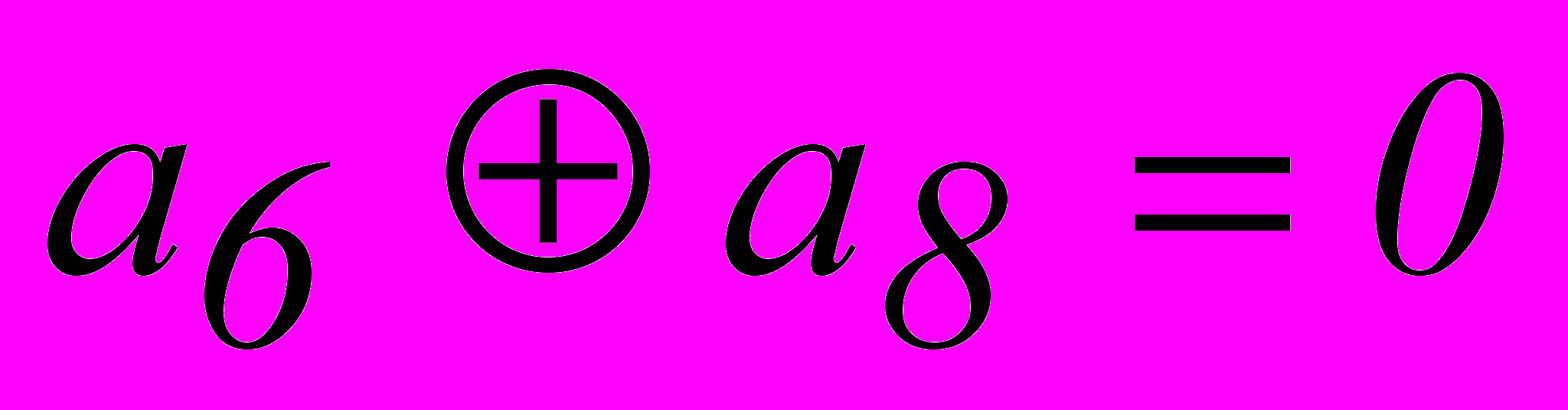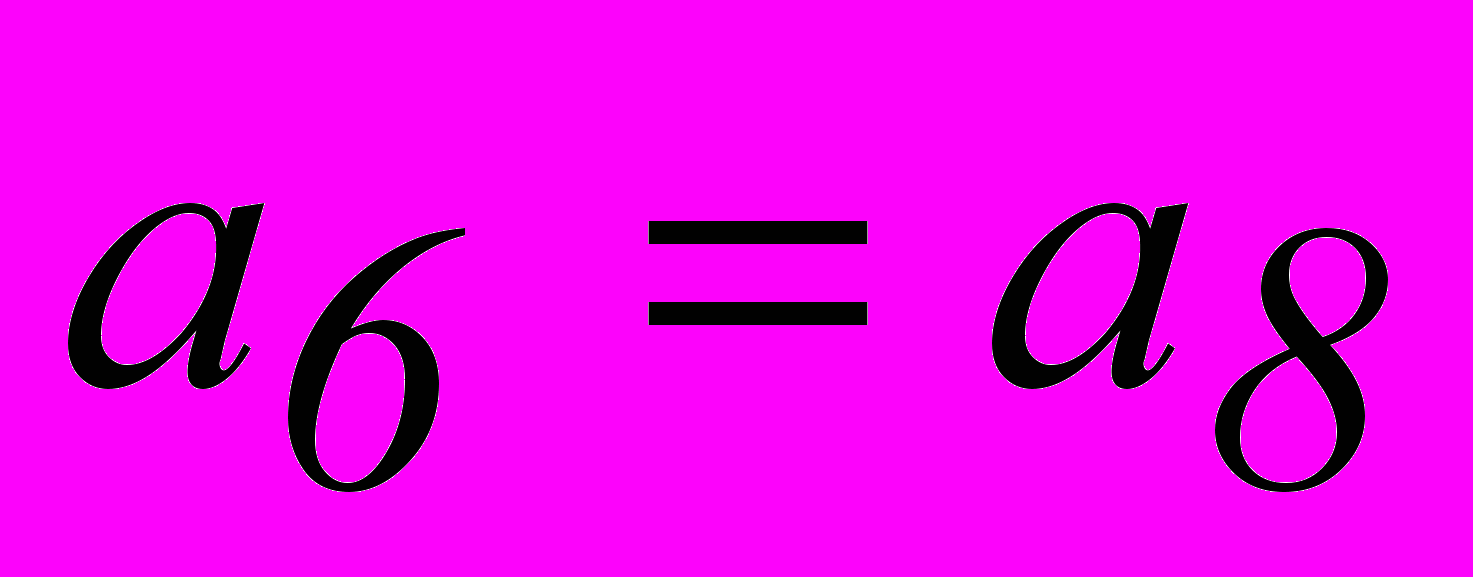
6.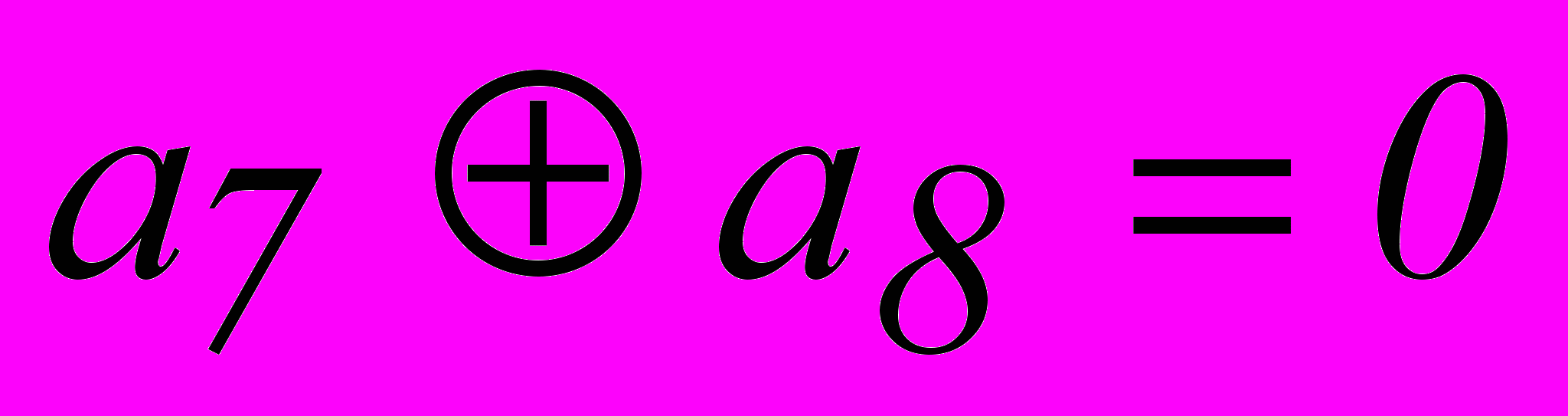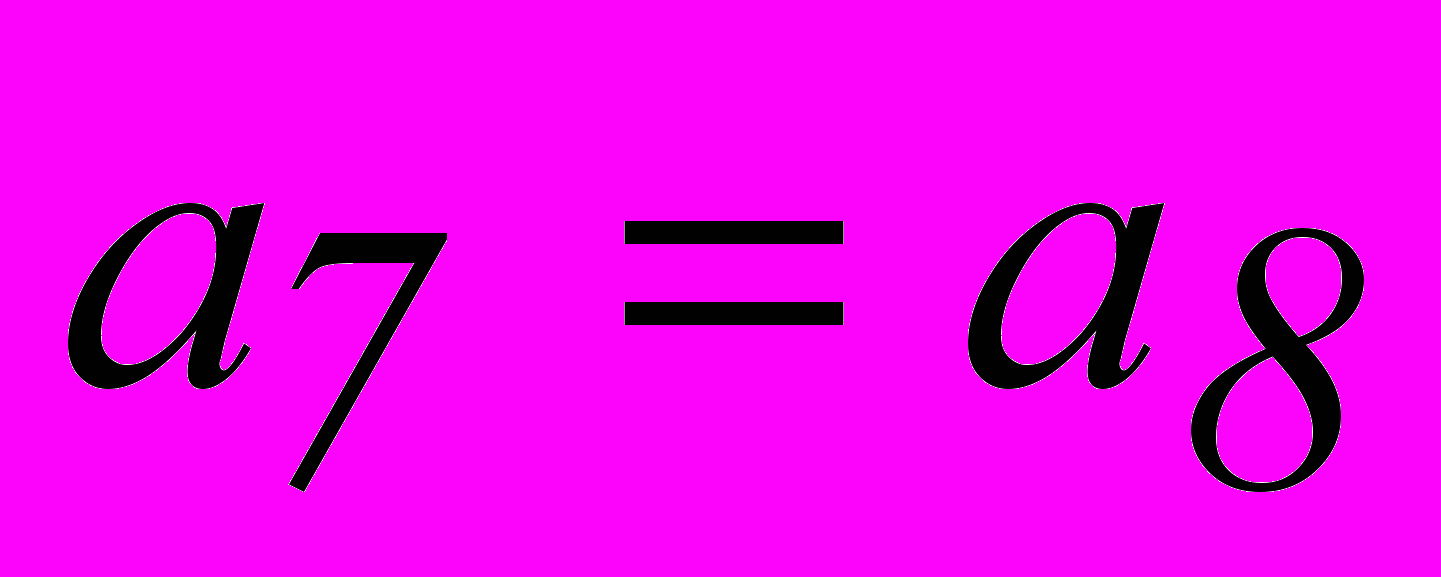

Эти уравнения, как и уравнение для кода (7,4), получаются из вертикальных столбцов опознавателей.


2.4. Мажоритарное декодирование групповых кодов


Мажоритарное декодирование базируется на системе проверочных равенств. Система последовательно должна быть разрешена относительно каждой из независимых переменных, причем в силу избыточности это можно сделать не единственным способом.

Любой символ выражается d различными независимыми способами через комбинации других символов. При этом может использоваться тривиальная проверка 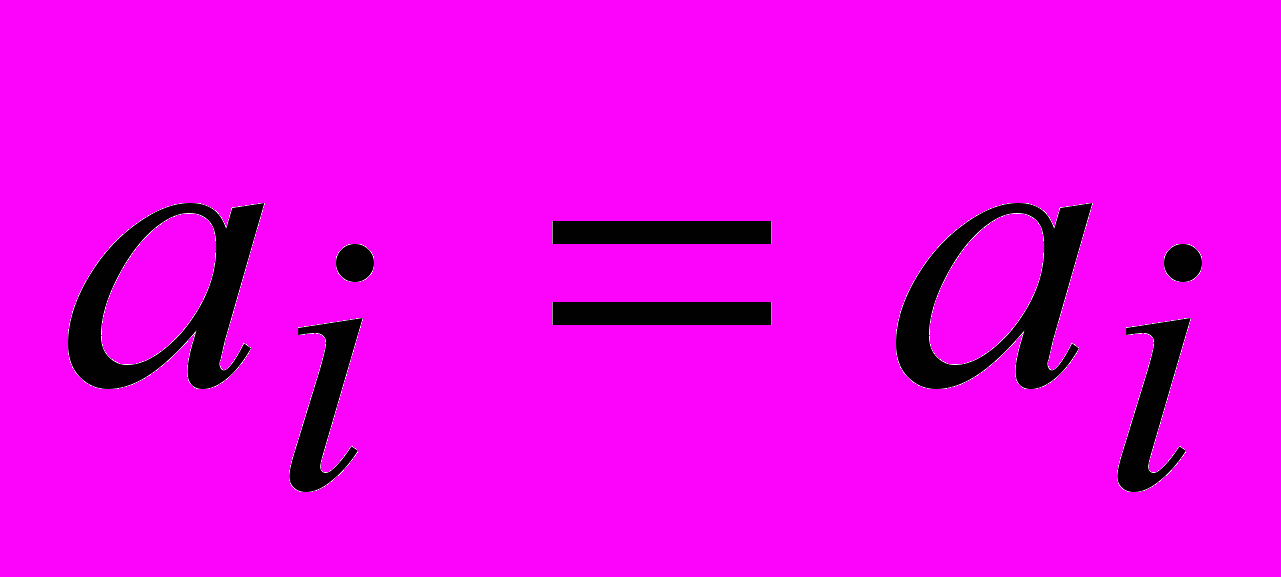. Результаты вычислений подаются на соответствующий этому символу мажоритарный элемент.

Последний представляет собой схему, имеющую d входов и один выход, на котором появляется единица, когда возбуждается больше половины его входов, и ноль когда число нолей на входах меньше половины. Если ошибки отсутствуют, то проверочные равенства не нарушаются и на выходе мажоритарного элемента получаем истинное значение символа. Если число проверок 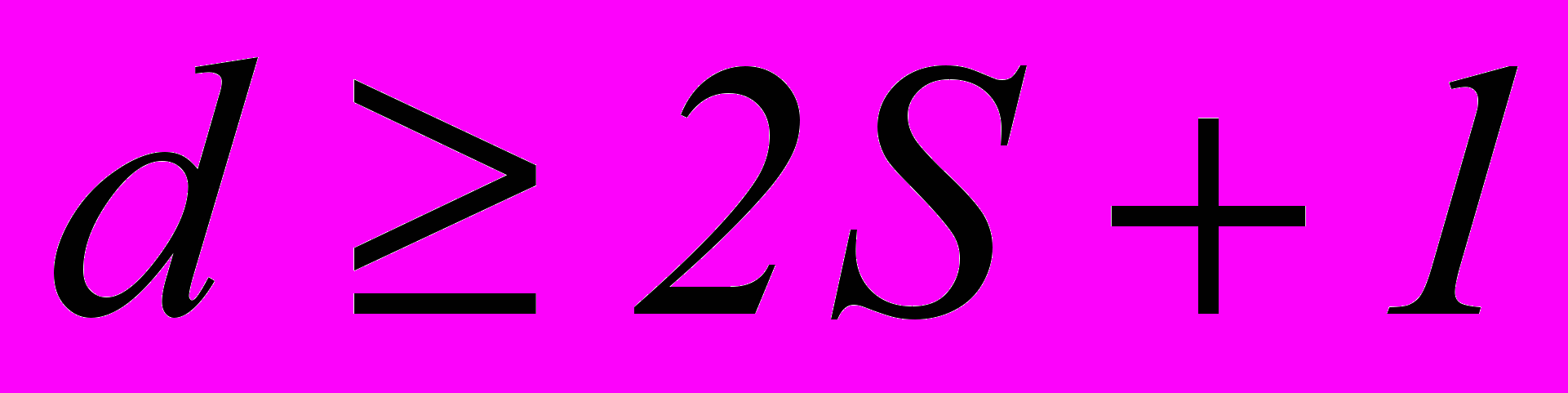, то появление ошибки кратности S и менее не приводит к нарушению более S проверок. Чтобы указанное условие выполнялось, любой (не проверяемый) символ должен входить не более, чем в одно проверочное равенство. В этом случае мы имеем дело с системой разделенных проверок.

Построим системы разделенных проверок для декодирования информационных символов рассмотренного ранее группового кода (8,2). Поскольку код рассчитан на исправление любых двойных ошибок, число проверочных равенств для определения каждого символа должно быть не менее 5. Подставив в равенства 1 и 2 значения , полученные из равенств 5 и 6, и записав их относительно , совместно с равенствами 3 и 4 и тривиальным равенством 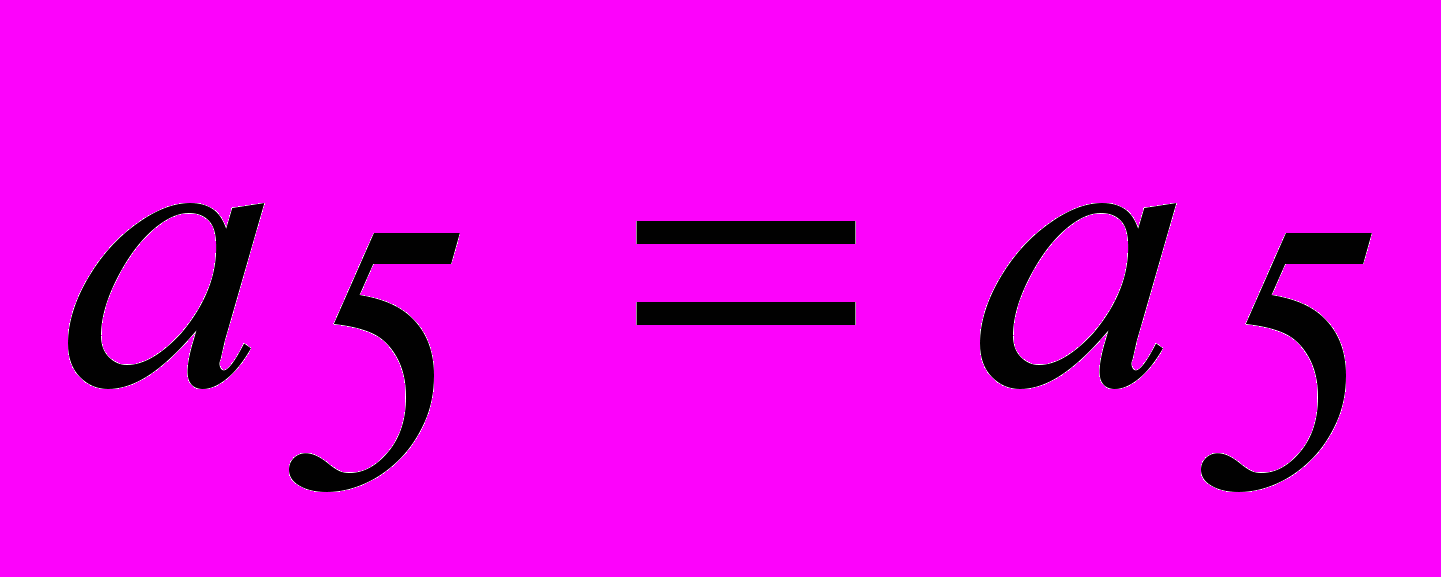получим систему разделенных проверок для символа . Аналогично получаем систему разделенных проверок и для символа .













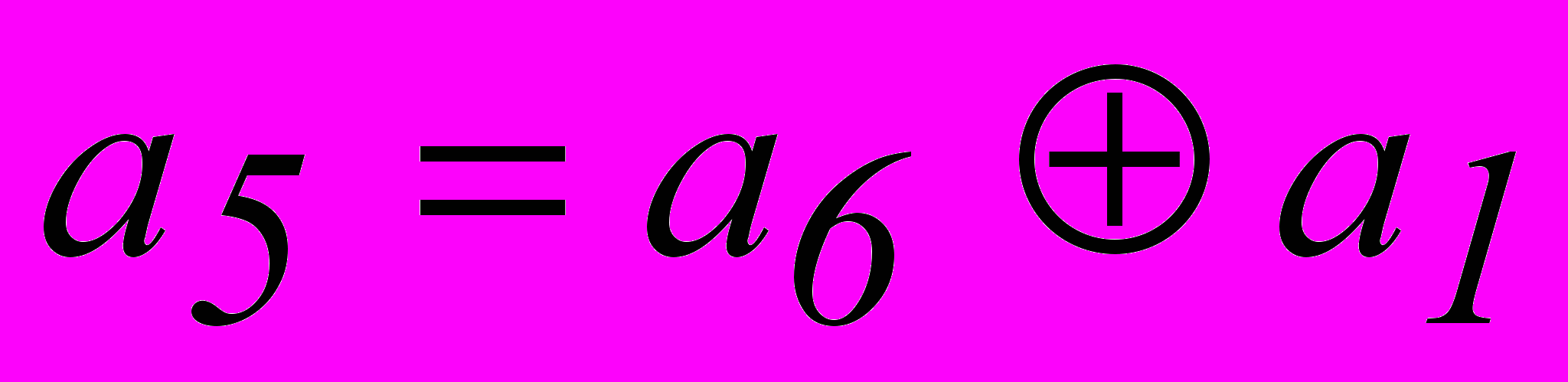
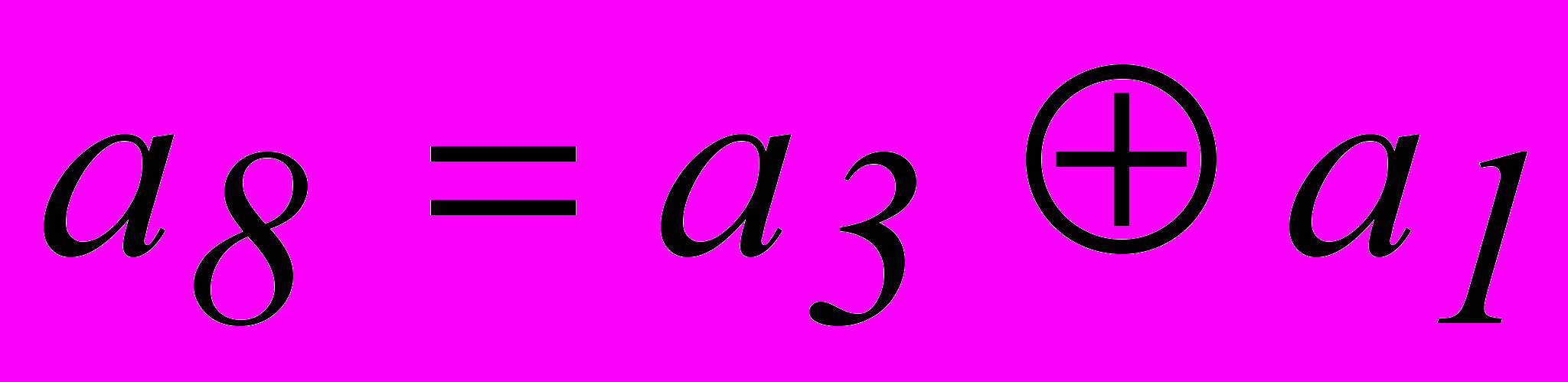
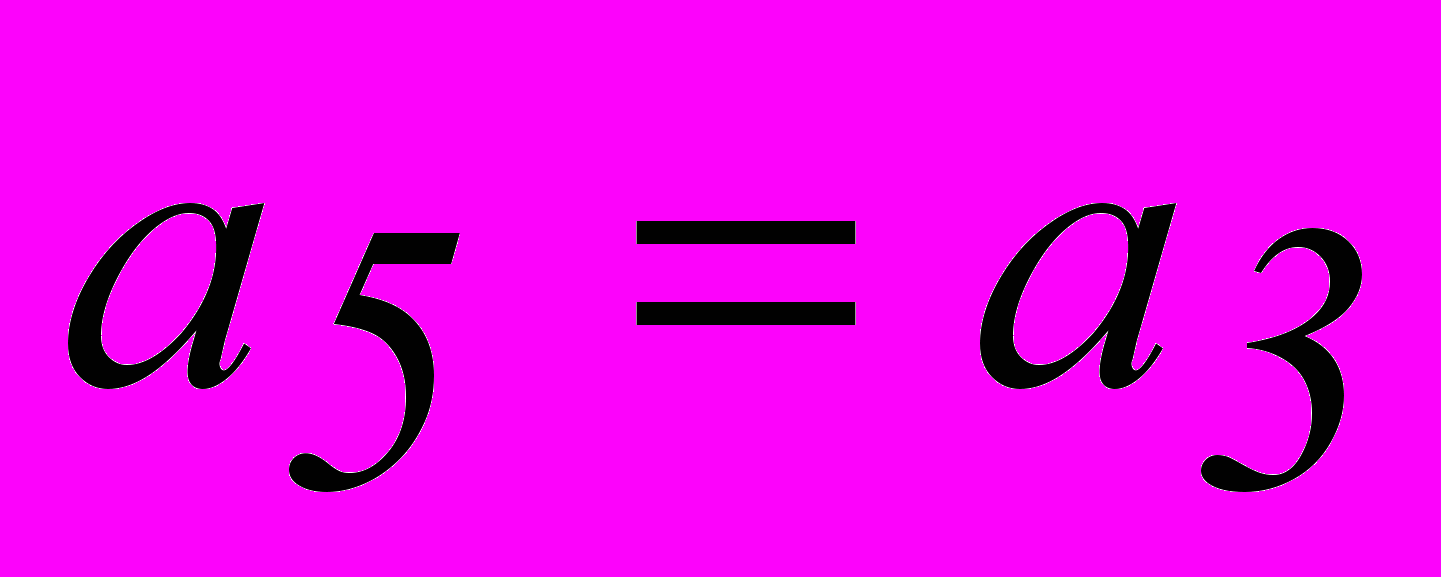
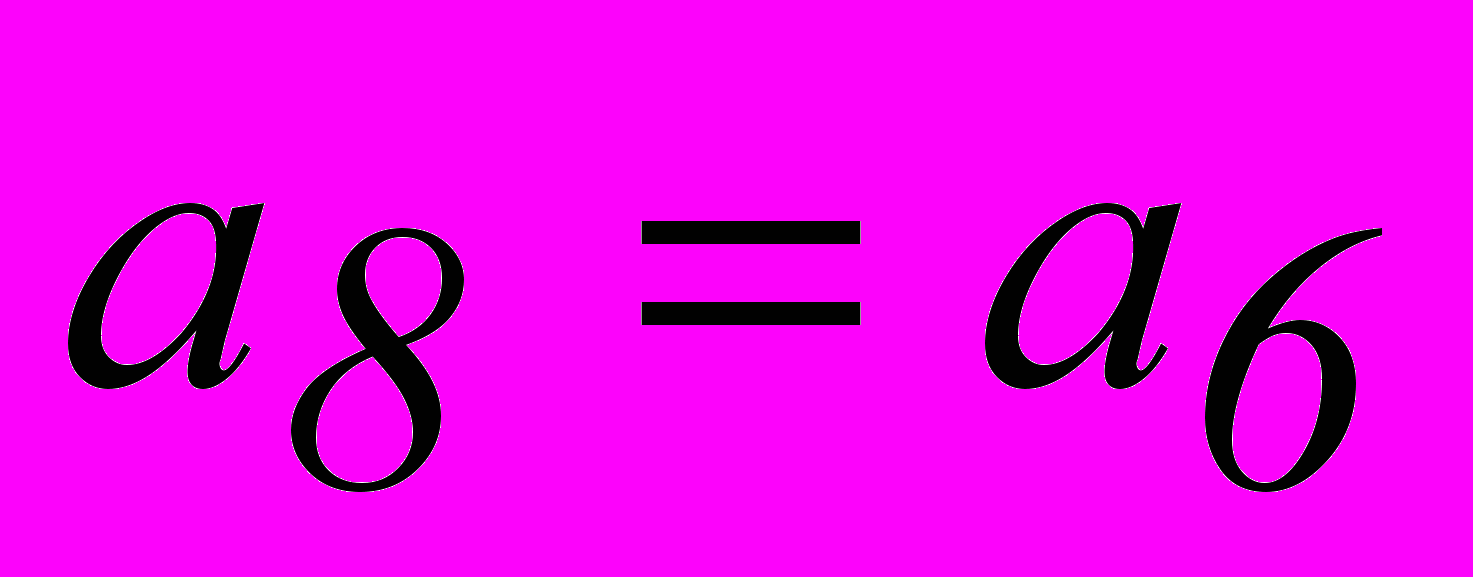
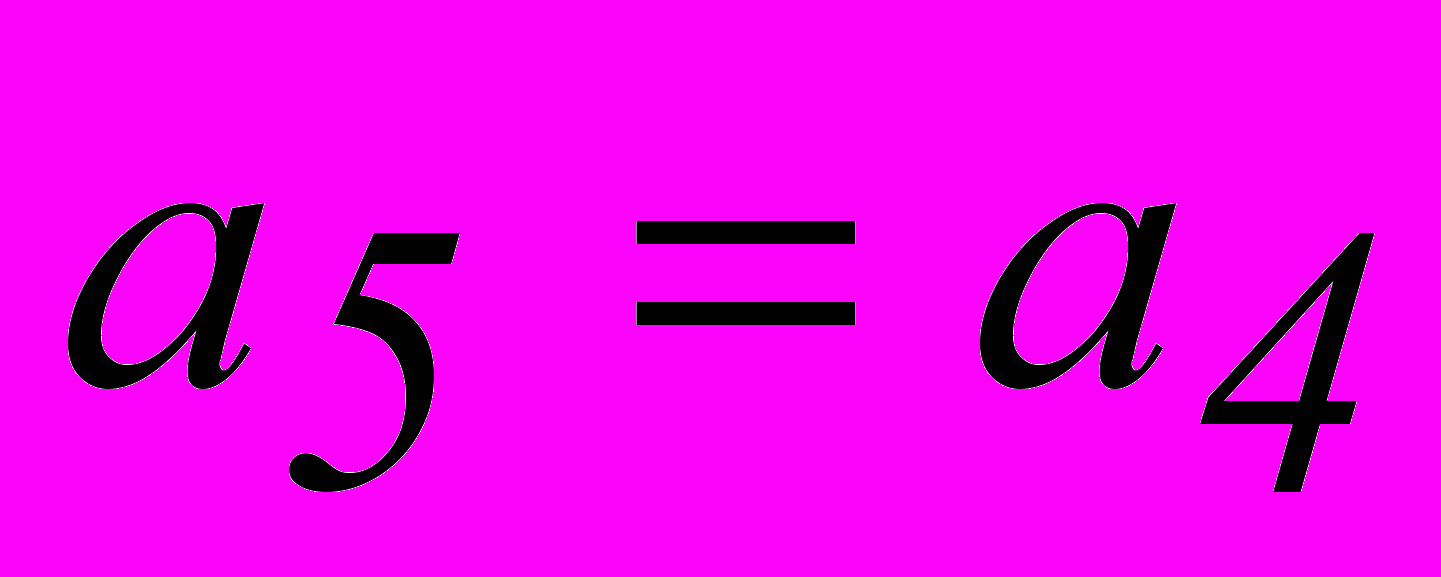
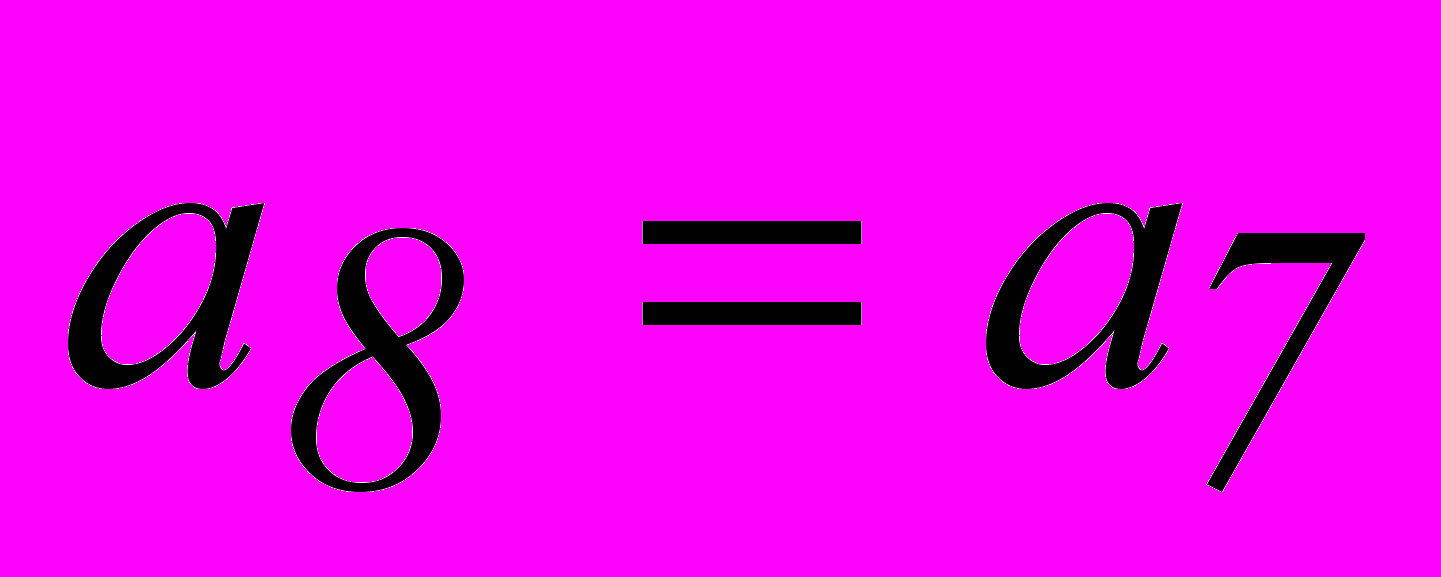
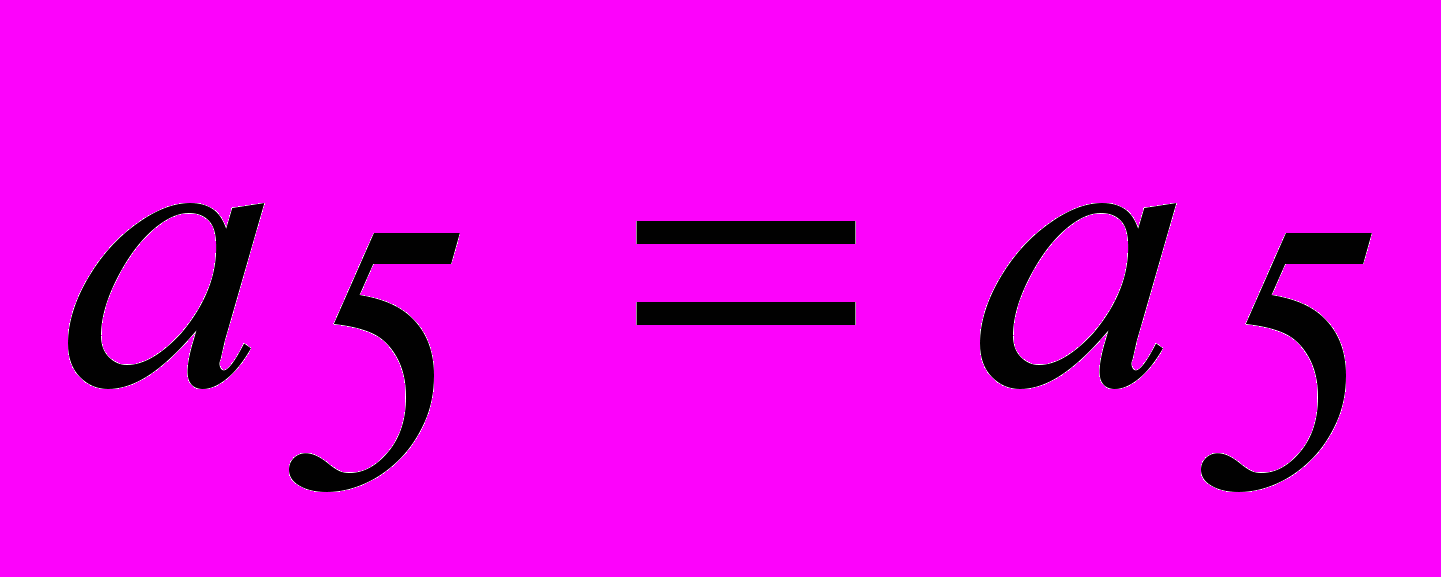
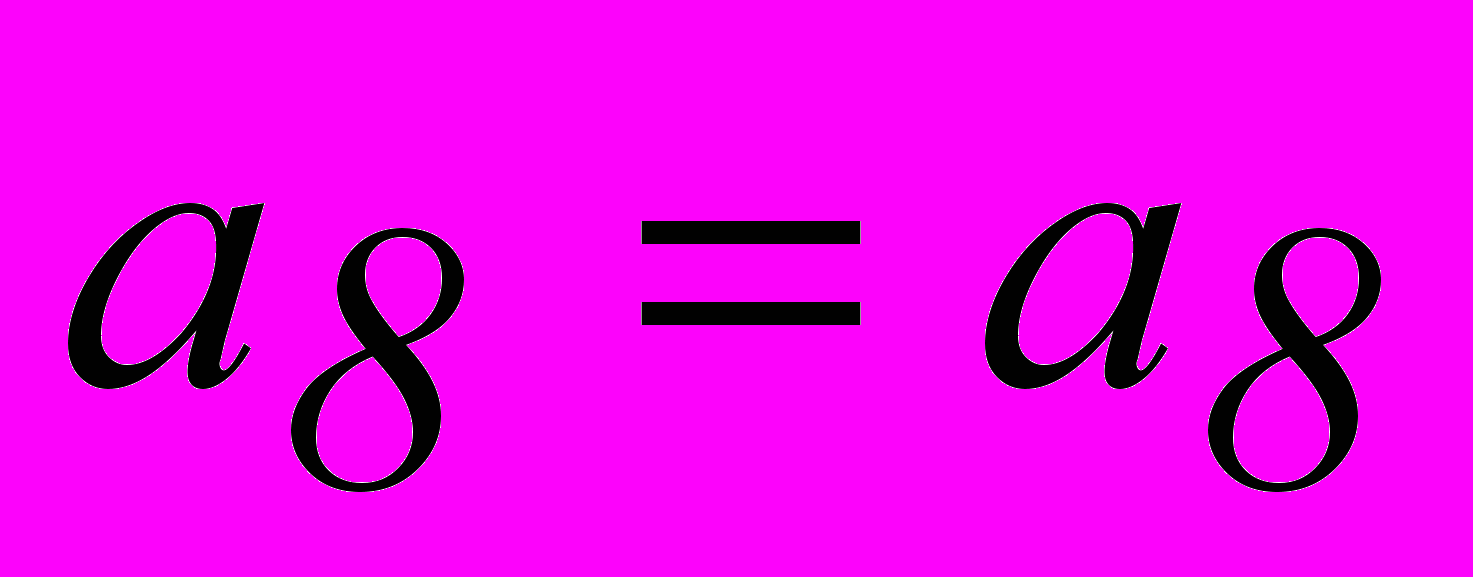
2.5. Описание программного обеспечения


Доступ ко всем возможностям программы осуществляется через главное меню.


Сборка cхемы:

На экране отображается заготовка схемы. Вам предлагается расставить соединения элементов. Текущее соединение отображается красной пунктирной линией, ее можно перемещать клавишами управления курсором. Клавиши <ПРОБЕЛ> или позволяют зафиксировать соединение или снять его (если оно было установлено).

Закончив сборку схемы нажмите , проверьте еще раз правильность схемы, и нажмите любую клавишу для продолжения работы.


Запуск cхемы :

Вам предлагается набpать пеpедаваемый код и вектоp ошибки. Они пpедставляются последовательностью '0' и '1', при пpевышении пpедельно допустимой длины стpоки pаздается звуковой сигнал.

Для выполнения схемой следующего такта нажимайте любую клавишу.


О помехозащищенных кодах:

Вы можете просмотреть текст, содержащий информацию о способах кодирования. При просмотре используются стандартные клавиши.


О программе:

Просмотр этого текста.


Выход:

Выход из программы.

Программа осуществляет моделирование системы с учетом задержек на элементах. Схему можно исправлять и запускать многократно, анализируя процесс прохождения информации.


ЗАДАНИЕ


Выполняется при домашней подготовке

1. Ознакомится с принципами построения групповых кодов.

2. Пользуясь табл. 2.1, 2.3, 2.4, 2.5, составить уравнения кодирования и декодирования для кодов:

(7,4), обеспечивающего коррекцию одиночных ошибок;

(8,4), обеспечивающего коррекцию одиночных ошибок и одновременное обнаружение двойных ошибок;

(7,3), обеспечивающего коррекцию двойных смежных ошибок (т.е. пачку ошибок не более двух символов);

(8,2), обеспечивающего коррекцию двойных независимых ошибок;

(9,3), обеспечивающего коррекцию пачек ошибок в трех и менее

разрядах.

3. Закодировать конкретные совокупности информационных символов, заданных персонально каждому студенту преподавателем, для кодов, указанных в п.2.

4. Для конкретных векторов ошибок ( по три для каждого кода), выбранных студентом из всего множества возможных ошибок, определить опознаватели ошибок.


Выполняется в лаборатории

1. Ознакомится с описанием программного обеспечения.

2. При помощи специальных команд войти в кафедральную сеть и запустить на выполнение программу pomeh.exe.

3. Собрать схему кодирования и декодирования для кода (7,4).

4. Протестировать ее для pазных кодовых комбинаций и вектоpов ошибок, исправляя схему пpи необходимости.

5. Пpоделать пункты 3 и 4 для кодов (7,3),(8,2),(9,3).


Требования к отчету


Отчет должен включать:

1. Уравнения кодирования и декодирования кодов, указанных в п.2 задания.

2. Совокупность кодовых комбинаций, соответствующих заданным информационным символам, по каждому из кодов.

3. Совокупность опознавателей ошибок, соответствующих заданным векторам ошибок, по каждому из кодов.

4. Схемы кодирования и декодирования для одного из кодов, указанных в п.2, причем отчеты бригады в совокупности должны содержать схемы реализации всех исследуемых кодов.


Контрольные вопросы


1. Какова математическая основа группового кода?

2. Как составляется таблица опознавателей?

3. В чем сущность мажоритарного декодирования?

4. Как определяются уравнения кодирования и декодирования?

5. Как построить код, исправляющий одиночные и одновременно

обнаруживающий двойные ошибки?

6. Как построить код, обнаруживающий четырехкратные ошибки?
   
7. Как построить код, обнаруживающий тройные ошибки?
   

ЛИТЕРАТУРА

1. Дмитриев В.И. Прикладная теория информации. – M.: Высш. шк., 1989. – 320с. (C. 202–239).
   
2. Темников Ф.Е., Афонин В.А., Дмитриев В.И. Теоретические основы информационной техники. М.: Энергия, 1979.–512с. (C. 131–171).
   

Лабораторная работа №103

ПОСТРОЕНИЕ И РЕАЛИЗАЦИЯ ЦИКЛИЧЕСКИХ КОДОВ

Целью работы является усвоение методов построения и технической реа­лизации кодирующих и декодирующих устройств циклических кодов.

3. Указания к построению кодов.
   

Математической основой циклических кодов является теория колец [1;2]. В качестве основных операций в циклическом коде используются операции сложения по модулю два и символического умножения, в котором для сохранения степени многочлена не выше (n-1) используется искусственный прием. Если степень многочлена после умножения на выше n-1, то он и принимается за результат умножения , а если выше , то он делится на другой многочлен (xⁿ+1) и в качестве результата умножения принимается остаток от деления.


3.1. Выбор образующего многочлена


Любой групповой (n,k) код может быть записан в виде матрицы, вклю­чающей k линейно-независимых строк по n символов. Среди всего многообразия таких кодов можно выделить коды, у которых строки обра­зующих матриц связаны дополнительным условием цикличности.

Все строки образующей матрицы такого кода могут быть получены цикли­ческим сдвигом одной комбинации: называемой образующей для данного кода. Коды, удовлетворяющие этому условию, получили название циклических ко­дов.

Сдвиг осуществляется справа налево, причем крайний левый символ каж­дый раз переносится в конец комбинации. Запишем, например, образующую матрицу кода, получающуюся циклическим сдвигом комбинации 001011:


G =

При описании циклических кодов n-разрядные кодовые комбинации пред­ставляются в виде многочленов фиктивной переменной х. Показатели степени у х соответствуют номерам разрядов (начиная с нулевого), а коэффициентами при х являются цифры 0 и 1 (поскольку мы рассматриваем двоичные коды).

Запишем, например, в виде многочлена образующую кодовую комбина­цию 001011



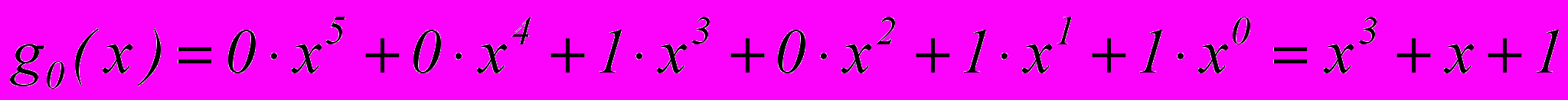
Действия над кодовыми комбинациями теперь сводятся к действию над многочленами.

Вышеупомянутый циклический сдвиг образующего многочлена без пере­носа единицы в конец кодовой комбинации соответствует простому умноже­нию на х. Например, вторая строка матрицы есть

g₀ (x)x=x⁴+x²+x (010110).

Циклический сдвиг строки матрицы с единицей в старшем разряде (слева) равносилен умножению соответствующего многочлена на х с одновре­менным вычитанием из результата многочлена х^п+1

Поскольку операции вычитания и сложения по модулю два тождественны, многочлен, соответствующий любой строке матрицы, может быть записан в виде

g_i(x)=g₀(x)xⁱ+С(xⁿ+1),

где С равно 1, если степень g₀(x)xⁱ превышает n-1, и нулю, если не превы­шает.

Если выбрать за образующий такой многочлен g₀(x), который является де­лителем двучлена xⁿ+1, то все многочлены матрицы, а поэтому и все много­члены кода (разрешенные кодовые комбинации), будут делиться на g₀ (x) без остатка. Ни один многочлен, соответствующий запрещенной кодовой комбина­ции, на образующий многочлен на цело не делится. Это свойство позволяет об­наруживать ошибки. По виду остатка можно определить и вектор ошибки, а, следовательно, и устранить ее.

Любая принятая кодовая комбинация h(x), содержащая ошибку, может быть представлена в виде суммы по модулю два неискаженной комби­нации кода f(x), делящейся на g₀(x) без остатка, и вектора ошибки e(x). Для од­нозначности декодирования каждому вектору ошибки должен соответствовать отличный от других остаток - опознаватель. Чем больше различных остатков может быть образовано при делении h(x) на g₀(x), тем больше разновидностей ошибок способен исправить данный циклический код.

Наибольшее число остатков, равное 2^m-1 (исключая нулевой), может обес­печить только неприводимый (простой) многочлен g₀(x) степени m , принадле­жащий показателю степени п, если m и n связаны соотношением n= 2^m-1.

В литературе по кодированию [1;2] доказано, что для любого т существует по крайней мере один неприво­димый многочлен степени т, принадлежащий показателю степени п, если n=2^m-1.

При известном числе информационных символов (к) задача, следова­тельно, сводится к тому, чтобы определить наименьшую степень т образую­щего многочлена, обеспечивающего обнаружение или исправление ошибок за­данной кратности. Зная п и т по имеющимся в ряде книг [2] таблицам много­членов, неприводимых при двоичных коэффициентах, можно выбрать и кон­кретный образующий многочлен.

Для исправления одиночных ошибок требуемая минимальная степень образующего многочлена (m) на­ходится из соотношения

2^т-1=2^п-k-1 C¹_n

Выберем, например образующий многочлен для случая к=4. Тогда п=7 и т=3.

В таблице неприводимых многочленов, принадлежащих степени п, нахо­дим два многочлена третей степени, так как х⁷+1=(х+1)(х³+х+1)(х³+х²+1).

Примем за образующий многочлен g(x)=x³+x²+1 (1101). Чтобы убедится, что каждому вектору ошибки соответствует отличный от других остаток, поде­лим каждый из этих векторов на g₀(x).

Векторы ошибок т младших разрядов имеют вид :





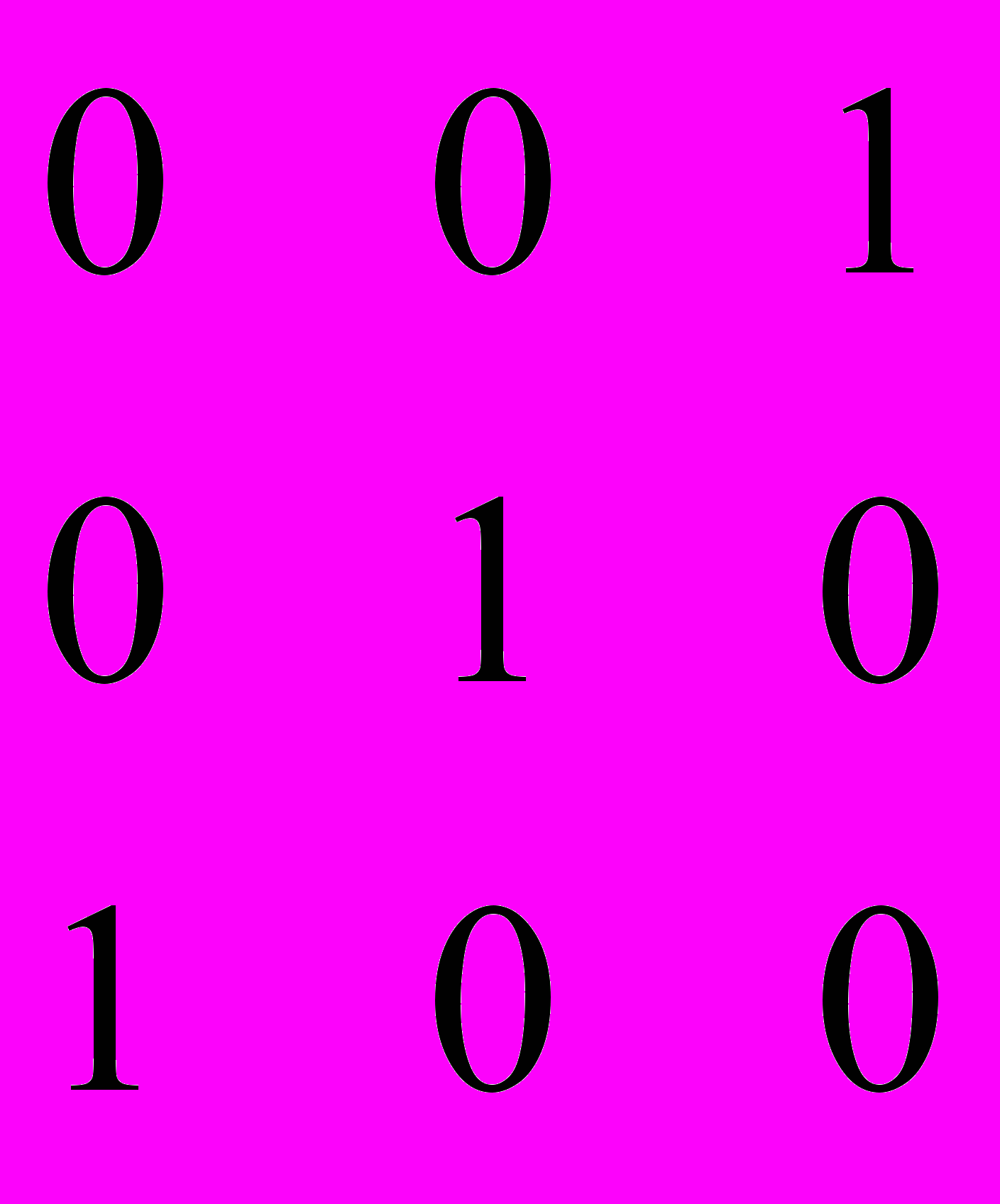
Степени соответствующих им многочленов меньше степени образующего многочлена g₀(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий ошибке в следующем разряде, получается при делении 1000 на 1101, т.е.

1000 1101

1101

101


Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g₀(x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки


1000000000 1101 Остатки

1101

1010 101

1101 111

1110 011

1101 110

01100 001

1101 010

001000 100

При последующем делении остатки повторяются.

Если выбрать в качестве образующего многочлена 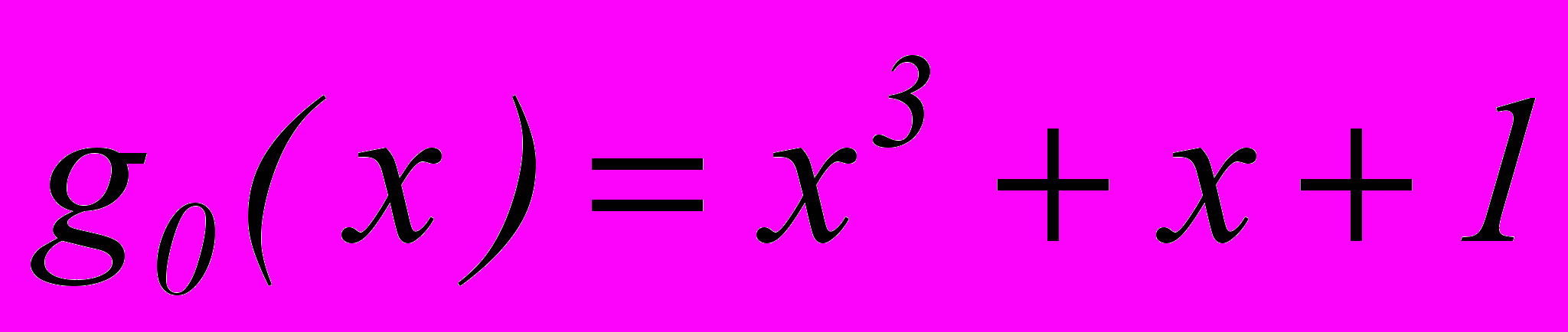, то тоже получим требуемое число различных остатков – 7.

Если k=5 и требуется исправлять тоже одиночную ошибку, то 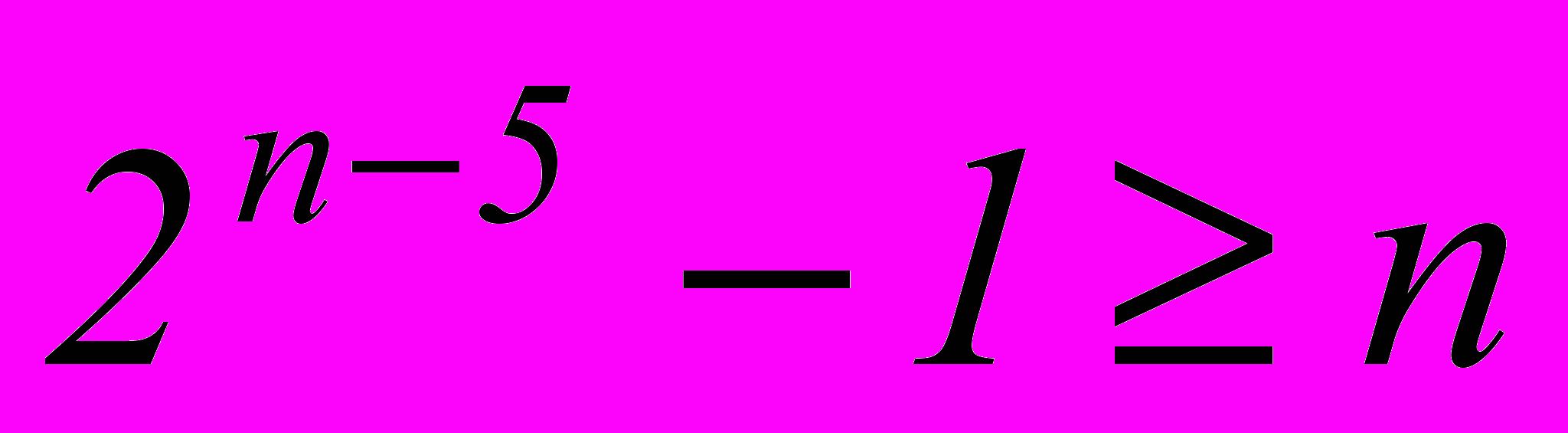. Откуда получаем n_min=9 и m= n – k =9–5=4. Примем 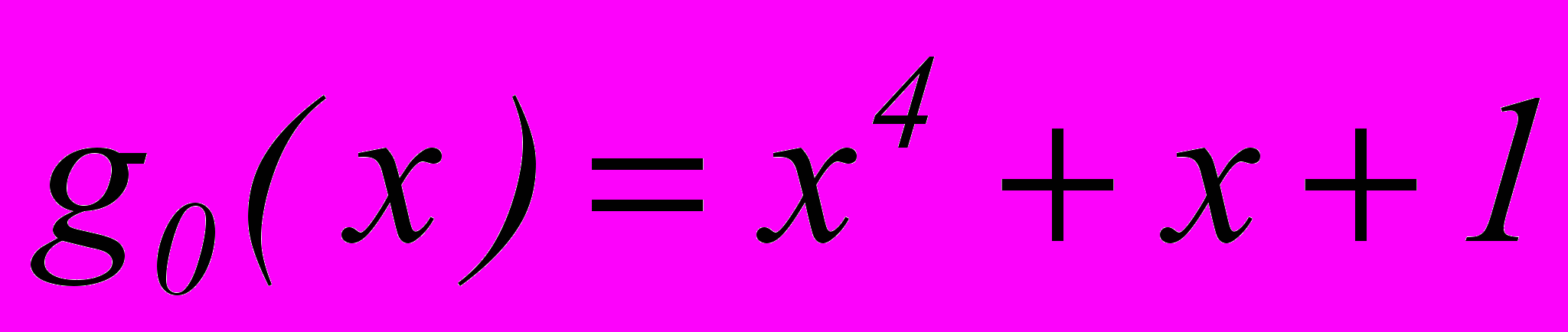. Этот образующий многочлен сохранится до k=11, так как неравенство 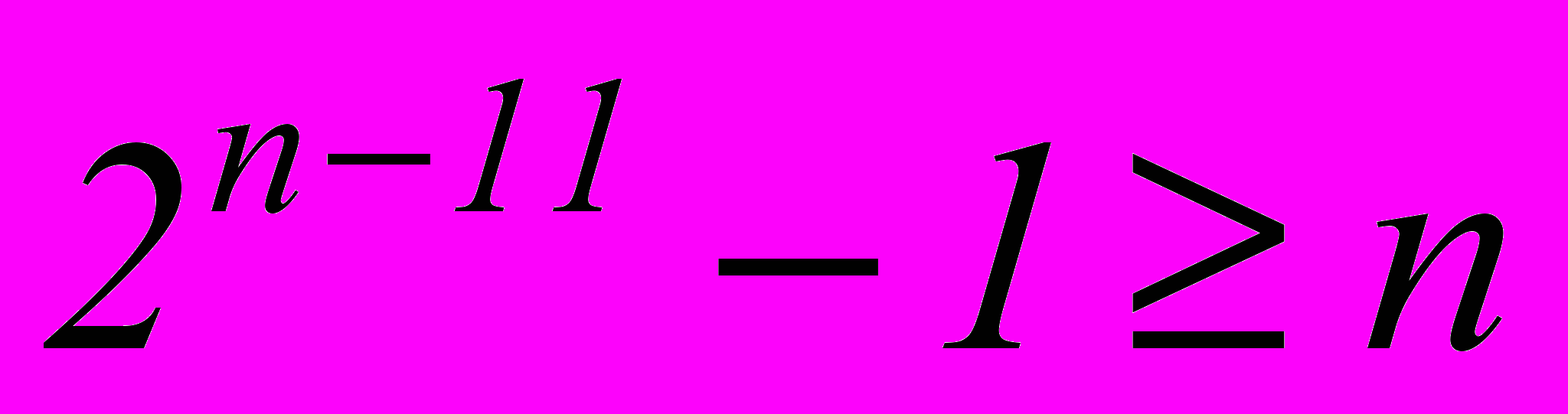будет выполняться при n_min=15 и m=4.