В. В. Демьянов Государственная Морская Академия им. В. Ф. Ушакова, Новороссийск

Вид материала

Документы

Содержание Эксперимент Майкельсона и его традиционная интерпретация V "эфирного ветра". Однако измерения Майкельсона и более поздние эксперименты показали, что Δt Эксперимент Майкельсона в оптических средах и его нерелятивистская интерпретация Обсуждение и выводы

Подобный материал:

• Совершенствование управления конкурентоспособностью предприятий сферы услуг (на примере, 350.16kb.
• Федеральное агентство по рыболовству правительство калининградской области балтийская, 39.6kb.
• «Государственная морская академия имени адмирала С. О. Макарова», 256.52kb.
• Ушакова ольга Владимировна нарушения функции поджелудочной железы при хронических вирусных, 270.36kb.
• Финансово-промышленные группы как фактор конкурентоспособности россии, 406kb.
• Орлова Анастасия Геннадьевна лауреат международных конкурс, 24.41kb.
• Военно-морская академия имени Адмирала Флота Советского Союза Н. Г. Кузнецова, 175.94kb.
• «Курская государственная сельскохозяйственная академия имени профессора И. И. Иванова», 325.11kb.
• Постановление от 10 августа 2010 №2752 постановление от от 10 августа 2010 №2752, 17.41kb.
• Министерство транспорта россии дальневосточная государственная морская академия имени, 4135.49kb.

Измерения на интерферометре Майкельсона в диэлектрических средах и теоретическая интерпретация наблюдаемого сдвига

интерференционной полосы


В.В.Демьянов

Государственная Морская Академия им. В.Ф.Ушакова, Новороссийск

e-mail: demjanov@nsma.ru


Экспериментально обнаружено, что отсутствующий в вакууме сдвиг X_m интерференционной полосы в опыте Майкельсона оказывается отличным от нуля при использовании в качестве светоноса диэлектрических сред (газов, жидкостей, твёрдых тел), показатель преломления которых n ≠ 1. Это открытие заставило концептуально по-новому интерпретировать физические процессы, протекающие в интерферометре Майкельсона. Я отказался от общепринятого правила с±V аддитивного сложения скорости V инертного тела со скоростью c света, как принципиально неприложимого к неинертному объекту, каковым является электромагнитная волна. Вместо этого я применил дорелятивистскую формула Френеля c/n ± V(1–1/n²) увлечения света движущейся оптической средой. Последняя, вместе с учетом физического эффекта лоренцева сокращения плеча L интерферометра, позволила построить теоретическую модель X_m ~ LΔε(1–Δε), где Δε = n²–1, которая воспроизвела в существенных чертах полученную в эксперименте параболическую зависимость X_m() от части диэлектрической проницаемости ε, связанной с вкладом только поляризации частиц светоноса. Из экспериментальной кривой с помощью выведенной таким образом формулы V²/с²= X_m/[X_oL (1)], где X_o  ширина интерференционной полосы и   длина волны, получен ожидаемый порядок величины абсолютной скорости Земли относительно неподвижного эфира. На параллели г. Обнинска в разное время суток в горизонтальной плоскости она менялась в пределах 140<V<480 км/ сек.


Эксперимент Майкельсона и его традиционная интерпретация


Эфир, по определению, – гипотетическая сплошная среда, служащая для переноса электромагнитного излучения и передачи взаимодействия. Предположительно Земля движется сквозь светоносный эфир с некоторой скоростью V. Для того, чтобы опытным путём определить скорость этого движения, Майкельсон [1–2] измерил время t, за которое свет преодолевает расстояние L от источника до возвращающего зеркала и обратно в двух направлениях: t_|| – параллельно V и 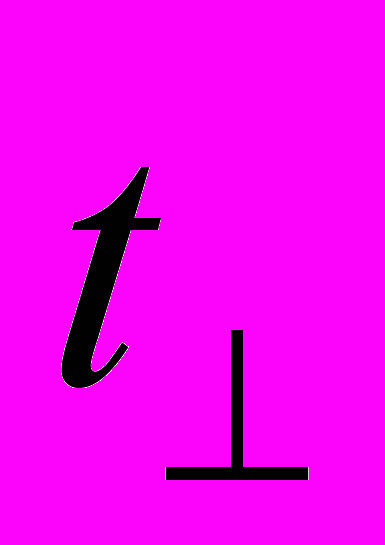– перпендикулярно направлению движения экспериментальной установки. Полученные экспериментальные данные были истолкованы следующим образом. Согласно Майкельсону, в равноплечном интерферометре должны выполняться следующие соотношения:

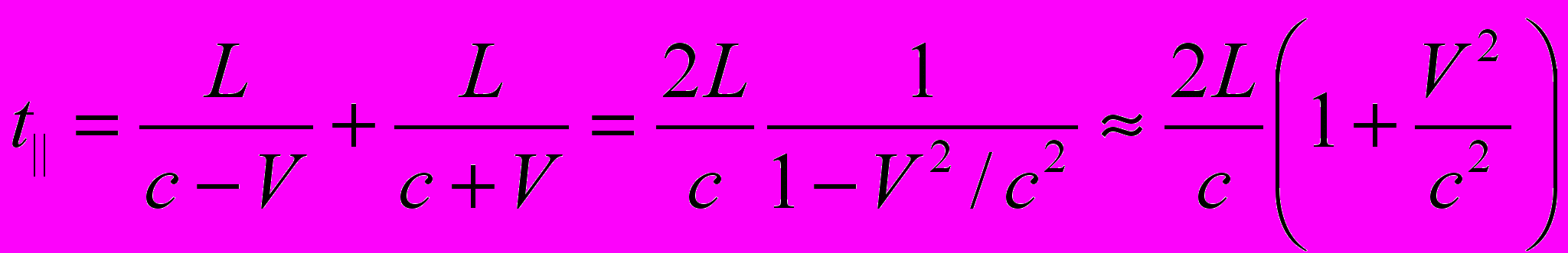, (1)

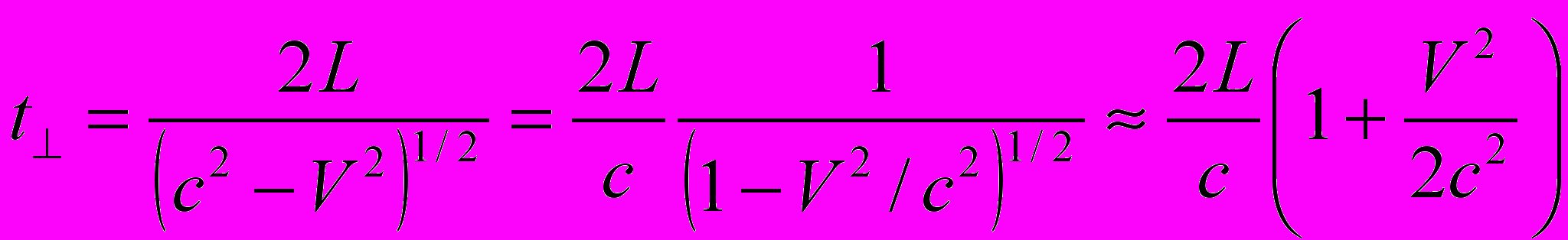. (2)


В таком случае, измеряя разность времен (2) и (1)

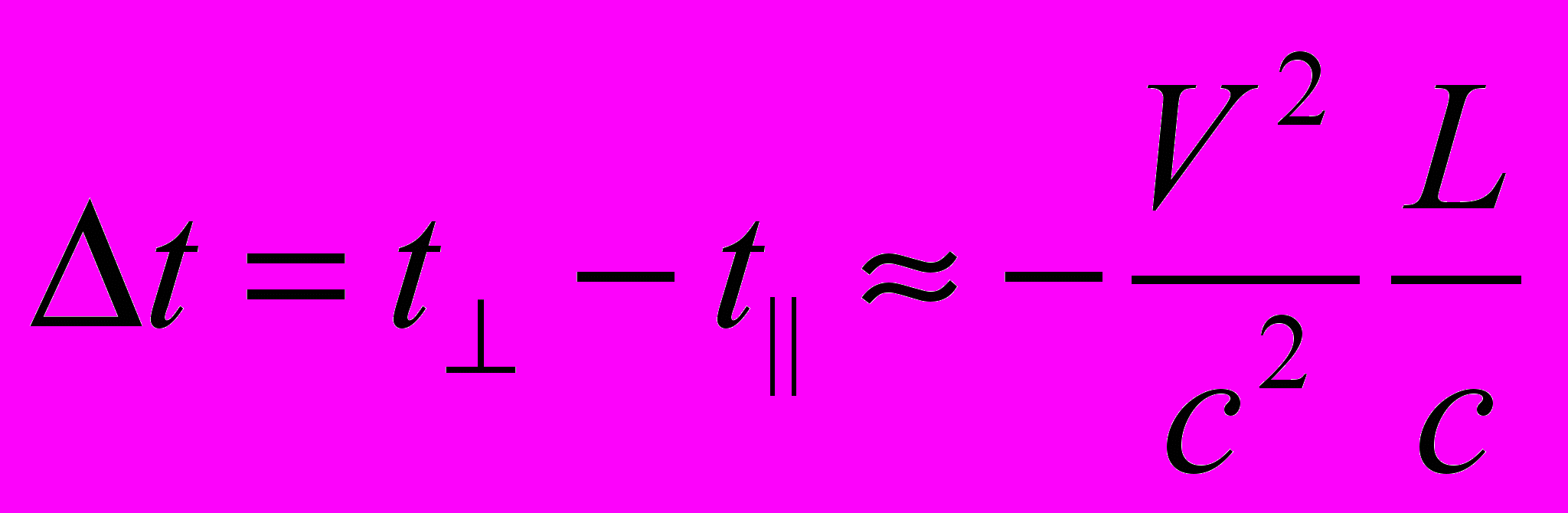(3)

можно было бы найти скорость V "эфирного ветра".

Однако измерения Майкельсона и более поздние эксперименты показали, что Δt равно нулю. Этому факту было дано объяснение в рамках физического эффекта лоренцева сокращения длины L движущегося со скоростью V тела:

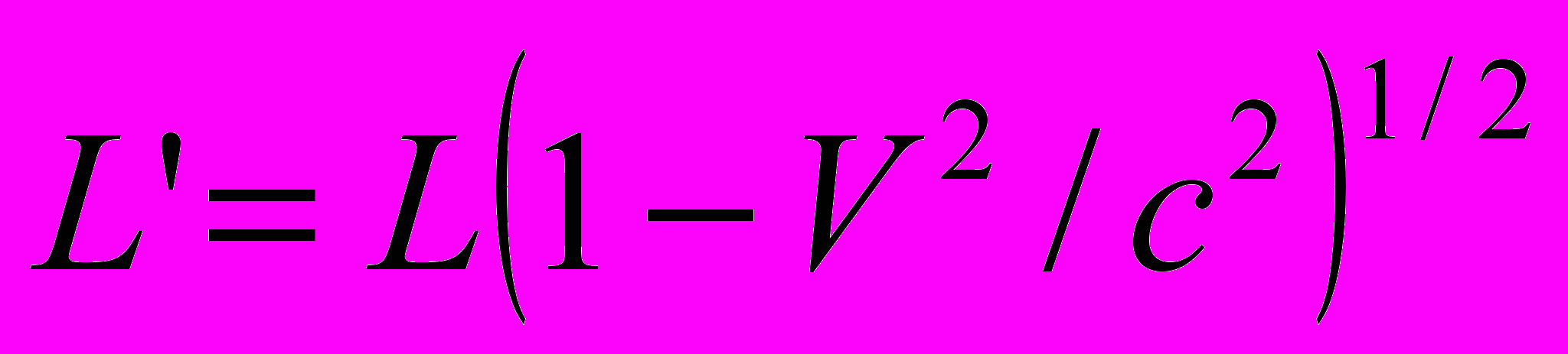. (4)

где L' – длина плеча интерферометра в (1). С учетом (4) получим вместо (1)

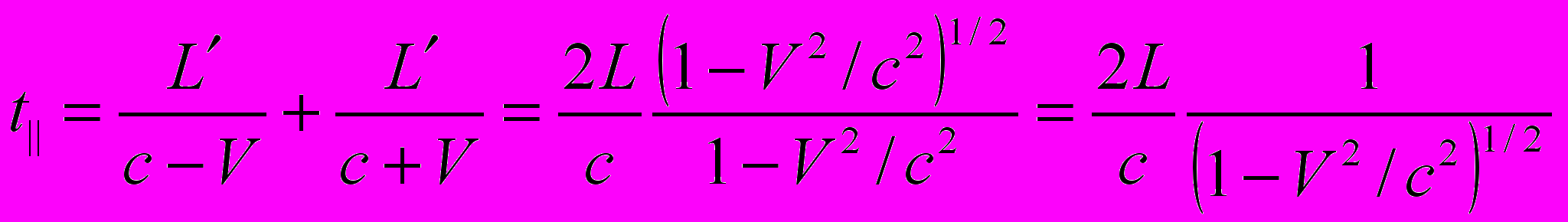. (5)

Из (5) и (2) имеем точное равенство 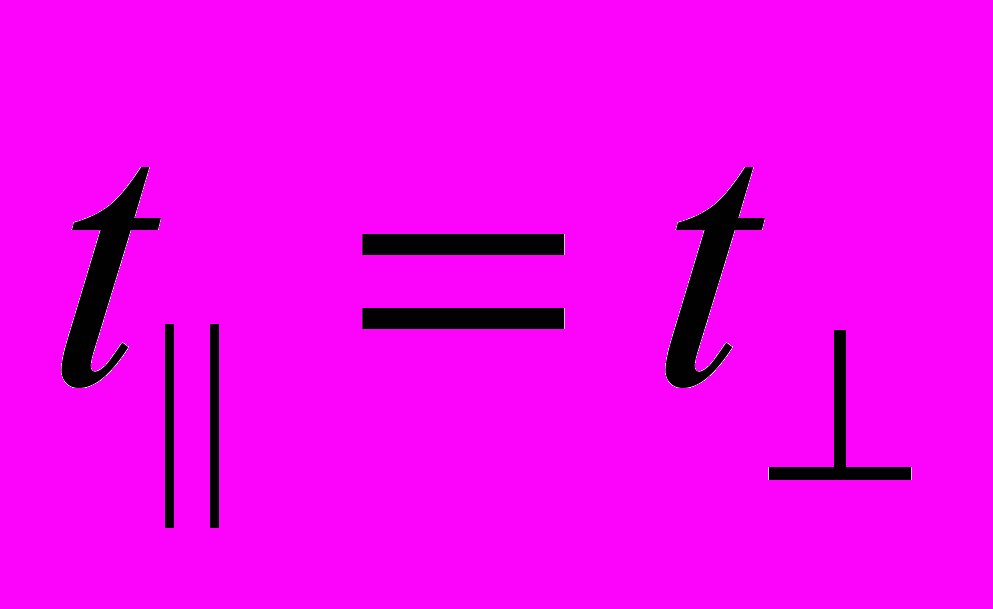, т.е. Δt = 0 .


Эксперимент Майкельсона в оптических средах и его нерелятивистская интерпретация


_{В 1968–1971 годах, будучи научным сотрудником Обнинского филиала НИФХИ им. Л.Я.Карпова, я измерил зависимость амплитуды смещения Xm интерференционной полосы от части проницаемости =n}²_{1 вклада частиц в полную проницаемость =n}² _{различных оптопрозрачных материалов [3]. Измеряемая разность Δt времён tt|| пропорциональна амплитуде смещения полосы Xm. На рис.1 показана найденная мной параболическая зависимость Xm(Δ) от вклада Δε=ε–1 частиц в диэлектрическую проницаемость ε оптической среды. Как видно из рисунка, выходное отношение сигнал/шум значительно улучшается для сред с показателем преломления n>1, где ε = n}²_{. В двух областях значений диэлектрической проницаемости, Δε→0 и Δε1, сигнал тонет в шумах прибора.}





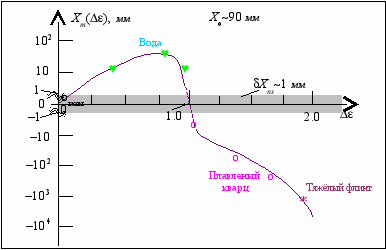
Рис.1. Зависимость сдвига X_m интерференционной полосы интерференционной полосы от вклада Δε поляризации частиц светоноса в полную диэлектрическую проницаемость ε = 1+Δε оптической среды – воздуха, воды, плавленого кварца и стекла "тяжелый флинт", соответственно. Измерения на газах проведены при длине плеча L=6.0 м, а на воде, плавленом кварце и стёклах при L=0.3 м в синем луче (все экспериментальные точки приведены к L=6 м); X₀ – ширина полосы, транслируемой на экран неподвижного кинескопа; δX_ns – уровень шума в интерферометре.


Для того, чтобы объяснить ход экспериментальной кривой, показанной на рис.1, я отверг, как несостоятельное, правило сложения с±V скорости света c со скоростью V поступательного движения частиц оптической среды, использованное Майкельсоном при выводе соотношений (5) и (2). Вместо аддитивного правила сложения скоростей я использовал формулу Френеля, ранее подтвержденную в опыте Физо, для зависимости скорости света от параметров движущейся оптической среды:

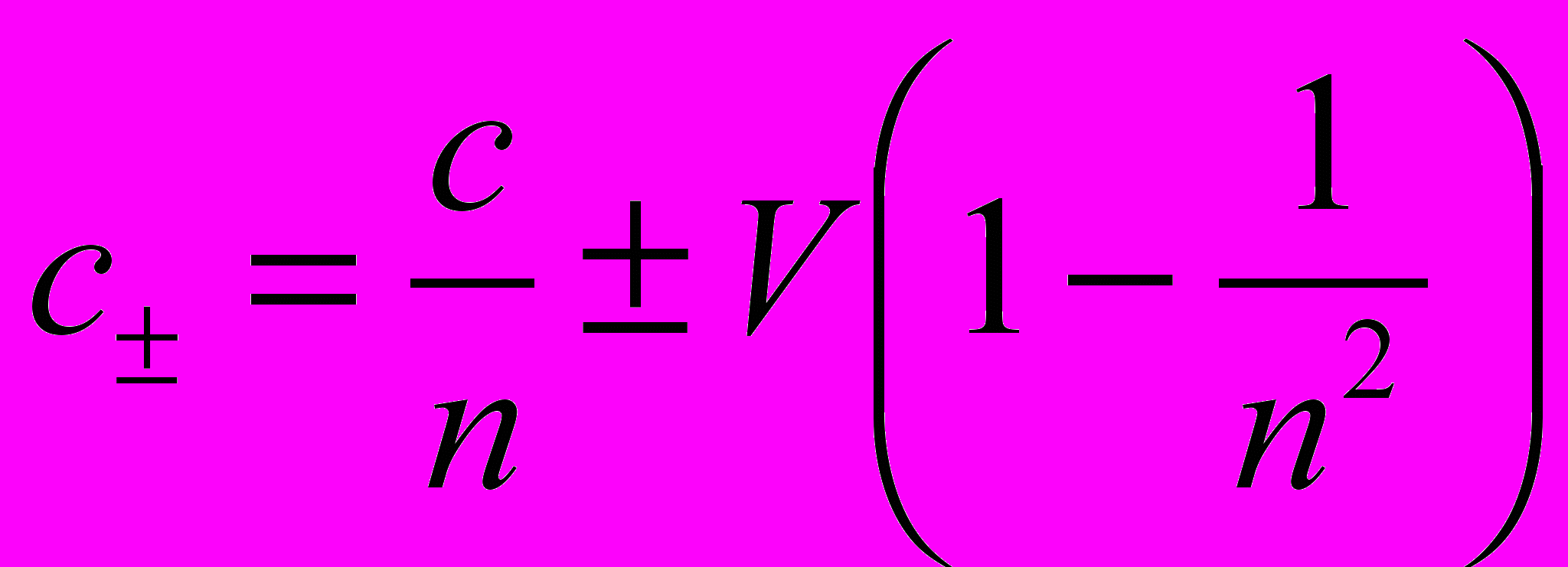. (6)

Замечу, что недавно формула Френеля была выведена [4] из уравнений Максвелла. Используя (6) вместо (1) будем иметь:

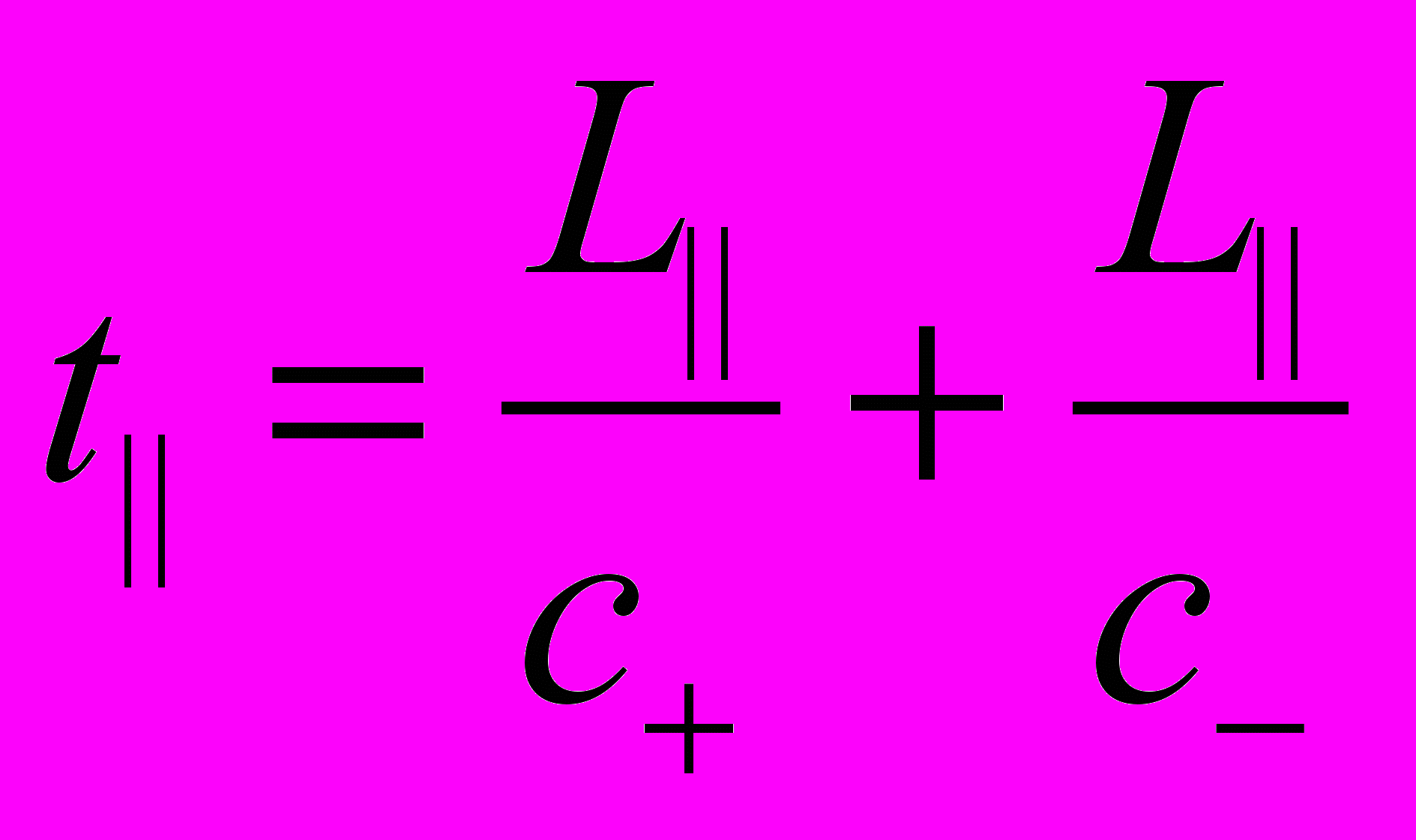, (7)

где c₊ и c_ – значения (6) для распространения света вдоль V и в противоположном направлении, соответственно. Как выяснилось, для воспроизведения экспериментальной кривой рис.1, в формулу (7) следует внести поправку на эффект лоренцева сокращения длины движущегося тела. Необходимое согласие с экспериментом получается, если в лабораторной системе отсчёта за оптический пробег света в параллельном плече интерферометра принять длину

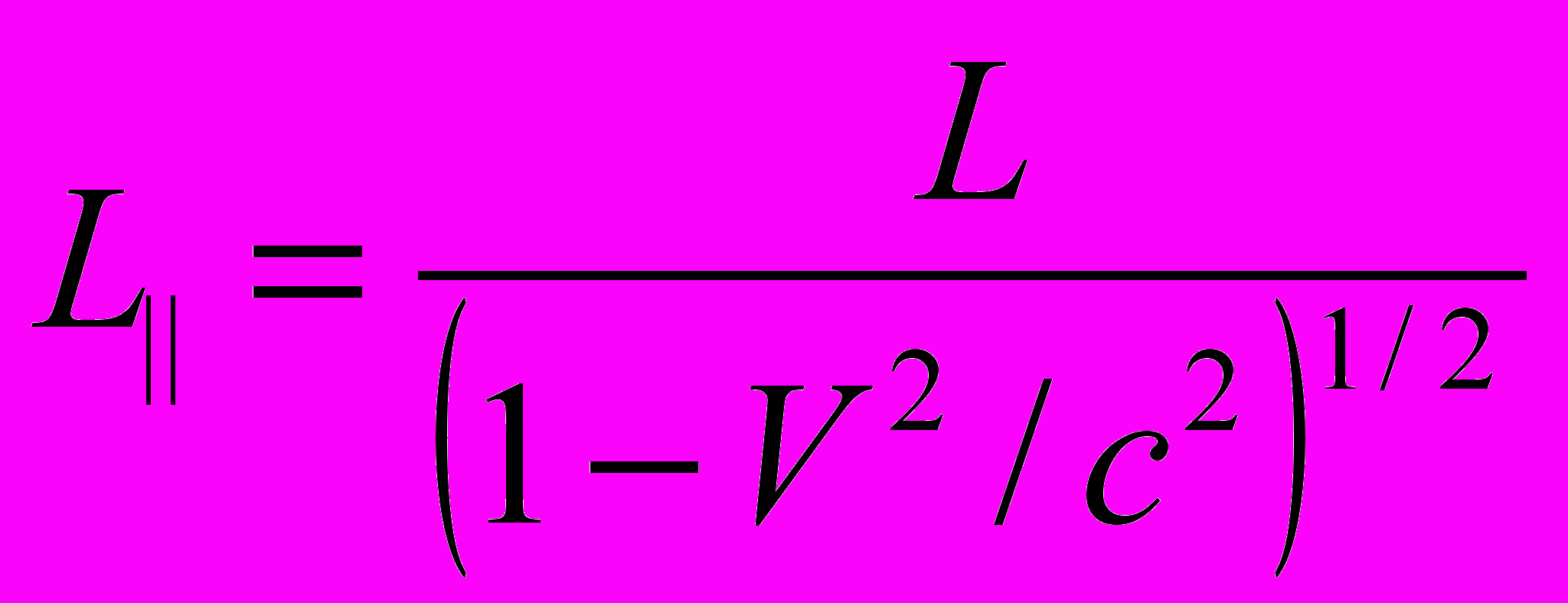. (8)

Именно эта последняя формула позволила правильно передать показанную на рис.1 зависимость. По-видимому, соотношение (8) является следствием того, что в оптических средах с невысокой проницаемостью свет большей частью пребывает в неподвижном эфире, в котором длина пробега L_|| больше длины L лоренц-сокращённого плеча подвижной инерциальной системы. Подставляя соответствующие значения (6) и (8) в (7), получим для времени пробега луча в направлении, параллельном V , и обратно





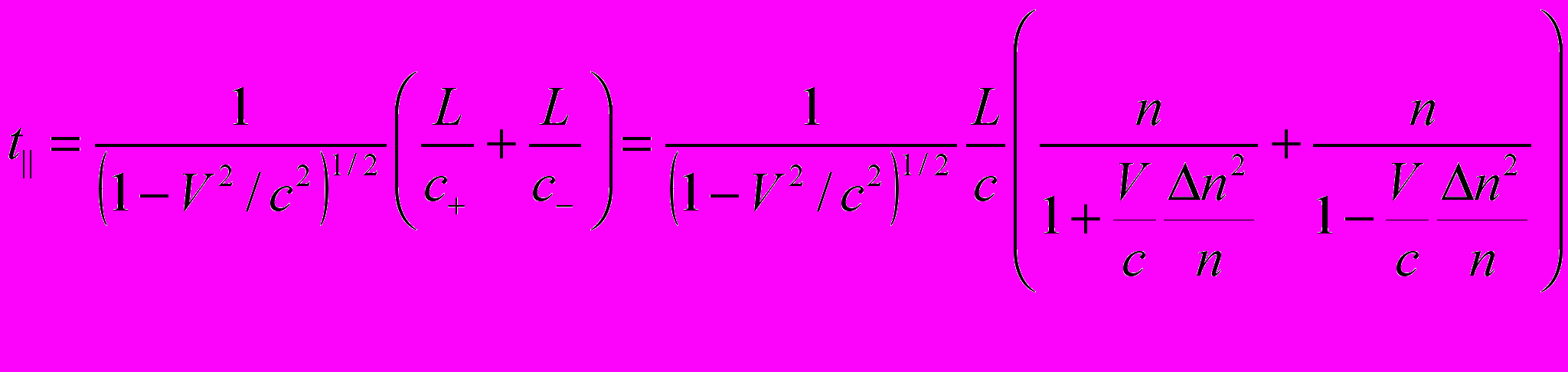
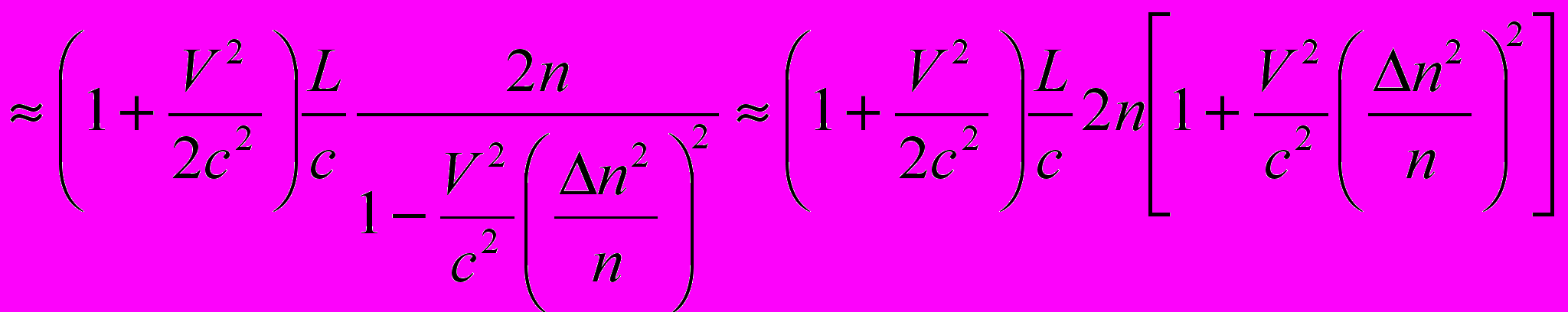
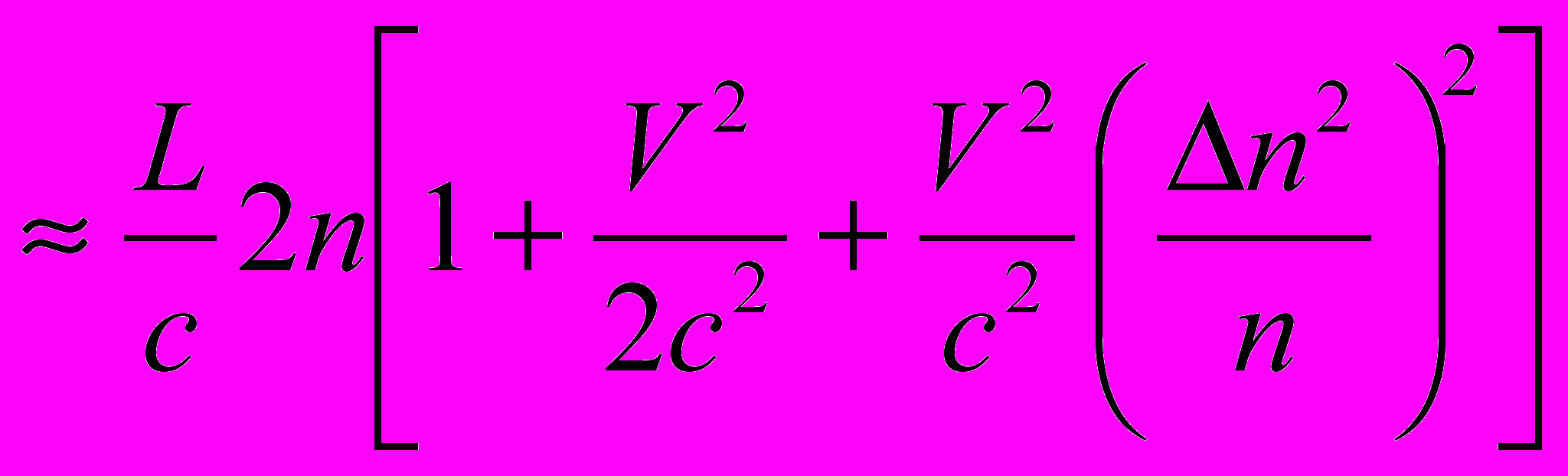. (9)

Для времени t_ распространения света туда и обратно в плече, перпендикулярном V , из (2) с учетом (6) получаем:

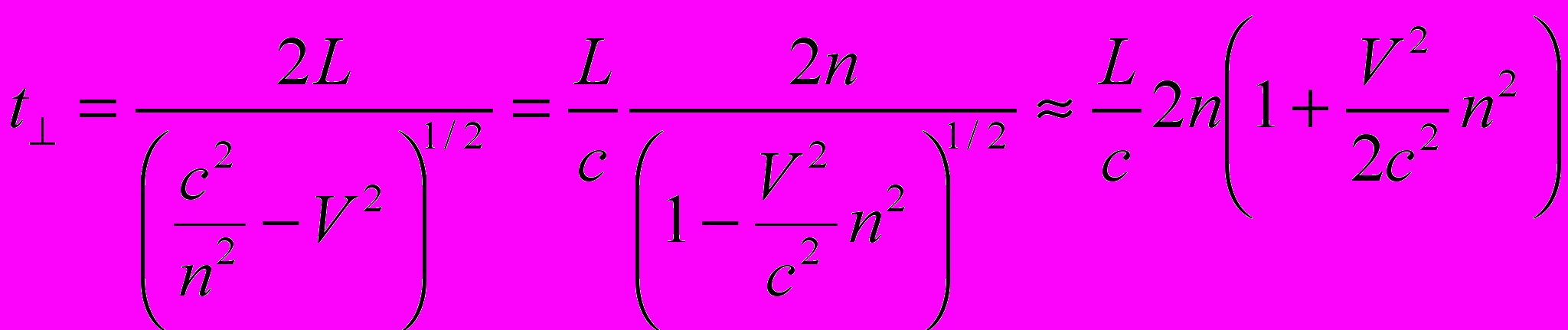. (10)

Вычитая (9) из (10), найдем

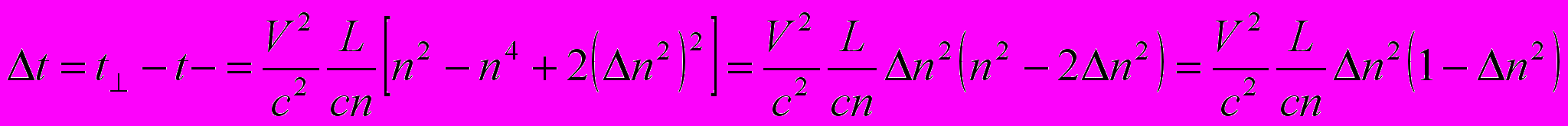. (11)

С учётом n = ε^1/2 и Δε =Δn²=n²1 получаем из (11) формулу (Демьянов 1971)

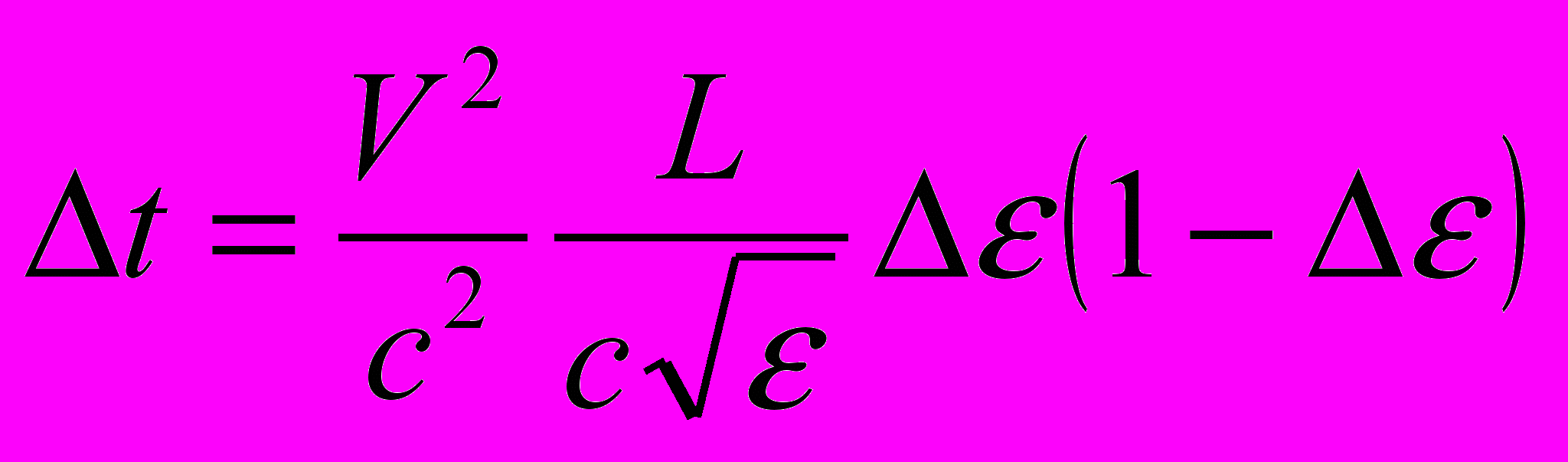, (12)

которая воспроизводит в существенных чертах экспериментальную кривую, показанную на рис.1. Из этой кривой и теоретической модели (12) получается оценка скорости V "эфирного ветра": 140480 км/сек. Заметим, что авторы [5] лишь недавно высказали соображение о целесообразности проведения эксперимента Майкельсона в оптических средах. Однако, полученная ими линейная модель X_m~LΔε не описывает опытов Физо и, разумеется, не способна воспроизвести полученные мной в диапазоне 0 <Δε<2 экспериментальные данные (см. рис.1). К тому же она основана на использовании эклектичной формы с/n±V, противоречащей формуле Френеля, выведенной [4] из уравнений Максвелла.


Обсуждение и выводы


На интерферометре Майкельсона при использовании в качестве светоносов оптических сред с показателем преломления, отличным от единицы, получен сдвиг интерференционной полосы X_m, тем значительнее повышающий отношение сигнал/шум, чем больше вклад  частиц в полную проницаемость светоносной среды (=1+). Выяснилось, что измеряемая разность t ~ X_m между временными интервалами прохождения света от источника до зеркала и обратно для направлений параллельно и перпендикулярно направлению движения интерферометра очень сильно зависит от показателя преломления n светоносной среды, причём не от всей проницаемости, а от её части =n²1, обусловленной только поляризацией частиц светоноса. Найденная параболическая зависимость X_m от показателя преломления оптической среды хорошо описываются теоретической моделью X_m~()² [3], основанной на дорелятивистской и негалилеевской формуле Френеля для увлечения света движущейся оптической средой. Таким образом, показана несостоятельность аддитивного правила сложения скорости света со скоростью движущегося инертного тела, используемого при выводе формулы Майкельсона.

В рамках предложенной интерпретации, концептуально отличной от традиционной, находит объяснение тот факт, что все известные измерения (см. например [6–7]) на интерферометре типа Майкельсона заканчивались отрицательным результатом: X_m0 и, следовательно, Δt0. В этих опытах экспериментаторы, как правило, стремились к тому, чтобы в той части прибора, где проходил свет, был лабораторный вакуум, т.е. Δε0. Либо опыты проводились с использованием гамма-лучей. В последнем случае Δε_γ=ε_γ1=0 из-за того, что диэлектрическая проницаемость оптических сред в гамма-лучах ε_γ=1 (то есть показатель преломления n_γ=1). Подстановка же Δε=0 в формулу (12) дает Δt=0.

В опытах МайкельсонаМорли [2] и Миллера [6] при достаточной длине плеча L≥10 м интерферометра фиксировался ненулевой эффект X_m≠0. Хотя и небольшой, но наблюдаемый в этих опытах сдвиг интерференционной полосы связан с тем, что они проводились не в вакууме, а при нормальном давлении воздуха, что соответствует Δε≈0,0006. Однако из-за использования неправильной формулы (3) указанные авторы получали многократно заниженную оценку абсолютной скорости Земли, лежащую в пределах шума прибора, 5–10 км/сек. Действительно, согласно (3), скорость V эфирного ветра ошибочно оценивалась из экспериментального значения Δt, как

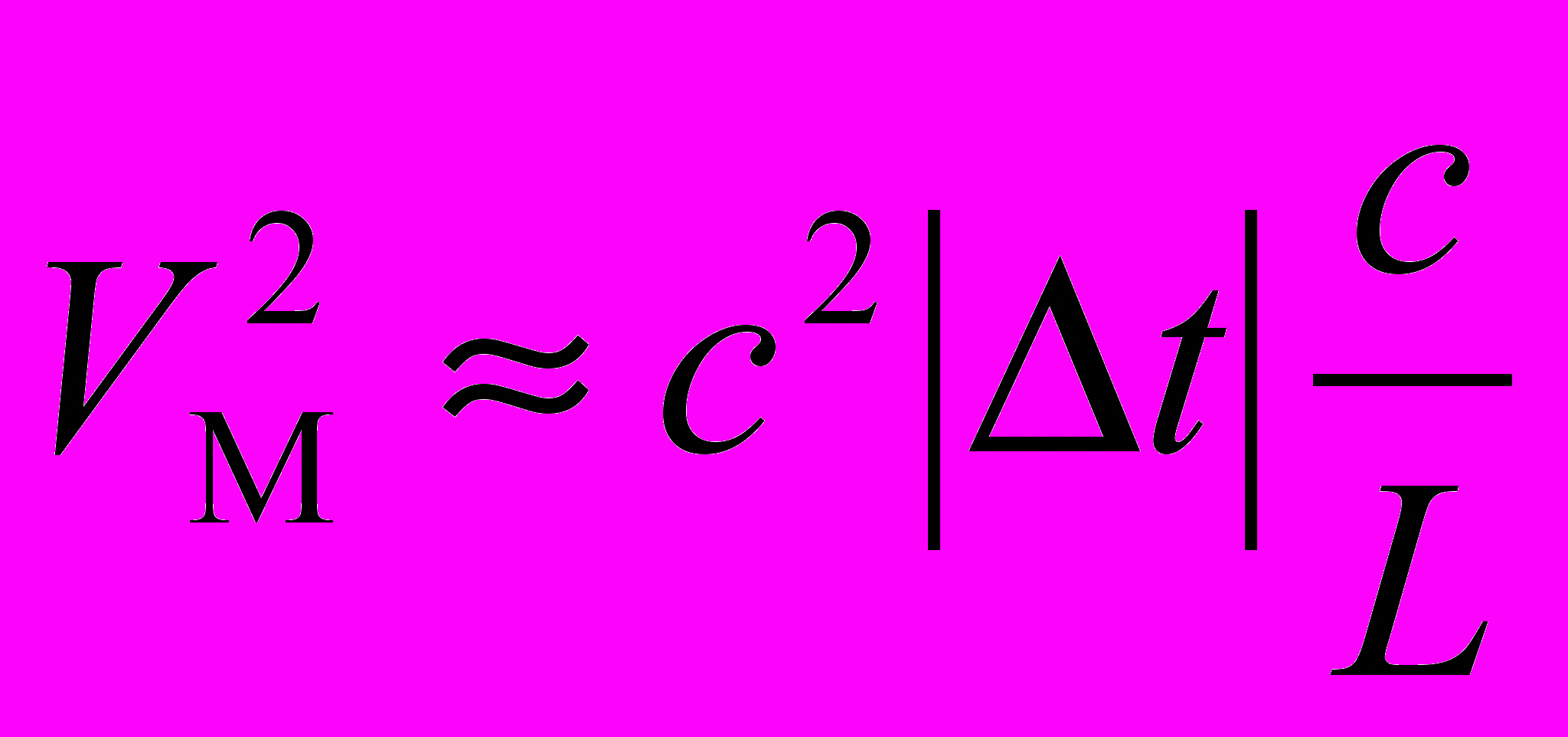. (13)

Правильная оценка V_Д , полученная из того же экспериментального значения Δt с помощью формулы (12) при Δε<<1, будет

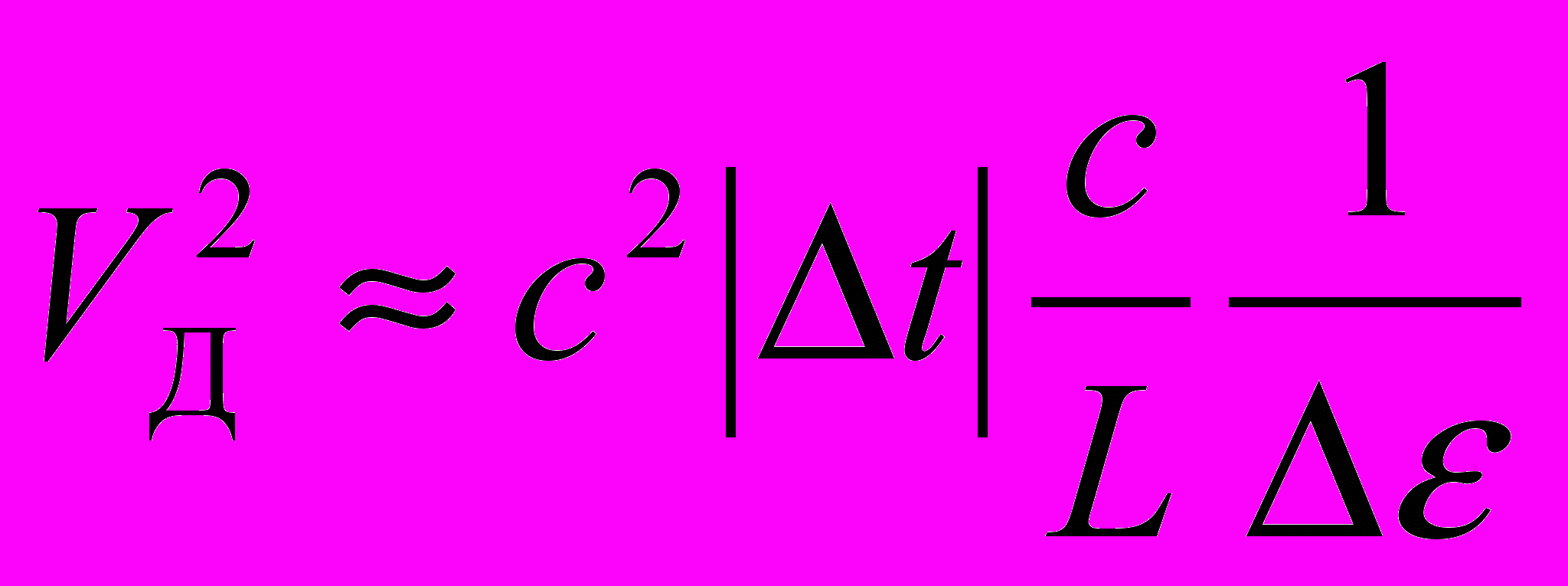. (14)

Сравнивая формулы (13) и (14), находим, что в [2] и [6] значение абсолютной скорости Земли было занижено в 0,0006^1/240 раз:

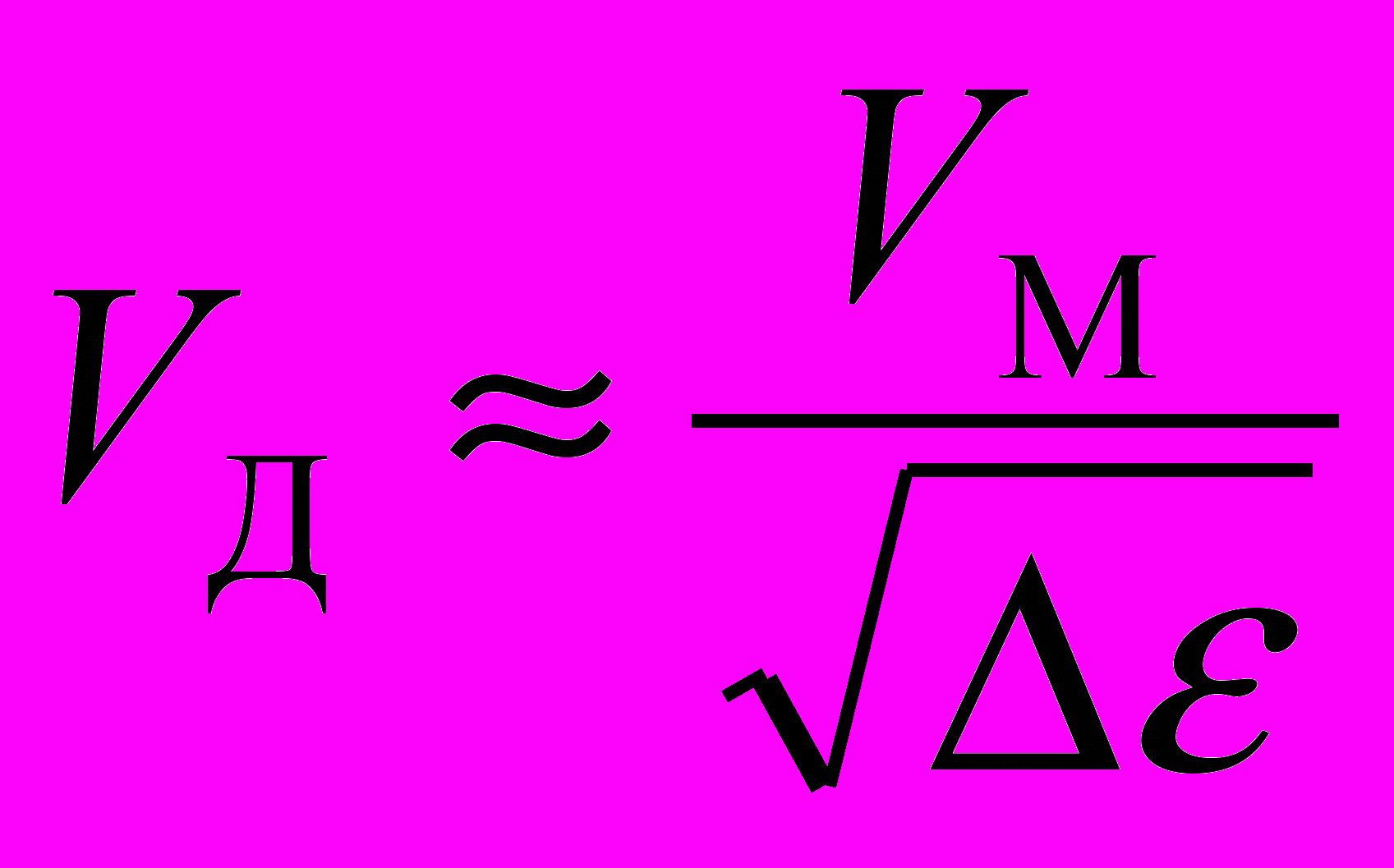. (15)

Использование правильной теоретической модели (12), учитывающий зависимость от , избавило меня от фатальной ошибки, в результате которой "эфирный ветер" оказывается незамеченным. Рассчитанная из экспериментальной кривой по формуле

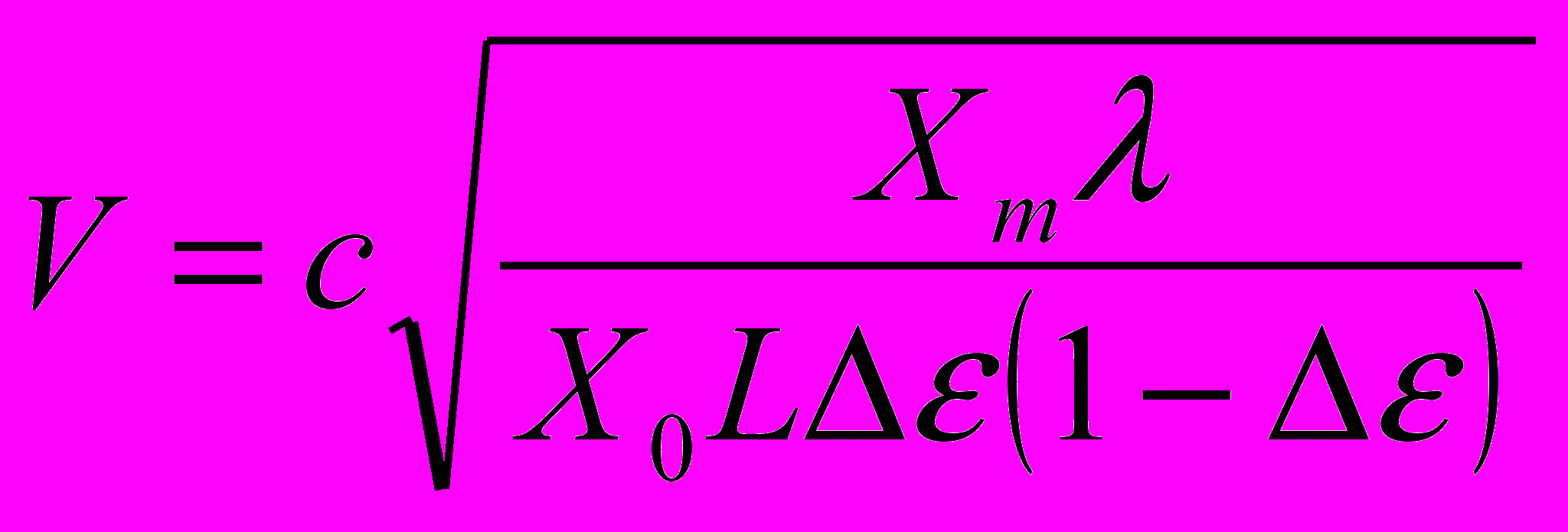, (16)

являющейся следствием формулы (12), абсолютная скорость Земли, в разное время суток в горизонтальной плоскости в г. Обнинске оказалась равной 150–500 км/сек.

Успех обнаружения абсолютного движения Земли относительно неподвижного эфира в моих опытах достигнут благодаря следующим инновационным моментам, определившим прорыв в трех основных направлениях:

- осознание того, что подвижной инерциальной системой в опытах типа Майкельсона является часть светоносной среды, проявляющая себя через поляризационный вклад  частиц в полную проницаемость светоноса =1+; это позволило правильно учесть относительность эффекта лоренцева сокращения плеча интерферометра;

- повышение чувствительности интерферометра к эфиру в сотни раз, по сравнению с прибором Майкельсона (фактически мной создан новый прибор для детектирования реакций эфира);

- переосмысление физической природы всех наблюдаемых эффектов в известных экспериментах электродинамики подвижных сред (от опытов Физо 1852-го года до моих, суммарно представленных на рис.1).

Полученные экспериментальные результаты и их теоретическая интерпретация указывают на конвенциональный характер специальной теории относительности, обусловленный искусственным распространением (расширением) аддитивного правила сложения скоростей (с_=cV) инертных тел на электромагнитные волны. По сути, специальная теория относительности оказывается артефактом этого расширения.


Литература


[1] A.A.Michelson. The relative motion of the Earth and the luminiferous aether, Am.J.Sci., ser.3, v.22, pp.120-129 (1881).

[2] A.A.Michelson, E.W.Morley. The relative motion of the Earth and the luminiferous aether, Am.J.Sci., ser.3, v.34, pp.333-345 (1887).

[3] В.В. Демьянов. Нераскрытая тайна великой теории, Новороссийск: МГА им. адм.Ф.Ф.Ушакова, РИО, 1-е издание 2005, 174 с.; 2-е издание 2009, 330 с.

[4] A.Drezet. The physical origin of the Fresnel drag of light by a moving dielectric medium, Eur.Phys.J. B, v.45, No 1, pp. 103-110 (2005).

[5] R. T. Cahill and Kirsty Kitto. Michelson-Morley Experiments Revisited and the Cosmic Background Radiation Preferred Frame, Apeiron, v.10, No 2, pp.104-117 (2003).

[6] D.C.Miller. Significance of the ether-drift experiment of 1925 at Mount Wilson, Science, v.68, No 1635, pp.433-443 (1926).

[7] J.Shamir, R.Fox. A new experimental test of special relativity, Nuovo Cim., v.62, No 2, pp.258-264 (1969).