Министерство образования Российской Федерации Казанский государственный технологический университет
| Вид материала | Документы |
| Ю.П.Козлов ВВЕДЕНИЕ Развитие гипотезы ломоносова Законы изменения частоты гравитационных полей вблизи тел |
- Дорогие коллеги!, 49.43kb.
- Формирование корпоративной компетенции студентов технического вуза в процессе внеучебной, 347.09kb.
- Российской Федерации Министерство образования и науки Российской Федерации Государственный, 343.55kb.
- Министерство образования и науки российской федерации южно-уральский государственный, 1544.17kb.
- Российской Федерации Министерство общего и профессионального образования Российской, 41.11kb.
- Министерство образования и науки российской федерации филиал федерального государственного, 24.82kb.
- Конкурс 2 «утверждаю», 3402.5kb.
- Программа 1-3 октября 2003 года Москва Организаторы и спонсоры Министерство образования, 141.3kb.
- Российской Федерации Читинский государственный университет иппк рабочая программа, 177.68kb.
- Рассматриваемые вопросы: Создание единого образовательного пространства «вуз-школа», 82.56kb.
Непреодолимое желание познать истину я стремился перенять у Ломоносова, метод научного познания природы – у Ньютона и Максвелла, упорство в эмпирических исследованиях – у Кеплера и Менделеева, широту и глубину мышления – у Толстого и Достоевского, краткость и выразительность слога – у Пушкина.
Я давно хотел создать труд, достойный моих учителей.
Ю.П.Козлов
ВВЕДЕНИЕ
В 1687 году вышел из печати труд Ньютона «Математические начала натуральной философии» /1/, в котором дается формулировка открытого им закона тяготения: сила притяжения между материальными частицами прямо пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Аналитическое выражение закона всемирного тяготения Ньютона записывается в виде:
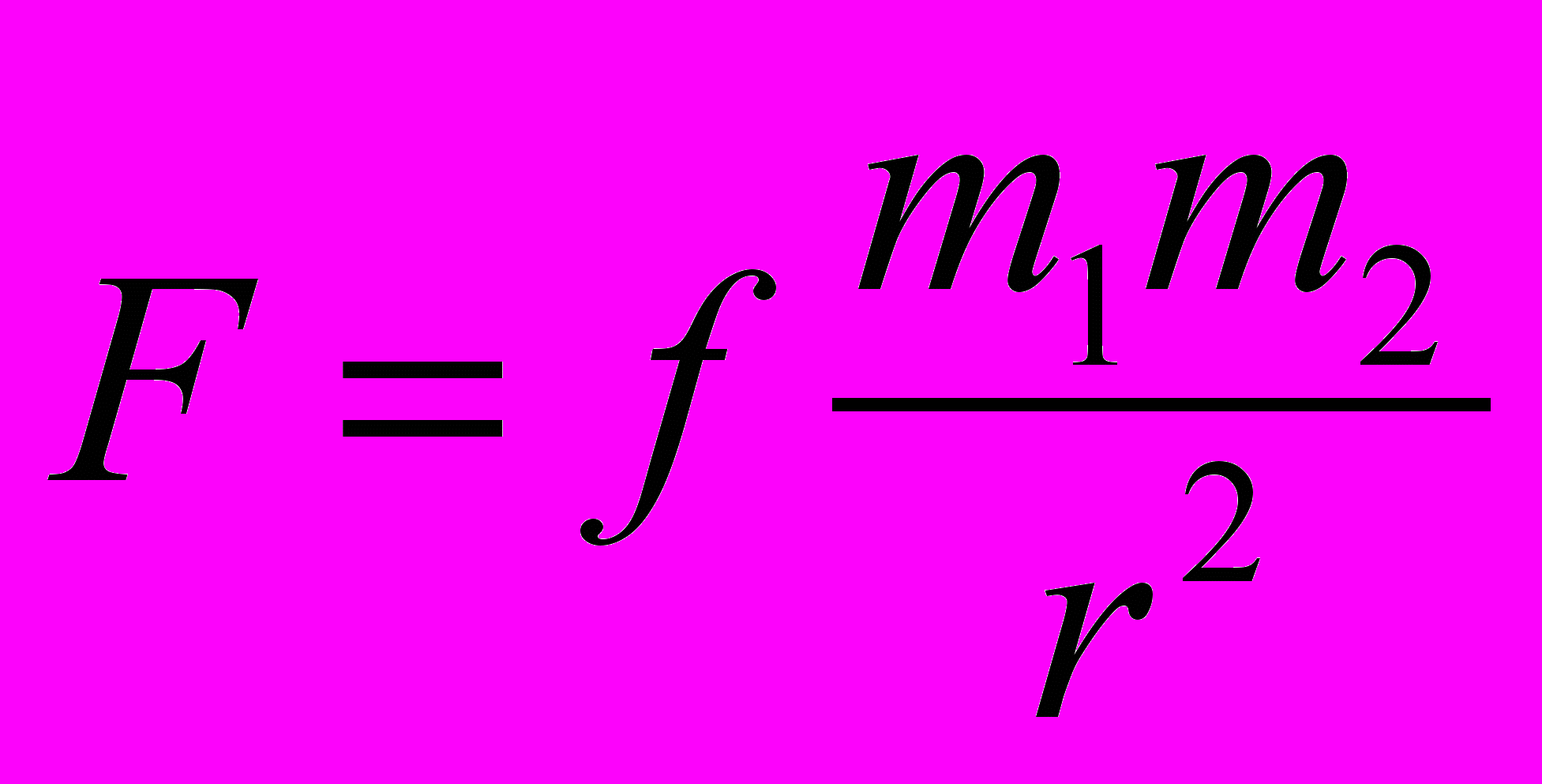 , (1)
, (1)где f – постоянная тяготения или гравитационная постоянная; m1, m2 – притягивающиеся массы; r – расстояние между частицами.
Из формулы (1) следует вывод о том, что гравитационная постоянная является величиной абсолютной, т.е. не зависящей от метода и места ее определения и вообще от каких-либо факторов.
В 1959-1961 годах на основании развития гипотезы Ломоносова о природе тяготения /2/ и эмпирических исследований результатов наблюдений и экспериментов, накопленных учеными к этому времени, нами была установлена новая, ранее неизвестная взаимосвязь между величиной ускорения силы тяжести на планетах, их объемом (массой) и расстоянием до Солнца, из которой следовал вывод о том, что гравитационная постоянная – имеет индивидуальное численное значение для каждой планеты и скачкообразно изменяется от одной планеты к другой. Соответственно было дано новое аналитическое выражение закона тяготения и его формулировка, а именно:
 , (2)
, (2)где а’ – постоянные величины; nA – частота гравитационного поля, в котором находится частица А; mА, mВ – массы притягивающихся частиц А и В; r – расстояние между частицами А и В.
В общем случае величина nA является переменной. Смысл формулы (2) можно выразить так: частица А притягивает к себе частицу В с силой, величина которой в данный момент прямо пропорциональна произведению масс частиц, частоте в данный момент гравитационного поля, в котором находится частица А (частоте nA гравитационного колебания ядер атомов частицы А), и обратно пропорциональна квадрату расстояния между частицами. Для установления силы притяжения, с которой частица В притягивает частицу А, в формуле (2) необходимо изменить соответственно индексы:
 , (3)
, (3)где nВ – частота гравитационного поля, в котором находится частица В.
На основании формул (2) и (3) можно сказать о том, что если частицы А и В находятся в гравитационных полях с различными характеристиками (nА nВ), то сила притяжения частицы В к частице А не равна силе притяжения частицы А к частице В (FA FB), т.е. третий постулат Ньютона в общем случае в явлении тяготения не применим, во всяком случае в той форме, в которой он сформулирован Ньютоном.
Гравитационная постоянная Ньютона имеет индивидуальное численное значение для каждой частицы и равна:
 , (4)
, (4)где nX – частота гравитационного поля. в котором находится притягивающая частица. Частота гравитационного поля Солнца изменяется плавно с изменением расстояния от его центра, а гравитационная постоянная для планет изменяется скачкообразно. Это значит, что не все значения частоты гравитационного поля Солнца могут удовлетворять формуле (4), а только те (и, следовательно, только на определенных расстояниях от Солнца), которые удовлетворяют существующей закономерности скачкообразного изменения гравитационной постоянной Ньютона. Видимо, только на этих расстояниях от Солнца в процессе эволюции смогли образоваться планеты.
Первое сообщение о том, что нами эмпирическим путем установлена новая закономерность в Солнечной системе, было отправлено в 1961 г. в Министерство высшего, среднего и специального образования РСФСР под названием «Всемирный закон тяготения на основе развития гипотезы Ломоносова о природе тяготения». Имеющиеся на сегодняшний день публикации по рассматриваемому вопросу в различных журнальных изданиях отмечены в приложении 2.
Несмотря на то, что после опубликования первой статьи прошло уже более 40 лет, работа в целом не получила ни желаемого распространения, ни должного признания, причинами чему, очевидно, являются, во-первых, необходимость для окончательного заключения о формулировке закона тяготения постановки специального эксперимента во внеземных условиях, во-вторых, очень большой авторитет Ньютона и увлеченность физиков-теоретиков общей теорией относительности, что мешает убедительно обосновать необходимость постановки эксперимента во внеземных условиях. Дело в том, что общая теория относительности остается хотя и строгой и последовательной, но недоказанной и насколько правильно она отображает реально существующий физический мир говорить пока преждевременно, а близкая сходимость результатов вычислений по формулам общей теории относительности и формулам Ньютона для сравнительно небольших скоростей и слабых гравитационных полей не является доказательством справедливости ни тех, ни других формул, тем более что до сего времени не проверена сама фундаментальная основа всех формул и всех теорий - зависимость численного значения гравитационной постоянной от места ее определения в космосе.
Каждый период развития естествознания выдвигает свои задачи перед человечеством, связанные с его трудовой деятельностью. В настоящее время наступил период освоения космоса, в который уже недостаточно мыслить категориями прежних постулатов и принципов; необходимо знать истинную среднюю плотность планет, осмыслить что такое «инерция», представить механизм движения частиц в пространстве и тем самым ответить на вопрос, Что такое энергия? Кроме этого вопрос будущего будет заключаться также в том, как зависят все свойства веществ (химические, физические, механические) от характеристик гравитационного поля, в котором эти вещества находятся. Неизбежно возникает проблема и о том, как влияют характеристики гравитационного поля на генную и имунную системы, на здоровье, продолжительность жизни и вообще возможность иметь потомство живых организмов в иных, чем на Земле, гравитационных полях. Все отмеченные вопросы взаимосвязаны. В настоящей работе делается попытка начать их изучение на основе установленных нами новых закономерностей.
РАЗВИТИЕ ГИПОТЕЗЫ ЛОМОНОСОВА
Открытый Ньютоном закон тяготения выдвинул перед наукой вопрос о вскрытии физической природы тяготения. Первым, кто попытался объяснить явление тяготения, был Ломоносов /2/. Полученные нами результаты исследования позволяют сказать, что идея Ломоносова в общем виде, как она была сформулирована им, призвана занять ведущее положение в науке. Гипотеза Ломоносова о том, что явление тяготения есть результат «…. приталкивания» тел друг к другу «ультракосмическими»
корпускулами, заполняющими мировое пространство, в работах последующих ученых приняла несколько иную модификацию, согласно которой ультракосмические частицы заменяются весьма жесткой и проникающей электромагнитной волновой радиацией.
В качестве дальнейшего развития гипотезы Ломоносова допустим, что ускорение тела, вызванное тяготением, пропорционально градиенту частоты гравитационного поля:
 , (5)
, (5)где а – коэффициент пропорциональности, постоянный для всех тел;
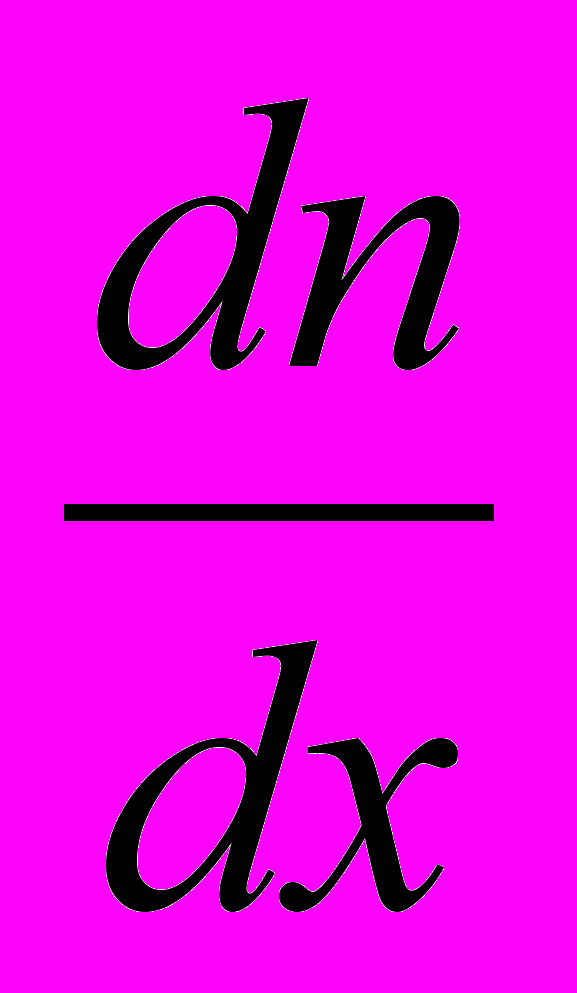 - градиент частоты. Ниже приводится конкретная форма этого выражения.
- градиент частоты. Ниже приводится конкретная форма этого выражения.ЗАКОНЫ ИЗМЕНЕНИЯ ЧАСТОТЫ ГРАВИТАЦИОННЫХ ПОЛЕЙ ВБЛИЗИ ТЕЛ
Эмпирические исследования результатов экспериментов и результатов наблюдений объектов Солнечной системы, накопленные учеными к настоящему времени, а также расчет ускорений силы тяжести на планетах по формуле (5) показывают, что частота гравитационного поля, в котором находится тело, уменьшается до нуля в центре тела по закону:
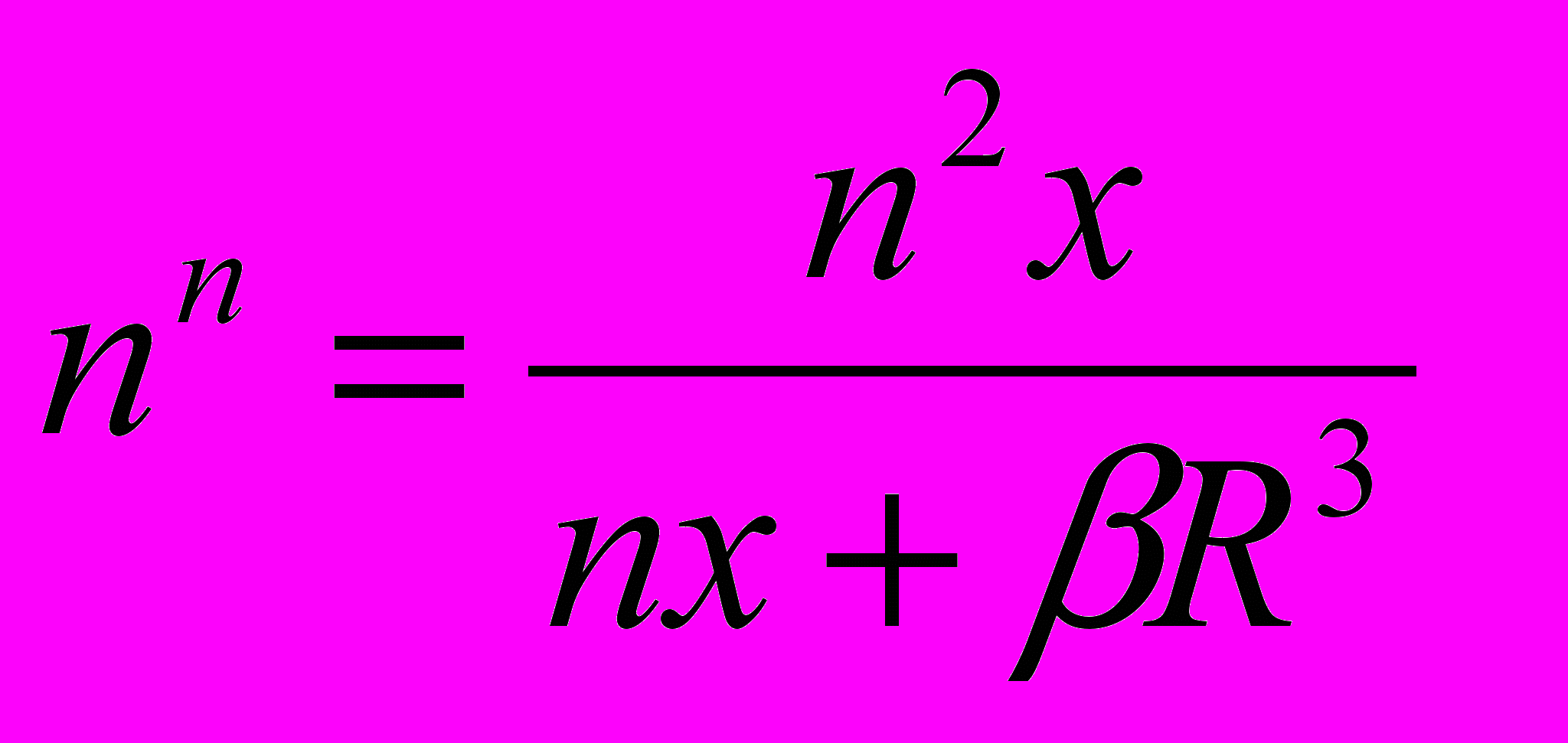 , (6)
, (6)который графически отображает кривая 1 (рисунок). Из тела как бы “выходит” гравитационное поле, частота которого уменьшается с увеличением растояния (х) от центра тела по закону:
 , (7)
, (7)который графически отображает кривая 2. В формулах (6) и (7)
n – частота гравитационного поля, в котором находится тело; R – радиус сферического тела; , - постоянные величины.

Расположение планет относительно «активного» (2) и «пассивного» (1) гравитационных полей Солнца (масштаб не соблюден)
Одно из свойств гравитационного поля, изменение частоты которого (nn) отображает кривая 1, заключается в том, что в нем существует градиент частоты, но оно не вызывает ускорения тел, находящихся в нем, согласно формуле (5), и поэтому его можно назвать «пассивным» гравитационным полем.
В отличие от «пассивного», гравитационное поле, изменение частоты которого (nа) характеризует кривая 2, можно назвать “активным” гравитационным полем, так как наблюдаемый в нем градиент частоты вызывает ускорение тел, находящихся в нем, согласно формуле (5), к центру тела, которое образовало это поле.
Величина ускорения к телу равна
 . (8)
. (8)Градиент частоты “активного” гравитационного поля равен
 . (9)
. (9)На основании изложенного произведен расчет Солнечной системы. Если через nг обозначить частоту гравитационного поля Галактики в том месте, в котором находится в настоящее время Солнце, то частота «активного» поля Солнца (nca) на расстоянии х от центра последнего равна
 , (10)
, (10)где Rс – радиус конденсированной части Солнца.
Частота «пассивного» гравитационного поля Солнца равна
 . (11)
. (11)Ускорение тел к Солнцу на расстоянии х равно
 . (12)
. (12)На рисунке показано расположение планет относительно обоих гравитационных полей Солнца.
Для планет (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн), находящихся в области, в которой максимальным полем (гравитационное поле, имеющее в данной точке пространства максимальную частоту по сравнению с другими полями) является “активное” гравитационное поле Солнца, ускорение на расстоянии x от центра планеты равно
 , (13)
, (13)где nса – частота «активного» поля Солнца на расстоянии, равном радиусу орбиты планеты; Rорб.пл. – радиус орбиты планеты.
Для планет (Уран, Нептун, Плутон), находящихся в области, в которой максимальным полем является «пассивное» поле Солнца, ускорение на расстоянии х от центра планеты равно
 , (14)
, (14)где nсn - частота «пассивного» поля Солнца на расстоянии, равном радиусу орбиты планеты.
Установлены следующие значения постоянных:
nг = 2,8531019 с-1, а = 5,7710-11 м2с-1,
= 1,7410-15 м-2, = 1,475107 м-2с-1,
Rс3 = 46,11024 м3, т.е. Rс = 3,59108 м.
Вычисленные значения ускорений по формулам (12), (13) и (14) помещены в таблице (для сравнения приведены литературные данные).
Ускорение силы тяжести на поверхности Плутона по закону Ньютона равно
 мс-2.
мс-2.Здесь приведен обратный расчет, поскольку у Плутона имеется спутник и величина ускорения силы тяжести для него была определена по кинетическому закону
 ,
,где v – скорость движения Харона по орбите; Rх – радиус орбиты. Потом уже вычислена масса.
Ускорение на поверхности Плутона по эмпирической формуле (14) равно
 мс-2.
мс-2.Сходимость результатов вычислений и наблюдений вполне удовлетворительная. Таким образом, кроме Меркурия и Венеры, все планеты и Солнце подчиняются общему правилу, заключающемуся в том, что величина ускорения силы тяжести для них является величиной пропорциональной кубу радиуса конденсированной части планеты.
Расстояние, на котором частоты “активного” и “пассивного” гравитационных полей равны, находится из условия
na = nn.
Поскольку х не может быть отрицательным, окончательно имеем
 . (15)
. (15)Для Солнца x0 = R0 = 1,421012 м.
Для планет значения x0 приведены в таблице.
| Параметры | Планета | |||||||||||
Мерку-рий | Вене- ра | Земля | Марс | Юпи- тер | Са- турн | Уран | Неп- тун | Плу- тон | Солнце | Луна | ||
| (видимая часть) | (конден- сирова-ная часть) | |||||||||||
| Вычисленное ускорение на планете по сравнению с 9,8 мс-2 | 0,96 | 1,31 | 1,00 | 0,35 | 2,15 | 0,96 | 0,80 | 1,14 | 0,068 | 27,9 | 115,0 | 0,165 |
| Наблюдаемое ускорение на планете по сравнению с 9,8 мс-2 | 0,415 | 0,904 | 1,00 | 0,392 | 2,52 | 1,05 | 0,95 | 1,134 | 0,073 | 27,9 | - | 0,165 |
| Частота гравитационного поля, в котором находится планета 1018с-1 | 39,0 | 21,0 | 15,33 | 9,90 | 3,00 | 1,61 | 3,00 | 4,50 | 6,00 | 28,55 | 109,55 | 9,30 |
| Среднее расстояние до Солнца, млн.км. | 58 | 108 | 150 | 228 | 778 | 1426 | 2869 | 4496 | 5900 | - | - | 0,3844 (до Земли) |
| Диаметр планеты в диаметрах Земли | 0,38 | 0,95 | 1,00 | 0,53 | 11,2 | 9,5 | 3,9 | 3,9 | 0,172 | 109,1 | 55,0 | 0,273 |
| Новое значение средней плотности планеты103 кгм-3 | 2,16 | 3,80 | 5,51 | 5,90 | 6,63 | 5,70 | 6,63 | 5,44 | 5,94 | 0,74 | 5,51 | 5,47 |
| х0 = R0 для планеты,м | 1,63105 | 5,57106 | 1,09107 | 2,26106 | 4,071010 | 3,321010 | 1,86109 | 1,17109 | 8,54104 | 1,421012 | 1.421012 | 2,78105 |
