Дремова

Вид материала

Литература

Содержание Идеальными объектами Квадрат, построенного на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Подобный материал:

• Л. А. Дрёмова "16" апреля 2012г. Расписание, 91.99kb.
• Владивостокский государственный медицинский университет, г. Владивосток  Устинова, 51.63kb.
• Меня зовут Дремова Елена Сергеевна, по образованию я экономист, 66.52kb.

Работу выполнила:

Буряк Анастасия

Ученица 6 класса

Новокиевской основной общеобразовательной школы


Руководитель:

Дремова

Татьяна Николаевна


С. Новокиевка 2009г.

План

1. Пифагор
   
2. Пифагоровы тройки
   
3. Таблица Пифагора
   
4. Теорема Пифагора
   
5. Литература
   

Пифагор


Родился на острове Самос около 580г. до н. э. Его отцом был некий Мнесарх из Самоса, человек благородного происхождения и образования. Спасаясь от тирании Поликрата, Пифагор около 530 до н. э. покинул Самос.

Историю его жизни трудно отделить от легенд, представляющих Пифагора в качестве полубога и чудотворца, совершенного мудреца и «великого посвященного» во все тайные доктрины греков и варваров. По предании., Пифагор объездил весь свет и собрал свою философию из различных систем, к которым имел доступ. Так, он изучал экзотические науки у брахманов Индии, астрономию и астрологию в Халдее и Египте. В Индии он и по сей день известен под именем Янваначарья («Ионийский учитель»). По возвращении он поселился в Кротоне, В Южной Италии, где проповедовал свое учение многочисленным последователям, часть которых образовала своего рода религиозный орден, или братство «посвященных». Этот орден фактически пришел в Кротоне к власти, однако из-за антипифагорейских настроений в конце VI в. до н. э. Пифагору пришлось удалиться в метапонт, где он умер в 500 году до н. э.

Пифагор стоял у истока греческой науки, был вынужден заниматься всем сразу: арифметикой и геометрией, астрономией и музыкой. Его целью было разобраться в строении Вселенной и человеческого общества (от движения звезд до политической борьбы).

Он первый заметил, что сила и единство науки основаны на работе с ИДЕАЛЬНЫМИ ОБЪЕКТАМИ. Например, прямая линия - это не тетива натянутого лука и не луч света: ведь они имеют небольшую толщину, а линия толщины не имеет. Несовершенные природные тела являются лишь грубоватым подобием идеальных математических сущностей

Первая научная модель мира, предложенная Пифагором - все природные тела и процессы суть искаженные подобия идеальных тел и движений - а закономерности идеальных объектов выражаются с помощью чисел.

«Числа правят миром через свойства геометрических фигур».

Пифагоровы тройки


Изучение свойств натуральных чисел привело пифагорейцев к еще одной «вечной» проблеме теоретической арифметики (теории чисел) – проблеме, ростки которой пробивались задолго до Пифагора в Древнем Египте и Древне Вавилоне, а общее решение не найдено и поныне. Начнем с задачи, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение

х² + у² = z² (1.1)

Сегодня эта задача именуется задачей Пифагора, а ее решения – тройки натуральных чисел, удовлетворяющих уравнению - (1.1) – называются пифагоровыми тройками. В силу очевидной связи теоремы Пифагора с задачей Пифагора последней можно дать геометрическую формулировку: найти все прямоугольные треугольники с целочисленными катетами х, у и целочисленной гипотенузой z.

Частные решения задачи Пифагора были известны в глубокой древности. В папирусе времен фараона Аменемхета I (ок. 2000 г. до н. э .), хранящемся в Египетском музее в Берлине, мы находим прямоугольный треугольник соотношением сторон 3 : 4 : 5 (3² + 4² = 5²). По мнению крупнейшего немецкого историка, математика М. Кантора (1829 - 1920), в Древнем Египте существовала особая профессия гарпедонаптов – «натягивателей веревок», которые во время храмов и пирамид различали прямые углы с помощью веревки, имеющей 12 (= 3 + 4 + 5) равноотстоящих узлов.

Надо сказать, что с Кантором категорически не согласен другой знаток древней математики – Ван дер Варден, хотя сами пропорции древнеегипетской архитектуры свидетельствуют в пользу Кантора. Как бы то ни было, сегодня прямоугольник с отношением сторон 3 : 4 : 5 называется египетским.

Сохранилась глиняная табличка, относящаяся к древневавилонской эпохе и содержащая 15 строк пифагорских троек. Помимо тривиальной тройки получаемой египетской (3, 4, 5) умножениями на 15 (45, 60, 75), здесь есть и весьма сложные пифагоровы тройки, такие, как (3367, 3456, 4825), и даже (12709, 13500, 18541)! Нет ни каких сомнений, что эти числа были найдены не простым перебором, а неким единым правилом.

Таблица Пифагора


Учение о правилах действия над числами у пифагорейцев называлось логистикой. В состав логистики входили арифметические действия с натуральными числами вплоть до извлечения квадратных и кубических корней, действия с дробями, техника вычислений на счетной доске. Хотя задачи вычислительной арифметики отвечали насущным потребностям жизни – торговле, строительству, расчету метательных орудий, логистика (искусство вычислять) по сравнению с арифмети (наукой о числах) считалась пифагорейцами наукой второго сорта и развивалась весьма слабо.

Как и в теоретической арифметике, числа камешки играли в логистике значительную роль. Они успешно использовались в первой в истории человечества «вычислительной машине» - абаке. Абак выглядел просто: это разлинованная плита, в каждой колонке которой камешки имели разные значения: единицы, десятки, сотни и т. д.

Но подсчитанные числа необходимо было запомнить, лучше записать. Так появляется письменное фиксирование чисел – нумерация, а затем и письменный счет.

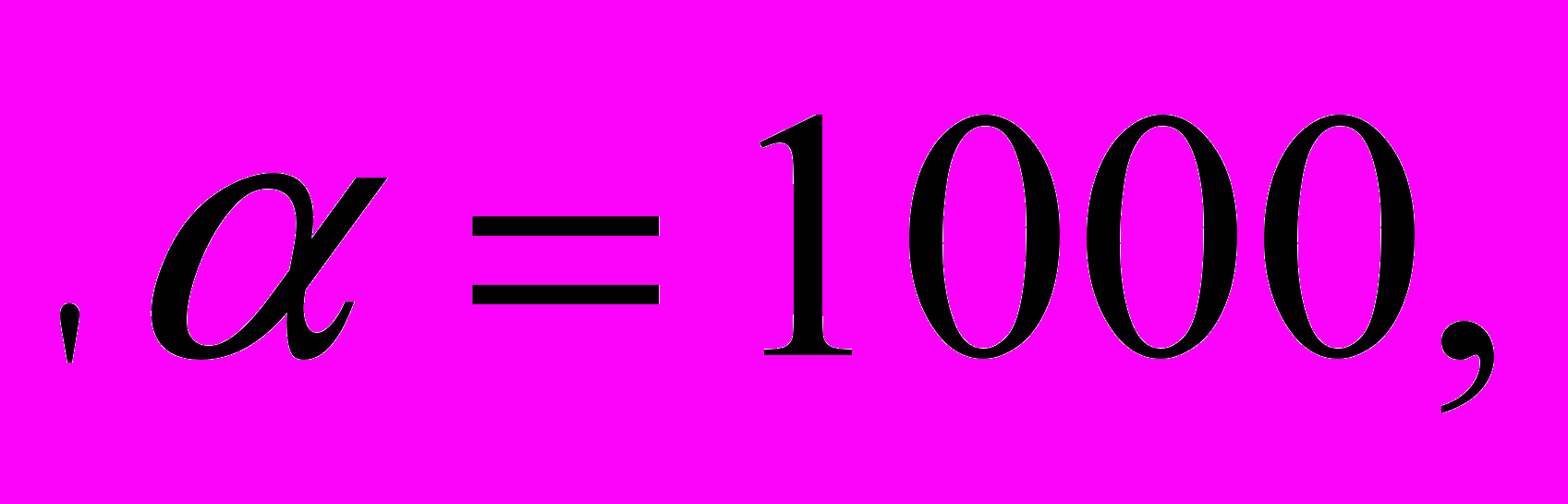
Для обозначения тысяч применялся штрих слева внизу буквы, например 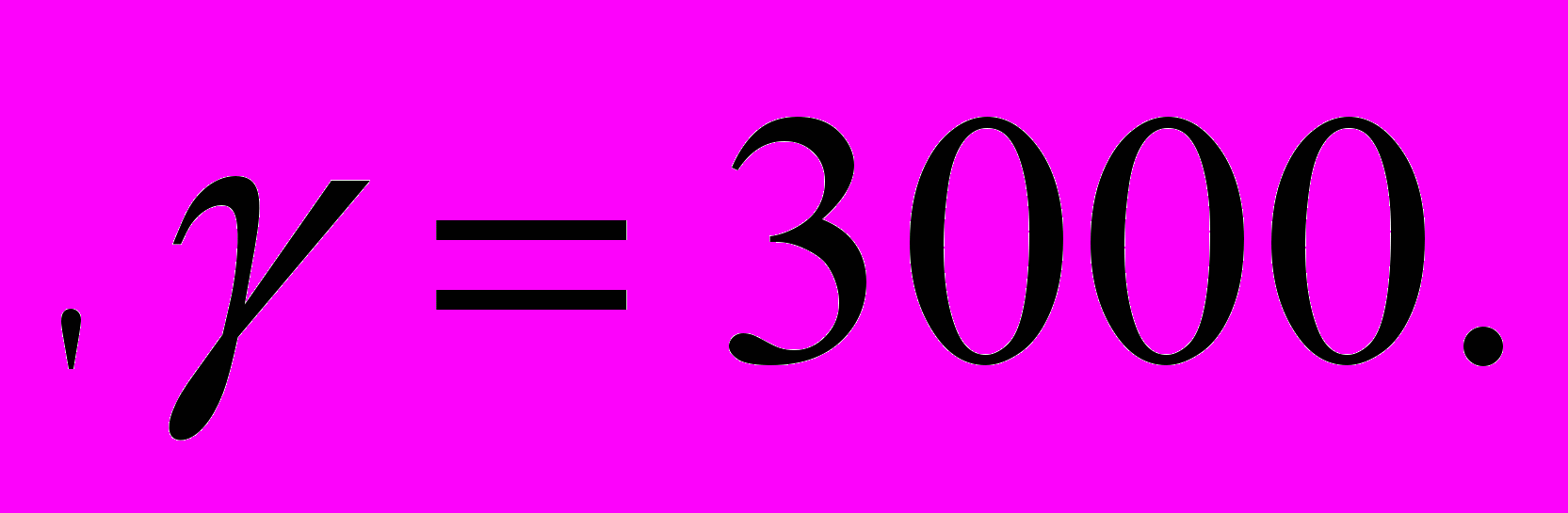Десятки тысяч обозначались знаком М с соответствующей буквой сверху, например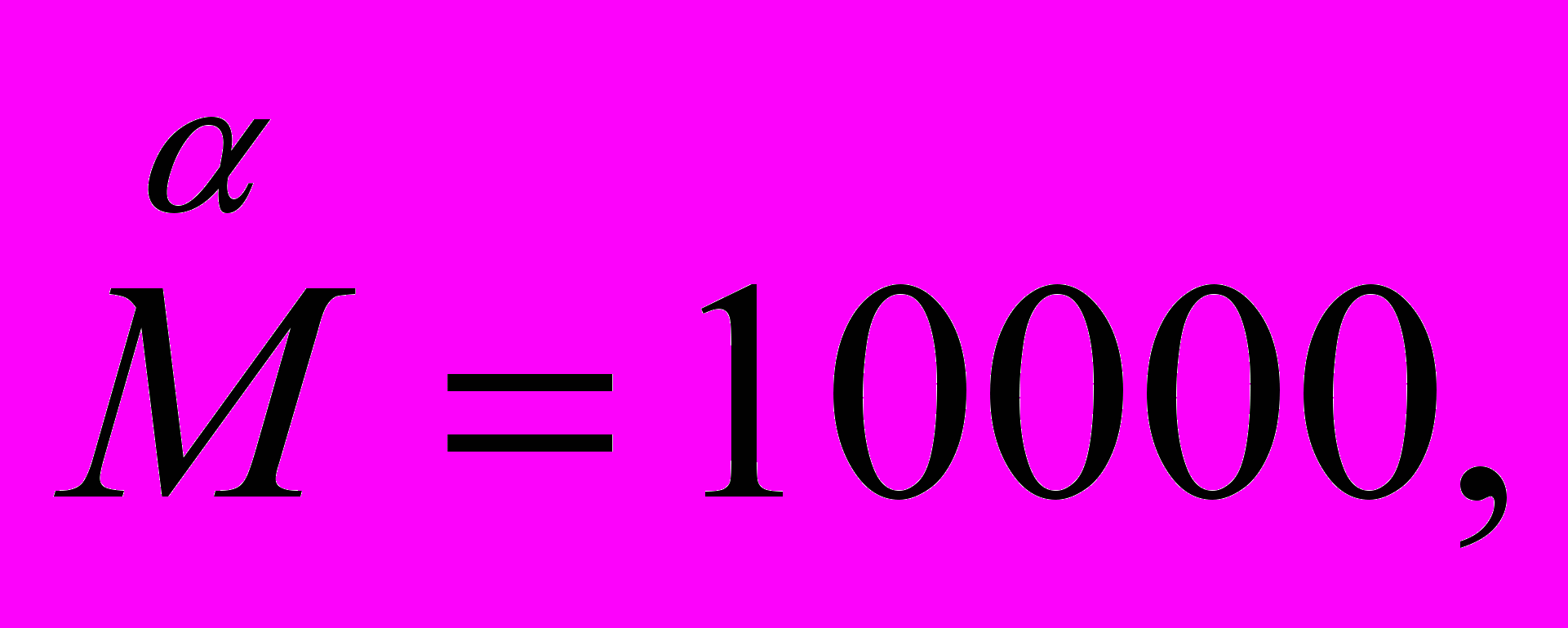

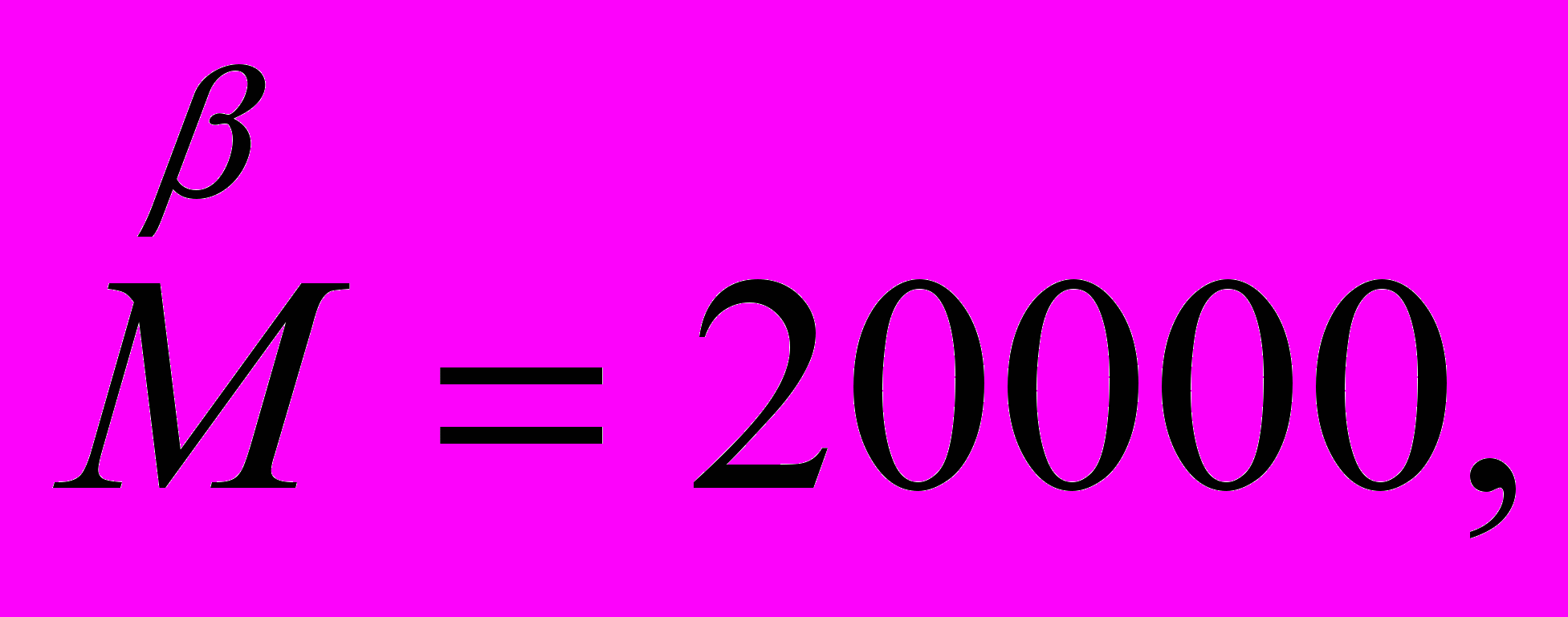
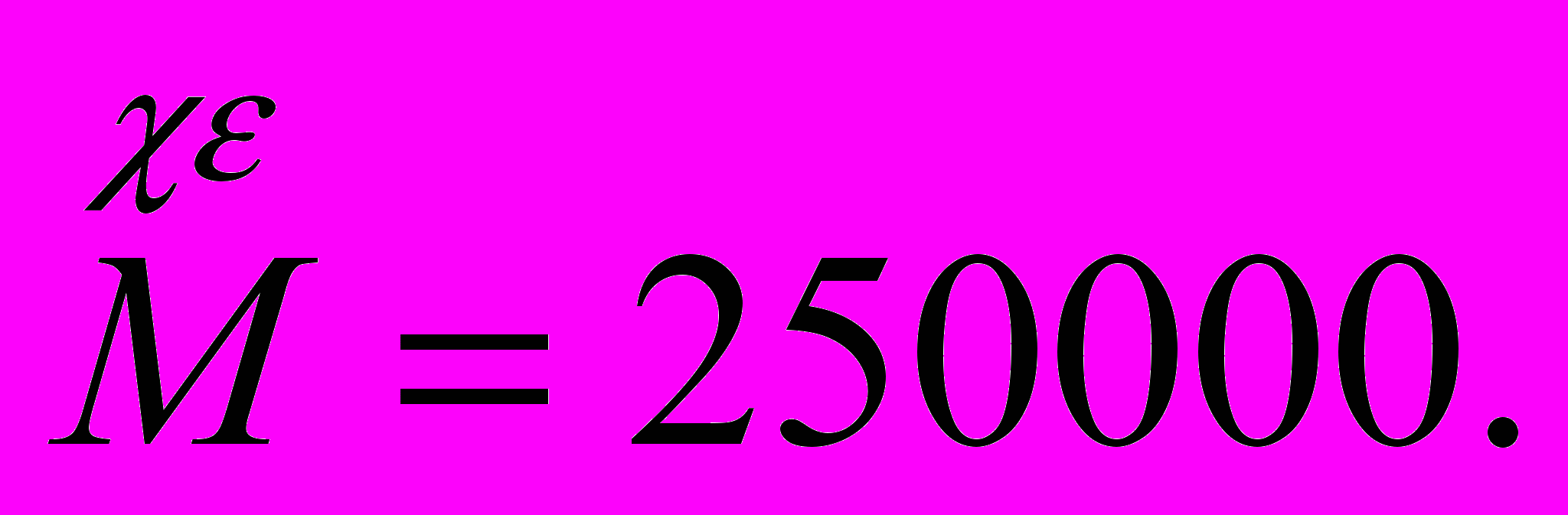
Для вычисления промежуточных результатов составлялись таблицы умножения.

Таблицу Пифагора нашли в сочинении «Введение в арифметику» непифагорейца Никомаха Геразского (I – II вв.)

Перед нами таблица Пифагора:



Таблица умножения таблица Пифагора стала эффективной лишь с изобретением десятичной позиционной системы счисления, когда все умножение свелось к умножению целых чисел от 1 до 9. Скорее всего таблица Пифагора была задумана не как таблица умножения, а как таблица, иллюстрирующая свойство пропорциональности чисел.

Теорема Пифагора


Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» - квадрате гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота – красота – значимость.

И хотя сегодня теорема Пифагора обнаружена в различных частных задачах и чертежах: и в египетском треугольнике в папирусе времен фараона Аменемхета I (ок. 2000 до н. э.), и в вавилонских клинописных табличках эпохи царя Хаммурапи (XVIII в. до н. э.), и в древнейшем китайском трактате «Чжоу – би щань цзинь» («Математический трактат о гномоне»), время создания которого точно не известно, но где утверждается, что в XII в. до н. э. китайцы знали свойства египетского треугольника, а к VI в. до н. э. и общий вид теоремы, и в древнеиндийском геометрическо - теологическом трактате VII – V вв. до н. э. «Сульва сутра» («Правила веревки»), - несмотря на все это, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадется.

Сегодня принято считать, что Пифагор дал первое доказательство носящей его имя теоремы. Увы, от этого доказательства также не сохранилось никаких следов. Поэтому нам ничего не остается, как рассматривать некоторые классические доказательства теоремы Пифагора (древнекитайское, древнеиндийское, доказательство Евклида, доказательство Аннариция).

Т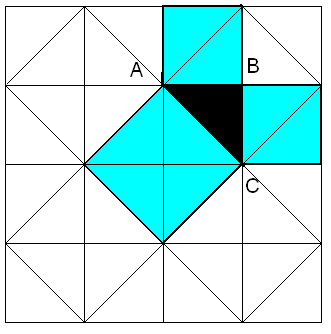еорема Пифагора. Квадрат, построенного на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах.

Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и началась теорема. В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для треугольника АВС: квадрат, построенный на гипотенузе АС содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.


Литература

1. Волошинов А. В. Пифагор: союз истины, добра и красоты. – М.: Просвещение, 1993.
   
2. Математика в школе. № 7, 2005г.