Geum.ru

Космологическая модель без сингулярностей

Вид материалаДокументы
Подобный материал:
Космологическая модель без сингулярностей


Мы исходим в своих исследованиях из предположения Эйнштейна о том, что в единой физической теории вообще не должно быть сингулярностей, а особое состояние в начале эволюции нестационарных моделей есть проявление ограниченности общей теории относительности. Мы далеки от мнения современных космологов-релятивистов, согласно которому сингулярность описывает реальное физическое состояние, с которого началась эволюция Вселенной.




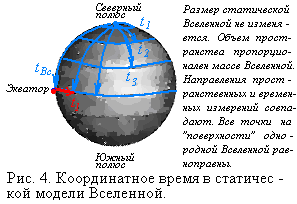
На рисунке 4 координатное время характеризует изменение радиуса кривизны пространства статической модели Вселенной. Здесь любая точка пространственно-временного направ-ления соответствует не определенной стадии расширения Вселенной, а времени, необходимому свету для прохождения от данной точки до точки наблюдения. Если исходить из единства гравитационного и электромагнитного поля и их связи с материей (веществом), тогда этой пространственно-временной диаграмме можно дать следующее объяснение.

Все вещество во Вселенной образует единое электромагнитное (или гравитационное) поле. Поскольку любой наблюдатель может наблюдать лишь половину Вселенной, условно говоря, лишь ту часть Вселенной, которая расположена между Северным или Южным полюсами и экватором. Когда наблюдатель «заглядывает» все дальше и дальше, охватывая, в конце концов, всю Вселенную вплоть до горизонта видимости, он взаимодействует со всей наблюдаемой массой Вселенной, с ее общим гравитационным полем. Если в качестве наблюдателя взять стабильную элементарную частицу (например, ядро атома водорода – протон), то так называемое сингулярное состояние вещества представляет собой всю массу Вселенной, втиснутую в пространство, занимаемое одной элементарной частицей. Поскольку отношение массы частицы к занимаемой ею поверхности Вселенной равно 1 кг/м² (Все пояснения можно найти в. разделе «Волновое пространство»), то плотность сингулярного состояния равна

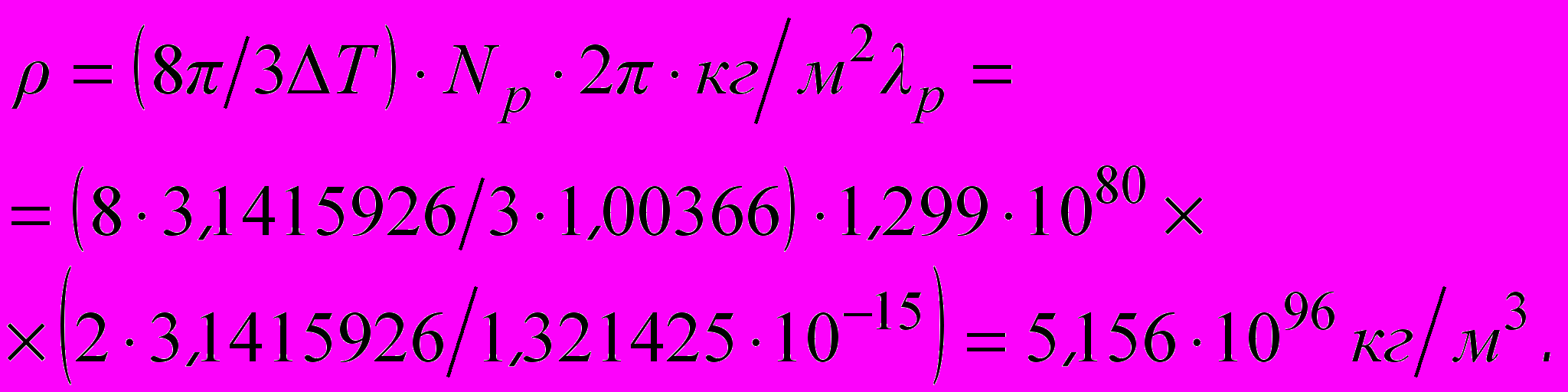(1.)

Используя полученные нами в разделе «Волновое пространство» соотношения, уравнение (1) можно представить в виде

(2)

Для преобразования уравнения (1) можно также использовать полученное нами соотношение для сечения томсоновского рассеяния свободными нерелятивистскими электронами:

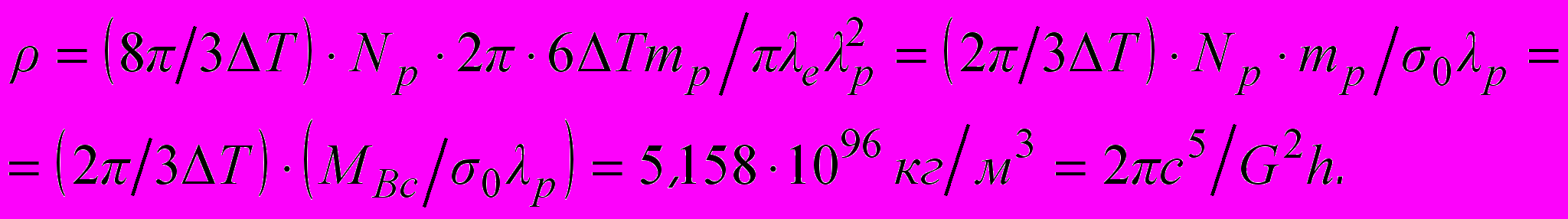(3)

Таким образом, коэффициент пропорциональности в законе всемирного тяготения Ньютона (гравитационная постоянная) определяется отношением мощности гравитационного излучения Вселенной (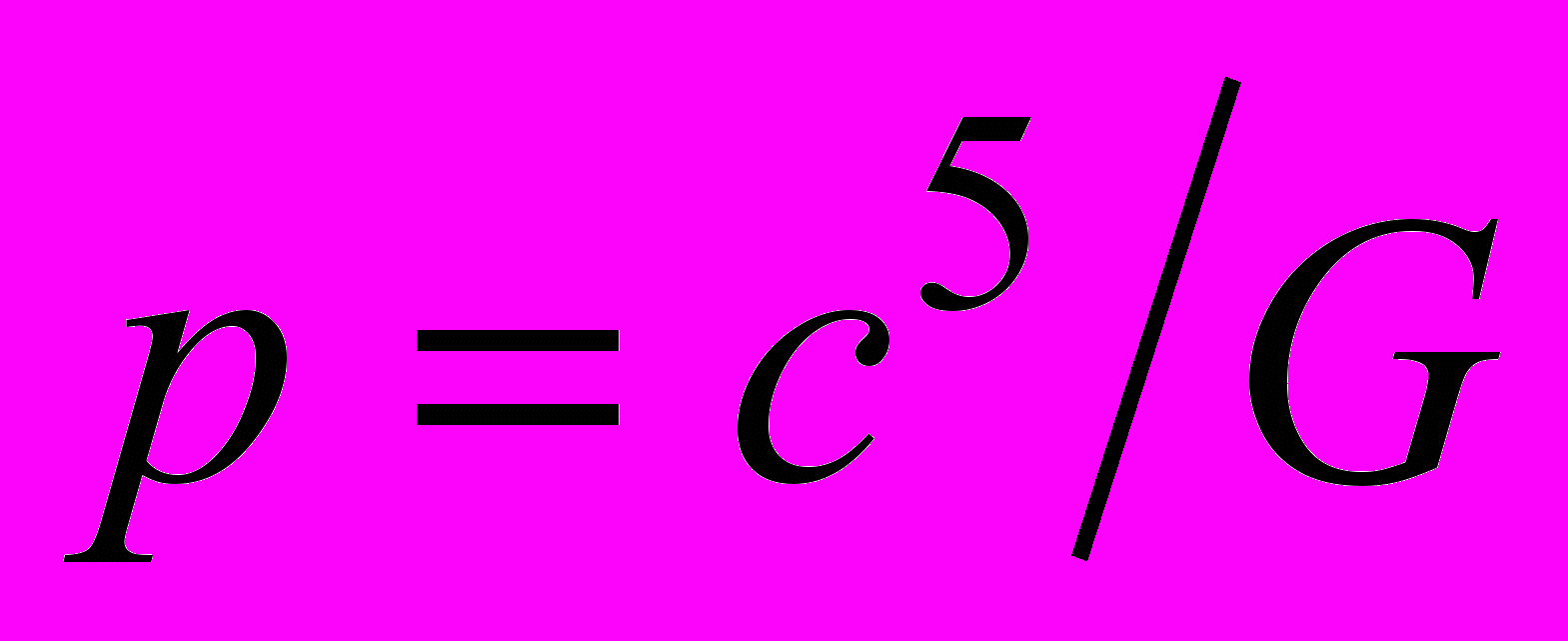, отнесенную к единице массы), к постоянной Планка:

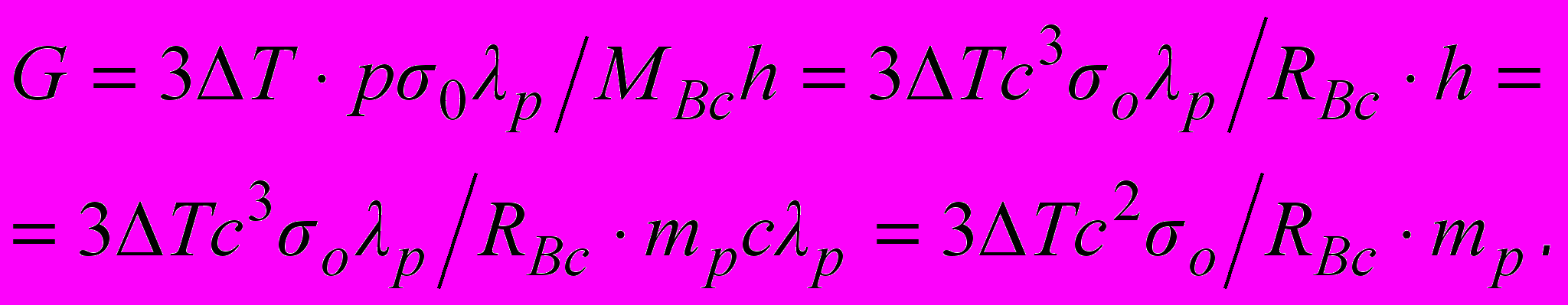(4)

Заменив величину ускорения 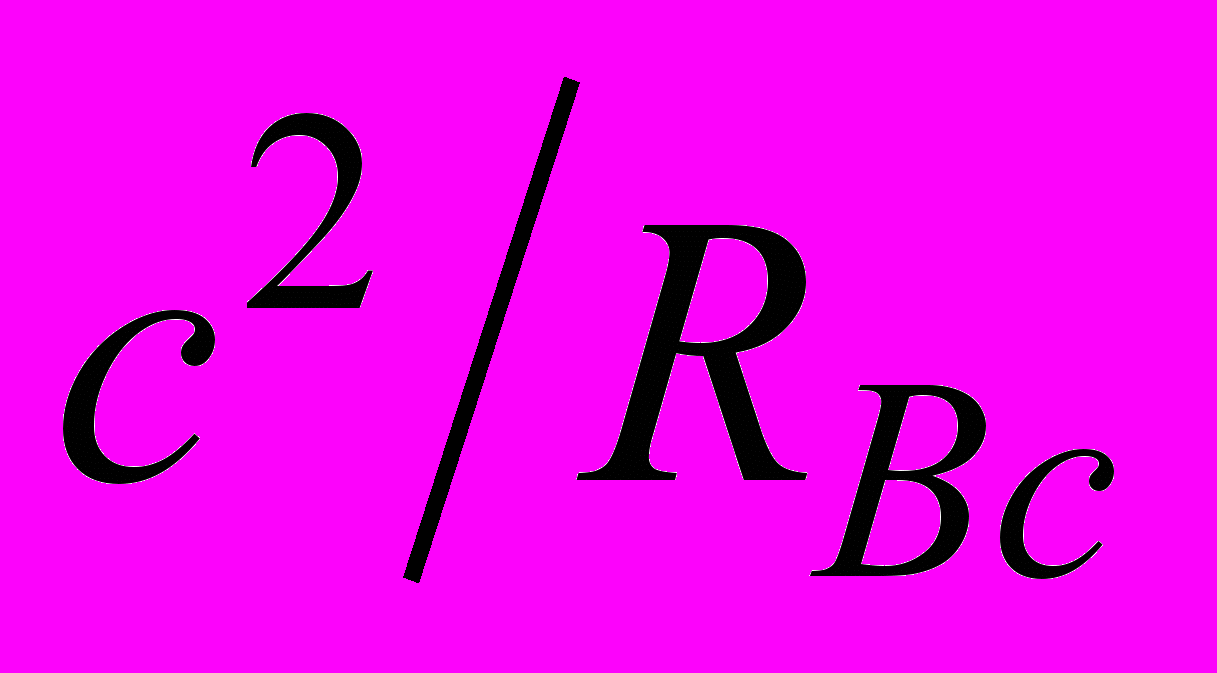на 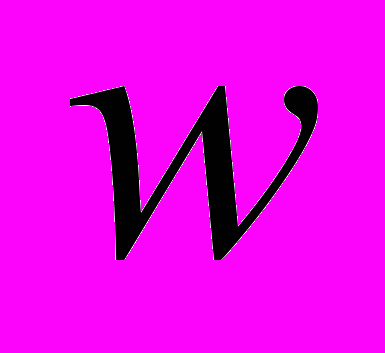, получаем:

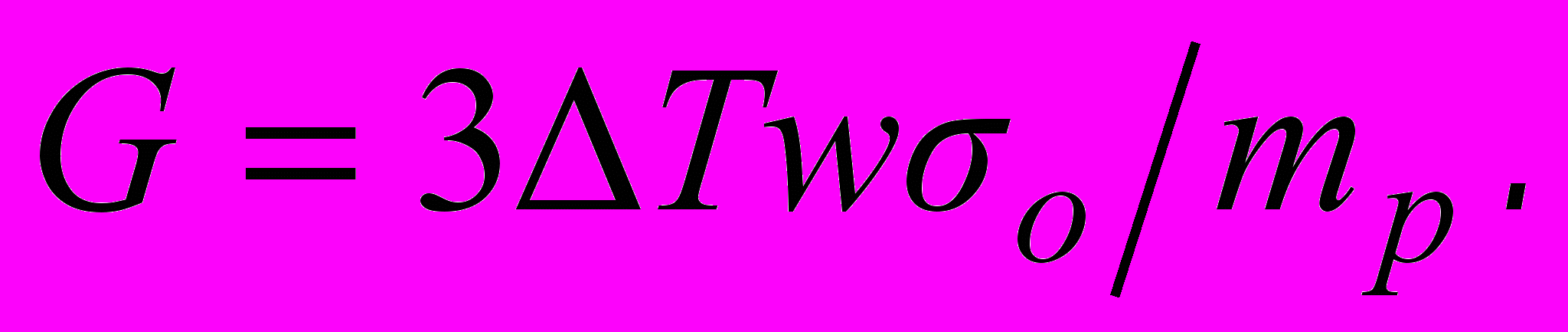(5)

Поскольку радиус статической Вселенной определяется соотношением 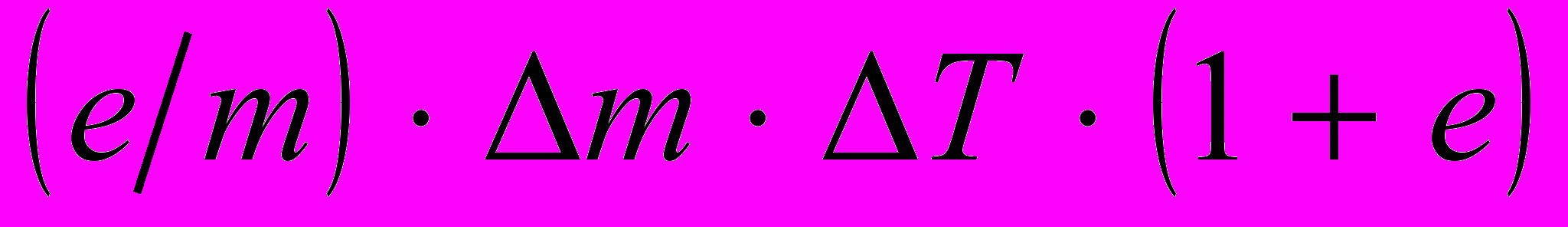, то выражение (4) можно записать в следующем виде:

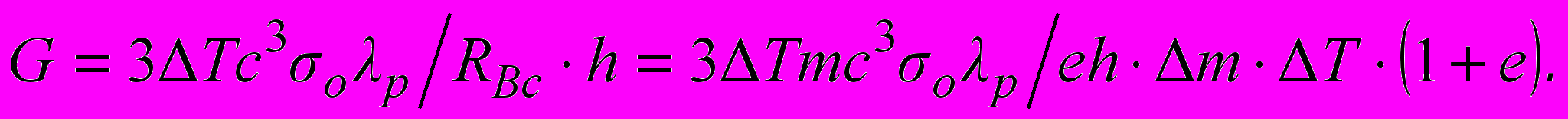(6)

Магнитный момент электрона (магнетон Бора) равен , следовательно, выражение (6) можно представить в виде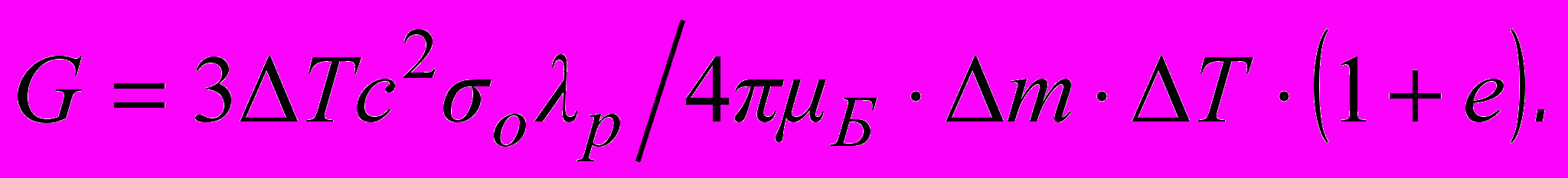

(7)

Таким образом, магнитный момент электрона имеет гравитационную по своей сути природу.

Можно определить и поправку к величине гравитационной постоянной или массе ядра атома водорода, которая равна поправке к величине магнитного момента электрона 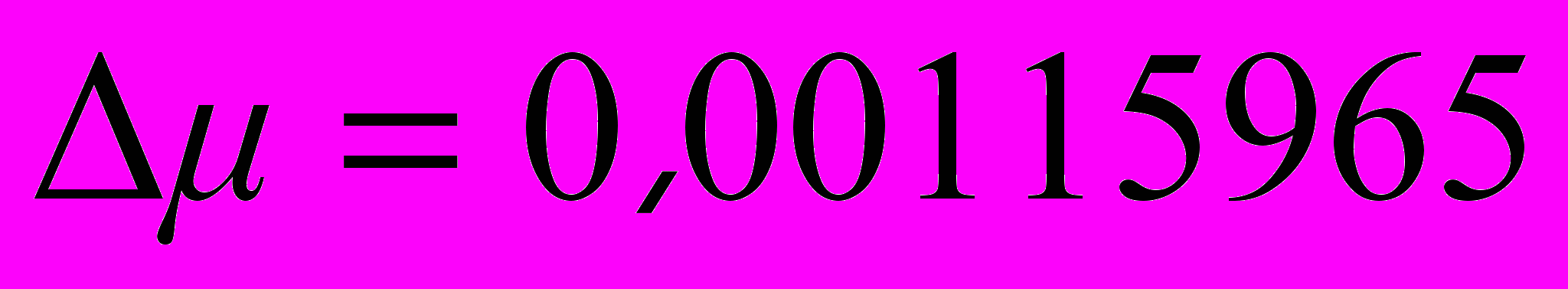. Сферическую поверхность ядра атома водорода можно представить в виде 8 взаимодействующих равносторонних треугольников, поэтому коэффициент 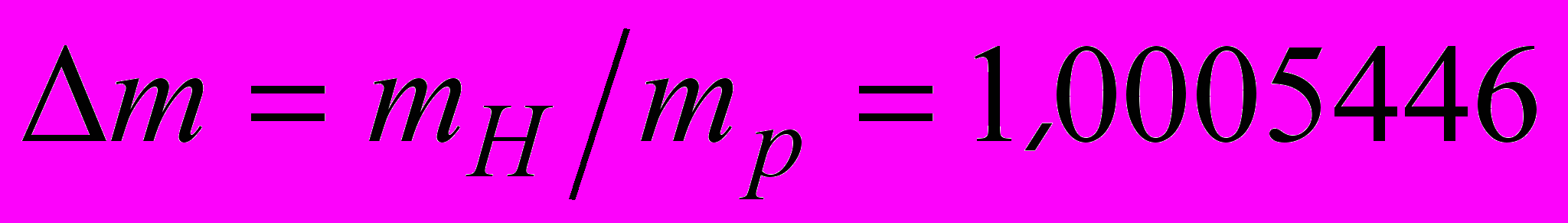возьмем в восьмой степени. Движение частицы в четырехмерном пространстве-времени возможно по четырем направлениям, поэтому коэффициент, связанный с эксцентриситетом орбиты 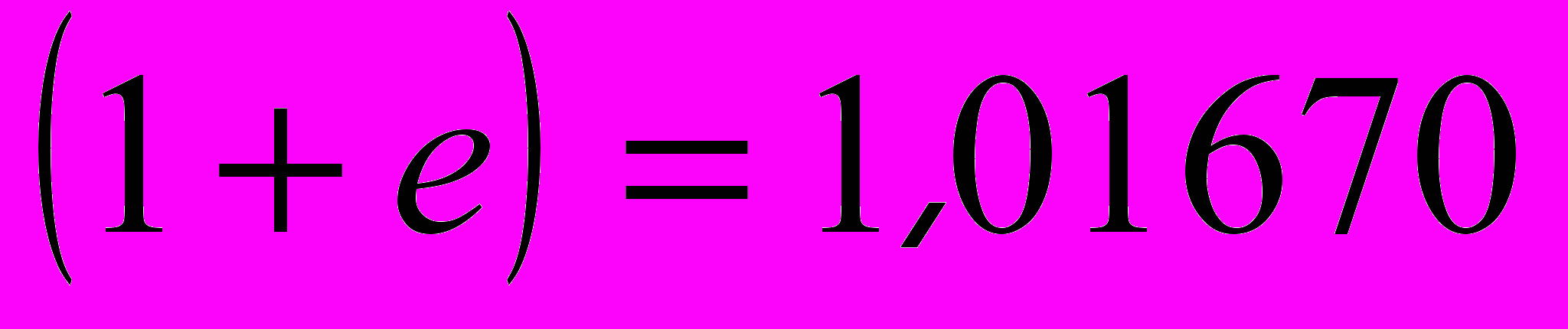возьмем в четвертой степени. Таким образом, с учетом численного коэффициента (10), соответствующему количеству независимых компонентов метрического тензора четырехмерного пространства-времени

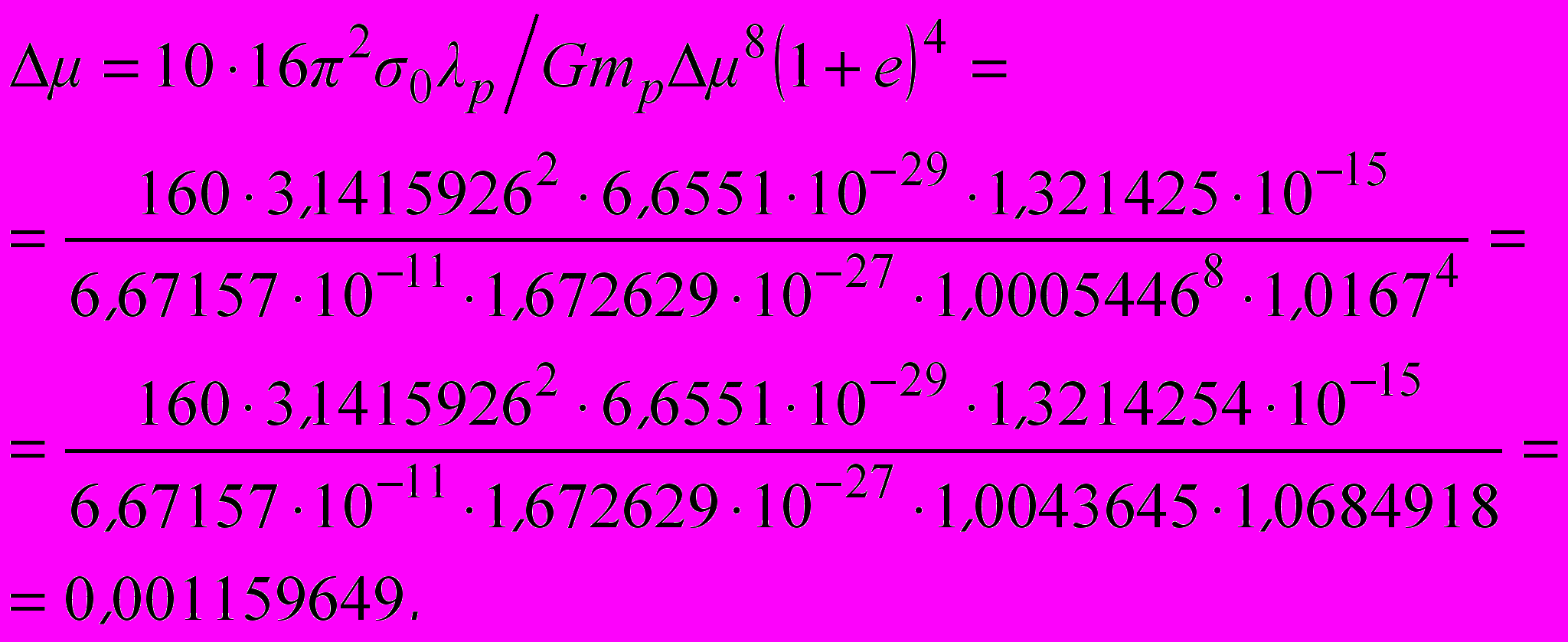(8)

Определить величину так называемой планковской плотности вещества можно для любой массы, включая Солнце:

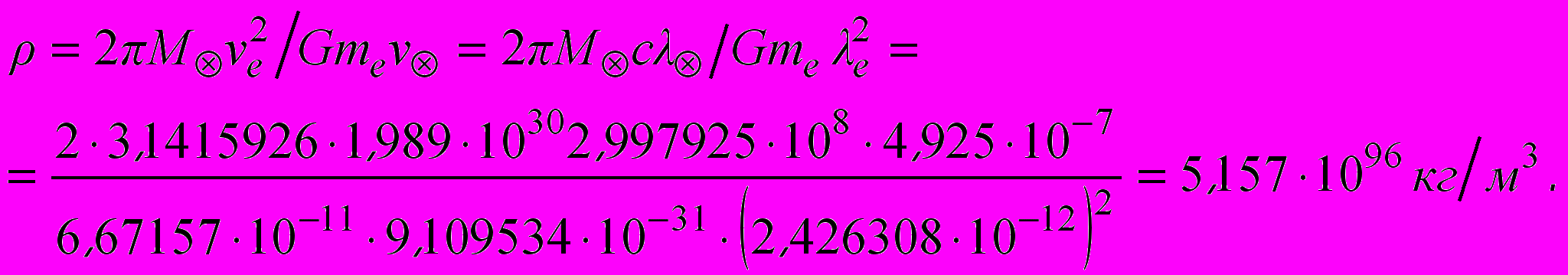(9)

Квадрат величины планковской плотности можно выразить также как отношение энергии частиц и античастиц вакуума (равной энергии вещества Вселенной) к площади земной орбиты и к квадрату гравитационного радиуса Солнца:

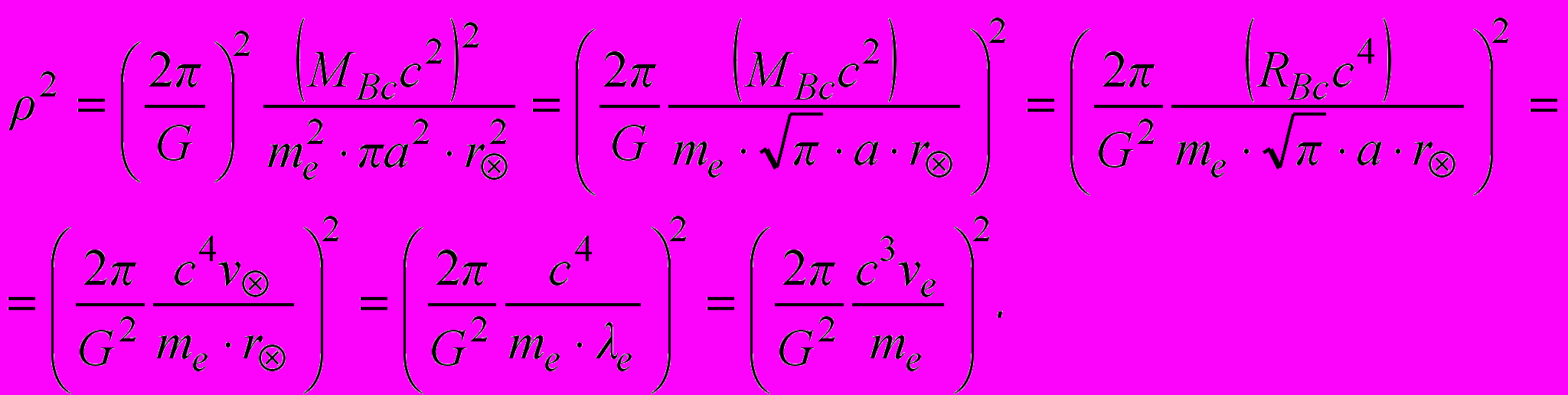(10)

Чтобы получить плотность вещества (и виртуальных частиц, порождаемым из вакуума гравитационным полем) во Вселенной, надо планковскую величину плотности умножить на отношение квадрата планковской длины к площади Вселенной:

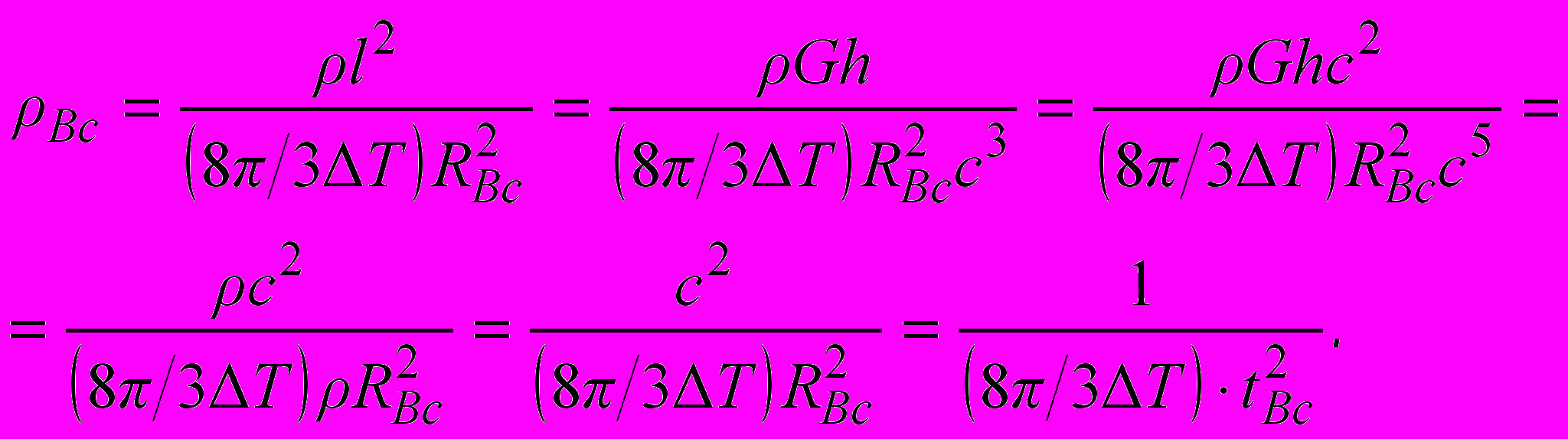(11)

Здесь величина 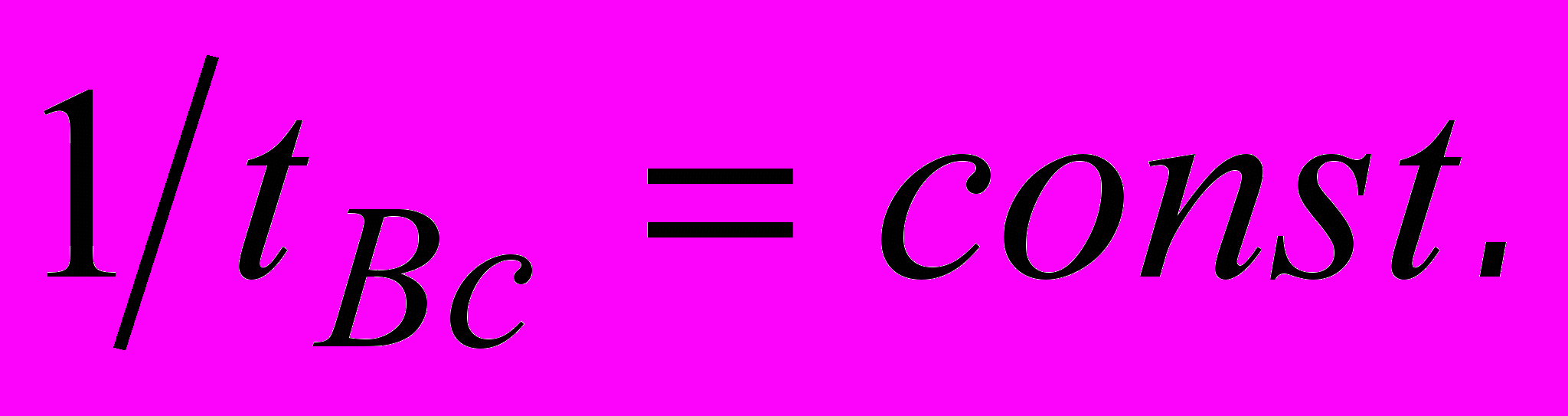равна постоянной Хаббла 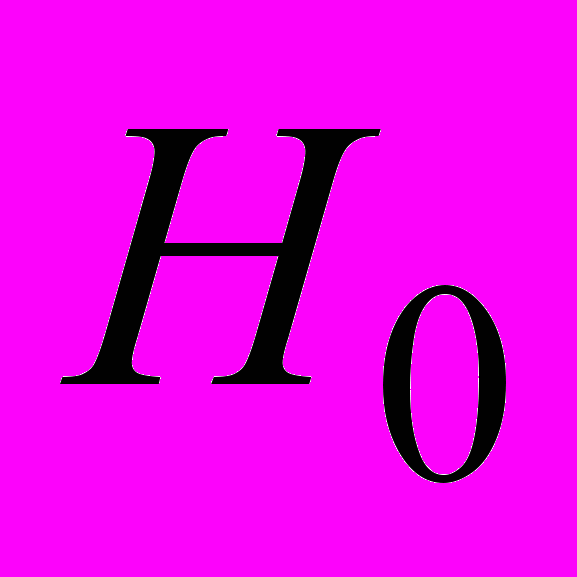для настоящего момента в теории расширяющейся Вселенной.

Какой же физический смысл имеет квадрат планковской длины? На орбите вокруг земли искусственный спутник движется с той скоростью, которую определяет гравитационный потенциал земли. Следовательно, скорость электрона на орбите вокруг ядра определяет гравитационный потенциал протона. Чем дальше от протона находится электрон (в том числе виртуальный, вакуумный), тем меньше его гравитационный потенциал. У «экватора» гравитационный потенциал протона, находящегося на «Северном полюсе» будет ничтожно мал, и его величина как раз равна квадрату планковской длины. На расстоянии, равном радиусу видимости Вселенной от данного протона общее количество протонов 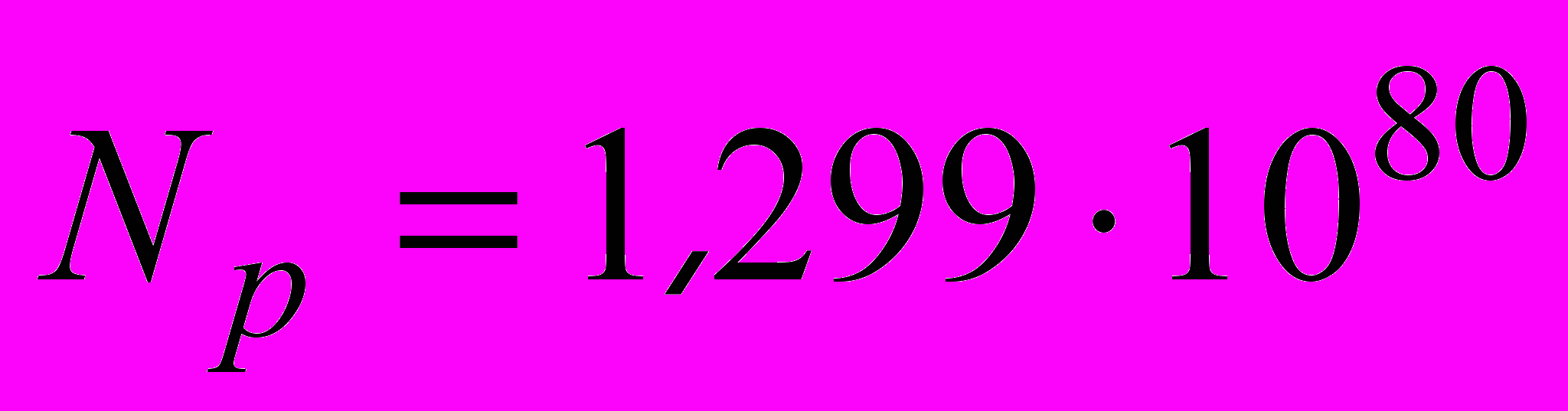. Спин протона 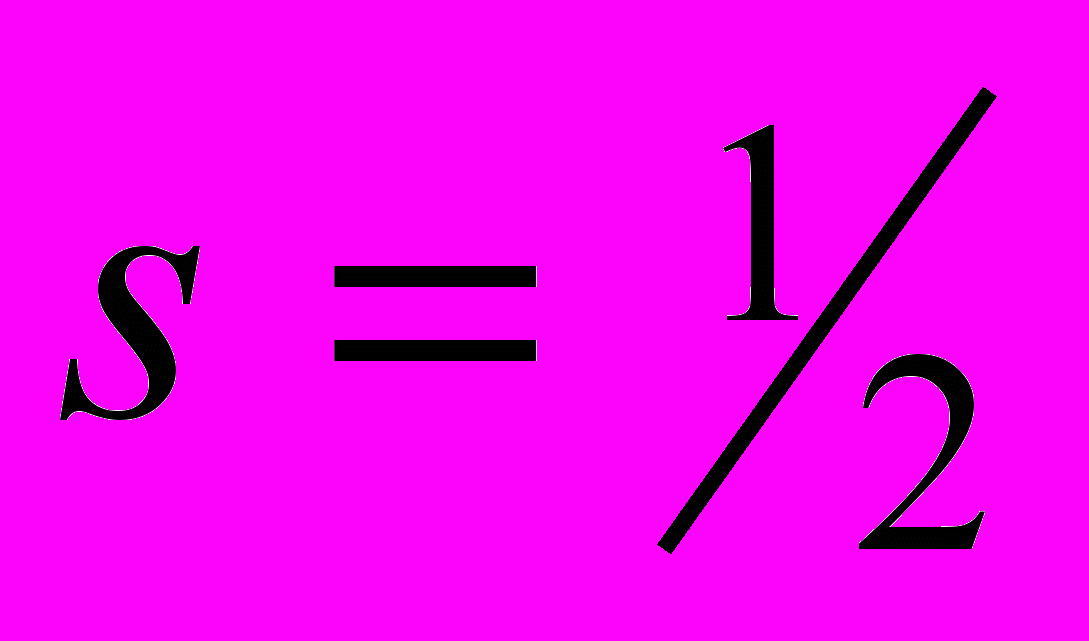. Тогда общий гравитационный потенциал, создаваемый всеми частицами Вселенной в четырехмерном пространстве-времени равен

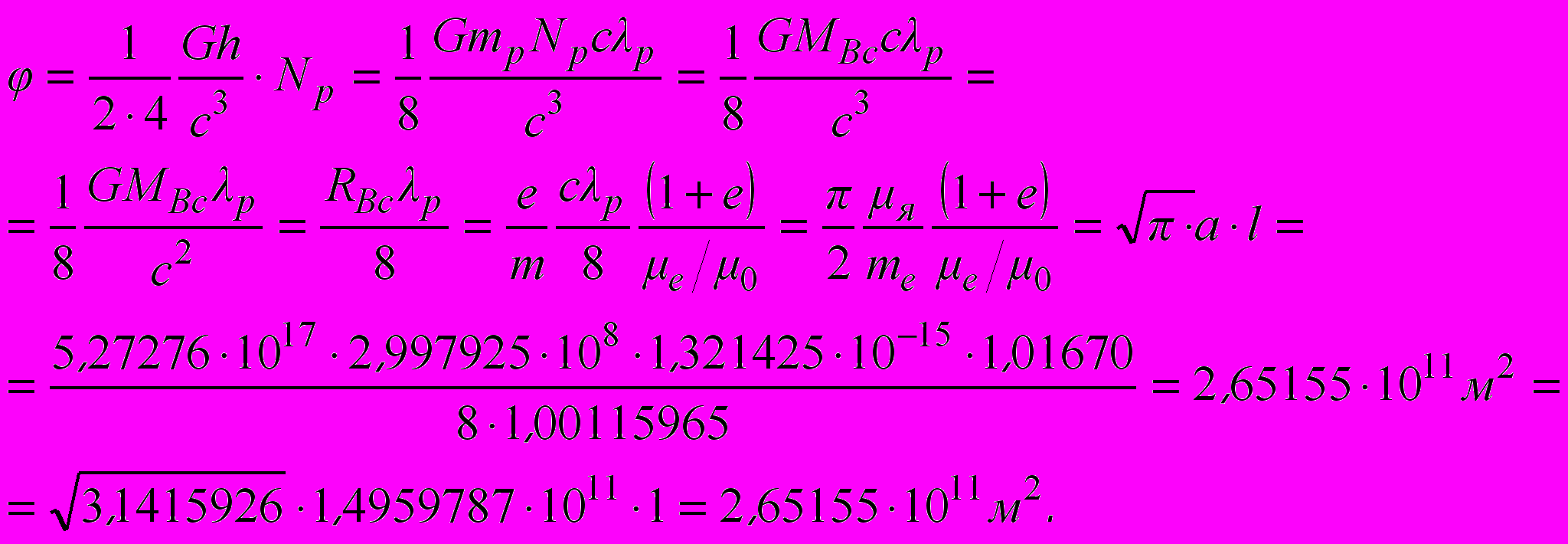(12)

Как мы полагаем, уже одного этого результата достаточно, чтобы утверждать, что уравнения единой теории поля работают.

Здесь e – заряд электрона, m – его масса, 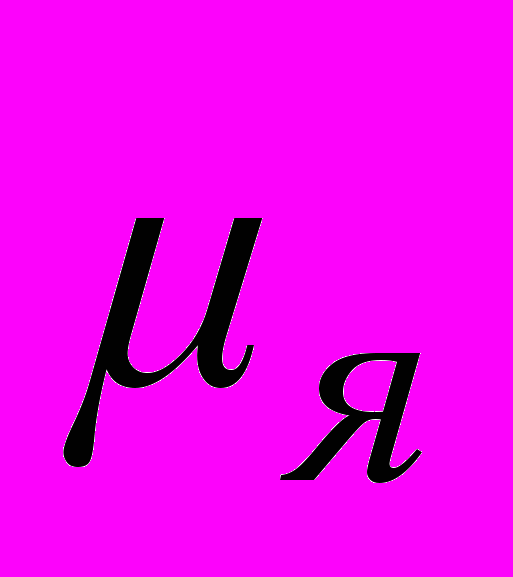- ядерный магнетон, 1+е - эксцентриситет орбиты Земли, 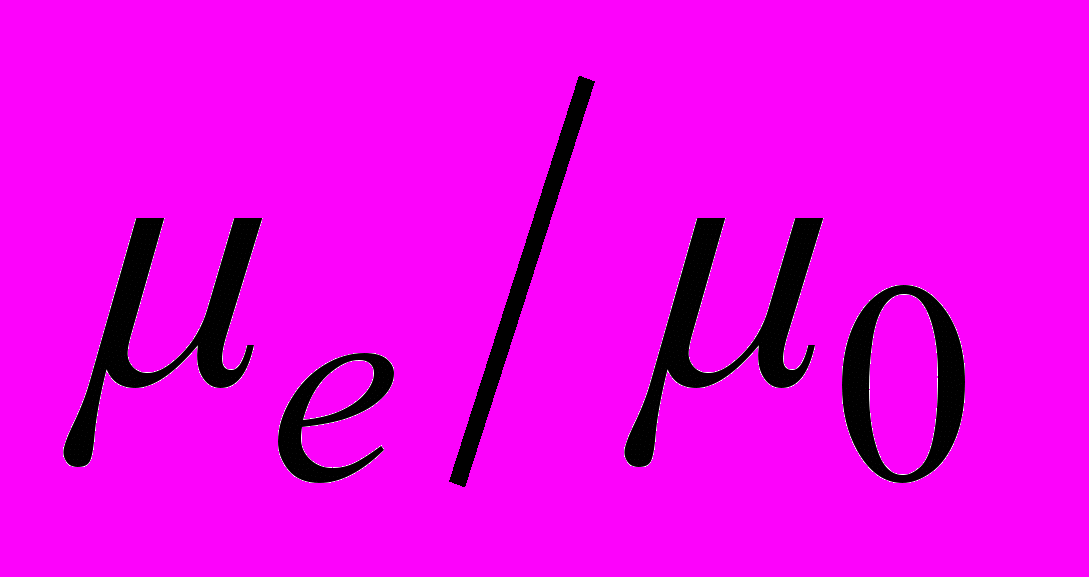– отношение аномального магнитного момента электрона к нормальному, 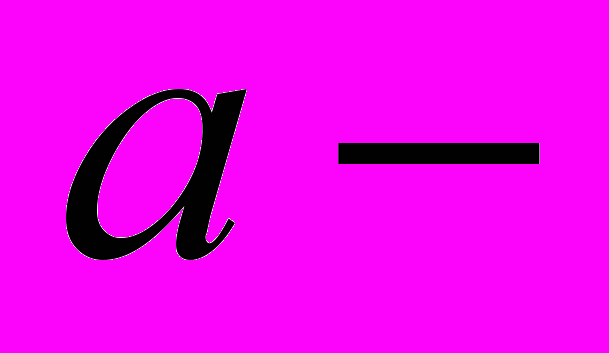среднее расстояние от Земли до Солнца, .

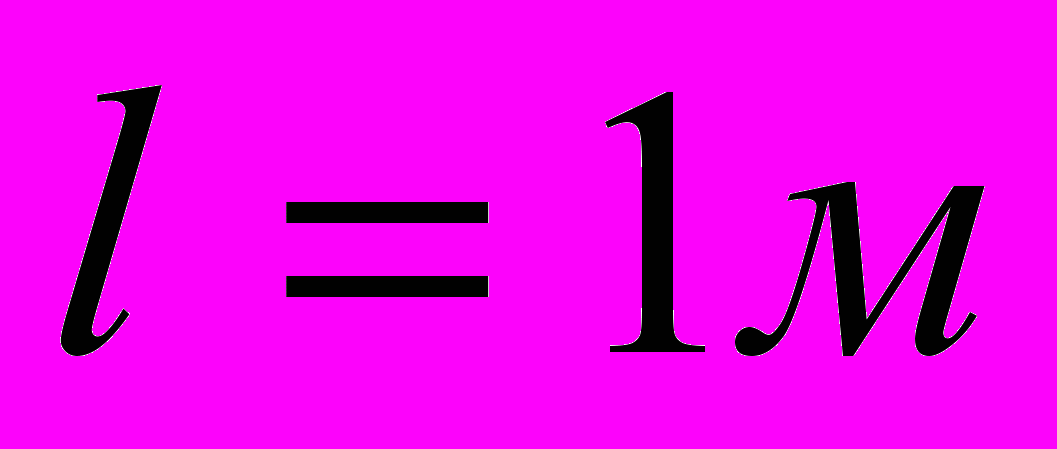Можно показать, что полученный выше результат имеет промежуточное (среднее геометрическое) значение между первой и второй космическими скоростями на поверхности Солнца, которые и определяют величину его гравитационного потенциала:

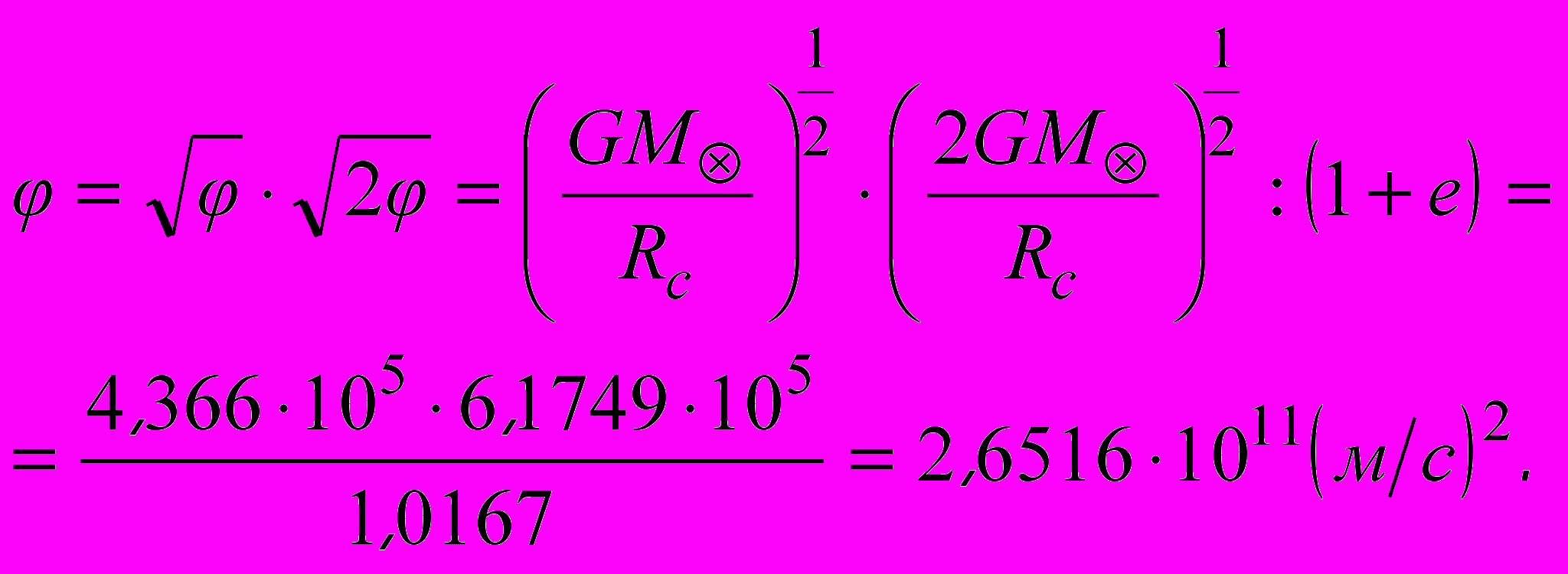(13)

В ньютоновой теории тяготения для описания гравитационного поля было достаточно единственного гравитационного потенциала. А Эйнштейн в своей теории предлагает использовать десять гравитационных потенциалов. Если каждому из 10 гравитационных потенциалов, создаваемых ядром атома соответствуют 10 виртуальных электронов вакуума, тогда можно ввести дополнительный коэффициент 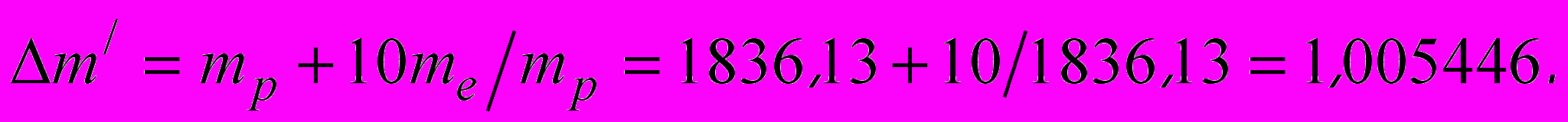Теперь умножим квадрат планковской длины на количество протонов на Солнце:

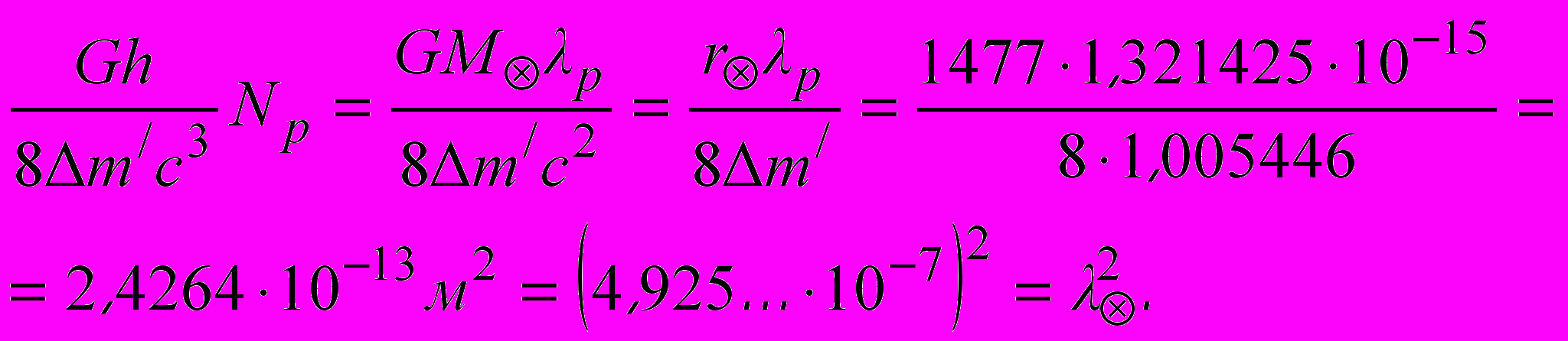(14)

Полученный результат точно равен длине волны фотона солнечного излучения максимальной интенсивности.

Таким образом, сингулярность не такая уж чудовищная вещь, где пасуют известные нам законы физики и, во всяком случае, она не имеет никакого отношения к так называемому «началу» Вселенной, ее рождению «из ничего». Так что не так страшен черт, как его малюют физические пророки.