Def. Пусть векторное пространство над или. Нормой

Вид материала

Документы

Содержание Def. Единичным шаром Def. Множество называется выпуклым Лемма. Единичный шар является выпуклым множеством. Доказательство. Def. Множество называется центрально-симметричным

Подобный материал:

• П-мерное векторное пространство, 201.59kb.
• Морозова Алена Витальевна. Требования к студентам : курс предполагает наличие знаний, 262.09kb.
• Iii. Численные методы алгебры. Лекция, 64.34kb.
• Теория множеств, операции над множествами. Круги Эйлера, 94.64kb.
• Информационный Бюллетень по Ведической философии, Цигуну, боевому ушу или Кун-фу, 285.8kb.
• Аналитическая геометрия с элементами линейной алгебры, 44.1kb.
• Аналитическая геометрия с элементами линейной алгебры, 54.48kb.
• Бхакти Тиртха Свами Духовный воин — 4 победа над врагами ума переводчик Гру И. Б. (Ишвара, 5040.91kb.
• Говорят, чем мы Винду сильнее любим, тем дольше грузится она. Пусть в Новом году, 22.39kb.
• Программа вступительного экзамена по специальности в магистратуру физического факультета, 209.43kb.

20. Нормированное векторное пространство

Def. Пусть 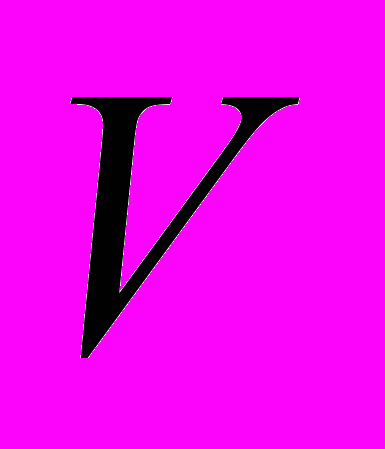- векторное пространство над 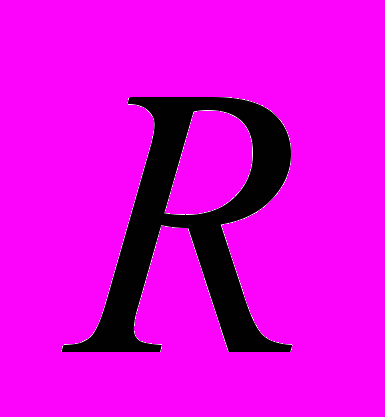или . Нормой называется функция 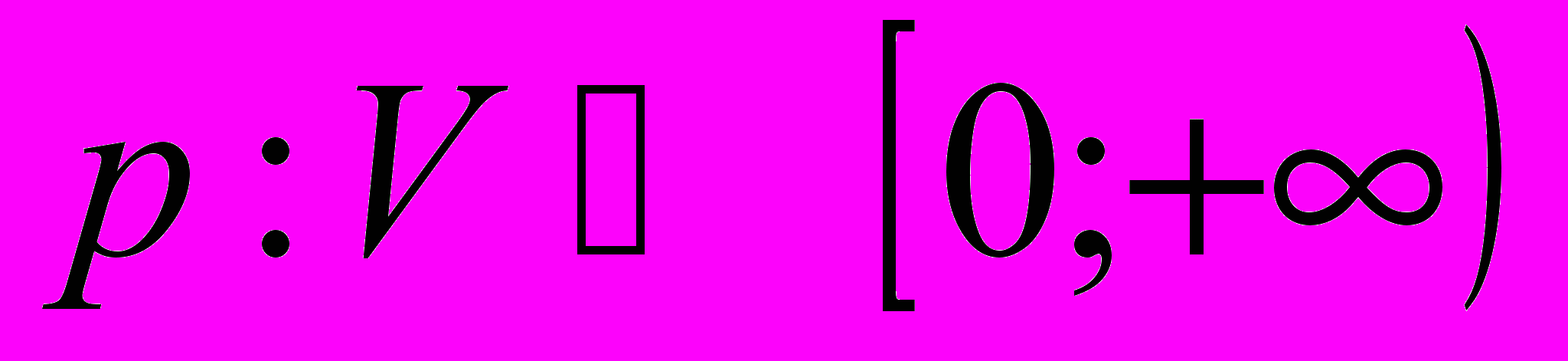со свойствами:

1) ;

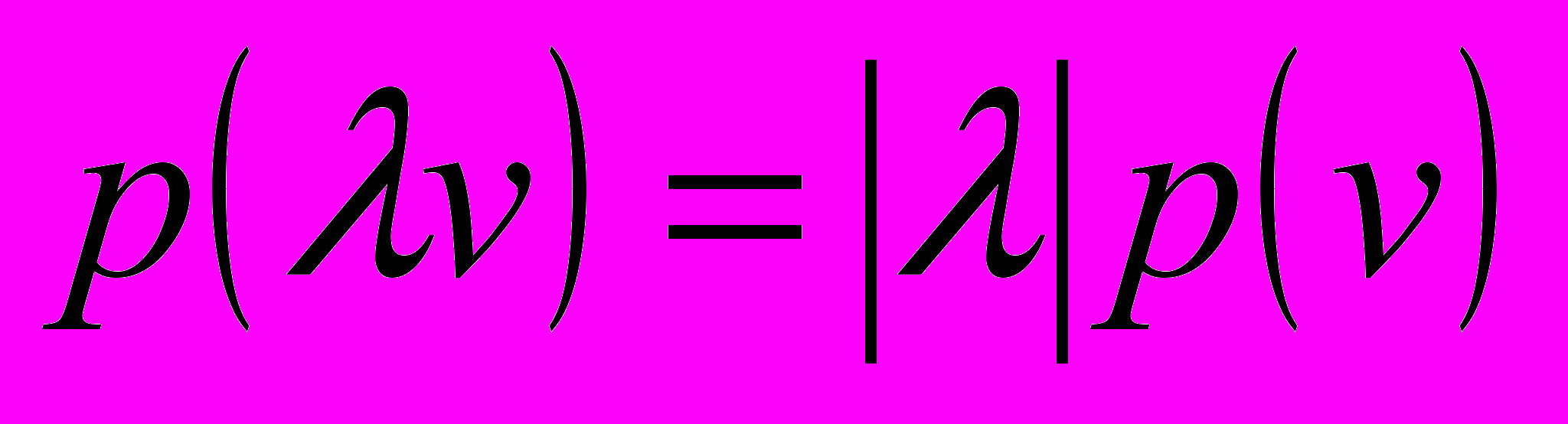2) ;

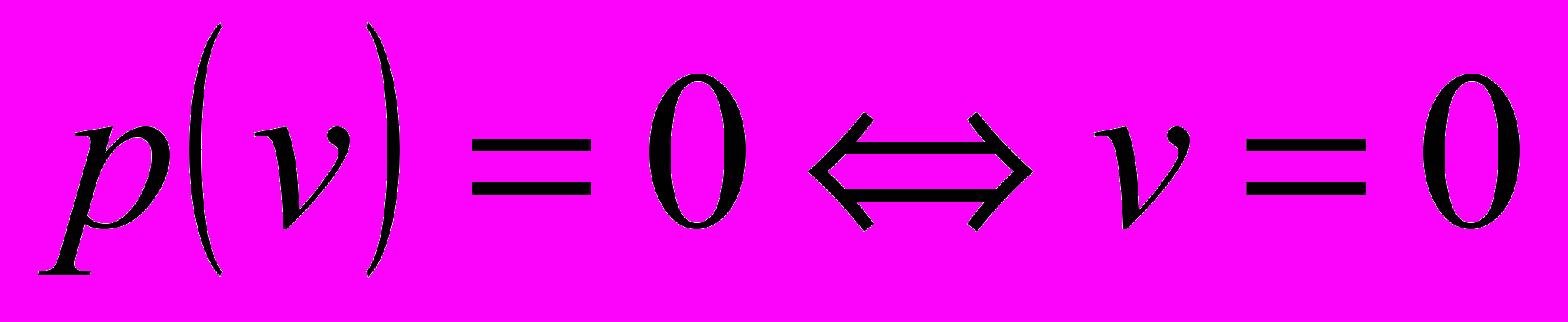3) 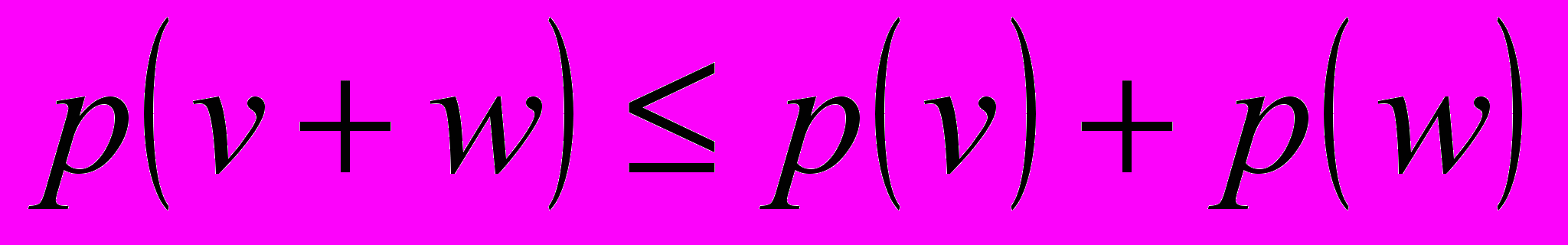(неравенство треугольника).


Обозначается норма как .


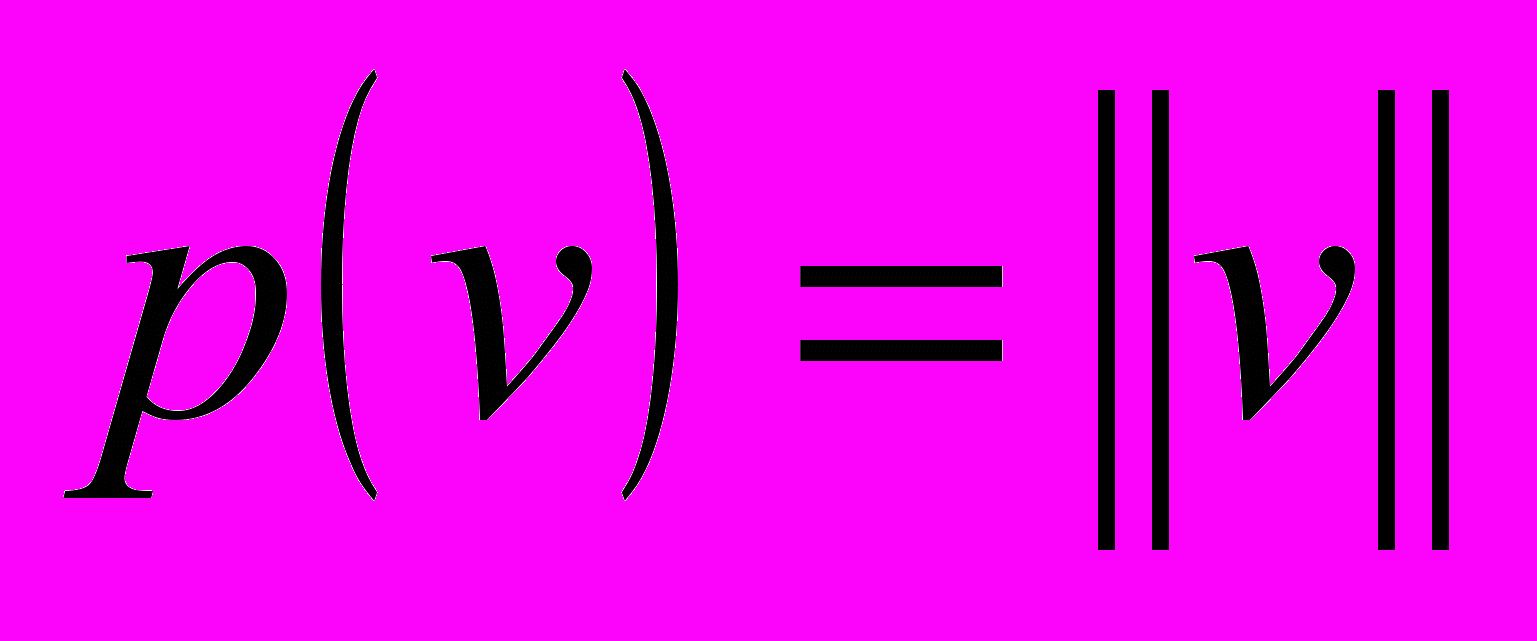Пример:Пусть 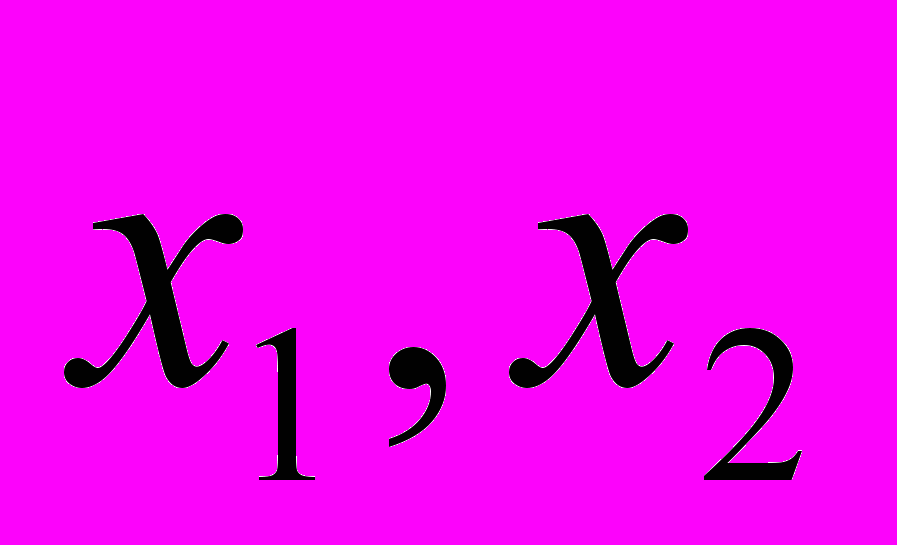- координаты на плоскости, тогда норму можно ввести аж несколькими способами: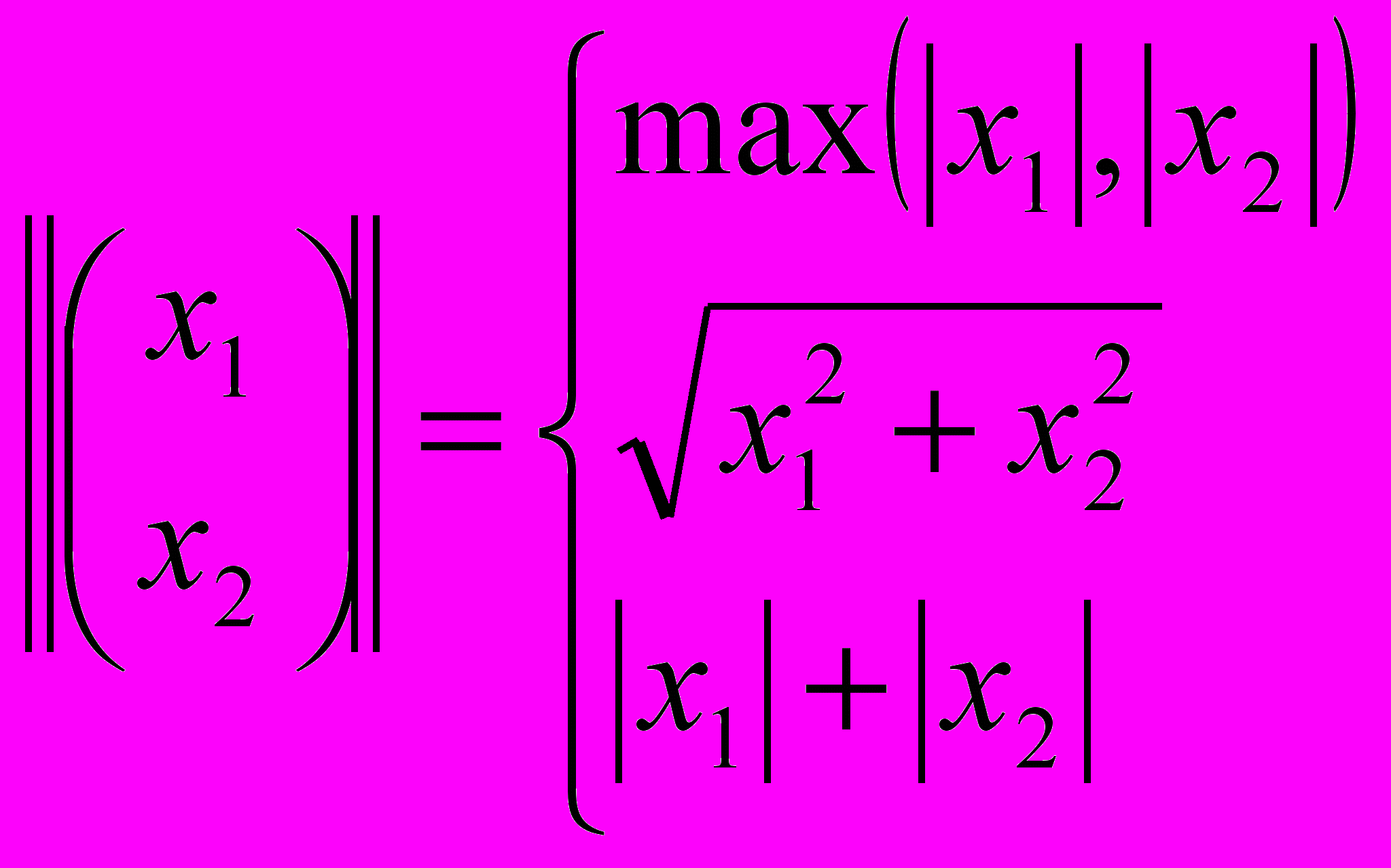




Def. Единичным шаром называется множество векторов, норма которых не превосходит единицу, т.е. .


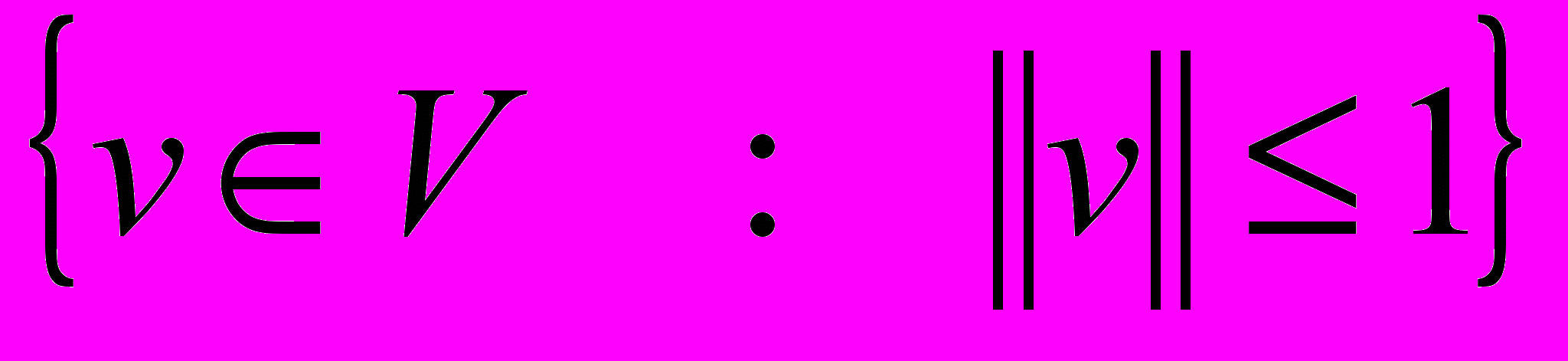Пример: Предыдущем примере единичным шаром будет: квадрат, ограниченный прямыми 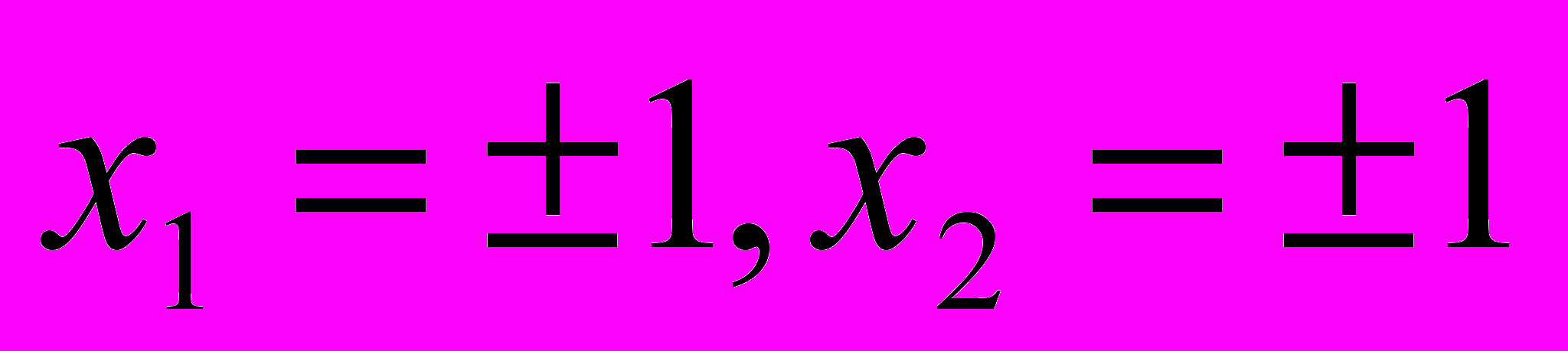, в случае первой нормы; круг радиуса 1 и с центром в начале координат в случае второй нормы; квадрат, ограниченный прямыми 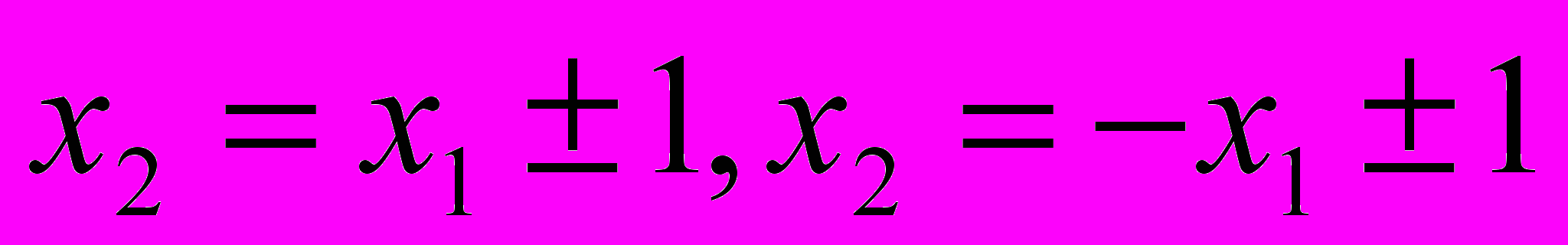в случае третей нормы.


Def. Множество 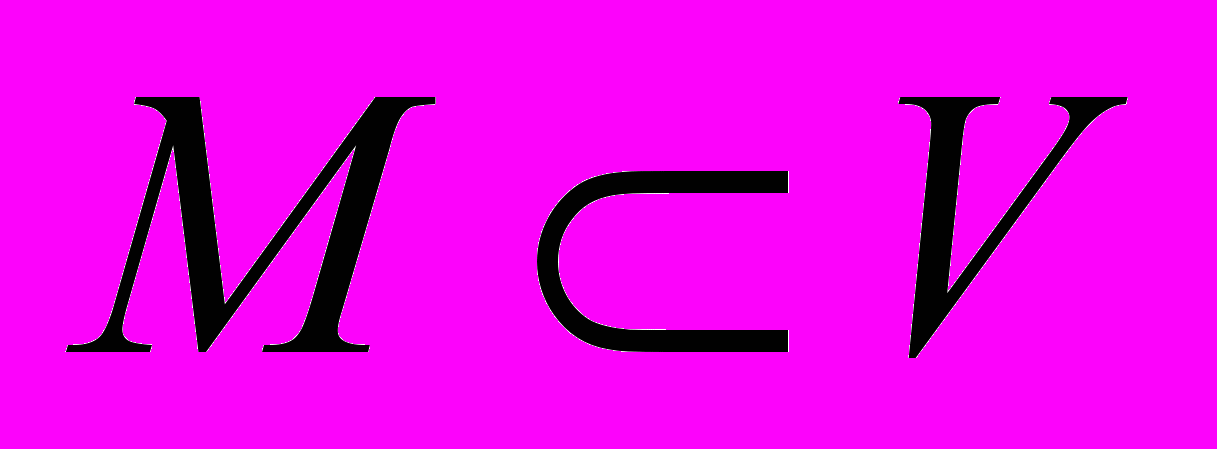называется выпуклым, есл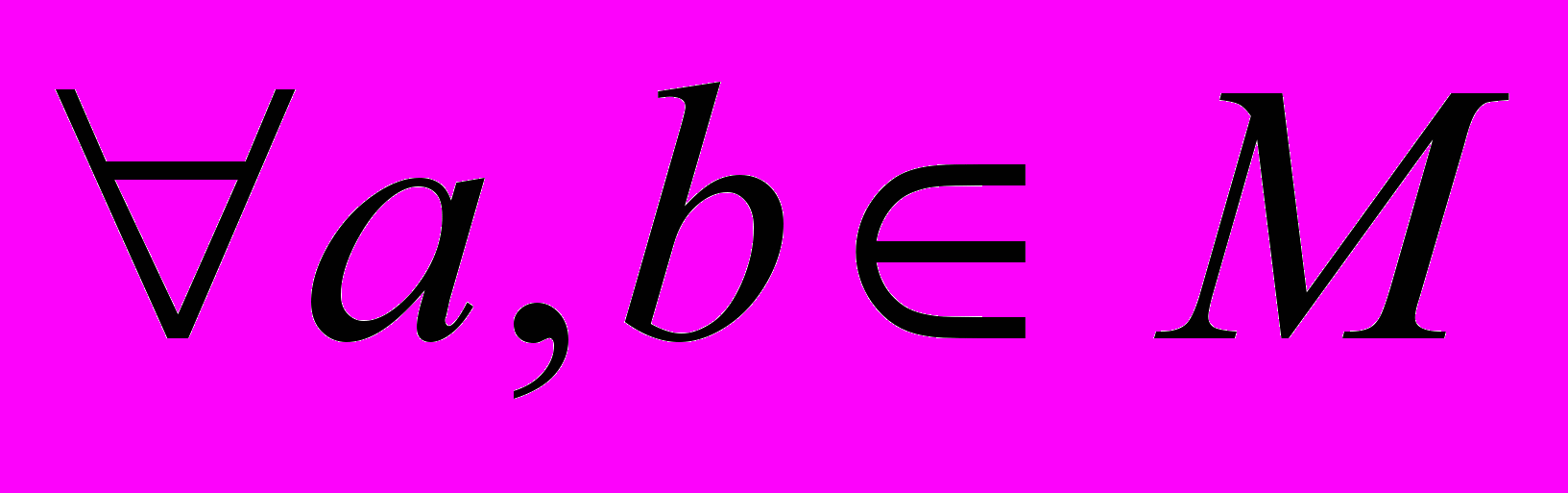и и 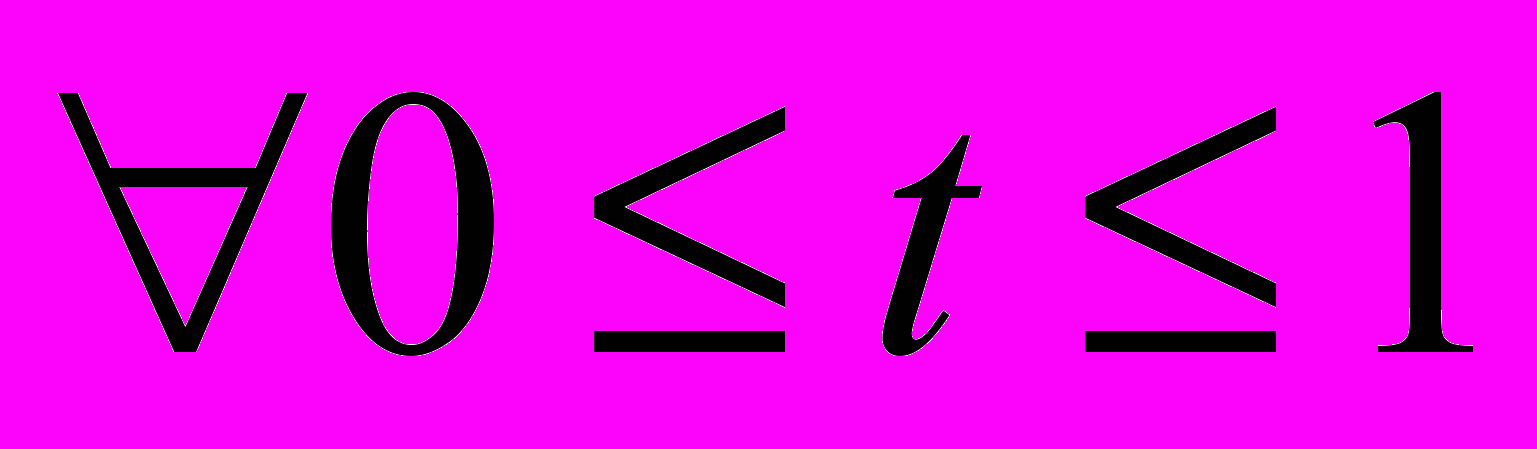точка 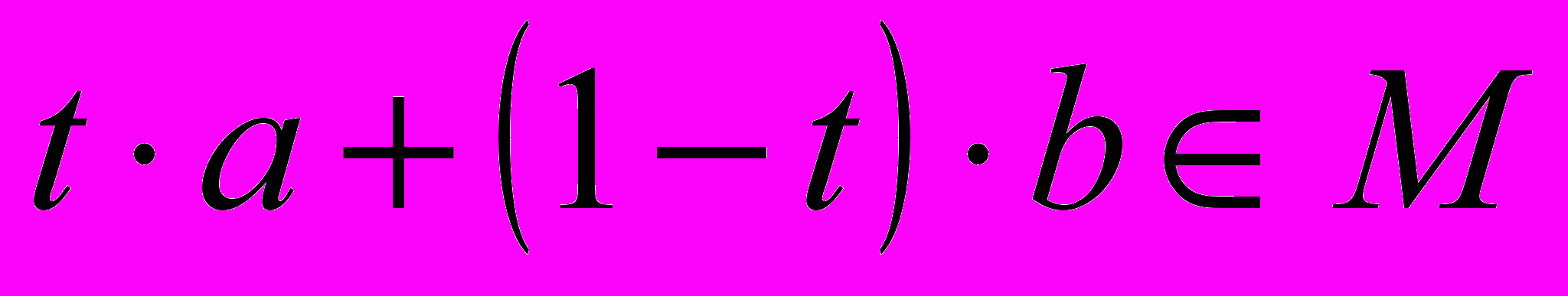, т.е., если две точки принадлежат множеству, то и весь отрезок, их соединяющий, должен этому множеству принадлежать.


Лемма. Единичный шар является выпуклым множеством.

Доказательство.

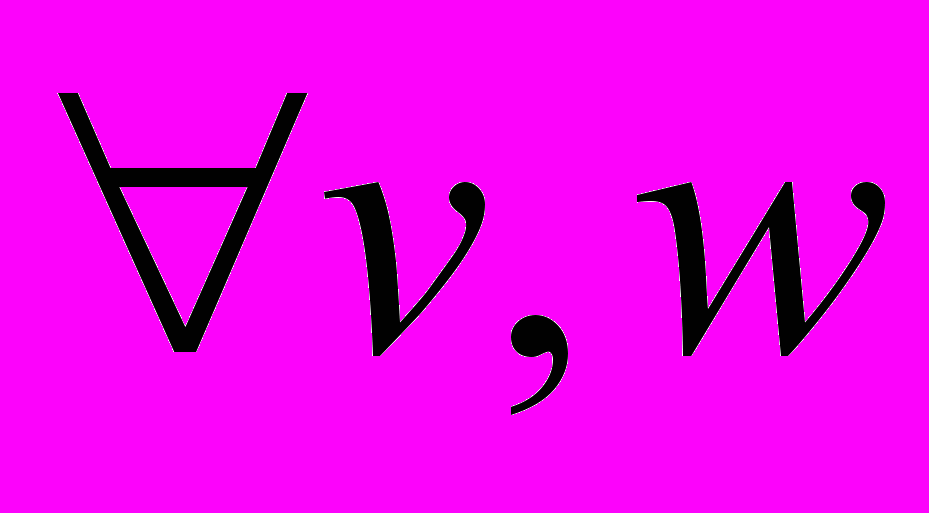, принадлежащих единичному шару, имеем , тогда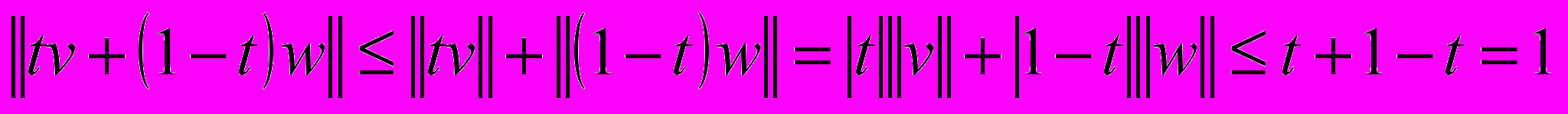

,

т.е. точка 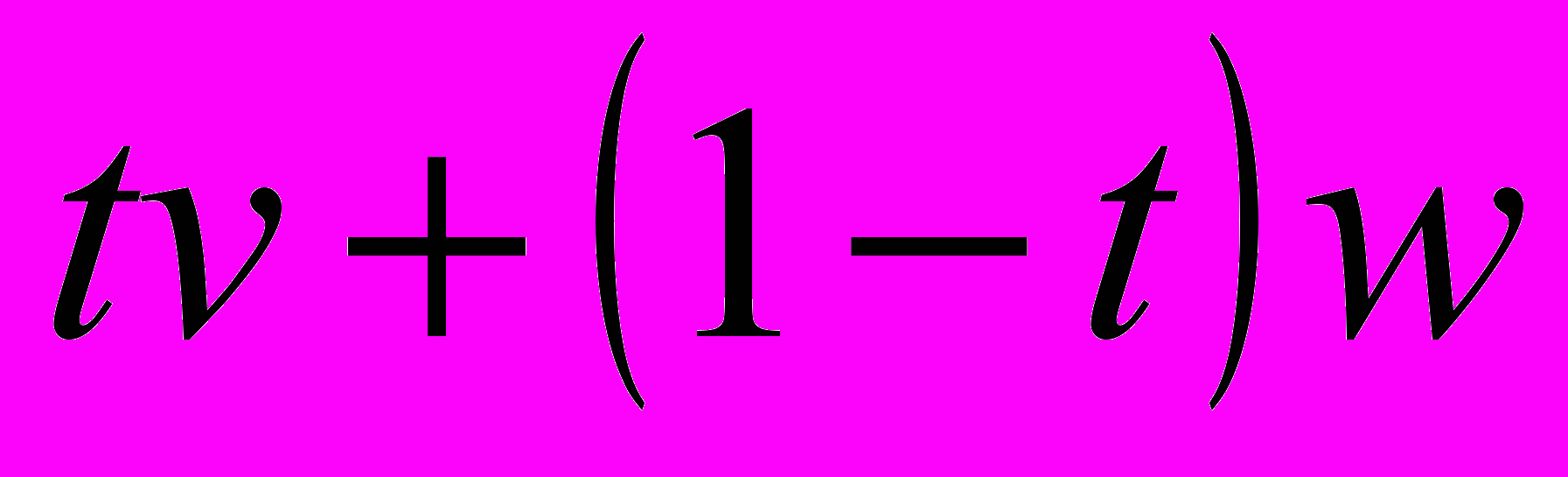тоже принадлежит единичному шару .

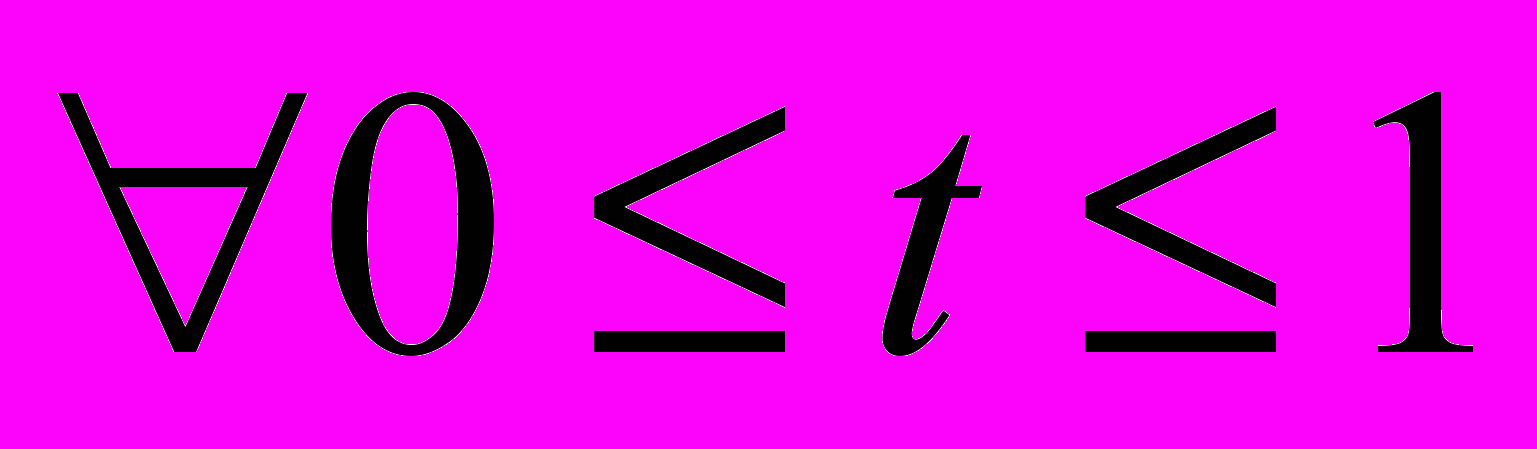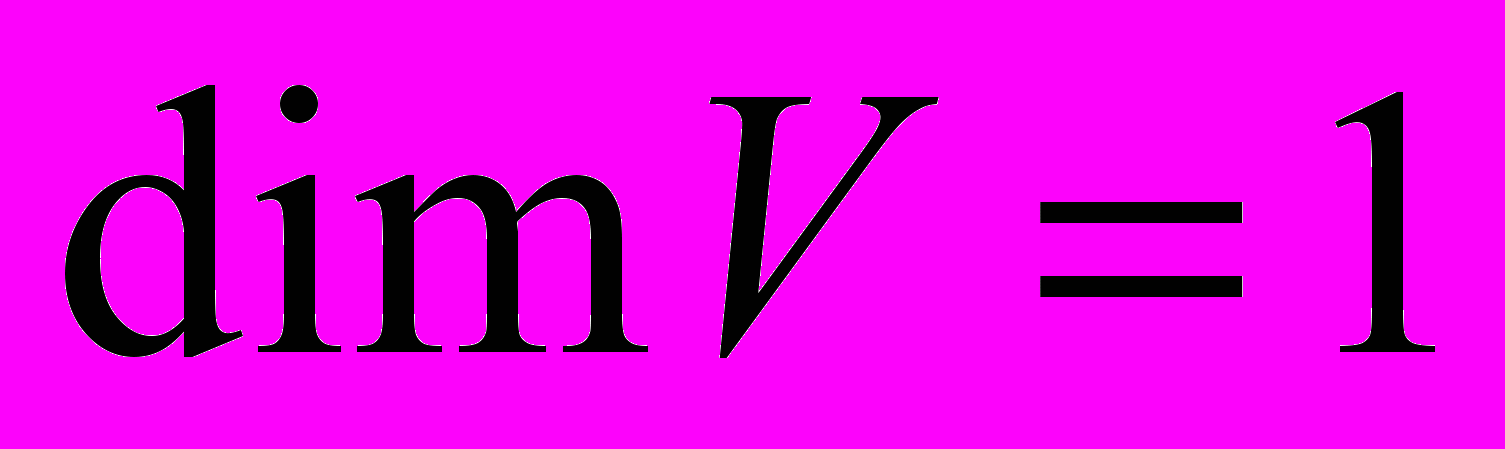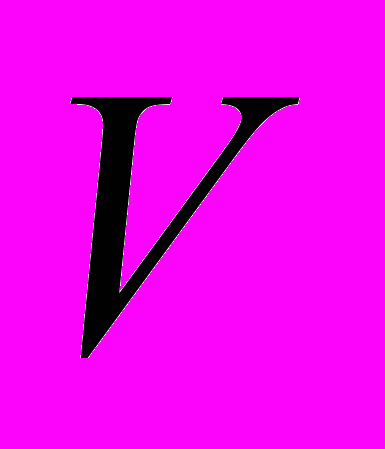Норма на одномерном вещественном и комплексном пространстве. Пусть и - пространство над 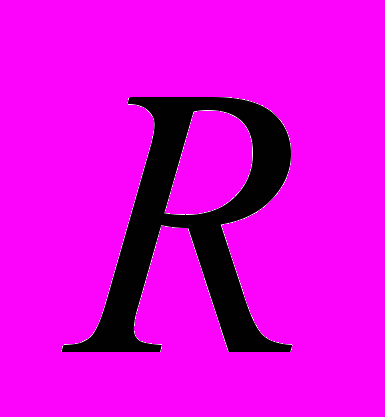. Возьмем произвольный вектор 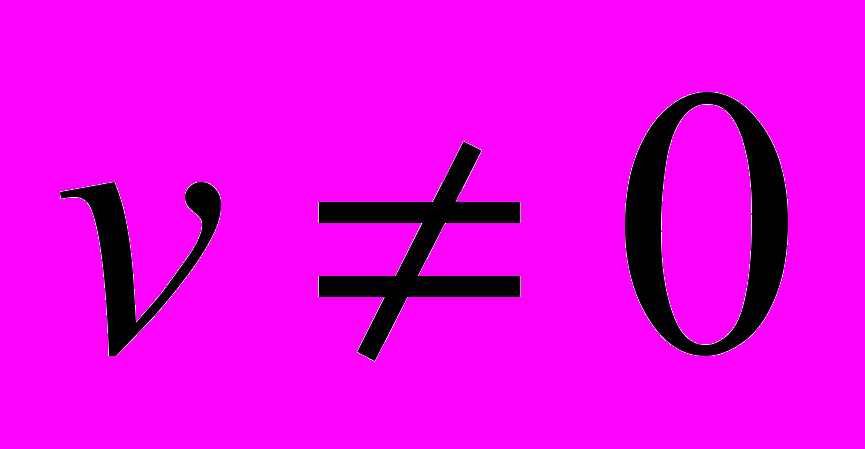в этом пространстве, тогда найдет такое числ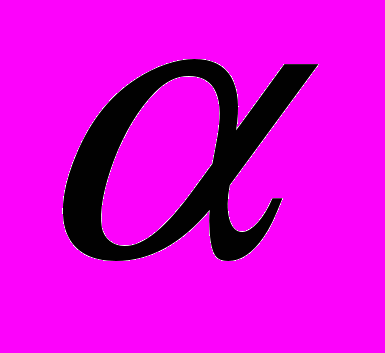о , что 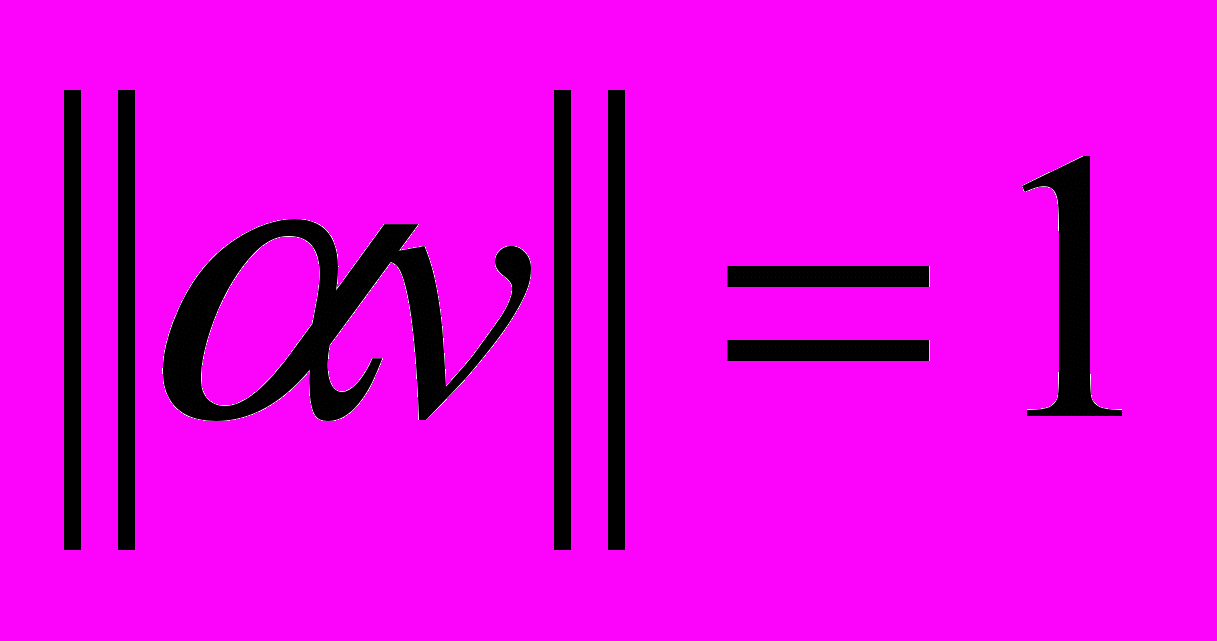, возьмем вектор 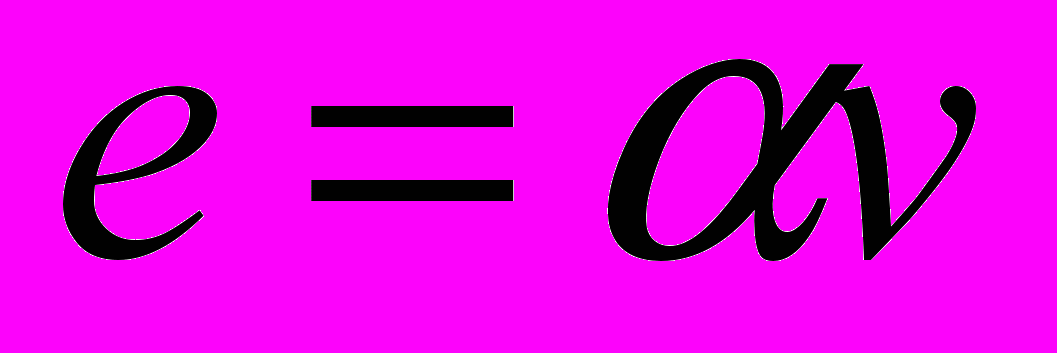в качестве базиса. Тогда единичный шар – это множество 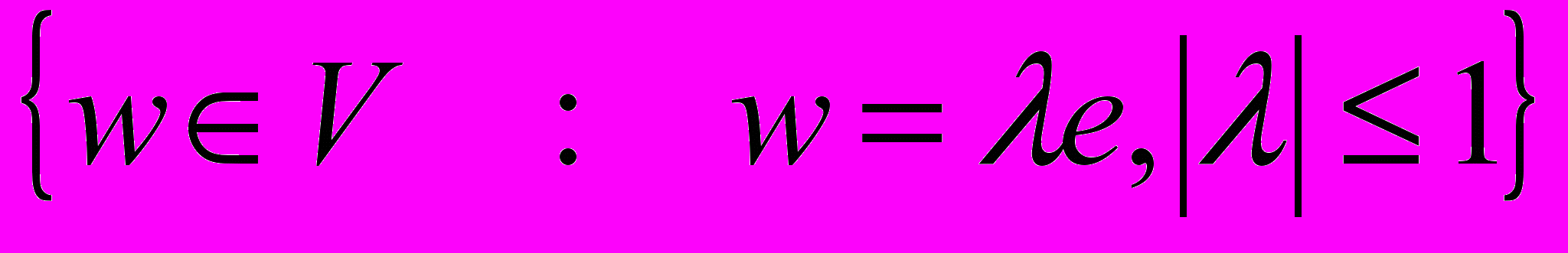, т.е. отрезок 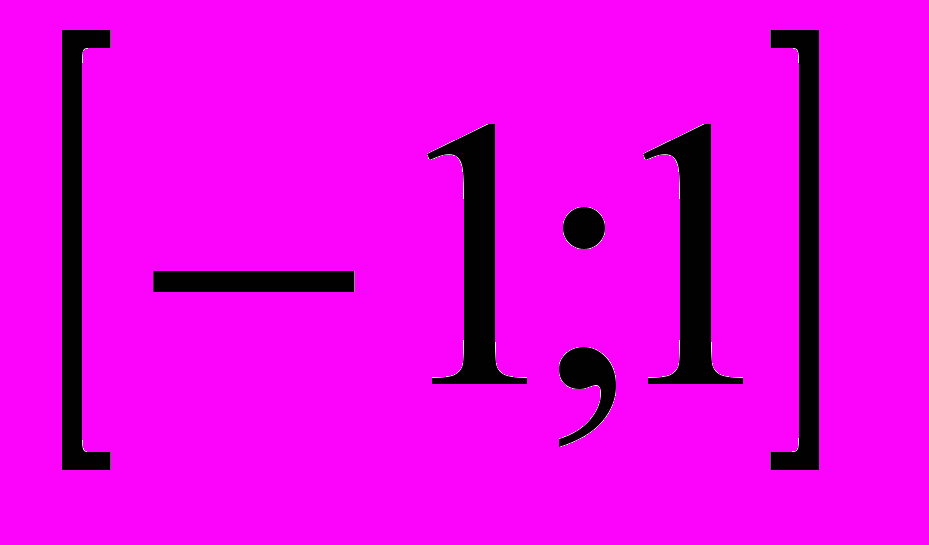на координатной прямой. Если 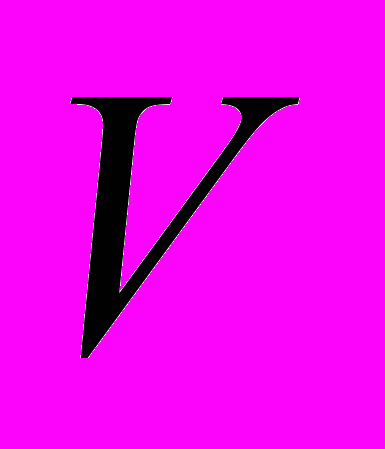- пространство над , то единичным шаром будет круг на комплексной плоскости радиуса 1 с центром в начале координат.

Def. Множество 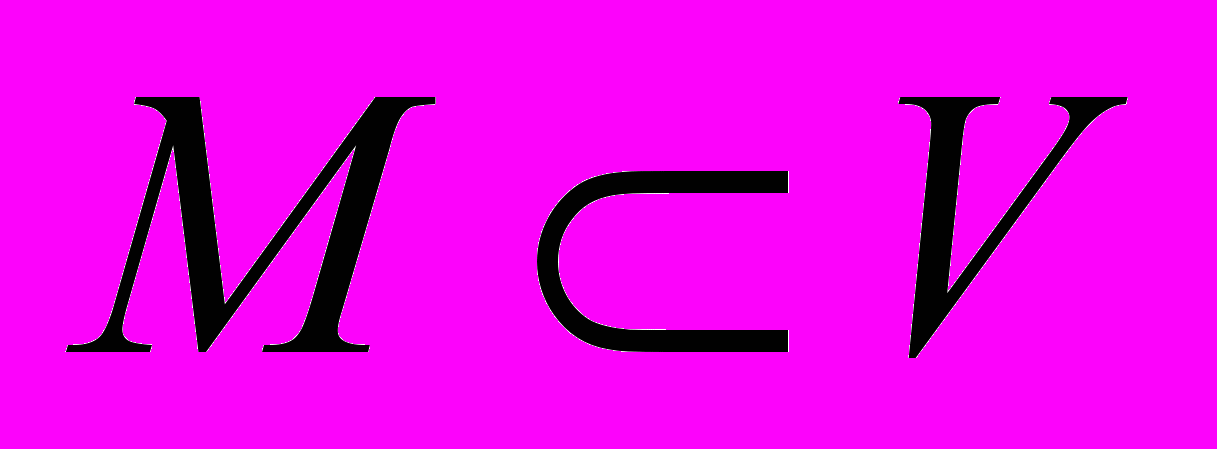называется центрально-симметричным, если его пересечение с любым одномерным пространством 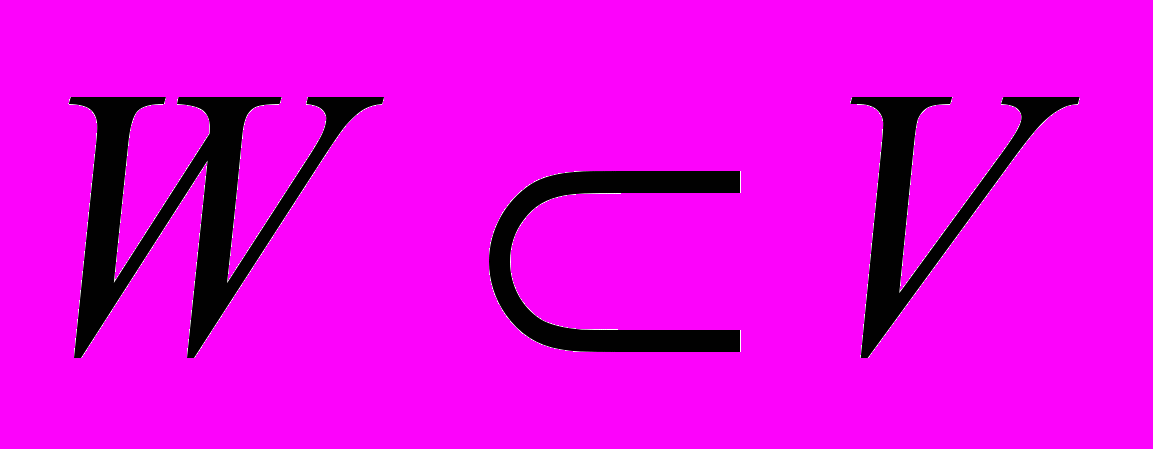имеет один из вышеописанных видов (отрезок или круг).


Пример: Очевидно, что единичный шар является центрально-симметричным множеством.


Теорема. Пусть 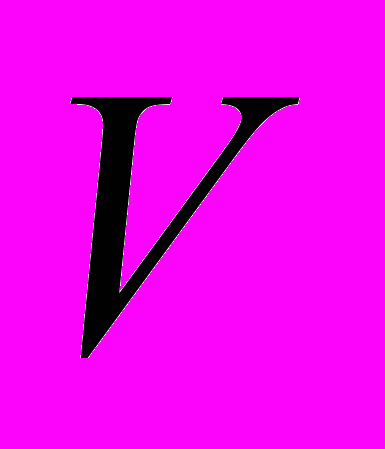- линейное пространство, 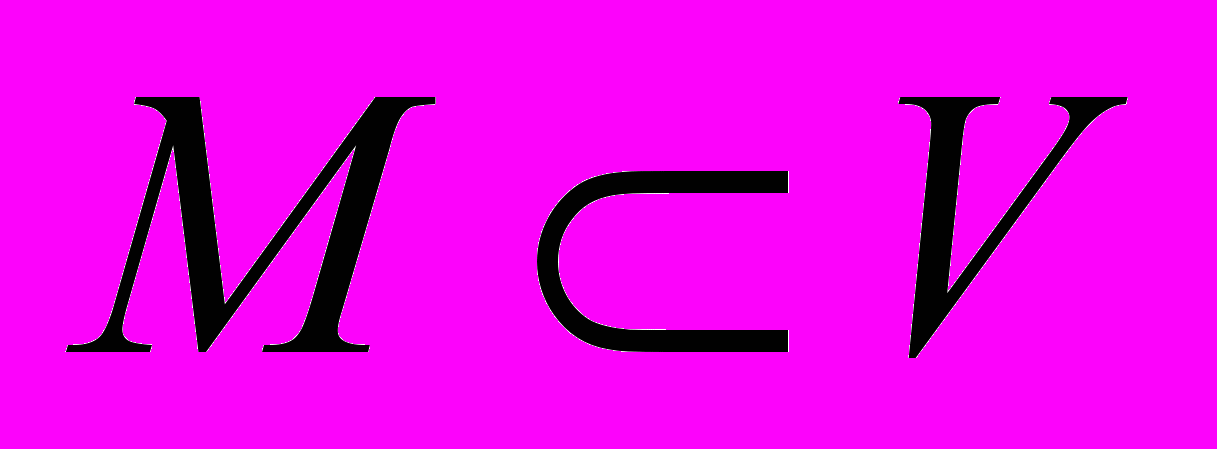центрально-симметрично и выпукло, тогда на пространстве 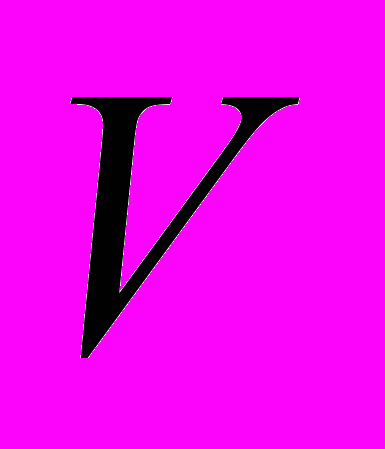существует такая норма, что для нее множество 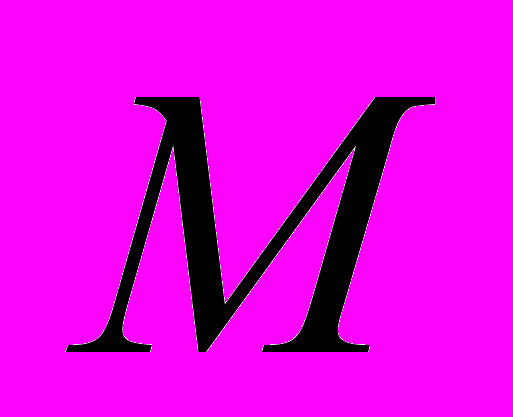является единичным шаром.

Доказательство. Пусть 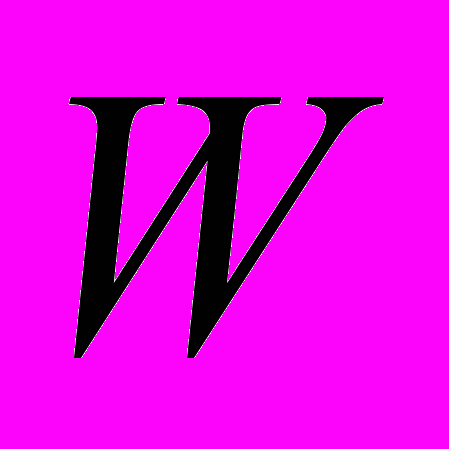- произвольное одномерное подпространство, тогда 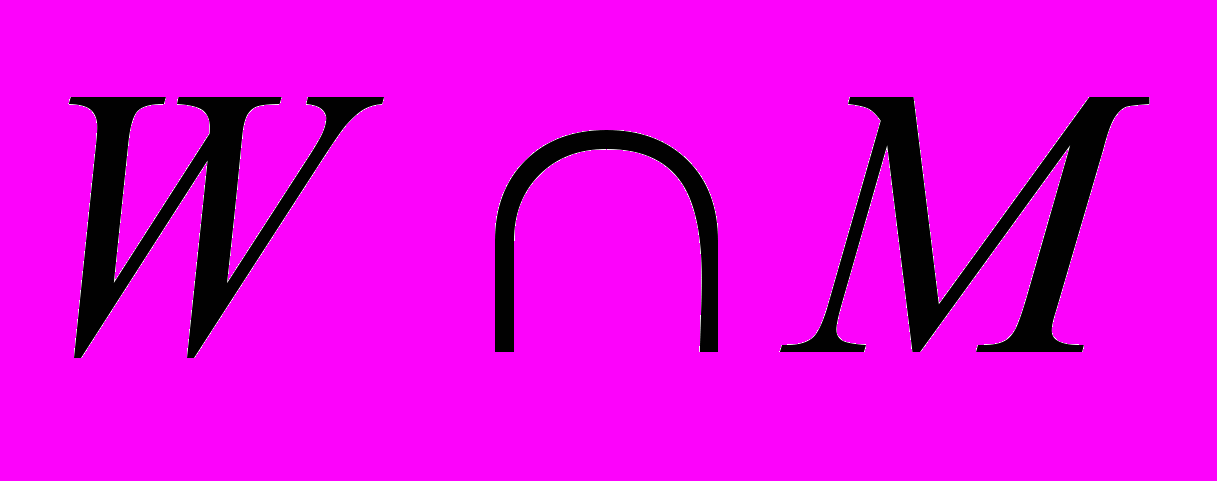устроено так же, как и единичные шары в одномерных пространствах, т.е. , т.ч. 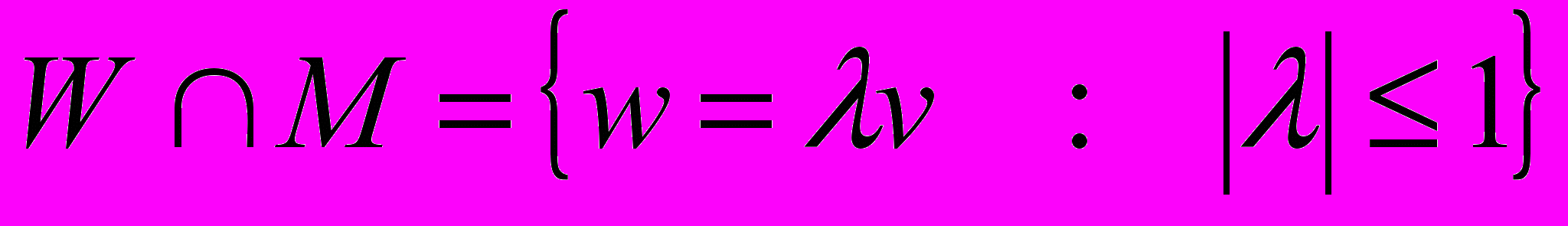. Определим норму следующим образом: 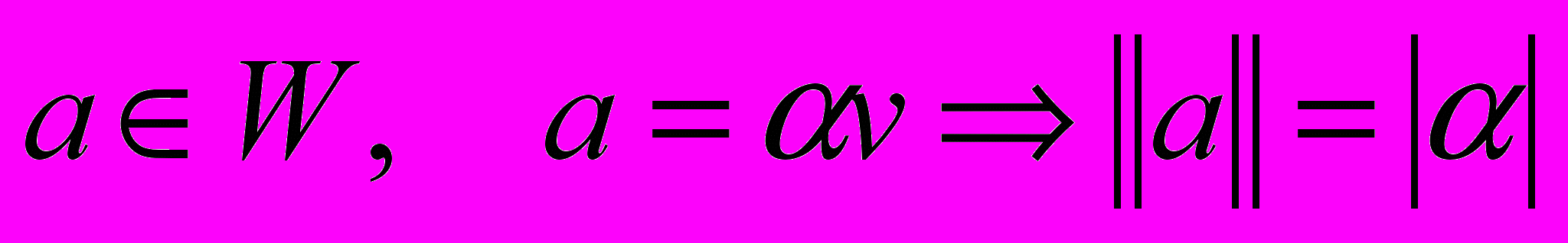. Покажем, что так определить норму можно лишь единственным образом. Пусть множество 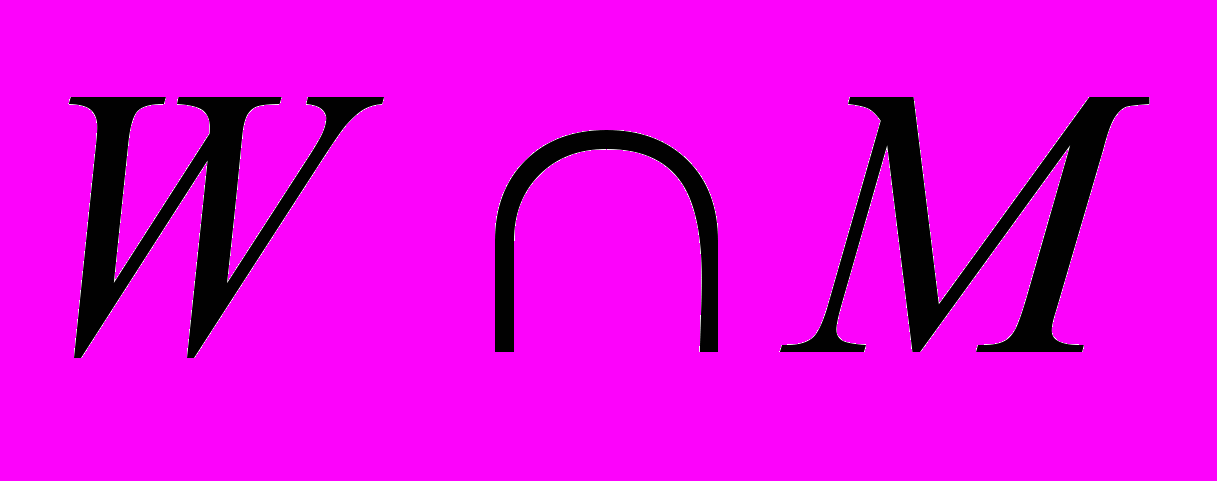задается каким-нибудь другим вектором 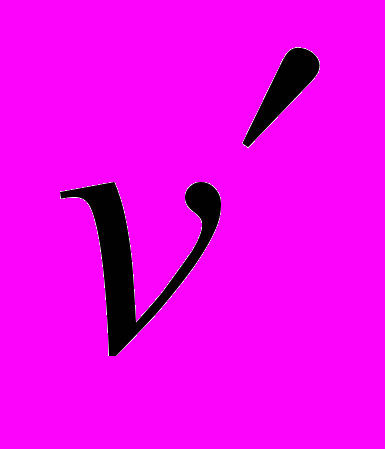, т.е. 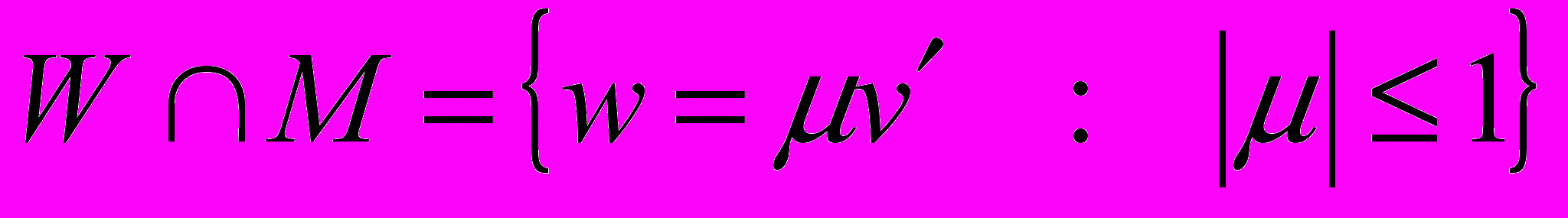. Тогда, т.к. 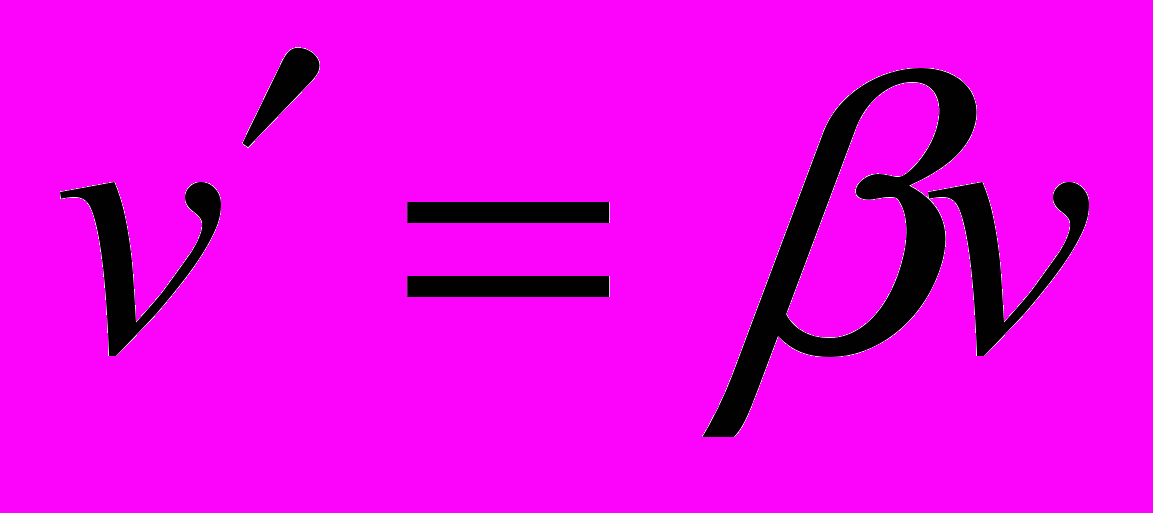, 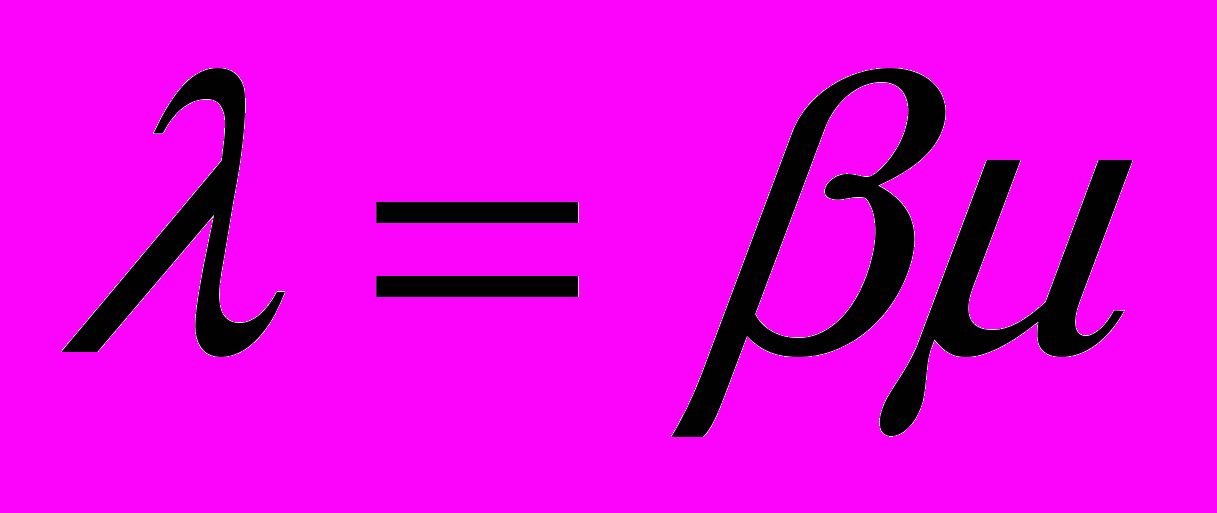и 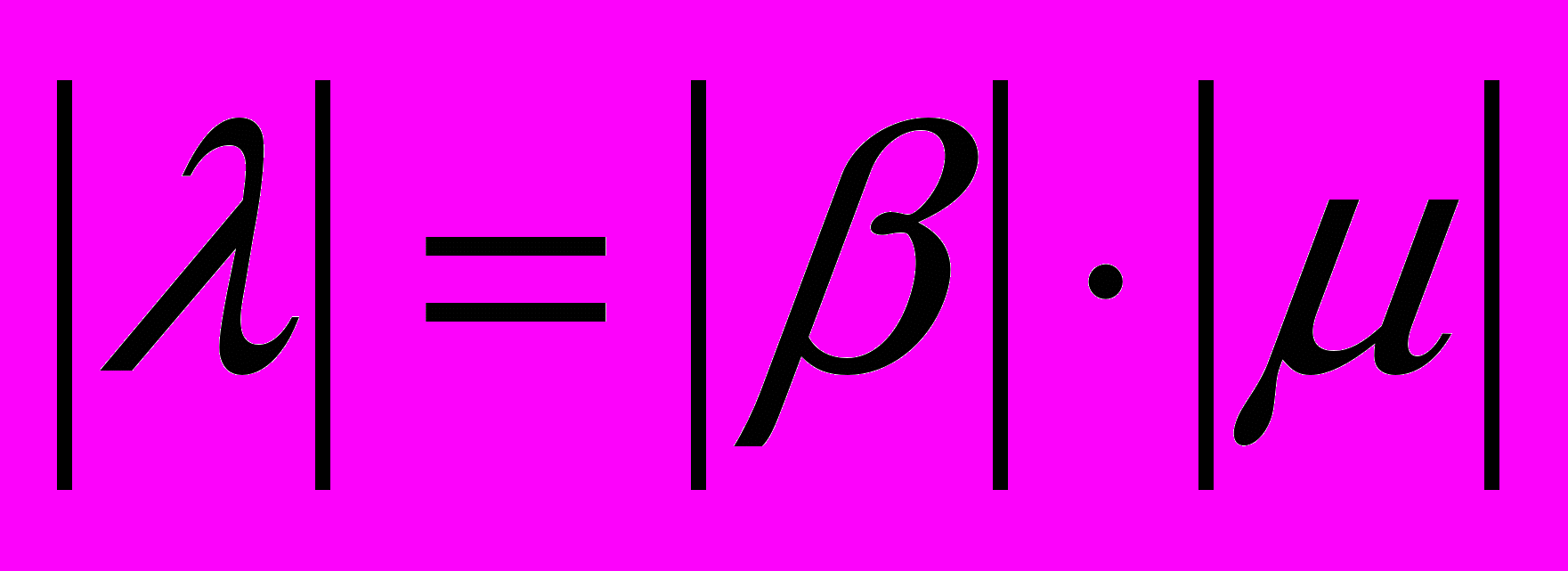. Мы получаем, что неравенства 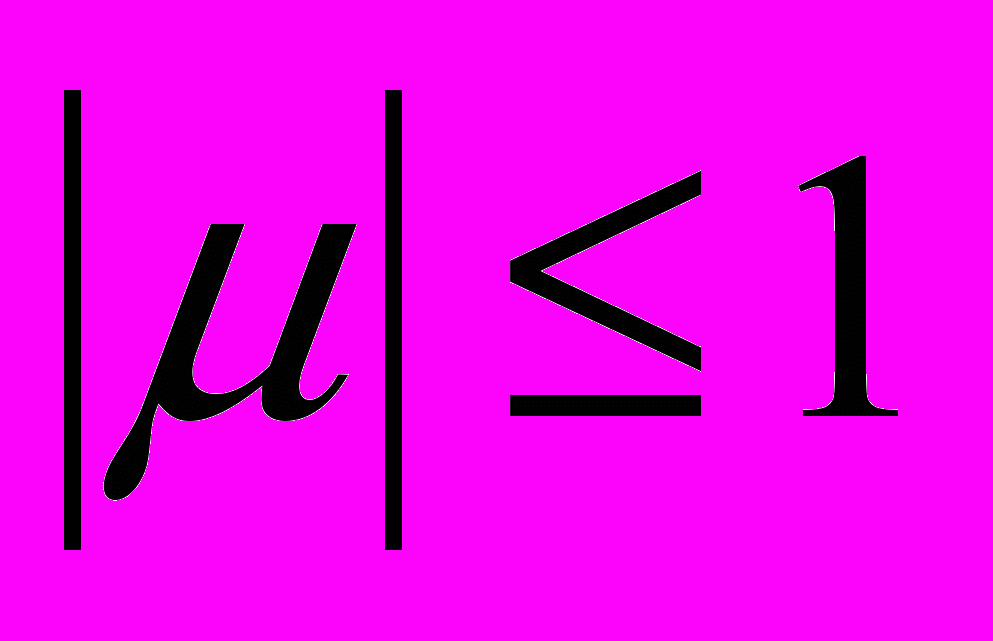и 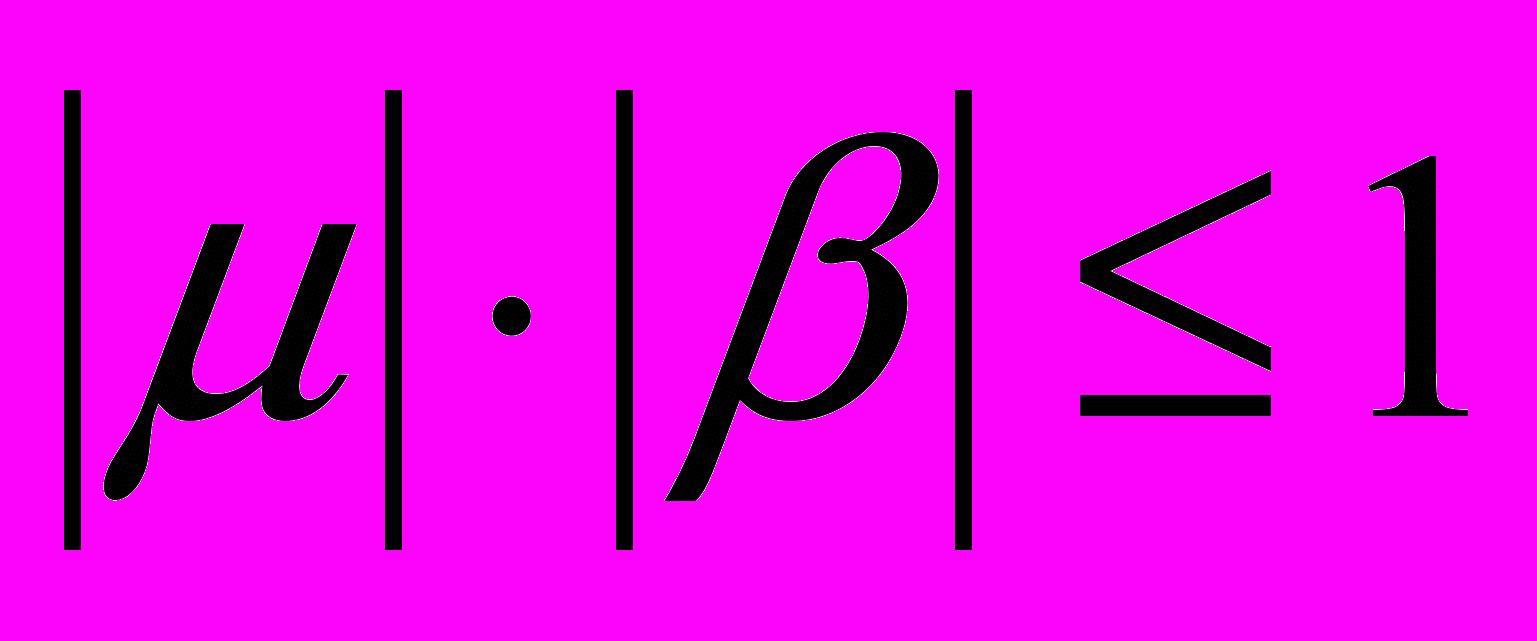должны бать равносильны (относительно ), следовательно, 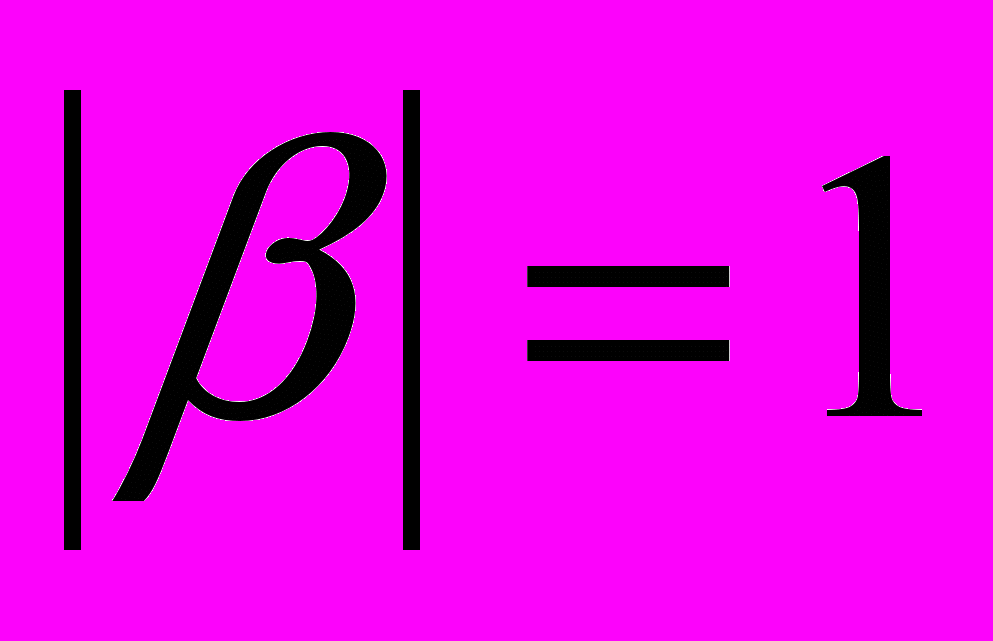и 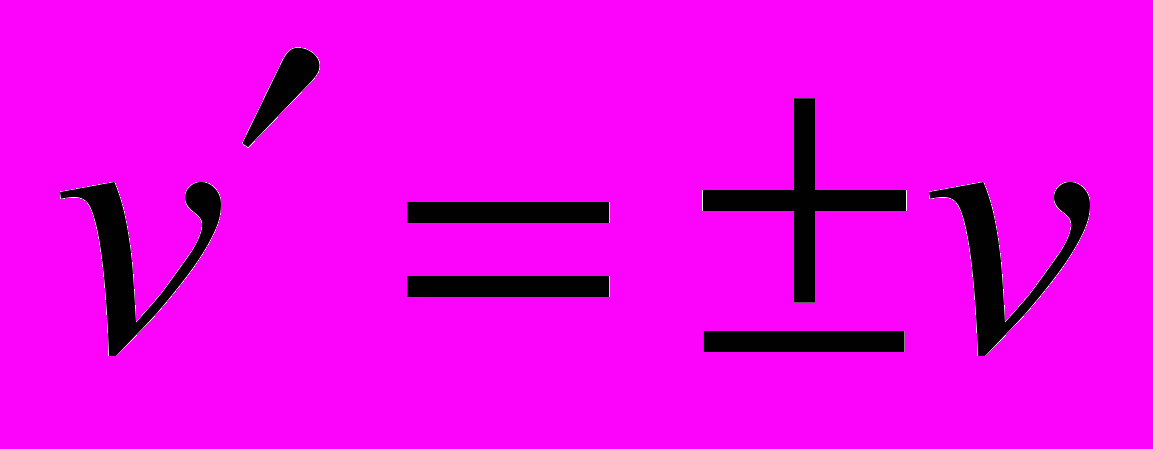. Если 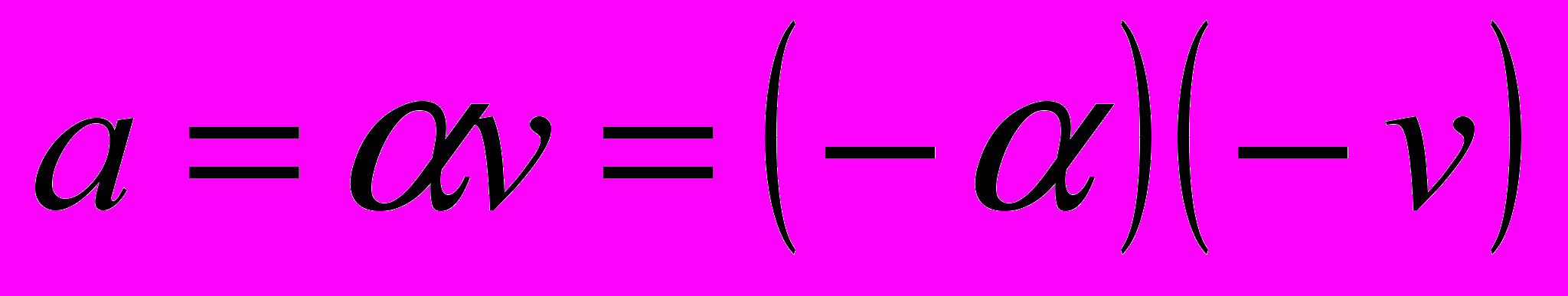, то его норма в обоих случаях равна .

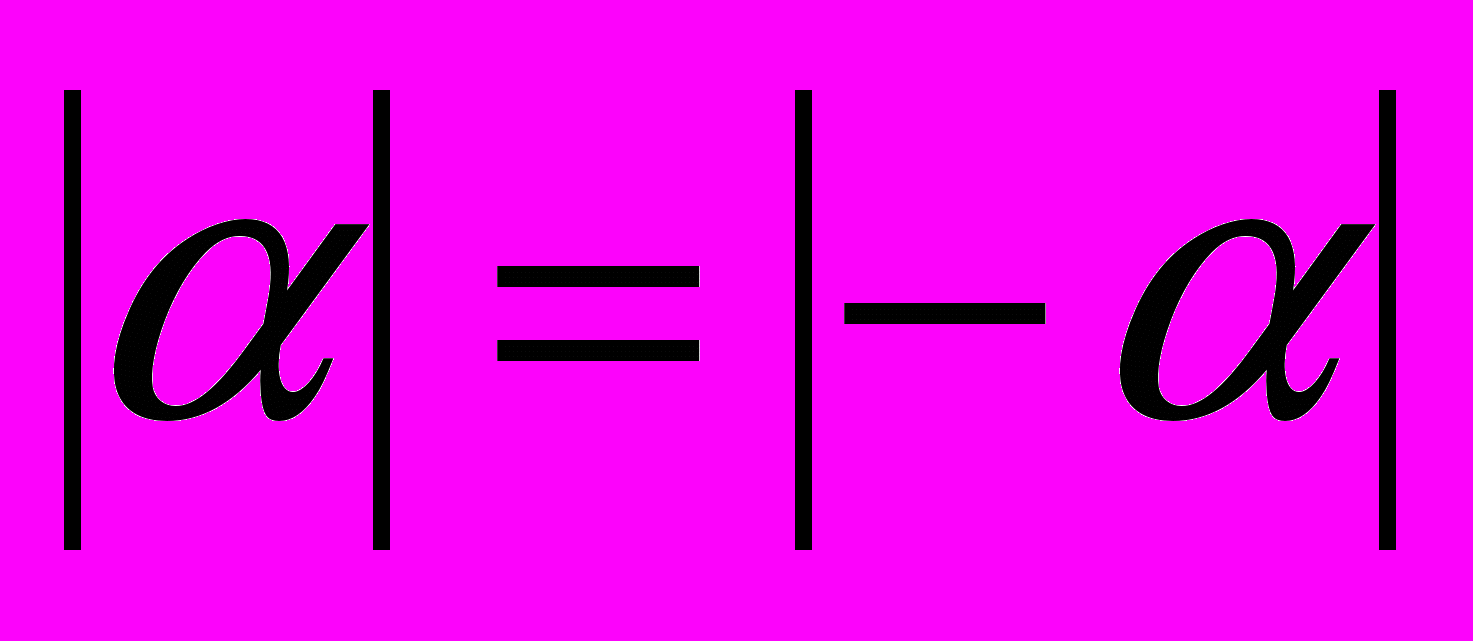Возьмем произвольный вектор 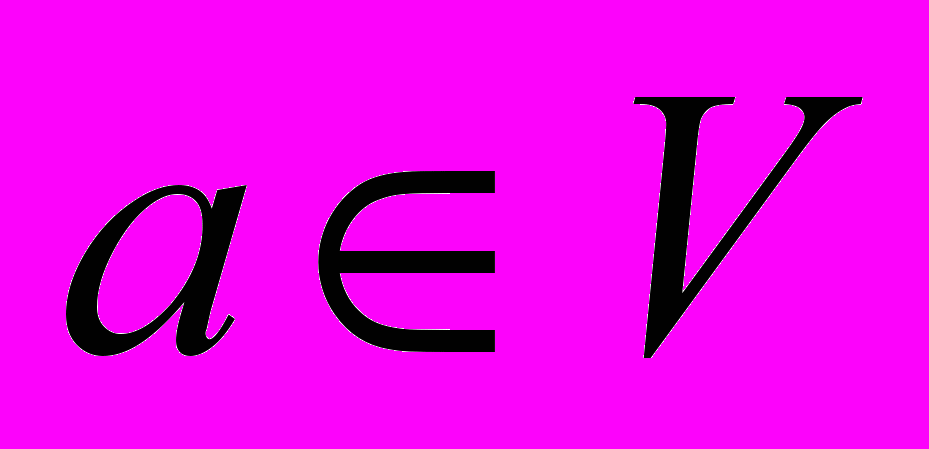, он задает одномерное пространство 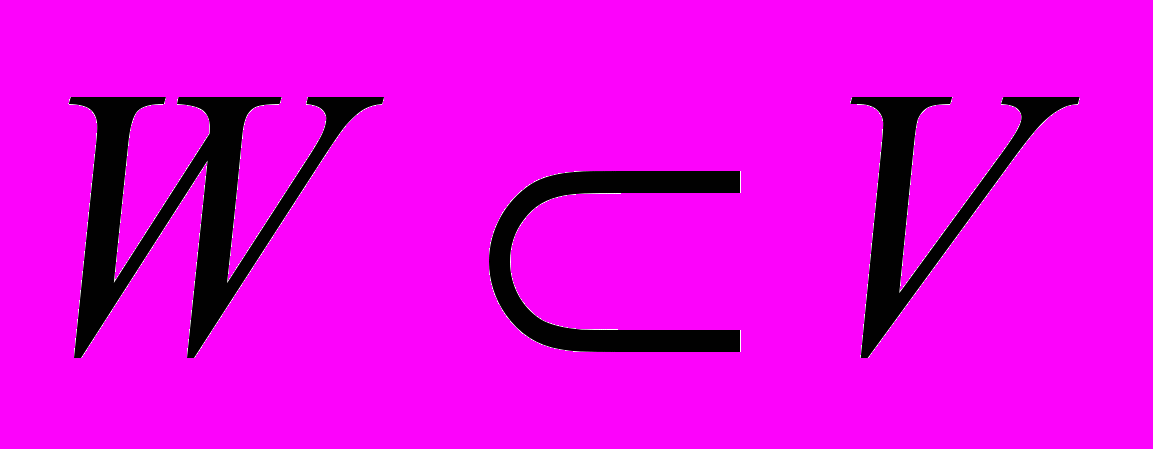, определим норму как показано выше. Проверим, будут ли выполнены необходимые условия нормы, первые два условия очевидны, а третье (неравенство треугольника) надо проверять:

Возьмем произвольные вектора 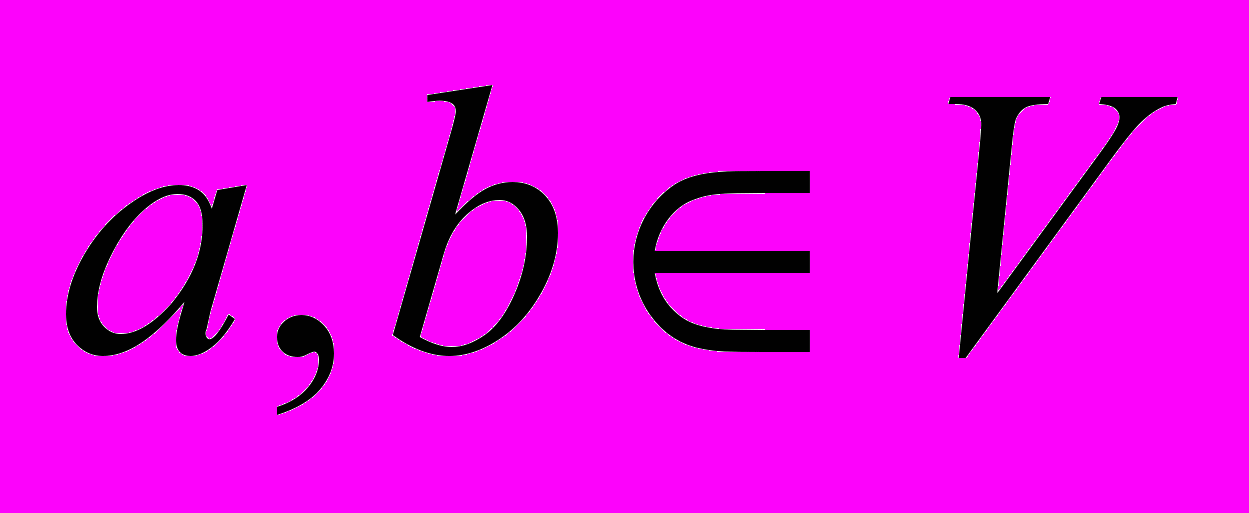, рассмотрим вектора 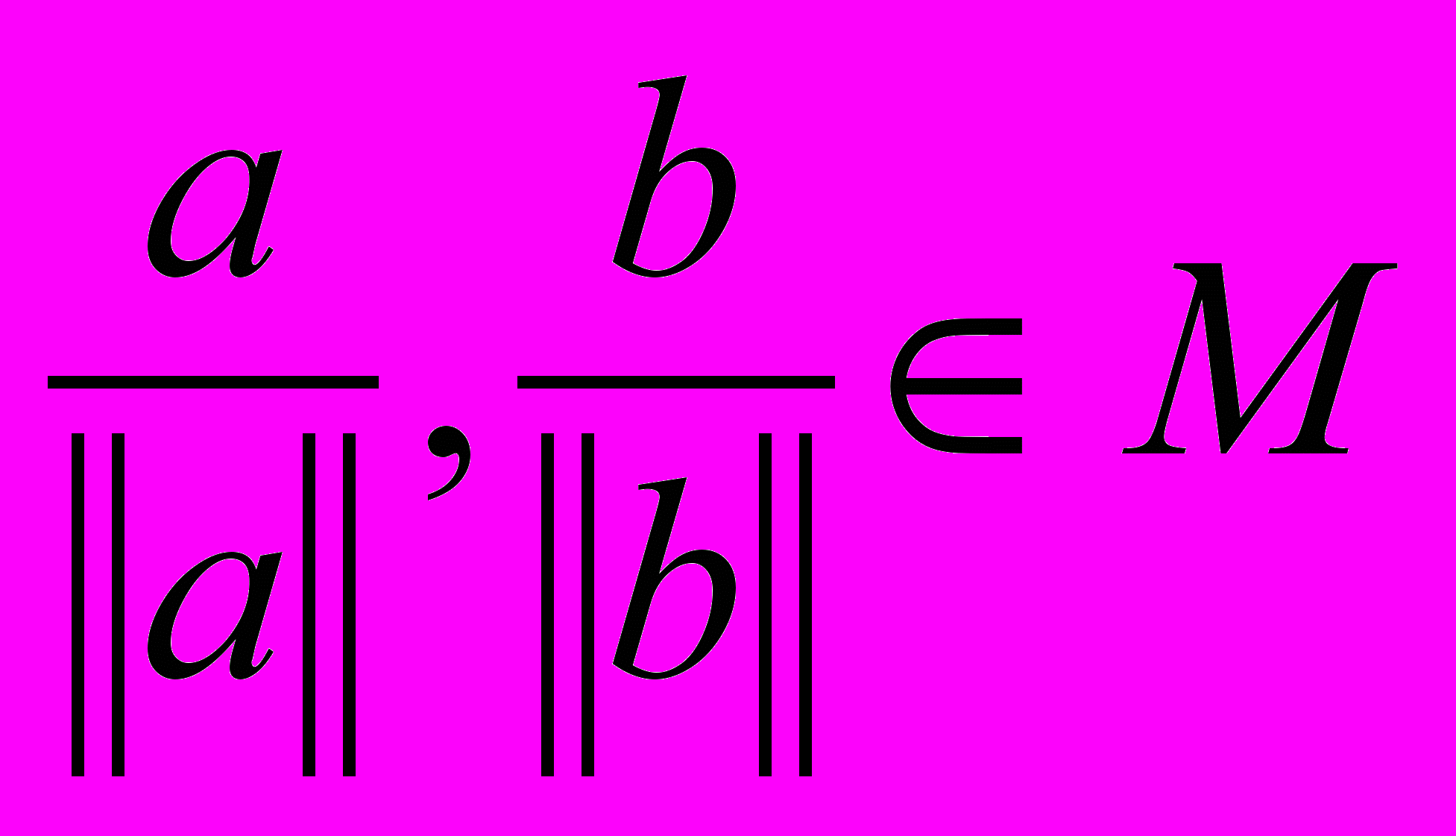, т.к. их норма равна 1. Т.к. множество 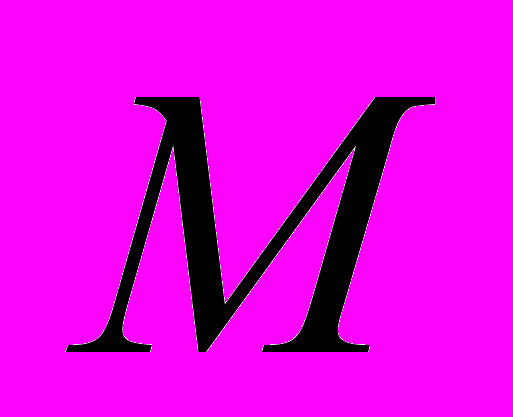выпукло, то 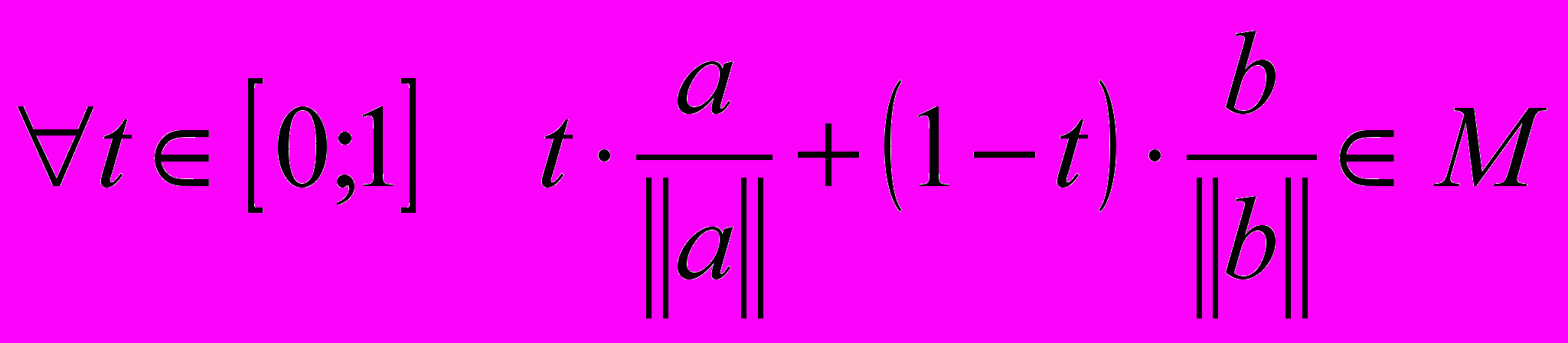. Возьмем , тогда точка , следовательно 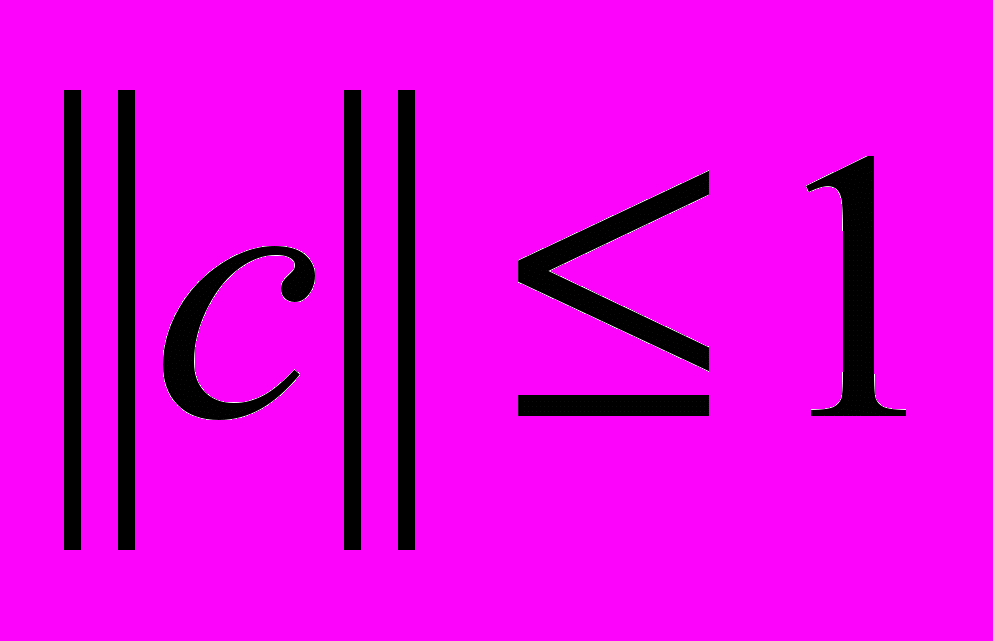. Т.е. 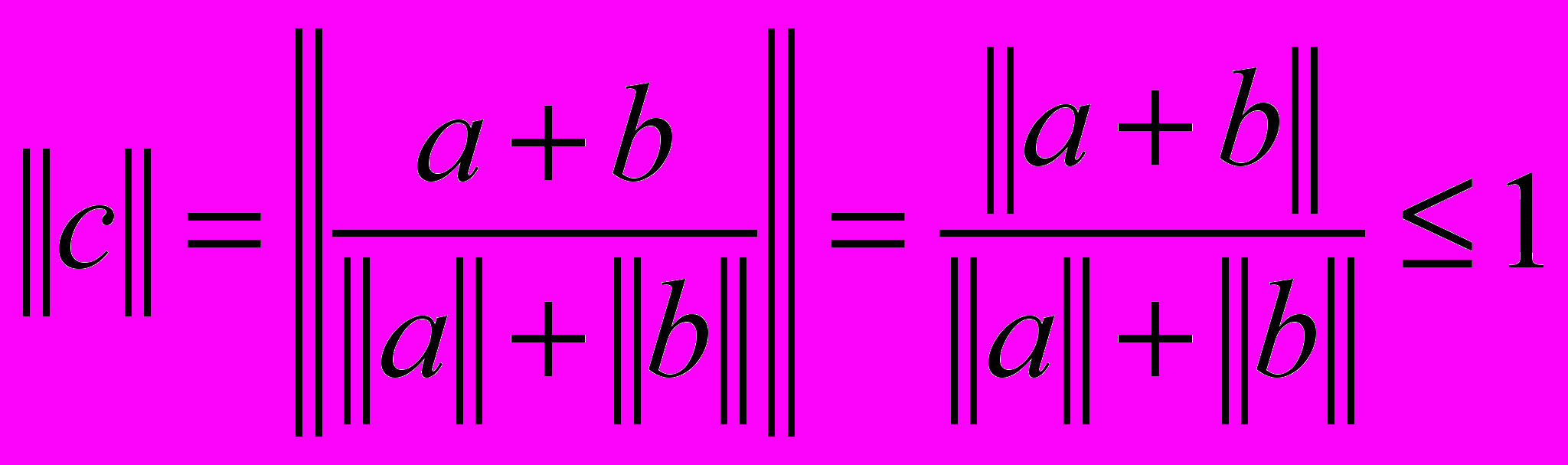, отсюда уже следует неравенство треугольника .#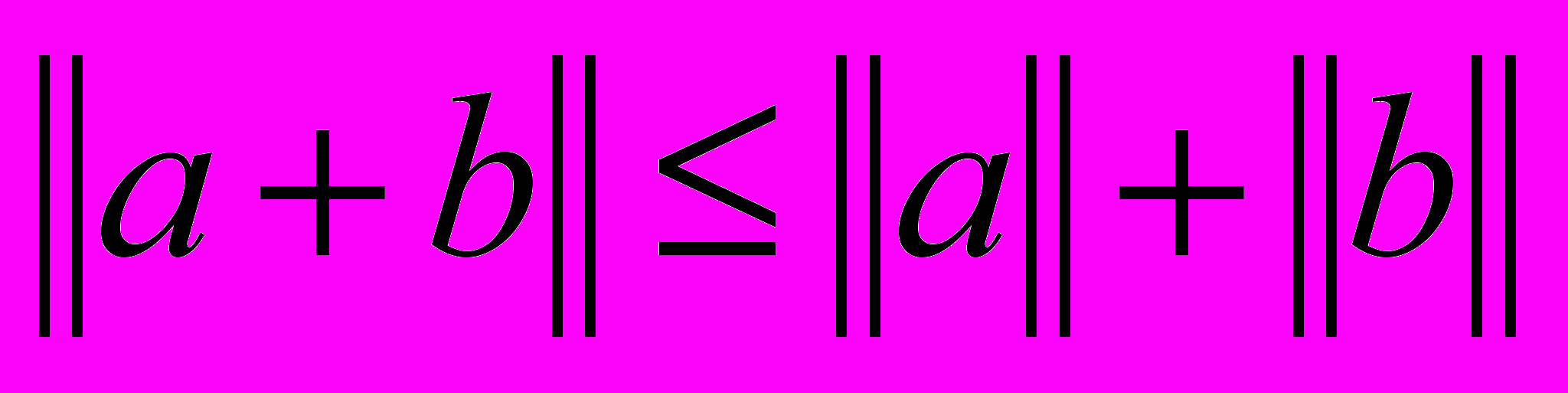