Математическая логика

Вид материала

Документы

Содержание Машина Тьюринга Т= полностью определяется

Подобный материал:

• Рабочая программа по дисциплине в 2-Математическая логика и теория алгоритмов шифр, 316.78kb.
• Программы кандидатского экзамена по специальности 01. 01. 06 "Математическая логика,, 50.44kb.
• Рабочая учебная программа по дисциплине математическая логика, 72.41kb.
• Рабочей программы учебной дисциплины дв2 Математическая логика и теория алгоритмов, 50.1kb.
• Рабочая учебная программа по дисциплине «Математическая логика и теория алгоритмов», 69.99kb.
• Н. В. Папуловская Математическая логика Методическое пособие, 786.38kb.
• Уакиев Валериан Савирович рекомендуемая литература, 334.04kb.
• Аннотация программы учебной дисциплины «Дискретная математика и математическая логика, 55.65kb.
• Логика компьютера, 210.22kb.
• Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.

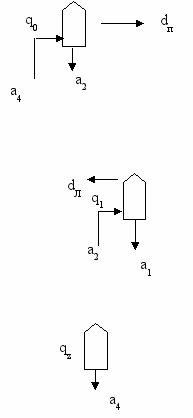
1) Пусть последовательность k₀ k₂ k_z имеет вид q₀ a₂ a₁ a₄ q₁ a₁ q_z a₄ a₂ (очевидно, что последовательность команд следующая: q₀ a₂  q₁ a₄ d_п, q₁ a₁ q_z a₂ d_Л).

Имеем следующую интерпретацию смены ситуаций:

a0

a2

a1

a0

a0

k₀

a0

a4

a1

a0

a0

k₁

a0

a4

a2

a0

a0

k_z


2) Машина Т=<a₀, a, q₀, q_z, q₀ a₀ q₀ a d_п, q₀ a q₀ a d_п> будет работать бесконечно, заполняя все ячейки ленты символами а вправо от начальной пустой ячейки (исходная информация на ленте - пустые символы а₀ в каждой ячейке ленты).

Примечания:

1. Соответствие, устанавливаемое машиной Тьюринга между теми исходными данными, к которым она применима ( то есть если она приводит к результату) и результатами ее работы представляет собой некоторую словарную функцию (в математическом смысле) Т(^*_исх^*_рез_исх_рез_пром.
   
2. Если для функции имеется машина ее реализующая, то говорят, что эта функция вычислима по Тьюрингу. Функция, для вычисления которой существует алгоритм, называется вычислимой.
   
3. Поскольку слово (^*, m) можно отождествить с натуральным числом (в m-ичной системе счисления), то уточнение понятия вычислимой словарной функции приводит и к уточнению понятия вычислимой числовой функции f:N^kN, kN. Тьюринг доказал. что класс числовых функций, вычислимых на машине Тьюринга, совпадает с классом частично-рекурсивных функций.
   

Формальное определение машины Тьюринга.

Машина Тьюринга Т= полностью определяется:

1. внешним алфавитом А=а₀, а_1… а_m;
   
2. Алфавитом внутренних состояний Q=q₀, q_1… q_n;
   
3. Программой , то есть совокупностью выражений Т(i, j) (i=0,n; j=0,m), каждое из которых имеет вид следующей команды q_j a_i  q_k a_L d_t (k=0,n; L=0,m; d_t  d_Л, d_п, d_н.
   

Машина Тьюринга есть формальная детерминированная система F.S==x, R>, порождающая множество L своих конфигураций (машинных слов) ₁ q_j a_i ₂ (₁, ₂А^*, ₁ и ₂ могут быть пустыми). Единственная аксиома – начальная конфигурация q₀ (А^*), правила вывода R – система команд (программа) Т(i, j).

Примечания:

1. Очевидно, что всякий алгоритм является формальной системой F.S, что следует из тезиса Тьюринга: «Любой алгоритм может быть реализован машиной Тьюринга».
   
2. Поскольку машина Тьюринга есть алгоритм, то записью последнего является программа , а алгоритмом выполнения – описание устройства машины Тьюринга.
   

Пример:

Построить машину Тьюринга для вычисления базисной рекурсивной функции f(x)=x+1, xN₀ Имеем T=0, Q=q₀, q_z, =

A\Q	q0	qz
a0	dн qz	a0 dн qz
	dn q0	dн qz

>
или