Математическая логика

Вид материала

Документы

Содержание Машина Тьюринга Т – название, закрепившееся за вычислительными абстрактными машинами некоторого точно охарактеризованного типа.

Подобный материал:

• Рабочая программа по дисциплине в 2-Математическая логика и теория алгоритмов шифр, 316.78kb.
• Программы кандидатского экзамена по специальности 01. 01. 06 "Математическая логика,, 50.44kb.
• Рабочая учебная программа по дисциплине математическая логика, 72.41kb.
• Рабочей программы учебной дисциплины дв2 Математическая логика и теория алгоритмов, 50.1kb.
• Рабочая учебная программа по дисциплине «Математическая логика и теория алгоритмов», 69.99kb.
• Н. В. Папуловская Математическая логика Методическое пособие, 786.38kb.
• Уакиев Валериан Савирович рекомендуемая литература, 334.04kb.
• Аннотация программы учебной дисциплины «Дискретная математика и математическая логика, 55.65kb.
• Логика компьютера, 210.22kb.
• Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.

Машина Тьюринга Т – название, закрепившееся за вычислительными абстрактными машинами некоторого точно охарактеризованного типа.

Содержательное понятие машины.

Машину Тьюринга Т=0, q_z, > удобно представлять в виде автоматически функционирующего устройства, способного находиться в конечном числе внутренних состояний Q=q₁…q_n-2, q_z и снабженного бесконечной внешней памятью – лентой. Среди состояний Q имеются два выделенных – начальное q₁ и заключительное q_z. Лента разделена на ячейки и потенциально бесконечна в обе стороны. В каждой ячейке ленты может быть записана любая из букв внешнего алфавита А=a₀, a₁…a_m (a₀ – пустая буква, то есть считается, что в пустой ячейке записана a₀). Функционирование машины обуславливает программа =q_j a_i  q_k a_L d_t.

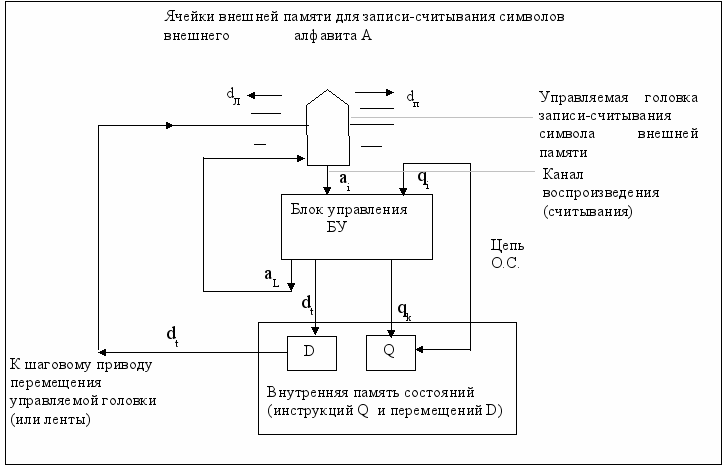
Схема такого устройства как совокупность стуктурно-связанных внутренней и внешней памяти, блока управления и управляемой головки

a0

a2

a5

ai

a9

a3

a5

a0

дает возможность имитировать алгоритмические процессы распознавания и порождения цепочек языка произвольного типа (по Хомскому).

На схеме:

а) Блок управления производит преобразование пары (цепочки из двух символов) q_j a_iQ*A в тройку q_k a_L d_t Q*A*D. Это означает, что если машина находится в состоянии q_j (то есть вычисляет инструкцию q_j), а управляемая головка считывает символ a_i из обозреваемой ячейки внешней памяти, то блок управления вырабатывает команду q_k a_L d_t, согласно которой:

1. машина переходит в состояние q_k (допускается k=j);
   
2. в обозреваемую ячейку ленты вместо символа a_i записывается символ a_L (допускается i =L);
   
3. управляющая головка (лента) перемещается на один шаг или остается на прежнем месте (d_Л – перемещение на один шаг влево, d_п – перемещение на один шаг вправо, d_н – оставаться на месте; d_Л, d_п, d_нD).
   

Итак, если блок управления осуществляет функциональное отображение:

Г_f: Q*A Q*A*D,

где q_j a_iQ*A, q_k a_L d_t Q*A*D, a_i, a_LА, q_j, q_kQ, d_t D= d_Л, d_п, d_н, то машину Тьюринга будем называть детерминированной и всюду определенной.

б) Данные (исходные, промежуточные и окончательные) машины есть цепочки символов (слова) в алфавите А, которые записываются на бесконечной ленте внешней памяти (каждый символ слова в отдельной ячейке) (А=А_исх А_промА_рез, а₀А_исх, а₀А_рез).

в) Элементарные шаги в рассматриваемой машине следующие:

1. изменение состояния машины и содержимого ячейки, обозреваемой управляемой головкой;
   
2. перемещение управляемой головки на один шаг влево ( вправо);
   

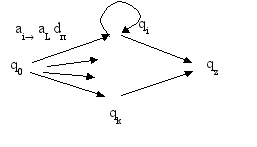
г) Детерминированность работы машины обуславливается программой ее работы , то есть совокупностью выражений (j, i) (j=0,n; i= 0,n), каждое из которых имеет один из следующих видов:

q_j a_i  q_k a_L d_н

q_j a_i  q_k a_L d_Л

q_j a_i  q_k a_L d_п,

где 0  k n, 0 L m.

В дальнейшем программу будем записывать в табличном виде:

A \ Q	q0	q1	…	qj	…	qz
a0
a1
…
ai				qk aL dt
…
am

или диаграммой переходов вида:




д) Начальная атрибуция (конфигурация машины) характеризуется следующим образом:

1. на ленте записано слово А^*;
   
2. управляемая головка указывает на ячейку ленты, в которой записан самый левый символ цепочки (слова),
   
3. машина находится в начальном состоянии q₀  Q;
   

Пример начальной конфигурации машины:

a0

a0

a2

a4

a7

a3

a9

a0

a0

a0

Символически эта конфигурация записывается как машинное слово q₀= q₀ a₂ a₄ a₇ a₃ a₉= k_0.

e) Текущая (промежуточная) ситуация (конфигурация) k_p есть машинное слова вида ₁ q_j a_i ₂, где ₁ и ₂ – цепочки символов алфавита А.

ж) Заключительная ситуация (конфигурация) k_z имеет вид q_z, где q_z – заключительное состояние машины, q_zQ, - результат работы машины из исходной ситуации по заданной программе, А^*.

Очевидно, что последовательность конфигураций k₀ k₁ k₂… однозначно определяется исходной конфигурацией k₀ и полностью описывает работу машины Тьюринга Т= =0, q_z, >, начиная с k₀= q₀ (А^*_исх, А_исхА). Эта последовательность конечна, если в ней встретится заключительная конфигурация k_z= q_z, и бесконечна в противном случае.

Пример: