Системантика
| Вид материала | Монография |
Содержание3. Алгоритмы поиска 1. Редукционная модель Тезис: Земля имеет форму шара. Общее правило |
3. Алгоритмы поиска
Всякий алгоритм можно записать в машинно-независимой форме в виде графа зависимости вычисляемых величин друг от друга. Последовательность выполнения отдельных операций в соответствии с этим графом создает поток данных. Машины, реализующие архитектуру их потока, называют машинами потока данных, которые представляют основные направления развития мультипроцессорных систем. Граф потока данных для вычисления корней квадратного уравнения показан на рис. 73, 74.
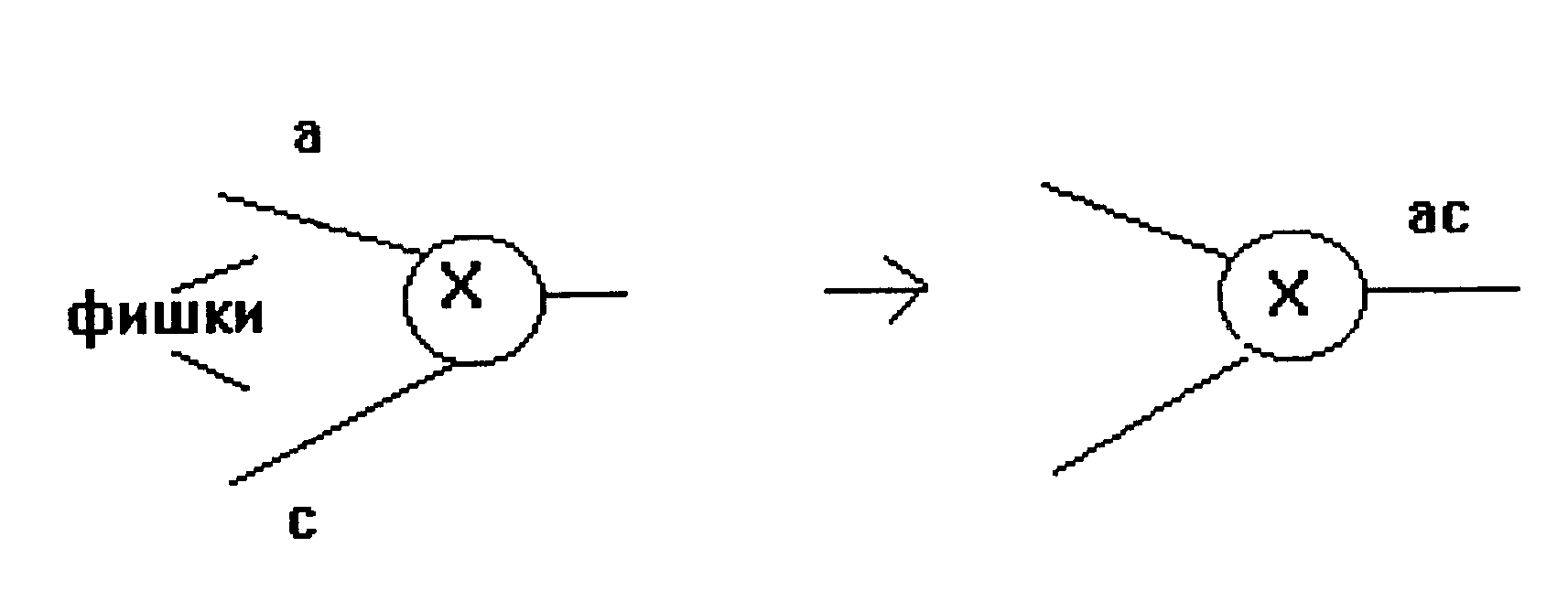
Рис. 74. Схема элементарного действия
На этом графе показан переход от исходных коэффициентов уравнения (а, с) к результатам счета (х1, х2). В узлах обозначены акторы, т. е. вершины, в которых включаются различные действия. Движущиеся числа обозначают фишками. Актор взводится, когда на всех входах присутствуют фишки (входные величины), и выстреливает, удаляя фишки с входных ребер и помещая их на выходные (рис. 74).
Функционирование таких сетей описывается сетями Петри.
Представим себе, что в каждом узле графа помещено по компьютеру и каждый процессор выполняет действие тогда и только тогда, когда на его вход поступают все нужные операнды. При этом каждый процессор выполняет специальную работу. Такой принцип построения вычислительной сети называется конвейерным.
При конвейерной обработке нет необходимости ждать выполнения всего процесса предыдущих операций. Достаточно, чтобы у предыдущей операции был выполнен хотя бы один первый этап (рис. 75, 76, 77).
Рис. 75. Схема конвейерной обработки
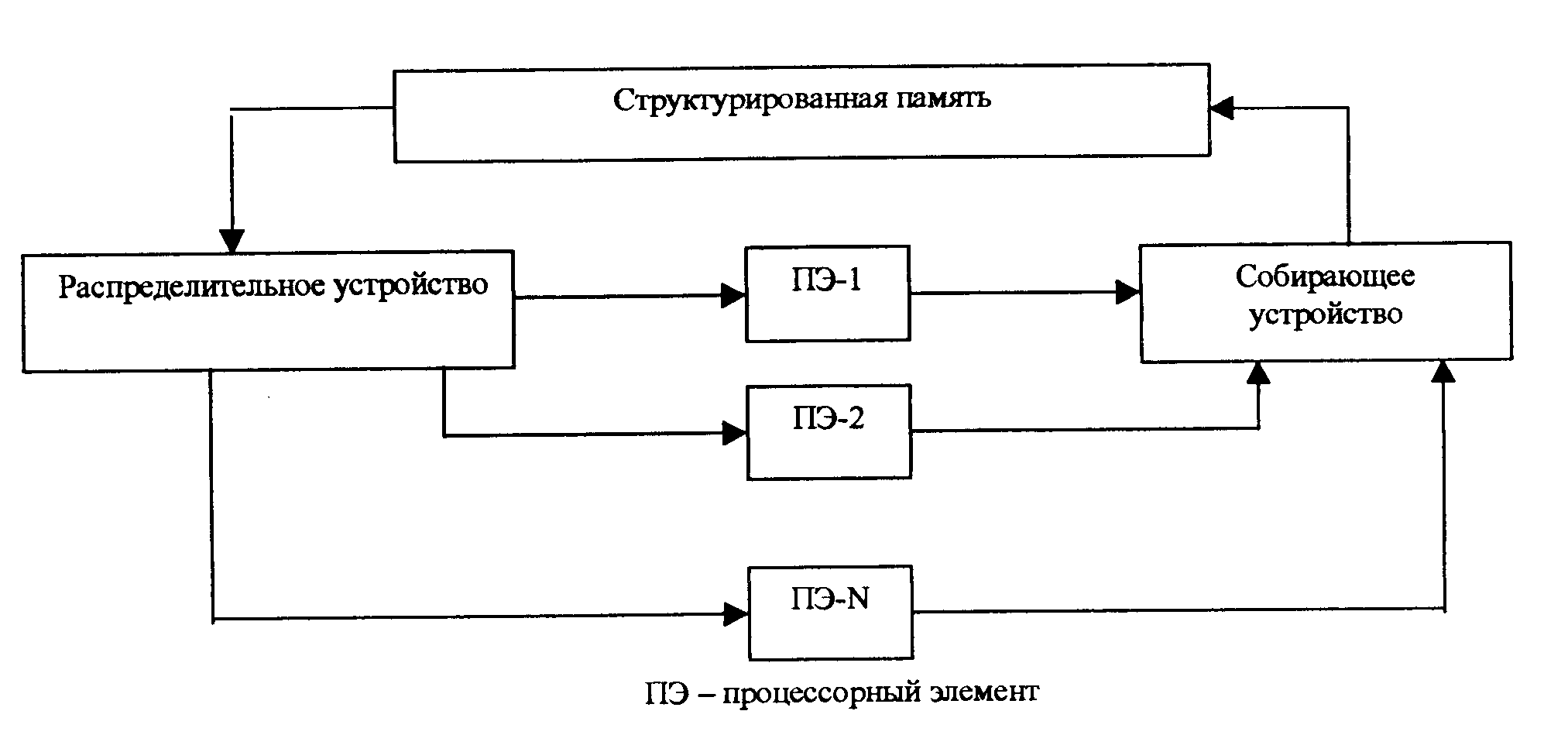
Рис. 76. Архитектура средств конвейерной обработки
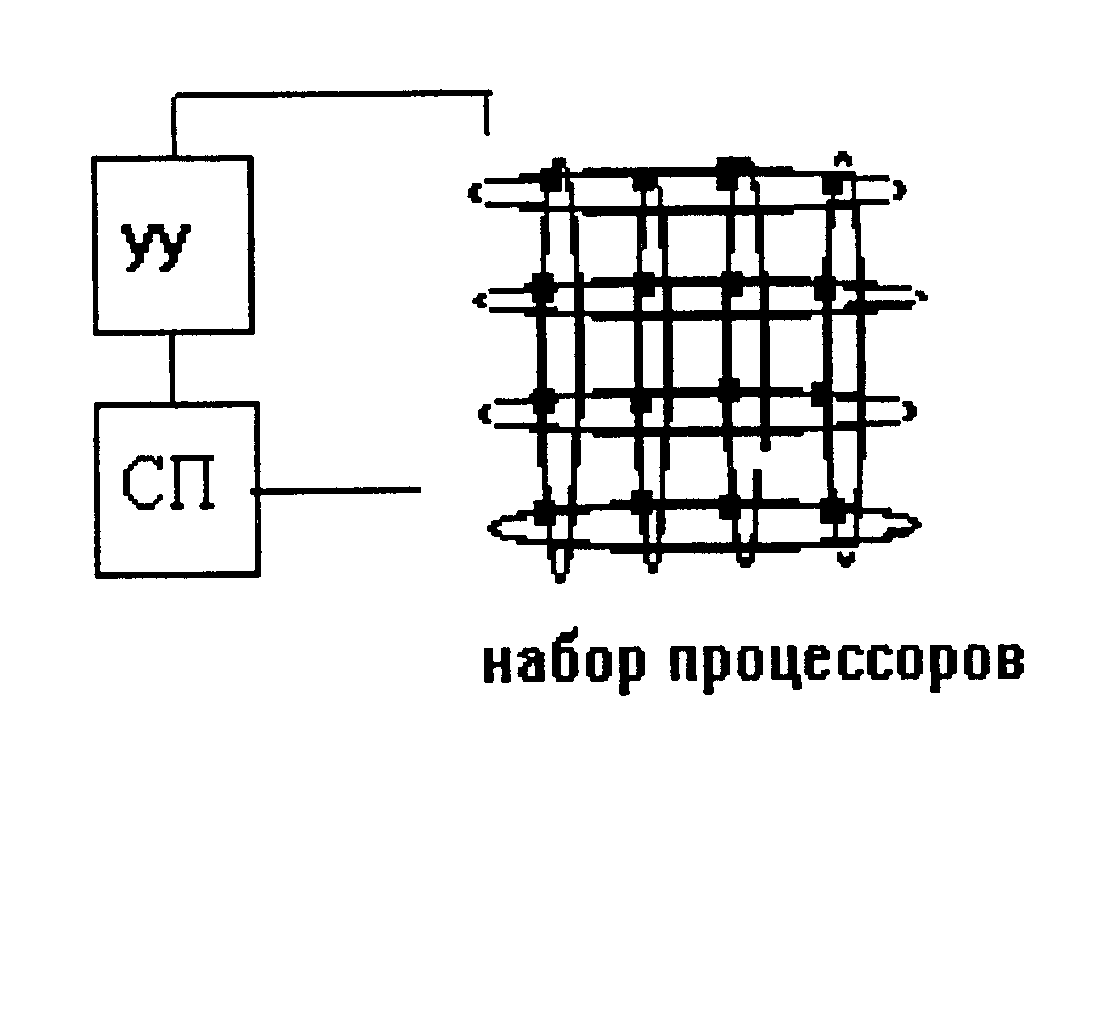
Рис. 77. Принципиальная схема машины потоков данных
* – процессор;
УУ – устройство управления;
СП – структурированная память
Процедурные знания можно представить как механизмы, выполняющие определенные действия. Существует набор элементарных операций, позволяющий путем их комбинации создать сколь угодно сложные механизмы. Набор элементарных операций, определяется составом машинных команд конкретных электронно-вычислительных машин.
Становится необходимым создать аппарат для полного, ясного и однозначного описания вычислительных процессов, реализующих процедурные знания, получивший название алгоритм.
Понятие алгоритма уже давно возникло в математике. Однако оно стало развиваться особенно быстро и получило практическое применение с появлением ЭВМ.
Глава X
ЛОГИЧЕСКИЙ ВЫВОД И ЭВРИСТИЧЕСКИЙ ПОИСК
1. Редукционная модель
Логика – это наука о способах доказательств и опровержений. Особую роль играют ее приложения в обработке текстовой информации. Различают логику индуктивную и дедуктивную. Обе эти логики определяют способы рассуждений, которые от истинных суждений (посылок) приводят к истинности суждений (следствий).
Индуктивная логика – это способ рассуждения от частного к общему, от фактов к обобщению. Индуктивная логика позволяет отделить форму от содержания в процессе познания исследуемой предметной области.
Дедуктивная логика определяет логический вывод от общего к частному. При этом новое положение выводится чисто логическим путем, т. е. по законам формальной логики, из предшествующих положений – посылок.
Любой компонент логического вывода является либо ранее доказанным положением, либо аксиомой, либо гипотезой. Результат логического вывода называется заключением.
При дедуктивном доказательстве тезис, являющийся частным случаем суждения, подводится под общее правило.
Суть доказательства состоит в том, чтобы общие правила, под которые подводится данный факт, были истинными. После чего правило распространяется на доказываемый тезис.
Тезис: Земля имеет форму шара. Общее правило: все планеты имеют форму шара. Рассуждение: если все планеты – шары, а Земля – планета, то Земля – шар.
В формальной логике различают три вида дедуктивных умозаключений, обеспечивающих при истинности посылок и соблюдении правил логики истинность заключения.
1. От общего к единичному или менее общему.
2. От одной общности к другой. Все нефтепродукты – органические вещества. Ни один из минералов не является органическим веществом. Ни один нефтепродукт не является неорганическим веществом.
3. От единичного к частному. Литий легче воды. Литий – металл. Следовательно, некоторые металлы легче воды.
Диалектика считает индукцию и дедукцию лишь особыми, но не самостоятельными видами познания, не изолированными друг от друга. Одно невозможно без другого.
Всякая научная дедукция является результатом предварительного индуктивного изучения предмета и основывается на этом изучении.
В свою очередь, индукция является подлинно научной только тогда, когда изучение отдельных частных явлений основывается на знании общих законов.
В отличие от методов формальной логики эвристика изучает закономерности и методику процессов поиска решения той или иной задачи на содержательном уровне, сводя к минимуму или ограничивая перебор возможного множества решений этой задачи, сокращает время по сравнению с формальными методами решения.
Главной темой начальной стадии работ по искусственному интеллекту, начавшихся в 50-х гг. прошлого века, явилась разработка теории эвристического поиска. Общая постановка его задачи в неформальном виде выглядит следующим образом: задана начальная и целевая ситуация, имеется набор операторов, изменяющих ситуации. Нужно найти последовательность преобразований или последовательность операторов, приводящих от начальной ситуации к целевой.
В случае игры в шахматы начальное положение на доске и множество позиций, в которых одна из сторон выигрывает, требуется найти последовательность ходов, преобразующих начальную ситуацию в целевую.
Исследовательским полигоном для различных методов эвристического поиска являлись всевозможные игры и головоломки. Некоторые из них стали классическими в литературе. Игры и задачи брались потому, что при относительно простых мирах, в них содержатся сложные ситуации.
В 60-х гг. ХХ в. появилась потребность проверить результаты на реальных мирах.
Стратегия поиска решений предусматривает разбиение исходной задачи на более простые до тех пор, пока решение не будет представлено в виде элементарных действий, выполняемых в определенном порядке. Задачу можно записать в виде:
Задача: = <So, Sn, {Fj}, {SFj}>,
где фигурные скобки обозначают множества. Эта модель называется редукционной (рис. 78).
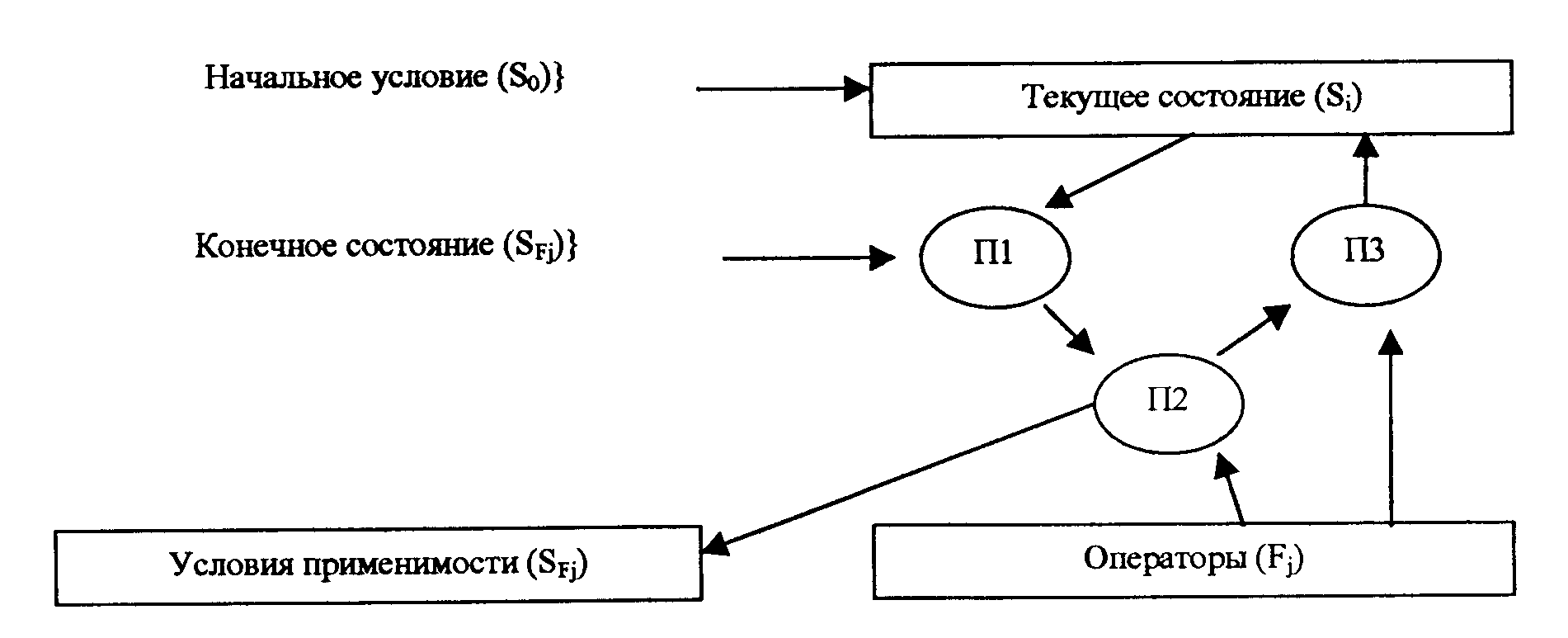
Рис. 78. Блок-схема редукционной модели
Процедура П1 осуществляет проверку на совпадение текущего состояния с целевым и вырабатывается список различий. Процедура П2 находит оператор, уменьшающий различие. Процедура П3 применяет оператор к начальному состоянию.
Рассмотрим в упрощенном варианте модель перестановки предметов (см. рис. 79).
Пусть имеется оператор Fр, с помощью которого мы переходим из S0 в SFp.
1) Fp; (S0) → SFp
2) Sk = Fp(SFp) – некоторое состояние.
3) Sk → Sn
K1 не находится на платформе 2. К4 не на К1.
Рассмотрим некоторые операторы:
F1: К1 → Р2
F2: К4 → К1
К2 на К1
F3: снять К2 с К1
К3 на К2
F4: снять К3 с К2
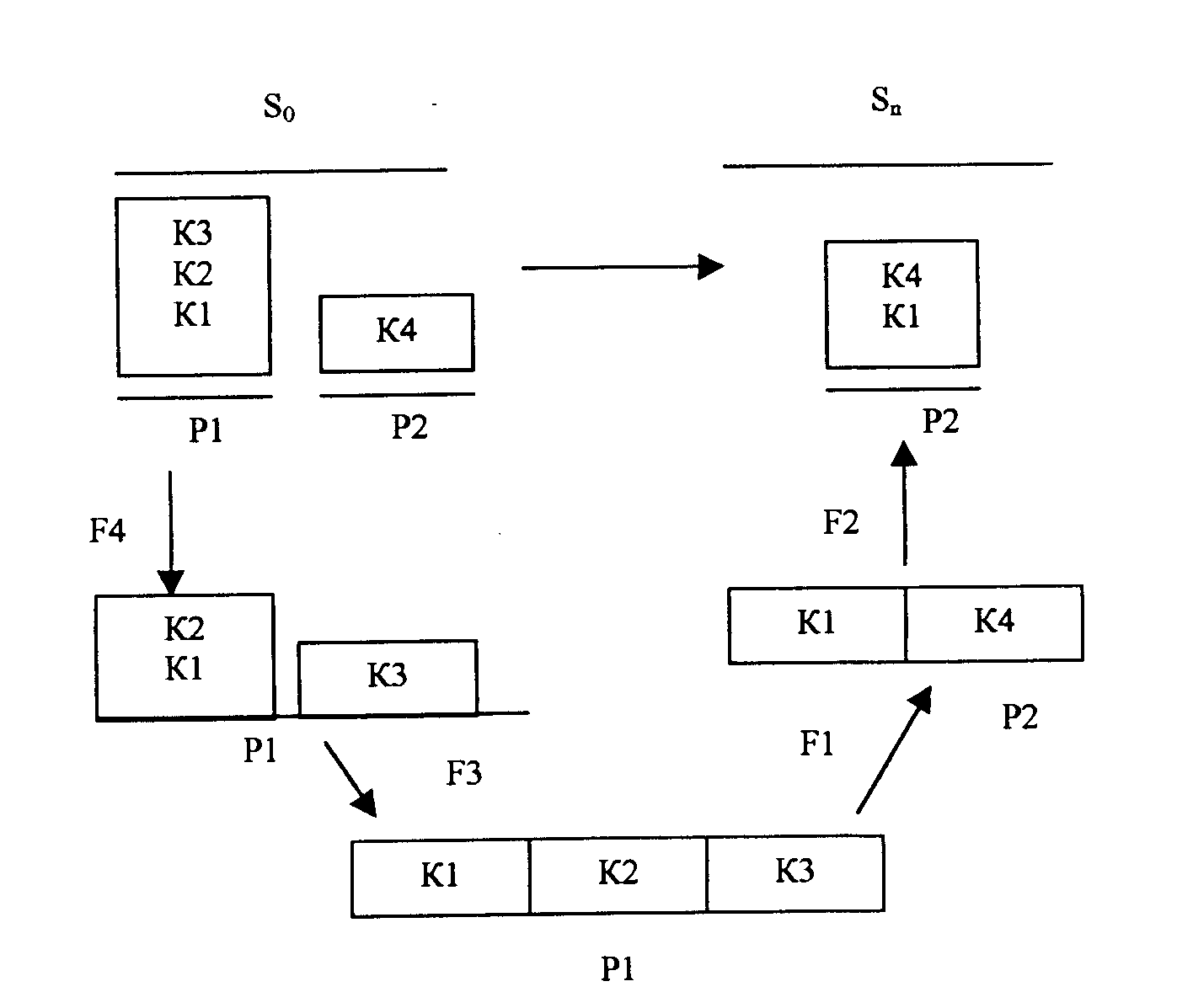
Рис. 79. Начальное, текущее и конечное состояние задачи
Таким образом, будет найдена следующая последовательность операций:
F4: снять К3 с К2;
F3: снять К2 с К1;
F2: перенести К1 на Р2;
F1: поставить К4 на К1.
Логический вывод включает не только объективное знание, отражающее достоверность результатов, но и субъективное, несущее возможность правдоподобных рассуждений.
Редукционная модель представляет процедурные знания в интеллектных системах. Она находит широкое применение при синтезе планов решения задач и принятия решений.
Принятие решения – сложный технологический процесс, который можно определить как выбор направления действия для достижения цели. Описания этого процесса используют классические, поведенческие и нечеткие модели принятия решений.
Согласно каждой из этих моделей, принимающий решение субъект не сравнивает непосредственно альтернативы. Он выбирает их либо с помощью таких учитываемых в поведенческой модели факторов, как конечный эффект или желаемый уровень поведения, либо на основе функций выигрыша, как в классическом случае. Исход, соответствующий каждой альтернативе, – это результат сложного сплетения всех переменных, описывающих внешние условия, со всеми переменными, характеризующими альтернативу.
Однако чем более аморфна проблема, тем труднее становится правильное предсказание этих переменных и, в конечном итоге, исхода.
В этих условия субъект обычно абстрагирует проблему и строит простую модель, а затем полученным из анализа модели исходом подменяет непредсказуемый исход первичной проблемы.
Для этой цели с семантических позиций осуществляется «размывание» вычисленного исхода. Нечеткое утверждение более пригодно для решения сложных проблем и более адекватно отражает семантическую сущность анализируемых человеком и компьютером понятий и утверждений.
Выигрыш – это выраженный в количественной форме исход, оцененный с учетом цели или системы предпочтений.
Поэтому выигрыш должен быть нечетким и не только потому, что зависит, по существу, от нечеткого исхода, но также и потому, что его значение получается в результате неоднозначной процедуры оценивания.
Желаемый уровень поведения также можно рассматривать как нечеткий, поскольку он опирается на неуловимые стремления субъекта достигнуть определенную цель. Желаемый уровень поведения сортирует альтернативы, сравнивая их с исходом. Поэтому нет необходимости быть абсолютно точным, поскольку рассматриваемая цель и исход сами по себе нечеткие.
Нечеткость дает ключ к углубленному исследованию семантической сущности принятия решений, начало которому положено А.А. Романовым1. При принятии решения нельзя игнорировать проблему различения. Степень различения информационных объектов можно определить как степень разделения множеств, характеризующих семантику каждого объекта. Семантически более определенная информация положительно релевантна по отношению к семантически менее определенной. Семантическая составляющая информации предполагает наличие некоторой семантической метрики для ее интерпретации. В качестве показателя семантической определенности информации можно использовать показатель размытости (меру энтропии) нечетких множеств.
Показатель семантической определенности информации по аналогии с показателем размытости нечеткого множества определяется как мера внутренней неопределенности, двусмысленности объектов семантической шкалы по отношению к некоторому свойству, характеризующему эти объекты и формально определяющему нечеткое множество объектов.
В настоящее время известен ряд показателей размытости нечеткого множества. Использование конкретного показателя зависит от вида решаемой задачи. В практике принятия решений часто бывает необходимо отнести объект к одному из двух классов, характеризующихся противоположными свойствами типа: «горячий – холодный», «хороший – плохой». Объекты могут обладать обоими противоположными свойствами в разной мере. Мера может включать вычисляемые пороговые значения.
Реализация действий заключается в превращении информационных сигналов о принятом решении в материально-энергетическое воздействие на объект.
Развитие моторного аппарата систем шло наряду с развитием рецепторно-сенсорного. Их взаимная связь обеспечивает материально-энергетическое взаимодействие моторного аппарата системы с внешним миром на основе информационного рецепторно-сенсорного взаимодействия.
В модели знаний интеллектной системы должны присутствовать модели обоих упомянутых систем.
В ходе эволюции выработались две схемы управления моторным аппаратом: рефлекторные и сознательные.
Рефлекторные движения возникают в ответ на пусковые сигналы от внешнего мира. Осознанные движения могут запускаться изнутри по памяти за счет собственной активности.
