Дослідження властивостей поверхневих циклотронних о-мод”
| Вид материала | Документы |
СодержаниеДослідження властивостей поверхневих циклотронних о-мод Е, Н ~ f(x) exp[i(k Ну(0) – величина магнітного поля на поверхні плазми, Н Список посилань |
- Робоча навчальна програма предмет Методи дослідження властивостей матеріалів (Р-32), 48.64kb.
- Стан поверхневих та підземних вод у басейні Дніпра протягом 2009 року Якісний стан, 599.58kb.
- Реферат Харків 2009, 139.06kb.
- Поняття юридичної науки та її місце в системі суспільних наук, 1990.39kb.
- Курс Викладач Жук Л. П. Дисципліна Методологія та організація наукових досліджень, 878.91kb.
- Міжнародні відносини: проблеми наукового дослідження, 138.24kb.
- Маркетингові дослідження зовнішнього ринку при здійсненні експортно-імпортних операцій, 27.09kb.
- Програма дослідження освітньо-виховної роботи в дошкільних навчальних закладах міста, 29.4kb.
- Маркетингові дослідження фірми (потік мк), 21.6kb.
- Удк 556. 52/554 еколого-гідроморфологічний аналіз умов та наслідків підвищення рівня, 272.15kb.
Дослідження властивостей поверхневих циклотронних О-мод 290786klyz
„Дослідження властивостей поверхневих циклотронних О-мод”
Напрямок: Фізика і астрономія; прикладна фізика.
Ключові слова: циклотронні поверхневі О-моди, неоднорідна плазма, хвильовий вектор, власна частота.
ВСТУП
Поширення електромагнітних хвиль у плазмі в напрямку, що є перпендикулярним магнітному полю, має цікаві особливості, які не виявляються при так званому «косому» поширенні. А саме, можлива поява нових слабко загасаючих гілок коливань – циклотронних хвиль, існування яких обумовлене скінченністю величини теплового ларморівського радіуса частинок плазми. Терміном «циклотронні хвилі» прийнято називати хвилі в плазмі із частотою розповсюдження близької до частоти обертання заряджених частинок у магнітному полі (т.зв. циклотронна частота) або її гармонікам.
Відомий цілий ряд фізичних явищ, пов'язаних із циклотронними хвилями, таких як, наприклад, випромінювання та розсіювання шумів на електронній та іонній циклотронній частотах, циклотронні резонанси в іоносфері та лабораторній плазмі, нестійкості на циклотронних частотах, що призводить до переходу плазми в турбулентний стан. Також у сучасних експериментальних плазмових установках широко використовується електронне циклотронне резонансне нагрівання та іонне циклотронне резонансне нагрівання. У цьому випадку енергія хвилі завдяки різним процесам передається частинкам плазми. У той же час відомо, що значна частина енергії хвилі втрачається в периферійній області плазми. Тому виникає питання про поверхневі хвилі.
Поверхневими називають хвилі, амплітуда яких максимальна на межі та зменшується вглиб плазми. ПХ (поверхневі хвилі) широко використовуються в багатьох областях фізики плазми, наприклад, у плазмовій електроніці [1, 2], мікрохвильових газових розрядах [3, 4] для виробництва плазми. Беручи до уваги те, що деякі типи ПХ можуть поширюватися навіть уздовж межі магнітоактивна плазма-метал [5, 6], можна очікувати, що дослідження ПХ будуть корисні при вивченні проблеми взаємодії плазми зі стінками термоядерних реакторів. Також корисним вивчення властивостей ПХ представляється з прикладної точки зору: їх можна використати для експериментального дослідження густини периферійної плазми [7]. З теорії [8] відомо два типи поляризації циклотронних хвиль: звичайні та незвичайні хвилі.
В даній роботі вперше розглянуто випадок поширення поверхневих циклотронних звичайно поляризованих хвиль в неоднорідній плазмі. Отримані залежності власної частоти хвилі від хвильового вектора для різних параметрів плазми, таких як товщина діелектрика, товщина прошарку плазми, відношення магнітного тиску до газового, для різних типів залежності неоднорідності густини від координати.
ДОСЛІДЖЕННЯ ВЛАСТИВОСТЕЙ ПОВЕРХНЕВИХ ЦИКЛОТРОННИХ О-МОД
При вивченні плазми і явищ, що відбуваються в ній, основними є система рівнянь Максвелла:
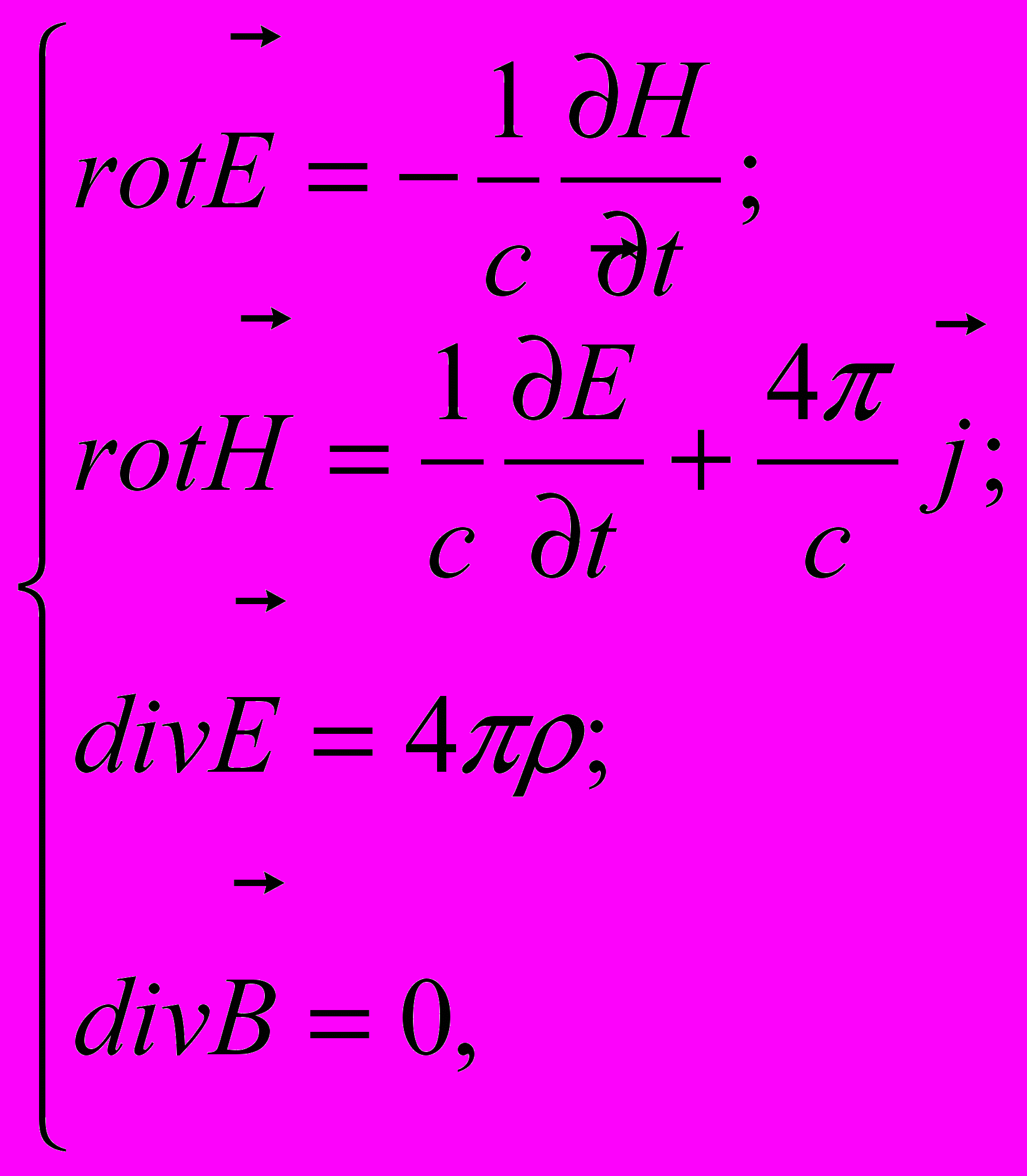 (1)
(1)де Е - напруженість електричного поля, H – напруженість магнітного поля, j – густина струму, ρ – об'ємна густина заряду, с – швидкість світла. Але, як відомо, циклотронні хвилі неможливо дослідити при гідродинамічному підході, вони з'являються тільки при адекватному урахуванні теплового руху частинок. Ця проблема вирішується за допомогою уведення функції розподілу частинок за швидкостями f(v). Щоб знайти її використовують рівняння Власова (рівняння самоузгодженого поля):
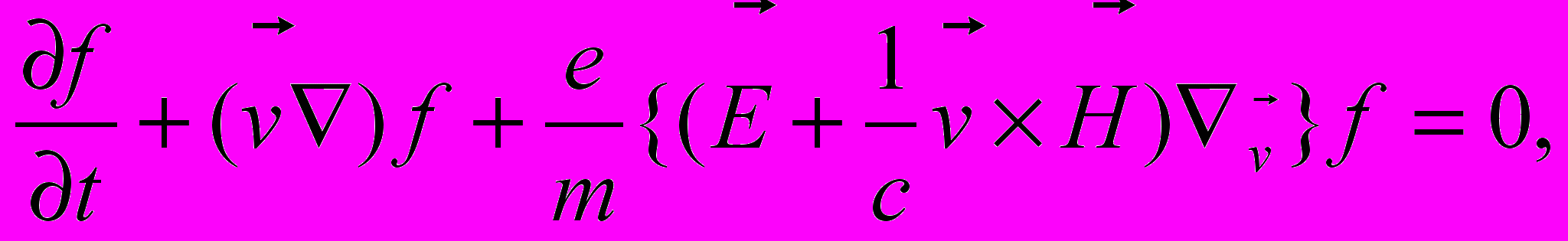 (2)
(2)де е - це заряд електрона, т – його маса,
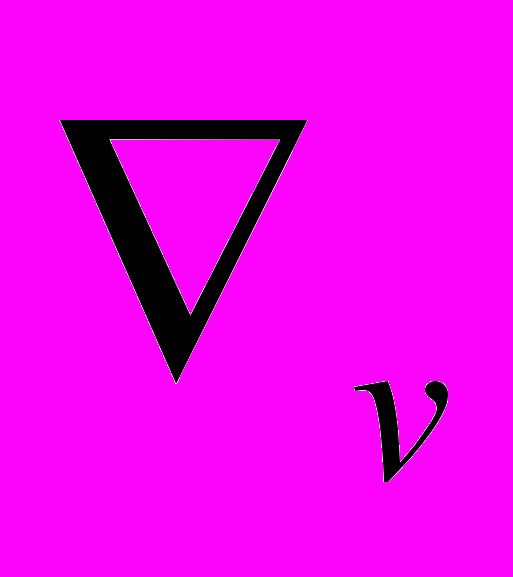 - градієнт у просторі швидкостей. Поля Е и H знаходять з рівнянь Максвелла (1) при урахуванні зв'язку j та ρ з f(v):
- градієнт у просторі швидкостей. Поля Е и H знаходять з рівнянь Максвелла (1) при урахуванні зв'язку j та ρ з f(v):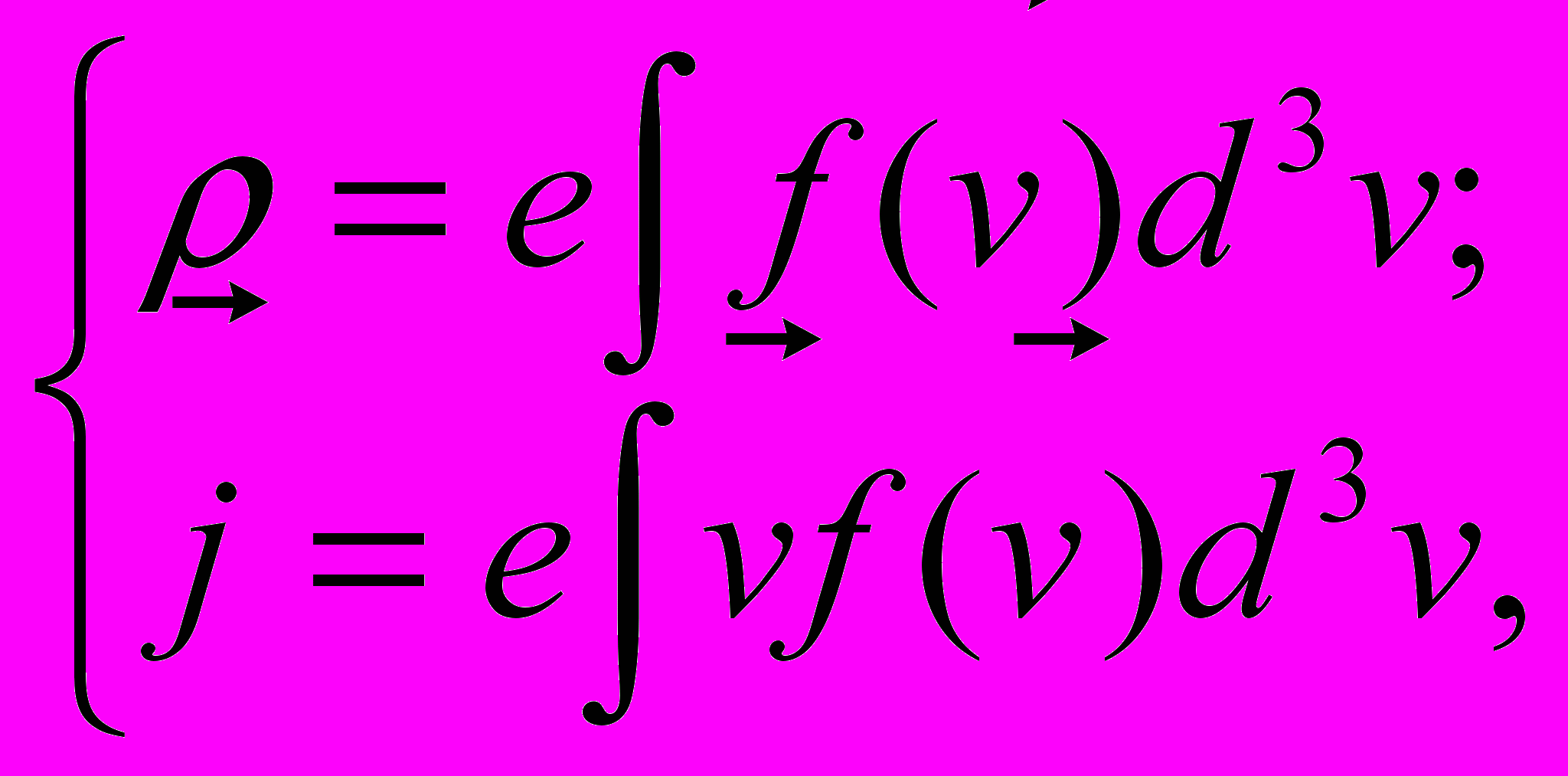 (3)
(3)Для електромагнітних коливань розв'язок рівняння (2) можна шукати у вигляді: f=f0+f1, де f1 – поправка до незбуреної функції f0. Виразивши f через Е і підставивши в рівняння (3), одержимо зв'язок між j та E. Для рівняння (2) можна використати метод інтегрування за траєкторіями, і взявши в якості f0 функцію розподілу Максвелла, можна одержати тензор діелектричної проникності [9].
Ми розглядаємо напівобмежену плазму (вона займає область х≥0), далі знаходиться шар діелектрика (-а≤х≤0, а – товщина прошарку), що межує із металевою стінкою хвилеводу. Магнітне поле спрямовано уздовж осі z, паралельно межі. Поля мають наступну функціональну залежність:
Е, Н ~ f(x) exp[i(k2y – ωt)], де ω – частота, k2 – у- компонента хвильового вектора. У цьому випадку система рівнянь Максвелла (1) розпадається на дві підсистеми: одна, з компонентами полів Ех, Еу та Нz описує Х-хвилю (незвичайно поляризовану моду), друга з компонентами Еz, Нх і Ну О-хвилю (звичайно поляризовану моду), яку тут і досліджено:
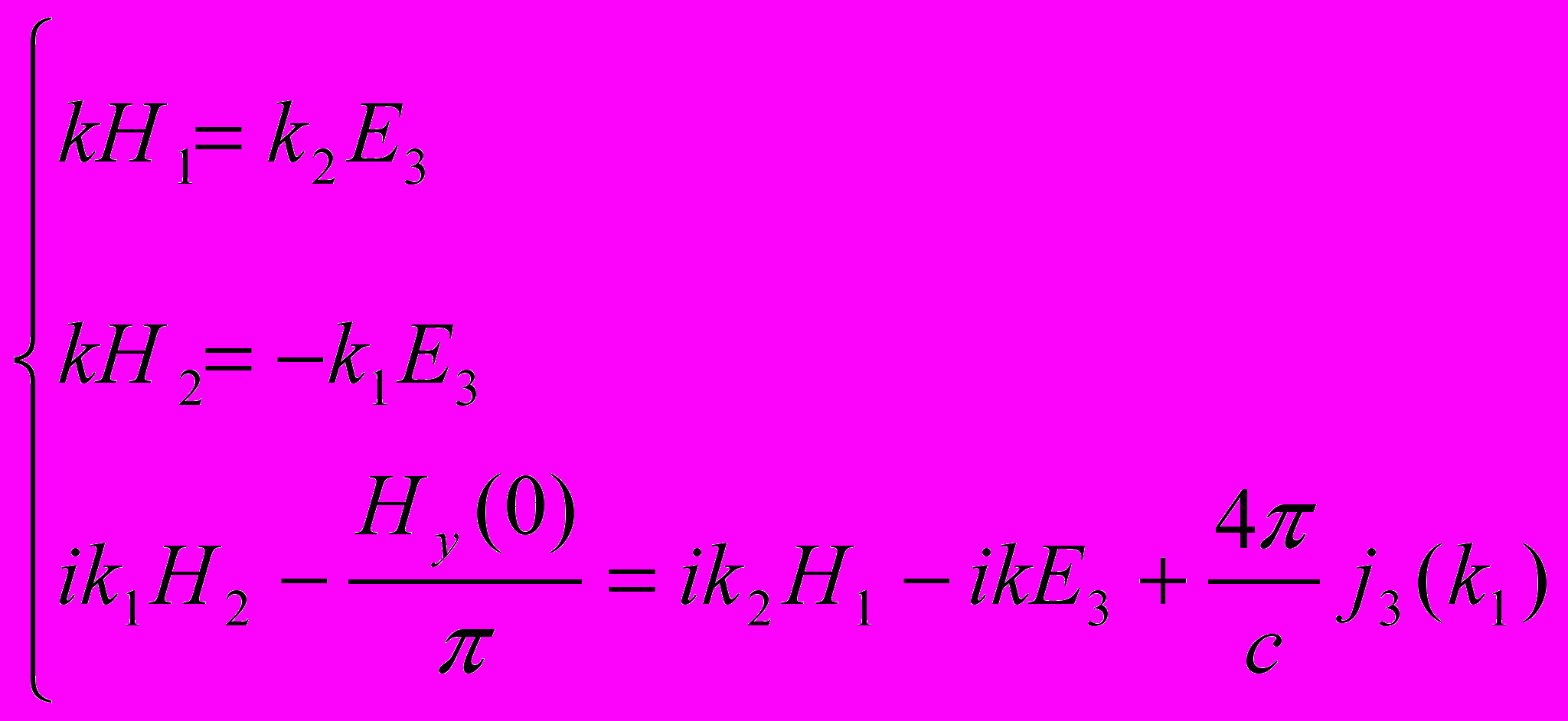 (4)
(4)де Ну(0) – величина магнітного поля на поверхні плазми, Н1 – Фур'є образ Нх, Н2 – Ну, Е3 – Еz, і j3 – jz, k=ω/c. Розв’язуємо цю систему для діелектрика (j3 та jz дорівнюють нулю), і для плазми. Застосовуємо крайові умови: на поверхні металу тангенціальна складова Е обертається в нуль, на межі плазма – діелектрик тангенціальні складові Е та Н є неперервними. В цьому випадку зручно користуватися неперервністю імпедансу Z=Ez/Hy. Прирівнявши Z діелектрика та плазми при х=0, отримаємо (у випадку повільних хвиль, k22>>k2) дисперсійне рівняння для першої гармоніки:
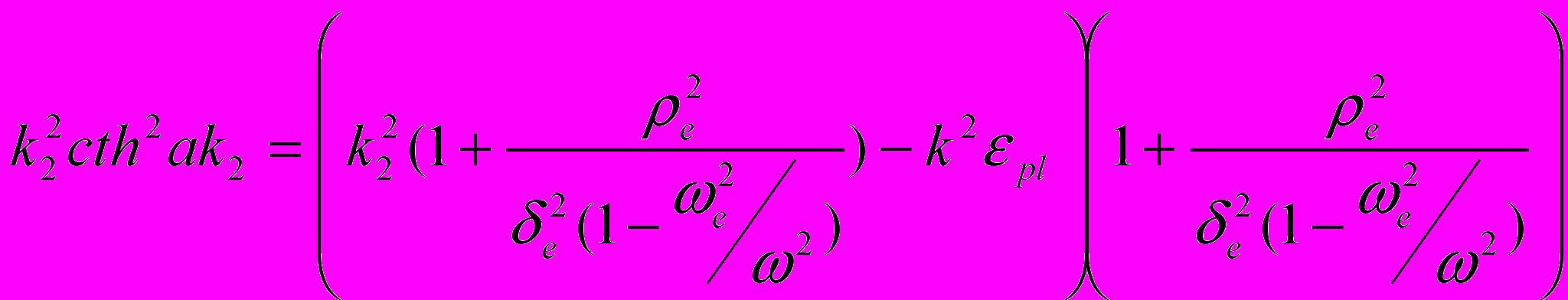 (5)
(5)де
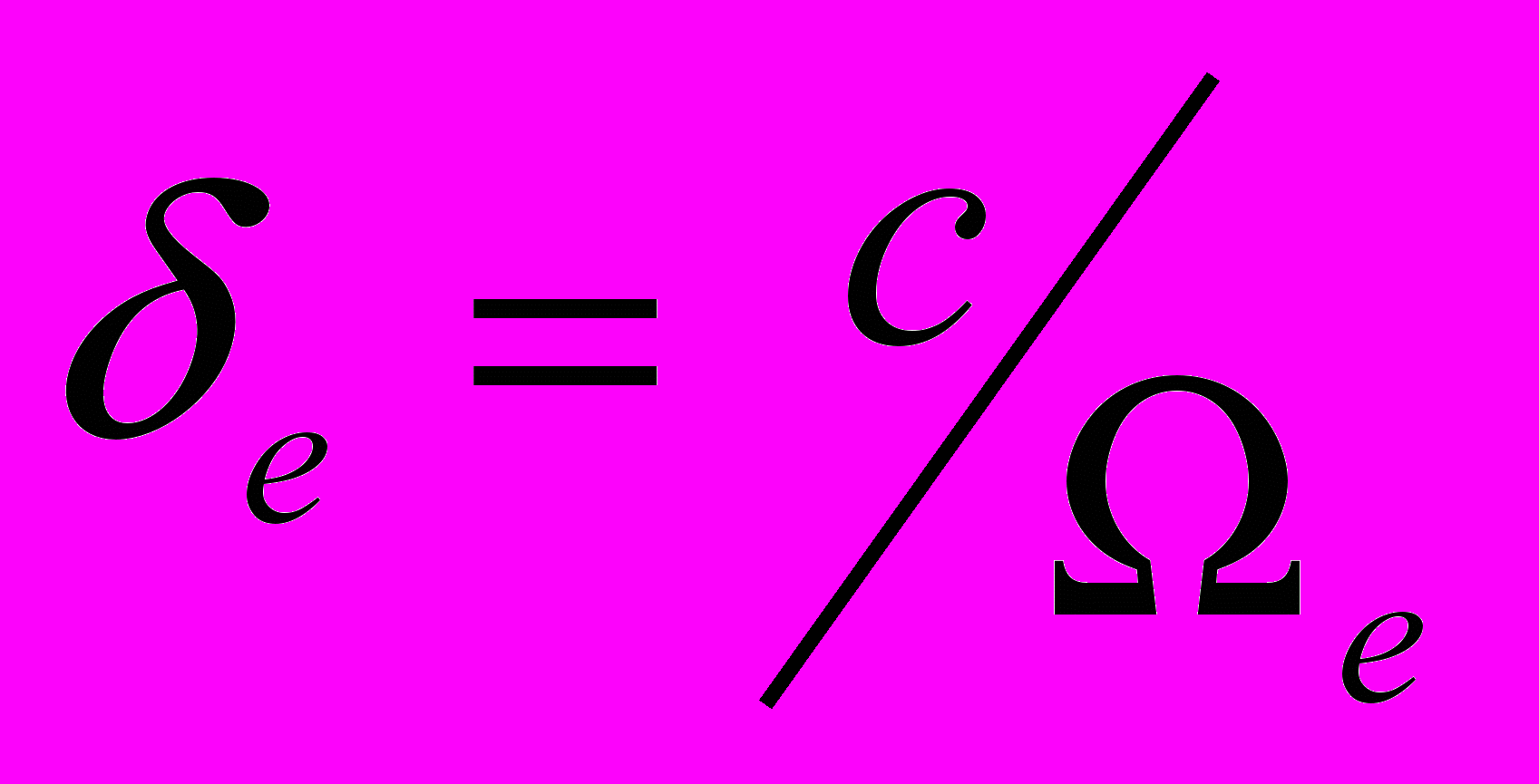 - глибина скін-слоя, εpl - діелектрична проникність холодної плазми:
- глибина скін-слоя, εpl - діелектрична проникність холодної плазми: 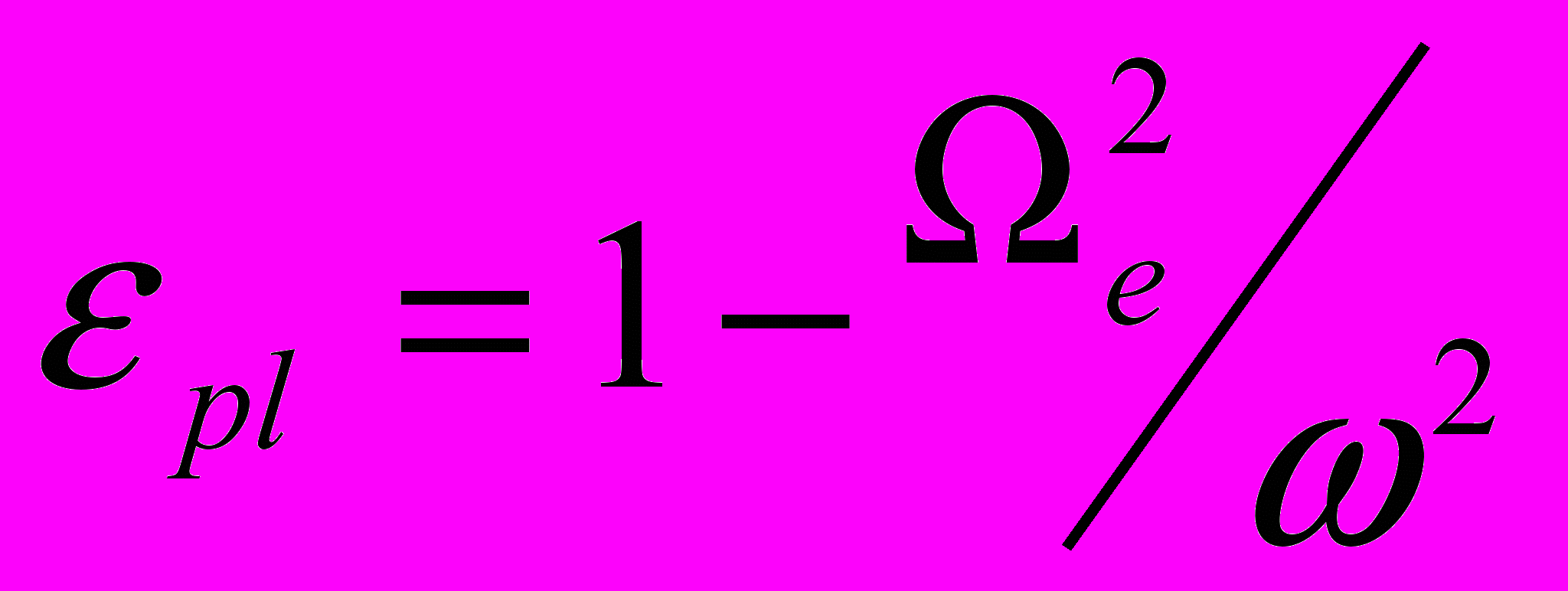 , ρе – ларморівський радіус електрона, Ωе – ленгмюрівська частота, k=ω/c. Розглянемо густу плазму, так що Ωе2/ω2 >> 1. У цьому випадку дисперсійне рівняння має наступний розв’язок:
, ρе – ларморівський радіус електрона, Ωе – ленгмюрівська частота, k=ω/c. Розглянемо густу плазму, так що Ωе2/ω2 >> 1. У цьому випадку дисперсійне рівняння має наступний розв’язок: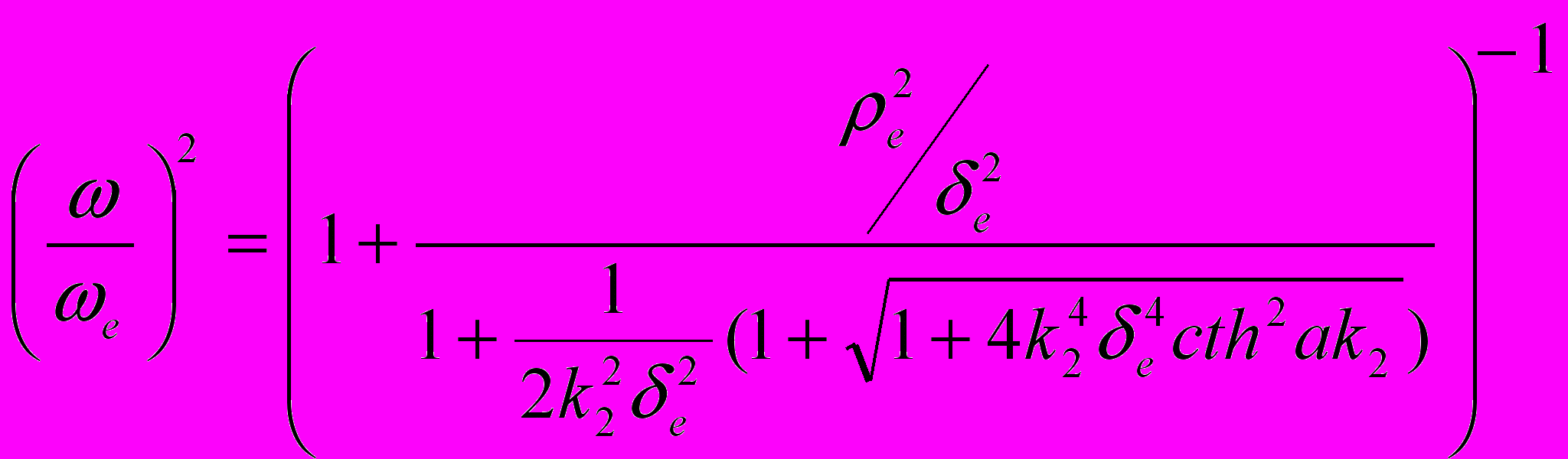 (6)
(6)де ωе – електронна циклотронна частота, сth(_ ) – гіперболічний котангенс. Цей вираз завжди менше одиниці, тобто частота ПЦЗХ є меншою від циклотронної.
Для О-хвилі немає принципової різниці між електронними та іонними хвилями (на відміну від Х-хвилі). З точністю до доданків порядку відношення маси електрона до маси іона, дисперсійні співвідношення мають такий же вигляд з належною заміною індексів e→i.
Тепер розглянемо як впливає неоднорідність на характеристики поверхневої хвилі. Густина зростає (або зменшується) від межі та виходить на постійне значення при х=d. Неоднорідний неперервний профіль плазми моделювався сходинковою функцією - шарами плазми з постійною густиною. Для кожного шару плазми розв’язувалася система рівнянь, що є аналогічною до (4). На межі кожного шару повинні виконуватися крайові умови неперервності Ez та Hy. З рівнянь (4) для кожного прошарку отримаємо наступні вирази:
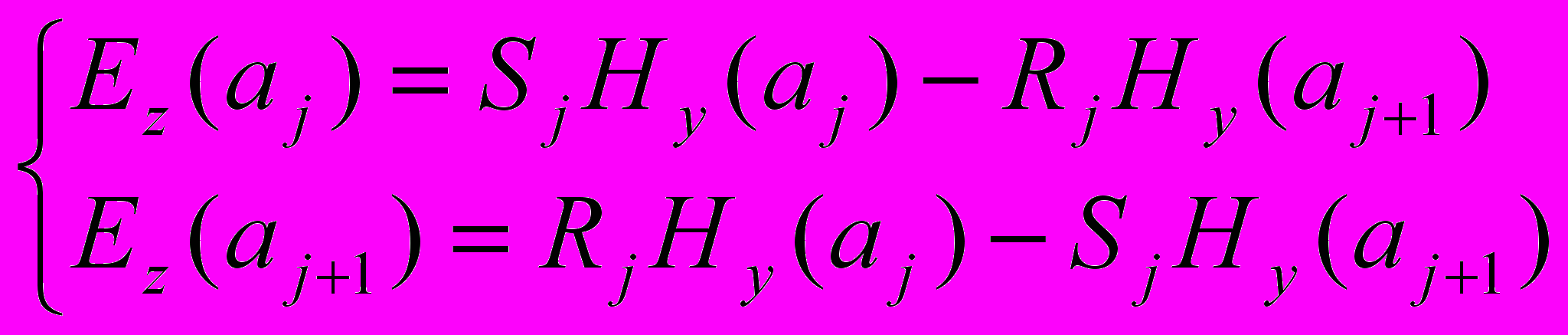 (7)
(7)де aj та aj+1 координати меж j-ого та (j+1)-ого шарів,
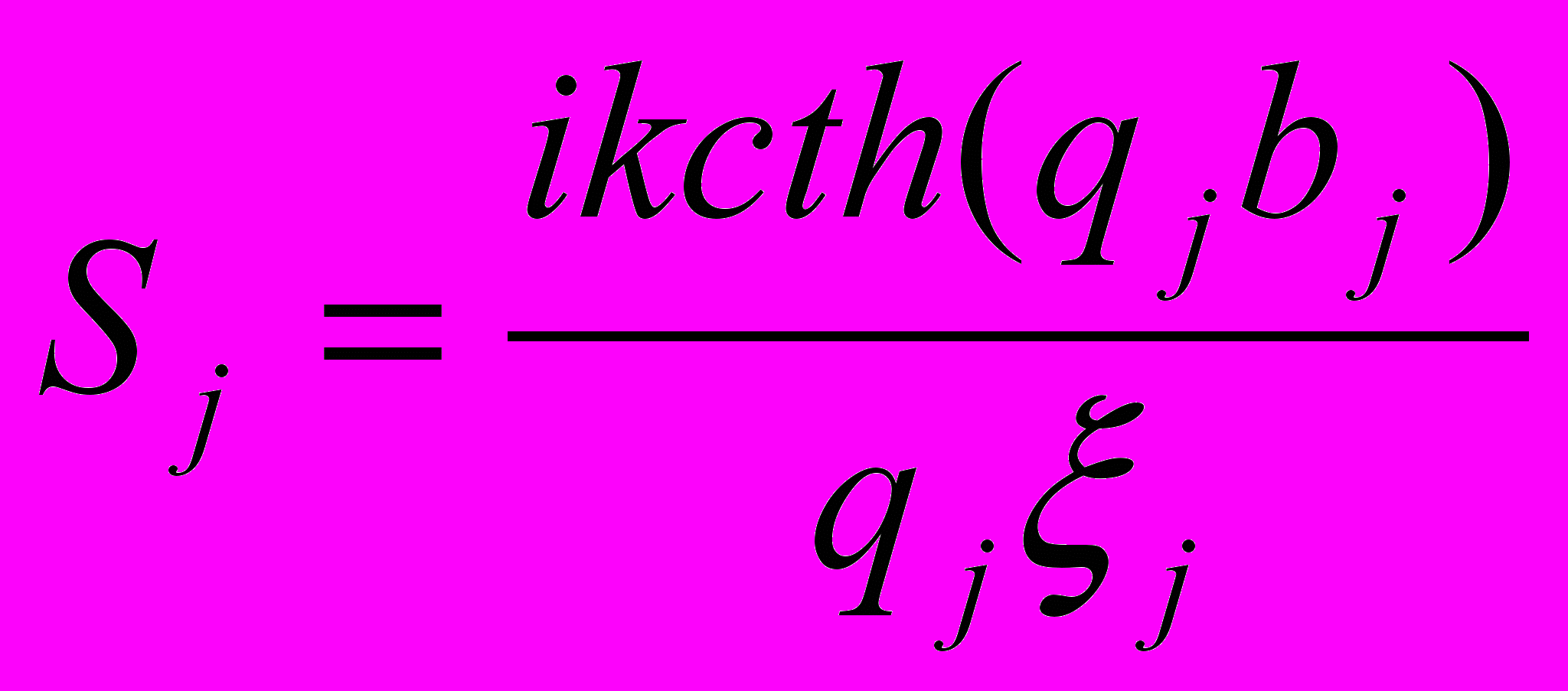 ,
, 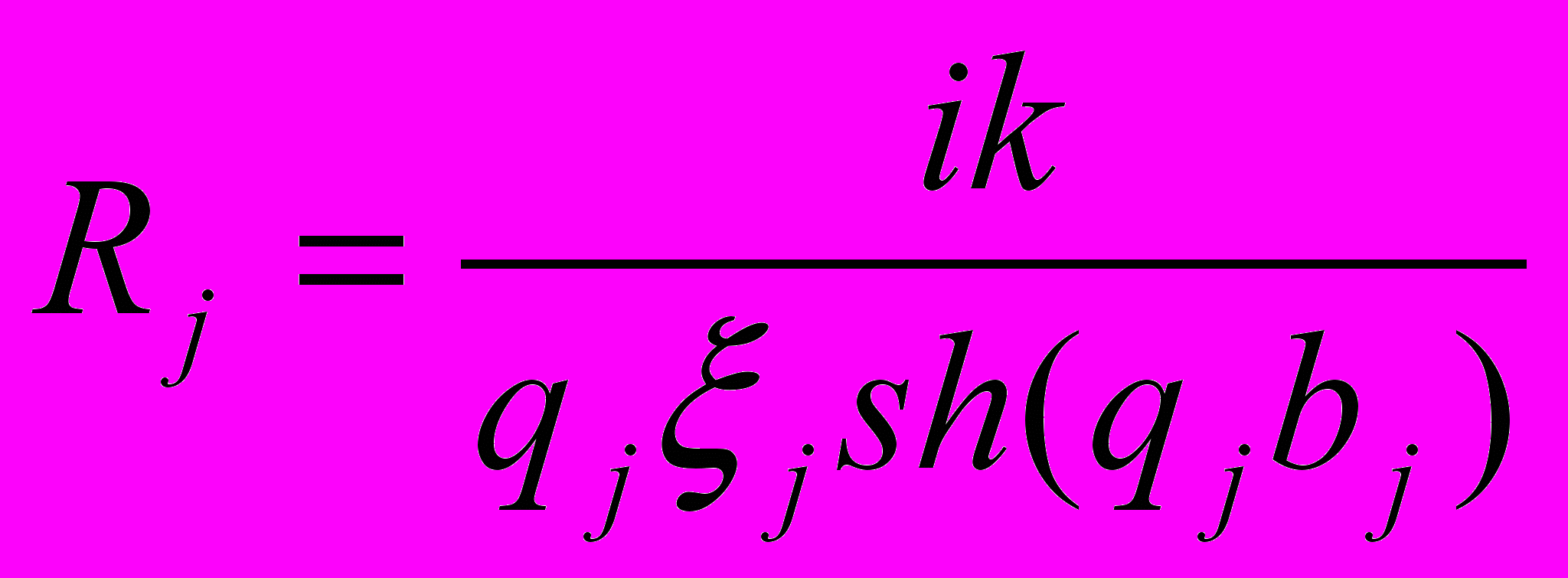 ,
, 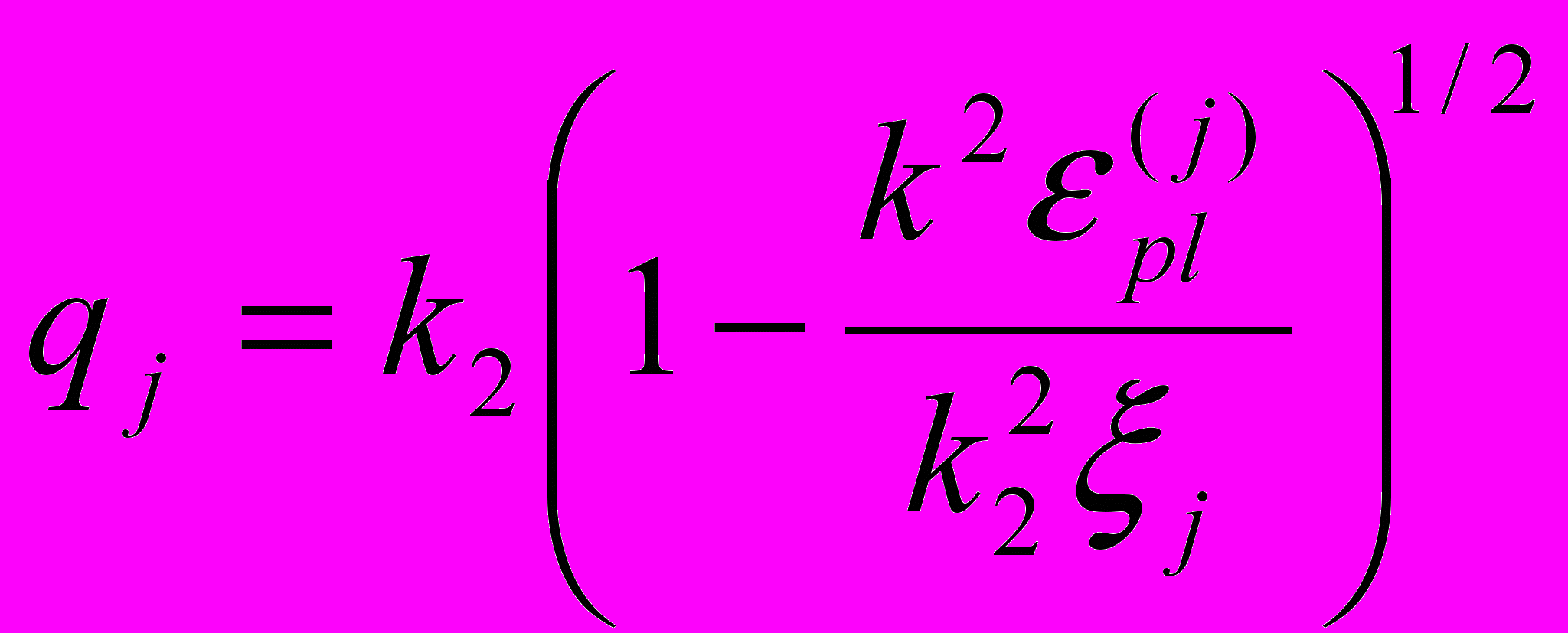 ,
, 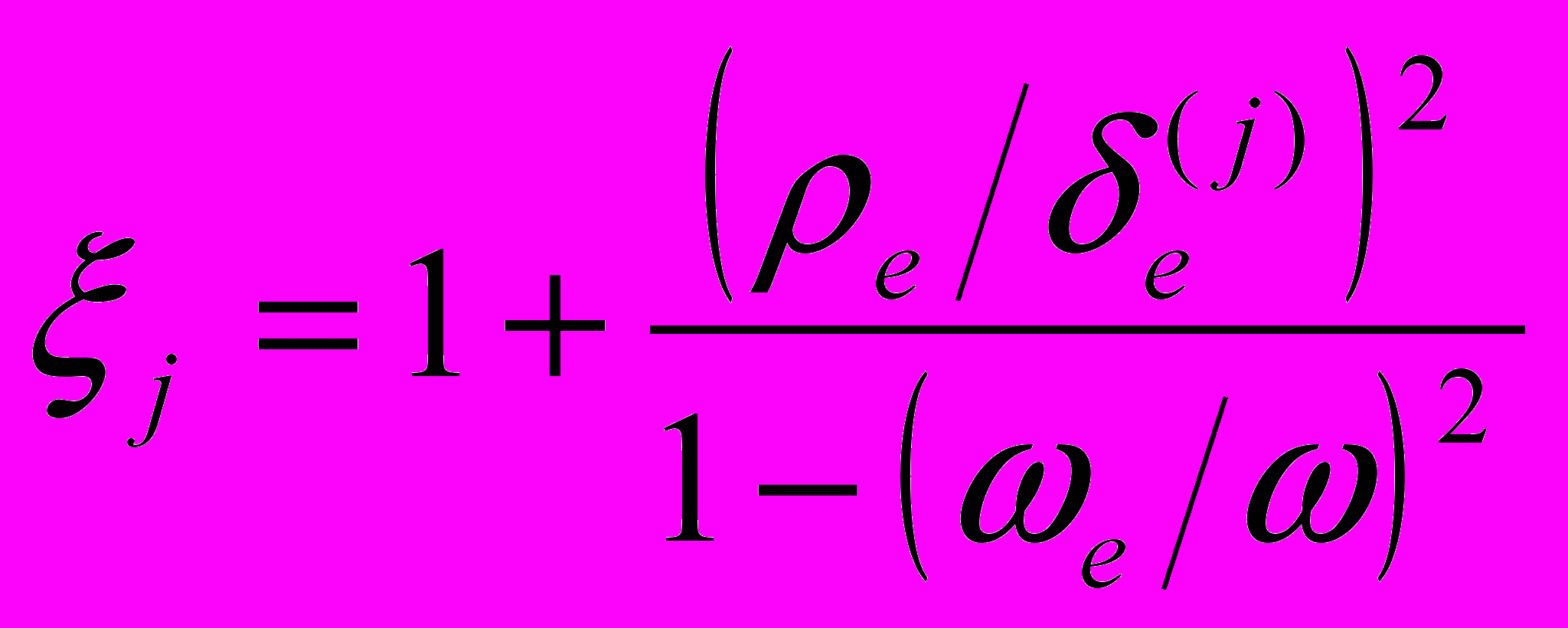 , bj – товщина j-ого прошарку. Для однорідної області плазми маємо: Zu=ik/(quξum), для діелектрика товщиною Ad і діелектричною проникністю ε:
, bj – товщина j-ого прошарку. Для однорідної області плазми маємо: Zu=ik/(quξum), для діелектрика товщиною Ad і діелектричною проникністю ε: 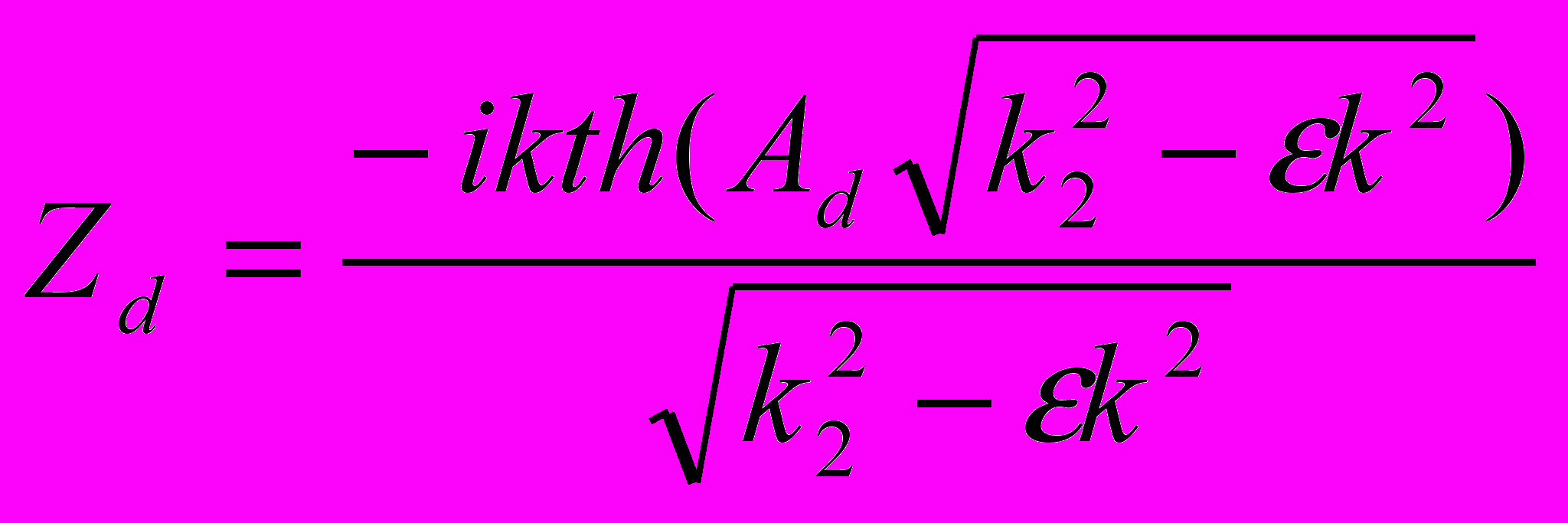 . Розв’язуючи спільно системи (7) і використовуючи умови неперервності тангенціальних складових електричного та магнітного полів, отримаємо рекурентні співвідношення:
. Розв’язуючи спільно системи (7) і використовуючи умови неперервності тангенціальних складових електричного та магнітного полів, отримаємо рекурентні співвідношення: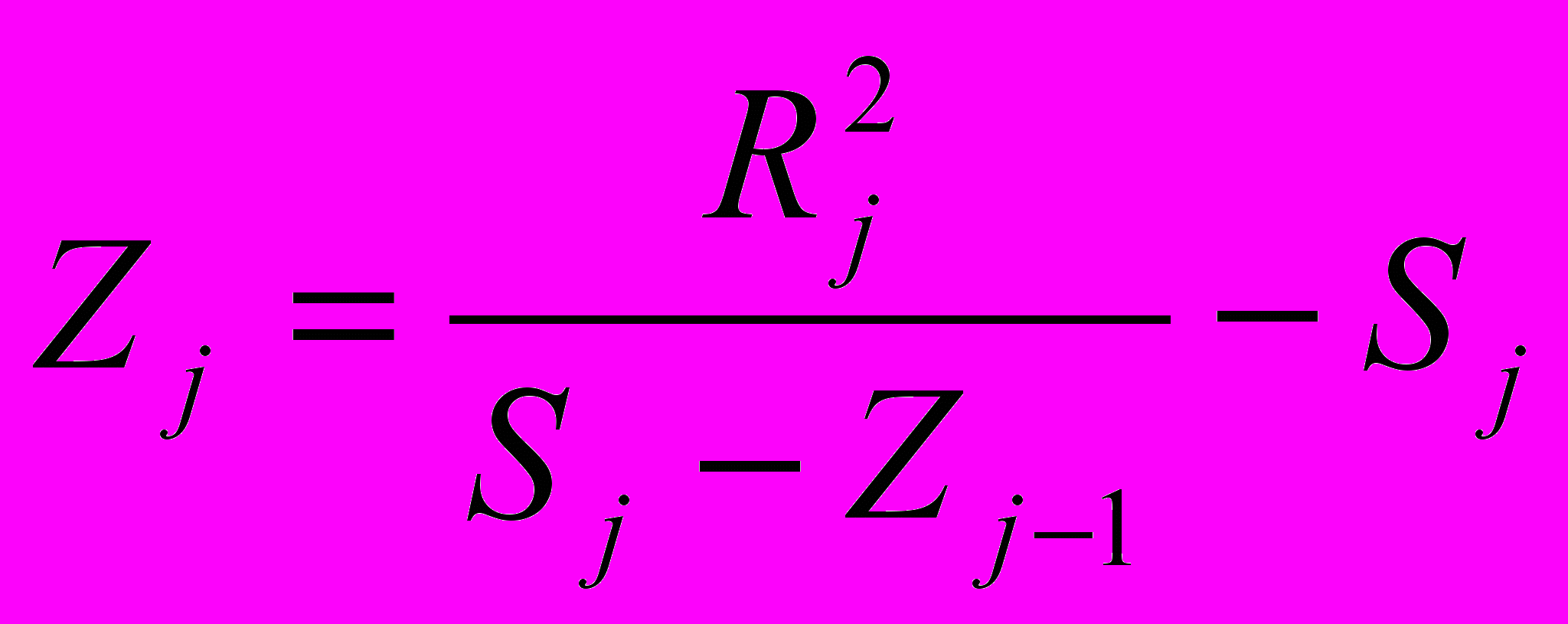
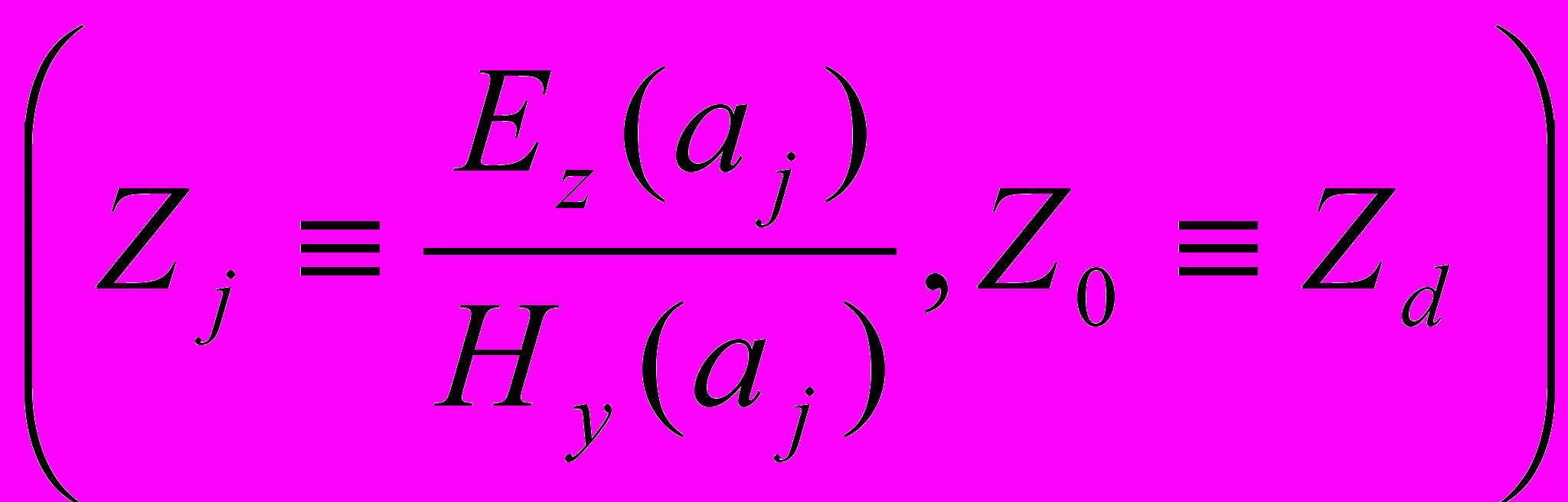 (8)
(8)і дисперсійне рівняння:
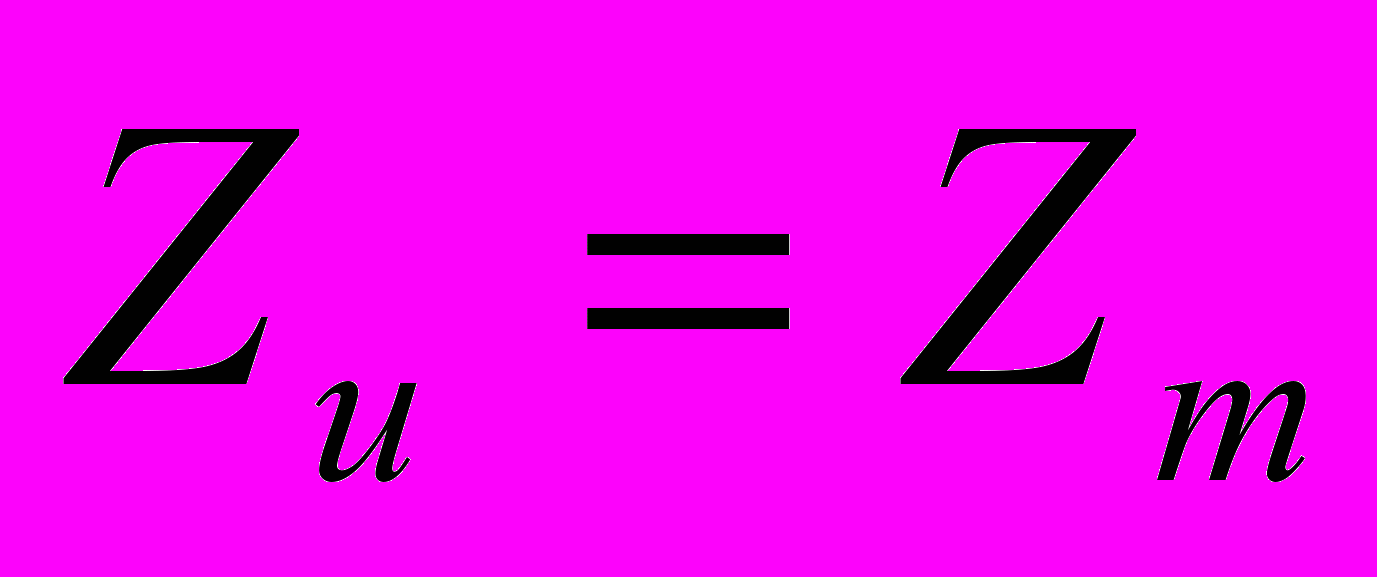 , (9)
, (9)де m – кількість прошарків розбивки. Рівняння (9) розв’язувалося числовим методом. У результаті з'являлося кілька гілок розв’язків (загальна кількість дорівнює т). Вони виникли в результаті використання модельної побудови (кожний розв’язок відповідає якійсь межі плазми), тому що поверхні розділу плазма – плазма на межі шару створено штучно. Для виділення потрібного розв’язку використовувався аналіз розв’язків для різної товщини діелектрика: при спрямуванні товщини діелектрика до нуля частота хвилі прямує до циклотронної (наприклад, див. рис. 2), а далі розв’язок має зникати. Це пов'язано з тим, що діелектрик служить прошарком між плазмою та металом, а на поверхні металу тангенціальні складові полів обертаються в нуль, тобто перестає існувати сама О-хвиля.
При побудові графіків частота нормувалася на циклотронну, а хвильове число – на ларморівський радіус. Для т≥20 розв’язки практично не відрізнялися (див. рис. 1). Тобто можна зробити висновок про те, що запропонований числовий метод є збіжним. Далі результати наведено для значення т=25.
Як було відзначено вище, розв’язок ω/ωе має прямувати до одиниці, коли Аdiel - товщини діелектрика зменшується, це видно з рис 2. При Аdiel ≥10ρe розв’язки не відрізняються, тобто діелектричний шар можна вважати нескінченним.
Також у роботі досліджувався спектр циклотронних хвиль при різних значеннях параметра
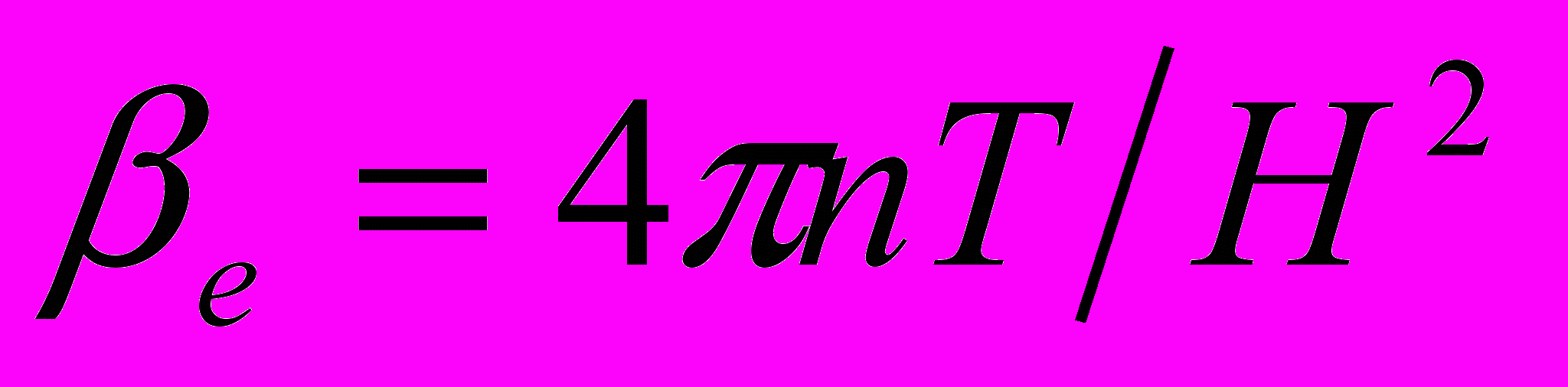 - відношення газового тиску до магнітного (див. рис. 3). При βе≥10 розв’язки не змінюються при збільшенні βе, тобто це значення є граничним, після якого можна вважати магнітний тиск нескінченно малим. При малому βе частота є близькою до циклотронної.
- відношення газового тиску до магнітного (див. рис. 3). При βе≥10 розв’язки не змінюються при збільшенні βе, тобто це значення є граничним, після якого можна вважати магнітний тиск нескінченно малим. При малому βе частота є близькою до циклотронної.Вплив на частоту величини і знаку градієнта наведено на рис.4 та 5, відповідно. Інтегральна густина плазми є однаковою для всіх випадків. Як видно з мал. 4 та 5 залежність частоти хвилі від густини плазми - інтегральна, тобто можна зробити висновок, що неоднорідність густини слабко впливає на частоту О-хвилі. Видно також, що частота підвищується зі збільшенням градієнта, від’ємний градієнт густини плазми призводить до зниження частоти хвилі.
У попередніх роботах [10, 11] враховувалася тільки одна складова хвильового вектора. В даній роботі взято до уваги обидві поперечні складові хвильового вектора. В цьому випадку він дорівнює
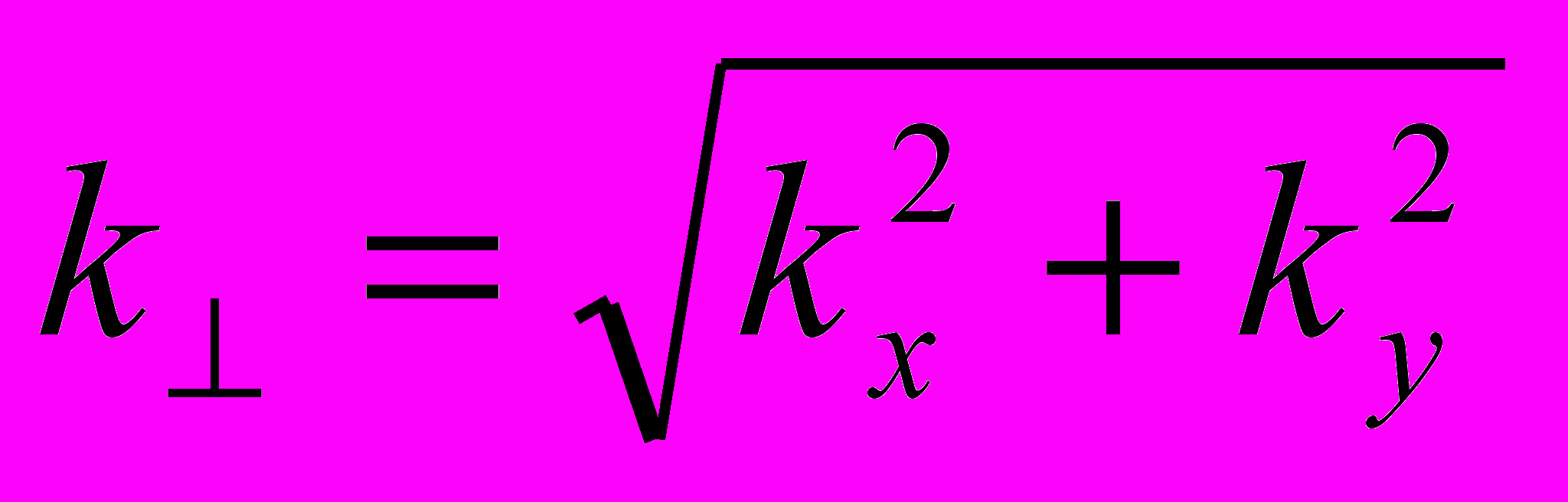 , коли раніше було просто
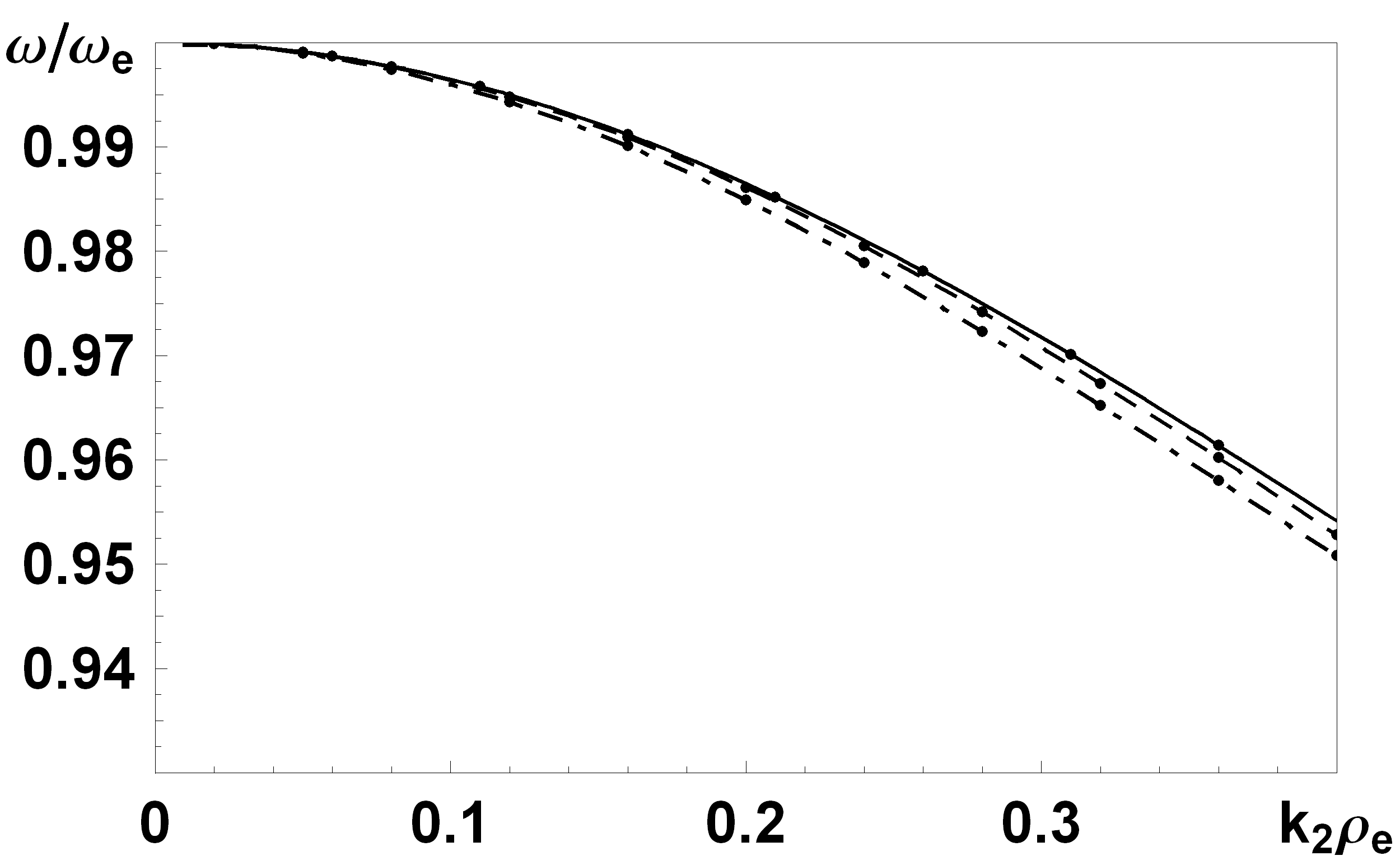
, коли раніше було просто 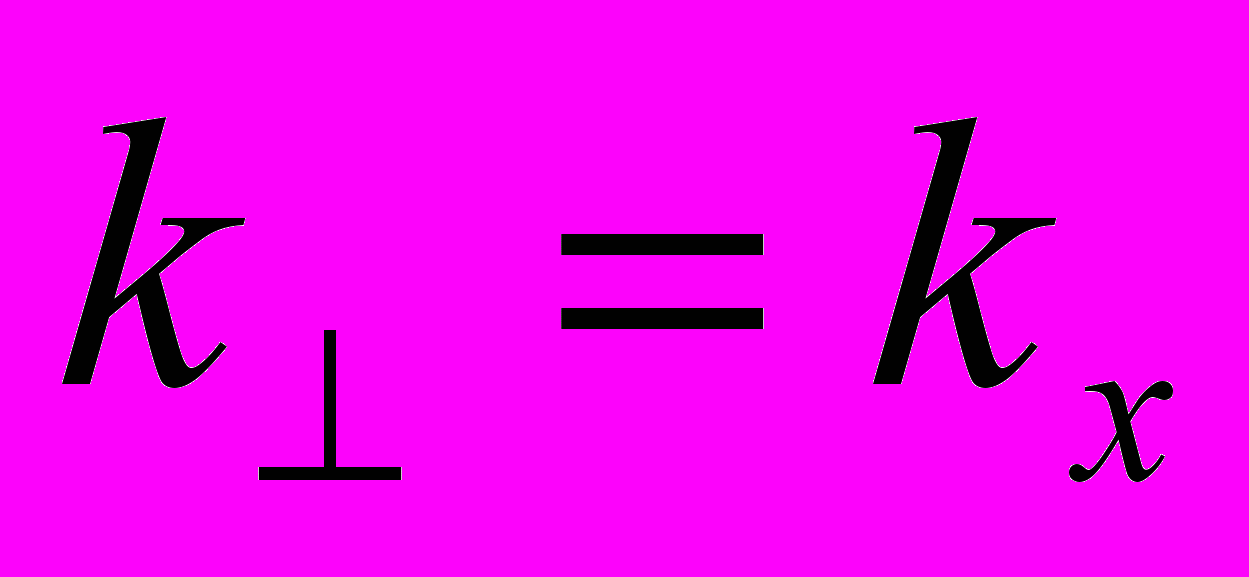 . Ця зміна призводить до того, що дисперсійне рівняння дещо змінюються, а це в свою чергу призводить до певного збільшення частоти (рис.6).
. Ця зміна призводить до того, що дисперсійне рівняння дещо змінюються, а це в свою чергу призводить до певного збільшення частоти (рис.6).Для прошарку плазми товщини
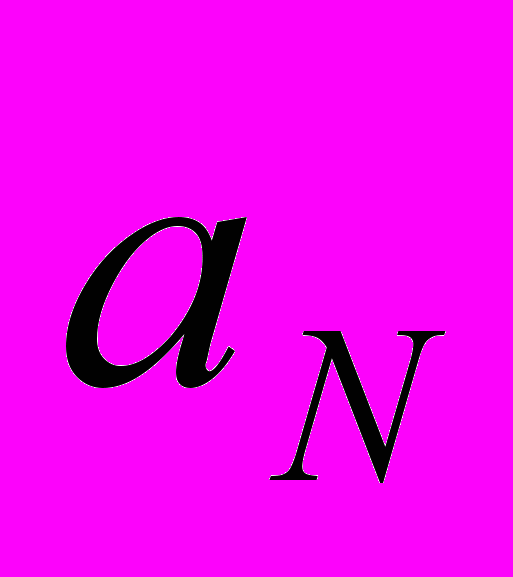 , який з обох боків обмежено діелектриком, товщиною
, який з обох боків обмежено діелектриком, товщиною 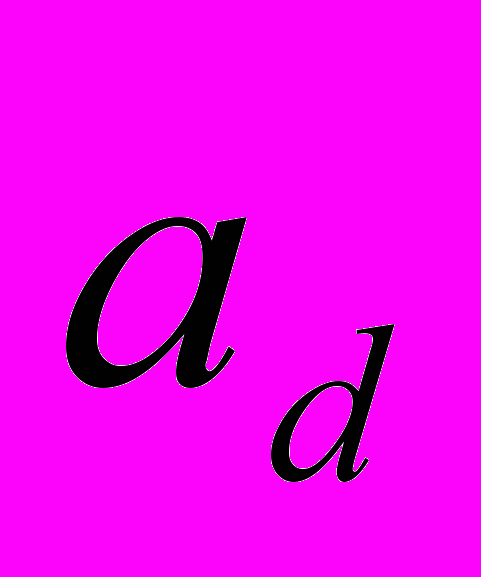 та діелектричною проникливістю
та діелектричною проникливістю 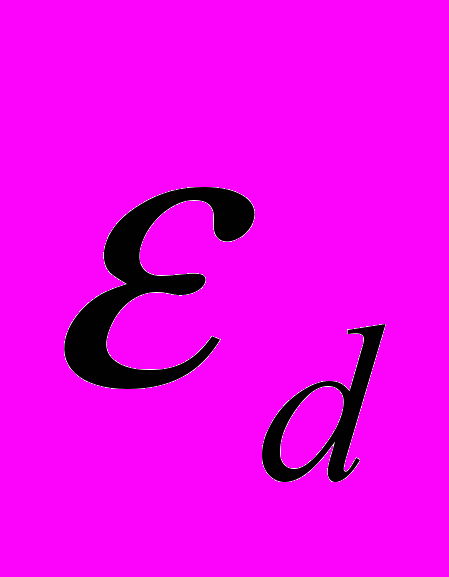 (з обох боків діелектрик є однаковим) дисперсійне рівняння змінюється:
(з обох боків діелектрик є однаковим) дисперсійне рівняння змінюється: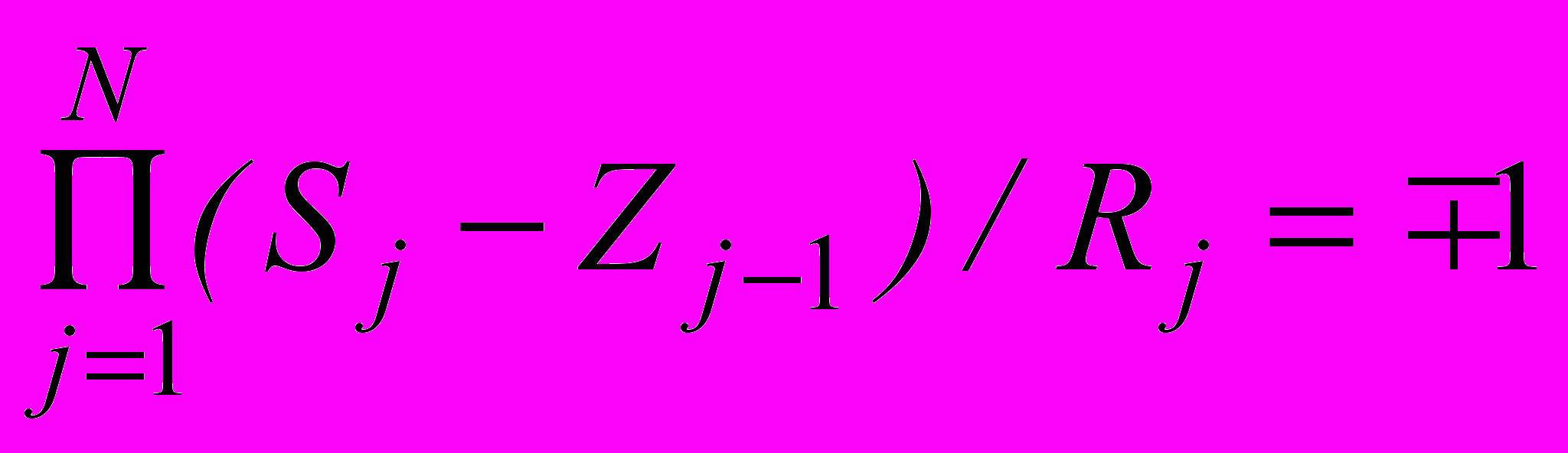 (10)
(10)де знак мінус відповідає симетричній моді (
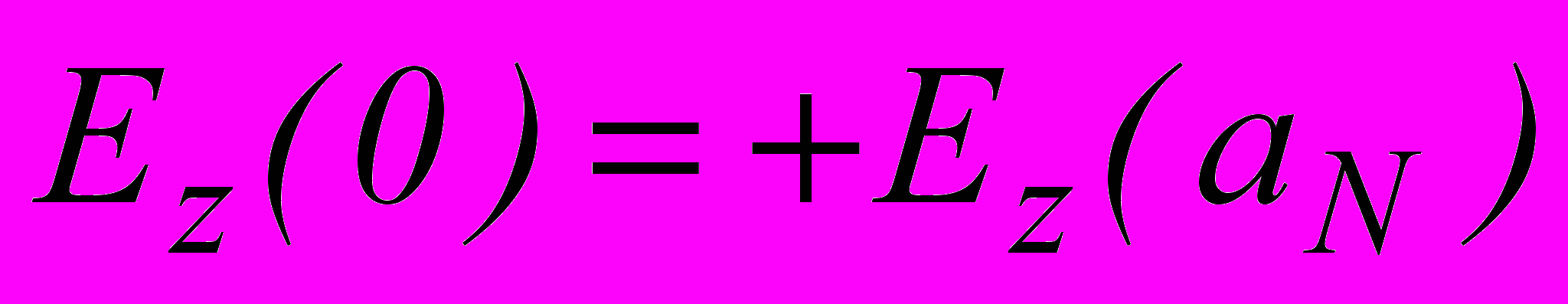 ,
, 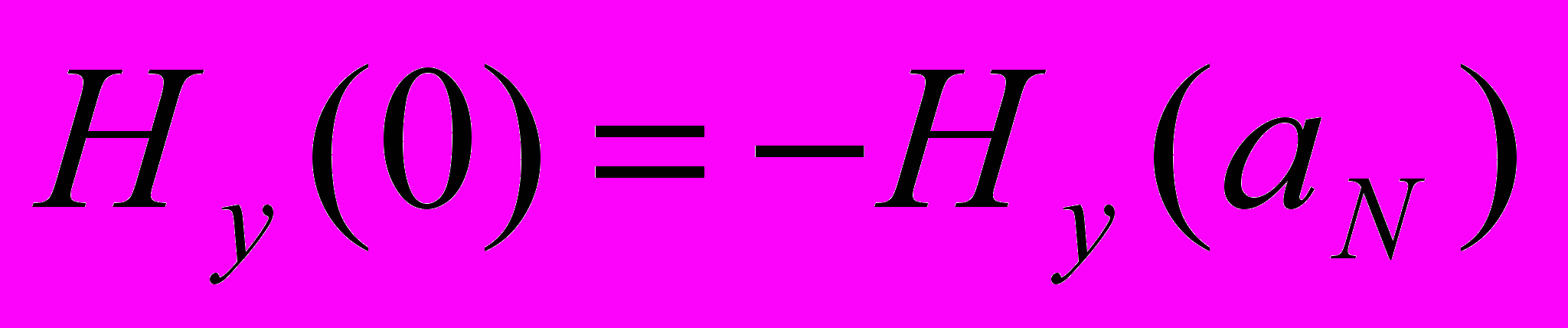 ), плюс – антисиметричній (
), плюс – антисиметричній (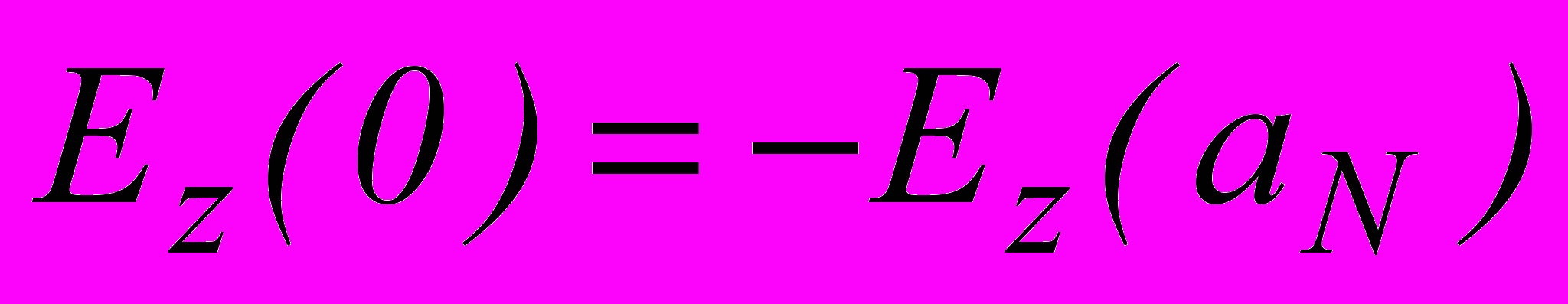 ,
, 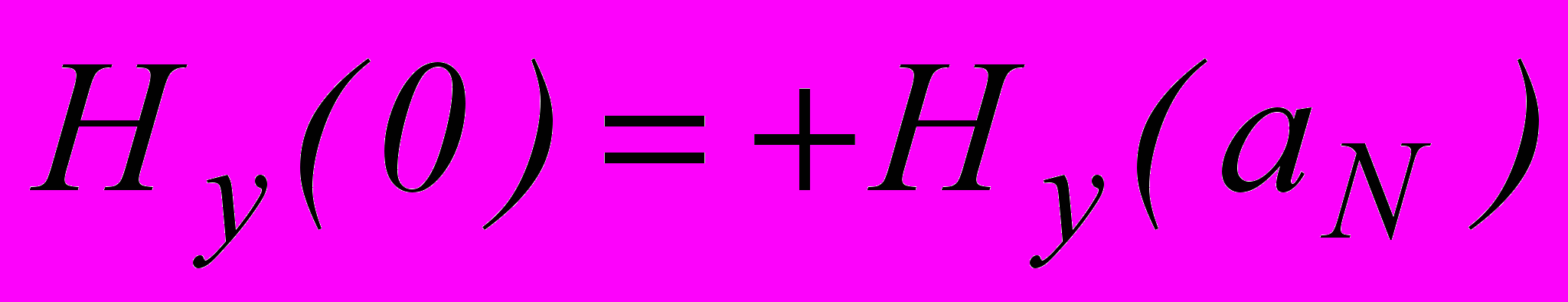 ).
). В однорідній плазмі розв’язок для тонкого слою
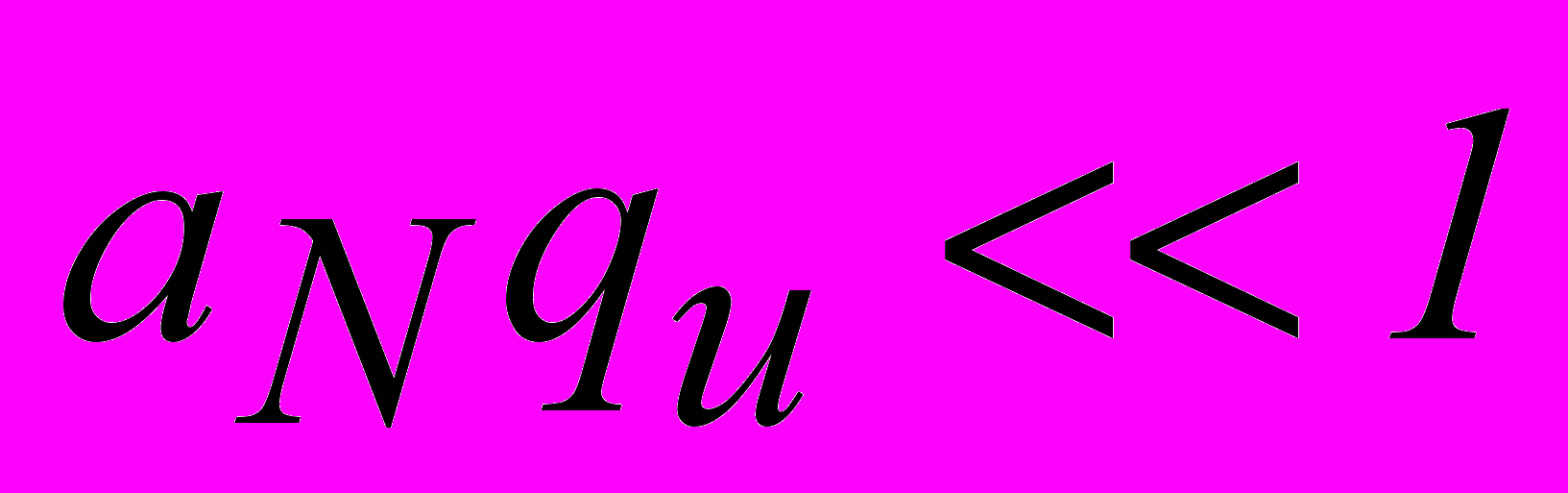 має вигляд:
має вигляд: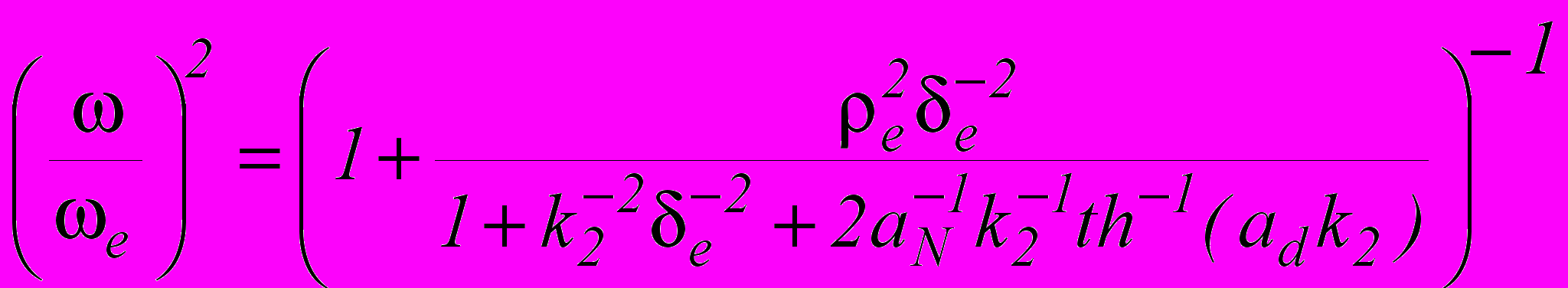 (11)
(11)Видно, що при зменшені товщини плазми частота прямує до циклотронної. Для товстого прошарку плазми (
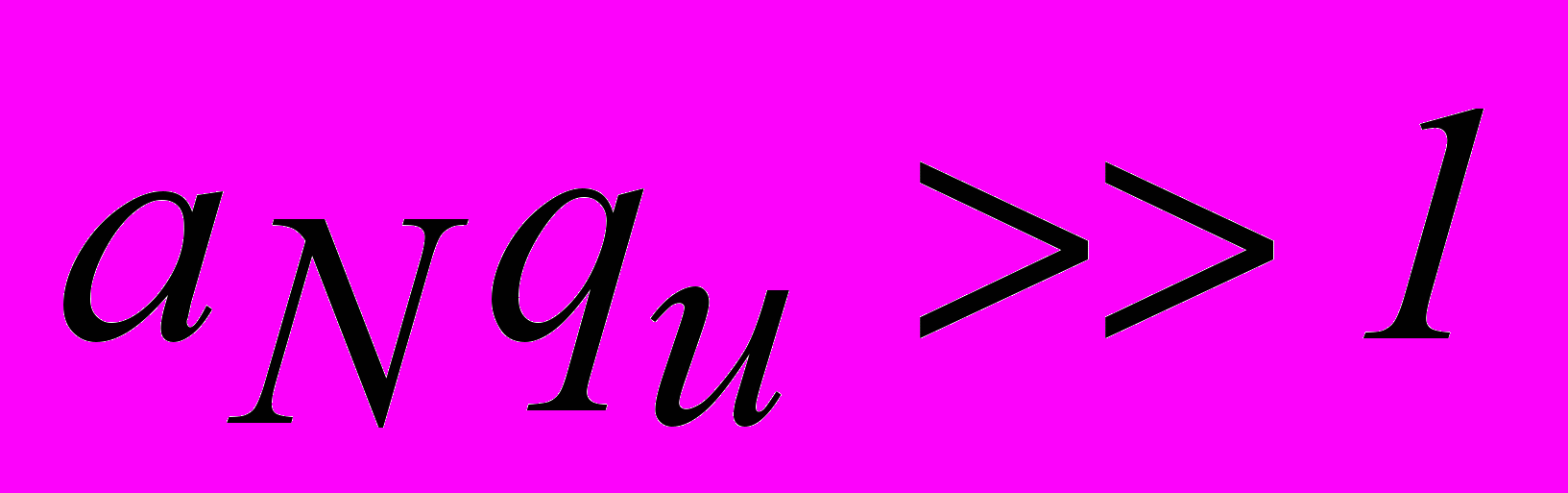 ) розв’язок дисперсійного рівняння для ПЦЗХ (11) співпадає з (6).
) розв’язок дисперсійного рівняння для ПЦЗХ (11) співпадає з (6).Рівняння (10) розв’язувалося методами числових розрахунків. Якісне поводження дисперсійних кривих для різної товщини діелектрика та різного відношення
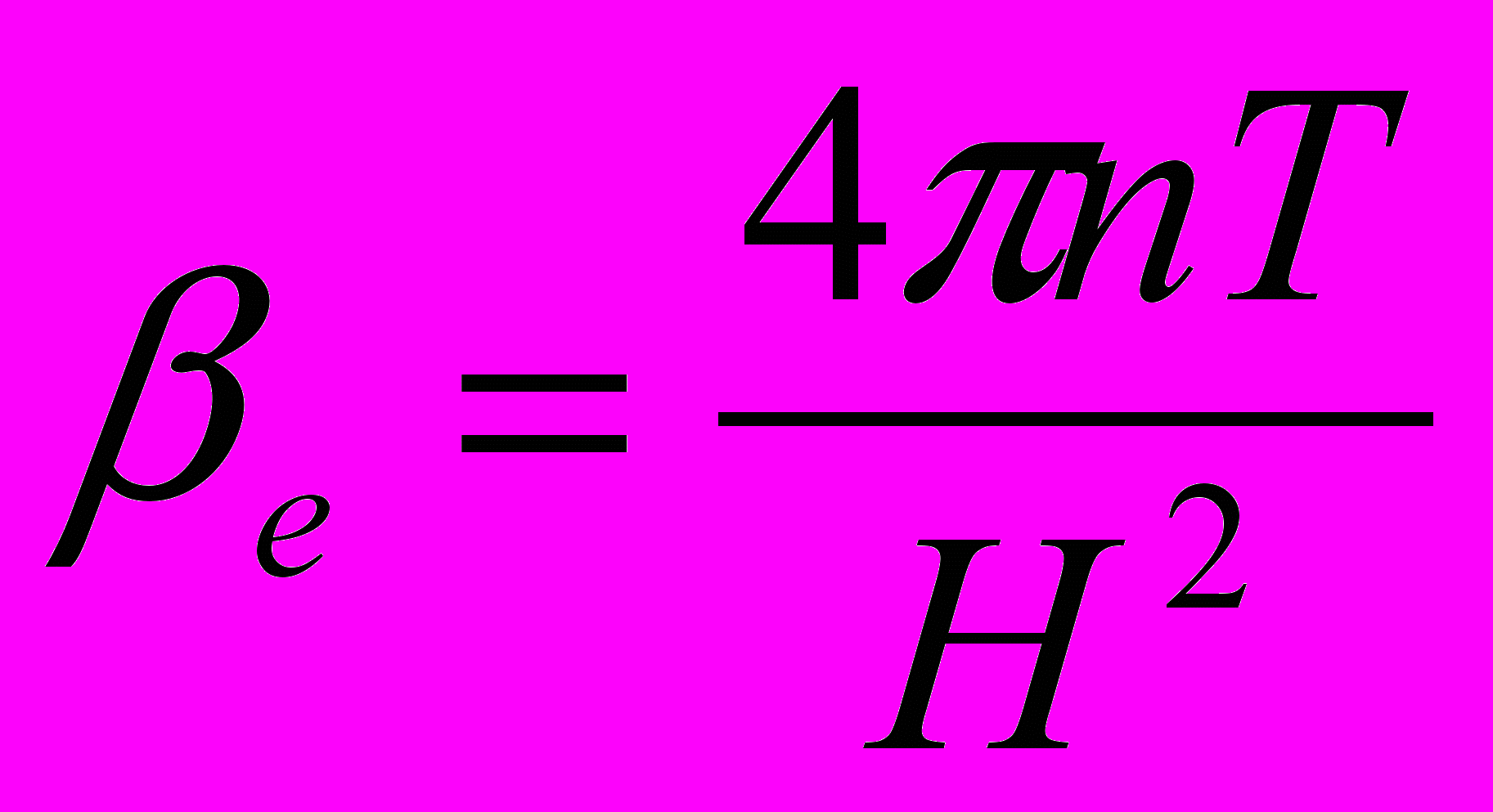 у випадках прошарку і напівобмеженої плазми співпадають. Цікавим є залежність від товщини шару плазми (див. рис.7). З розрахунків видно, що зі зменшенням товщини шару плазми частота ПЦЗХ збільшується. Товщину
у випадках прошарку і напівобмеженої плазми співпадають. Цікавим є залежність від товщини шару плазми (див. рис.7). З розрахунків видно, що зі зменшенням товщини шару плазми частота ПЦЗХ збільшується. Товщину 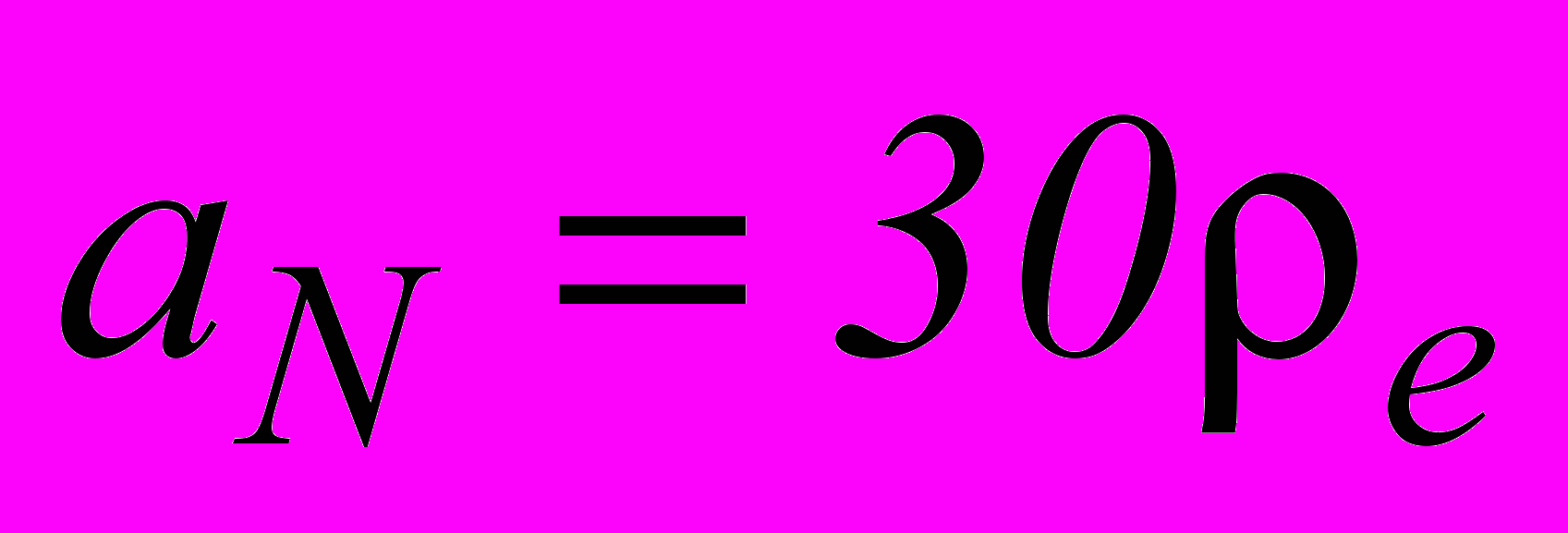 можна вважати еквівалентною напівобмеженій плазмі, тому що різниця розв’язків у цих випадках не перевищує однієї десятої відсотка.
можна вважати еквівалентною напівобмеженій плазмі, тому що різниця розв’язків у цих випадках не перевищує однієї десятої відсотка.Градієнт густини у випадку шару плазми зменшує частоту ПЦЗХ на відміну від напівобмеженої плазми (див. рис.8 та рис.9). На рис.8 представлено залежність частоти від величини градієнта для випадків параболічної та четвертої степені залежності густини від координати., на рис.9 – від знака градієнта: додатнього та від’ємного. Від’ємний градієнт означає, що на поверхні плазми густина є більшою, а вглиб плазми її величина спадає. У всіх випадках залежність густини є симетричною відносно центру шару плазми.
На рис.10 показано залежність глибини проникнення від хвильового вектора для різної товщини шару плазми. Видно, що залежність слабко відрізняється від лінійної (особливо для тонких шарів плазми).
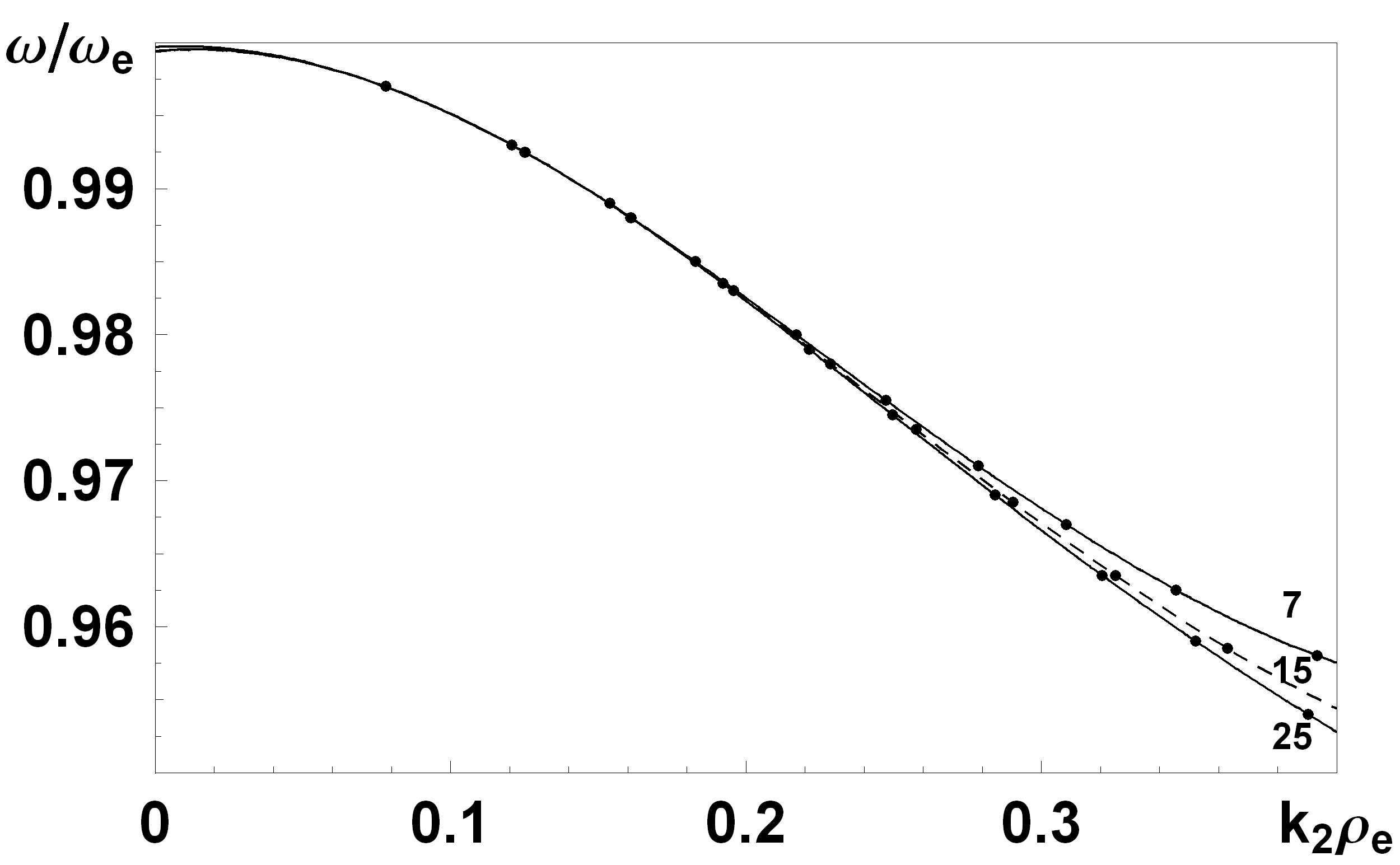 | 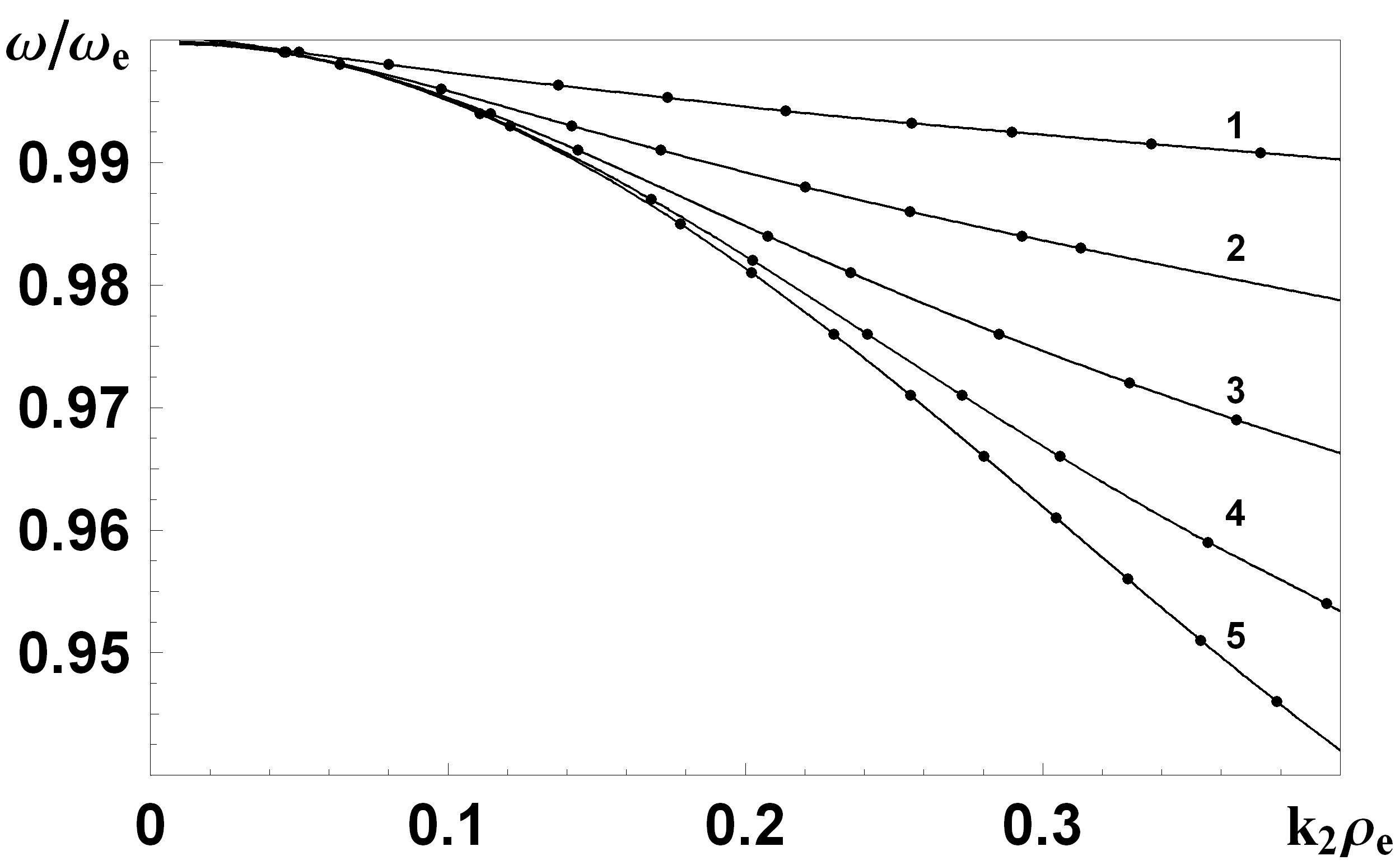 |
| Рис.1 Розв’язки для різної кількості прошарків розбиття. | Рис.2 Залежність частоти від хвильового вектора при різних товщина діелектрика. Цифрами 1,2,3,4 та 5 підписані криві з 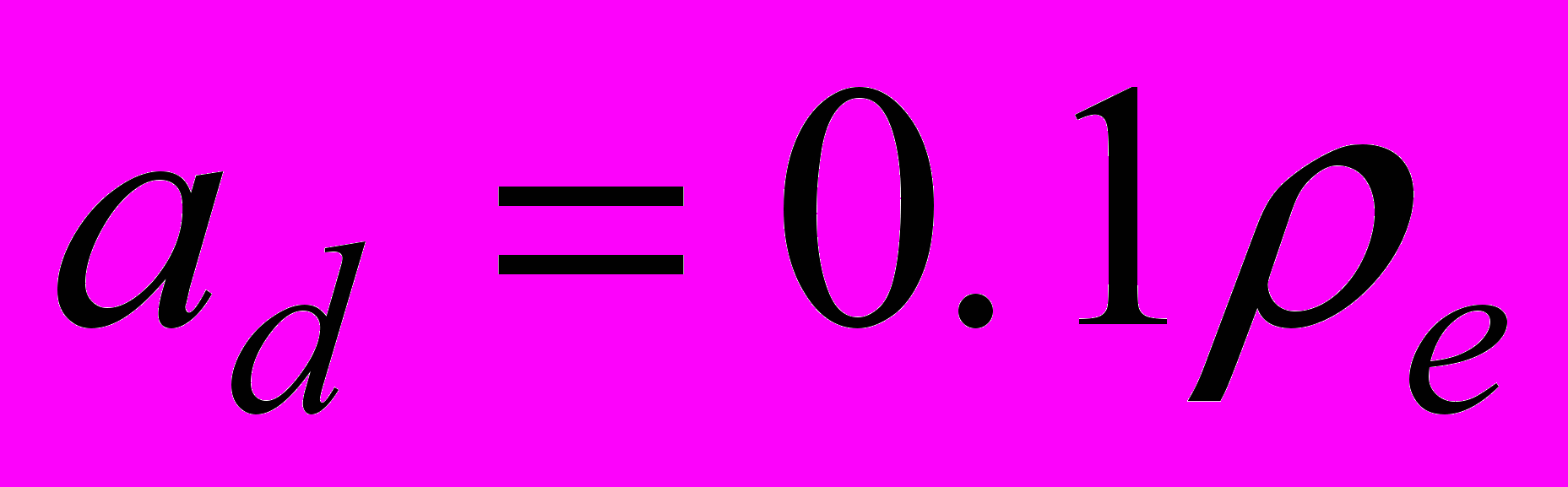 , , 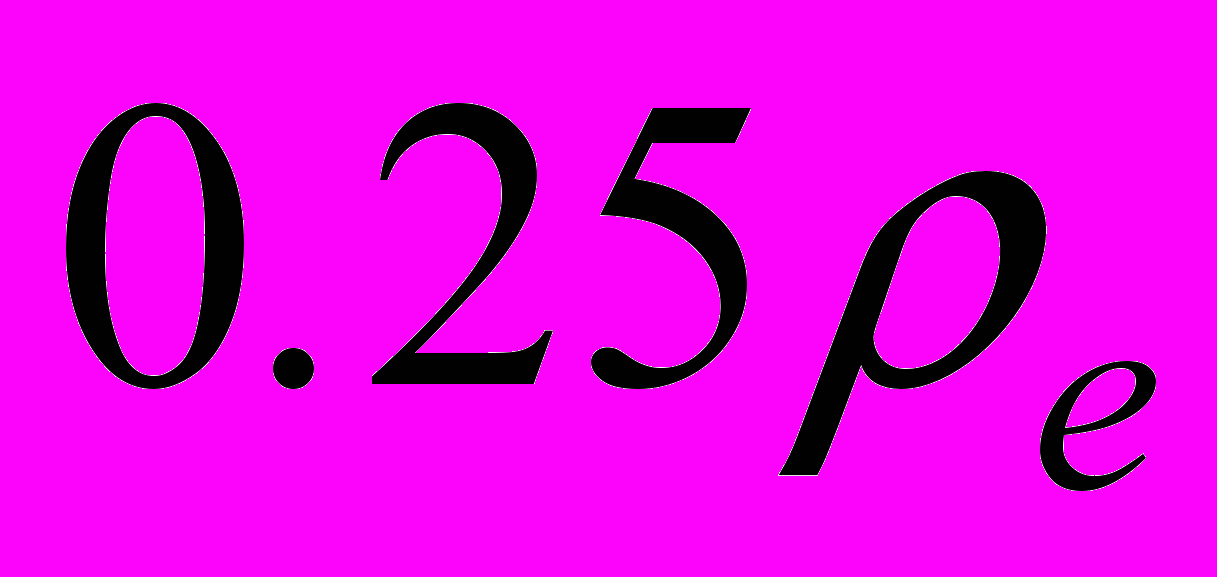 , , 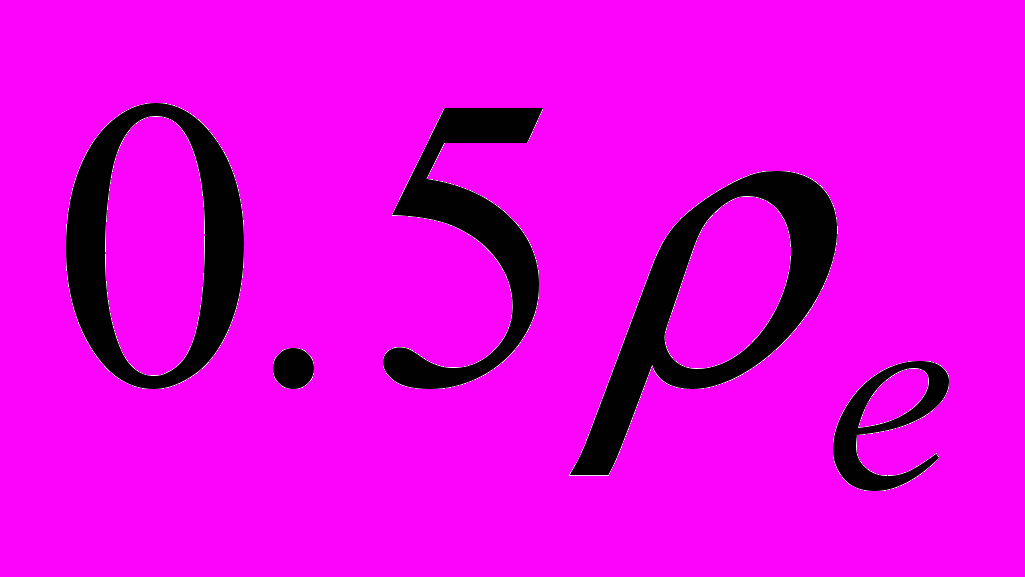 , , 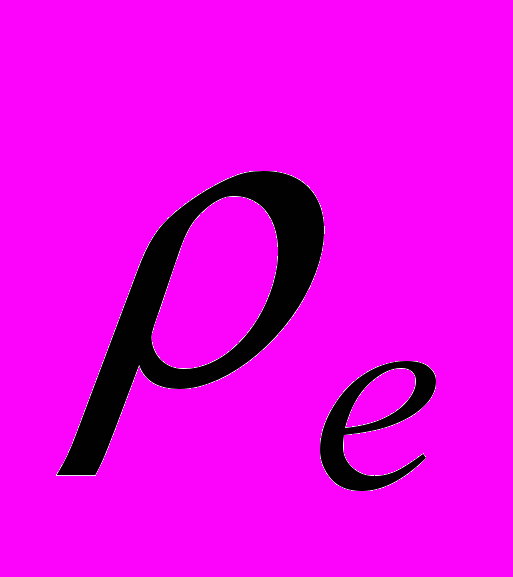 та та  , відповідно. , відповідно. |
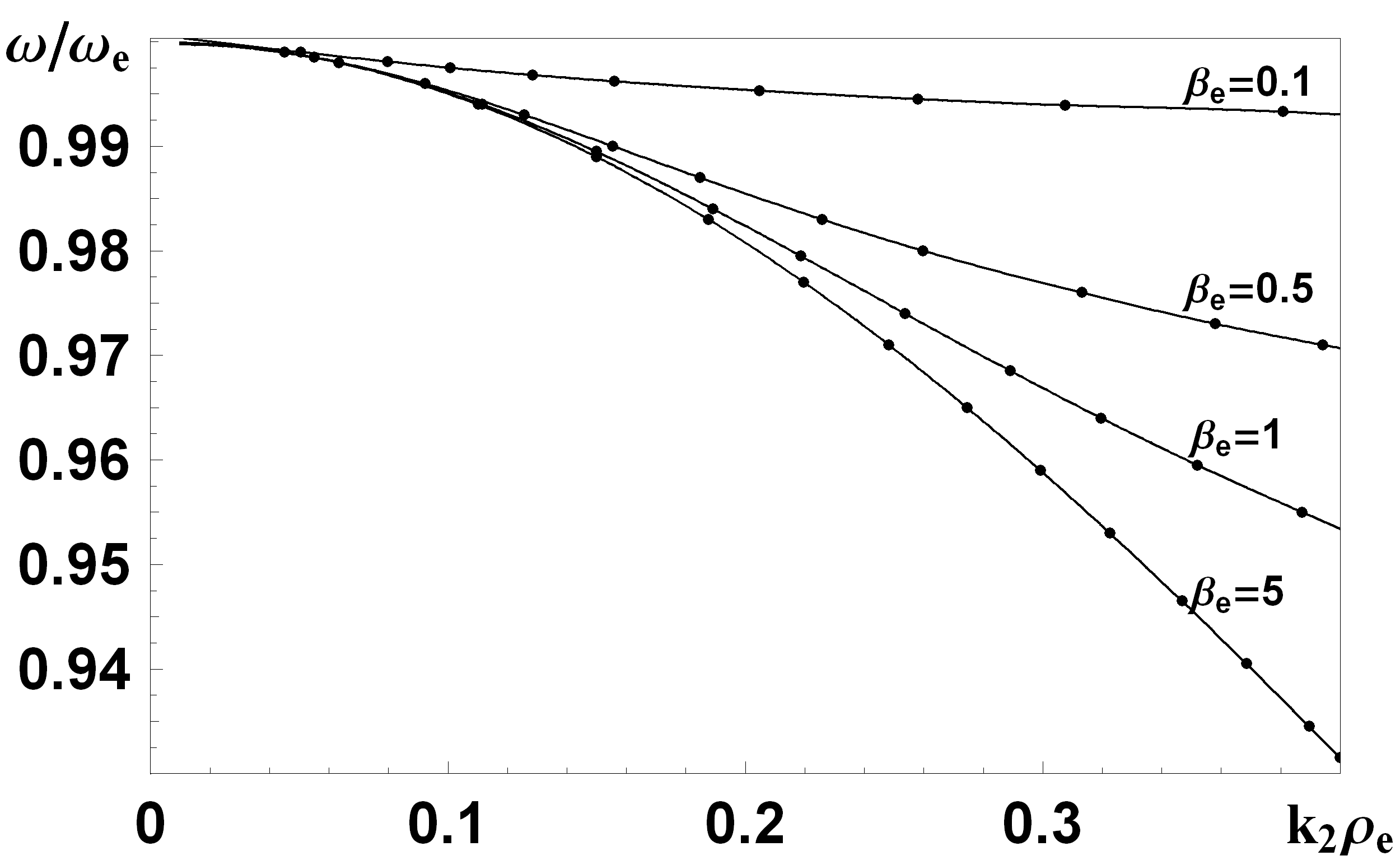 | 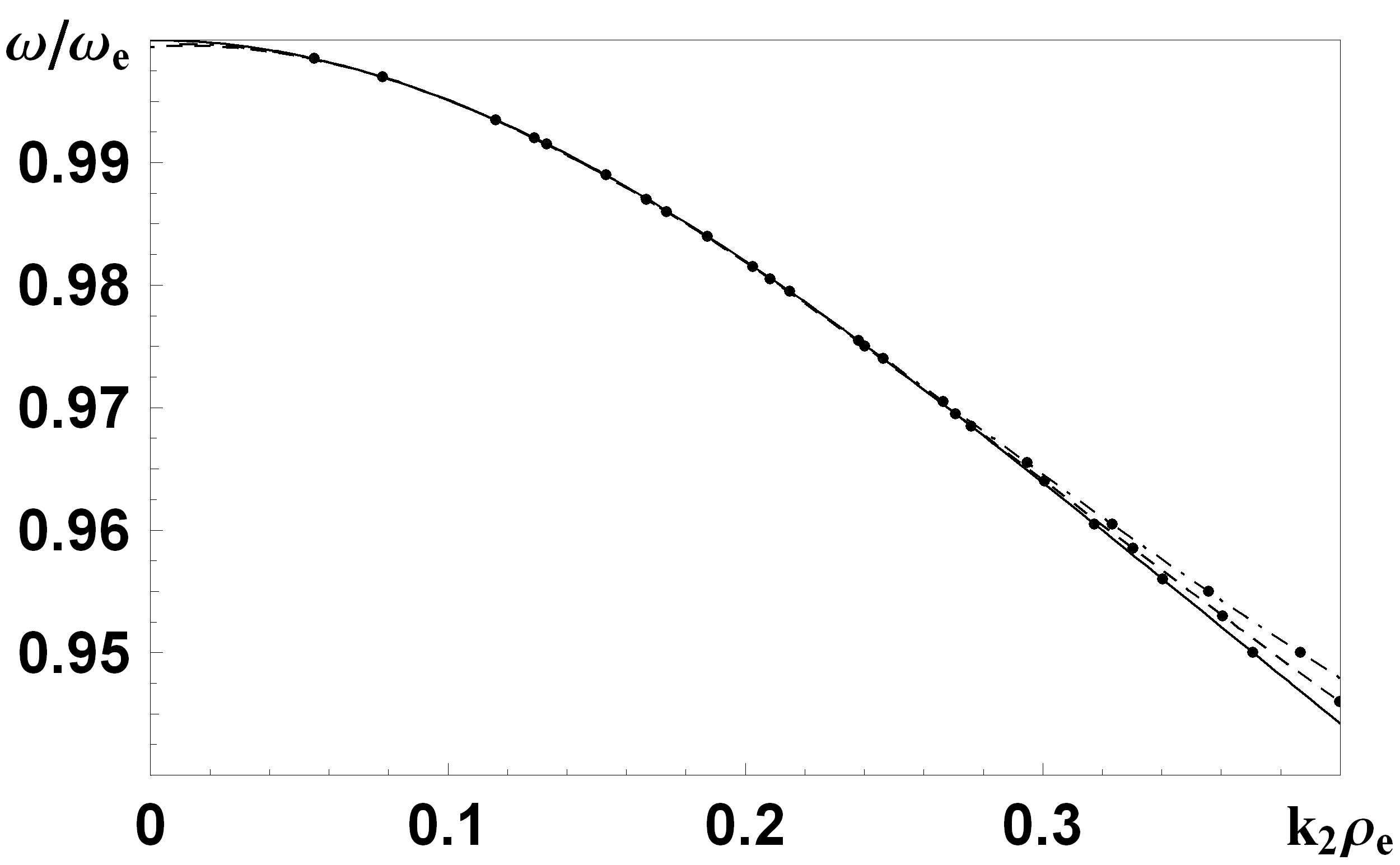 |
| Рис. 3. Дисперсійні характеристики при різних значеннях параметра 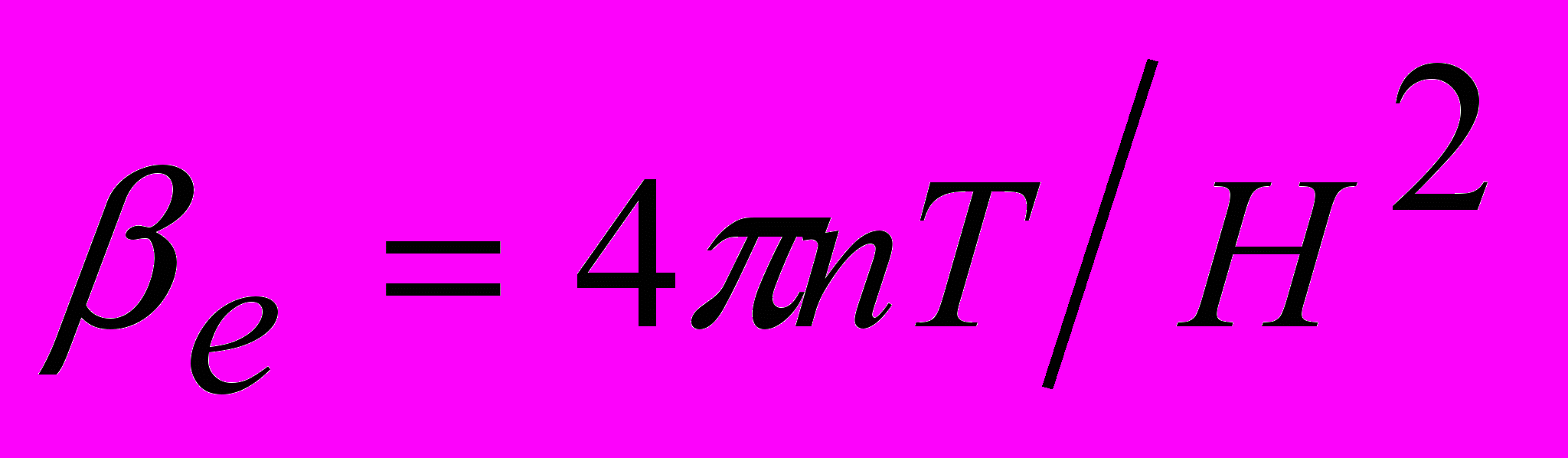 . . | Рис. 4. Частотні характеристики для різних залежностей густини плазми від координати. Сполошна крива відповідає однорідному випадку, штрих-пунктирна - 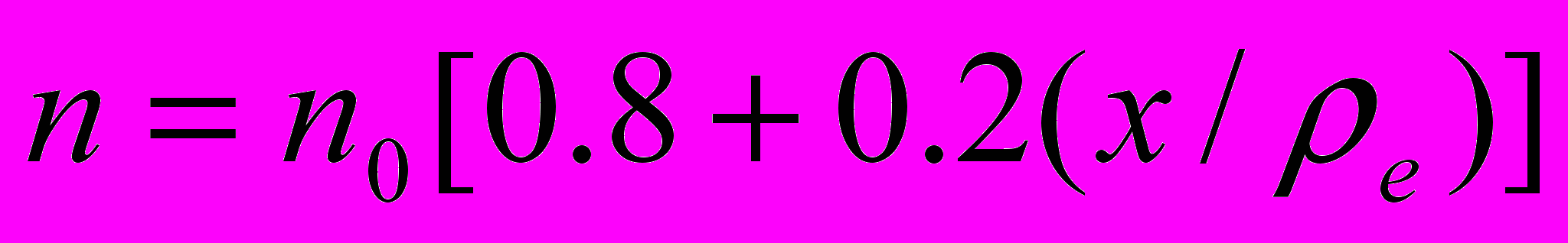 , штрихова - , штрихова -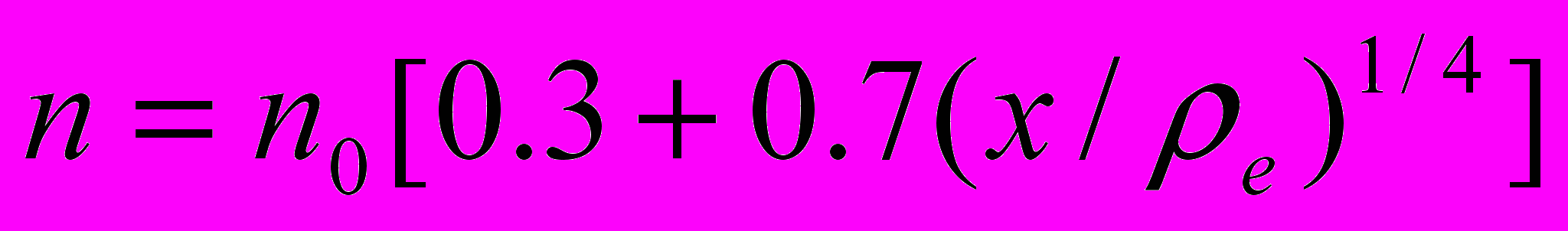 |
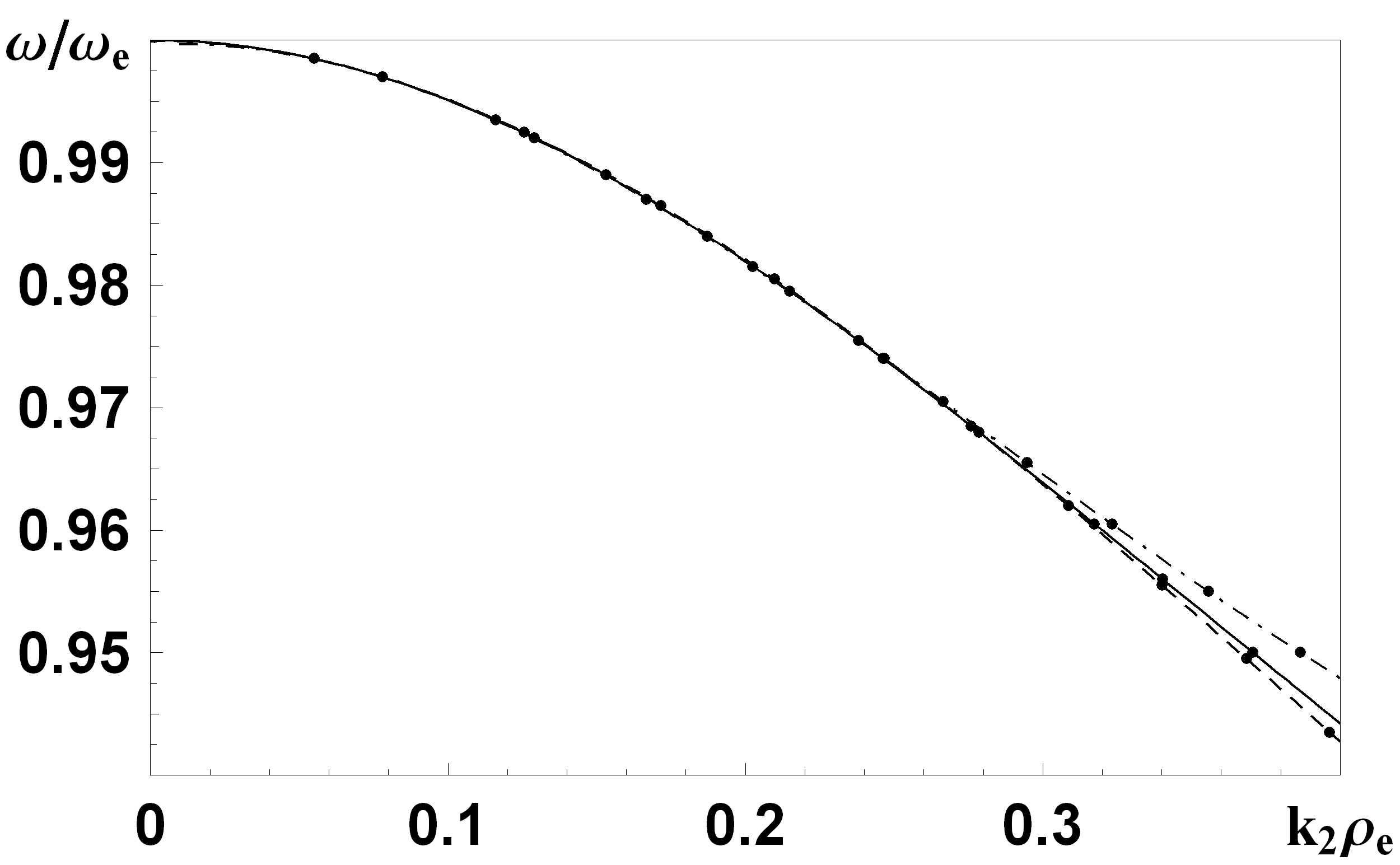 | 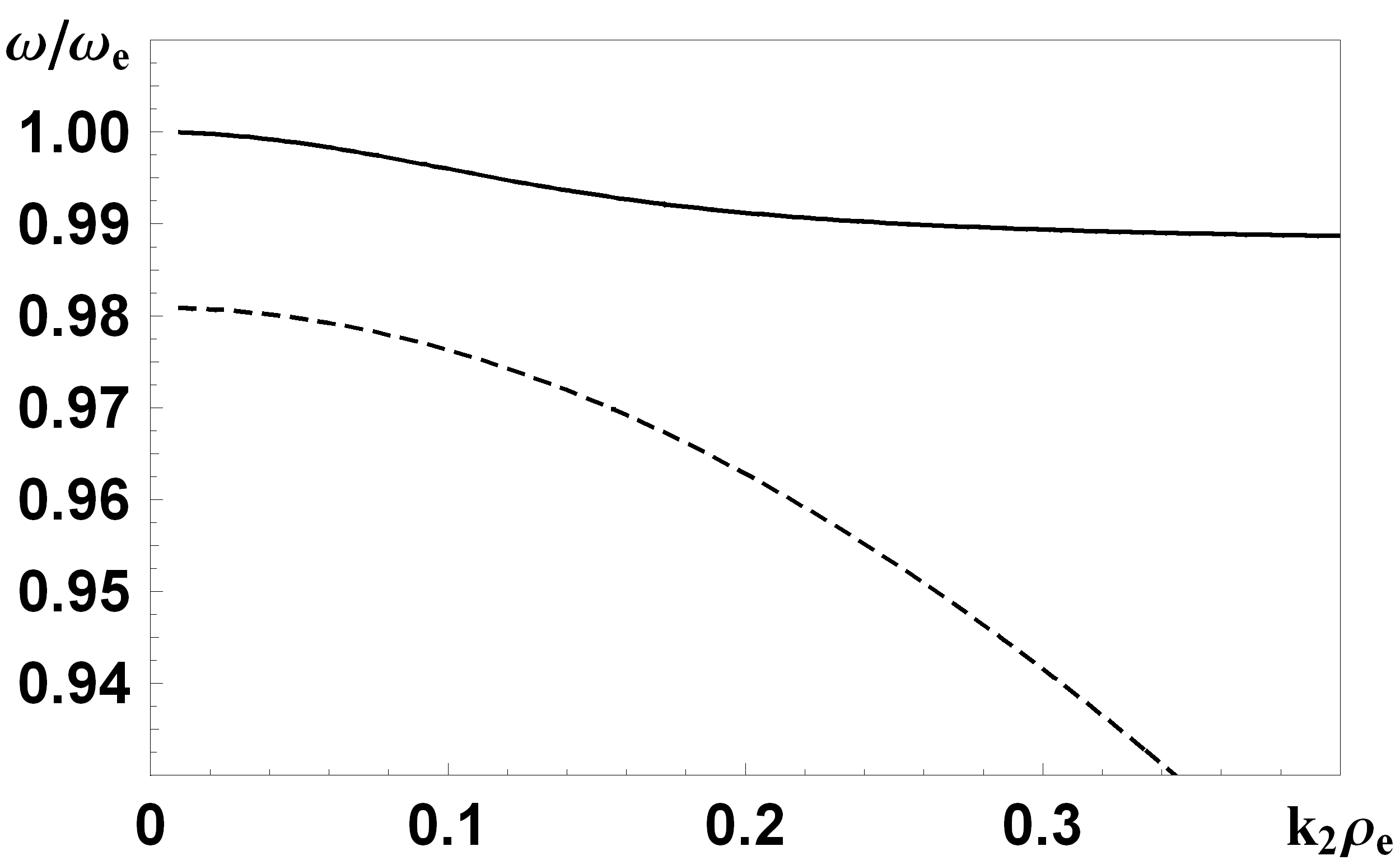 |
| Рис. 5. Частотні характеристики для різних залежностей густини плазми від координати. Сполошна крива відповідає однорідному випадку, штрих-пунтрирна – додатньому градієнту, штрихова - від’ємному. | Рис. 6. Сполошна лінія – враховані дві складові, штрихова – одна складова хвильового вектора. |
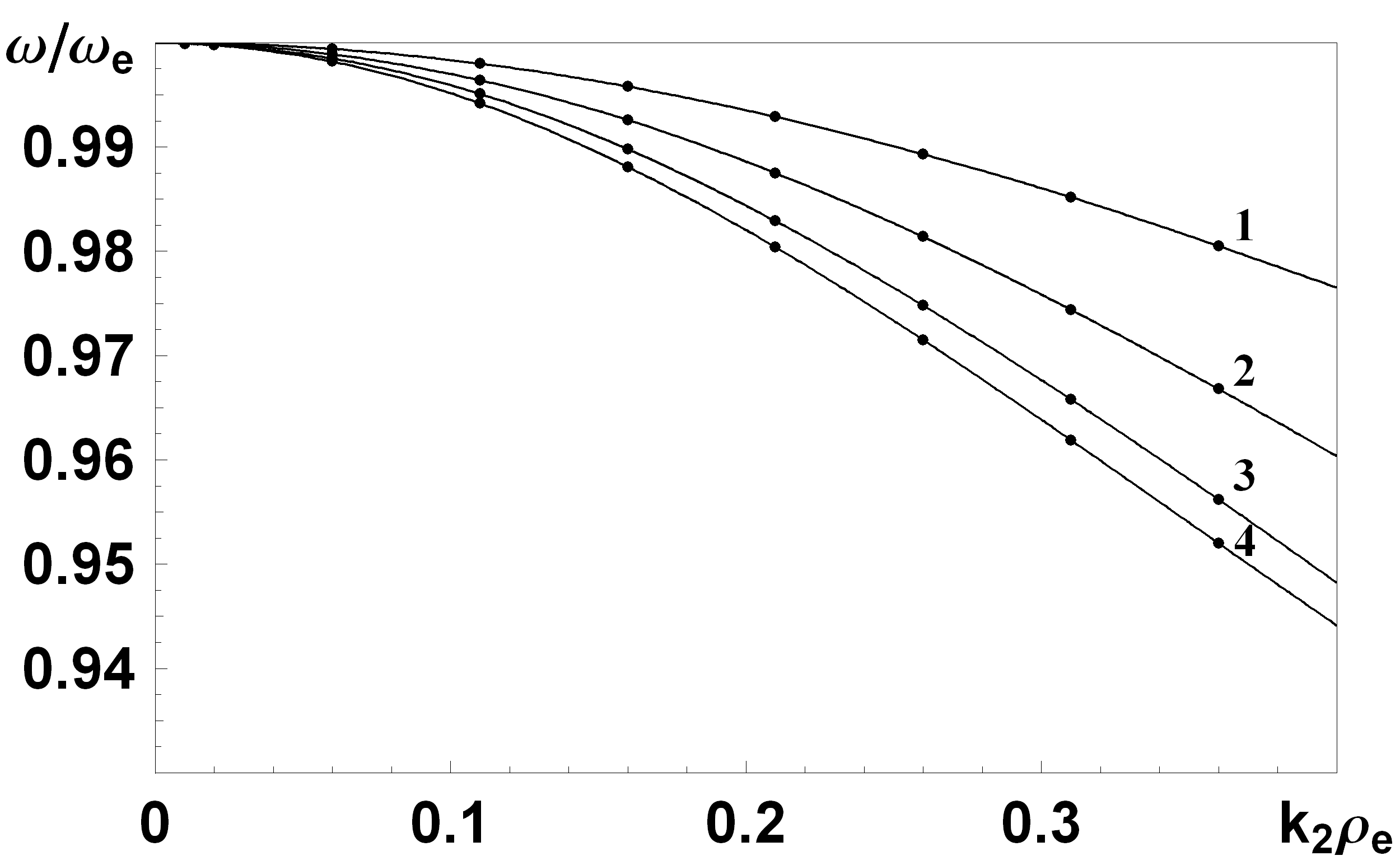 | 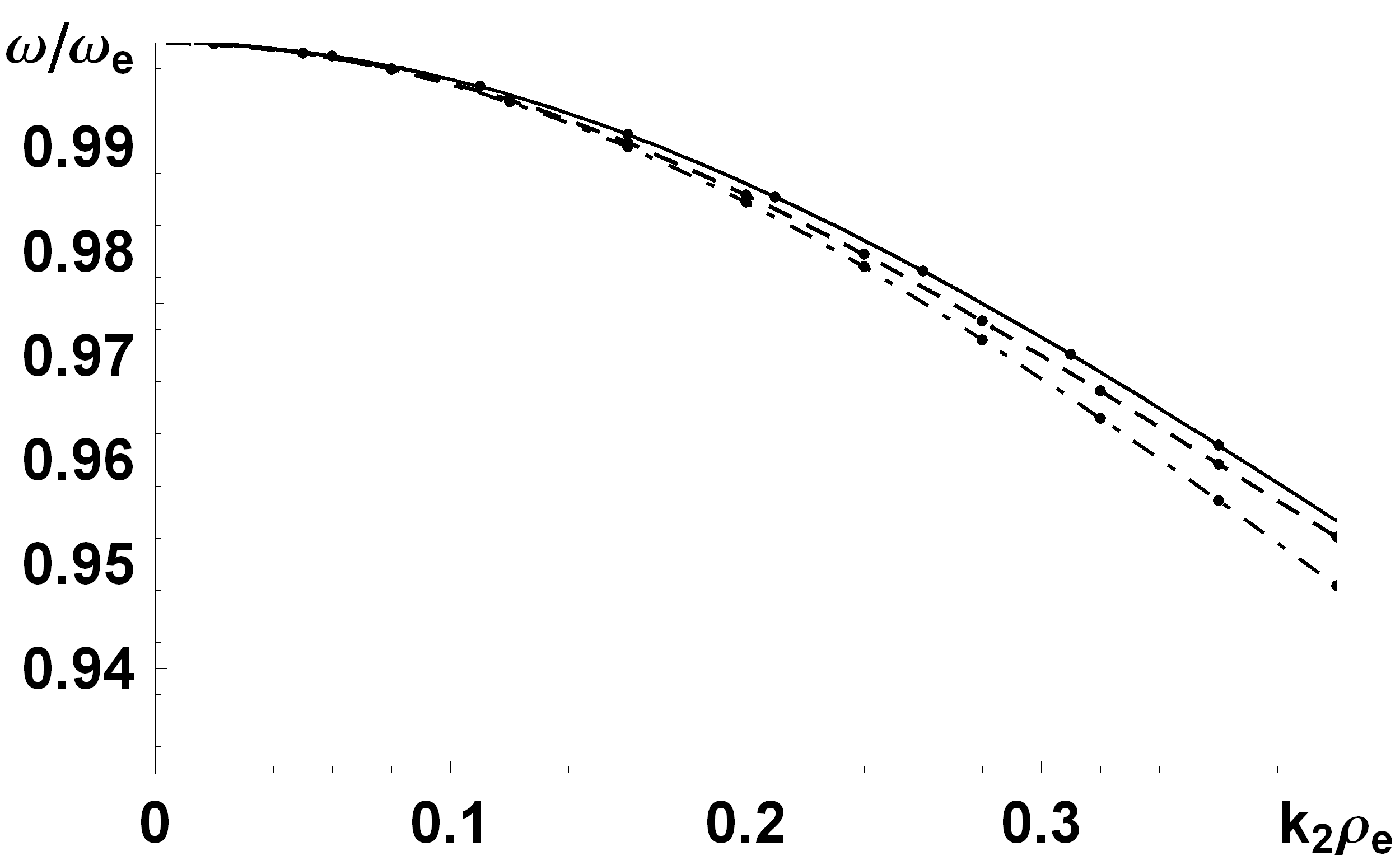 |
| Рис. 7. Залежність частоти від хвильового вектора для різної товщини плазми. Цифри 1,2,3 та 4 відповідають випадкам 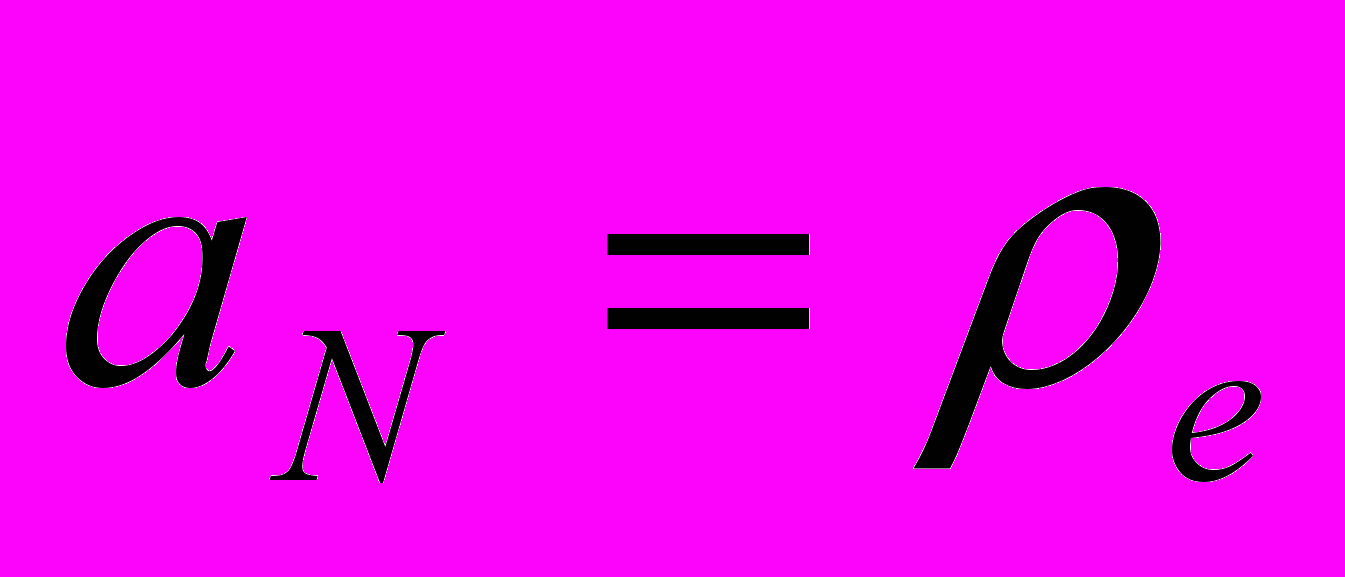 , , 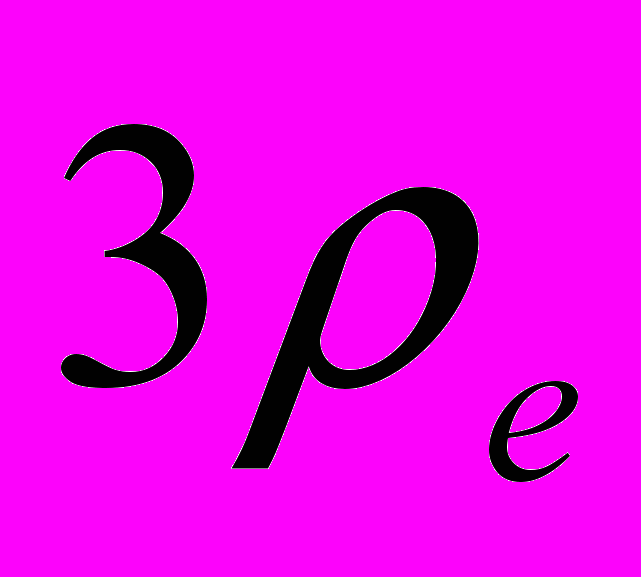 , , 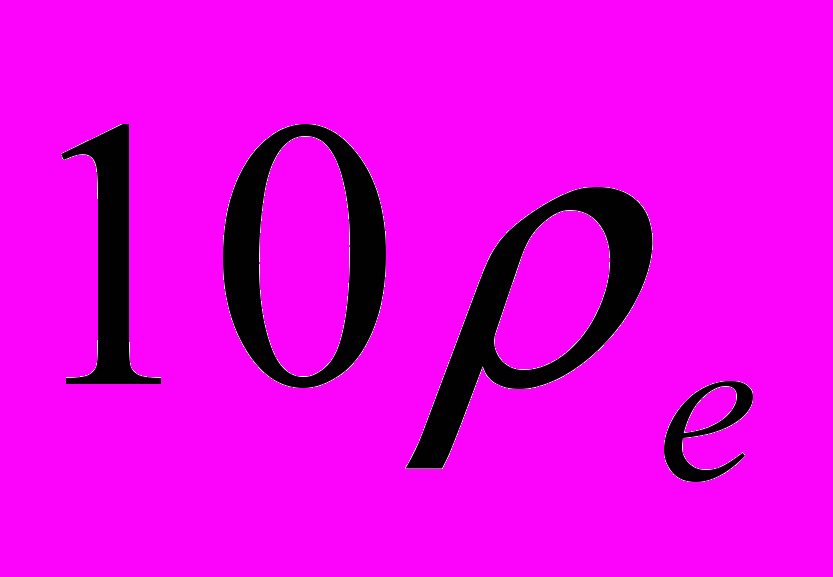 та напівобмеженій плазмі, відповідно. та напівобмеженій плазмі, відповідно. | Рис. 8. Залежність частоти від хвильового вектора для різних профілів плазми. Сполошна крива відповідає однорідному випадку, штрихова - параболічна залежність густини від координати, штрих-пунктир – залежність х4. |
 | 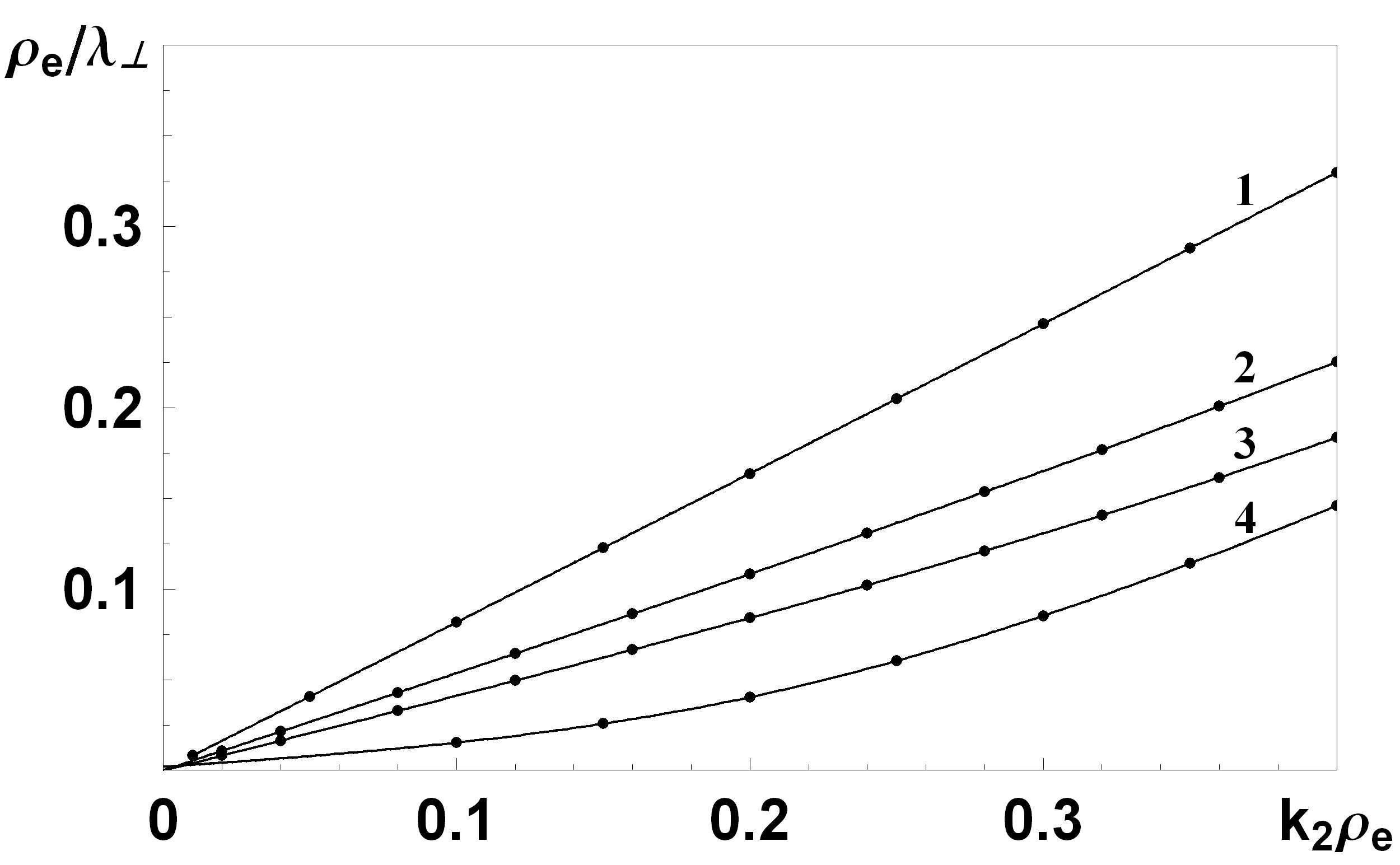 |
| Рис. 9. Залежність частоти від хвильового вектора для різних профілів плазми. Сполошна крива відповідає однорідному випадку, штрих-пунктирна – від’ємний градієнт, штрихова – додатній. | Рис. 10. Залежність глибини проникнення від хвильового вектора для різних товщини плазми. Криві 1-4 відповідають значенням 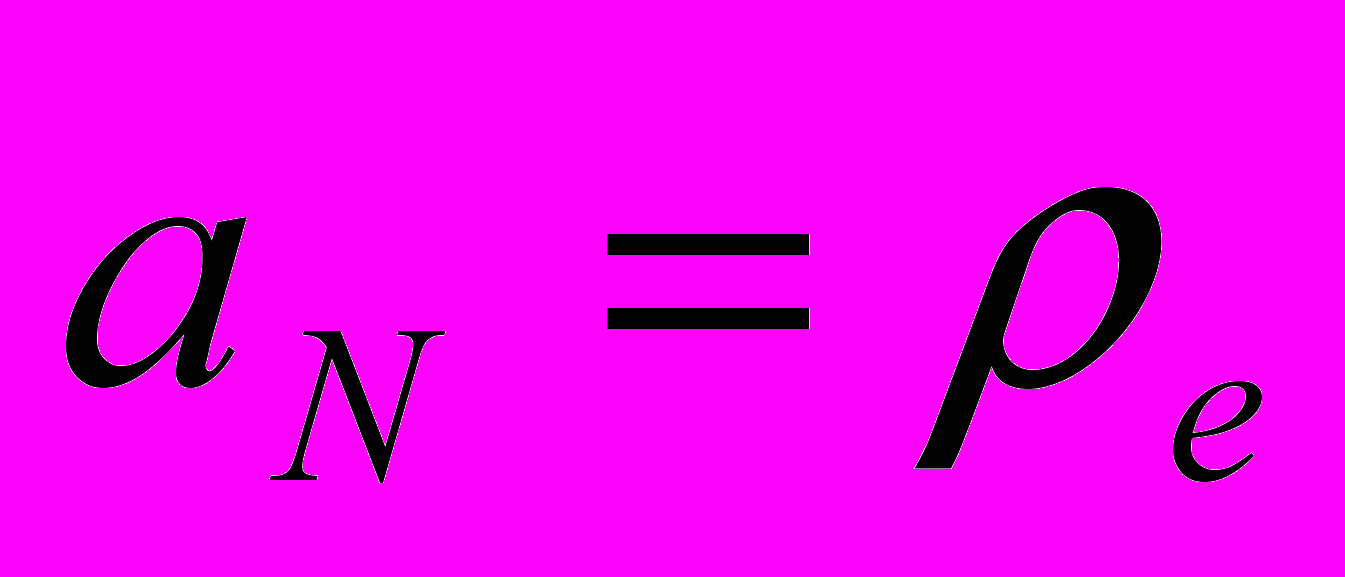 , , 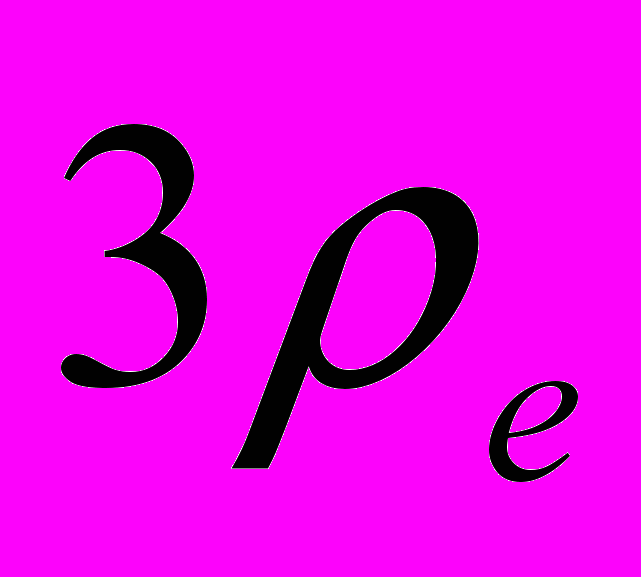 , , 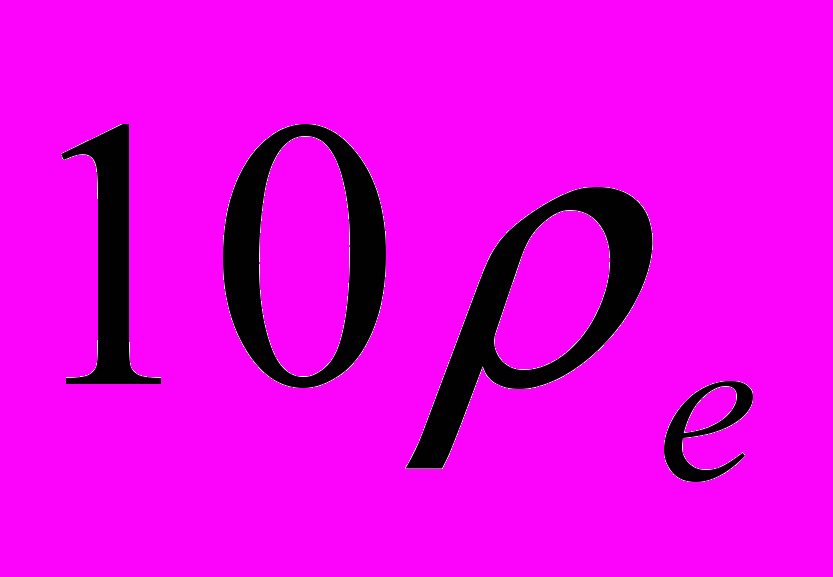 та напівобмеженій плазмі, відповідно. та напівобмеженій плазмі, відповідно. |
На завершення наведемо відомості про експерименти стосовно ПЦЗХ. Так у статті [12] наведено результати експериментів, які проводилися в адіабатичній плазмовій пастці з магнітним полем типу пробкотрона. Автори досліджували радіальні та осьові профілі плазми, а також збудження та поширення поверхневих циклотронних хвиль. Було доведено існування поверхневих циклотронних хвиль, виміряні частотні характеристики цих хвиль, її азимутальний та радіальний профіль. Отже ПЦЗХ не є просто теоретичною абстракцією, а реально існують та їх можна спостерігати експериментально.
ВИСНОВКИ
У даній роботі наведено результати дослідження циклотронних хвиль у плазмі. Розглянуто поверхневу О-моду (поверхневу циклотронну звичайно поляризовану хвилю). Звичайно поляризовані ПЦХ характеризуються аномальною дисперсією, напрямок групової та фазової швидкостей у цих хвиль є взаємно протилежним.
Моделювання неоднорідної плазми сходинковою функцією є гарним наближенням для розрахунків дисперсії хвиль, частота яких слабко залежить від густини плазми. Додатній градієнта густини призводить до зростання частоти ПЦЗХ, а від’ємний градієнт - до зниження частоти у випадку напівобженої плазми. В випадку прошарку плазми наявність градієнту призводить до зниження частоти.
Товщину плазмового прошарку
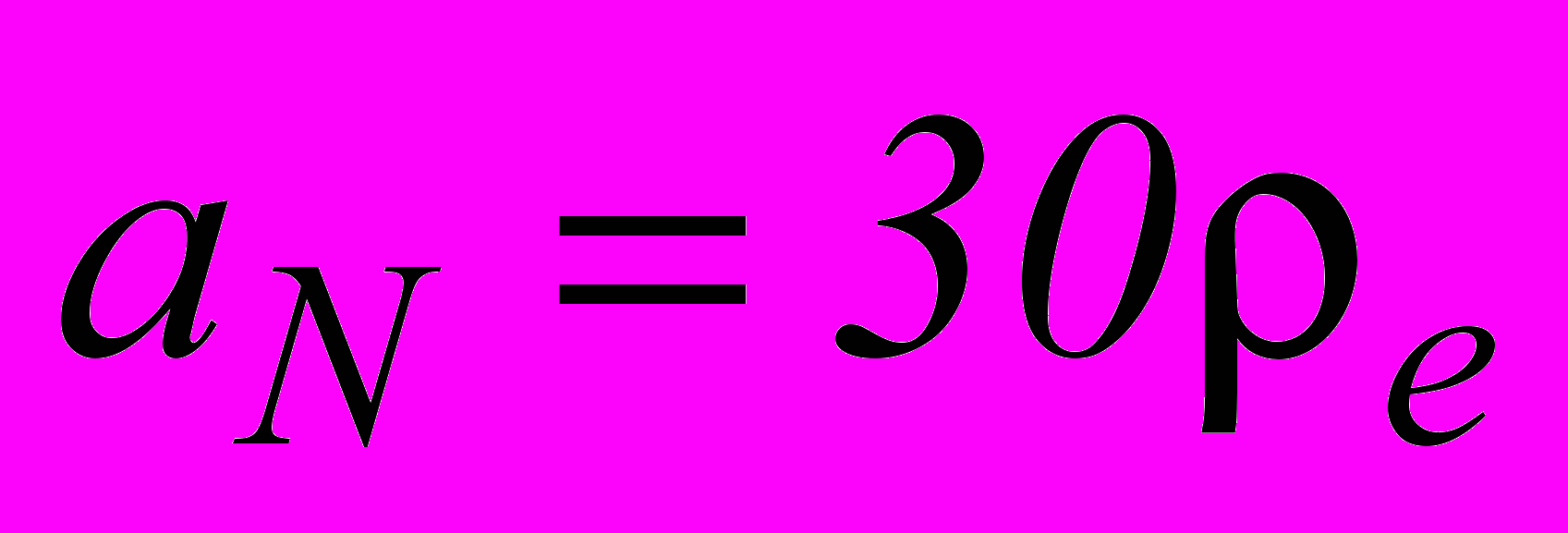 можна вважати еквівалентною напівобмеженій плазмі. При зменшенні товщини діелектрика частота ПЦЗХ прямує до циклотронної. Зменшення групової швидкості призводить до посилення загасання цих хвиль, тому на відміну від незвичайно поляризованих поверхневих циклотронних хвиль, звичайно поляризовані хвилі не можуть поширюватися уздовж поверхні розділу плазма-метал.
можна вважати еквівалентною напівобмеженій плазмі. При зменшенні товщини діелектрика частота ПЦЗХ прямує до циклотронної. Зменшення групової швидкості призводить до посилення загасання цих хвиль, тому на відміну від незвичайно поляризованих поверхневих циклотронних хвиль, звичайно поляризовані хвилі не можуть поширюватися уздовж поверхні розділу плазма-метал.При прямуванні до нуля параметра
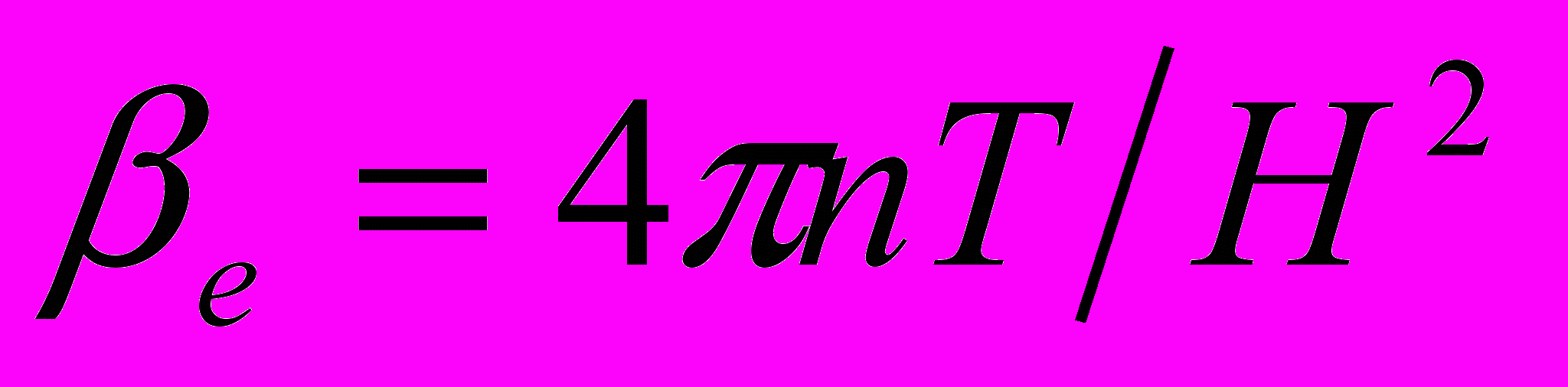 (відношення газового тиску до магнітного) частка ω/ωе → 1; при βе≥10 можна знехтувати магнітним тиском. Врахування другої складової хвильового вектора призводить до підвищення частоти ПЦЗХ.
(відношення газового тиску до магнітного) частка ω/ωе → 1; при βе≥10 можна знехтувати магнітним тиском. Врахування другої складової хвильового вектора призводить до підвищення частоти ПЦЗХ.Залежність глибини проникнення ПЦЗХ до плазми приблизно дорівнює
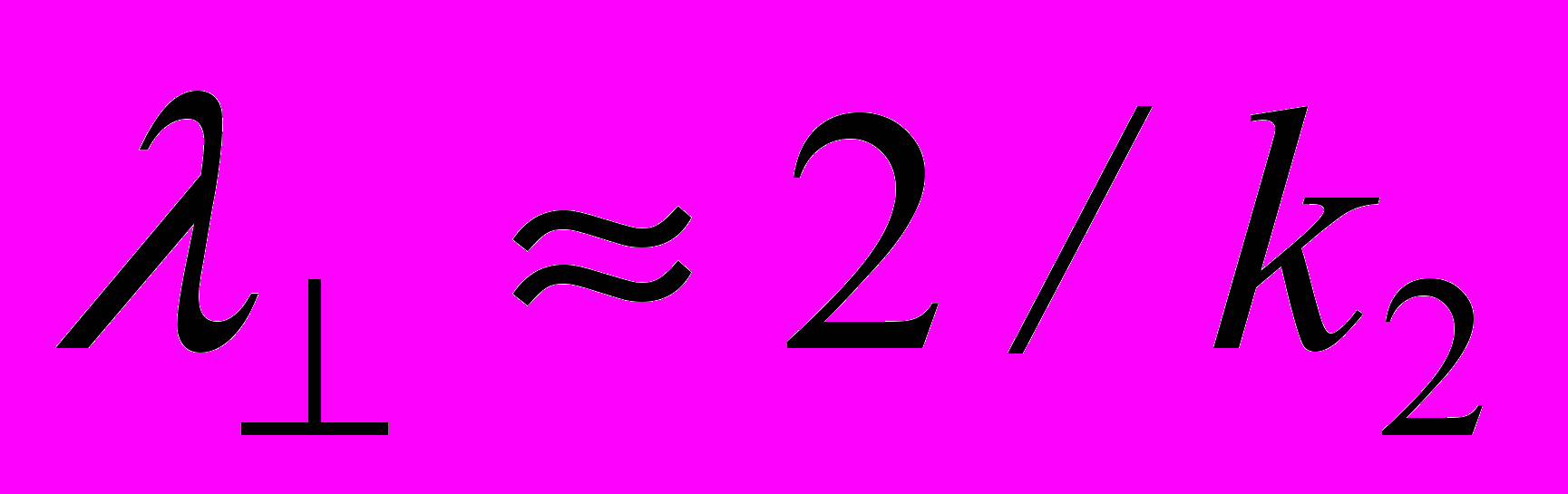 , при цьому зростання товщини шару плазми призводить до зростання глибини проникнення.
, при цьому зростання товщини шару плазми призводить до зростання глибини проникнення.Отримані результати представляються корисними для більш повного розуміння фізичних явищ в обмеженій плазмі.
СПИСОК ПОСИЛАНЬ
- Nagatsu M., Naito K., Ogino A., Nanko S. // Plasma Sources Sci. Technol. 2006. v.15. p. 37
- Белецкий Н.Н., Булгаков А.А., Ханкина С.И., Яковенко В.М. Плазменные неустойчивости и нелинейные явления в полупроводниках. - Киев: Наукова думка, 1984
- Margot J., Moisan M. Surface wave sustained plasmas in static magnetic fields for study of ECR discharge mechanisms. - Microwave Exited Plasmas. Ed. by M. Moisan and J. Pelletier. - Amsterdam: Elsevier, 1992
- Nagatsu M., Naito K., Ogino A., Nanko S. // Plasma Sources Sci. Technol. 2006. v.15. p. 37
- Azarenkov N.A., Girka V.O., Sporov A.E. Physica Scripta, vol.55, p.339 (1997)
- Azarenkov N.A., Girka V.O., Kondratenko A.M., Sporov A.E. Plasma Physic Cont. Fusion, vol.39, p.375 (1997)
- Dine S., Booth J-P., Curly G. A., Jolly J., Guillon J. // Plasma Sources Sci. Technol. 2005. v.14. p. 777
- Ахиезер А.И., Ахиезер И.А., Половин Р.В. и др. Электродинамика плазмы - М.: Наука, 1974
- Франк-Каменецкий Д.А. Лекции по физики плазмы.- М. Атомиздат (1968)
- Girka V.O. Plasma Physic Cont. Fusion, vol.42, p.999 (2000)
- Girka V.O. J. Plasma Physic, vol.68, №2, p.129 (2002)
- Tarey R. D., Akhtar M. K., Ganguli A. Plasma Sources Sci. Technol., vol. 8, p. 519
