Geum.ru

Лекция 15. Выбор в условиях неопределенности 1 риск в экономике. Ценность (!!!) Риска

Вид материалаЛекция

Содержание


Переход от вероятностей к оценке риска: математическое ожидание
Иные характеристики риска: изменчивость (среднеквадратичное отклонение, дисперсия)
Каков математическое ожижание жребия орел-решка, где выигрыш определяется в зависимости от номера попытки с выпадением орла след
Подобный материал:
Лекция 15. ВЫБОР В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ 1


РИСК В ЭКОНОМИКЕ. ЦЕННОСТЬ (!!!) РИСКА

  • Риск в экономике: примеры
  • Примеры рисковых «благ». Обобщение: все (!) «блага» (товары) являются в той или иной степени рисковыми. Если степень риска низка, то мы можем считать, что его нет. Что значит низкая степень риска?
  • Какова ценность рисковых благ? Почему они вообще имеют ценность, если они связаны с риском? Как можно определить ценность рисковых действий?
  • Почему люди предъявляют спрос на рисковые блага (товары)?
  • Какова практическая значимость оценки рисковых благ?
  • Как описать риск? Вероятность, математическое ожидание и дисперсия
  • Чем отличается объективная оценка риска от субъективной?
  • Братья Бернулли, Крамер и Санкт-Петербургский парадокс: как он родился?
  • В чем собственно парадокс? Противоречие между математическим ожиданием выигрыша и его субъективной оценкой



  • Риск в экономике: примеры



    • Кораблекрушение
    • Пожар
    • Организация нового предприятия
    • Посещение стоматолога
    • Хирургическая операция
    • Сдача экзамена
    • Выдача кредита банком
    • Участие в лотерее
    • Закупка фруктов для последующей продажи
    • Женитьба (замужество)
    • Назовите такое наше действие или желание, которое не было бы связано с риском…


Обобщение: все (!) «блага» (товары, действия) являются в той или иной степени рисковыми. Если степень риска низка, то мы можем считать, что его нет.

Следствие для теории: изучить как ведет себя человек в ситуациях связанных с риском:
  • Как он воспринимает риск
  • Как он оценивает риск
  • Какие факторы и как влияют на оценку риска
  • Как принимаются решения относительно рисковых благ



  • Что значит низкая степень риска? Чем отличается субъективная оценка риска от объективной? Как описать риск? Вероятность, математическое ожидание и дисперсия


Пример: переход улицы на красный свет. Возможная выгода – экономия времени. Возможные издержки – ущерб здоровью. Что означает объективная оценка риска в этом случае? Под объективной оценкой риска понимается информация о риске, независящая от восприятия риска данным человеком. Что это за информация?
    • Частота ДТП при переходе на красный свет (в скольких случаях из 1000 переходов на красный имеет место ДТП)
    • Каково распределение тяжести последствий ДТП
    • Какова возрастная структура попадающих в ДТП
    • Каково распределение тяжести последствий ДТП по выделенным возрастным группам
    • каков половой состав пешеходов попадающих в ДТП

каково распределение попадающих в ДТП по уровню зрения, физической силе, быстроте реакции, профессии, темпераменту, доходу, цвету волос, цвету одежды в момент ДТП, стоимости одежды в момент ДТП, расовой и национальной принадлежности и т.д.


Краткое отступление: что такое информация вообще? Определение Клода. Шеннона (Shannon Claude Elwood, 1916 – 2001): «информация это то, что устраняет неопределенность».


Имея объективные статистические данные мы можем построить функцию вероятности попадания в ДТП, а также функции вероятности тяжести последствий ДТП для конкретного человека. Они будут иметь следующий вид

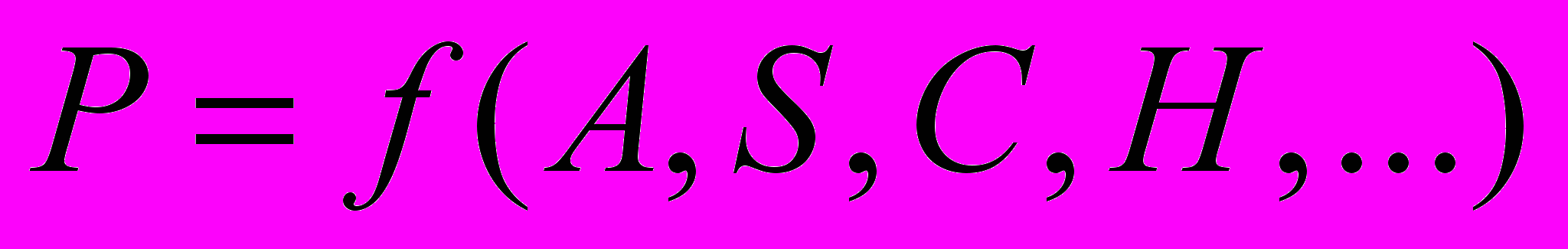, где

Например, функция может иметь вид

…….


Или функция вероятности того, что в ДТП у человека будет перелом (ушиб, ссадина, сотрясение мозга и т.д.) будет иметь вид

…..


Теперь рассмотрим, что означает субъективная вероятность

Это оценка данным конкретным человеком вероятности попасть в ДТП. От чего зависит ваша оценка такой вероятности? От того, как родители пугали в детстве? От вашей скорости бега? От любви к острым ощущениям?...


Далее, рассмотрим в когда используется объективная, а в когда субъективная вероятность?

Мы часто не обладаем объективной информацией. Поэтому нам ничего не остается как полагаться на наши субъективные оценки. Например, если мы хотим скупаться в незнакомом озере и не знаем какое там дно.


Переход от вероятностей к оценке риска: математическое ожидание

Человека интересует не только и не столько вероятность некоторого события сама по себе, но его возможные последствия, - положительные или отрицательные, - выгоды или потери. Например, вас интересует, не только вероятность выигрыша в лотерею, но и сумма выигрыша. Как оценить возможные выгоды или потери? Их оценивают посредством (заменяют) математического ожидания. Математическое ожидание (в речи часто сокращают – матожидание) это произведение вероятности события на его количественную оценку. Например, если вы покупаете лотерейный билет за 10 рублей и вероятность выиграть 100 рублей вы оцениваете в 10%, то матожидание выигрыша будет:


100*0,1 + 0*0,9 – 10 = 0! Что показывает матожидание? Оно показывает среднюю величину выигрыша, если бы вы покупали данную лотерею достаточно много раз.


Иные характеристики риска: изменчивость (среднеквадратичное отклонение, дисперсия)


  • Какова ценность рисковых благ? Почему они вообще имеют ценность, если они связаны с риском? Как можно определить ценность рисковых действий?
  • Почему люди предъявляют спрос на рисковые блага (товары)?
  • Какова практическая значимость оценки рисковых благ?
  • Братья Бернулли, Крамер и Санкт-Петербургский парадокс: как он родился?
  • В чем собственно парадокс? Противоречие между математическим ожиданием выигрыша и его субъективной оценкой


Каков математическое ожижание жребия орел-решка, где выигрыш определяется в зависимости от номера попытки с выпадением орла следующим образом

…….


Тогда математическое ожидание выигрыша будет

иметь вид


ЕР =




Даниил Бернулли (Bernoulli, Daniel, Гронинген, 8 февраля 1700 г. – Базель, 17 марта 1782 г.)

Швейцарский математик и естествоиспытатель. Принадлежал к знаменитой семье ученых, родоначальник которой Якоб Бернулли был выходцем из Голландии. В 1725-33 гг. работал в Петербургской Академии наук сначала на кафедре физиологии, затем математики. После возвращения в Швейцарию - профессор в Базеле на кафедре физиологии (1733) и механики (1750-77). В 1728-78 гг. в изданиях Петербургской АН, почетным членом которой он состоял после отъезда из России, опубликовал 47 работ.

В 1738 г. предложил решение так называемого Санкт-Петербургского парадокса, автором которого является его двоюродный брат Николай Бернулли. В решении была использована гипотеза об убывающей предельной полезности дохода.


Бернулли Д. Опыт новой теории измерения жребия . Вехи экономической мысли. Сост. и общ. ред. В. М. Гальперина. СПб., 1999. Т. 1 : Теория потребительского поведения и спроса. С. 11-27. Впервые опубликовано на латыни в 1738 г. в Записках Петербургской Академии Наук.

Швейцарец по происхождению, Бернулли был математиком и физиком-теоретиком; он родился в Гронингене 8 февраля 1700 г. и скончался в Базеле 17 марта 1782 г.


Даниил Бернулли был членом действительно выдающейся семьи, три поколения которой подарили миру не менее 8 талантливых математиков, трое из которых - Джеймс старший (1654-1705 гг.), Джон старший (1667-1748 гг.) и Даниил - в истории науки являются звездами первой величины.


Несмотря на то, что изначально Даниил Бернулли изучал медицину, в 1725 г. он согласился занять место математика в только что основанной Императорской Академии в Санкт-Петербурге, но в 1733 г. вернулся в Базель, где с успехом возглавлял кафедры анатомии и ботаники, психологии (1743 г.) и физики (1750-77 гг.).


Он был избран членом всех главных европейских научных обществ, существовавших в те дни, включая те, что находились в Лондоне, Париже, Берлине и Санкт-Петербурге и вел активную научную переписку с Эйлером и Голдбахом.


Будучи оригинальным мыслителем и плодовитым писателем, Бернулли работал во многих направлениях, но самый важный вклад он внес в область механики, гидродинамики и математики. Вместе с Эйлером, близким другом детства, они не менее 10 раз выигрывали или делили с кем-либо ежегодную премию Парижской Академии. В его шедевре, "Гидродинамика" (1738 г.), содержится основанный на уравнении Бернулли расчет равномерного потока невязкой, не сжимающейся жидкости и самое первое математическое представление кинетической теории газов с учетом закона Бойля.


Бернулли внес важный вклад в развитие статистики и теории вероятности, который включает одно из первых приложений метода максимального правдоподобия к теории ошибок и исследование эффективности прививок от оспы. Тем не менее, самым известным его вкладом в эту область определенно стал труд 1738 г. "Specimen theoriae novae de mensura sortis", в котором рассматриваются полезность, "моральное ожидание" и санкт-петербургский парадокс.


Санкт-петербургский парадокс (названный так, поскольку работа Бернулли появилась в Комментариях Санкт-Петербургской Академии) касается игры, которая впервые была упомянута Николаем Бернулли (племянником Даниила) в его переписке с Монтмортом: монета подкидывается n раз до тех пор, пока не выпадет "орел"; затем выплачивается 2 в степени n дукатов. Парадоксально, но математическое ожидание выигрыша представляет собой бесконечно большую величину, хотя здравый смысл приводят к заключению, что справедливым вознаграждением за участие в игре должна быть ограниченная сумма.


Бернулли предположил, что парадокс может быть разрешен, если заменить математическое ожидание моральным, в котором вероятность умножается на личную полезность, а не на цены, выраженные в деньгах. Утверждая, что дополнительная полезность обратно пропорциональна текущей удаче (и прямо пропорциональна приросту удач), Бернулли пришел к заключению, что полезность является линейной функцией логарифма денежной цены, и показал, что в этом случае моральное ожидание от игры будет конечной величиной.


Строго говоря, использование Бернулли логарифмической полезности не разрешило парадокса: если полезность неограниченна, то всегда можно найти соответствующий расходящийся ряд. Следует также отметить, что и не он был первым, кто использовал именно этот путь для решения парадокса. В 1728 г. в письме Николаю Бернулли швейцарский математик Габриель Крамер отмечал, что если полезность ограничена или пропорциональна квадратному корню из денежной цены, то моральное ожидание будет конечной величиной. Но только благодаря трудам Бернулли это решение вошло в литературу и, несмотря на имевшую в начале место (и эксцентричную) критику Д'Аламбера, к началу 19 века в большинстве научных трудов появился раздел, посвященный моральному ожиданию и самому парадоксу.


5.1. Описание риска 168

Вероятность 168
Математическое ожидание 169
Вариабельность 169
Принятие решений 173

5.2. Предпочтения в области риска 174

Различные предпочтения в области риска 176