Программа дисциплины высшая математика для студентов специальности 080507 «Менеджмент организаций» -бакалавры
| Вид материала | Программа дисциплины |
- Учебно-методический комплекс для студентов специальности 080507 «Менеджмент организаций», 493.27kb.
- Программа дисциплины сд. Ф. 04. Информационные технологии управления для студентов, 168.36kb.
- Методические рекомендации по выполнению контрольной работы по дисциплине «Инновационный, 80.89kb.
- Программа дисциплины сд. Ф. 11. Экологический менеджмент для студентов специальности, 230.43kb.
- Программа дисциплины сд. Ф «стратегический менеджмент» для студентов специальности, 128.75kb.
- Программа дисциплины сд. Ф инновационный менеджмент для студентов специальности 080507, 263.74kb.
- Программа дисциплины дс. 01. «Финансовый менеджмент» для студентов специальности 080507, 227.28kb.
- Программа дисциплины сд. Ф. 01. Стратегический менеджмент для студентов специальности, 149.47kb.
- Программа преддипломной практики для специальности 080507. 65 "Менеджмент организации", 125.78kb.
- Программа дисциплины 2500 сд. Ф. 14 «управленческий учёт» для студентов специальности, 420.39kb.
Министерство образования Российской Федерации

ОБНИНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ АТОМНОЙ ЭНЕРГЕТИКИ (ИАТЭ)
| | УТВЕРЖДАЮ |
| | Проректор по учебной работе ___________________ С.Б.Бурухин |
| | “______”____________ 2008 г. |
ПРОГРАММА ДИСЦИПЛИНЫ
ВЫСШАЯ МАТЕМАТИКА
Ф1. для студентов специальности 080507
«Менеджмент организаций» -бакалавры
Форма обучения: очная
Объем дисциплины и виды учебной работы по очной форме в соответствии с учебным планом
| Вид учебной работы | Всего часов | Семестры | |||
| | | 1 | 2 | 3 | |
| Общая трудоемкость дисциплины | 315 | 118 | 118 | 134 | |
| Аудиторные занятия | 159 | 68 | 68 | 68 | |
| Лекции | 102 | 34 | 34 | 34 | |
| Практические занятия и семинары | 57 | 20 | 17 | 20 | |
| Лабораторные работы | | | | | |
| Курсовой проект (работа) | | | | | |
| Самостоятельная работа | 156 | 50 | 50 | 56 | |
| Расчетно-графические работы | | | | | |
| Вид итогового контроля (зачет, экзамен) | | экзам | экзам | экзам | |
Обнинск 2008
Программа составлена в соответствии с Государственным образовательным стандартом высшего профессионального образования для специальности 080507 «Менеджмент организаций» - бакалавры
Программу составил:
доцент кафедры высшей математики ___________________Р.Т.Галусарьян
Программа рассмотрена на заседании кафедры высшей математики (протокол
№2 _____от_ 16.10___ 2008 г.)
Заведующий кафедрой высшей математики
профессор ___________________ Е.А.Сатаев
“____”_____________ 2008__ г.
СОГЛАСОВАНО
| Декан факультета СЭФ профессор_______________ В.Н.Тябин “____”_____________ 2008__ г. | Начальник Учебно – методического Управления____________Соколова Ю.Д. “______”_________2008___г. |
1. Цели и задачи дисциплины.
Основная цель изучения курса высшей математики – дать студенту необходимый математический аппарат, с помощью которого студент может решать экономические задачи.
В курсе излагаются сведения по основным разделам высшей математики:
- дифференциальное и интегральное исчисления функции одной переменной;
- элементы аналитической геометрии и линейной алгебры;
- дифференциальное исчисление функции многих переменных;
- числовые и функциональные ряды, ряды Фурье;
- кратные интегралы;
- дифференциальные уравнения.
2. Требования к уровню освоения содержания дисциплины.
В результате изучения дисциплины студент должен уметь:
- вычислять предел функции, находить производные при различных способах задания функции;
- проводить полное исследования функции;
- решать задачи на экстремум (в том числе и задачи экономического содержания);
- пользоваться аппаратом векторной и линейной алгебры;
- вычислять интегралы и использовать их при решении задач;
- находить частные производные, решать задачи на безусловный и условный экстремум;
- вычислять кратные интегралы и применять их при решении задач;
- Находить общие и частные решения дифференциальных уравнений 1-го и 2-го порядков.
3. Содержание курса «Высшая математика»
Лекции: 1-й семестр– 17 лекций по 2ч.
| Содержание лекции | Лит-ра [2] |
| Элементы аналитической геометрии и линейной алгебры | |
| Л1.(2ч) Определители 2-го и 3-го порядков. Методы их вычисления. Системы линейных уравнений с тремя переменными. Случай единственного решения. Решение по правилу Крамера и методом Гаусса | Гл10,§2 |
| Л2.(2ч) Точка и прямая в прямоугольной системе координат на плоскости. Расстояние между двумя точками. Деление отрезка в данном отношении. Различные виды уравнения прямой на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности двух прямых. Расстояние от точки до прямой. | Гл3,§2,6 |
| Л3.(2ч) Кривые второго порядка . Канонические уравнения окружности, эллипса, гиперболы и параболы. Основные параметры этих кривых. Приведение уравнений кривых к каноническому виду. | Гл3,§7 |
| Л4.(2ч) Векторная алгебра. Действия над векторами. Проекция вектора на ось. Разложение вектора по базису 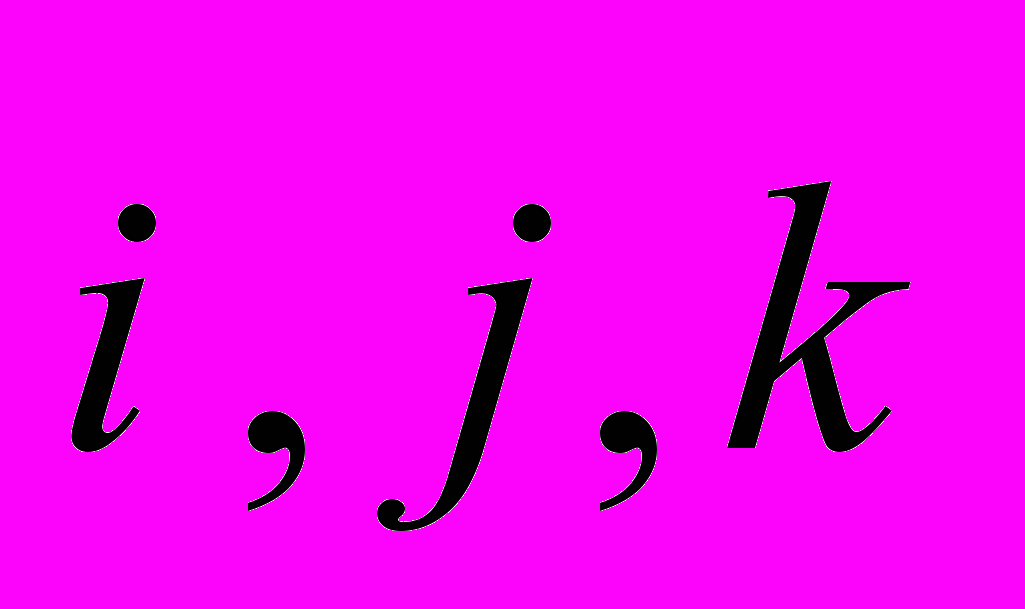 . Скалярное и векторное произведение двух векторов. Угол между двумя векторами. Условие коллинеарности и ортогональности двух векторов. Смешанное произведение трех векторов. Условие компланарности трех векторов. Объем параллелепипеда. . Скалярное и векторное произведение двух векторов. Угол между двумя векторами. Условие коллинеарности и ортогональности двух векторов. Смешанное произведение трех векторов. Условие компланарности трех векторов. Объем параллелепипеда. | Гл9,§2-8 |
| Л5.(2ч) Прямая и плоскость в пространстве. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору (нормали). Уравнение плоскости проходящей через три данные точки. Угол между плоскостями. Расстояние от точки до плоскости. Различные виды уравнения прямой в пространстве Угол между двумя прямыми. Угол между прямой и плоскостью. | Гл9, §11-13 |
| Л6.(2ч) Матрицы. Умножение матрицы на число, сложение матриц. Умножение матриц. Обратная матрица и метод ее нахождения. Решение линейных систем матричным способом. Ранг матрицы и методы его вычисления. | Гл10, § 1 |
| Л7.(2ч) Системы линейных уравнений. Условие совместности системы (теорема Кронекера – Капели) линейных неоднородных уравнений. Случай определенного решения. Решение методом Гаусса и методом Жордана. Нахождение общего решения линейной неоднородной системы (случай неопределенного решения). Нахождение фундаментальной системы решений для однородной системы. | Гл10, § 3,4 |
| Математический анализ | |
| Л8.(2ч) Числовые множества. Понятие о точной грани. Существование точной грани у ограниченного множества. Элементарные функции и их графики. Гиперболические функции. Функции: 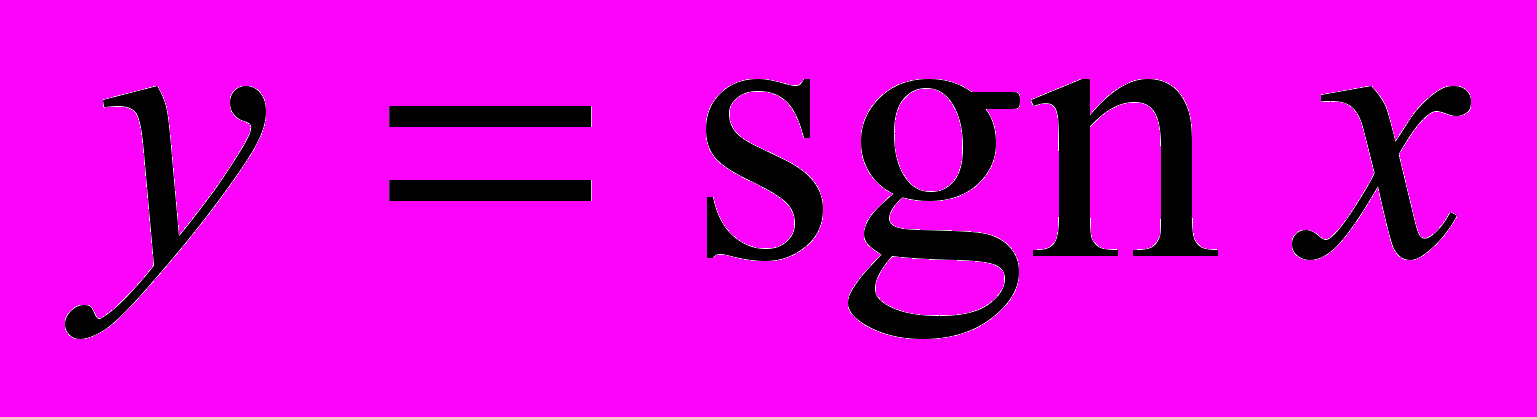 (сигнум- знак), (сигнум- знак), 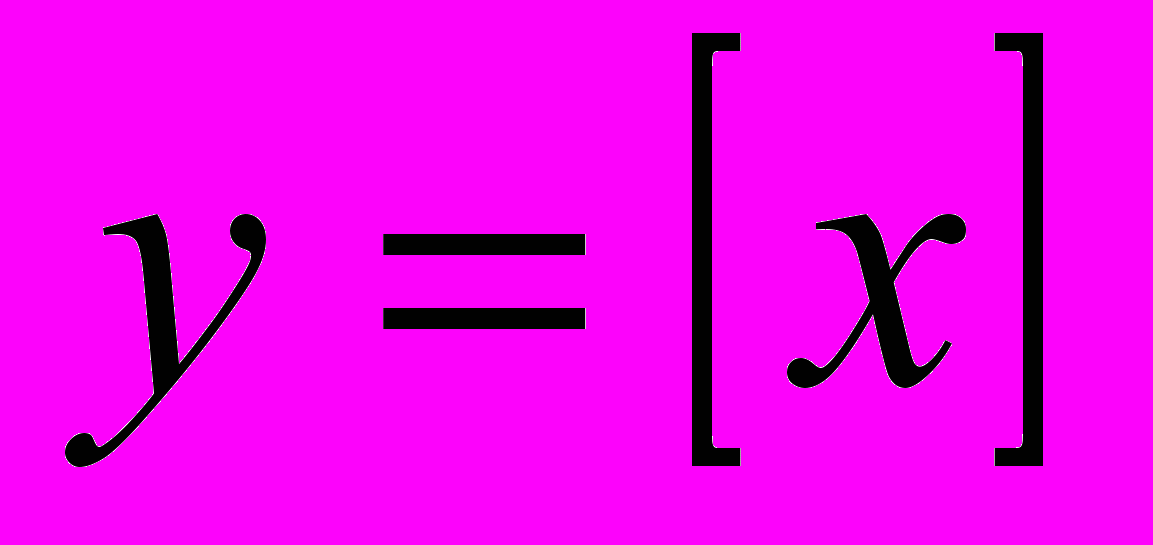 - целая часть числа, - целая часть числа, 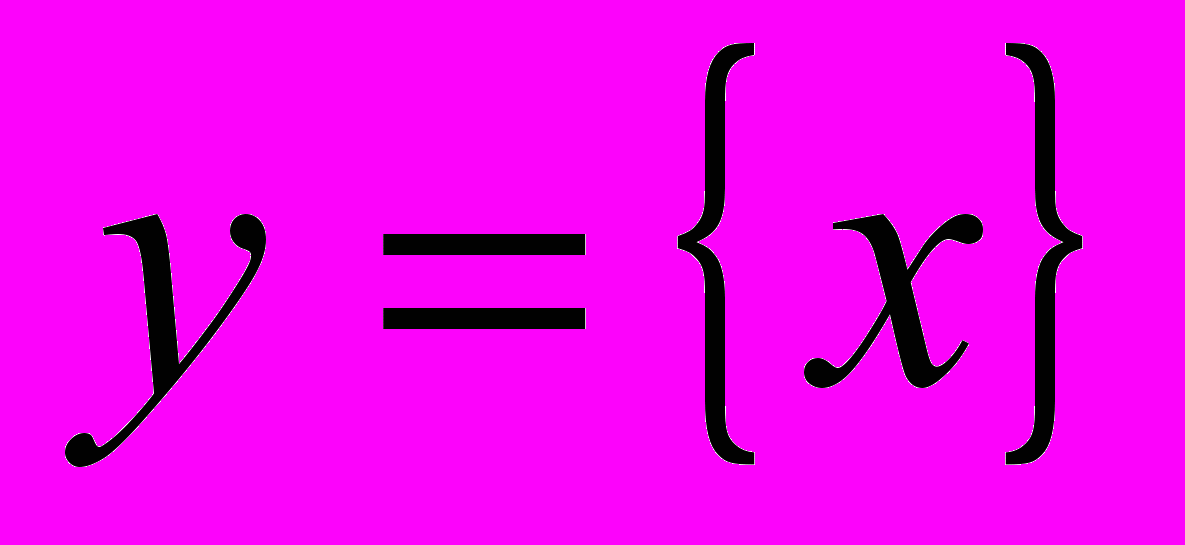 - дробная часть числа. - дробная часть числа. | Гл1, § 1-4 |
| Л9.(2ч) Простейшие функции, встречающиеся в экономике: линейные и квадратичные кривые спроса и предложения. Понятие о точке равновесия и максимальной прибыли. Числовая последовательность. Предел числовой последовательности. Критерий Коши (без доказательства). Арифметические свойства предела. | Гл2, § 1,2 |
| Л10.(2ч) Существование предела у монотонной ограниченной последовательности. Число е. Различные определения предела функции. Односторонние пределы. Арифметические свойства предела. Свойства функции, имеющей предел: ограниченность, сохранение знака. | Гл2, § 3 Гл4, § 2 |
| Л11. (2ч) Непрерывность функции в точке. Свойства функции, непрерывной в точке. Непрерывность элементарных функций. Два замечательных предела. Бесконечно малые и бесконечно большие функции. Эквивалентные бесконечно малые. Применение эквивалентности при вычислении предела функции. | Гл4, § 5,7,8 |
| Л12. (2ч) Сравнение бесконечно малых и бесконечно больших функций. Односторонняя непрерывность. Точки разрыва. Классификация точек разрыва. | Гл4, § 6,9 |
| Л13. (2ч) Свойства функции, непрерывной на отрезке. Сохранение знака, достижение наибольшего и наименьшего значения функции, непрерывной на отрезке. Понятие о равномерной непрерывности. Теорема Кантора (без доказательства). | Гл4, § 10 |
| Л14. (2ч) Понятие о производной. Необходимое условие дифференцируемости. Производная сложной функции. Правила дифференцирования. Таблица производных. Вывод формул производных некоторых функций: y=sinx, y=tgx, y=lnx, y=xn, y=arcsinx. Геометрический смысл производной. Уравнение касательной и нормали. Понятие эластичности функций: эластичность спроса, эластичность предложения. | Гл5, § 1,2 |
| Л15. (2ч) Дифференциал функции. Геометрически смысл, инвариантность. Дифференциал дуги. Производные и дифференциалы высших порядков. Дифференцирование неявных и параметрически заданных функций. | Гл5, §3, 10,11 |
| Л16. (2ч) Основные теоремы анализа. Теоремы Ферма, Ролля и Лагранжа. Теорема Коши. Формула Тейлора. Применение формулы Тейлора при вычислении предела функции. | Гл6, § 1,3 |
| Л17. (2ч) Правило Лопиталя. Применение правила Лопиталя при вычислении предела функции. | Гл6, § 2 |
Лекции: 2-й семестр– 17 лекций по 2ч.
| Содержание лекции | Лит-ра [2] |
| Л1.(2ч) Исследование функции с помощью производной. Условие монотонности. Необходимое и достаточные условия существования экстремума функции. | Гл6,§4 |
| Л2.(2ч) Наибольшее и наименьшее значения функции на отрезке. Применение методов исследования функции в экономике. Решение задач на оптимизацию. Задача получения максимальной прибыли. | Гл6,§4 |
| Л3.(2ч) Понятие о выпуклости и вогнутости графика функции. Точка перегиба. Необходимое и достаточное условие перегиба. Асимптоты графика функции. Схема полного исследования функции и построение графика. | Гл3,§4,5 |
| Л4.(2ч) Интегральное исчисление функции одной переменной. Первообразная и неопределенный интеграл. Свойства интеграла. Таблица интегралов. Метод компенсирующего множителя и метод введения под знак дифференциала. Интегрирование по частям. Метод замены переменной в неопределенном интеграле. | Гл7,§1-4 |
| Л5.(2ч) Интегрирование функций, содержащих квадратный трехчлен в знаменателе. Интегрирование рациональных дробей с помощью представления их в виде суммы простейших дробей (случаи различных и кратных действительных корней). Интегрирование рациональных дробей (случай комплексных корней). | Гл7, §5 |
| Л6.(2ч) Интегрирование тригонометрических и гиперболических выражений. Интегрирование простейших иррациональностей. Тригонометрические подстановки. Интегрирование дифференциальных биномов. | Гл7, § 6 |
| Л7(2ч). Определенный интеграл. Интегральные суммы. Критерий интегрируемости. Свойства определенного интеграла. Вычисление интеграла по формуле Ньютона-Лейбница. Применение интеграла для нахождения суммарного дохода с помощью предельного дохода. | Гл8, § 1-4,7 |
| Л8.(2ч) Интегрирование четных и нечетных функций на симметричном интервале. Замена переменной и интегрирование по частям в определенном интеграле. | Гл8, § 8 |
| Л9.(2ч) Геометрические приложения интеграла. Площадь плоской фигуры: 1)вычисление в прямоугольной системе координат, 2) вычисление в параметрической форме , 3) вычисление в полярных координатах. | Гл8, § 10 |
| Л10.(2ч) Вычисление длины дуги. Объем тела по площади сечения. Объем тела вращения. Поверхность тела вращения. | Гл8,§10 |
| Л11. (2ч) Приближенное вычисление определенного интеграла. Метод прямоугольников, метод парабол (формула Симпсона). Применение определенного интеграла в экономике: добавочная выгода производителя, нахождение капитала по известным инвестициям. | Гл8, § 12 |
| Л12. (2ч) Функции многих переменных. Арифметическое (метрическое) пространство. Понятие функции многих переменных. Понятие о линии уровня. Линии уровня производственных функций (изокванты). | Гл11, § 1.2 |
| Л13. (2ч) Предел и непрерывность функции многих переменных. Свойства непрерывных функций. Частное и полное приращения функции. Понятие о частных производных и их геометрический смысл. | Гл11, § 3,4 |
| Л14. (2ч) Касательная плоскость и нормаль к поверхности. Дифференциал. Частные производные сложных функций. Дифференцирование неявных функций. Теорема существования (без доказательства ) | Гл12, § 1,2,4 |
| Л15. (2ч) Частные производные высших порядков. Теорема Шварца о равенстве смешанных производных. Дифференциалы высших порядков. Формула Тейлора. Вывод формулы для функции двух переменных. | Гл12, §6,7 |
| Л16. (2ч) Экстремум. Необходимые и достаточные условия существования экстремума. Критерий Сильвестра. | Гл12, § 8 |
| Л17. (2ч) Наибольшее и наименьшее значения функции многих переменных в замкнутой области. Условный экстремум. Метод Лагранжа. Решение задачи о максимальной прибыли методом Лагранжа. | Гл12, § 9 |
Лекции: 3-й семестр– 17 лекций по 2ч.
| Содержание лекции | Лит-ра [2] |
| Л1.(2ч) Числовые ряды. Понятие о сходимости. Необходимый признак сходимости. Признаки сравнения. Достаточные признаки Даламбера и Коши. | Гл14,§1,2 |
| Л2.(2ч) Интегральный признак Коши. Знакопеременные ряды. Теорема Лейбница для знакочередующихся рядов. Абсолютная. и условная сходимость. | Гл14, §3,4 |
| Л3.(2ч) Функциональные ряды. Область сходимости. Равномерная сходимость. Теорема Вейерштрасса. Дифференцирование и интегрирование функциональных рядов. | Гл14,§5 |
| Л4.(2ч) Степенные ряды. Теорема Абеля. Радиус и центр сходимости. Разложение функций в степенные ряды по формуле Тейлора. Дифференцирование и интегрирование степенных рядов. Применение разложения функции в ряд Тейлора для приближенного вычисления интегралов. | Гл14,§4 |
| Л5.(2ч) Системы ортонормированных тригонометрических функций. Ряды Фурье. Теорема Дирихле. Коэффициенты Фурье Разложение функций в ряд Фурье в интервале (-, ). Разложение в ряд Фурье по синусам и по косинусам. Разложение функций в ряд Фурье в интервалах ( -l, l ), ( a, b ). | Гл14, §5 |
| Л6.(2ч) Определение двойного интеграла. Свойства двойного интеграла. | Гл13,§ 1 |
| Л7(2ч). Методы вычисления двойного интеграла. | Гл13,§ 2 |
| Л8.(2ч) Определение тройного интеграла. Свойства тройного интеграла. Методы вычисления. | Гл13, § 10 |
| Л9.(2ч) Замена переменных в двойных и тройных интегралах. Криволинейные координаты. Якобиан. Вычисление двойных интегралов в полярных и обобщенных полярных координатах. | Гл13, § 10 |
| Л10.(2ч) Вычисление тройных интегралов в цилиндрических и сферических координатах. Геометрические приложения кратных интегралов. Площадь плоской фигуры: 1) в прямоугольной системе координат, 2) в полярной системе координат. | Гл13, §10 |
| Л11. (2ч) Площадь поверхности тела. Объем фигуры. Вычисление объема тела с помощью тройного интеграла: в прямоугольной системе и в сферической системе координат. | Гл13, § 4 |
| Л12. (2ч) Понятие о математическом программировании. Решение задач на оптимизацию методами линейного программирования. Решение экономических задач методами линейного программирования. уровня производственных функций (изокванты). | Гл12, § 9 |
| Дифференциальные уравнения | |
| Л13. (2ч) Понятие о дифференциальном уравнении 1-го порядка. Общее решение. Частное решение. Особое решение. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения 1-го порядка. Нахождение общего и частного решения. | Гл15, § 1 |
| Л14. (2ч) Линейные дифференциальные уравнения и уравнения Бернулли. Решение этих уравнений методом Бернулли и методом вариации. Уравнения в полных дифференциалах. Решение методом объединения частных интегралов. | Гл15, § 1 |
| Л15. (2ч) Понятие о дифференциальных уравнениях второго и высших порядков. Общее и частное решение. Уравнения, допускающие понижение порядка: 1) 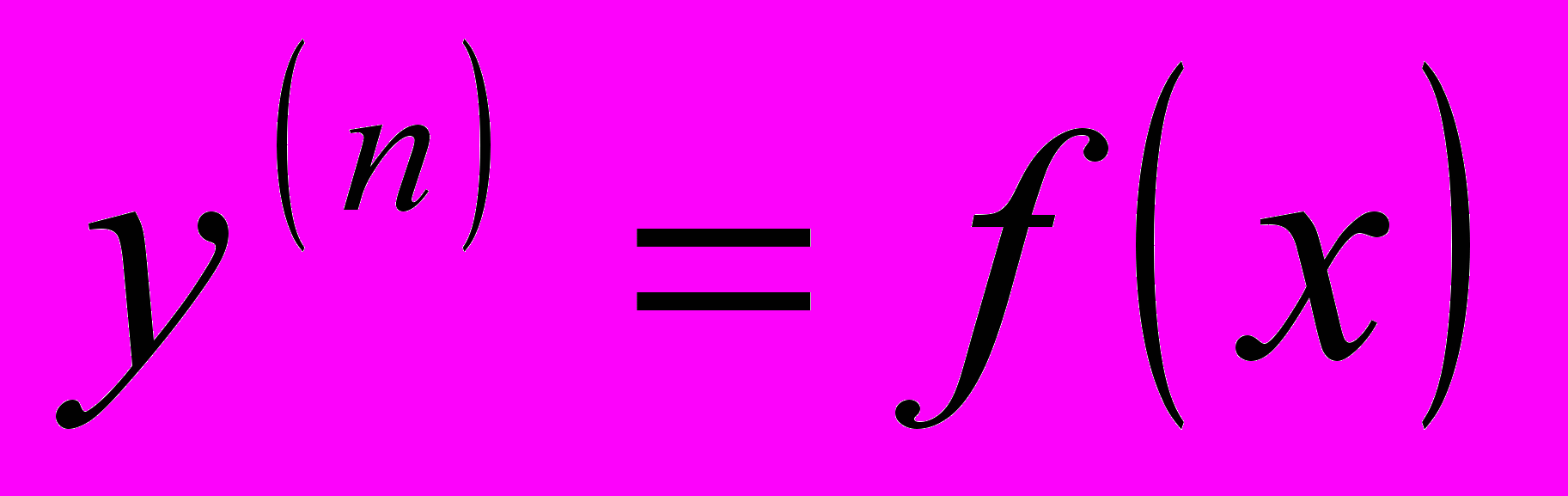 , 2) , 2) 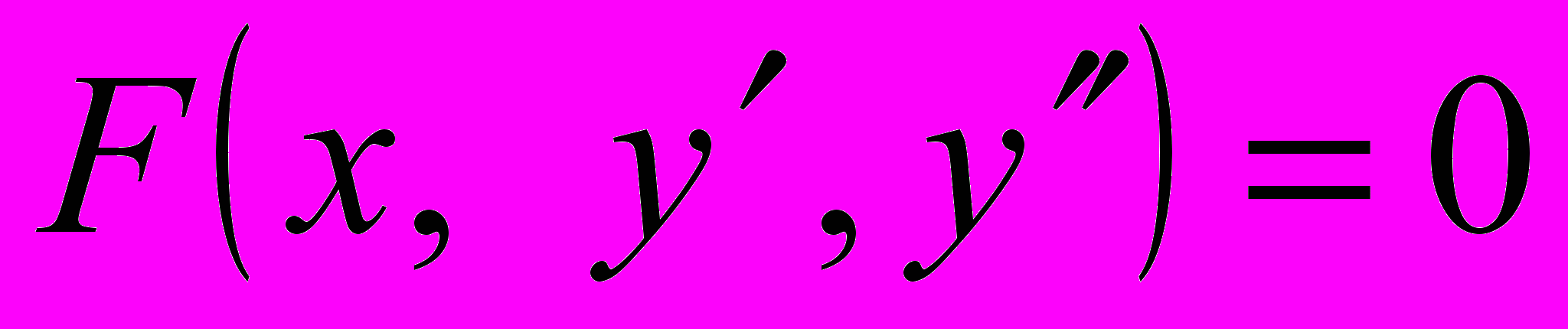 , 3) , 3) 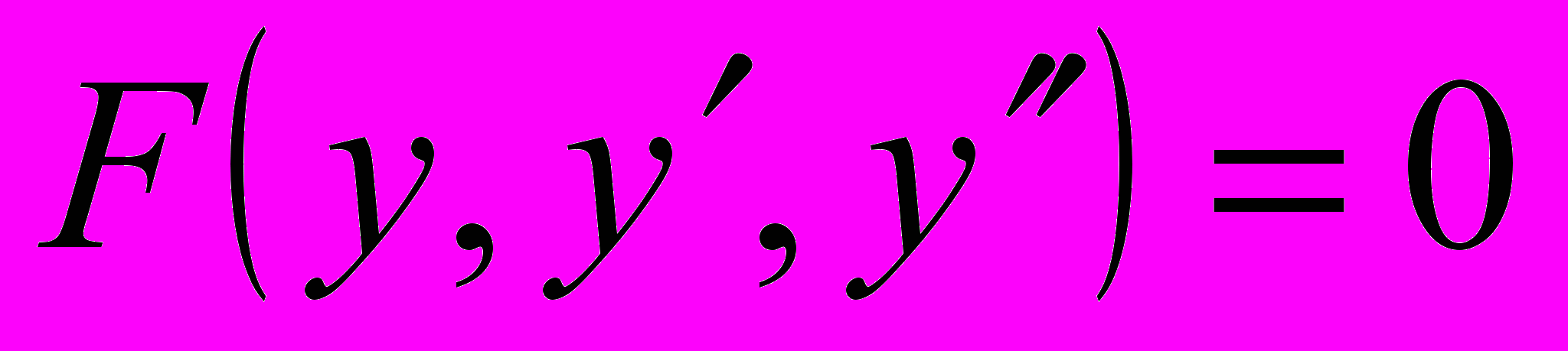 . . | Гл15, §2 |
| Л16. (2ч) Линейные дифференциальные уравнения второго и высших порядков. Свойства частных решений. Понятие о фундаментальной системе частных решений. Определитель Вронского. Свойство определителя Вронского. Теорема о структуре общего решения однородного уравнения. Неоднородные уравнения высших порядков. Свойства частных решений. Теорема о структуре общего решения неоднородного уравнения. Линейные дифференциальные уравнения второго и высших порядков с постоянными коэффициентами. Нахождение общего решения однородного уравнения. Характеристическое уравнение. Фундаментальная система частных решений. Общее решение однородного уравнения. | Гл15, § 3 |
| Л17. (2ч) Неоднородные линейные уравнения высших порядков с постоянными коэффициентами. Нахождение частного решения неоднородного уравнения в зависимости от вида правой части. Нахождение частного решения неоднородного уравнения методом вариации произвольных постоянных – методом Лагранжа. | Гл15, § 4 |
Семинары : 1-й семестр - 10 семинаров по 2ч.
Литература:
1. Г.Н.Берман «Сборник задач по курсу математического анализа».
2. Д.В.Клетеник «Сборник задач по аналитической геометрии»
3. П.Рябушко «Сборник индивидуальных заданий по высшей математике» (1-й том).
4. Л.А.Кузнецов «Сборник заданий по высшей математике»
5. Р.Т.Галусарьян «Сборник задач и упражнений по курсу Высшая математика, ч. 1 и 2,
Обнинск-2008»
6. Р.Т.Галусарьян «Введение в математический анализ», Обнинск-2002
7. Р.Ф.Апатенок «Сборник задач по линейной алгебре и аналитической геометрии».
8. Сборник задач по высшей математике для экономистов под редакцией В.И.Ермакова
| Семинар 1 Определители 2-го и 3-го порядка и методы их вычисления. Свойства определителя. Системы двух линейных уравнений. Системы трех линейных уравнений. Решение по правилу Крамера и методом Гаусса. [2] №1204 – 1207, 1211 – 1216, 1236 – 1241. [5] Семинар № 1 [8] № 4.15 – 4.22, 4.36 – 4.40, 6.2, 6.3 |
| Семинар 2 Аналитическая геометрия на плоскости. Уравнение прямой на плоскости. Расстояние между двумя точками. Деление отрезка в данном отношении. Расстояние от точки до прямой. Кривые 2-го порядка. Канонические уравнения окружности, эллипса и гиперболы [2] № 223, 226, 227, 236 – 238, 243 – 252, 270 – 276, 397, 398, 444. [8] № 2.21 – 2.27, 3.4 – 3.9, 3.13 – 3.24; [5] Семинар № 2, 3 |
| Семинар 3 Векторная алгебра. Действия над векторами. Скалярное произведение двух векторов. Угол между векторами. Условия коллинеарности и ортогональности векторов. Векторное произведение. Смешанное произведение трех векторов. Условие компланарности трех векторов. [2] № 750, 754, 757, 777, 780, 787, 795, 796, 814, 819, 820, 826, 835, 839, 840, 851, 857, 860, 874, 876, 877. [8] № 1.20 – 1.29; [3] ИДЗ 2.1. и 2.2. (стр.67-83). [5] Семинар № 4 Семинар 4 Плоскость и прямая в пространстве. Общее уравнение плоскости. Угол между плоскостями. Расстояние от точки до плоскости. Канонические и параметрические уравнения прямой. Угол между двумя прямыми. Угол между прямой и плоскостью.Построить плоскости: 1) 3х+2у+4z—12=0, 2) x—2y—6=0, 3) 2y—5=0. [2] № 915, 916, 917, 921, 924—929, 941, 945, 1008, 1009,1012, 1013, 1023, 1040. [3] ИДЗ 3.1. (стр. 97—103 ); [5] Семинар № 5 |
| Семинар 5 Матрицы. Действия над матрицами. Обратная матрица. Решение матричных уравнений Решение системы линейных уравнений матричным методом. Решение однородной системы линейных уравнений. Нахождение фундаментальной системы решений. Нахождение общего решения неоднородной системы. [7] 1.30(б),1.50 , 1.51 , 1.82 , 1.129 ,1.131 , 1.167 ,1.175 , 1.178 , 1.207 , 1.209 , 1.211 ,1.226, 2,24, 2.47, 2.57, 2.109; [ [5] Семинар №6, 7 Рейтинговая контрольная работа № 1 «Элементы аналитической геометрии и линейной алгебры» проводится на лекции |
| Семинар 6 Построение графиков элементарных функций. Графики степенных функций и дробно- линейных функций. Графики функций, содержащих модули. Применение свойств элементарных функций при построении графика функции. Графики гиперболических функций, целой и дробной части числа [5] или [6]глава 1 № 2.6, 2.7, 2.8, 3.1 – 3.30, 3.31 – 3.60 . ИДЗ – [5] или [6] глава1 § 4 Варианты контрольных работ |
| Семинар 7 Числовая последовательность. Вычисление предела числовой последовательности. Предел отношения многочленов. Теорема о главном члене. Вычисление предела функции: по определению, методом разложения на множители, методом освобождения от иррациональности. Второй замечательный предел [6] 2.1- 2.7, 2.13 – 2.22, 2.29 – 2.37, 2.41-2.45, 2..50-2.57 или [7] глава 2 № 1 -7, 13 – 22, 29 – 37, 41 – 46, 50 – 57. [ 1] № 180,181, 185, 192, 245 – 267, 272 – 286, 291 – 310 |
| Семинар 8 Первый замечательный предел. Эквивалентные бесконечно малые. Таблица эквивалентных бесконечно малых. Применение эквивалентности при вычислении предела функции. Сравнение бесконечно малых. Непрерывность и точи разрыва. Классификация точек разрыва. Асимптоты графика функции. Построение графика функции. 5] или [6] № 112, 113,119, 124, 128, 130, 133, 135, 140,142, 149, 162,165, 170 – 174. [1] № 317, 350, 355,357, 375. Рейтинговая контрольная работа №2 (Предел и непрерывность) проводится на лекции |
| Семинар 9 Дифференцирование явных функций. Дифференцирование сложных функций. Логарифмическое дифференцирование. Дифференциал. Производные и дифференциалы высших порядков. Формула Лейбница. [5] № 2.227 – 2.278 [1] № 467, 471, 486, 490, 507 – 513, 524 – 531, 541, 543, 551 – 559, 588 – 597, 629 – 638, 650 – 665, 1008, 1015, 1029, 1034, 1039, 1040, 1088 |
| Семинар 10 Дифференцирование неявных и параметрически заданных функций. Разложение функции по Формуле Тейлора. Применение правила Лопиталя и формулы Тейлора при вычислении предела функции. [1] № 789 – 811, 829 – 856, 936 – 949, 1330 – 1360, 1498 - 1528. [6] № 2.254 – 2.324 |
Семинары : 2-й семестр - 17ч. за семестр
Литература к семинарским занятиям:
1. Г.Н.Берман «Сборник задач по курсу математического анализа».
2. А.П.Рябушко «Сборник индивидуальных заданий по высшей математике»
3.Р.Т.Галусарьян «Введение в математический анализ», Обнинск-2002
| Семинар 1 (2ч) Неопределенный интеграл. Интегрирование методом введения под знак дифференциала или методом компенсирующего множителя. Интегрирование с помощью подстановки и интегрирование по частям [1] № 1691 – 1790. 1870 – 1890, 1832 – 1868. |
| Семинар 2 (2ч) Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование рациональных дробей. Интегрирование тригонометрических и гиперболических функций. Интегрирование иррациональных выражений. Тригонометрические подстановки. [1] № 1940 – 1955, 2012 – 2055, 2068 - 2089. [2] ИДЗ 8.1 , 8.2, 8.3, 8.4 |
| Семинар 3 (2ч) Вычисление определенного интеграла по формуле Ньютона-Лейбница. Интегрирование по частям и замена переменной в определенном интеграле. Вычисление несобственных интегралов. [1] № 2233, 2235, 2240, 2252, 2253, 2261, 2263, 2275, 2285, 2286, 2294, 2367, 2370 – 2372, 2378, [2] ИДЗ 9.1 – 3адачи 1 –8 |
| Семинар 4 (2ч) Вычисление площади фигуры с помощью интеграла. Применение интеграла. Длина дуги, объем по площади сечения, объем и площадь поверхности тела вращения. [1] 2381, 2382, 2391, 2393, 2400,2405, 2407, 2461, 2468, 2479, 2491, 2494, 2496, 2500, 2505, 2507, 2512. 2519, 2525, 2537, 2547, 2561. Контрольная работа: « Определенный интеграл. Несобственные интегралы. Геометрические приложения интеграла» пишется на лекции |
| Семинар 5 (2ч) Функции многих переменных. Построение области определения. Частные производные и дифференциалы любого порядка для явных функций. [ 1 ] 2984, 2988, 2992, 2996, 2999, 3043, 3044, 3054, 3068, 3070, 3101, 3105, 3184, 3196. [ 2 ] ИДЗ 10.1 |
| Семинар 6 (2ч) Дифференцирование сложных функций, неявных функций. Касательная плоскость и нормаль. [ 1 ] 3125, 3129, 3136 – 3138, 3140, 3142, 3162, 3165, 3178, 3204, 3416, 3421. [ 2 ] ИДЗ 10.2 |
| Семинар 7 (2ч) Формула Тейлора. Разложение по формуле Тейлора. Приближенное Вычисление значений функции с помощью формулы Тейлора. [ 1 ] 3246, 3249, 3251, 3257 |
| Семинар 8 (2ч) Экстремум функции многих переменных. [ 1 ] 3260, 3271, 3274, 3276 – 3278. |
| Семинар 9 (1ч) Наименьшее и наибольшее значение функции. Условный экстремум. [ 1 ] 3281, 3282, 3286, 3290, 3292 - 3294, 3296, 3410, 3414, 3421. Контрольная работа по теме: «Функции многих переменных» проводится на лекции |
Семинары : 3-й семестр - 10 семинаров по 2ч.
Литература :
1. Г. И. Берман « Сборник задач по курсу математического анализа ».
2. Л. А. Кузнецов « Сборник заданий по высшей математике ».
3. А.Ф.Филиппов «Сборник задач по дифференциальным уравнениям».
4. А.П.Рябушко «Сборник индивидуальных заданий по высшей математике» 2-й том).
| Семинар 1 Числовые ряды. Сходимость. Необходимое условие. Признаки Даламбера и Коши. Признаки сравнения. Знакочередующиеся ряды. Знакопеременные ряды. Абсолютная и условная сходимость [ 1 ] 2728, 2732, 2735, 2756, 2759, 2763, 2766, 2767, 2773, 2741, 2742, 2745, 2749, 2751. [ 2 ] Глава 6. Ряды. Задачи № 1 – 8. |
| Семинар 2 Область сходимости функциональных рядов. Равномерная сходимость. Дифференцирование и интегрирование рядов. Ряд Тейлора. Разложение функций в ряд Тейлора-Маклорена. [ 1 ] 2803, 2807, 2812, 2814, 2816, 2817, 2819, 2823, 2825, 2878, 2885. [ 2 ] Глава 6. Ряды. Задачи № 9, 10,12-15. |
| Семинар 3 Ряды Фурье. Разложение функции в ряд Фурье. [ 1 ] 4373, 4276, 4378, 4380, 4383, 4391- 4394. Рейтинговая контрольная работа № 1 «Числовые и функциональные ряды. Ряды Фурье» проводится на лекции |
| Семинар 4 Двойные интегралы. Методы вычисления в прямоугольной системе координат. Тройные интегралы. Методы вычисления в прямоугольной системе координат. [ 1 ] 3517, 3519, 3523, 3522, 3524, 3488, 3491 [ 2 ] ИДЗ. Глава 7. Задачи № 1 - 5. |
| Семинар 5 Двойные интегралы в полярных и обобщенных полярных координатах. Применение двойных и тройных интегралов. Вычисление объема фигуры и площади пластины [ 1 ] 3526, 3530, 3537, 3540, 3546, 3556 – 3558, 3562, 3564, 3568, 3571, 3578, 3590. Рейтинговая контрольная работа № 2 «Кратные интегралы» проводится на лекции |
| Семинар 6 Понятие о дифференциальном уравнении 1-го порядка. Общее решение. Частное решение. Дифференциальные уравнения с разделяющимися переменными. Однородные дифференциальные уравнения 1-го порядка. Нахождение общего и частного решения. [3] № 51 – 65, 101 – 123 [1] № 3901 – 3910, 3913 – 3917, 3934 – 3947 |
| Семинар 7 Линейные дифференциальные уравнения и уравнения Бернулли. Решение этих уравнений методом Бернулли и методом вариации. Уравнения в полных дифференциалах. Решение методом объединения частных интегралов. [3] № 136 – 153, 186 – 191 [1] № 3954 – 3960, 3965 – 3968, 4038 – 4044. 4050 – 4054 [4] ИДЗ – 11.1 (стр.290) |
| Семинар 8 Понятие о дифференциальных уравнениях второго и высших порядков. Общее и частное решение. Уравнения, допускающие понижение порядка: 1) 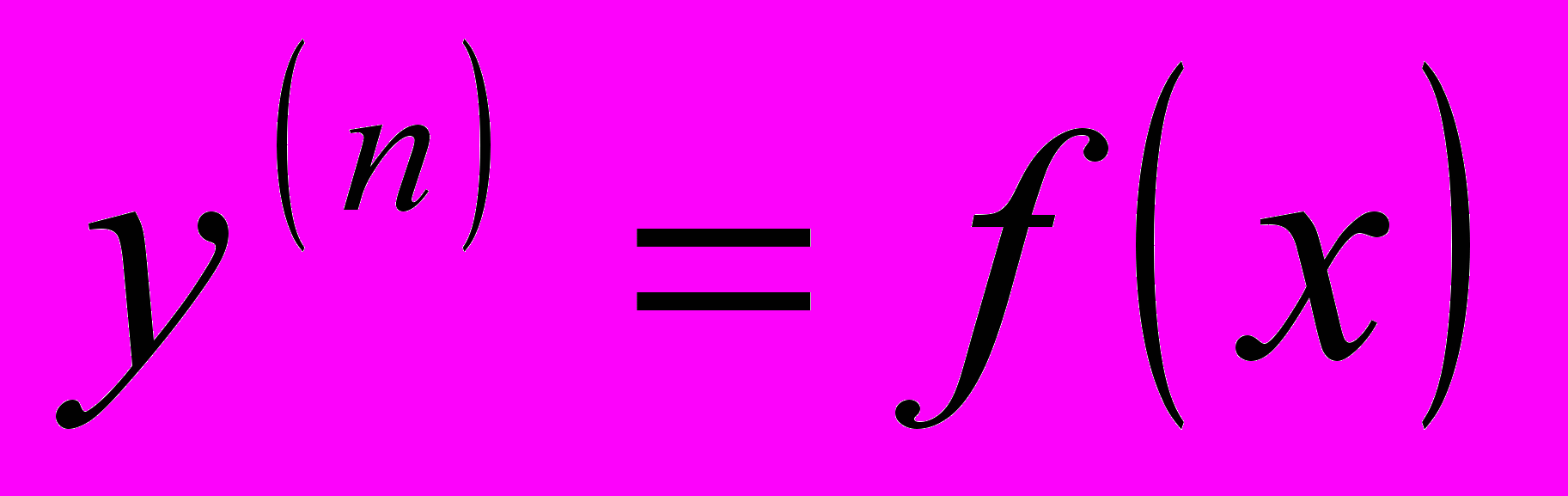 , , 2) 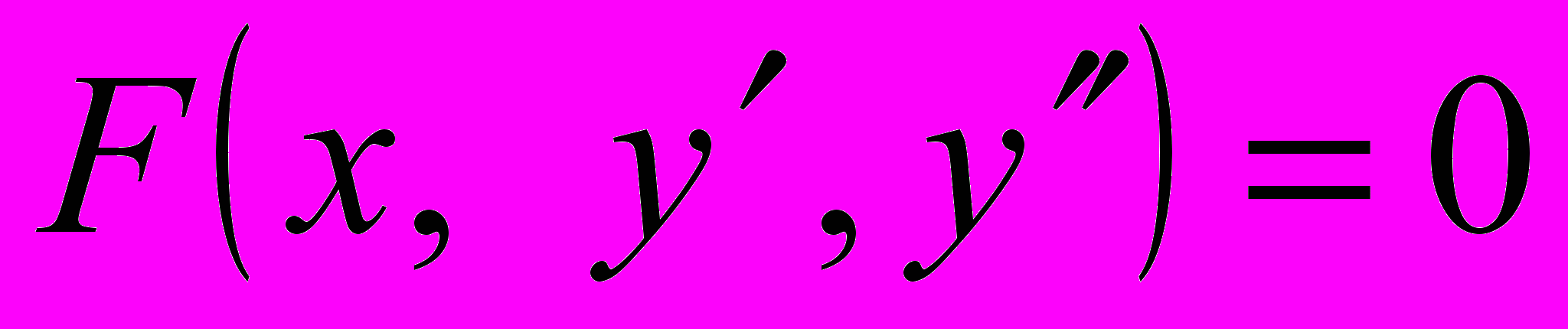 , 3) , 3) 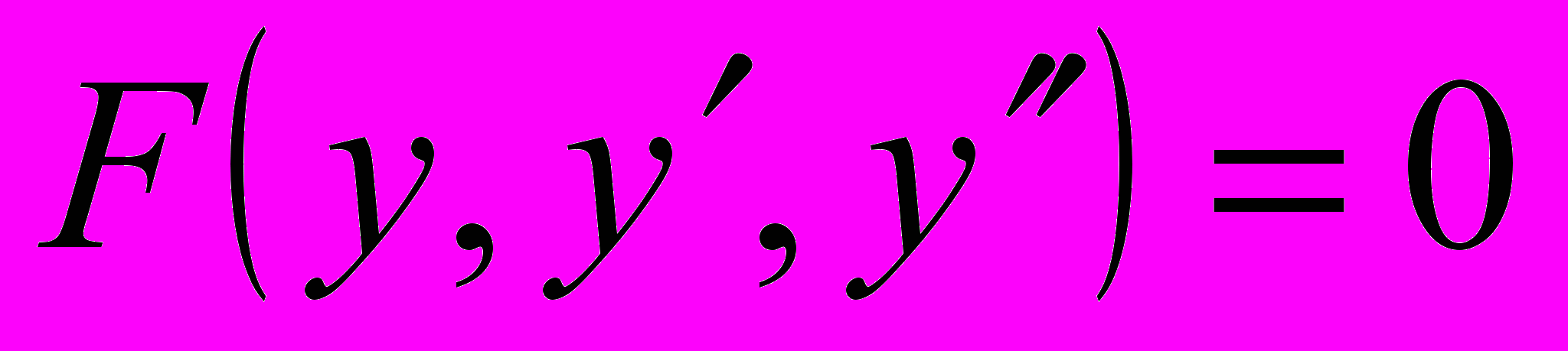 . .[3] № 421 – 440, 451 – 454 [1] № 4155 – 4178, 4189 – 4192 [4] № ИДЗ – 11.2 (стр.301) |
| Семинар 9 Однородные линейные уравнения с постоянными коэффициентами. Нахождение общего и частного решений. Линейные неоднородные уравнения. Нахождение общего решения как суммы общего однородного и частного неоднородного. [3] № 511 – 519, 53 – 540, 582,586 [1] № 4251 – 4264,4268 – 4274 |
| Семинар 10 Линейные неоднородные уравнения (продолжение). Решение методом вариации. Нахождение частного решения. [3] № 575 – 580, 583,585 [1] № 4276, 4280, 4281, 4283,4284 [4] № ИДЗ – 11.3 (стр.314) Рейтинговая контрольная работа № 32 «Дифференциальные уравнения» проводится на лекции |
3.2. Лабораторный практикум – не предусмотрен
3.3. Курсовые проекты (работы) – не предусмотрены
3.4. Формы текущего контроля
| Раздел(ы) | Форма контроля | Неделя |
| 1 сем | три контрольные работы: 1) Элементы аналитической геометрии и линейной алгебры, 2)Предел функции. 3)Производная ИДЗ по Рябушко [3] | 8,13,17 |
| 2 сем | три контрольные работы: 1)Исследование функции и неопределенный интеграл, 2) Определенный интеграл и его применение, 3)Функции многих переменных, ИДЗ по Рябушко [3] | 3, 9.15 |
| 3 сем | две контрольные работы
ИДЗ-дифференциальные уравнения-Рябушко [3] | 8,16 |
3.5. Самостоятельная работа:
1.выполнение домашних заданий,
2. подготовка ИДЗ,
3. повторение теоретического материала.
Контроль самостоятельной работы:
1.проверка домашних заданий,
2. прием ИДЗ.
4.1. Рекомендуемая литература
Литература к лекционным занятиям:
Основная
1. Общий курс высшей математики для экономистов: Учебник/Под ред. В.И.Ермакова
- М.:ИНФРА-М, 2001. (200)
2. Щипачев В.С. “Высшая математика”, Москва, 1990. (200)
Дополнительная
3. Ильин В.А., Позняк Э.Г. “Основы математического анализа”, ч1,ч2. (150)
4. Колесников А.Н. «Краткий курс математики для экономистов», М – 1997
5. Коршунова Н.И., Плясунов В.С. «Математика в экономике», М – 1996
Литература к семинарским занятиям:
1. Г.Н.Берман «Сборник задач по курсу математического анализа». (200)
2. Б.П.Демидович «Сборник задач и упражнений по математическому анализу». (200)
3. А.П.Рябушко «Сборник индивидуальных заданий по высшей математике» (100)
4. Л.А.Кузнецов «Сборник заданий по высшей математике» (200)
5. Р.Т.Галусарьян «Сборник задач и упражнений по высшей математике», Обнинск-2008 (50)
6. Р.Т.Галусарьян «Введение в математический анализ», Обнинск-2003 (100)
7. Д.В.Клетеник «Сборник задач по аналитической геометрии» (200)
8. А.Ф.Филиппов «Сборник задач по дифференциальным уравнениям» (200)
9. Р.Ф.Апатенок ”Сборник задач по линейной алгебре и аналитической геометрии “. (100)
