Взадачах рассматриваемого класса параметры размещения {
| Вид материала | Задача |
- Элективный курс по математике для учащихся 9 класса тема: «уравнения и неравенства,, 248.15kb.
- Isbn 978-5-7262-1377 нейроинформатика 2011, 136.96kb.
- Дневные программы обучения без размещения. Кроме занятий в школе курс Junior Day Programme, 162.83kb.
- Проекта, 43.2kb.
- Вопрос Параметры звука, 183.33kb.
- Лобанов Михаил Михайлович (научный сотрудник Института экономики ран, аспирант географического, 74.38kb.
- Рабочая программа элективного курса по математике «Знакомьтесь: модуль и параметры!», 100.3kb.
- Программа обучения на курсах продвижения сайтов: Тема Виды и методы продвижения сайтов, 61.1kb.
- Темы контрольных работ по индустрии гостеприимства Классификация средств размещения, 9.25kb.
- За курс 9 класса билет, 42.57kb.
Оcобенности программной реализации нелинейных оптимизационных задач размещения геометрических объектов
Novozhilova M.V., Chub I.А., Belenchenko I.V., Murin М.N.
Рассмотрим класс задач оптимизационного геометрического проектирования [1], состоящих в поиске оптимального размещения конечного набора T={Ti}, i=1,2,…I, геометрических объектов произвольной пространственной формы (int Ti ), геометрические характеристики которых могут изменяться, в заданной области Т0 без взаимных наложений при наличии различных ограничений и критериев качества размещения.
В общем случае геометрическая информация gi [1] об объекте Тi состоит из:
- совокупности пространственных форм {si}, составляющей объект Т;
- набора метрических характеристик {mi}, определяющих размеры точечных множеств, имеющих пространственную форму {s};
- параметров размещения {ui} объекта Тi в области Т0 [1].
В задачах рассматриваемого класса параметры размещения {ui} объекта Тi в области Т0 могут содержать как параметры трансляции
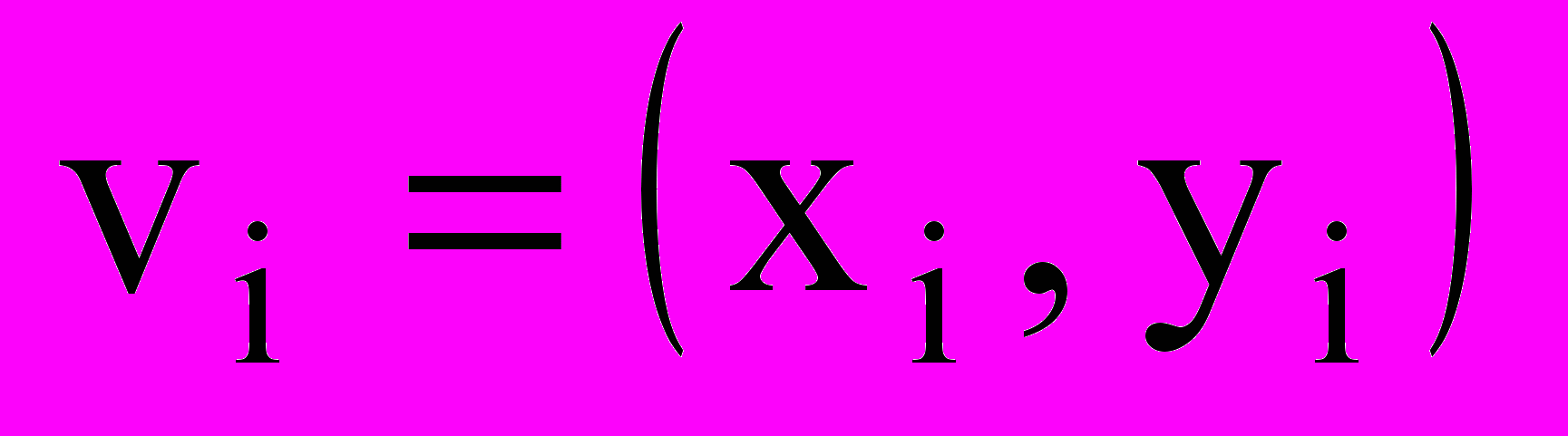 , так и угловой параметр
, так и угловой параметр  .
.Оптимизационные задачи такого рода возникают во многих областях человеческой деятельности – управление ресурсами проекта, задачи энергосбережения, задачи раскроя материалов. К данной задаче в указанной постановке могут быть сведены также задачи оптимизации распределения ресурсов в календарном планировании [2].
В общем случае рассматриваемый класс задач относится к многомерным многоэкстремальным задачам нелинейного невыпуклого математического программирования со специфичной областью допустимых решений, что затрудняет или делает невозможным применение классических методов условной оптимизации [3]. Эффективные точные методы решения задач практической размерности отсутствуют. Однако несомненная прикладная значимость таких задач вызывает необходимость создания и развития вычислительных методов решения оптимизационных задач размещения, основанных на современном математическом инструментарии.
Кроме того, решение задач данного класса необходимо подразумевает учет специфики области допустимых решений задачи и создание оригинального программного обеспечения.
В Украине ведущей в этом направлении является научная школа проф. Стояна Ю.Г. (г. Харьков).
Приведем некоторые постановки задач рассматриваемого класса.
Задача 1. Поиск оптимального размещения конечного набора неориентированных многоугольных геометрических объектов в заданной многосвязной многоугольной области.
Пусть есть набор
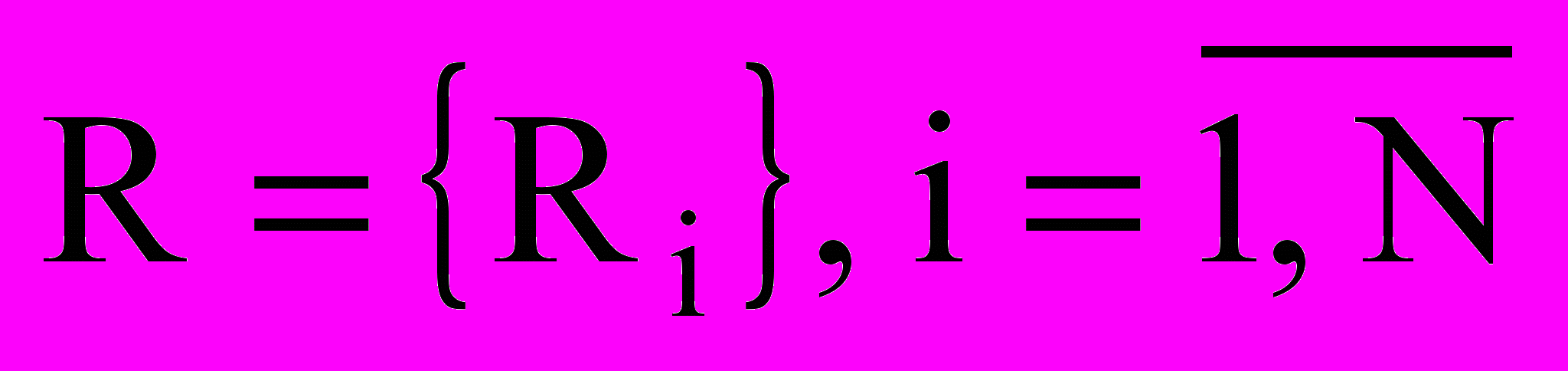 выпуклых неориентированных многоугольников, заданных в арифметическом евклидовом пространстве
выпуклых неориентированных многоугольников, заданных в арифметическом евклидовом пространстве 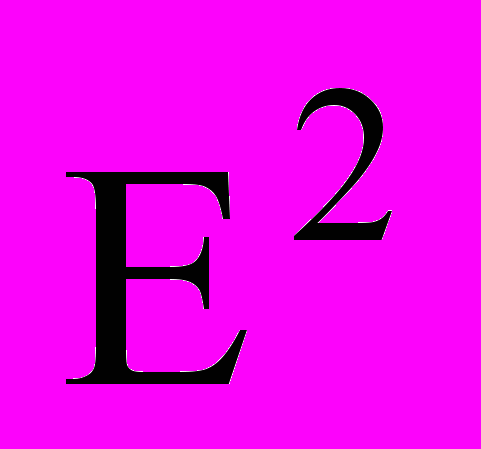 , и область размещения
, и область размещения 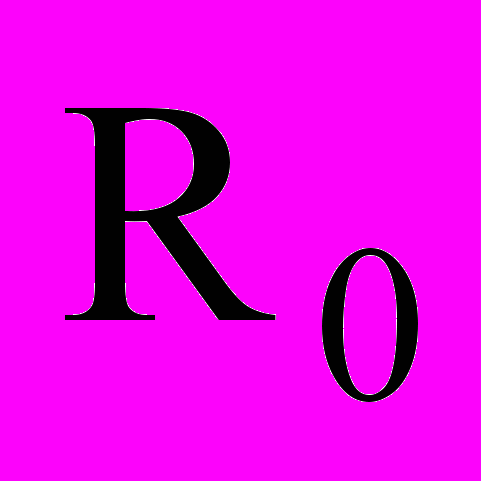 вида
вида 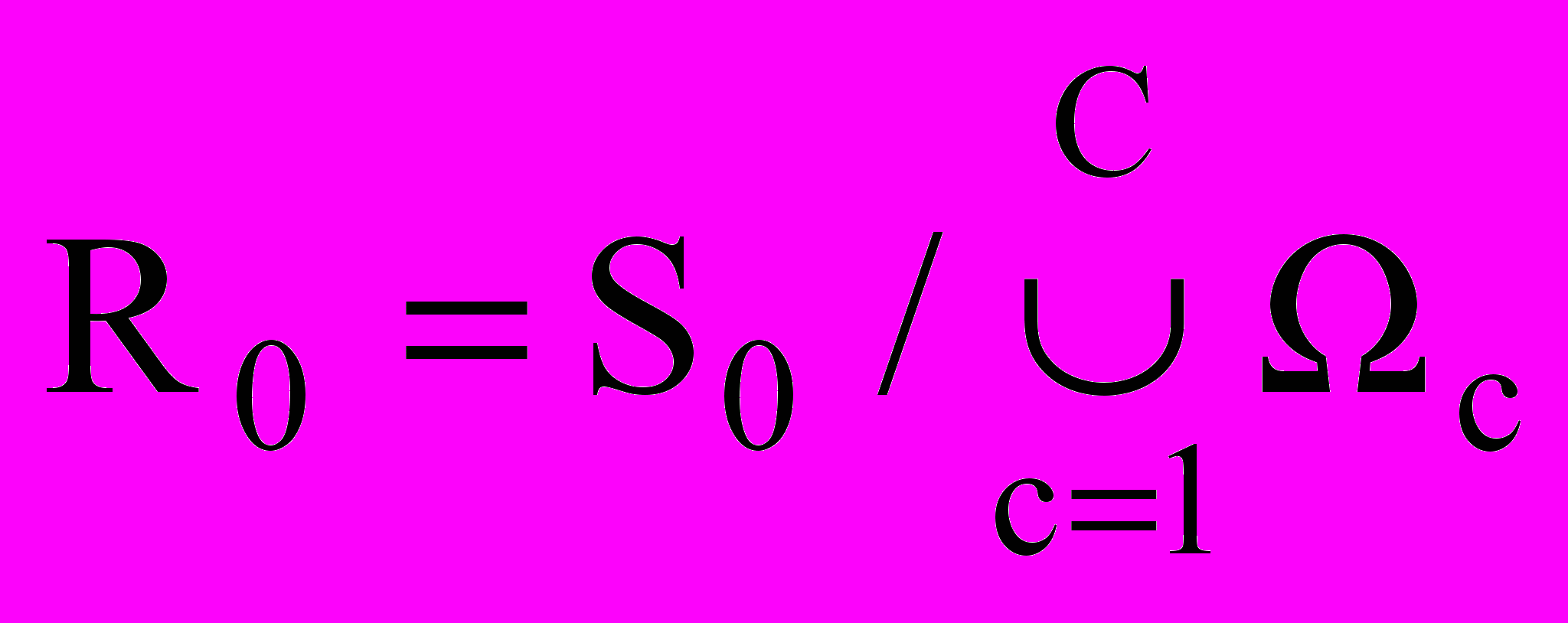 , (1)
, (1)где
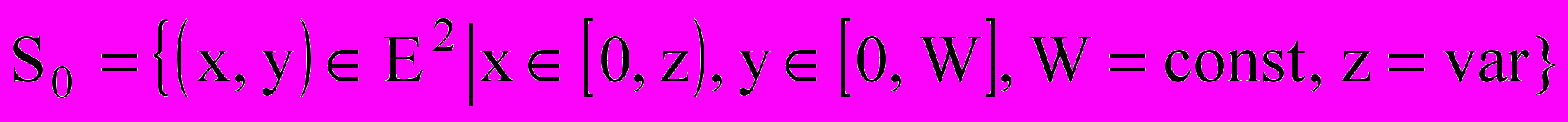 – полубесконечная полоса,
– полубесконечная полоса, 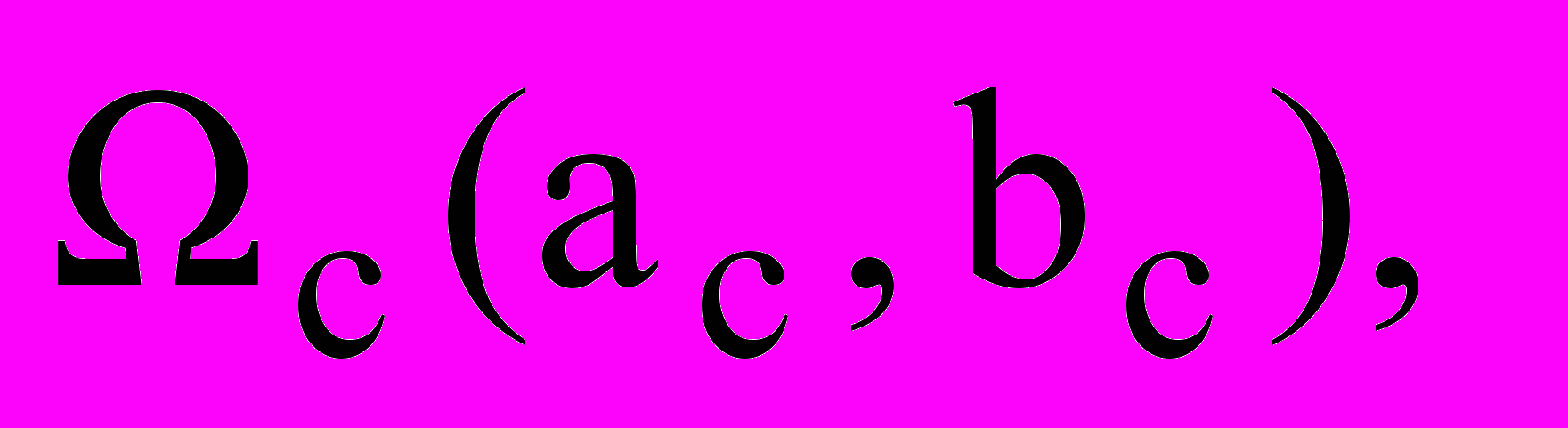
 – множество выпуклых областей запрета,
– множество выпуклых областей запрета, 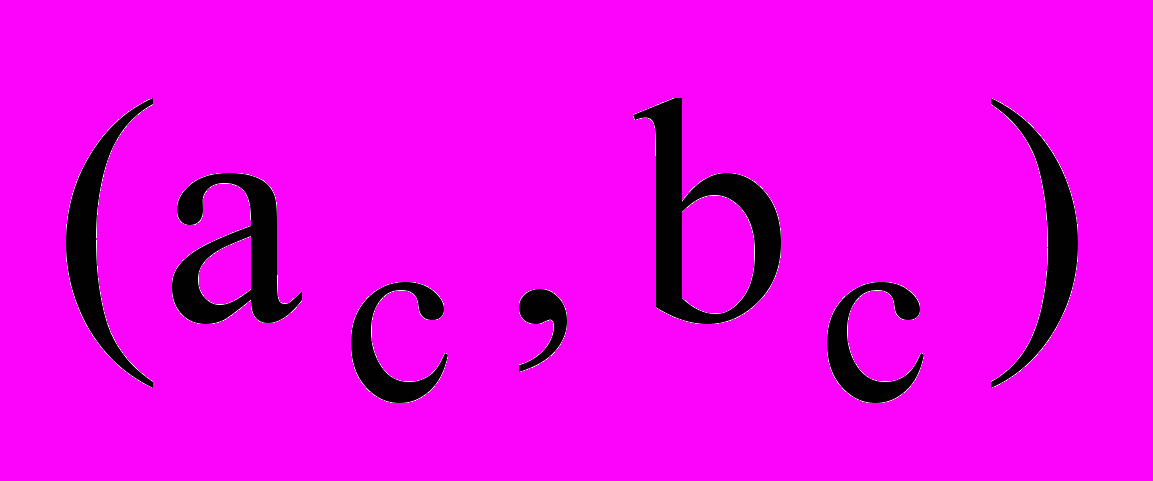 – фиксированные параметры.
– фиксированные параметры. Объект
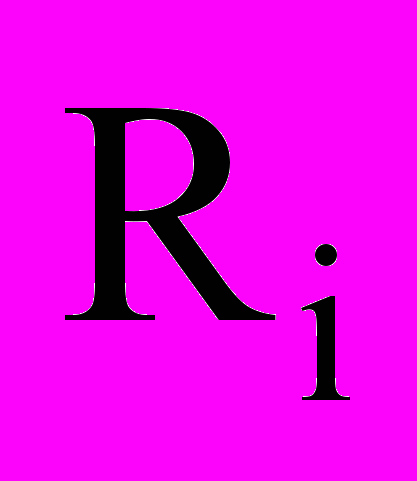 задается упорядоченным против часовой стрелки набором
задается упорядоченным против часовой стрелки набором 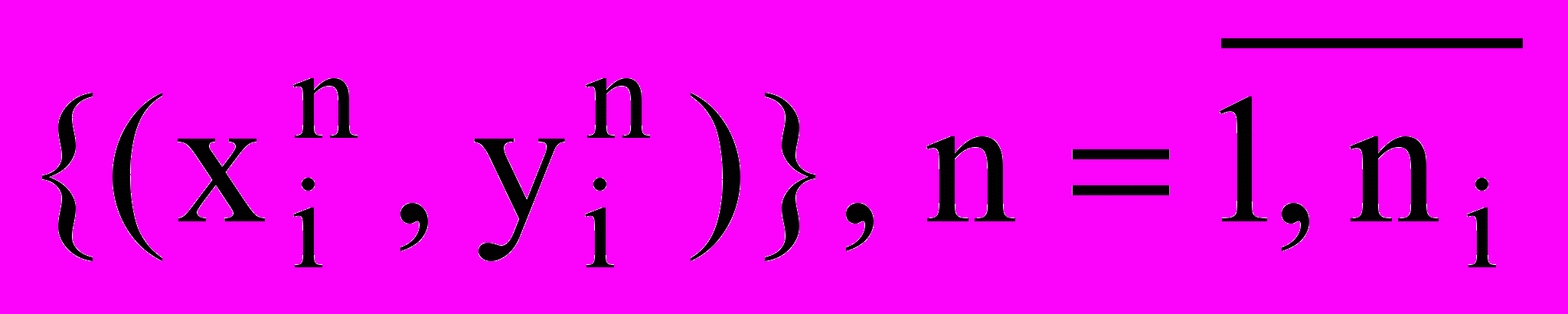 координат его вершин в собственной системе координат
координат его вершин в собственной системе координат 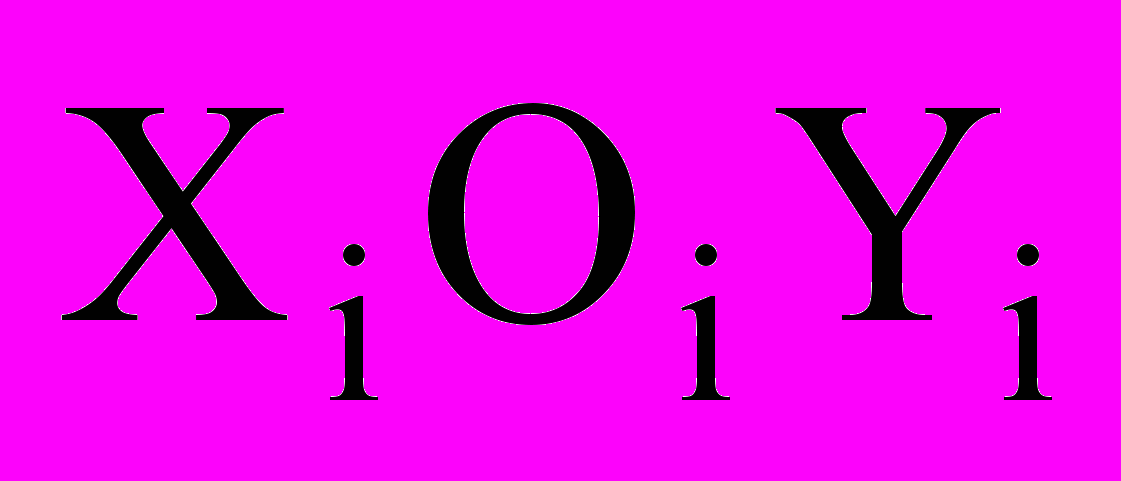 ,
, 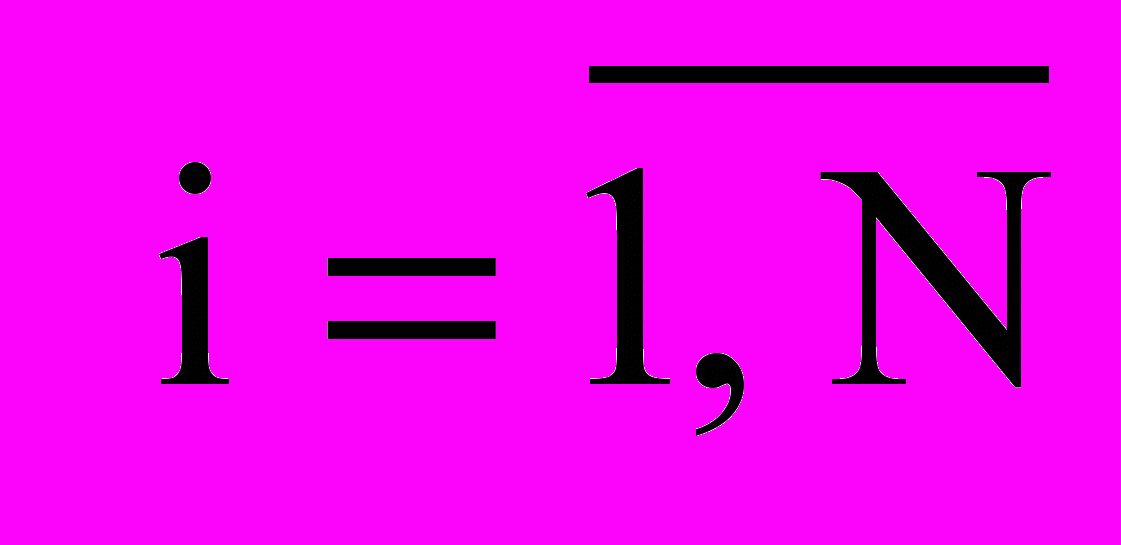 .
. Положение
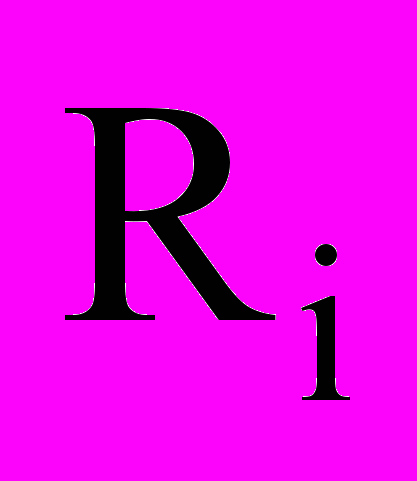 в общей системе координат
в общей системе координат  , связанной с областью
, связанной с областью 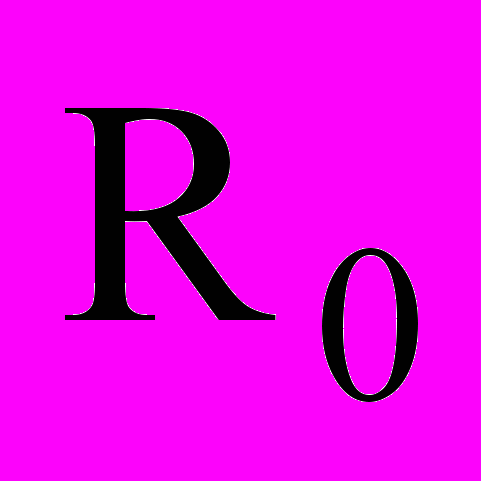 , задается вектором параметров размещения
, задается вектором параметров размещения 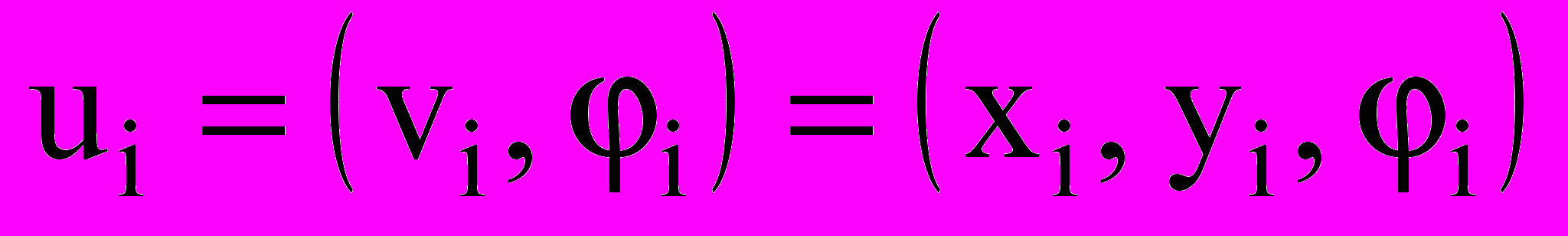 , который определяет полюс объекта – начало его собственной системы координат
, который определяет полюс объекта – начало его собственной системы координат 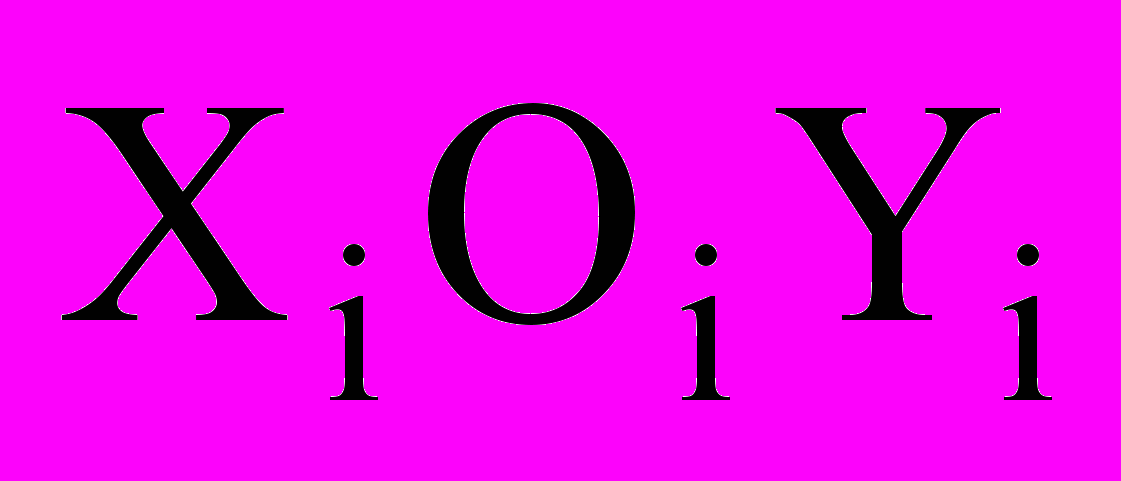 . При этом компонента
. При этом компонента 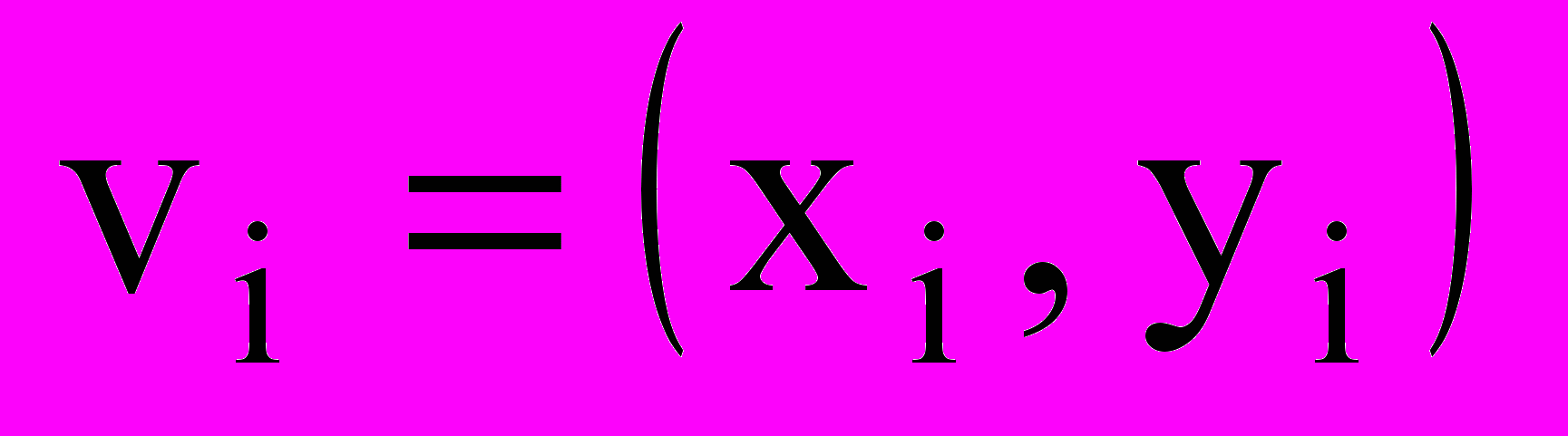 задает трансляцию
задает трансляцию 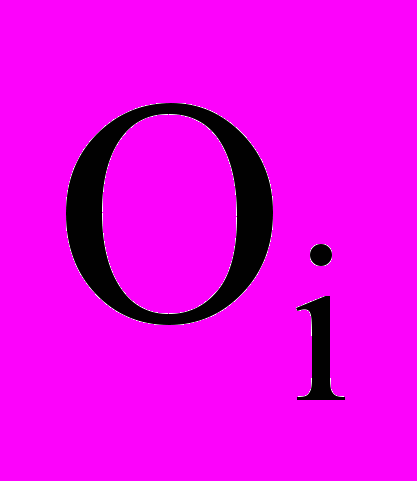 , а угловой параметр
, а угловой параметр  поворот системы координат
поворот системы координат 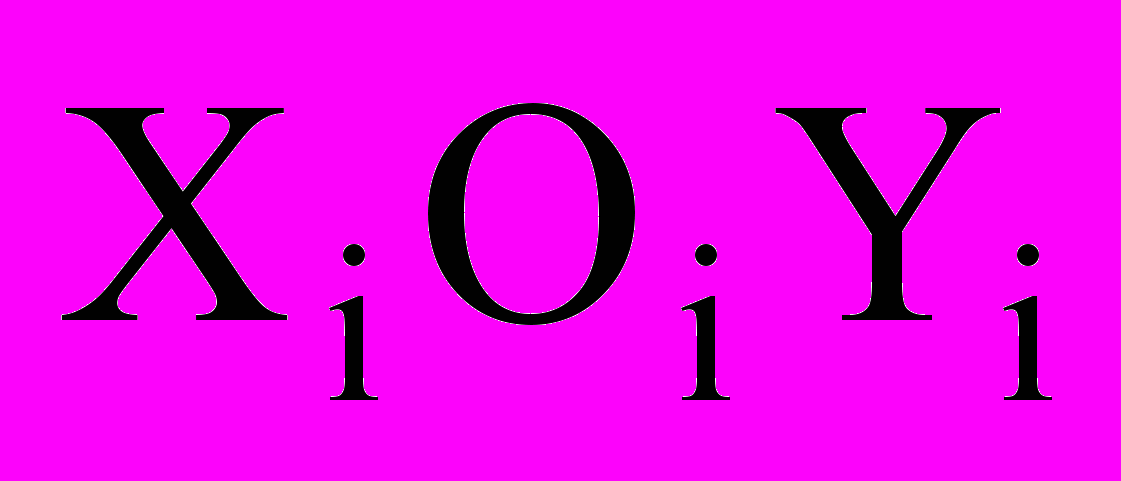 относительно
относительно 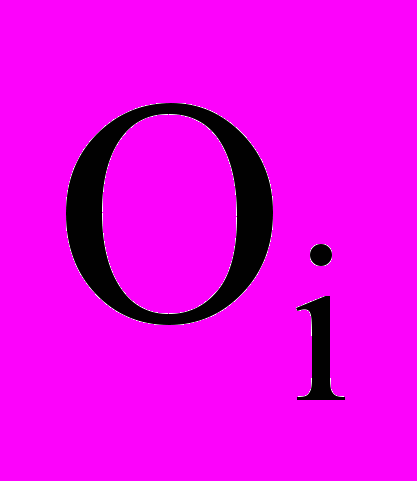 (рис. 1).
(рис. 1). Необходимо разместить набор
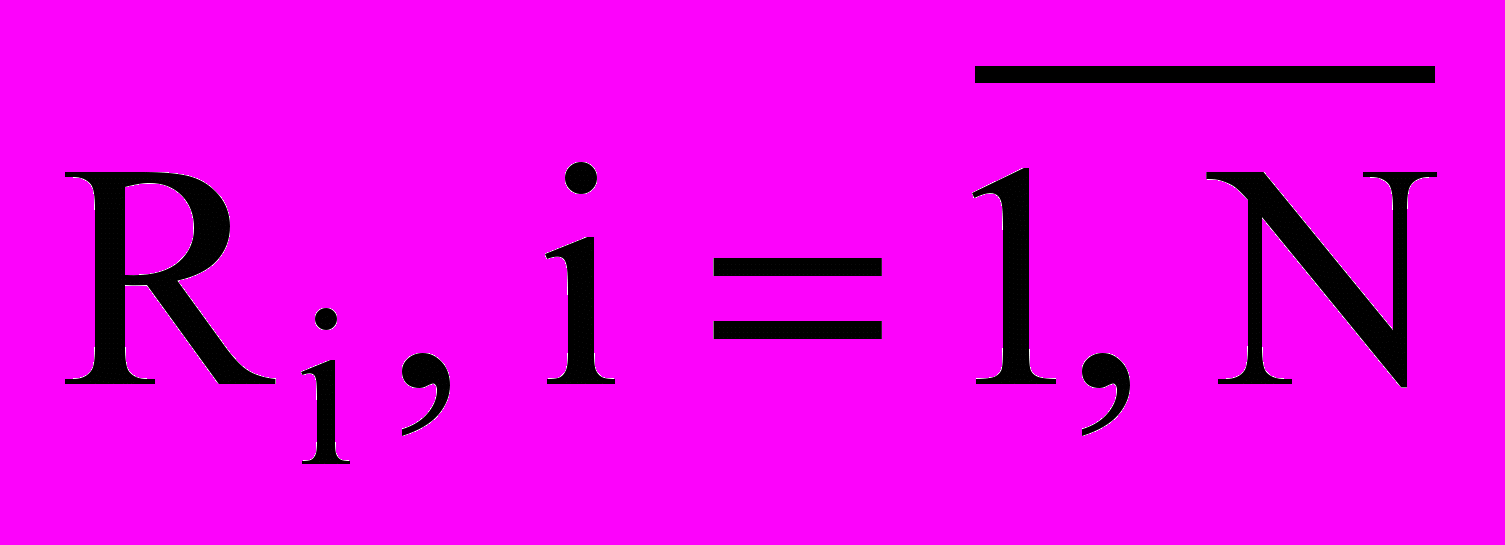 объектов без взаимных наложений в области
объектов без взаимных наложений в области 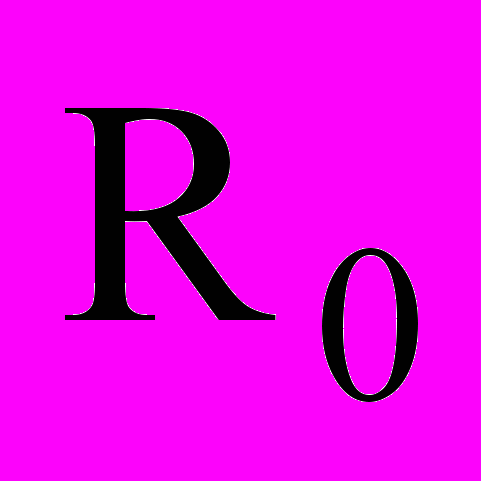 так, чтобы длина занятой части полосы
так, чтобы длина занятой части полосы  была минимальной.
была минимальной.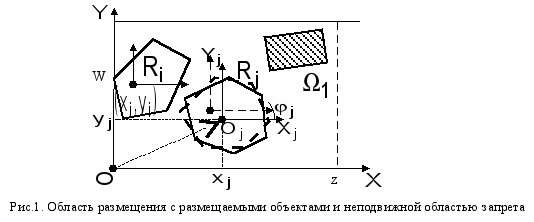
Математическая модель Задачи 1 имеет вид:
найти:
 , (2)
, (2)где
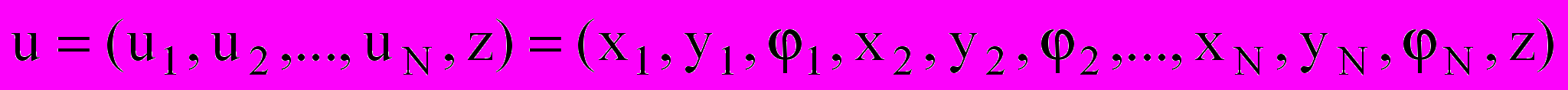 ;
; 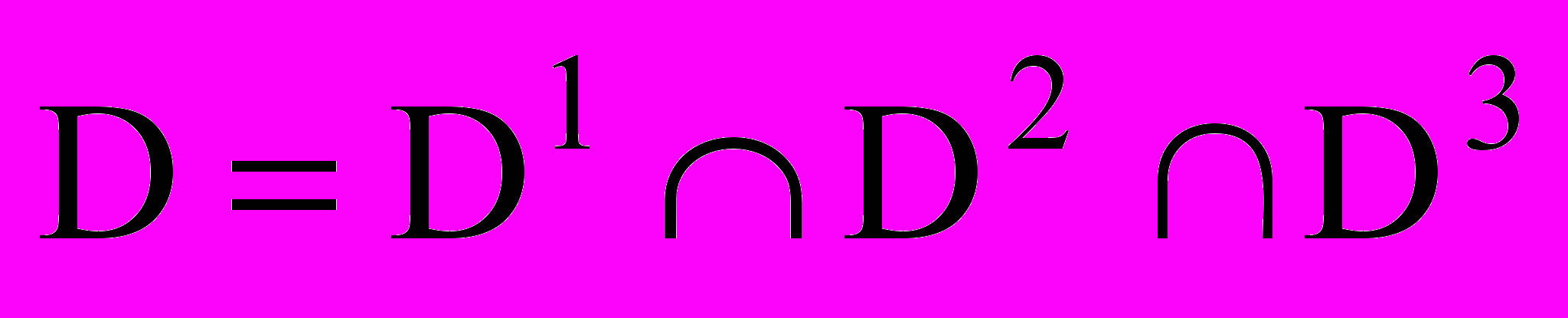 область допустимых решений задачи;
область допустимых решений задачи; 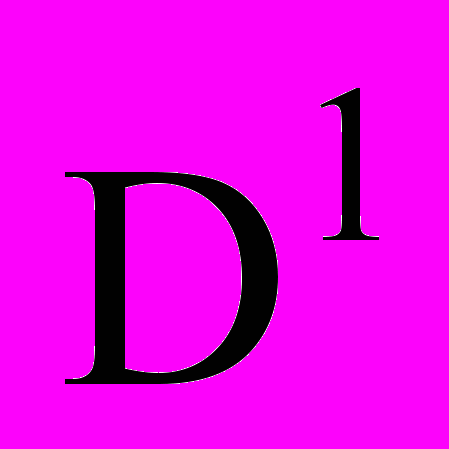
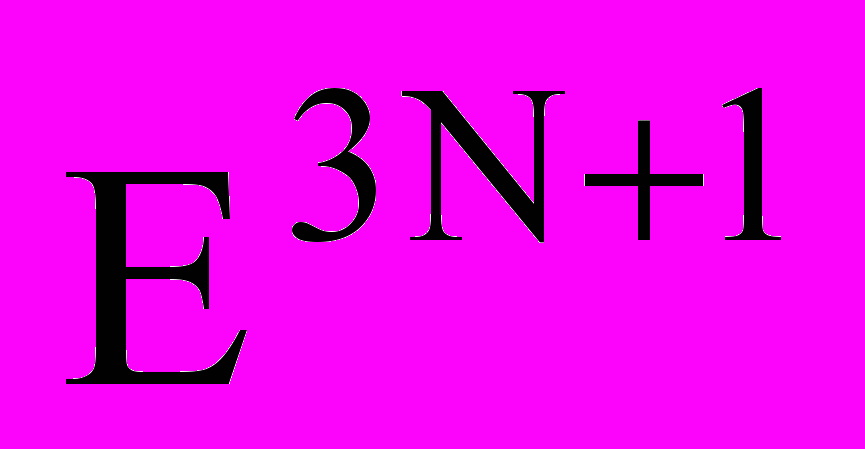 – подобласть, выделяемая ограничениями на размещение в полосе
– подобласть, выделяемая ограничениями на размещение в полосе 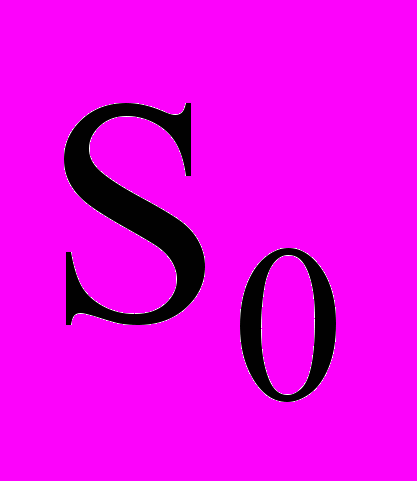 ;
; 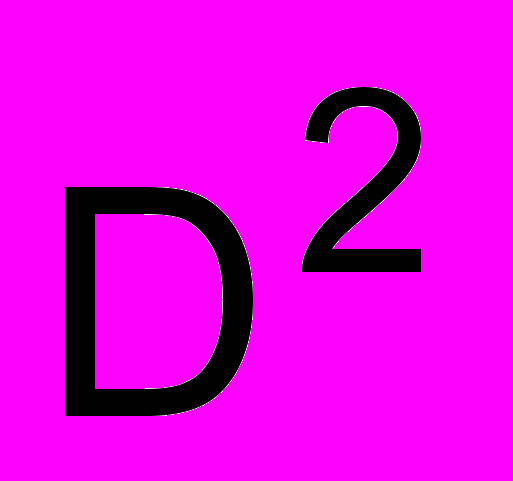
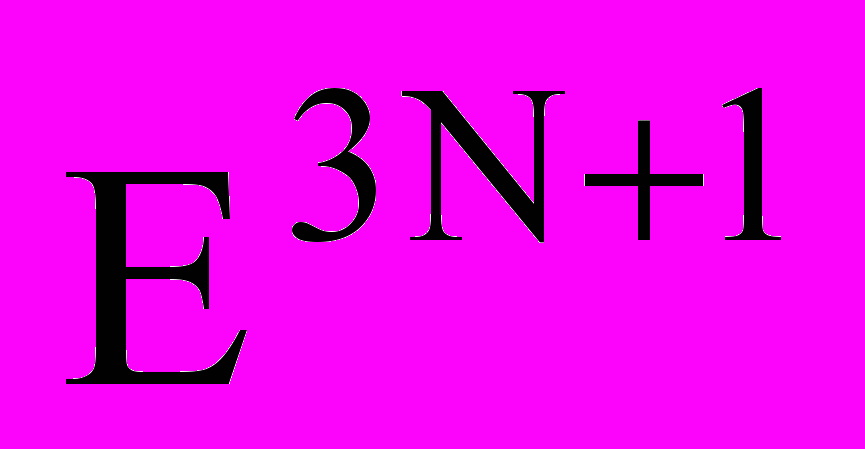 ,
, 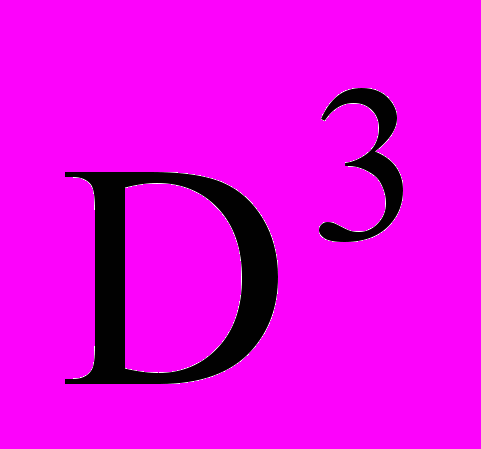
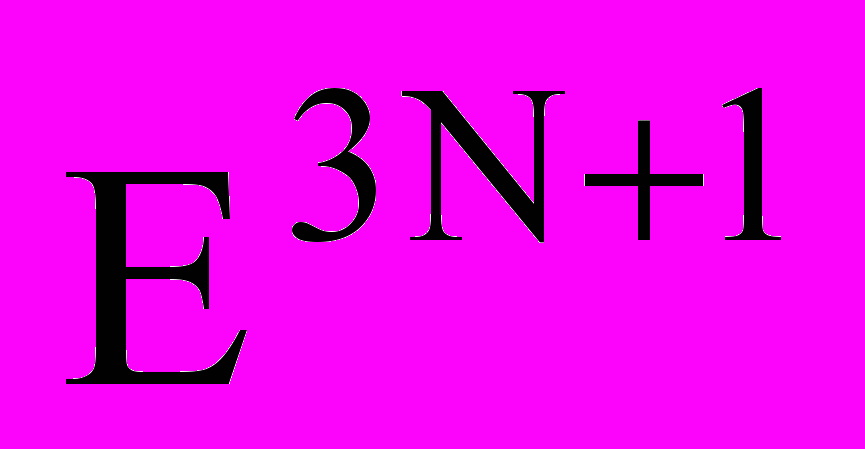 задаются условиями попарного взаимного непересечения (
задаются условиями попарного взаимного непересечения (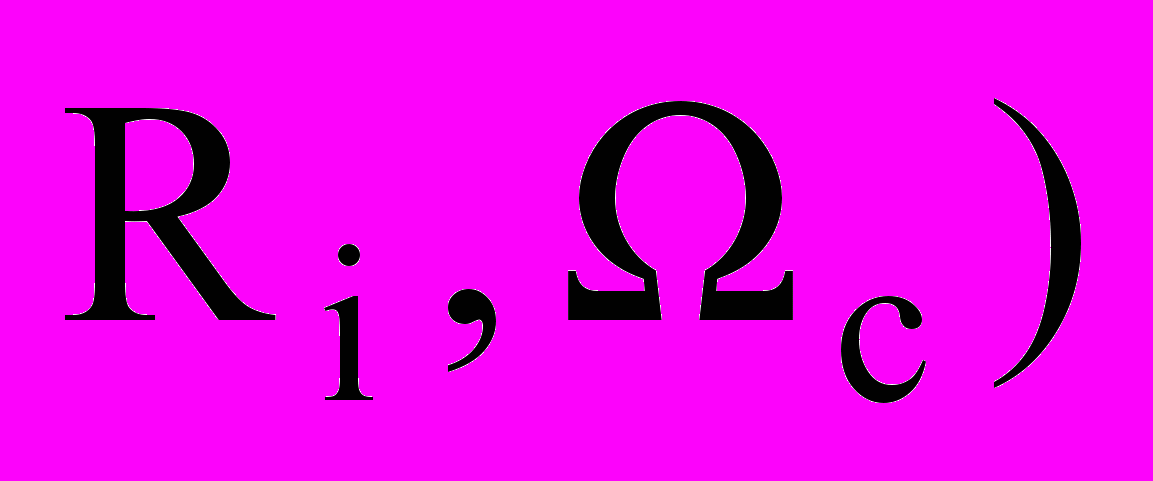 ,
, 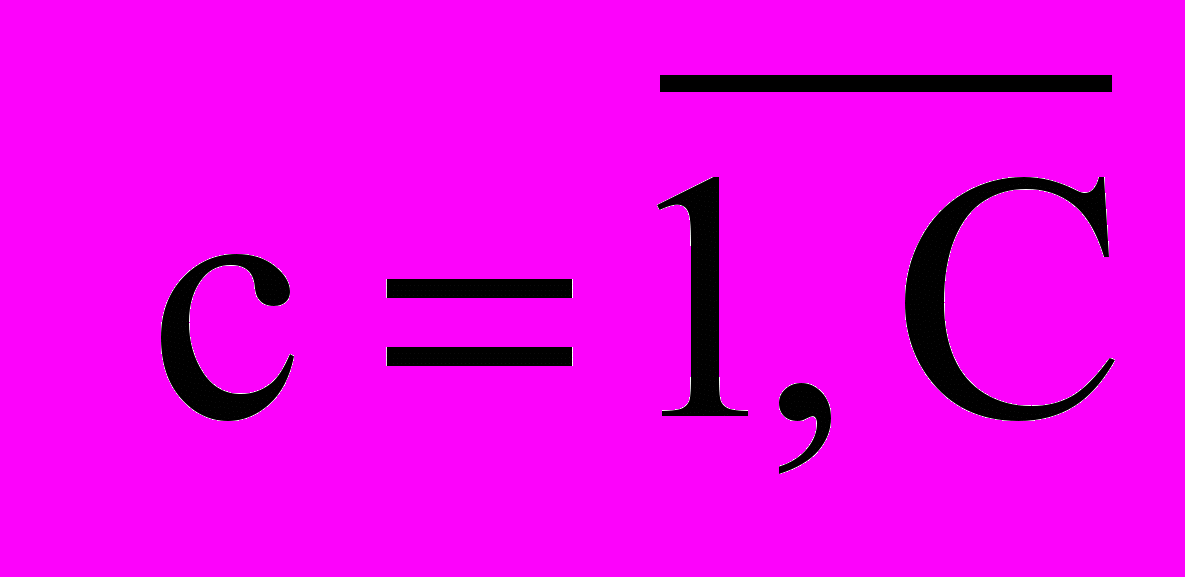 , и условиями попарного взаимного непересечения объектов размещения
, и условиями попарного взаимного непересечения объектов размещения 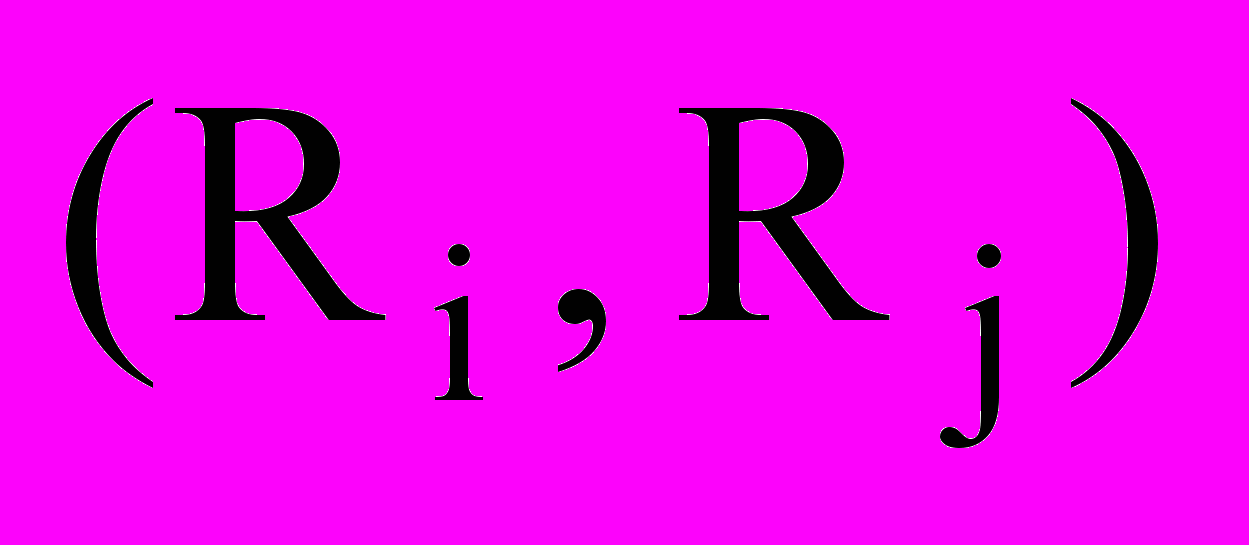 ,
, 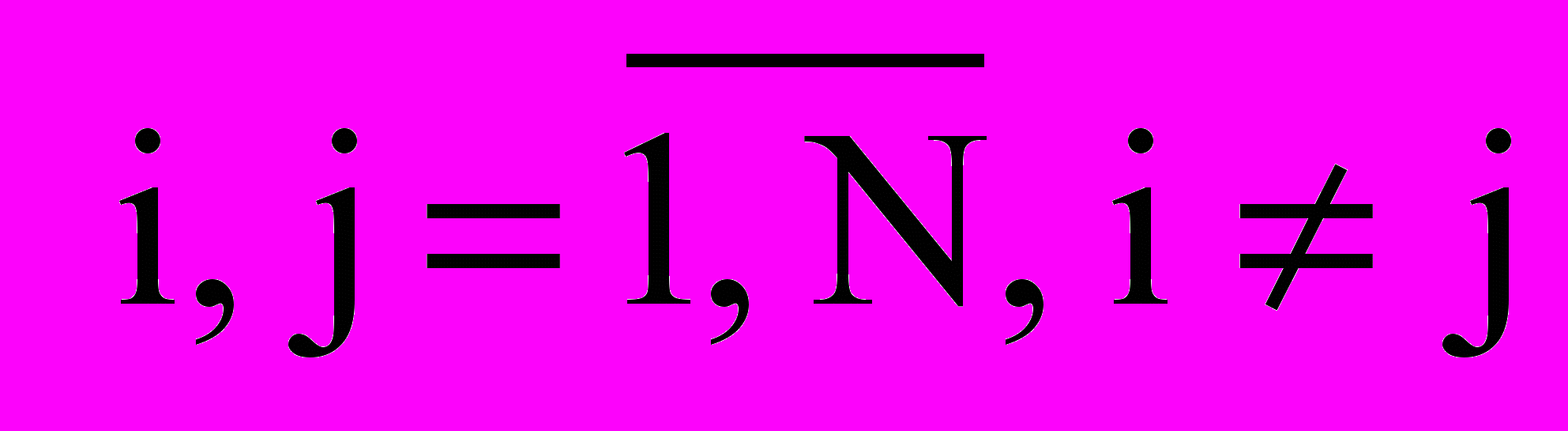 соответственно.
соответственно. Задача 2. Поиск оптимального размещения конечного набора прямоугольных геометрических объектов с изменяемыми метрическими характеристиками.
Пусть заданы область размещения R0 E2 (s0 = «прямоугольник», m0= (W, Z), W – const, Z – var) и конечный набор R = {Ri}, i=1,…, I объектов размещения (si = «прямоугольник», mі= (аі, bi), аі, bi – var, ui=(хi,уi) - параметры размещения объекта Ri в E2) (рис.2).
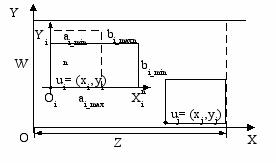
Рис.2.
Метрические характеристики аi и bi объектов Ri в процессе размещения могут изменяться
ai[ai min, ai max], bi[bi min, bi max], ai min >0, bi min > 0. (3)
причем площадь Si размещаемых объектов остается неизменной:
bi= Si / ai. (4)
Необходимо разместить набор объектов Rі в полубесконечной полосе R0 без наложений друг на друга так, чтобы величина Z была минимальной:
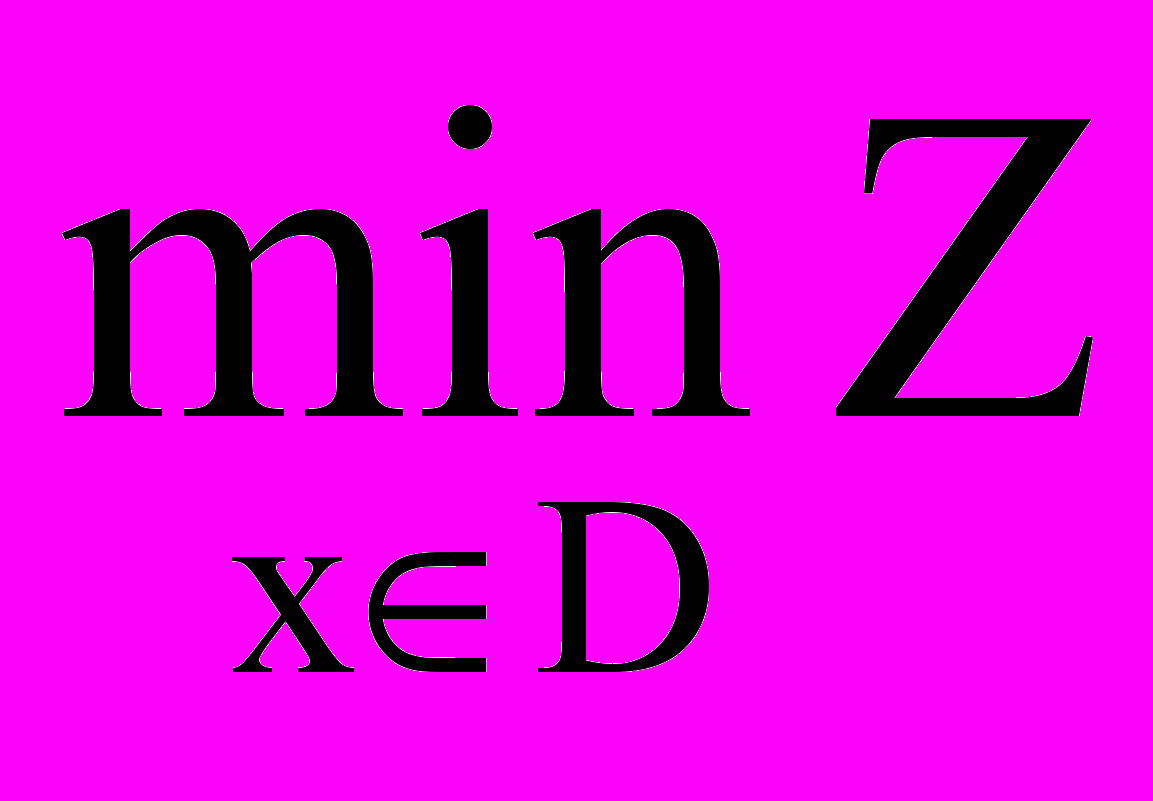 , (4)
, (4)где область допустимых решений D =D1 Ç D2 определяется условиями
D1: intRi (хi, уi, аі, bi) Ç intRj (хj, уj, аj, bj) = Æ, i,j=1,2,…,N, ij, (5)
D2: Ri (хi, уi, аi) R0, i=1,2,…,N. (6)
Задача 3. Поиск оптимального распределения ресурсов проекта во времени с учетом различной динамики изменения стоимости ресурсов
Рассмотрим проект, который состоит из N работ (операций) R=R{Ri}, i=1, 2,…, N. На множестве работ R задано условие частичной упорядоченности вида Ri
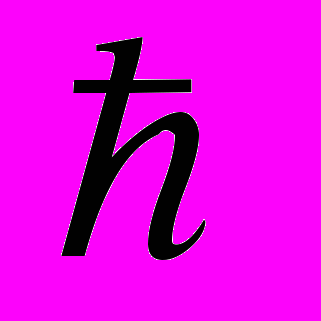 Rj, i, j {1,2, …N}, i j, определенное конкретной последовательностью выполнения работ. Для каждой работы Ri известны ее величины ресурсов, необходимых для ее выполнения:
Rj, i, j {1,2, …N}, i j, определенное конкретной последовательностью выполнения работ. Для каждой работы Ri известны ее величины ресурсов, необходимых для ее выполнения: 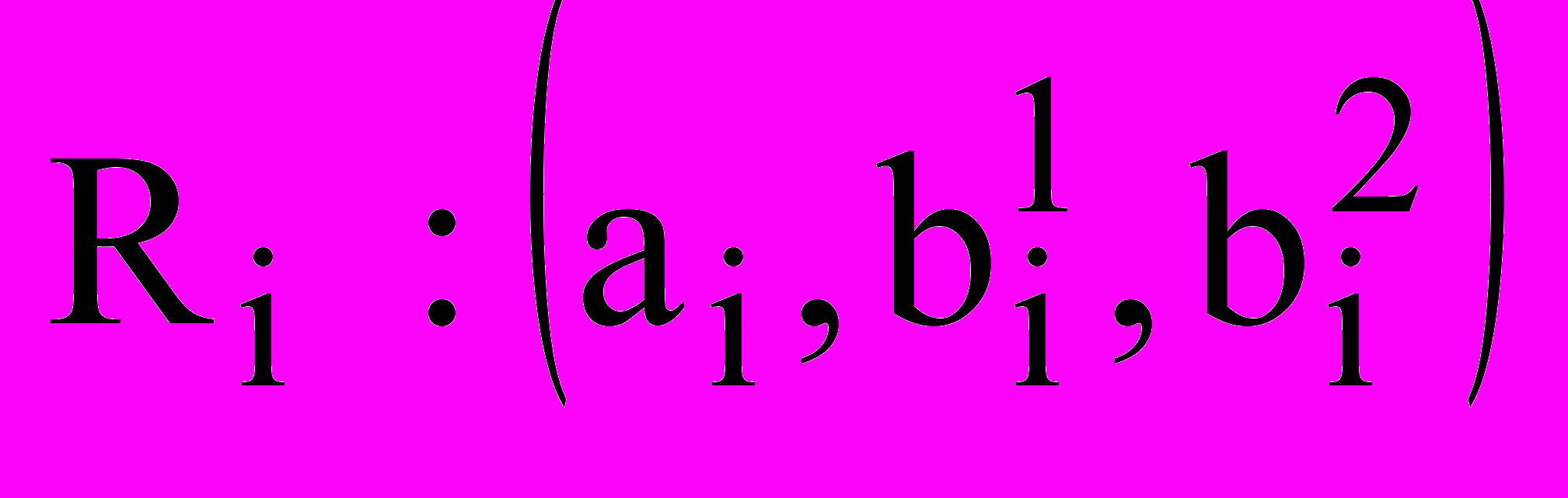 : где
: где  продолжительность работы,
продолжительность работы, 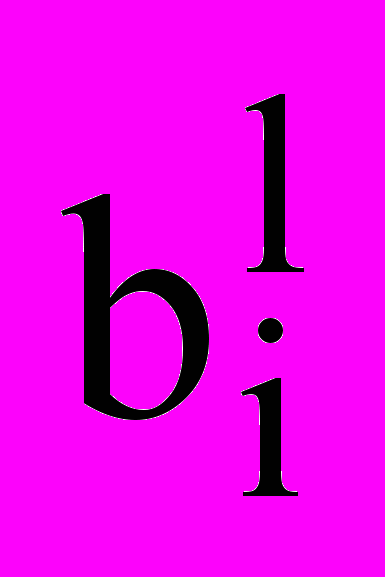 два других вида ресурсов в стоимостном выражении.
два других вида ресурсов в стоимостном выражении.В пространстве ресурсов Е3 работа
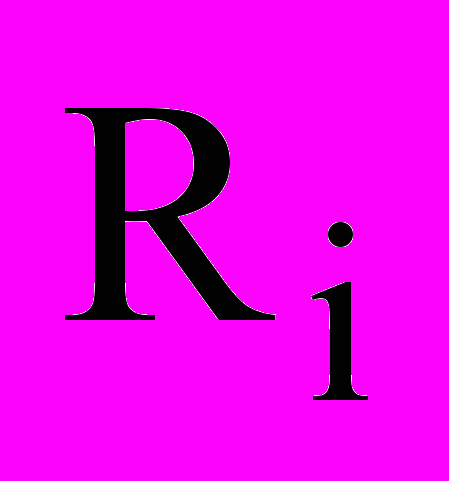 параллелепипед. Положение каждой работы
параллелепипед. Положение каждой работы 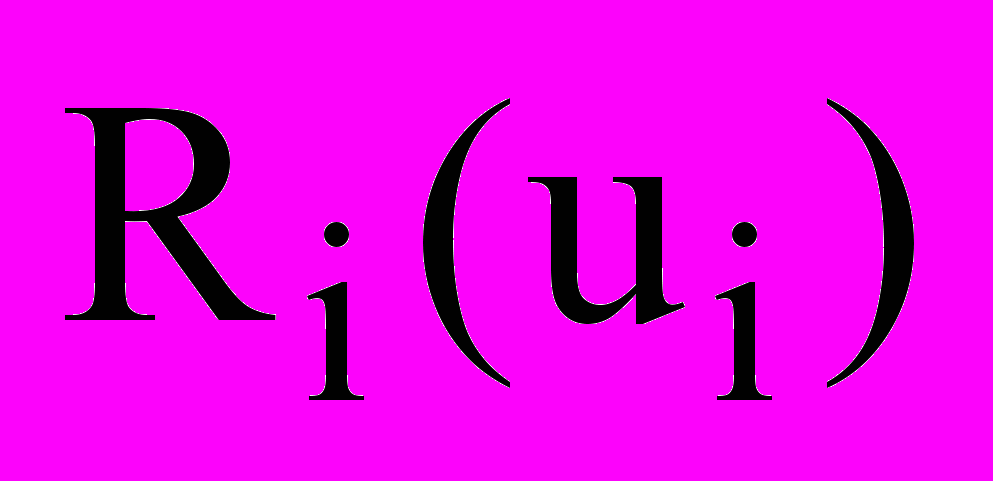 в Е3 характеризуется вектором параметров размещения ui=
в Е3 характеризуется вектором параметров размещения ui=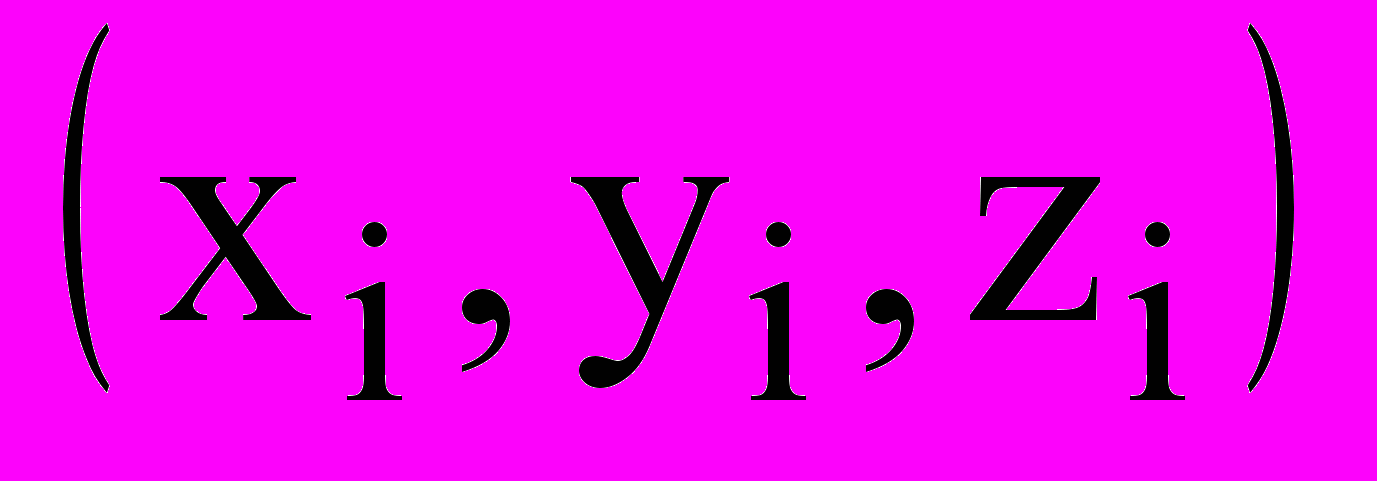 , задающим положение полюса собственной системы координат XiYiZi. Ограничения на возможные ресурсы проекта в целом выделяют в Е3 параллелепипед R0:(TM,B1M,B2M), где TМ время, максимально возможное для выполнения данного проекта, B1M, B2M максимальное финансовое обеспечение проекта по видам ресурсов.
, задающим положение полюса собственной системы координат XiYiZi. Ограничения на возможные ресурсы проекта в целом выделяют в Е3 параллелепипед R0:(TM,B1M,B2M), где TМ время, максимально возможное для выполнения данного проекта, B1M, B2M максимальное финансовое обеспечение проекта по видам ресурсов. Дисконтирование инвестиционных затрат по видам ресурсов учитывается изменением метрических характеристик объектов
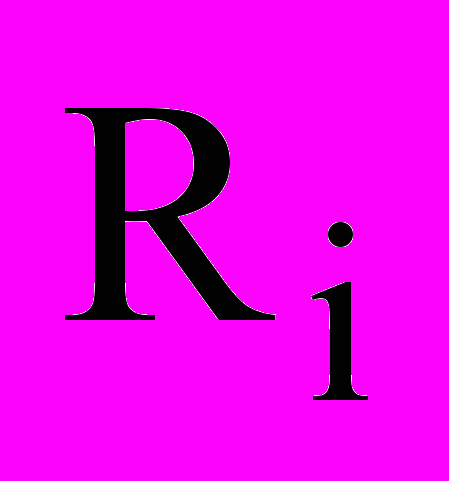 (что моделирует применение показателя наращения денег V(t)1) по линейному закону вида
(что моделирует применение показателя наращения денег V(t)1) по линейному закону вида 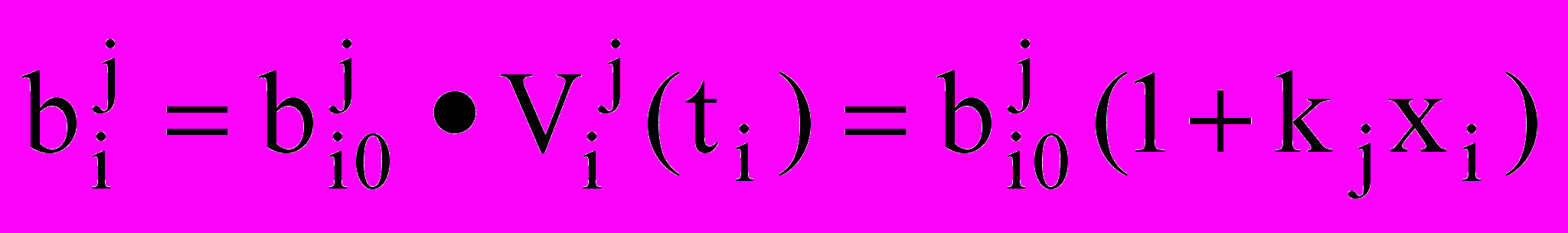 , j=1,2. (7)
, j=1,2. (7)Тогда задача оптимального распределения ресурсов проекта может быть представлена в виде: найти
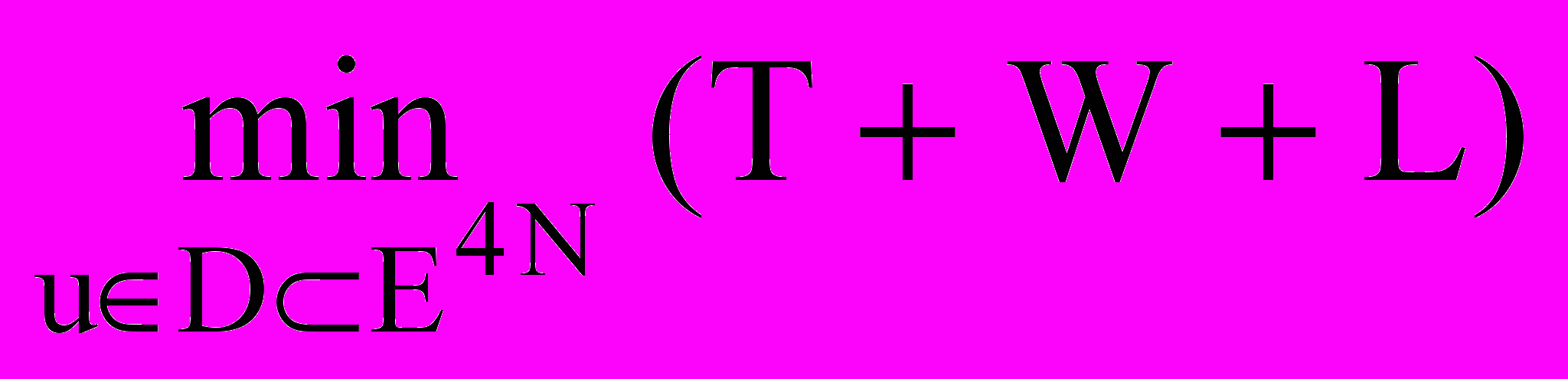 , (8)
, (8)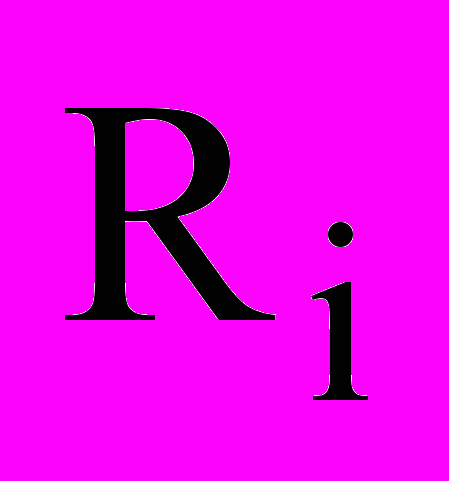
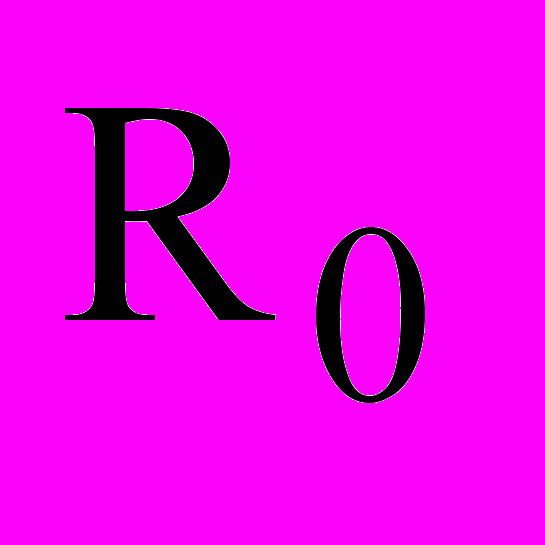 , (9)
, (9)D:
 , (10)
, (10)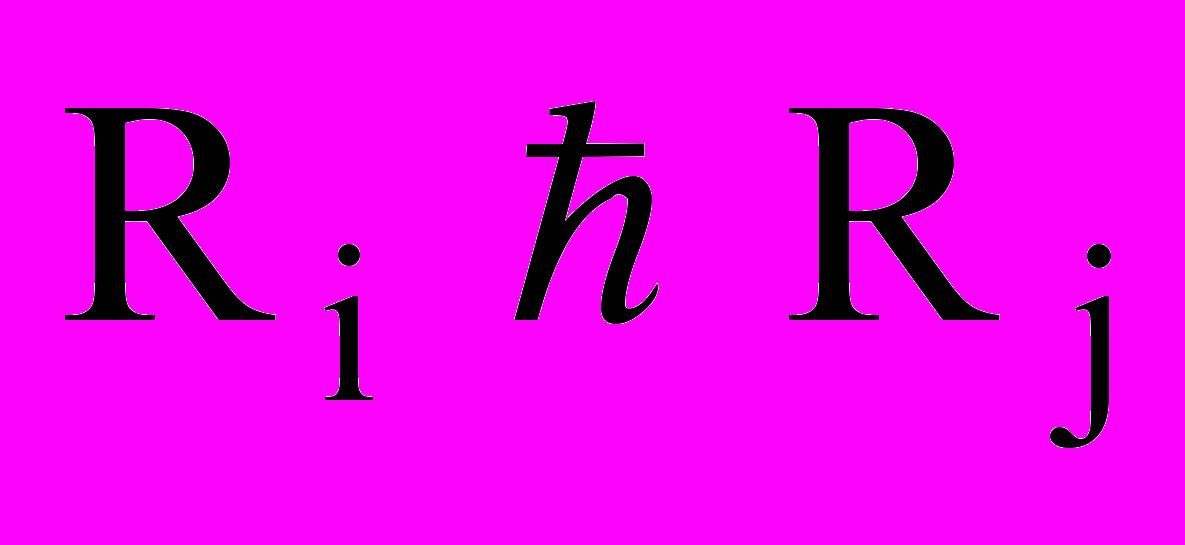 ,
, 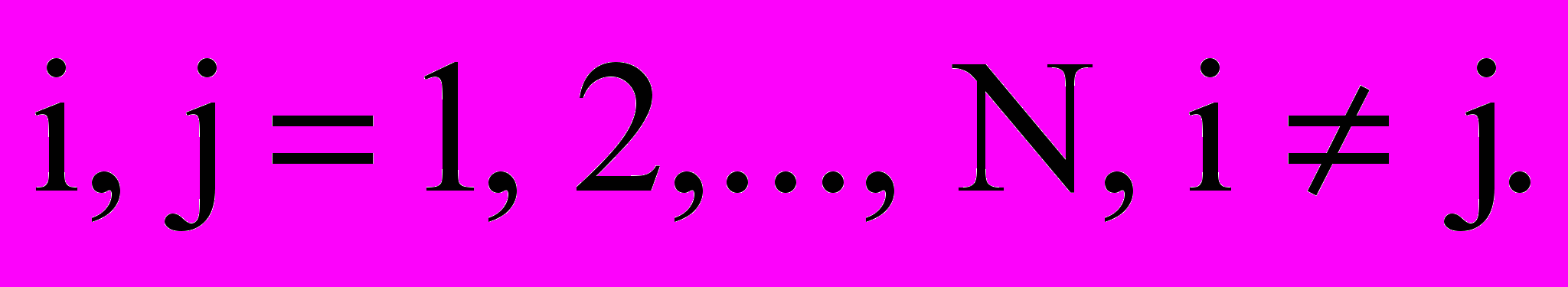 (11)
(11)Несмотря на разнообразие постановок задач, основными ограничениями на область допустимых решений D являются геометрические ограничения на размещение объекта Ri в области размещения R0 и условия попарного взаимного непересечения объектов.
Основные свойства оптимизационных задач 1-3. таковы:
Свойство 1. Область D невыпуклое, несвязное ограниченное точечное множество, имеющее кусочно-гладкую границу
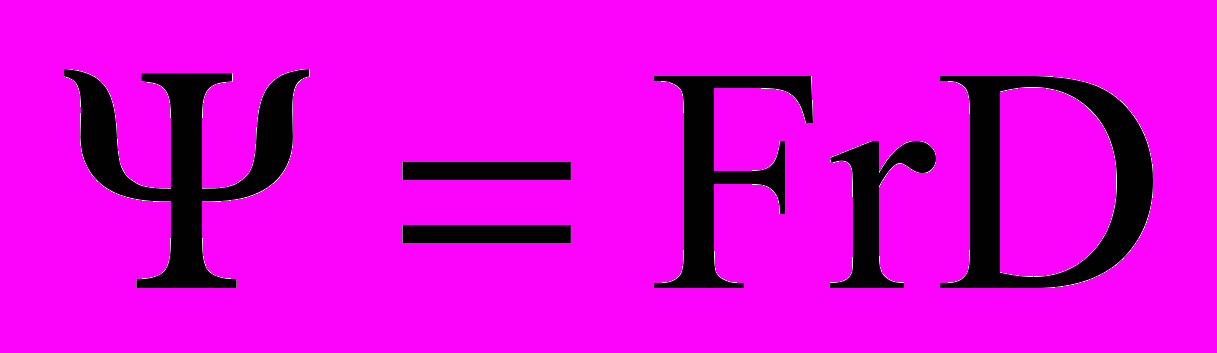 .
. Свойство 2. Область D допускает представление в виде объединения конечного числа выпуклых подобластей Dg вида
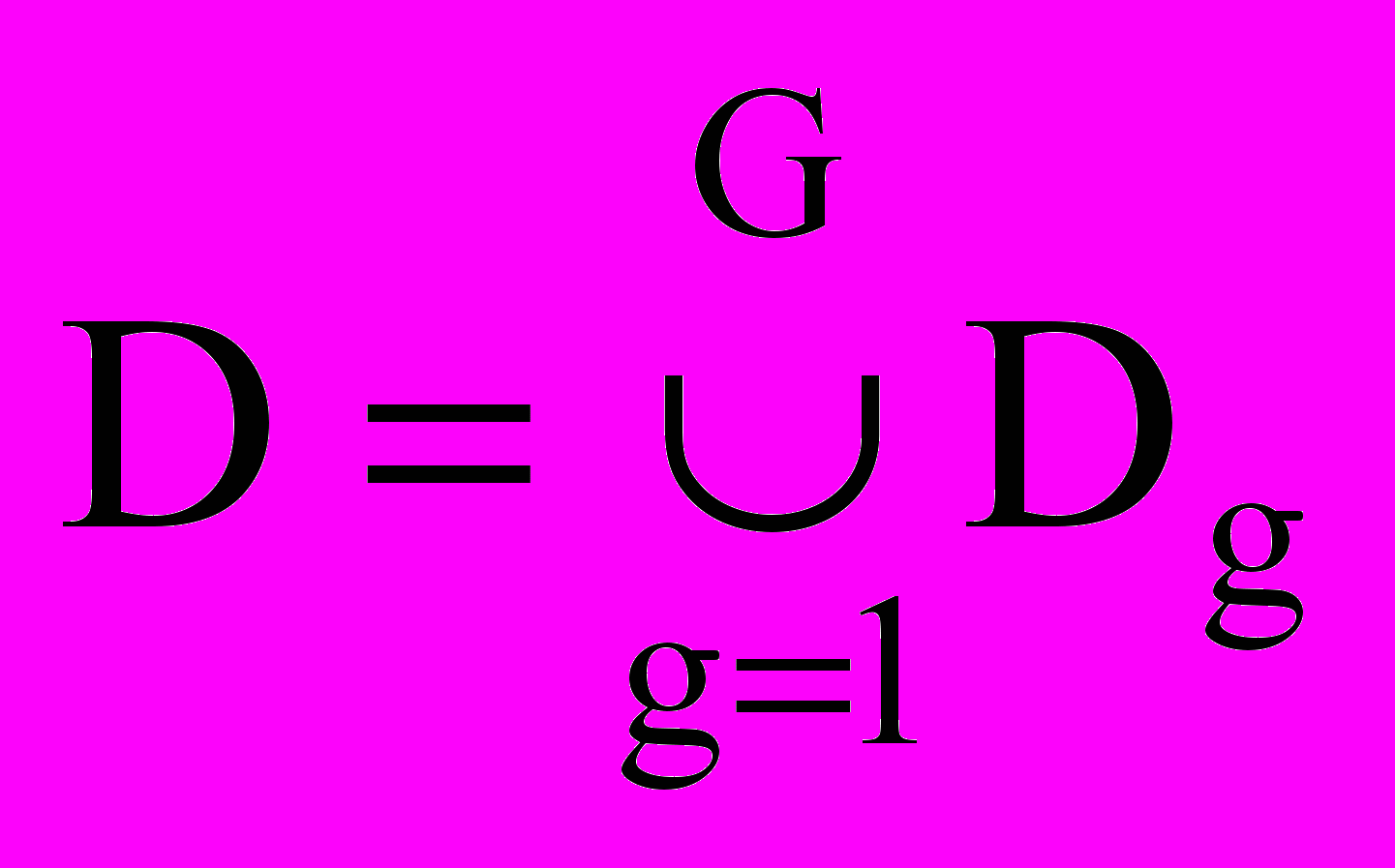 ,
, 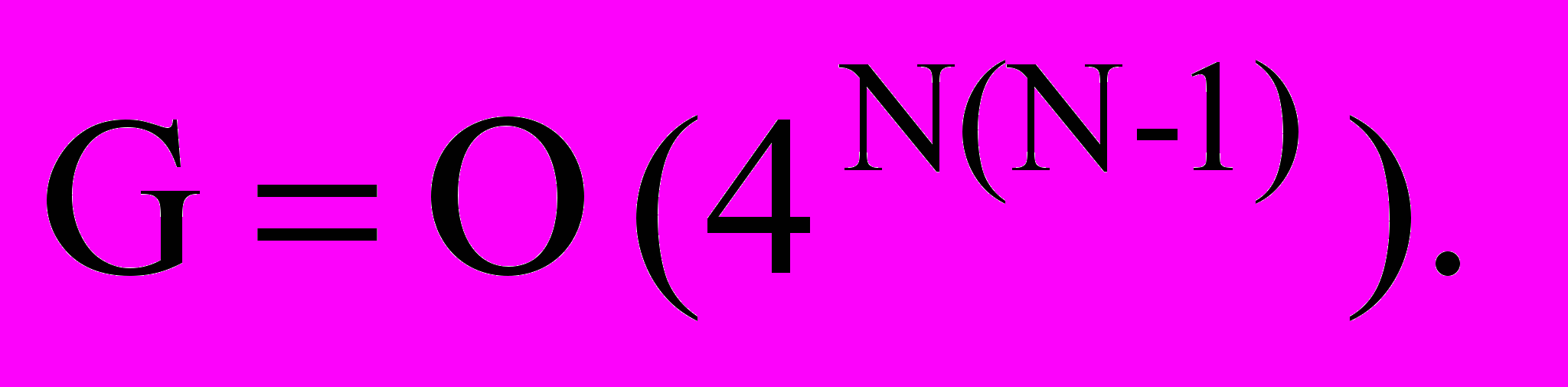 (12)
(12)Алгоритмическая и программная реализация математических моделей представленных задач предполагает учет следующих факторов: 1) неточность задания исходных данных задачи (вектора метрических характеристик набора объектов размещения и области размещения), 2) наличие вычислительной ошибки метода решения, вызванной нелинейностью функций ограничений области допустимых решений D и, возможно, функции цели. Кроме того, область допустимых решений D является существенно вырожденной – оптимальная вершина области описывается переопределенной системой уравнений, что вызывает необходимость разработки и реализации специальных программных средств учета ошибок округления алгоритма решения задачи.
В работе основное внимание уделено анализу второго фактора, для чего проведен анализ свойств области допустимых решений математических моделей представленных задач, построена линеаризация основных ограничений области допустимых решений, позволяющая с наперед заданной точностью свести рассматриваемые нелинейные оптимизационные задачи к набору задач линейного программирования.
ЛИТЕРАТУРА
1. Стоян Ю.Г., Яковлев С.В. Математические модели и оптимизационные методы геометрического проектирования. – К.: Наук. думка, 1986. – 268 с.
2. Управление проектами: Справочное руководство / Под ред. И.И. Мазура и В.Д. Шапиро. – М.: Высшая школа, 2000. – 875 с.
3. Гилл Дж., Мюррей К., Райт М. Практическая оптимизация. – М.: Наука, 1984, 459с.
