Труды V всероссийской научно-технической конференции "нейроинформатика-2003", ч. 1, с. 211

Вид материала

Документы

Содержание Постановка задачи 1. Суть алгоритма 2. Поиск идентификатора

Подобный материал:

• Программа всероссийской научно-технической конференции студентов, аспирантов и молодых, 1095.52kb.
• Вторая всероссийская научно-техническая конференция Мехатронные системы, 52.5kb.
• Уважаемые коллеги!, 138.01kb.
• Сборник статей по материалам Всероссийской научной конференции. 23-24 апреля 2003, 1941.16kb.
• Основные направления конференции, 107.24kb.
• Программ а 4-ой Всероссийской с международным участием научно-технической конференции, 119.57kb.
• Программ а 6-ой Всероссийской с международным участием научно-технической конференции, 125.51kb.
• Труды международной научно-практической интернет-конференции, 6066.9kb.
• Бондаренко С. В. Модель социализации пользователей в киберпространстве, 82.89kb.
• Министерство образования Российской Федерации Санкт-Петербургский государственный политехнический, 2776.63kb.

Труды V Всероссийской научно-технической конференции "НЕЙРОИНФОРМАТИКА-2003", ч.1, с.211.


Б.В.КРЫЖАНОВСКИЙ, В.М.КРЫЖАНОВСКИЙ

Институт оптико-нейронных технологий РАН, Москва

Московский инженерно-физический институт

iont@iont.ru , kryzhanov@mail.ru


ХЕШ-ФУНКЦИЯ НА ОСНОВЕ ВЕКТОРНОГО ПЕРСЕПТРОНА^*


Аннотация

В данной работе предлагается простой алгоритм, позволяющий производить быстрый ассоциативный поиск изображения по его ключу при наличии больших искажений. В работах [1-3] описана параметрическая нейросеть, обладающая большой емкостью памяти и способностью восстанавливать вектор при большом искажении. Предложенная в данной работе схема векторного персептрона базируется на результатах, полученных [1-3].


Постановка задачи

Имеется множество N-мерных векторов 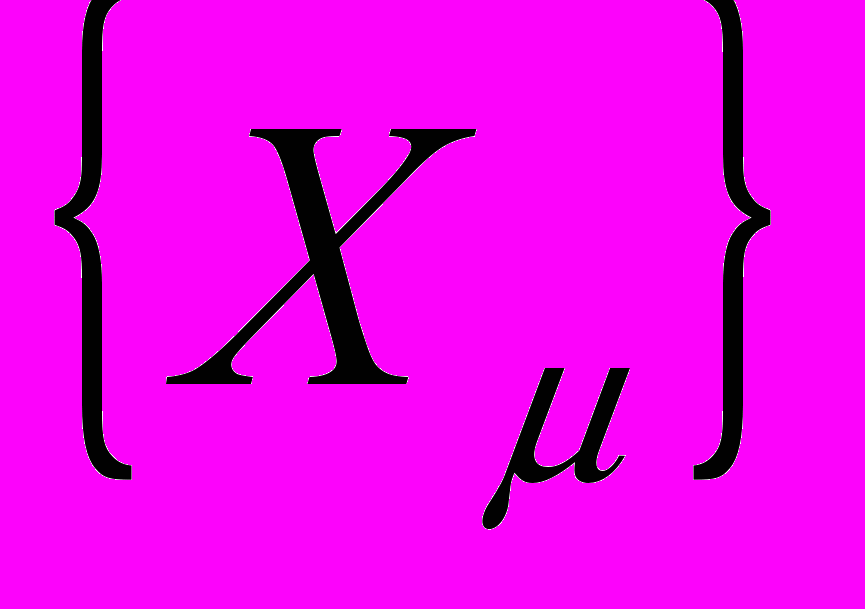, каждому вектору из этого множества поставлен в соответствие однозначным образом ключ (идентификатор - ). По искаженному образу необходимо восстановить ключ, по которому впоследствии однозначно определяется вектор 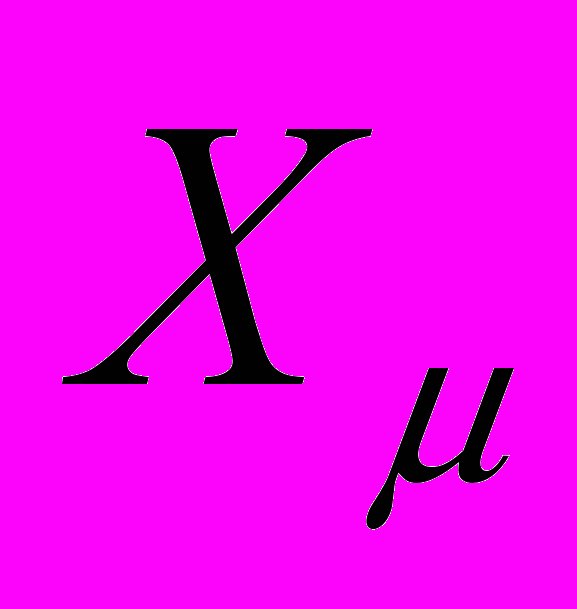, где 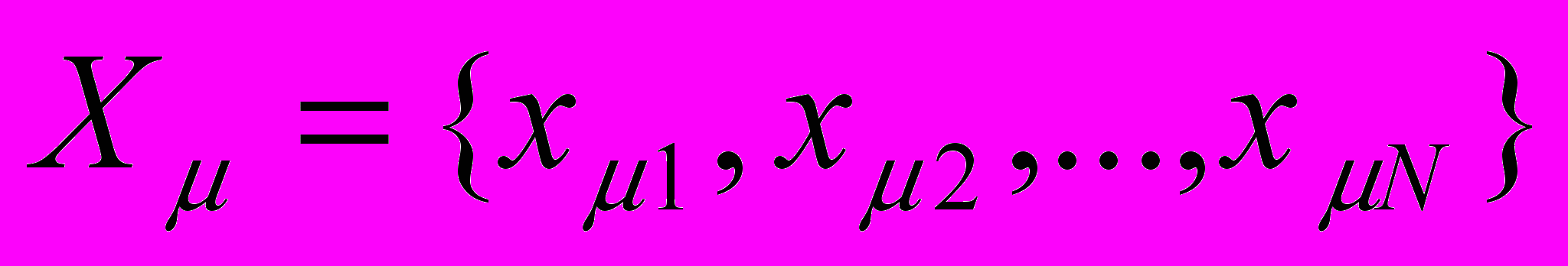, (=1,2,…,M), 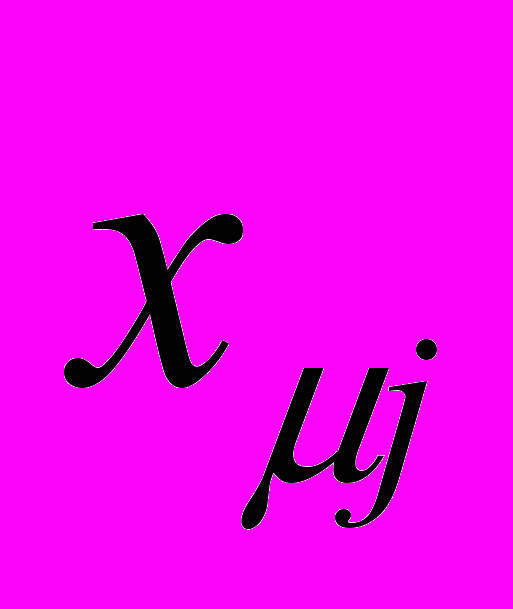- некоторый единичный вектор направленных вдоль одного из орт-векторов q-мерного векторного пространства, задающий состояние j-го нейрона.

Решающий эту задачу персептрон, представлен на рис.1. Он состоит из двух слоев нейронов, где каждый нейрон входного слоя связан со всеми нейронами выходного слоя. Алгоритм его работы реализован следующим образом.


N


1. Суть алгоритма:

• Для каждого образа 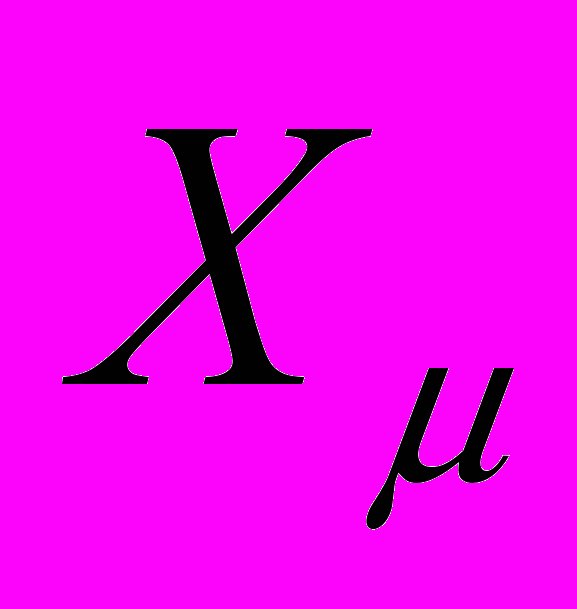генерируется дополнительный вектор 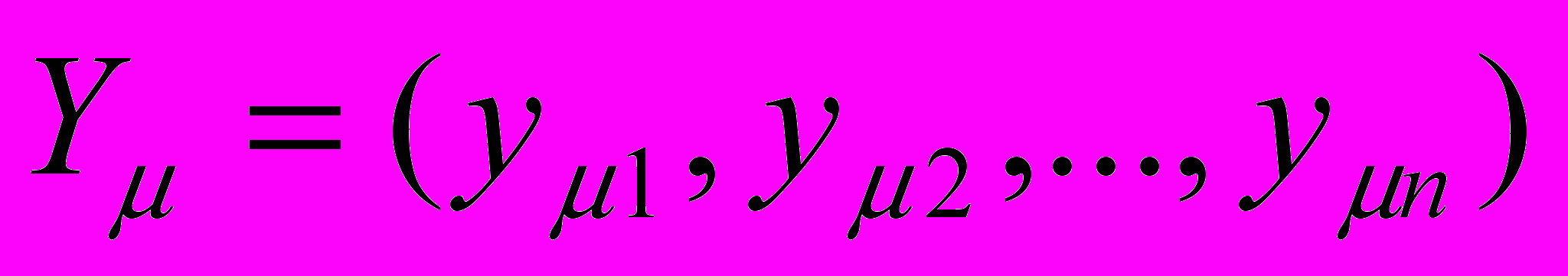, число компонент которого достаточно для кодировки ключа данного образа: последовательность номеров орт-векторов q-мерного векторного пространства, вдоль которых направлены единичные векторы 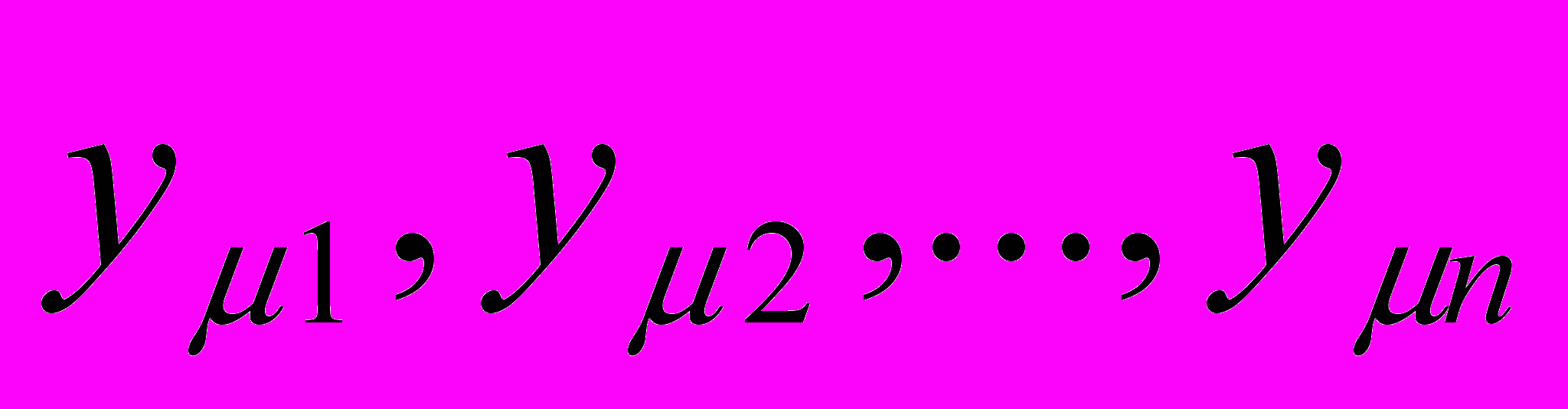, есть число μ в q-ичной записи. Иными словами 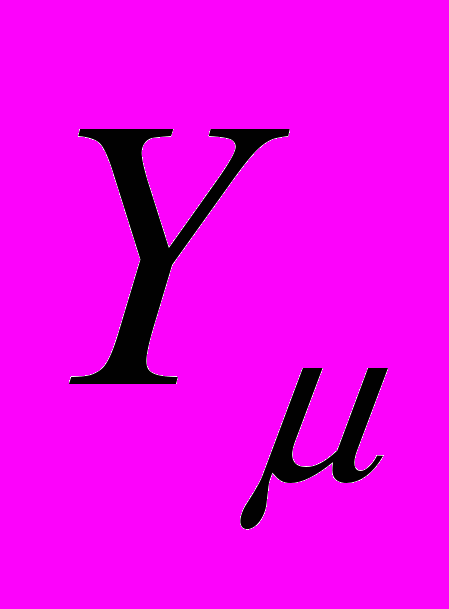есть кодировка номера μ.
  
• Формируем новый, модифицированный, набор векторов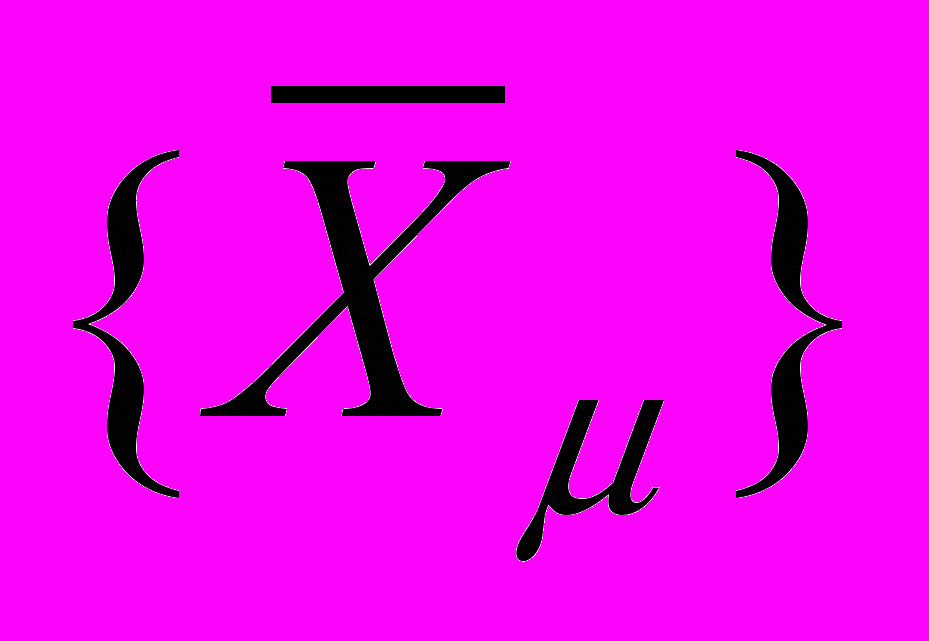размерности (N+n) по правилу «конкатенации» ,
  
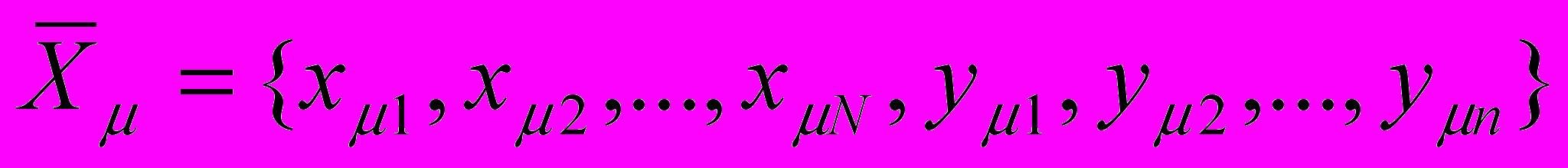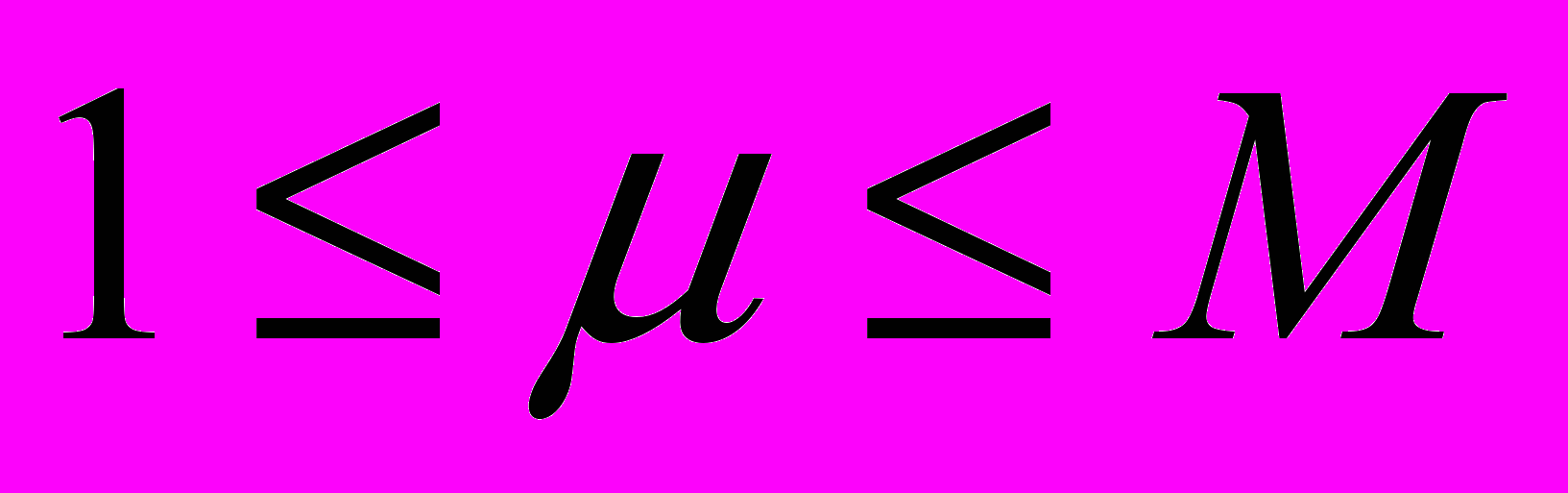
• На основе полученных векторов строим векторную нейросеть (рис.1), состоящую из (N+n) нейронов с q состояниями [3], где веса синоптических межсвязей вычисляются по обобщенному правилу Хебба:
  

, , ,

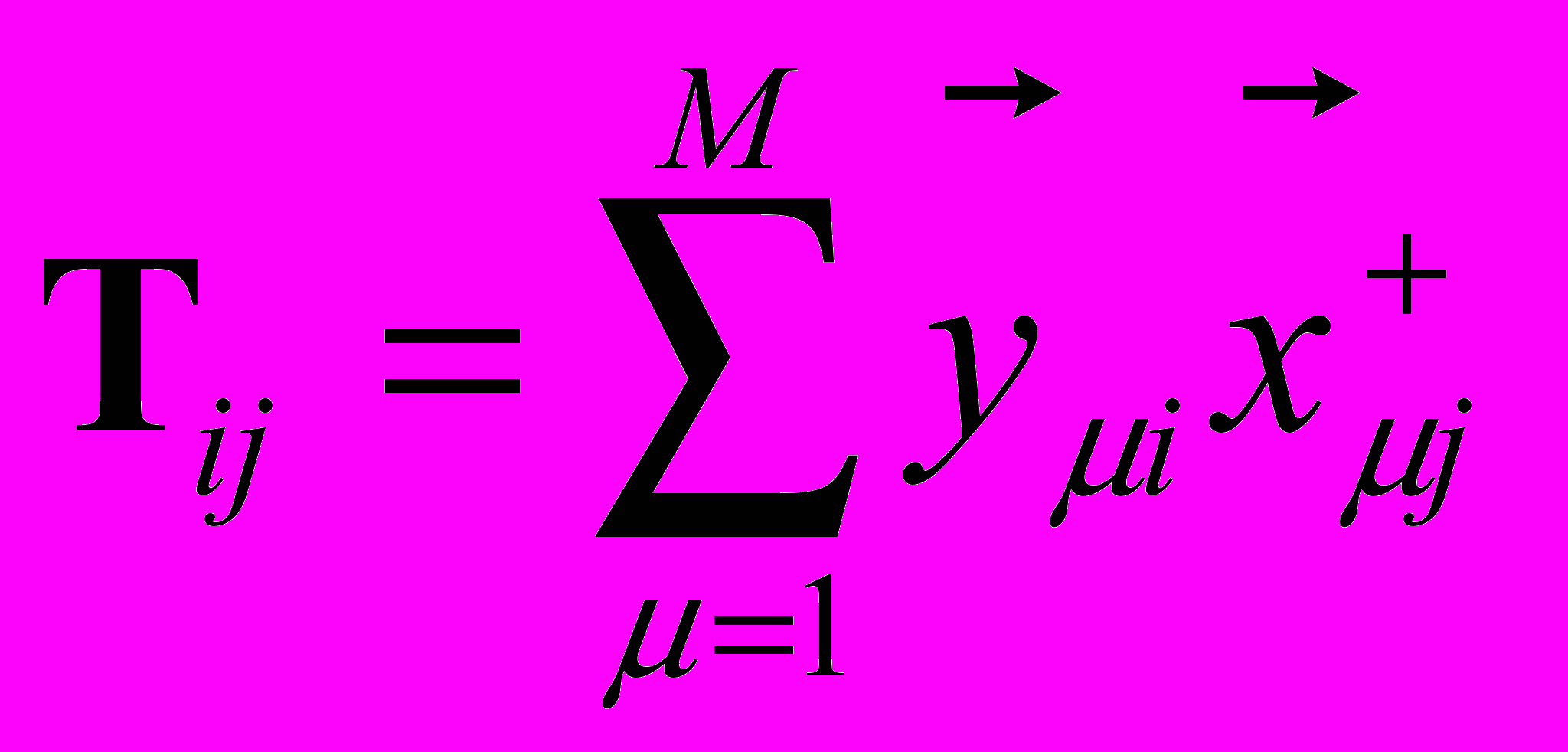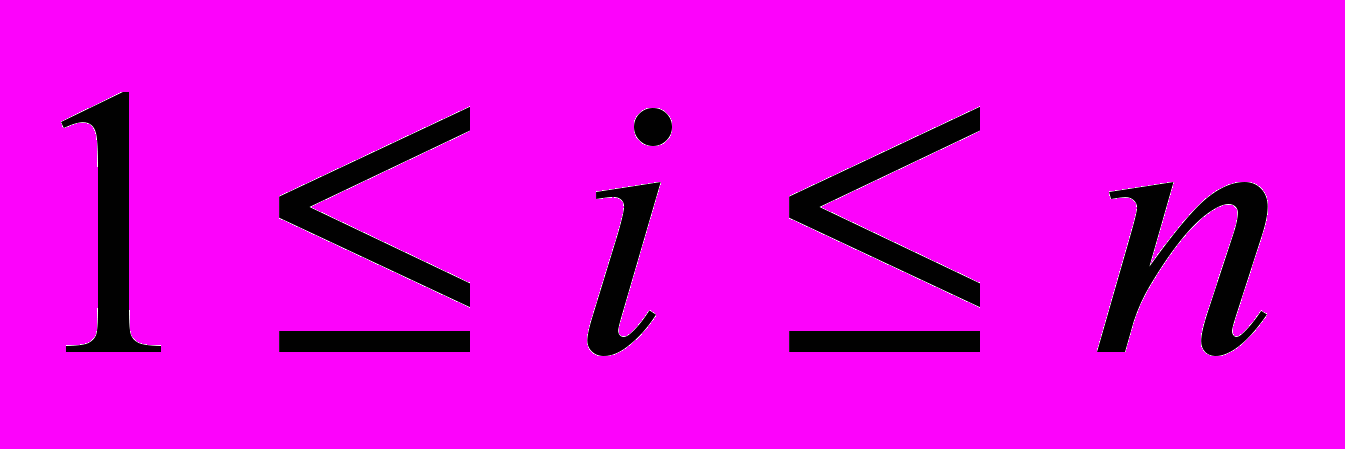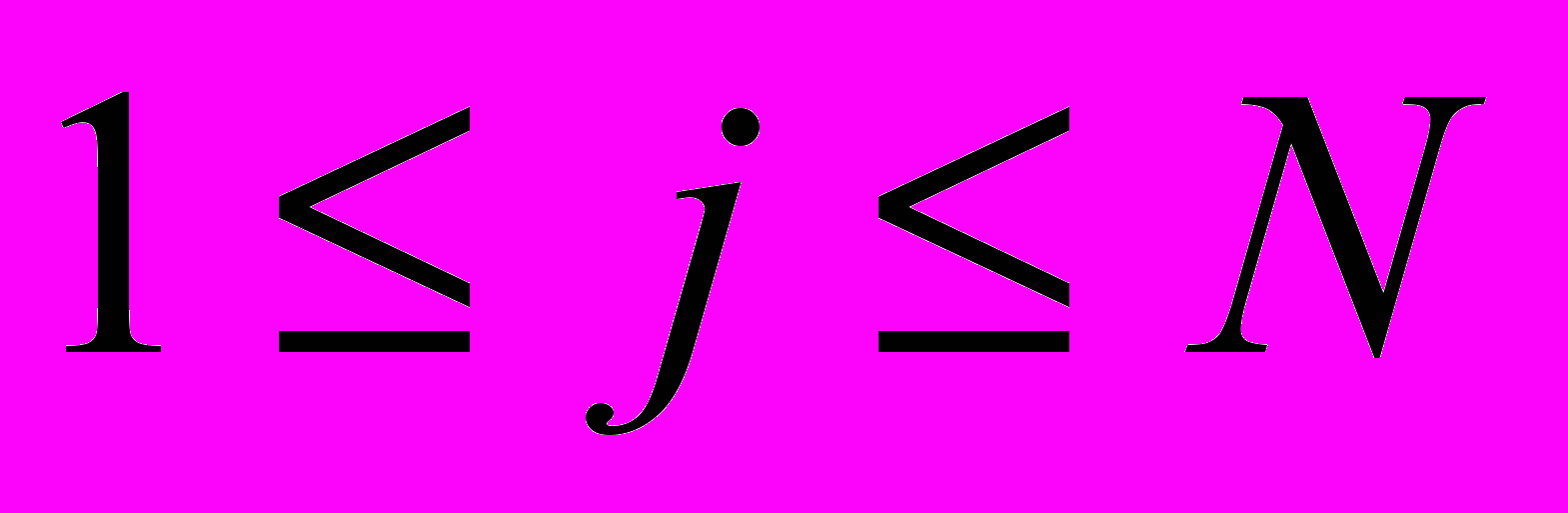где 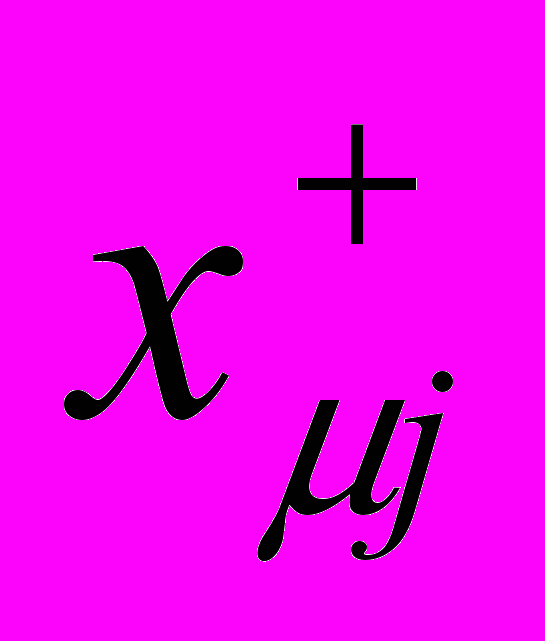- вектор-строка, а величина межсвязи T_ij между i-м и j-м нейронами не скаляр, как в обычной модели Хопфилда, а qq матрица.


2. Поиск идентификатора

• Пусть на вход сети подается некий образ 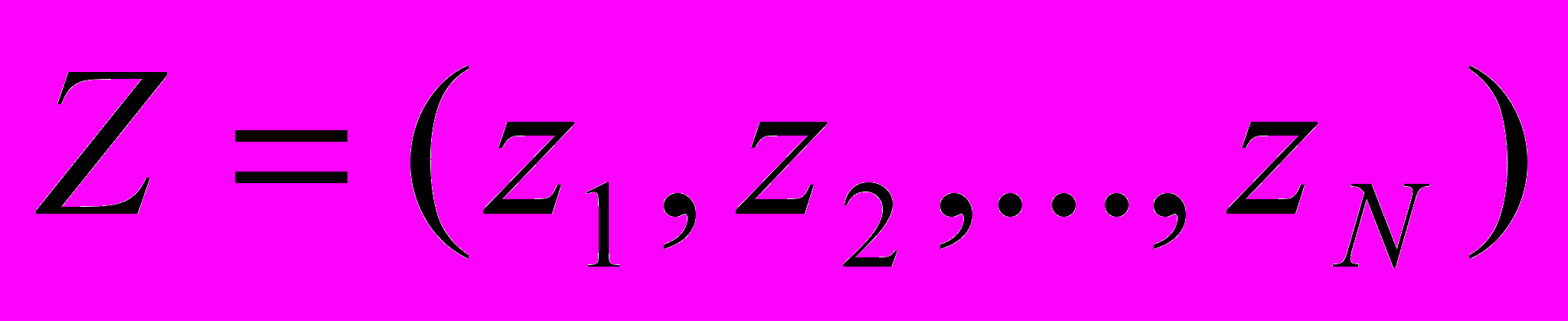, представляющий из себя искаженный вариант некоторого m-го эталонного паттерна .
  
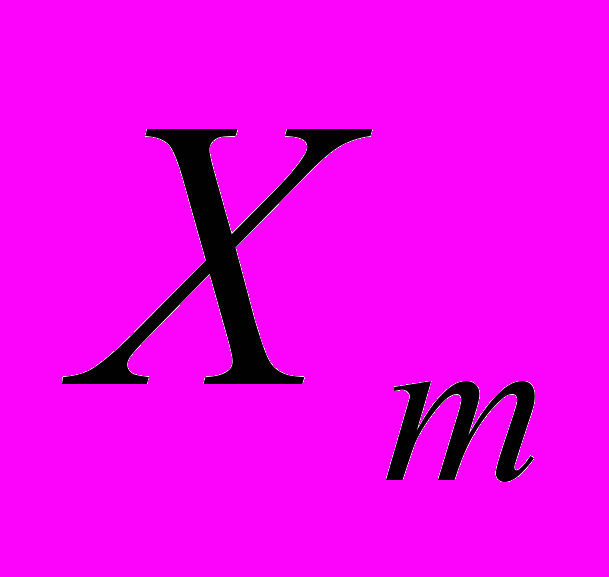• Для каждого i-го выходного нейрона считаем локальное поле со стороны нейронов входного слоя:
  

, ,

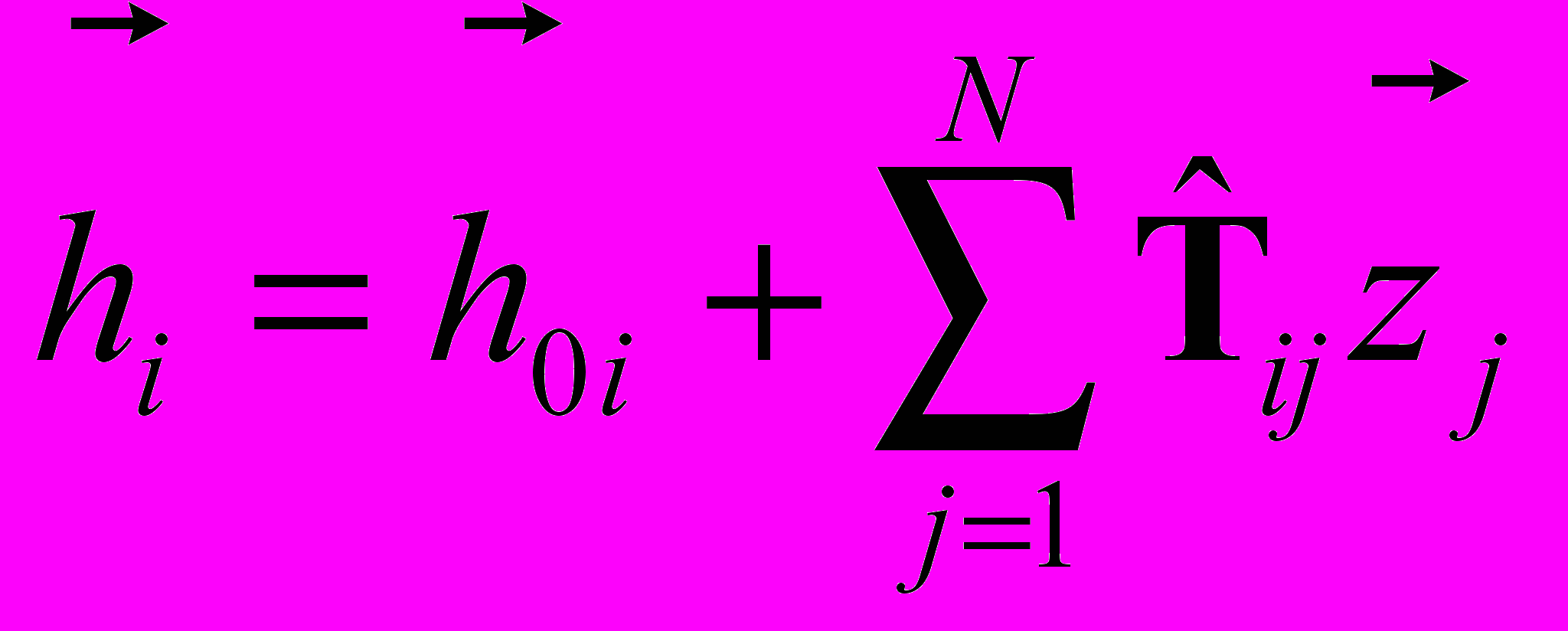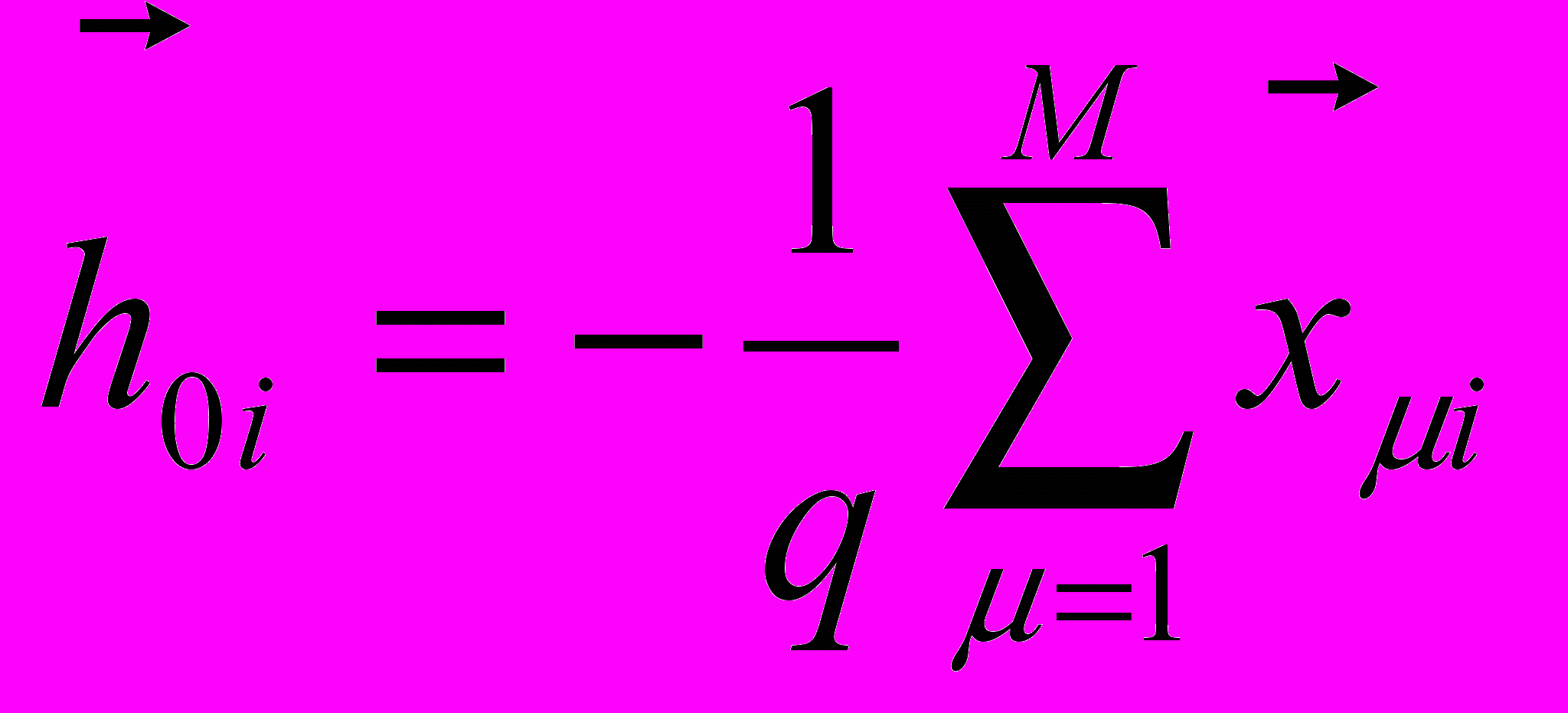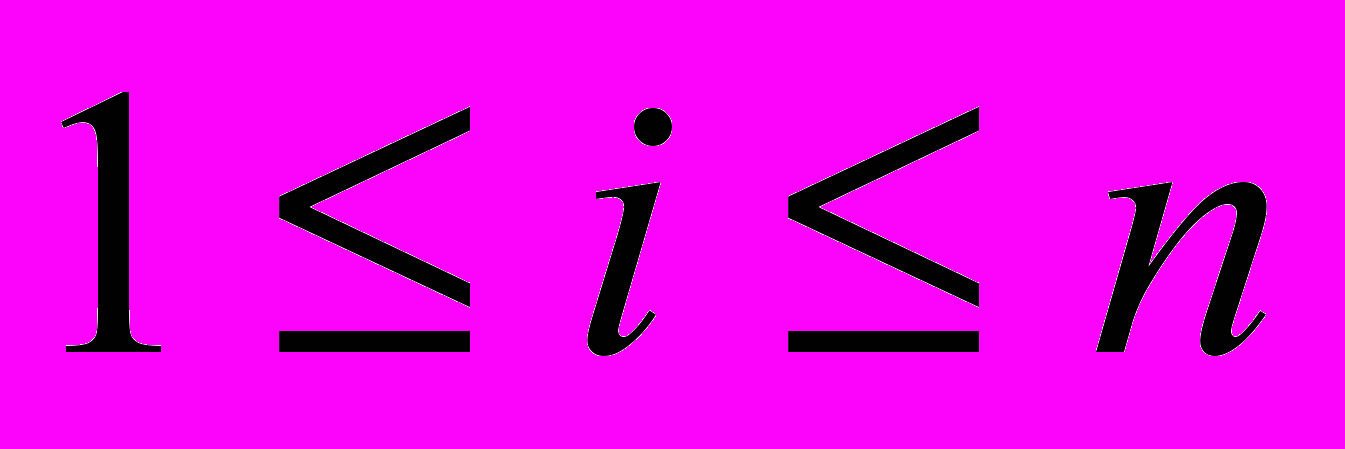
• Под воздействием локального поля i-й выходной нейрон ориентируется вдоль орта, направление которого наиболее близко направлению внешнего поля. При этом, восстанавливается кодирующий выходной вектор .
  
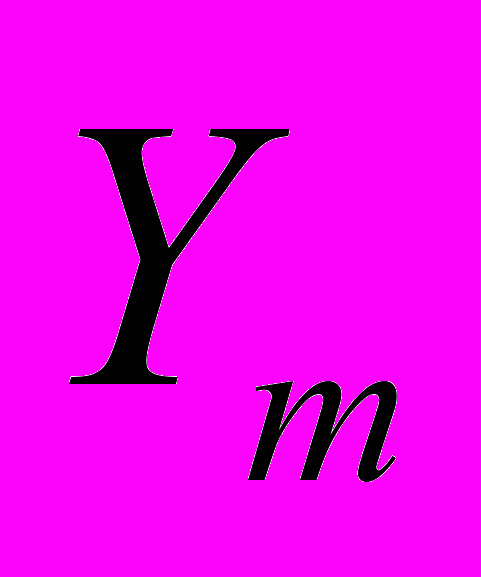• Обозначим через 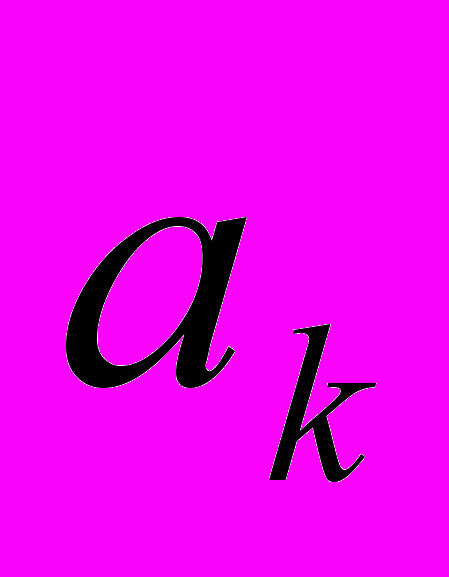номер орта, вдоль которого направлен вектор 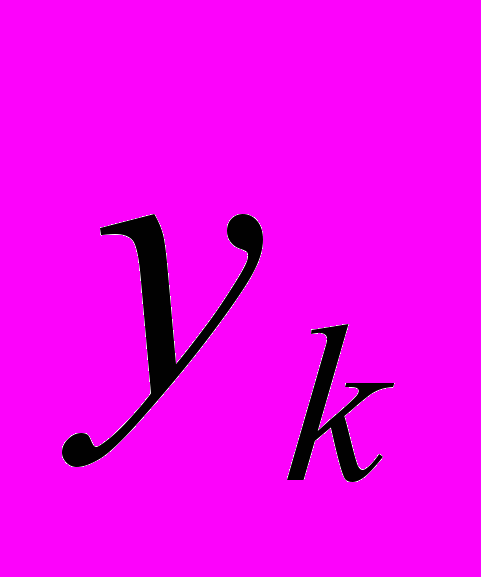. Тогда номер эталона, искажением которого является вектор Z, определится выражением .
  

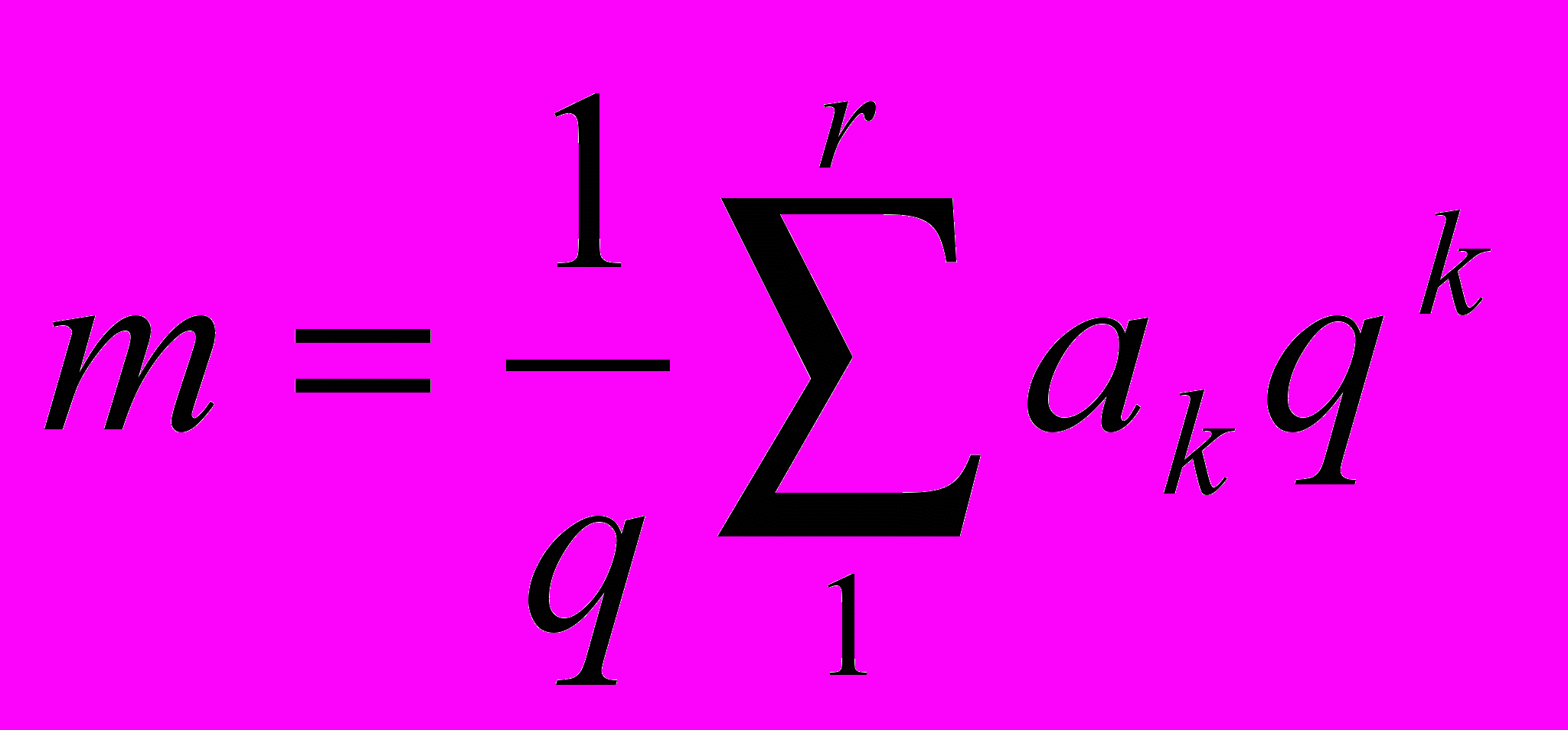Вероятность того, что номер m вектора определен неверно, задается выражением





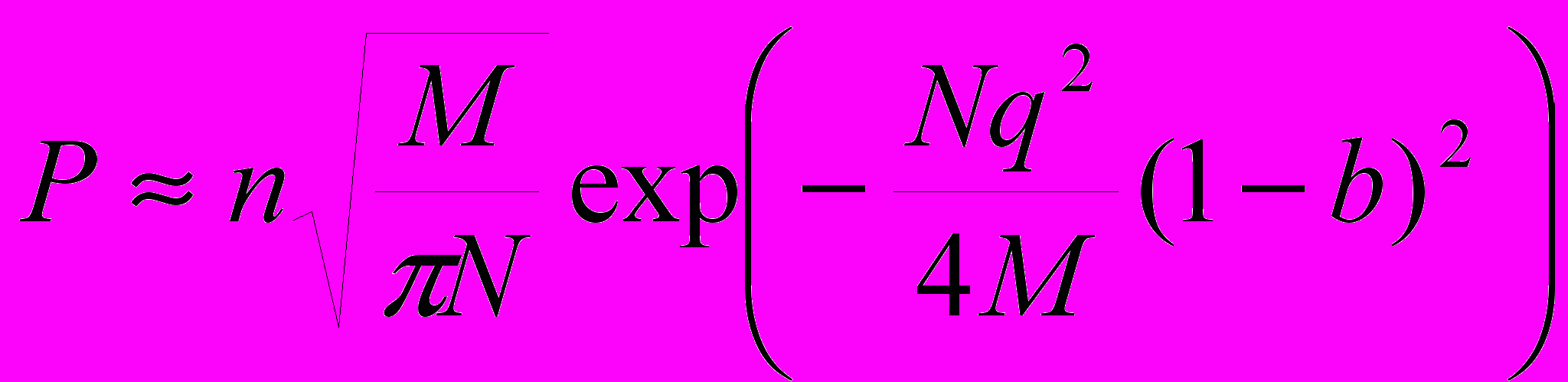
где b – параметр шума, т.е. вероятность того, что i-я компонента входного вектора искажена.

Число образов, которые можно записать при заданных параметрах (величине искажений b и ошибке распознавания P₀)



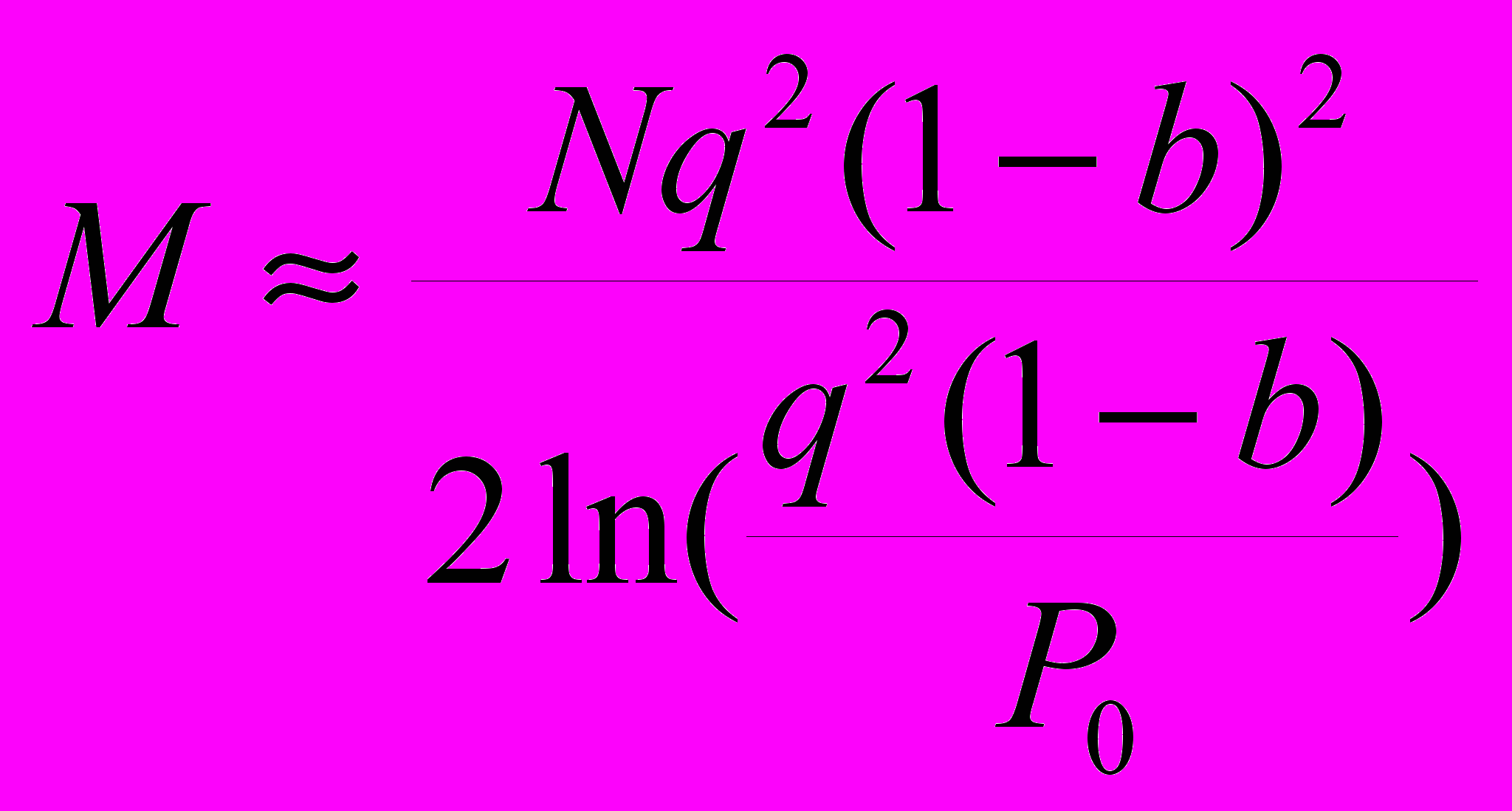
Как известно, быстрый поиск при наличии больших искажений (зашумленности) входных данных крайне затруднен. Одним из вариантов решения этой задачи является применение векторного персептрона.


Список литературы:

1. Б.В.Крыжановский, А.Л.Микаэлян. ”О распознающей способности нейросети на нейронах с параметрическим преобразованием частот ”. Доклады АН, сер. мат.физика, т. 383, №3, с.318-321, 2002.
   
2. B.V.Kryzhanovsky, V.M.Kryzhanovsky, A.L.Mikaelian and A.Fonarev. “Parametric dynamic neural network recognition power". Optical Memory&Neural Network, Vol. 10, №4, pp.211-218 (2001).
   
3. Б.В.Крыжановский, А.Л.Микаэлян. ”Ассоциативная память, способная распознавать сильно скоррелированные образы ”. Доклады АН, информатика, т 390, №1, с.27-31, 2003.
   
4. Б.В. Крыжановский, В.М. Крыжановский. Распознавание коррелированных образов с помощью векторной нейросети. Сборник трудов II-й международной конференции «Интегрированные модели и мягкие вычисления в искусственном интеллекте», с.321-327, Коломна-2003.