А. В. Савельев Уфимский государственный авиационный технический университет

Вид материала

Документы

Содержание 2.1. Логика спинальных ганглиев. 2.2. Переменная логическая структура нейросетей и принцип Дэйла. 2.3. Логика нейронов Пуркинье. 2.4. Хаотическая логика.

Подобный материал:

• А. В. Репин Уфимский государственный авиационный технический университет, Уфа e-mail:, 31.84kb.
• Гоувпо уфимский государственный авиационный технический университет Кафедра информатики, 300.86kb.
• "Философские науки", 789.13kb.
• Экономические интересы государства как акционера, 409.15kb.
• Уфимский государственный авиационный технический университет, 137.84kb.
• Уфимский Государственный Авиационный Технический Университет Кафедра вмиК отчет, 188.41kb.
• Разработка устройств для измерения сверхслабых полей естественного излучения, 793.23kb.
• Совершенствование инструментария управления реализацией федеральных целевых программ, 377.01kb.
• Тимирханов валентин Рахимович моделирование лингвофилософских явлений в свете имяславской, 773.94kb.
• Практическом освоении студентами научно-теоретических положений изучаемой дисциплины, 110.46kb.

А.В. Савельев

Уфимский государственный авиационный технический университет

gmkristo@mail.ru


логика нейронов и нейросетей¹


Аннотация

В работе приведены результаты исследования возможных путей изучения логических свойств нейронов и построения новых логических элементов. Отмечается примитивизм fuzzy-логики, применяющейся в настоящее время для моделирования нейронной логики. Поскольку, вопреки существующим взглядам, нейрон не является тривиальным в логическом отношении, отмечается необходимость более тонкого исследования и моделирования логических свойств нейронов различных типов. В качестве примеров приводятся разработанные ранее автором моделирующие схемы и структурные алгоритмы логики спинальных ганглиев, нейронов с переключением медиатора при экзоцитозе, нейронов Пуркинье мозжечка, хаотической логики.


1. Введение. В отношении нейрокомпьютерных технологий на сегодняшний день ассоциируется обычно с Fuzzy-логикой [1], являющейся модификацией классической логики с использованием теории размытых множеств, разработанной Л. Заде [2]. Однако, следует заметить, что введение вероятностных параметров размытых множеств означает признание неизвестным скрытых закономерностей формирования размытости, то есть недостаточность детализации. Это вполне соответствует грубому представлению нейрона как элемента 40 – 50 гг. Мак-Каллока – Питса [3]. Однако, на наш взгляд, к настоящему моменту нейробиологией накоплено большое количество знаний, позволяющих выйти за пределы формального элемента Мак-Каллока – Питса и, соответственно, примитивности логики, воспринимаемой на сегодняшний день как нейронную. Чтобы осуществить это требуется значительно более глубокое моделирование нейрона, в том числе, как логического элемента [4].

2.1. Логика спинальных ганглиев. Свойства нейрона как логического элемента чрезвычайно многообразны. Логические свойства нейрона могут проявляться в избирательном реагировании его, как, например, в конвергентных нейронах спинальных ганглиев, на активизацию синапсов, связанных с низкопорговыми или высокопороговыми рецепторами, спайковыми ответами обычной или увеличенной длительности [5]. Таким образом, это расширяет традиционные представления о нейроне, как элементарной «on-off»-ячейке, поскольку аналогично реальному нейрону вводится логическая модальность по вариациям длительности самих спайков. При этом реализуется пороговая логика с динамически изменяемым порогом, текущая величина которого определяется мгновенным состоянием конкуренции между количеством активированных синапсов, связанных с высокопороговыми или низкопороговыми рецепторами. Функционирование такого логического нейроподобного элемента в составе нейросети дает возможность воспроизводить генетические самоорганизующиеся алгоритмы переключения его логики (рис. 1).

Логические свойства нейрона могут проявляться также в мотонейронах, реагирующих быстрыми Na⁺-спайками, соответствующими быстрым движениям эффекторов, или медленными Са²⁺-спайками, обеспечивающими медленные движения эффекторов [6]. В этом случае дополнительными логическими свойствами могут быть наделены не только длительность и амплитуда спайков, но также продолжительность и глубина следовой зоны гиперполяризации, соответствующей рефракторному периоду, что и определяет, собственно, «быстроту» спайков. Устройство является также логическим анализатором количества активированных синапсов, изменяя нейронную логику при активации в сети нейрона-пейсмекера, что наблюдается обычно при медленных движениях эффектора. Бинарная логика этого устройства служит для управления тринарной логикой по аксонному выходу мотонейрона. При использовании устройства по [6] повышается точность моделирования реальных мотонейронов за счет воспроизведения тонких нейрофизиологических механизмов зависимости спайковой активности от стимуляции синаптических входов, расширяются функциональные возможности устройства за счет управления эффекторами в различных режимах воспроизведения реакции убегания и тонической активности, повышается гибкость управления эффекторами благодаря введению дополнительных элементов, моделирующих генерацию спайков различной природы в одном аксоне. Логика работы в этом случае реализуется переключением различных динамических характеристик активного проведения по аксону [7] и может осуществлять распознавание активизации нейронов-пейсмекеров в эффекторной сети мотонейронов. В связи с этим устройство может быть использовано в миостимуляторах, в том числе, в кардиостимуляторах, обеспечивая логическое регулирование без физической обратной связи и системы датчиков. И в том, и в другом случаях нейрон обнаруживает более богатую логику, кроме традиционно учитывающейся тривиально пороговой, а следовательно, обладает более богатой и гибкой функциональностью, что позволяет значительно сокращать размерность нейросети, требуемой для решения поставленных задач.





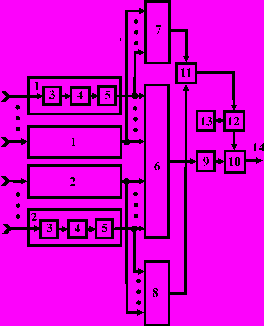
Рис. 1. Логический нейроподобный элемент, реализующий синергетические взаимодействия между низкопороговыми и высокопороговыми рецепторами (а.с. # 1645975)

2.2. Переменная логическая структура нейросетей и принцип Дэйла. Свойства нейрона как нетривиального логического элемента могут проявляться также при переключении его на различные виды экзоцитоза – использующего холинергический тип и нехолинергические типы медиатора. Установлено [8], что принцип Дэйла [9] о том, что на всех окончаниях одного аксона выделяется один и тот же медиатор, является грубым упрощением, характерным лишь для нейронов определенных групп. Неоднократно показывалось его нарушение, в частности, присутствие в одном аксоне как холинергических, так и нехолинергических видов экзоцитоза. В функциональном отношении это может выражаться как в различных динамических характеристиках передачи импульсов по сети, так и в динамическом изменении конфигурации нейросети под действием как различных входных воздействий, так и в виде реакции на ответы своих нейронов. При этом такая логика работает «по выходу», т.е. качественное состояние нейрона определяется характером потока его же выходной информации – определенным видом спайковой последовательности, как в вычислителе экзоцитоза [10], являющимся анализатором степени «пачечности» своих разрядов. Такая логика, кроме того, снижает высокую степень неопределенности нейроподобных элементов, выражающуюся в одинаковой частоте выходных импульсных последовательностей, соответствующей множеству равномощных состояний активированных входов нейрона, что является существенным недостатком элементов обычно применяемой пороговой логики. Устройство может использоваться также в качестве анализатора импульсных кодовых последовательностей, в виде семантического фильтра. Выступая, таким образом, как переключательные элементы по входо-выходным соединениям, такие нейроны могут формировать искусственные нейросети с переменной структурой, что может позволить более полно использовать их адаптивные механизмы пластичности, например, при управлении техническими устройствами или при решении сложных вычислительных задач.

2.3. Логика нейронов Пуркинье. В то же время, количественные показатели пачечности могут служить логическими состояниями нейрона, причем, с градацией, превышающей обычную двузначную логику и могут реализовывать многозначную, бесконечнозначную, непрерывную логику, логику «неисключенного четвертого» и т.д. Такое управление характером логических свойств нейрона может осуществляться, например, модуляцией со стороны лиановидного волокна, конвергирующего с нейроном Пуркинье мозжечка [11], контактирующего с его дендритами на большей части их протяжения и многократно повторяющего их дихотомические ветвления (рис. 2).

Рис. 2. Взаимосвязь между лиановидным волокном (темные участки) и дендритом (Д) клетки Пуркинье. Фото Uchizono K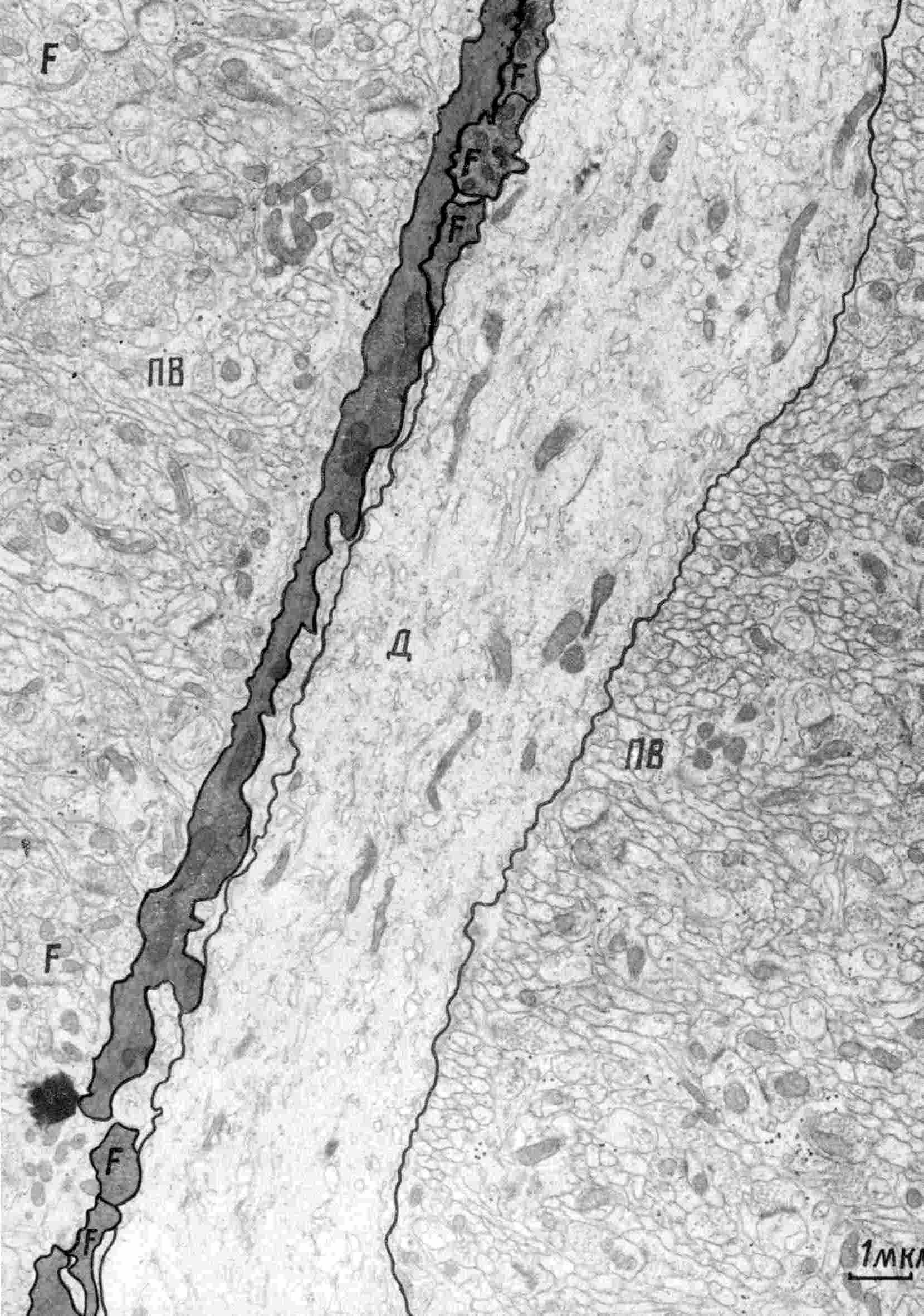

На протяжении всего контакта с дендритом лиановидное волокно образует последовательный ряд преимущественно возбуждающих синапсов. Раздражение ЛВ вызывает колебательные деполяризационные потенциалы в клетках Пуркинье, что может приводить к ращеплению выходного импульсного потока на пачки. Параметры колебательных деполяризационных потенциалов, управляющих логическими свойствами нейрона Пуркинье, зависят не только от приходящих возбуждающих стимулов по лиановидному волокну, но, в большей мере, от состояния возбуждения или торможения самих нейронов Пуркинье, величины результирующей деполяризации или гиперполяризации, а также от положения ЛВ на дендритах нейрона Пуркинье. В данном случае лиановидное волокно является не только простым входом, но соответствующим сопроцессором для самого нейрона Пуркинье ввиду сложного характера контактирования с ним. Таким образом, топология такого контакта определяет функциональные особенности комплекса и, соответственно, сети клеток Пуркинье (рис. 3А, В). Сочетание градуального изменения общего порога клетки Пуркинье с изменением количества генерируемых в пачках спайков под действием модуляции лиановидного волокна моделирует k-значность нейронной логики [12].

Граф логической структуры контакта клетки Пуркинье с лиановидным волокном является упрощенной моделью топологии контактирования, не учитывающей сложную объемную геометрию этого контакта, дендрита клетки Пуркинье и самого лиановидного волокна. Однако, такой граф достаточно хорошо отображает именно логические свойства такого контакта, выражающиеся, в том числе, в характере сигнальных связей синапсов лиановидного волокна. Ребра графа имеют физическое значение межсинаптических задержек в распространении пре- и постсинаптических потенциалов, соответственно по лиановидному волокну и дендриту клетки Пуркинье. Сюда же могут относиться и собственно синаптические задержки выделения медиатора. Сложный контакт лиановидного волокна с дендритом клетки Пуркинье значительно увеличивает вычислительные свойства каждой отдельной клетки Пуркинье без объединения их в сеть, реализуя разностную схему, описанную графом (рис. 3). Граф, соответствующий логической структуре контакта клетки Пуркинье с LF изображен на рис. 3. Учитывается, что LF образует с клеткой Пуркинье последовательную серию возбуждающих синапсов, количество тормозящих синапсов значительно меньше, причем, в отличие от возбуждающих, они могут образовывать реципрокные связи. Можно заметить также фрактальное подобие графа соединения клетки Пуркинье и лиановидного волокна в части обратных связей с логикой соединения участка нейросети мотонейронов с клетками Реншоу ([13]). Этот факт может свидетельствовать о структурном иерархическом представительстве низших двигательных механизмов в высших центрально-мозговых механизмах. Возможно, что рассмотрение такой логической организации этих мозговых структур сможет помочь решению проблемы о связи мысли и движения.





Рис. 3


2.4. Хаотическая логика. В устройстве [14] реализуется совершенно новый тип логики для технических устройств, предложенный авторами и позволяет реализовать хаотическую логику работы нейрона на макроуровне. Бинарные отношения могут кодироваться степенью детерминированности или хаотичности сигнала аналогично явлениям, наблюдаемым во многих нейронах некоторых отделов нервной системы, если учитывать реальные процессы, происходящие в их функционирующих аксонах. Детектирование таких состояний не представляет труда и может осуществляться аналогично детектированию их в реальной нервной системе [15]. Согласно теории нейронного ансамбля А.Б. Когана [16] и вероятностного характера связей между нейронами в ансамбле до обучения, робастный характер этих связей понимается относительно целенаправленной активности ансамбля. Учитывая нашу концепцию автофрактальности нейрона, т.е. возможности построения самого нейрона в виде нейросети [17], мы распространили эти положения, весьма справедливые для нейронного ансамбля, и на нервную клетку. Хаотические режимы может иметь результат функционирования нервной клетки (как нейросети) – частота спайковых разрядов, проявляющиеся при определенных качественных состояниях нейрона, распознаваемых предложенной схемой. Фактически, устройство воспроизводит динамические свойства нейрона как странного аттрактора не ниже 4-го порядка, имеющего хаотические режимы (каскады Фейгенбаума) при определенных значениях изменяемых параметров. Устройство может служить нейроном-детектором в задачах распознавания образов, принятия решений, управления, кодирования информации, а также в биомедицинской кибернетике в качестве электростимулятора или в гибридных техно-биологических системах. С теоретической точки зрения предложенное решение может выражать новый взгляд в понимании механизмов кодирования информации в нервной системе. В устройстве [18] реализован механизм продуцирования эндогенных спонтанных разрядов, присутствие которого характерно для многих нейронов нервной системы, в особенности, мотонейронов, обеспечивающих поддержание некоторого тонуса иннервируемой мышечной системы в разомкнутом положении. В результате на выходе формируется быстрый Na⁺-спайк при отсутствии сигналов на синаптических входах или когда эти сигналы малой интенсивности, или уравновешиваются тормозящими сигналами так, чтобы суммарные ВПСП с выхода сумматора 4 не превышали порог нейрона. Время, проходящее с момента начала «молчания» нейрона (т.е. отсутствия ритмической импульсации на выходе) до времени генерации спонтанного Na⁺-спайка содержит случайную составляющую, отражающую роль флуктуации эндогенных процессов нейрона. Таким образом, в логику переключения нейрона вносится случайная составляющая, однако, происходит это не по амплитуде, а по длительности межимпульсного интервала, т.е. по факту появления спайка. За счет этого при надпороговых воздействиях на нейрон он работает как детерминированный элемент, а в отсутствии внешних воздействий – как стохастический, что само по себе также может образовывать дополнительный логический информационный канал. Хаотизация логических свойств нейрона может выражаться в возникновении эндогенных спонтанных разрядов после продолжительной волны деполяризации ([19]), что является указанием на механизм информационной обработки нейроном таких волн в смысле феномена Швиндта – Крилла [20]. После такого воздействия спонтанный спайк может возникать даже если дно следовой гиперполяризации опускается до уровня потенциала покоя [21]. Нейрон самопроизвольно «уходит» от потенциала покоя к порогу, следовательно, в дендритах при этом течет аксиальный ток к соме, т.е. дендриты устойчиво деполяризованы. Механизм образования таких спайков отражен в [21]. В отличие от [20], объясняющих такой феномен инерционностью мембранных каналов именно входящего тока, активируемых деполяризацией, или А. Гутмана [22], объясняющего феномен Ш-К ВАХ мембраны нейрона, нами предложено объяснение этого явления, основанное на гистерезисе не мембраны, а логических свойств нейрона. Таким образом, можно говорить об особом виде гистерезисной логики [23].

3. Заключение. XIX-XX века открыли путь логики в математику, являющейся до этих пор преимущественно лишь уделом философов и схоластов. Б. Рассел поистине пророчески писал: «Тот факт, что вся математика есть не что иное, как символическая логика – величайшее открытие нашего века» [24]. Это имело грандиозные последствия. Именно логическому обоснованию математики и выразимости математических операций и объектов средствами логики мы обязаны возникновению и развитию компьютерной техники и автоматизации вычислений вообще [25]. Однако, логики, лежащие в основе современной математики, весьма примитивны даже в смысле моделирования естественных рассуждений. Этот факт неизбежно присутствует во всей математике, что ограничивает ее применимость, в том числе, к воспроизведению свойств природных объектов, в том числе, биологических. Как показывают наши исследования, логика биологических объектов является логикой «третьего уровня», поскольку представляет собой иной более сложный уровень по сравнению с логикой социальных взаимодействий. Эту логику можно назвать логикой «второго уровня», однако, даже ни она, ни ее элементы не используются в существующих системах математической логики, несмотря на явно выраженную потребность в развитии технических устройств от индивидуальных к социальным. Логики, представляющие на сегодняшний день фундамент современной математики по нашей классификации можно считать логиками «первого уровня» или же определить их как «индивидуальные» логики. Таким образом, исследование биологических объектов на предмет их логической организации может дать прогресс не только в области их моделирования, но и для реконструкции самого математического аппарата [26].


Список литературы

1. Круглов В.В., Дли М.И., Голунов П.У. Fuzzy-logic и искусственные нейронные сети. М., 2001.
   
2. Zadeh L.A. Quantitative Fuzzy Semantics // Inform. Sciences. 1970. № 3. Р. 0000-0176.
   
3. McCulloch W.S., Pitts W.H. Bull. Math. Biophysics. 1943. № 5. Р. 115-133.
   
4. Савельев А.В. Нейрокомпьютеры в изобретениях // Нейрокомпьютеры: разработка и применение. 2004. № 2-3. С. 33-49.
   
5. Ильясов Б.Г., Савельев А.В., Колесников А.А. Логический нейроподобный элемент. А. с. № 1645975 // Бюлл. № 16. 1991.
   
6. Савельева Н.А., Савельев А.В. Устройство для моделирования мотонейрона. А. с. № 1324044 // Бюлл. № 26. 1987.
   
7. Савельев А.В. Самоорганизационная нейрологика // Моделирование неравновесных систем. 2004.
   
8. Swanson L.W. Neuropeptides – new vistas on synaptic transmission // Trends in NeuroSciences. 1983. Vol. 6. № 8. Р. 294-295.
   
9. The Brain. Scientific American, Sep., 1979.
   
10. Савельев А.В., Савельева Н.А., Колесников А.А., Жуков А.Г. Устройство для моделирования нейрона. А. с. № 1645973 // Бюлл. 16. 1991.
    
11. Межецкая Т.А., Савельева Н.А., Савельев А.В., Колесников А.А. Устройство для моделирования нейрона Пуркинье. А.с. № 1497626 // Бюлл. 18. 1989.
    
12. Савельев А.В. Коллизионная нейрологика парадоксов // В сб. материалов III Всеcсибирского конгресса женщин-математиков. Красноярск: КГТУ, 2003.
    
13. Савельев А.В. Устройство для моделирования нейрона. А. с. № 1292494 // 1987.
    
14. Газутдинов И.Ф., Лакомкин И.М., Савельев А.В., Сергеев Н.А. Устройство для моделирования нейрона. А. с. № 1564654 // Бюлл. № 18. 1990
    
15. Савельев А.В. Образование упорядоченных структур в синаптической щели электрического синапса // Журнал проблем эволюции открытых систем, Казахстан, Алматы. 2003. № 1.
    
16. Коган А.Б. Функциональная организация нейронных механизмов мозга. М.: Медицина, 1979. 224 с.
    
17. Базарова Д.Р., Демочкина Л.В., Савельев А.В. Новая нейробионическая модель онтогенеза // Нейроинформатика-2002. 2002. Т. 1. С. 97-106.
    
18. Ильясов Б.Г., Савельев А.В., Колесников А.А. Устройство для моделирования мотонейронов. А. с. № 1585810 // Бюлл. № 30. 1990.
    
19. Жуков А.Г., Савельева Н.А., Савельев А.В. Устройство для моделирования нейрона. А. с. № 1672482 // Бюлл. № 31. 1991.
    
20. Schwindt P., Crill W.E. Factors influencing motoneuron rhythmic firing: result from a voltage-clamp study // J. Neurophysiol. 1982. V. 48. Р. 873-890.
    
21. Савельева Н.А., Савельев А.В. Устройство для моделирования нейрона. А. с. № 1436720 // 1988.
    
22. Гутман А., Свирскис Г. Теоретический анализ поляризации омического нейрона, наведённой полем постоянного тока // Биофизика. 1995. Т. 40. Вып. 3.
    
23. Савельев А.В. Хаотические режимы в нейронах и нейросетях // Моделирование неравновесных систем. 2004.
    
24. Russell В. The Principles of Mathematics, George Allen & Unwin, London, 1903.
    
25. Lomova J.J., Savelyev A.V. Pythagorean syndrome and numerical nature of information // в сб. тр. I Всесибир. Конгресса женщин-математиков, Красноярск, 2000. С. 123-124.
    
26. Savelyev A.V. Neuronic logic // Paper in CSIT’2003 Proceedings, Ufa, usatu. 2003. Vol. 3. Р. 57-64.