Гоувпо уфимский государственный авиационный технический университет Кафедра информатики
| Вид материала | Документы |
- А. В. Репин Уфимский государственный авиационный технический университет, Уфа e-mail:, 31.84kb.
- Уфимский Государственный Авиационный Технический Университет Кафедра вмиК отчет, 188.41kb.
- Тимирханов валентин Рахимович моделирование лингвофилософских явлений в свете имяславской, 773.94kb.
- "Философские науки", 789.13kb.
- Экономические интересы государства как акционера, 409.15kb.
- Уфимский государственный авиационный технический университет, 137.84kb.
- Разработка устройств для измерения сверхслабых полей естественного излучения, 793.23kb.
- Совершенствование инструментария управления реализацией федеральных целевых программ, 377.01kb.
- Практическом освоении студентами научно-теоретических положений изучаемой дисциплины, 110.46kb.
- А. В. Савельев Уфимский государственный авиационный технический университет, 128.55kb.
ГОУВПО
Уфимский государственный авиационный технический университет
Кафедра информатики
| 100 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 90 | | | | | | | | | | | | |
| 80 | | | | | | | | | | | | |
| 70 | | | | | | | | | | | | |
| 60 | | | | | | | | | | | | |
| 50 | | | | | | | | | | | | |
| 40 | | | | | | | | | | | | |
| 30 | | | | | | | | | | | | |
| 20 | | | | | | | | | | | | |
| 10 | | | | | | | | | | | | |
| | | | | | | | | | | | | |
| Моделирование и анализ работы электронных схем |
| |
| |
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
| к курсовой работе по | КТвНиП |
| 1308.327353.000ПЗ |
| (обозначение документа) |
| Группа | | | Фамилия, И., О. | Подпись | Дата | Оценка |
| АП-529М | | |||||
| | | |||||
| Студент | Пятков П.А. | | | | ||
| Консультант | Минасова Н. С. | | | | ||
| Принял | Минасова Н. С. | | | | ||
Уфа 2011 г
Содержание
Моделирование и анализ работы электронных схем 3
Введение 4
1 Постановка задачи 5
2 Проектирование системы 7
3 Средства и приемы программирования 17
4 Реализация системы 18
5 Описание пользовательского интерфейса 31
Заключение 36
Список используемой литературы: 37
Приложение А 38
Приложение Б 51
Приложение В 53
Введение
Повышение требований к функциональности и надежности бортовых энергетических комплексов обуславливает широкое использование новых информационных технологий, способных объединять все стадии разработки и производства в единый виртуальный процесс проектирования изделий, который оперирует с общей, полностью цифровой, моделью. Такая информационная среда позволяет разрабатывать многовариантные конфигурации изделий на стадии концептуального проектирования, интегрировать все этапы рабочего проектирования, моделировать и тестировать основные фазы производственного процесса, начиная с гибких автоматизированных участков изготовления комплектующих изделий и кончая сборкой компонент и созданием прототипа. При этом необходимо комплексно учитывать внутренние и внешние факторы, влияющие на тепловую и электрическую стойкость силовых приборов.
1Постановка задачи
К числу основных внутренних факторов относятся особенности структурных и функциональных принципов построения силовых комбинированных МОП – биполярных коммутирующих устройств. В связи с этим выявлены наиболее важные паразитные элементы структуры силовой ячейки MOSFET транзистора и двух основных структур IGBT транзистора: NPT-структуры и РТ-структуры. Установлено влияние внутренних сопротивлений и емкостей, а также паразитных n-p-n транзистора на область безопасной работы исследуемых классов силовых приборов. Кроме того, установлено, что в интегральной структуре МОП – биполярных транзисторов может сформироваться p-n-р транзистор, включающий следующую последовательность слоев: р+ - коллектор (эмиттер) / n – дрейфовая зона (база) / р+ - ячейка (коллектор), которые представляют вместе с n-p-n транзистором также и тиристорную цепь.
В свою очередь, внешние факторы, определяющие разброс характеристик и нестабильность рабочих режимов работы энергетических комплексов, связаны с используемыми конструктивно-технологическими решениями, влияющими на то, в какой степени разброс параметров силовых приборов сказывается на стабильности характеристик всего комплекса. Для оценки влияния внешних факторов предлагается процедура, включающая два взаимосвязанных этапа: анализ влияния топологии схемы при заданном диапазоне изменения параметров силовых приборов и оценку воздействия величины разброса параметров силовых приборов применительно к выбранной конфигурации (топологии) энергетического комплекса.
Особое место в анализе схемотехнических и конструктивных факторов, влияющих на стабильность характеристик силовых коммутирующих устройств, занимают интеллектуальные силовые модули, конструктивные особенности которых обеспечивают минимальные значения переходных тепловых сопротивлений и распределенных индуктивностей силовых шин в сочетании с высоким напряжением изоляции, что в сумме гарантирует стабильность их характеристик.
Проведенный анализ внутренних и внешних факторов, определяющих область безопасной работы энергетических комплексов, позволил разработать эффективную вычислительную процедуру, используемую при исследовании чувствительности временных характеристик энергетических комплексов применительно к динамическому режиму работы последних в случае значительного числа учитываемых варьируемых параметров. Указанная вычислительная процедура базируется на принципах структурно-топологического анализа основных конструктивных вариантов энергетических комплексов с использованием универсальных физических моделей их элементов в приращениях.
2Проектирование системы
2.1Построение функциональной модели
На рисунке 2.1.1 представлена функциональная схема системы.
Входными данными являются тип элементов электронной схемы и величина изменения температуры. На выходе программы получаем величину изменения токов в ветвях схемы.
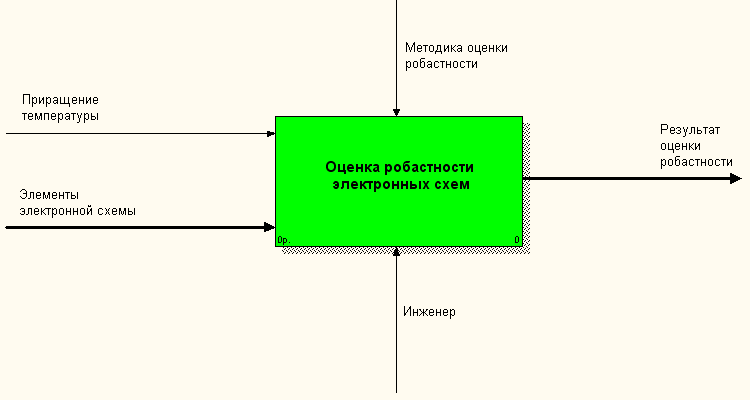
Рисунок 2.1.1 - Функциональная схема системы
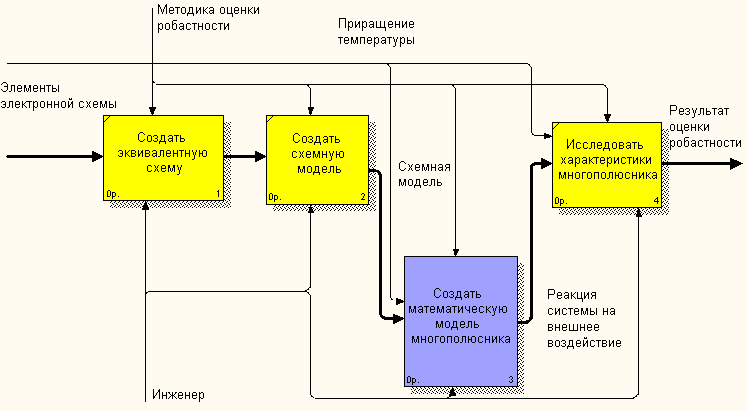
Рисунок 2.1.2 - Первый уровень декомпозиции
На рисунке 2.1.2 представлен первый уровень декомпозиции системы. На первом этапе создается эквивалентная схема в приращениях. Далее система описывается при помощи системы уравнений, которая записана в виде матрицы. Элементами матрицы являются эквивалентные сопротивления элементов схемы, вычисленные с учетом изменения условий внешней среды.
2.2Построение структурно-функциональной модели
На рисунке 2.2.1 представлена структурно-функциональная модель системы.
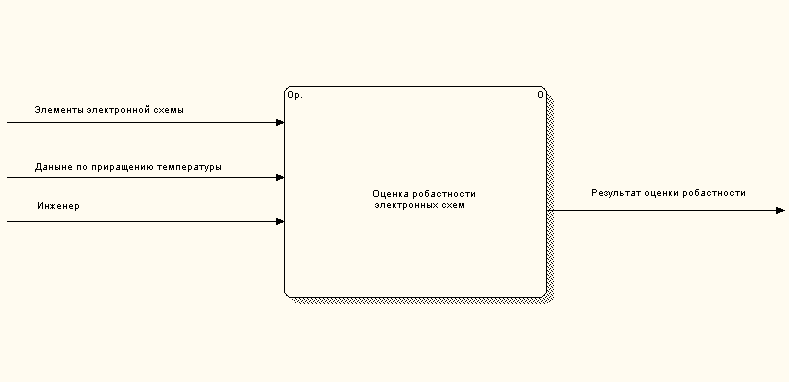
Рисунок 2,2,1 - Исходная контекстная диаграмма
На рисунке 2.2.2 представлен первый уровень декомпозиции структурно-функциональной модели.
Из базы данных берется информация о параметрах элементов. При построении эквивалентной схемы учитывается изменение температуры окружающей среды. На основании решения уравнений, полученных при создании математической делается вывод о воздействии внешних условий на работу схемы и эта информация заносится в базу данных результатов расчета.
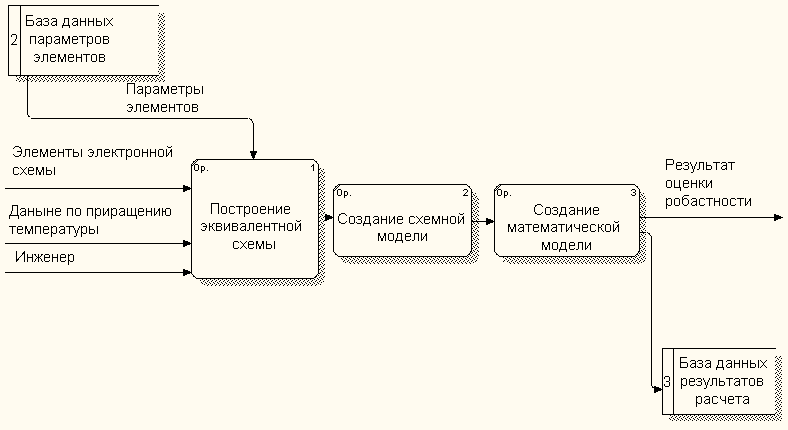
Рисунок 2.2.2 - Результат декомпозиции контекстной диаграммы
2.3Описание математической модели
Считаем, что исходная модель исследуемого устройства представлена его эквивалентной схемой в виде электрического многополюсника. Поскольку на этапе схемотехнического проектирования математические модели БИВС формируются для определенного базового набора элементов, рассмотрим в качестве такого набора универсальную совокупность. Она включает в себя: линейный и нелинейный резистор, линейную и нелинейную емкость, линейную и нелинейную индуктивность, независимые источники тока и напряжения, зависимые (управляемые) источники - источник тока, управляемый током или напряжением, и источник напряжения, управляемый напряжением или током.
Естественным и простым путем для описания информации является изображение направленного графа, соответствующего данной схеме. Для того чтобы компактно выразить уравнения второго закона Кирхгофа в виде единственного матричного уравнения, необходимо ввести матрицу контуров Ва, соответствующую направленному графу схемы.
Хотя направленный граф полностью описывается соединениями и опорными направлениями ветвей сложной схемы, эта форма выражения неудобна для записи в программу ЭВМ. Для записи в цифровом виде наиболее удобно представление информации в виде матриц.
Для того чтобы компактно выразить уравнения второго закона Кирхгофа в виде единственного матричного уравнения, необходимо ввести матрицу контуров Ва, соответствующую направленному графу схемы.
Для направленного графа с n ветвями и nn ориентированными контурами матрица контуров будет
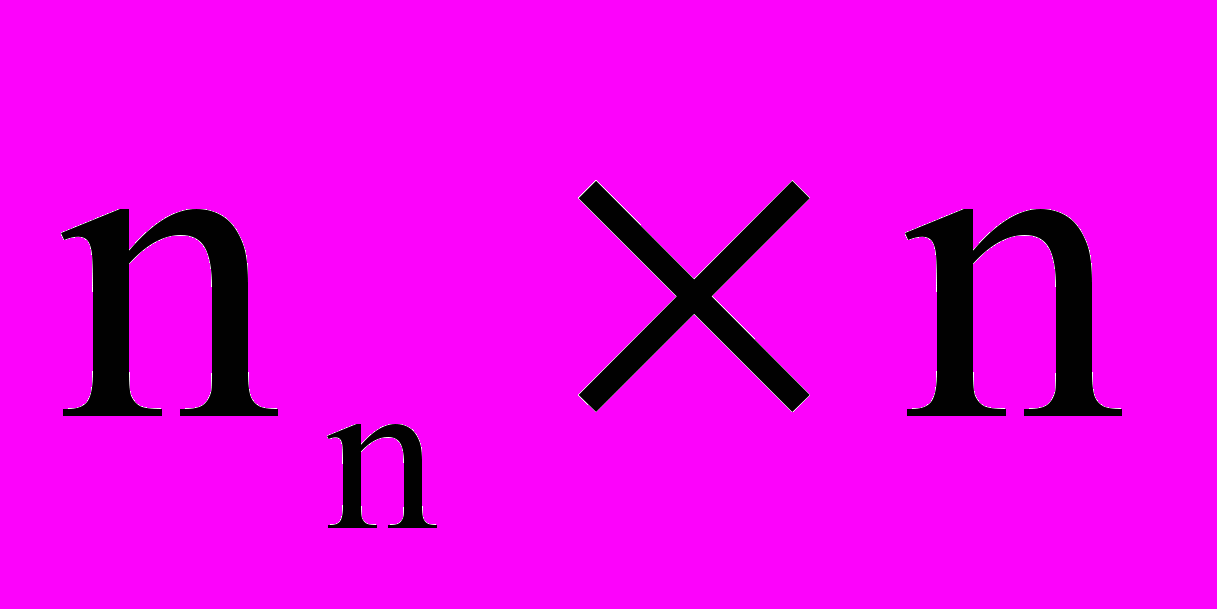 матрицей:
матрицей: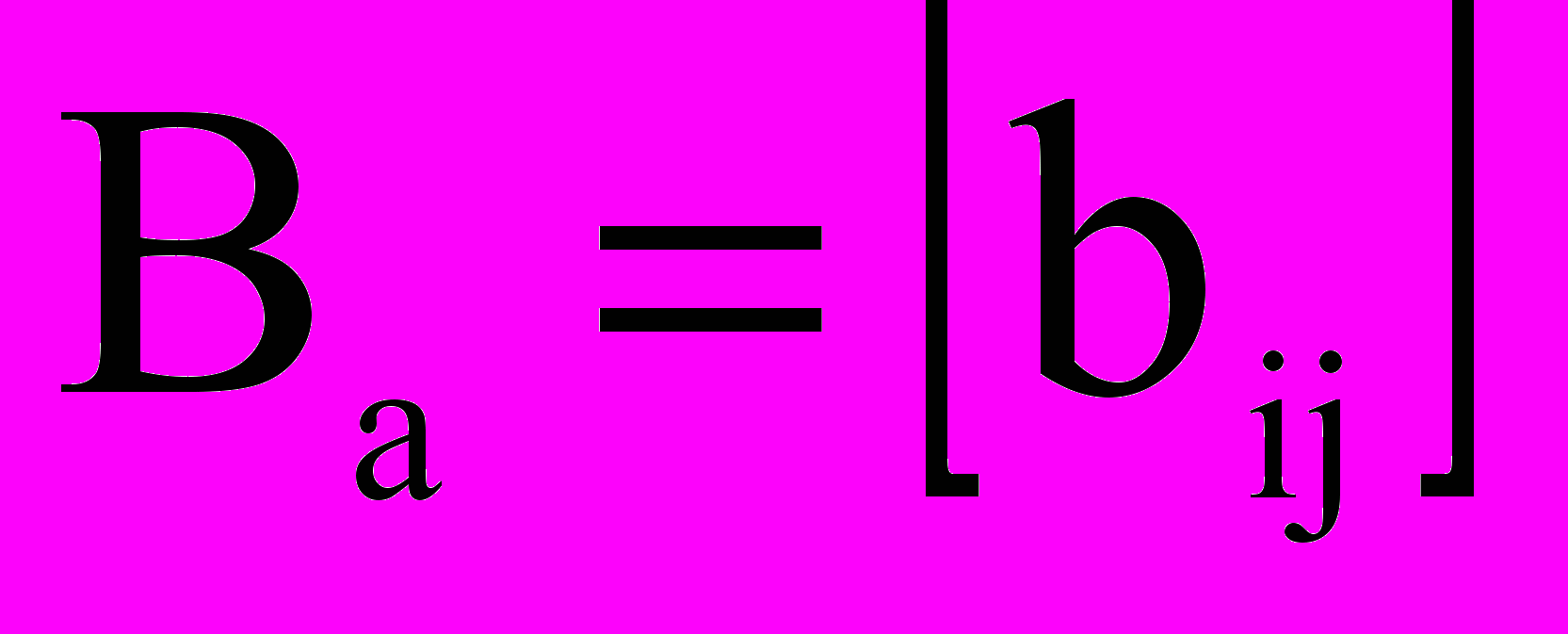 (1)
(1)где
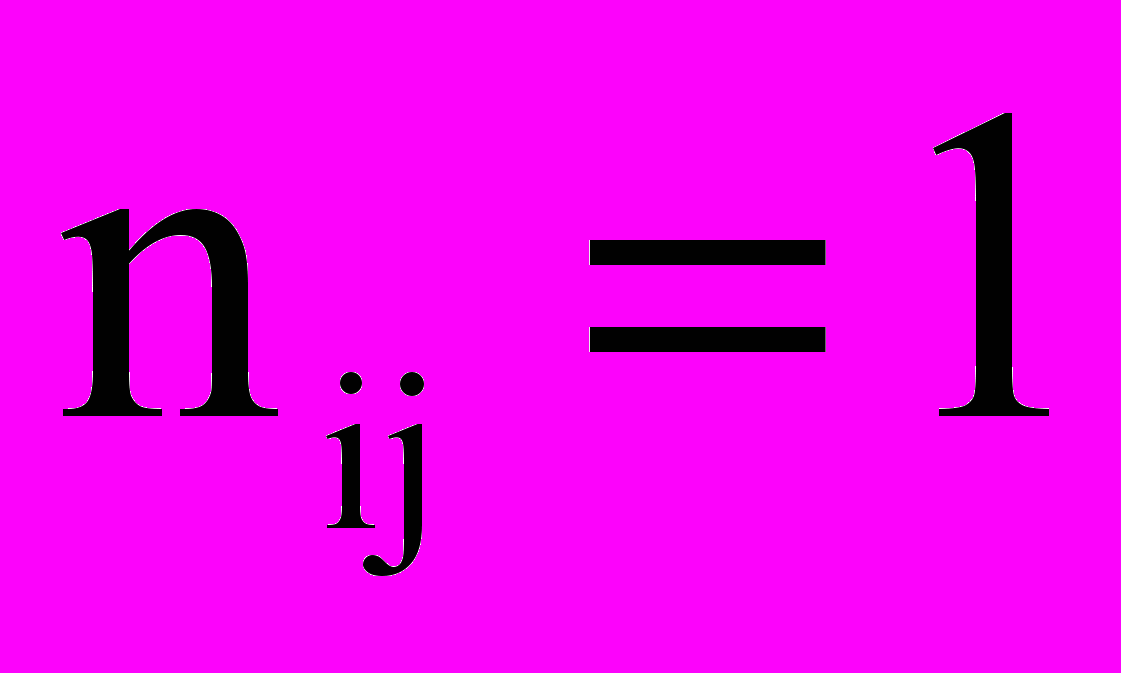 , если ветвь j входит в контур i и их направление одинаково;
, если ветвь j входит в контур i и их направление одинаково;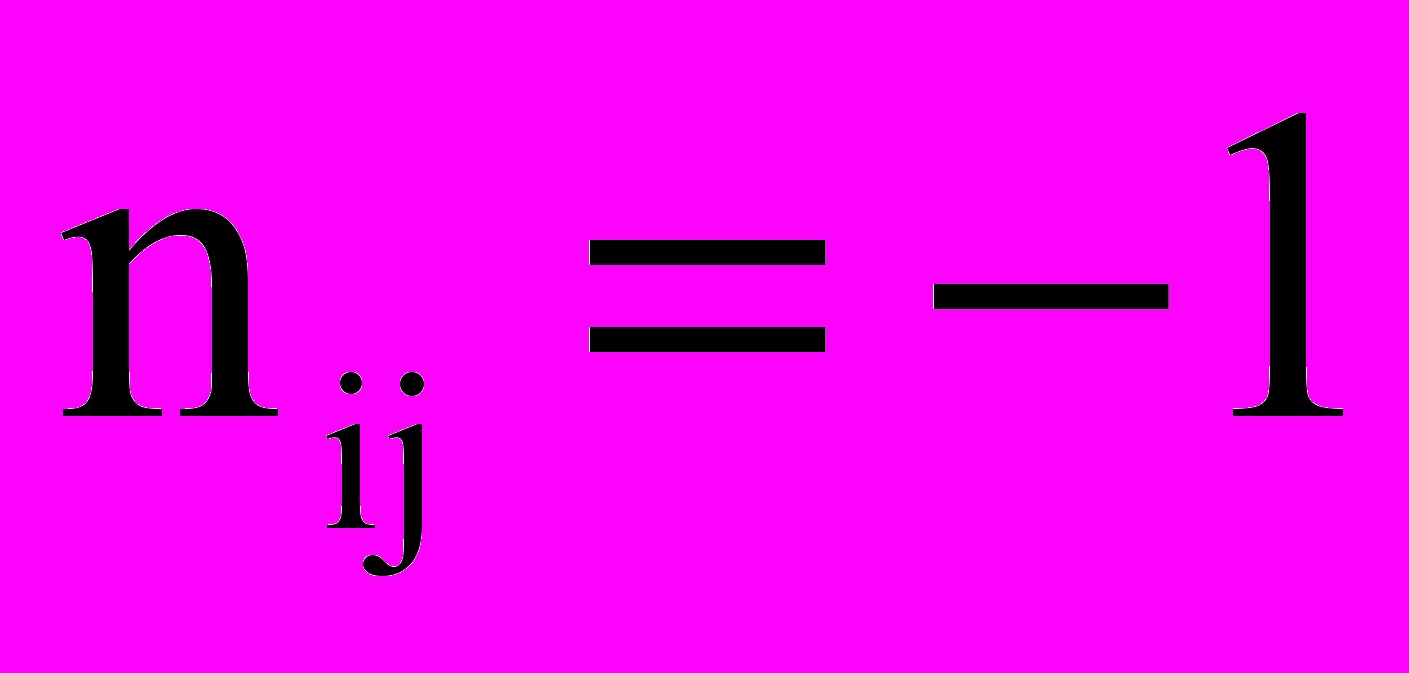 , если ветвь j входит в контур i и их направление
, если ветвь j входит в контур i и их направление противоположно;
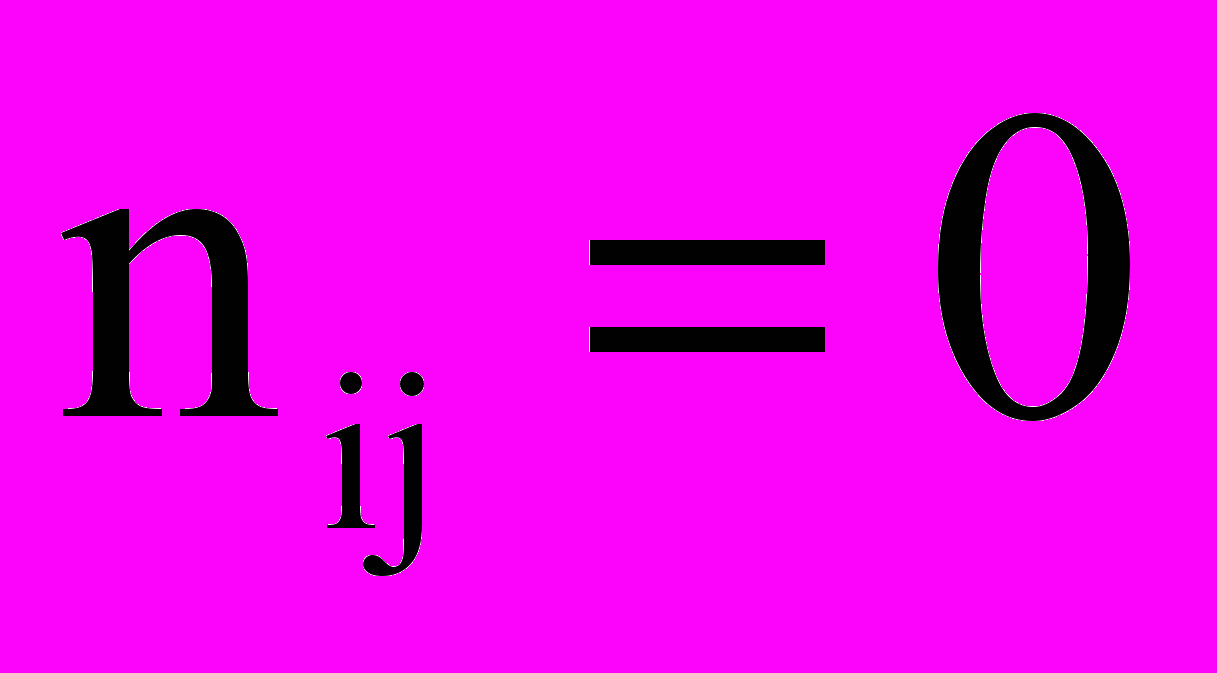 , если ветвь j не входит в контур i.
, если ветвь j не входит в контур i.Рассмотрим многополюсник, содержащий n ветвей и k узлов, тогда максимальное число неизвестных переменных составляет 2n – ток и напряжение на каждой ветви.
Обобщенная математическая модель многополюсника будет состоять из n топологических и n параметрических уравнений. Действительно, топологические уравнения:
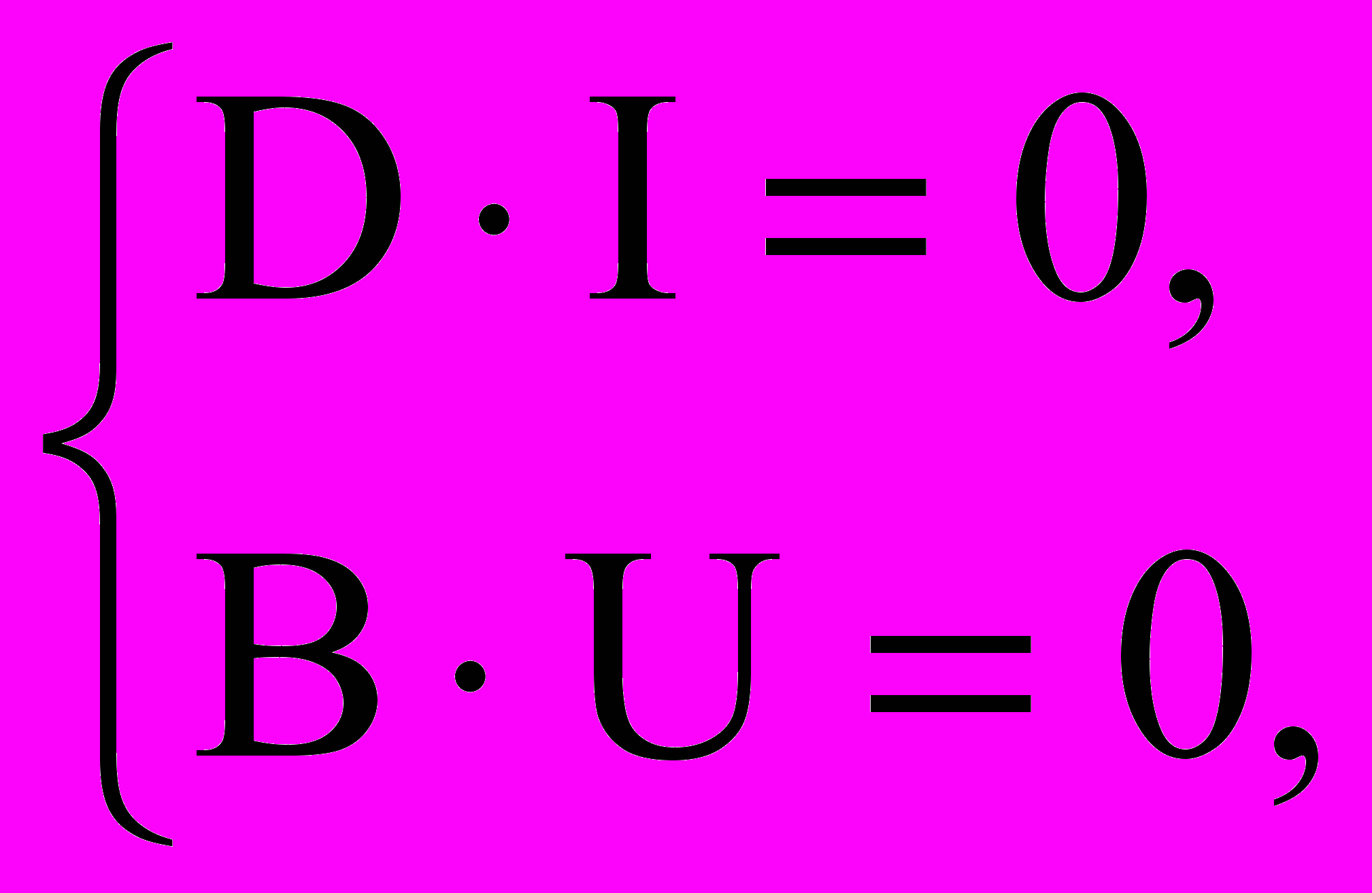 (2)
(2)где D – матрица главных сечений (k-1) уравнений;
В – матрица главных контуров (n-k+1) уравнений.
А также n параметрических уравнений, полученных ранее для всех видов ветвей. Например, для резистивных ветвей параметрические уравнения имеют вид:
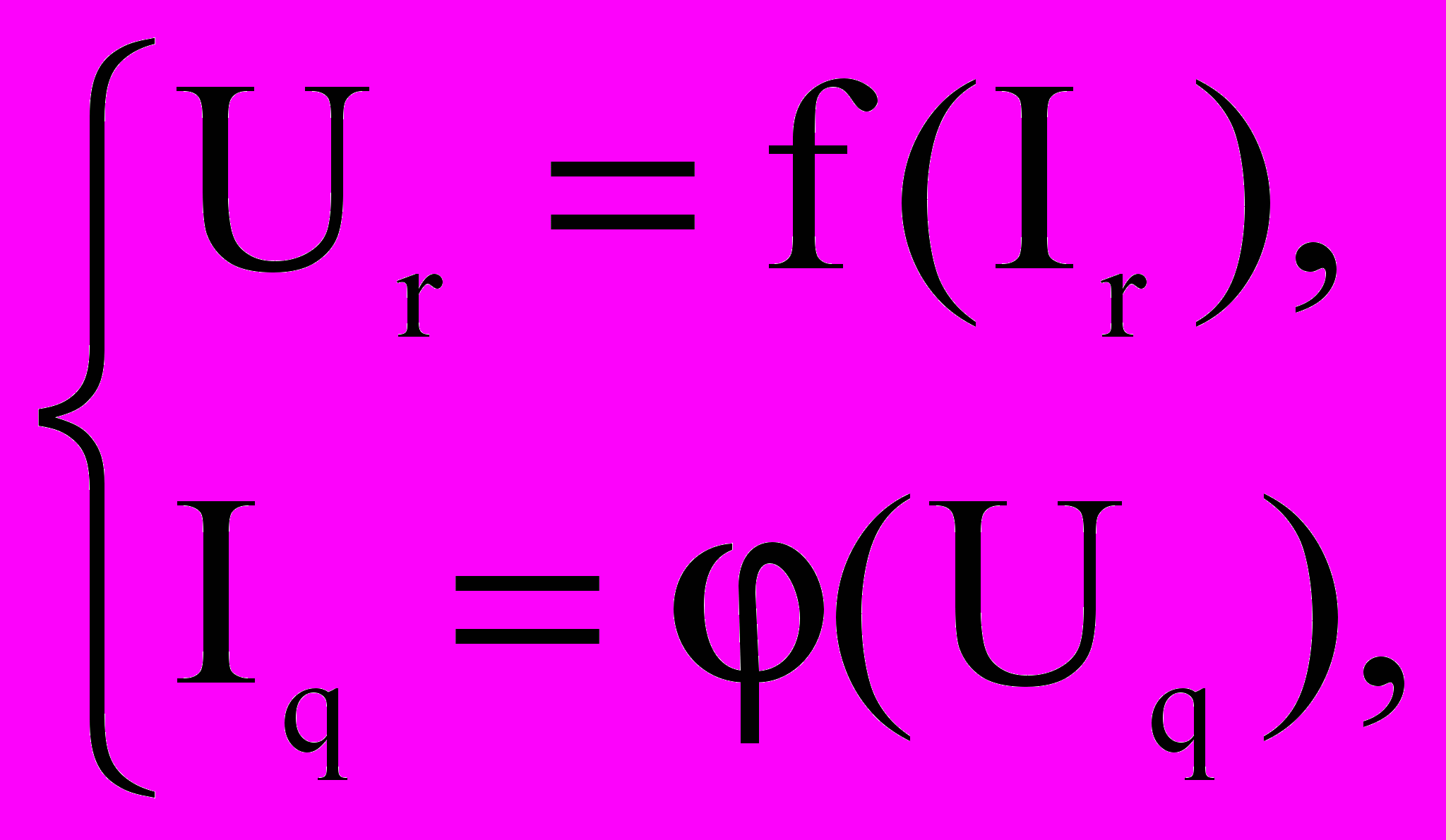 (3)
(3)где r=1,2,…,nz – для z – ветвей;
q=1,2,…,ny – для у – ветвей (
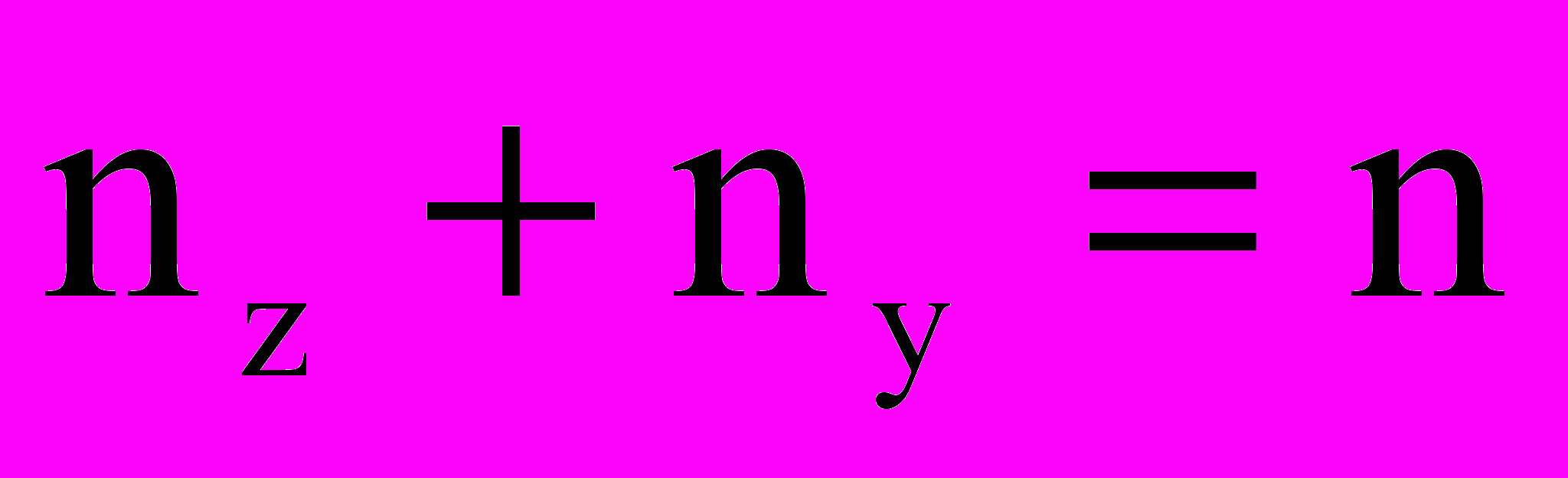 ).
).Таким образом, модель в полноразмерном гибридном базисе будет включать в себя 2n уравнений с 2n неизвестными.
Поскольку топология многополюсника для номинального и возмущенного режимов остается неизменной, то можно записать:
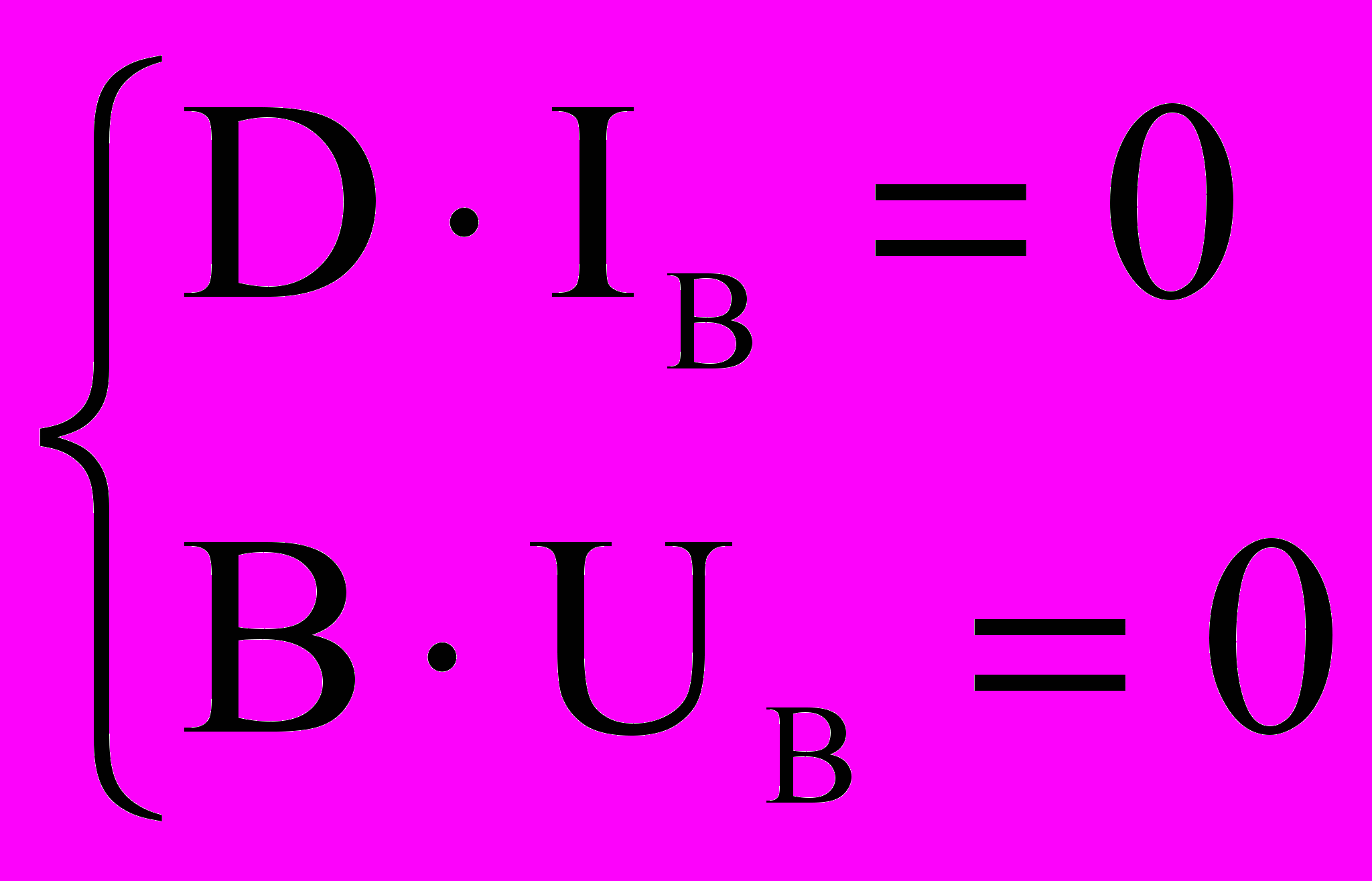 (для возмущенного режима) (4)
(для возмущенного режима) (4)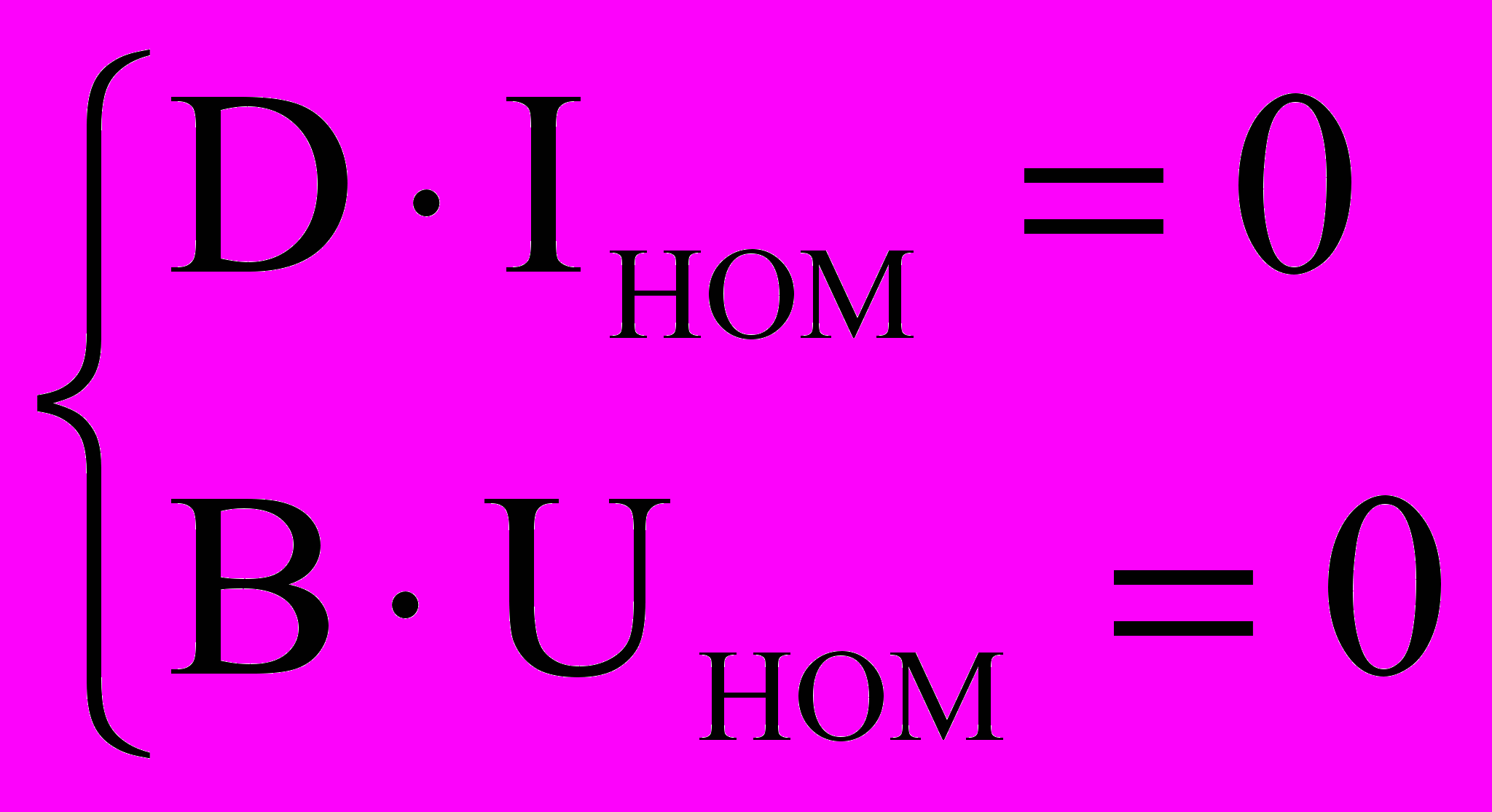 (для номинального режима) (5)
(для номинального режима) (5)Вычитая почленно уравнение (2.47) из (2.46), получим:
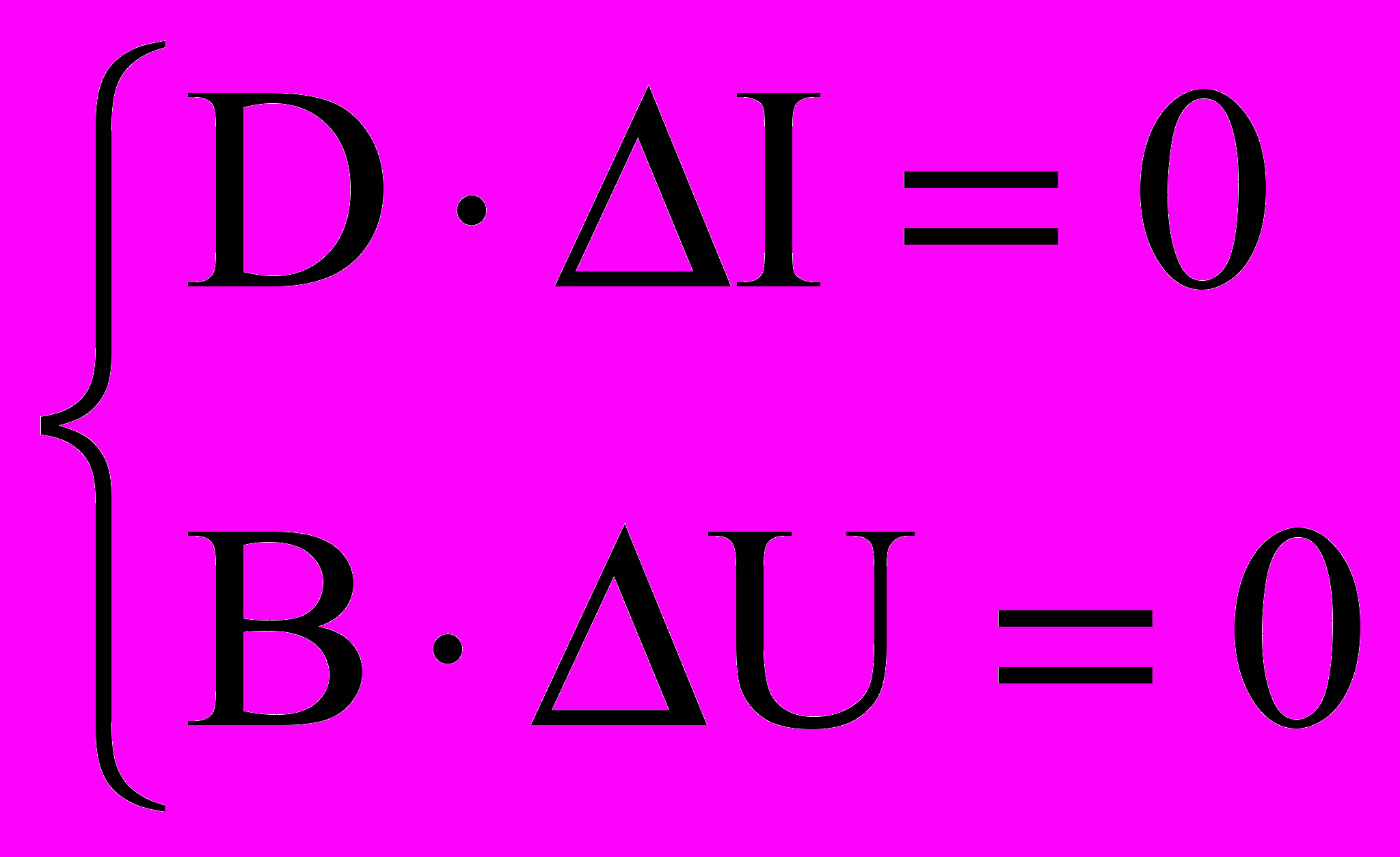 (6)
(6)Проведем декомпозицию ветвей, т.е. выделим особые ветви, к которым отнесем реактивные и нелинейные ветви. А все остальные отнесем к резистивным z и y ветвям. Тогда можно записать декомпозированную форму для векторов приращений токов и напряжений:
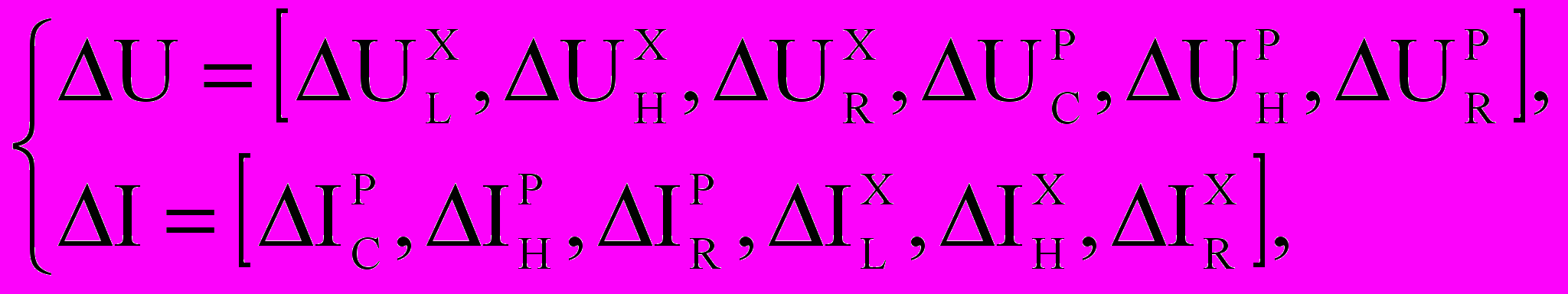 (7)
(7)где ,
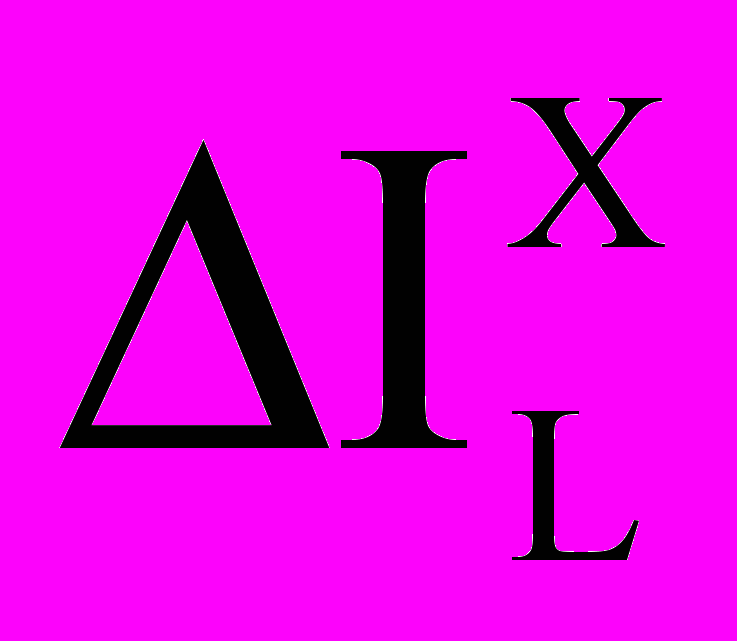 – приращения напряжений и токов на индуктивных
– приращения напряжений и токов на индуктивных хордах;
,
 – приращения напряжения и тока на емкостных ребрах;
– приращения напряжения и тока на емкостных ребрах;,
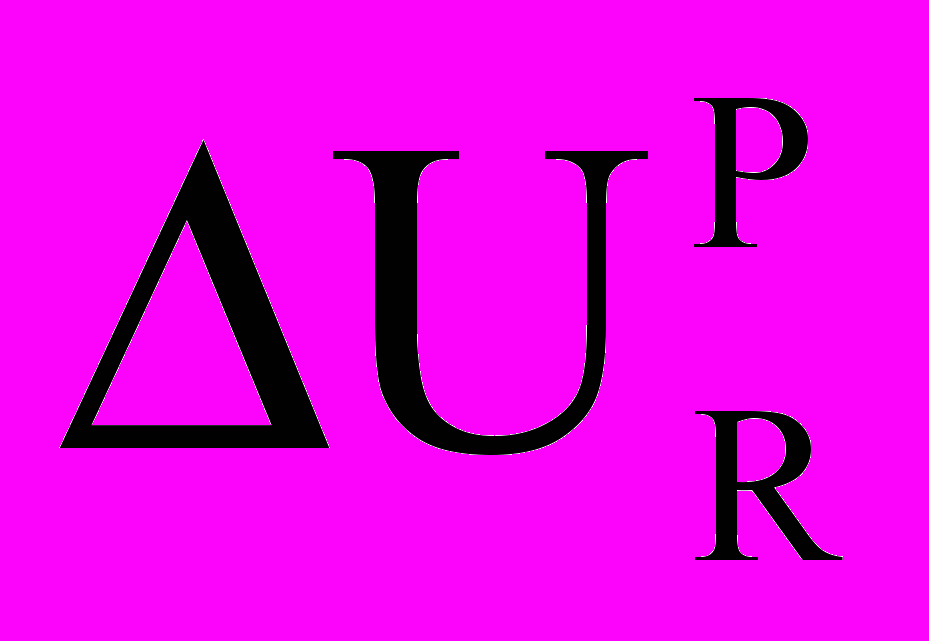 ,
,  ,
, 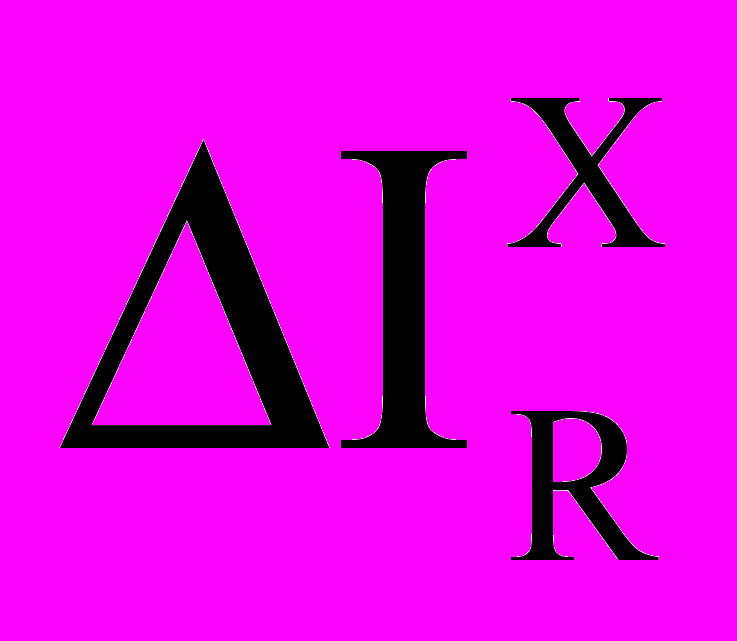 - приращения напряжения и тока на
- приращения напряжения и тока на резистивных ребрах и хордах;
,
 ,
,  ,
, 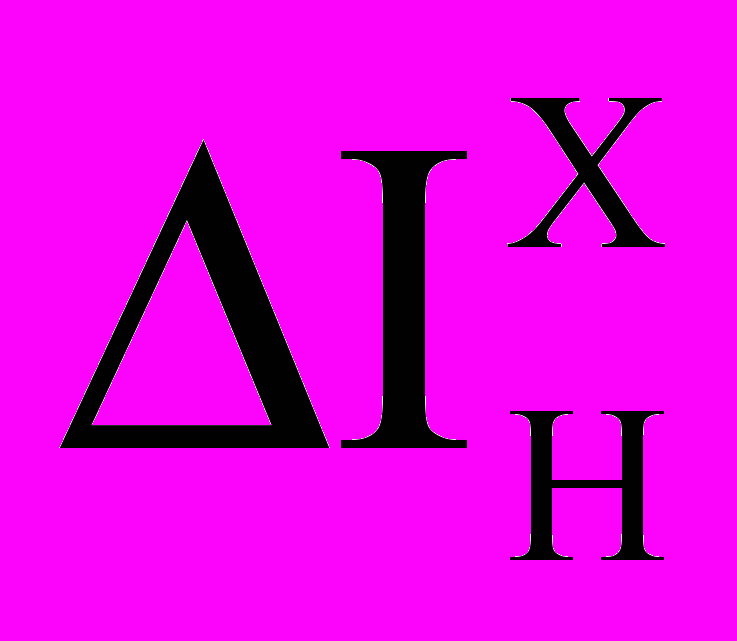 - приращения напряжения и тока на
- приращения напряжения и тока на нелинейных ребрах и хордах.
Используя (6), запишем первое уравнение системы (4) в следующем виде:
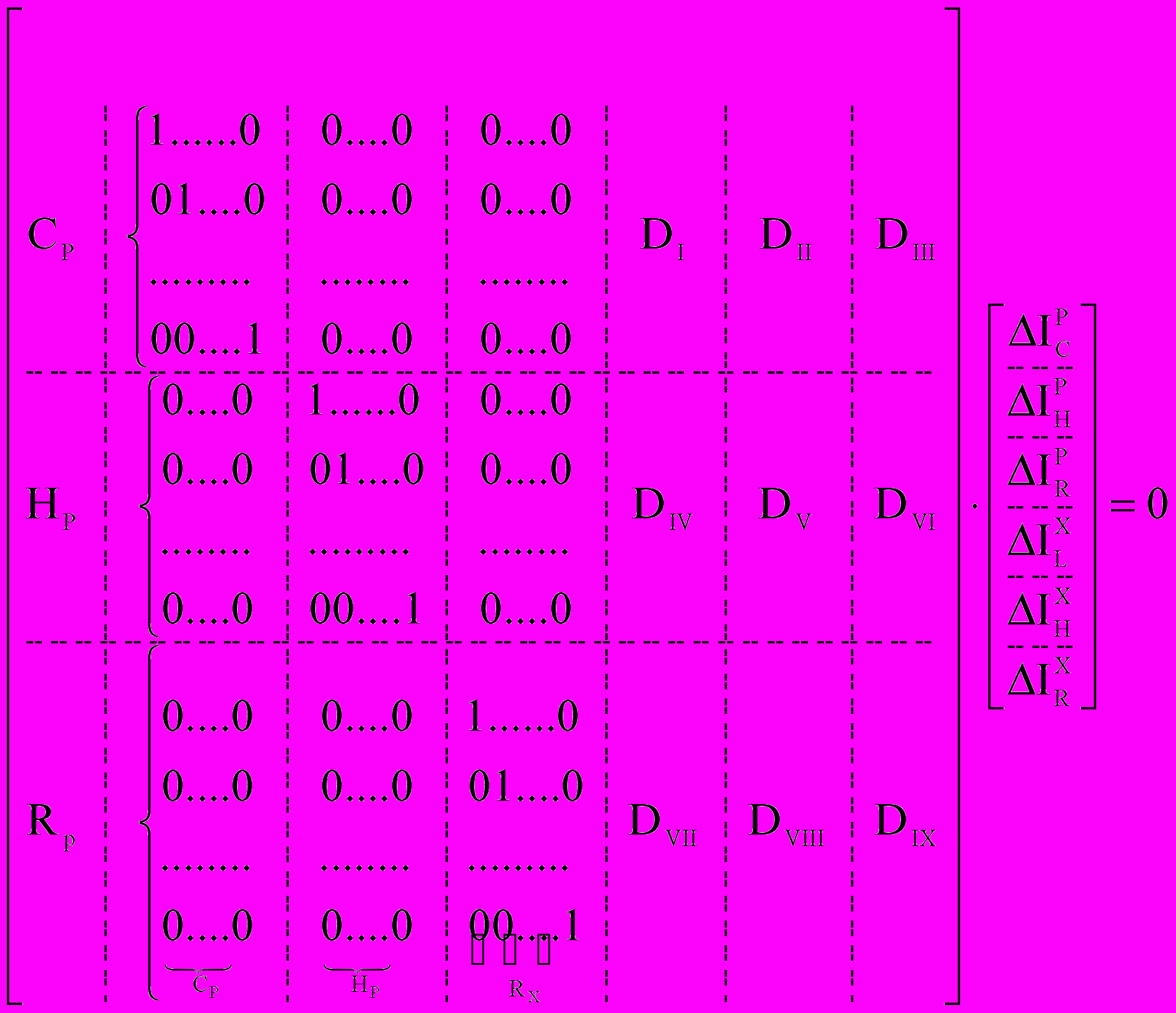 (8)
(8)Либо:
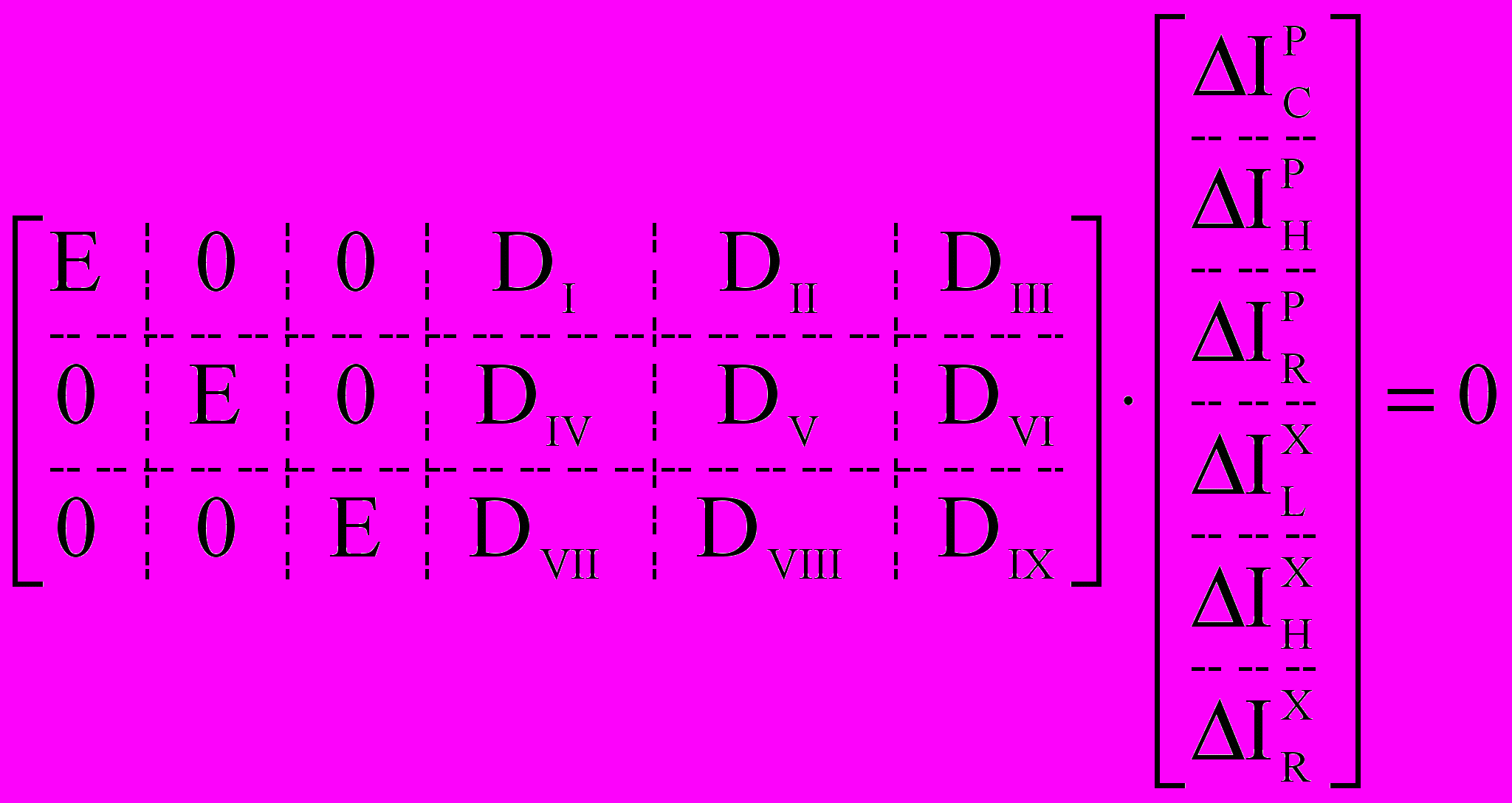 (9)
(9)где Е – единичная матрица.
Выражение (8) можно переписать в другой форме:
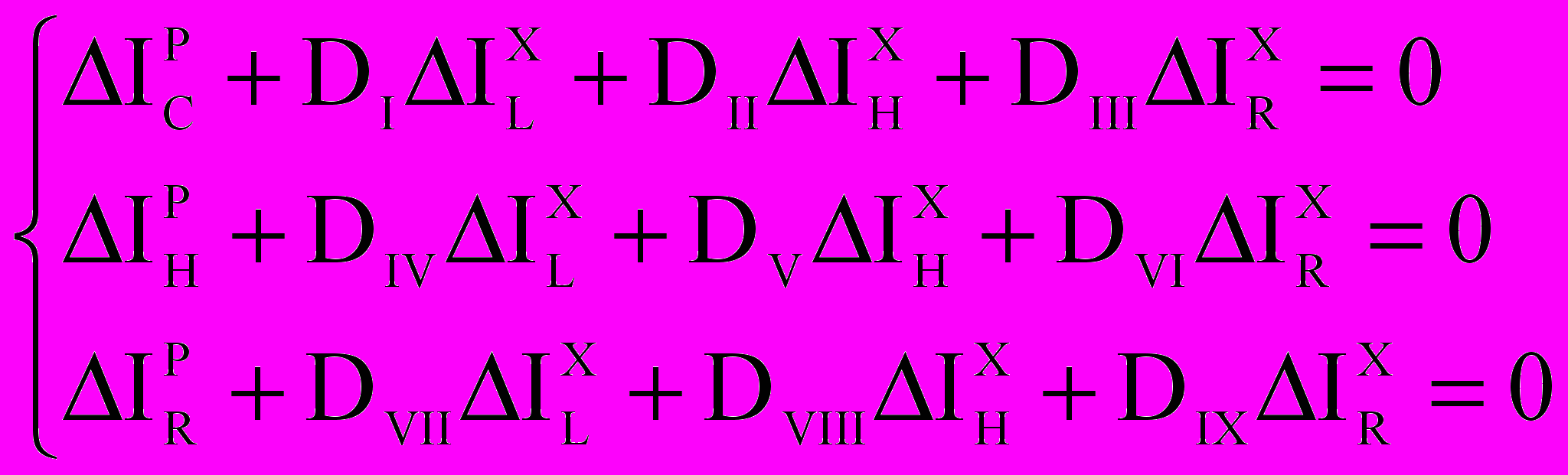 (10)
(10)Разрешим систему уравнений (10) относительно приращений токов на емкостных, нелинейных и резистивных ребрах:
 (11)
(11)Применяя аналогичные рассуждения о декомпозиции системы топологических уравнений, для второго уравнения системы (11), получим:
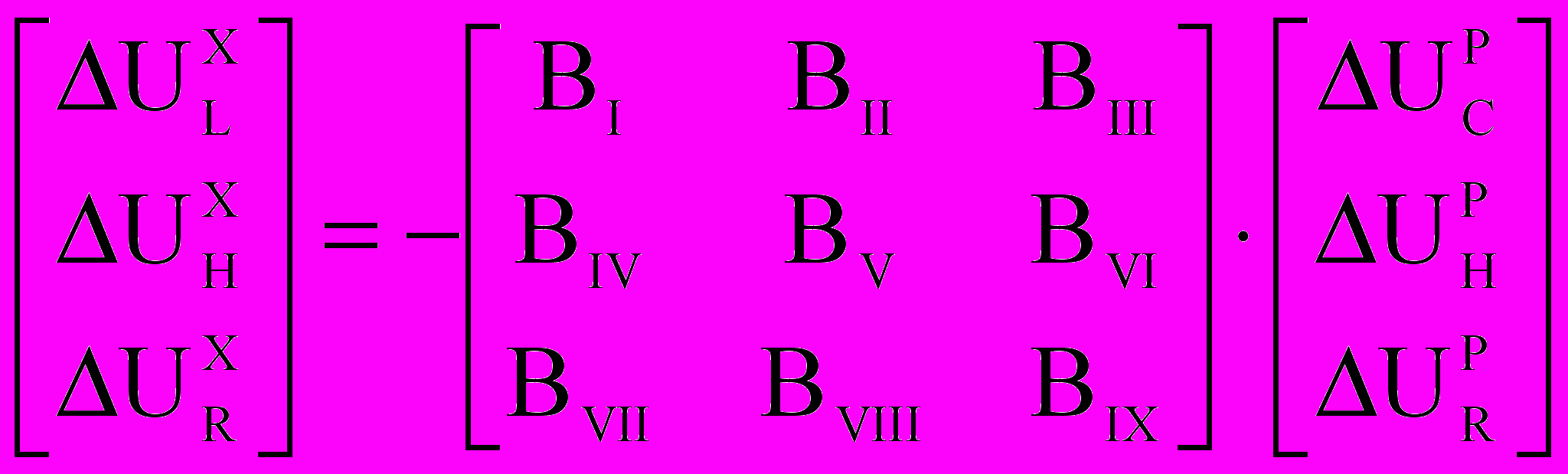 . (12)
. (12)Сформируем из (11) и (12) три группы уравнений в гибридном базисе:
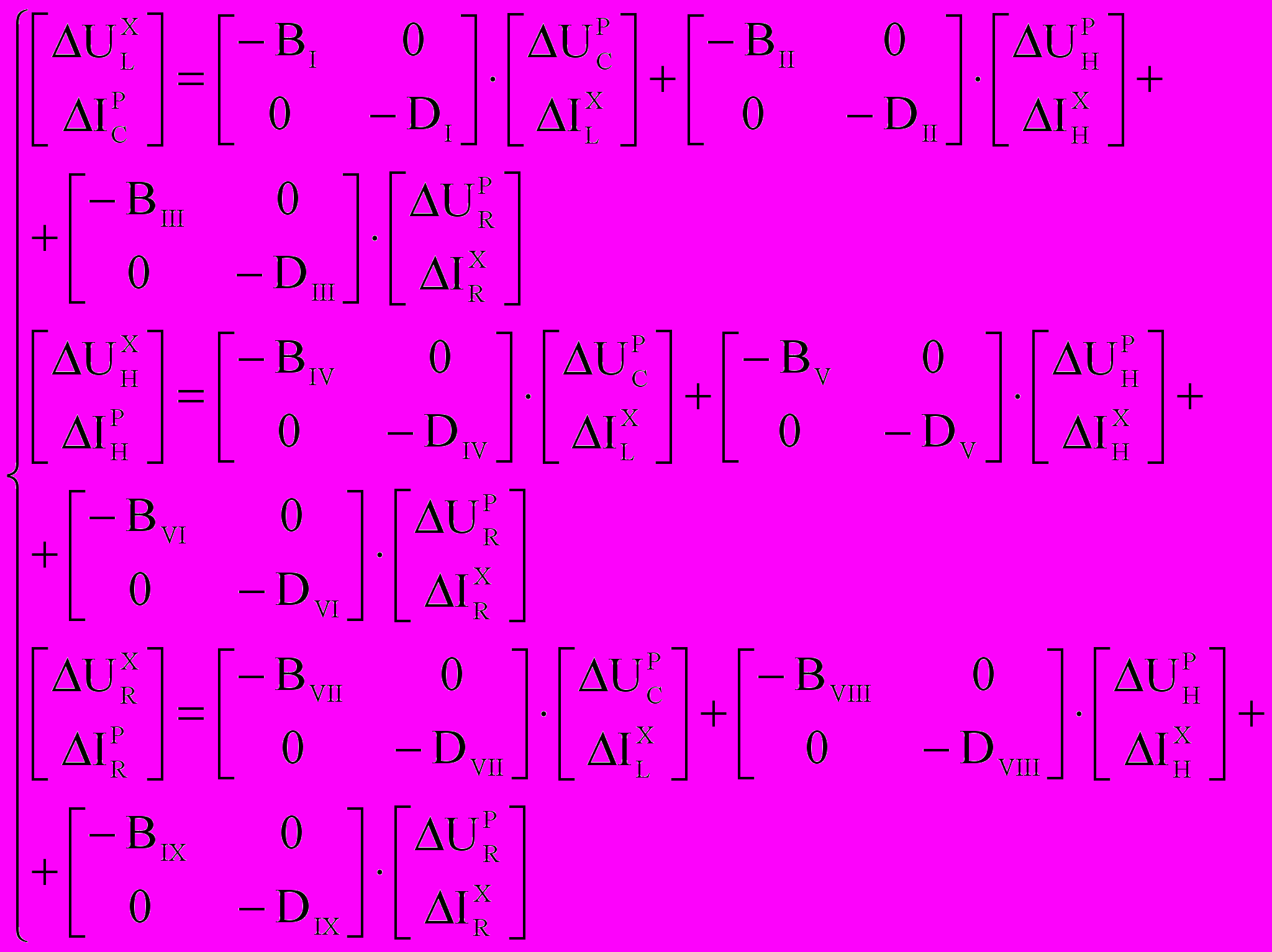 (13)
(13)Используя полученные уравнения можно исследовать робастность электронных схем практически любой сложности.
3Средства и приемы программирования
При разработке данной программы использовались следующие компоненты:
TForm, TLabel, TChart, TMainMenu, TEdit, TButton, TStringGrid, TGroupBox, TPaintBox, TSaveDialog, TImage.
Для ввода параметров схемы используется компонент TEdit. Значения введенных пользователем параметров элементов заносятся в соответствующий массив.
Для выбора типов элементов используются компоненты TGroupBox и TRadioButton. В каждом поле GroupBox можно расположить несколько кнопок выбора RadioButton. Это делает возможным выбор различных видов элементов для каждого типа элемента. Значения типов элементов заносятся в соответствующий массив.
Для передачи массива типов элементов и массива значений эквивалентных сопротивлений элементов на следующую форму используются компоненты TStringGrid.
Так информация об этих массивах пользователя не интересует, то для свойства Visible компонента TStringGrid установлено значение false.
Для отображения выбранной пользователем схемы используется компонент TPaintBox, на котором при помощи функций LineTo и MoveTo рисуется выбранная схема. Для рисовании схемы также были созданы процедуры рисования отдельных элементов, таких как конденсаторы, резисторы, индуктивности и источники ЭДС.
Для визуализации результатов анализа схемы используется компонент TChart, на котором отображаются графики зависимости токов от изменения температуры окружающей среды.
4Реализация системы
4.1Обоснование и выбор средства программирования
Для написания программного средства была выбрана среда С++ Builder, которая предоставляет широкие возможности для реализации подобного рода задач
Достоинством данной среды является то, что в ней реализована идея подлинно визуальной разработки программ. Интегрированная среда системы (Integrated Development Environment, IDE) обеспечивает продуктивность многократного использования визуальных компонентов в сочетании с усовершенствованными инструментами и разномасштабными средствами доступа к базам данных. Основное предназначение IDE – радикально ускорит производительный цикл разработки сложнейших программных проектов для различных областей применения.
Профессиональные средства языка C++ интегрированы в визуальную среду разработки. C++Builder предоставляет быстродействующий компилятор с языка Borland C++.
Конструирование по способу "drag-and-drop " позволяет создавать приложение простым перетаскиванием захваченных мышью визуальных компонентов из Палитры на форму приложения. Инспектор объектов предоставляет возможность оперировать со свойствами и событиями компонентов, автоматически создавая заготовки функций обработки событий, которые наполняются кодом и редактируются в процессе разработки.
4.2Описание работы программы
В данной программе производится анализ резистивного многополюсника.
Для линейного резистора исходная схема имеет вид, показанный на рисунке 1(а).
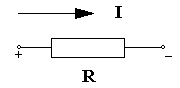
а)
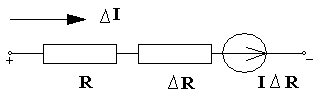
б)
Рисунок 4.2.1 - Схема линейного резистора (а) и его схема в приращениях (б)
В невозбужденном режиме линейный резистор характеризуется уравнением по закону Ома:
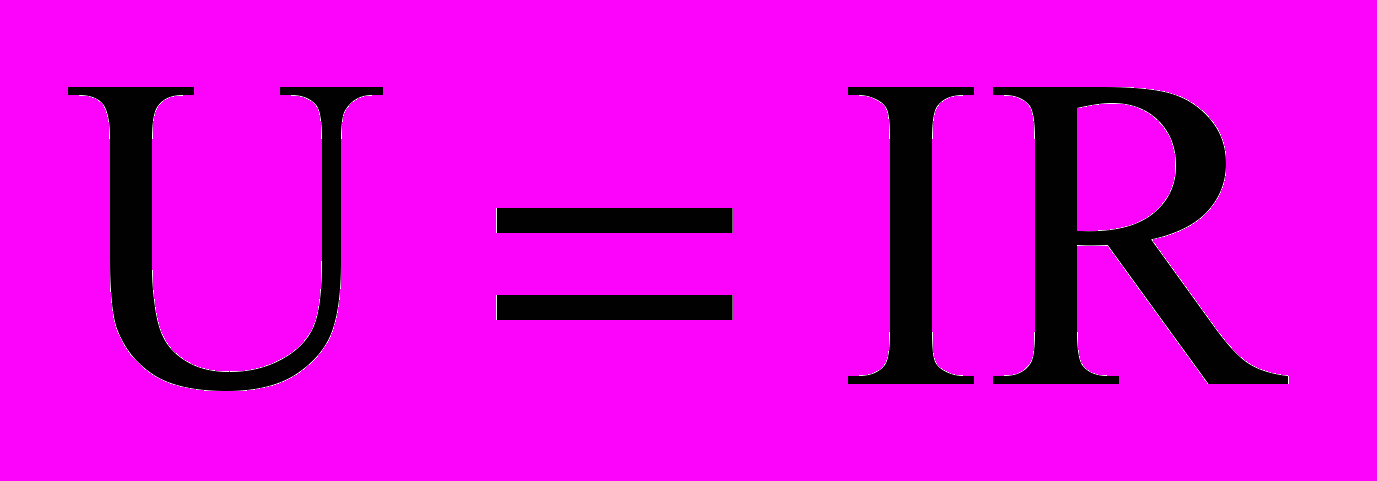 (14)
(14)Предположим, что под влиянием неких внешних и/или внутренних факторов изменились параметры элемента, т.е. параметры получили некое конечное приращение. Тогда уравнение (1) примет следующий вид:
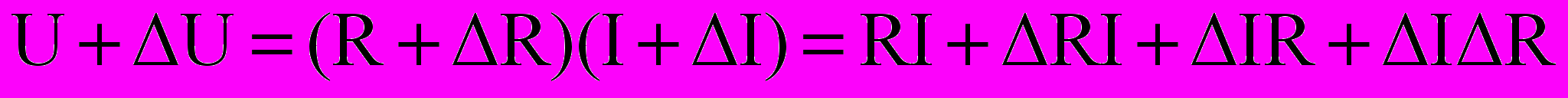 (15)
(15)Из приведенных уравнений можно определить характеристику в возбужденном режиме:
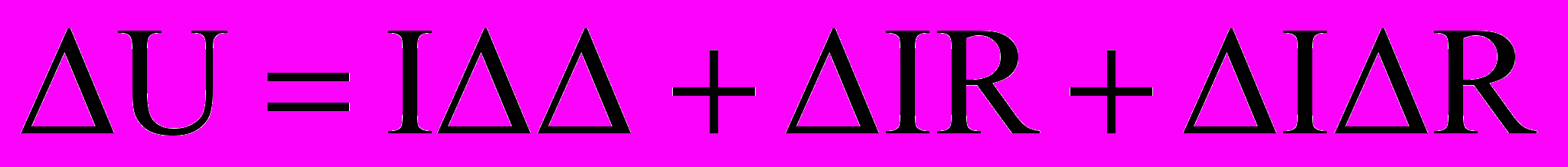 (16)
(16)Большинство исследователей отбрасывают последнее слагаемое уравнения (3),считая произведение двух приращений очень малым и стремящимся к нулю. Однако, для исследования чувствительности электронных схем по отношению к изменению параметров внешней среды на взгляд авторов целесообразно считать произведение приращений
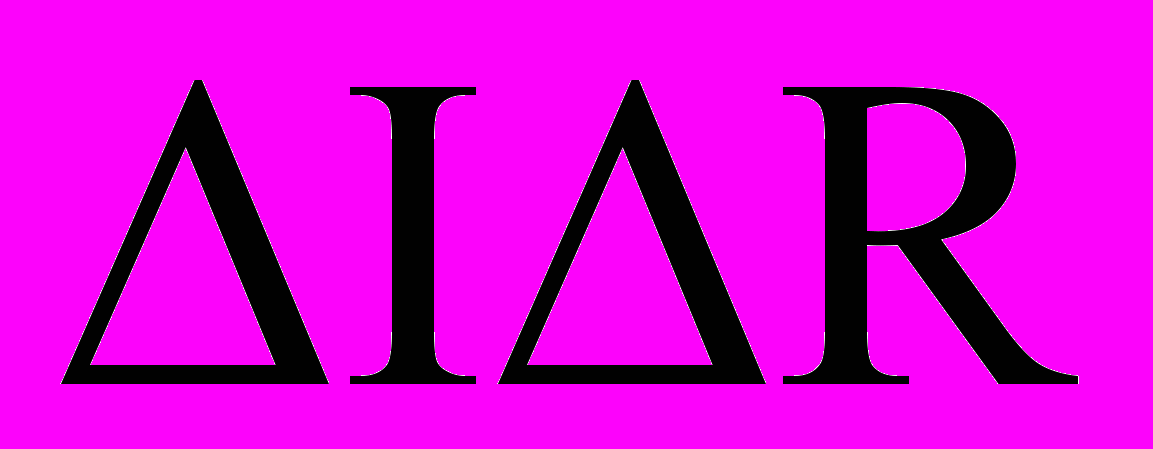 конечным и не стремящимся к нулю. Таким образом, можно получить более точную схему линейного сопротивления в приращениях.
конечным и не стремящимся к нулю. Таким образом, можно получить более точную схему линейного сопротивления в приращениях. Из формулы для температурного коэффициента сопротивления
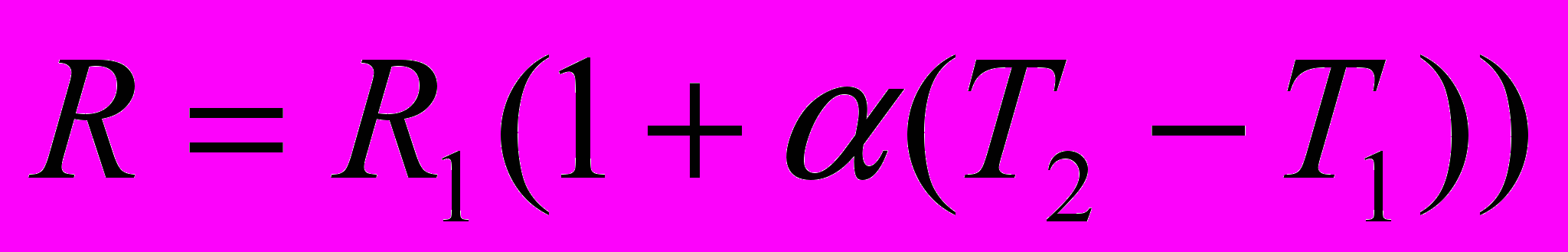 (17)
(17)Определим сопротивление резистора при повышении температуры:
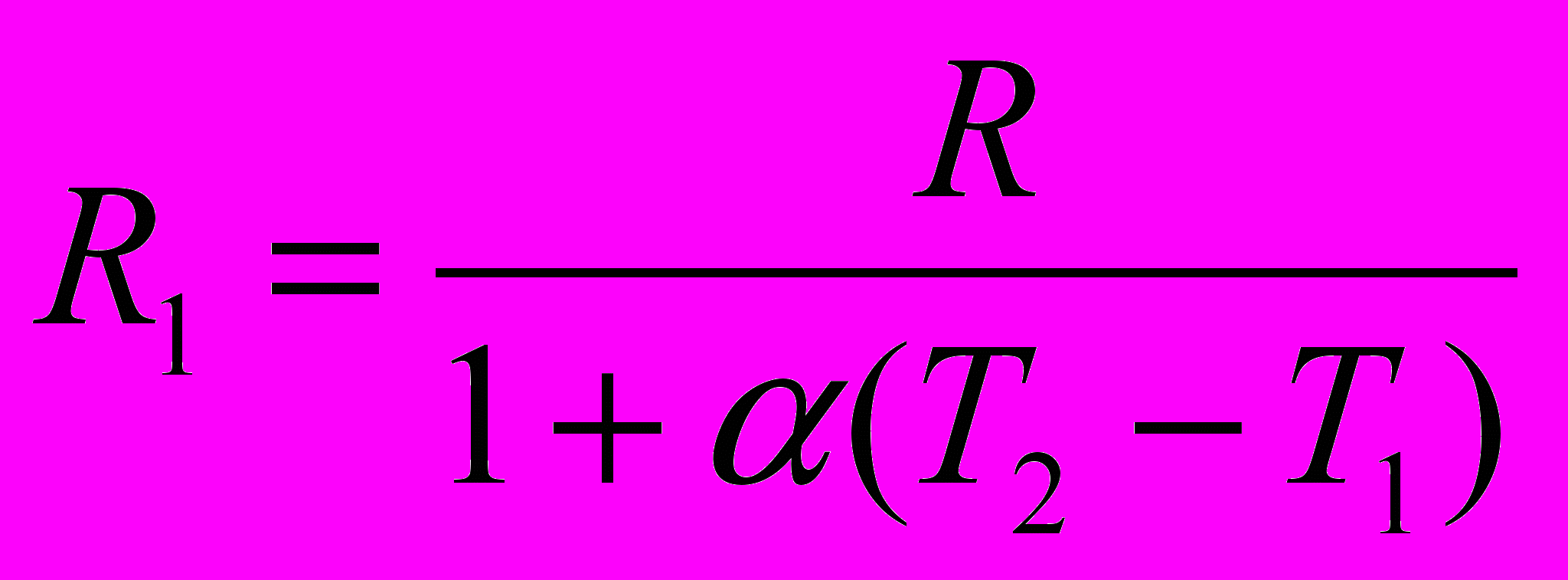 (18)
(18)В качестве материала резистора примем железо, температурный коэффициент которого
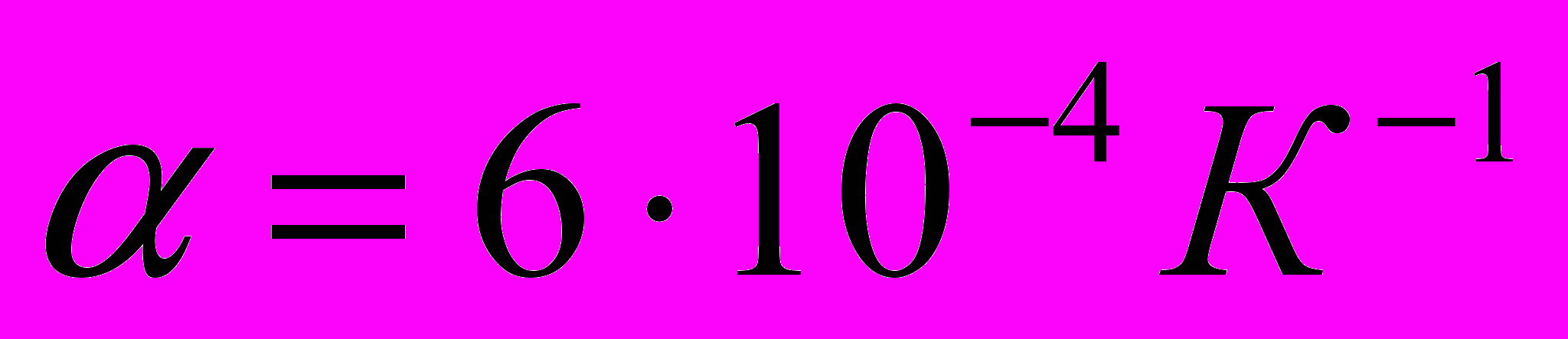 .
.В качестве схемы для анализа выберем схему, приведенную на Рис.2.
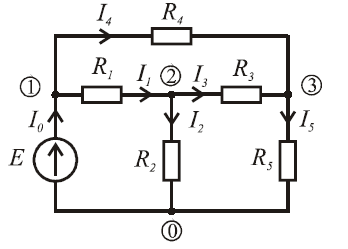
Рисунок 4.2.2 - Схема для анализа
Для нахождения токов в схеме составим уравнения по методу контурных токов:
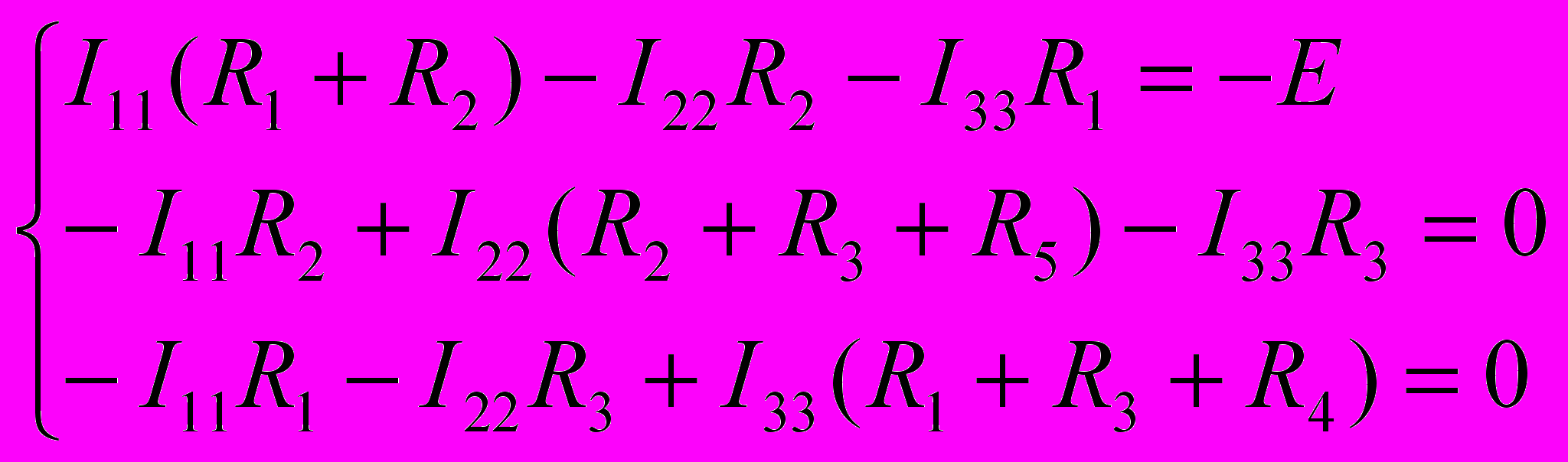 (19)
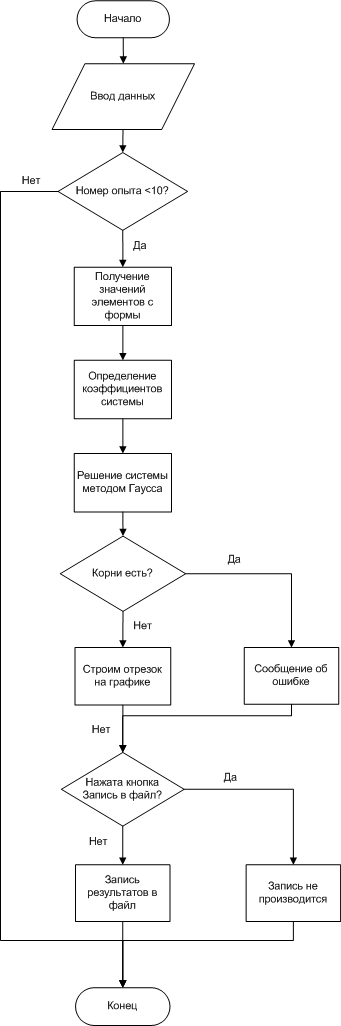
(19)Для решения этой системы уравнений применим метод Гаусса.
Расчет системы производится 10 раз для значений температуры окружающей среды от 0 до 100 градусов, с шагом 10. Данные о значениях токов выводятся на график.
4.3Фрагменты исходных кодов, реализующие основные алгоритмы
решаемой задачи
При помощи кнопок RadioButton пользователь осуществляет выбор типа элемента схемы (сопротивление или индуктивность). Создается два массива:
В первом массиве a[n] содержатся типы элементов, а во втором b[n] их значения. Для передачи данных на вторую форму предусмотрены скрытые элементы формы StringGrid1 и StringGrid2.Значения массивов записываем в String Grid и открываем новое окно:
//вывод массива а
int i;
for(i=0; i<=5;i=i+1)
{
StringGrid1->Cells[i][0]=FloatToStr(a[i]);
}
//вывод массива b
for(i=0;i<=5;i=i+1)
{
StringGrid2->Cells[i][0]=FloatToStr(b[i]);
}
Form2->Show();
В новой форме при движении мышью вызывается процедура рисования исходной схемы:
PB->Canvas->MoveTo(30,50);
PB->Canvas->LineTo(30,20);
PB->Canvas->LineTo(56,20);
PB->Canvas->MoveTo(108,20);
PB->Canvas->LineTo(134,20);
PB->Canvas->LineTo(134,50);
PB->Canvas->MoveTo(82,102);
PB->Canvas->LineTo(30,102);
PB->Canvas->MoveTo(82,102);
PB->Canvas->LineTo(134,102);
DrawE(30,50,1); //Источник ЭДС
Схема рисуется при помощи процедур рисования резистора, индуктивности и источника ЭДС:
//Процедура рисования сопротивления
void TForm2::DrawR(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+12,y1);
PB->Canvas->LineTo(x1+12,y1-8);
PB->Canvas->LineTo(x1+12,y1+8);
PB->Canvas->LineTo(x1+40,y1+8);
PB->Canvas->LineTo(x1+40,y1);
PB->Canvas->LineTo(x1+52,y1);
PB->Canvas->MoveTo(x1+40,y1);
PB->Canvas->LineTo(x1+40,y1-8);
PB->Canvas->LineTo(x1+12,y1-8);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+12);
PB->Canvas->LineTo(x1-8,y1+12);
PB->Canvas->LineTo(x1+8,y1+12);
PB->Canvas->LineTo(x1+8,y1+40);
PB->Canvas->LineTo(x1,y1+40);
PB->Canvas->LineTo(x1,y1+52);
PB->Canvas->MoveTo(x1,y1+40);
PB->Canvas->LineTo(x1-8,y1+40);
PB->Canvas->LineTo(x1-8,y1+12);
}
}
//Процедура рисования индуктивности
//---------------------------------------------------------------------------
void TForm2::DrawL(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+17,y1);
PB->Canvas->LineTo(x1+20,y1-8);
PB->Canvas->LineTo(x1+23,y1);
PB->Canvas->LineTo(x1+26,y1-8);
PB->Canvas->LineTo(x1+29,y1);
PB->Canvas->LineTo(x1+32,y1-8);
PB->Canvas->LineTo(x1+35,y1);
PB->Canvas->LineTo(x1+52,y1);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+17);
PB->Canvas->LineTo(x1-8,y1+20);
PB->Canvas->LineTo(x1,y1+23);
PB->Canvas->LineTo(x1-8,y1+26);
PB->Canvas->LineTo(x1,y1+29);
PB->Canvas->LineTo(x1-8,y1+32);
PB->Canvas->LineTo(x1,y1+35);
PB->Canvas->LineTo(x1,y1+52);
}
}
//Процедура рисования источника ЭДС
void TForm2::DrawE(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+22,y1);
PB->Canvas->LineTo(x1+22,y1-8);
PB->Canvas->LineTo(x1+22,y1+8);
PB->Canvas->MoveTo(x1+52,y1);
PB->Canvas->LineTo(x1+32,y1);
PB->Canvas->LineTo(x1+32,y1+18);
PB->Canvas->LineTo(x1+32,y1-18);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+24);
PB->Canvas->LineTo(x1+18,y1+24);
PB->Canvas->LineTo(x1-18,y1+24);
PB->Canvas->MoveTo(x1,y1+52);
PB->Canvas->LineTo(x1,y1+32);
PB->Canvas->LineTo(x1-8,y1+32);
PB->Canvas->LineTo(x1+8,y1+32);
}
}
//---------------------------------------------------------------------------
Далее, при нажатии кнопки “Заполнить таблицу” происходит заполнение таблицы уравнений по методу контурных токов:
n=3;
X=new float [n] ;
for (int i=0; i
{
for (int j=0; j
{
A[i][j]=NULL;
}
X[i]=NULL;
}
StringGrid5->Cells[0][0]=FloatToStr(b[0]+b[1]);
StringGrid5->Cells[0][1]=FloatToStr(-b[1]);
StringGrid5->Cells[0][2]=FloatToStr(-b[0]);
StringGrid5->Cells[1][0]=FloatToStr(-b[1]);
StringGrid5->Cells[1][1]=FloatToStr(b[1]+b[2]+b[4]);
StringGrid5->Cells[1][2]=FloatToStr(-b[2]);
StringGrid5->Cells[2][0]=FloatToStr(-b[0]);
StringGrid5->Cells[2][1]=FloatToStr(-b[2]);
StringGrid5->Cells[2][2]=FloatToStr(b[0]+b[2]+b[3]);
StringGrid5->Cells[3][0]=FloatToStr(-b[5]);
StringGrid5->Cells[3][1]=0;
StringGrid5->Cells[3][2]=0;
Далее, при нажатии на кнопку “Найти токи методом Гаусса” происходит решение системы уравнений контурных токов и дальнейший расчет значений токов в ветвях схемы. Расчет производится 10 раз. На основе расчетов строятся графики зависимости токов от температуры.
for (int m=1; m<10; m++)
{
StringGrid5->Cells[0][0]=FloatToStr((b[0]+b[1])/(1+6*0.001*m));
StringGrid5->Cells[0][1]=FloatToStr(-b[1]/(1+6*0.001*m));
StringGrid5->Cells[0][2]=FloatToStr(-b[0]/(1+6*0.001*m));
StringGrid5->Cells[1][0]=FloatToStr(-b[1]/(1+6*0.001*m));
StringGrid5->Cells[1][1]=FloatToStr((b[1]+b[2]+b[4])/(1+6*0.001*m));
StringGrid5->Cells[1][2]=FloatToStr(-b[2]/(1+6*0.001*m));
StringGrid5->Cells[2][0]=FloatToStr(-b[0]/(1+6*0.001*m));
StringGrid5->Cells[2][1]=FloatToStr(-b[2]/(1+6*0.001*m));
StringGrid5->Cells[2][2]=FloatToStr((b[0]+b[2]+b[3])/(1+6*0.001*m));
StringGrid5->Cells[3][0]=FloatToStr(-b[5]);
StringGrid5->Cells[3][1]=0;
StringGrid5->Cells[3][2]=0;
Memo1->Lines->Clear ();
for (int i=0; i
{
for (int j=0; j
{
TryStrToFloat(StringGrid5->Cells[j][i],A[i][j]);
}
}
Memo1->Lines->Add (" Решение системы методом Гаусса: ");
Memo1->Lines->Add ("");
if (!fl1) {
Memo1->Lines->Add ("Матрица приводится к ступенчатому виду: ");
l=0;
for (int i=0; i
{
for (int j=n-1; j>i; j--)
{
if (A[j-1][l]
{
for (int k=0; k
{
r=A[j][k] ;
A[j][k]=A[j-1][k] ;
A[j-1][k]=r;
}
l=0;
}
else
{
if (A[j-1][l]==A[j][l])
{
l++;
j++;
}
if (l==n+1)
{
j--;
l=0;
}
}
}
}
for (int k=0; k
{
for (int i=k; i
{
r=A[i][k] ;
for (int j=k; j
{
A[i][j]=A[i][j]/r;
}
}
for (int i=k+1; i
{
for (int j=k; j
{
A[i][j]=A[i][j]-A[k][j];
}
}
}
X[n-1]=A[n-1][n]/A[n-1][n-1] ;
for (int i=n-2; i>=0; i--)
{
r=A[i][n] ;
for (int j=i+1; j<=n-1; j++)
r=r-A[i][j]*X[j];
X[i]=r/A[i][i];
}
String s="";
for (int i=0; i
{
s="";
for (int j=0; j
{
s+=FloatToStr (A[i][j])+" ";
}
Memo1->Lines->Add(s);
}
Memo1->Lines->Add("");
Memo1->Lines->Add("Величины контурных токов: ");
for (int i=0; i
{
if (X[i]!=NULL)
{
Memo1->Lines->Add ("I"+IntToStr(i+1)+IntToStr(i+1) +" = "+FloatToStr(X[i])+",А");
}
else
{
Memo1->Lines->Add("Нет корней!");
break;
}
}
Memo1->Lines->Add("");
Memo1->Lines->Add("Величины токов в ветвях равны: ");
Memo1->Lines->Add ("I0=" + FloatToStr(-X[0])+",А" );
Memo1->Lines->Add ("I1="+FloatToStr(-X[0]+X[2])+",А");
Memo1->Lines->Add ("I2="+FloatToStr(X[1]-X[0])+",А");
Memo1->Lines->Add ("I3="+FloatToStr(-X[1]+X[2])+",А");
Memo1->Lines->Add ("I4="+FloatToStr(-X[2])+",А");
Memo1->Lines->Add ("I5="+FloatToStr(-X[1])+",А");
this->Series1->AddXY(m,-X[0],"",clTeeColor);
this->Series2->AddXY(m,-X[0]+X[2],"",clTeeColor);
this->Series3->AddXY(m,X[1]-X[0],"",clTeeColor);
this->Series4->AddXY(m,-X[1]+X[2],"",clTeeColor);
this->Series5->AddXY(m,-X[2],"",clTeeColor);
this->Series6->AddXY(m,-X[1],"",clTeeColor);
}
5Описание пользовательского интерфейса
В главном окне программы пользователь может ввести значения всех элементов схемы.
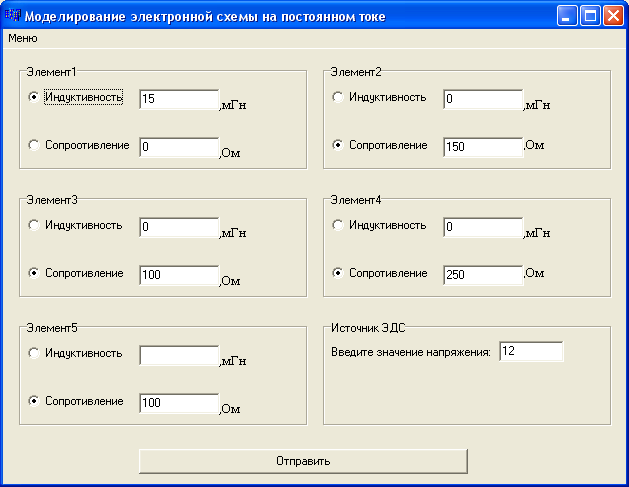
Рисунок 5.1 - Главное окно программы
При нажатии “Меню – Выбрать схему для моделирования” пользователь может выбрать одну из предложенных схем. В данной работе реализовано моделирование схемы с резистивными элементами.
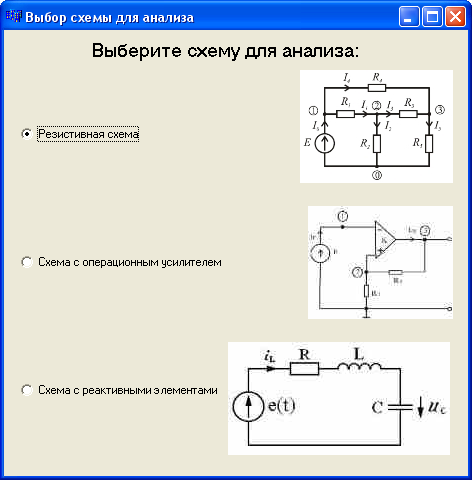
Рисунок 5.2 - Исходная схема для моделирования
После отправки значений элементов схемы открывается следующее окно, в котором, для удобства пользователя, отображается моделируемая схема.
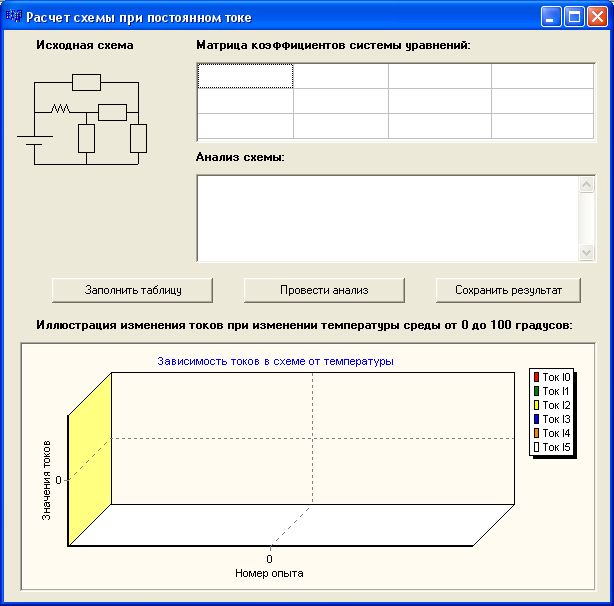
Рисунок 5.3 - Окно программы Расчет схем на постоянном токе
При нажатии кнопки “Заполнить таблицу” происходит заполнение таблицы, введенными пользователем в первой форме, данными. Так как расчет производится на постоянном токе, сопротивления индуктивностей стремятся к нулю,
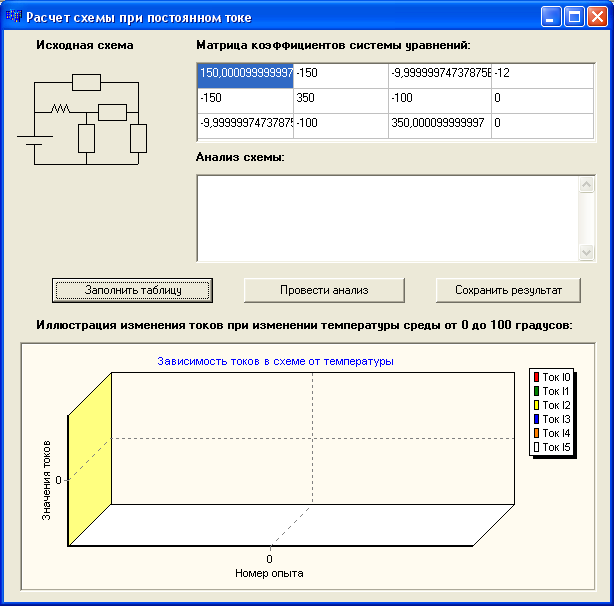
Рисунок 5.4 - Заполнение коэффициентов системы уравнений
При нажатии кнопки “Найти токи методом Гаусса” производится расчет схемы при 10-ти различных значениях температуры. Строится график зависимости токов от температуры. Значения токов в последнем опыте выводятся в окно пользователя.
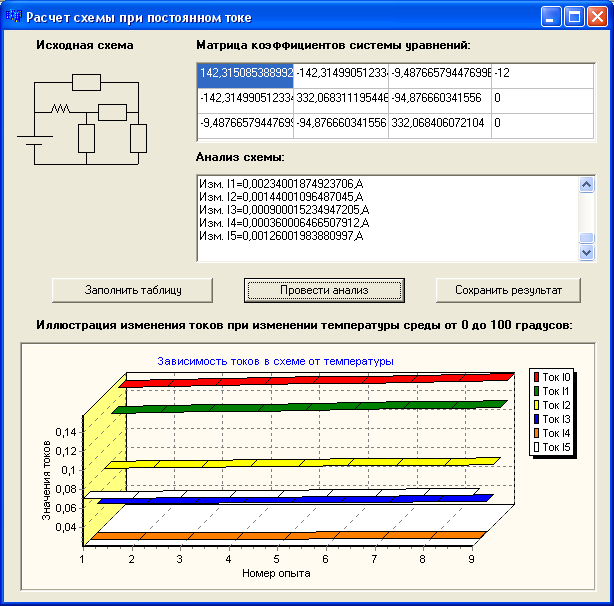
Рисунок 5.5 - Окно с результатами опыта
Заключение
В данной работе было оценено влияние температуры на токи в ветвях цепи.
При значительном изменении температуры окружающей среды токи в ветвях схемы также изменяются.
При увеличении температуры на 100 градусов наибольшему влиянию подвергается ток I0, который возрастает на 0,008 А.
Менее всего подвержен воздействию температуры ток I4, который увеличился на 0,001А.
Исследование чувствительности различных схемотехнических вариантов построения энергетических комплексов позволяет установить степень влияния вариации параметров компонентов на характеристики проектируемого устройства, а также определить, в каком направлении следует проводить изменения в процессе схемотехнического проектирования, при настройке и отладке спроектированного устройства.
Список используемой литературы:
- Чуа Л.О., Лин Пен-Мин «Машинный анализ электронных схем: Алгоритмы и вычислительные методы». – М.: Энергия, 1980. – 640 с., ил.
- Бондарев А.В. Вычислительная процедура исследования чувствительности временных характеристик энергетических комплексов
- Архангельский А. Я. Программирование в C++ Builder 6 / А. Я. Архангельский.— 2-е изд. — Москва: БИНОМ, 2005 .— 1162 с.: ил.
- Либерти Дж. Освой самостоятельно С++ за 21 день: учеб. пособие / Либерти Дж. — 3-е изд. — М.: Вильямс, 2001.— 816 с. : ил.
- Ашарина И. В. Объектно-ориентированное программирование в C++: лекции и упражнения: учебное пособие для студентов высших учебных заведений / И. В. Ашарина.— Москва: Горячая линия - Телеком, 2008 .— 319 с.: ил.
Приложение А
(обязательное)
Unit1.h
//---------------------------------------------------------------------------
#include
#pragma hdrstop
#include "Unit3.h"
#include "Unit1.h"
#include "Unit2.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//первый массив содержит тип элементов 3-сопротивление
//2-индуктивность
//второй массив содержит номинал элементов в Ом, ф и Гн
float a[7];
float b[7];
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button1Click(TObject *Sender)
{
//первый элемент
if (RadioButton2->Checked)
{
a[0]=2;
b[0]=0.0001;
}
if (RadioButton3->Checked)
{
a[0]=3;
b[0]=StrToFloat(Edit3->Text);
}
//второй элемент
if (RadioButton5->Checked)
{
a[1]=2;
b[1]=0.0001;
}
if (RadioButton6->Checked)
{
a[1]=3;
b[1]=StrToFloat(Edit6->Text);
}
//третий элемент
if (RadioButton8->Checked)
{
a[2]=2;
b[2]=0.0001;
}
if (RadioButton9->Checked)
{
a[2]=3;
b[2]=StrToFloat(Edit9->Text);
}
//четвертый элемент
if (RadioButton11->Checked)
{
a[3]=2;
b[3]=0.0001;
}
if (RadioButton12->Checked)
{
a[3]=3;
b[3]=StrToFloat(Edit12->Text);
}
//пятый элемент
if (RadioButton14->Checked)
{
a[4]=2;
b[4]=0.0001;
}
if (RadioButton15->Checked)
{
a[4]=3;
b[4]=StrToFloat(Edit15->Text);
}
//шестой элемент
a[5]=4;
b[5]=StrToFloat(Edit16->Text);
//вывод массива а
int i;
for(i=0; i<=5;i=i+1)
{
StringGrid1->Cells[i][0]=FloatToStr(a[i]);
}
//вывод массива b
for(i=0;i<=5;i=i+1)
{
StringGrid2->Cells[i][0]=FloatToStr(b[i]);
}
Form2->Show();
}
//---------------------------------------------------------------------------
void __fastcall TForm1::N2Click(TObject *Sender)
{
Form3->Show();
}
//---------------------------------------------------------------------------
Unit2.h
//---------------------------------------------------------------------------
#include
#pragma hdrstop
#include "Unit1.h"
#include "Unit2.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm2 *Form2;
int a[7];
float b[7];
int n=0,l=0;
float r=0,p=0;
const x=100;
float A[x][x];
float *X;
float *Y;
bool fl1=false;
//---------------------------------------------------------------------------
__fastcall TForm2::TForm2(TComponent* Owner)
: TForm(Owner)
{
}
//---------------------------------------------------------------------------
void TForm2::DrawR(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+12,y1);
PB->Canvas->LineTo(x1+12,y1-8);
PB->Canvas->LineTo(x1+12,y1+8);
PB->Canvas->LineTo(x1+40,y1+8);
PB->Canvas->LineTo(x1+40,y1);
PB->Canvas->LineTo(x1+52,y1);
PB->Canvas->MoveTo(x1+40,y1);
PB->Canvas->LineTo(x1+40,y1-8);
PB->Canvas->LineTo(x1+12,y1-8);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+12);
PB->Canvas->LineTo(x1-8,y1+12);
PB->Canvas->LineTo(x1+8,y1+12);
PB->Canvas->LineTo(x1+8,y1+40);
PB->Canvas->LineTo(x1,y1+40);
PB->Canvas->LineTo(x1,y1+52);
PB->Canvas->MoveTo(x1,y1+40);
PB->Canvas->LineTo(x1-8,y1+40);
PB->Canvas->LineTo(x1-8,y1+12);
}
}
//---------------------------------------------------------------------------
void TForm2::DrawC(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+22,y1);
PB->Canvas->LineTo(x1+22,y1-8);
PB->Canvas->LineTo(x1+22,y1+8);
PB->Canvas->MoveTo(x1+52,y1);
PB->Canvas->LineTo(x1+32,y1);
PB->Canvas->LineTo(x1+32,y1+8);
PB->Canvas->LineTo(x1+32,y1-8);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+24);
PB->Canvas->LineTo(x1+8,y1+24);
PB->Canvas->LineTo(x1-8,y1+24);
PB->Canvas->MoveTo(x1,y1+52);
PB->Canvas->LineTo(x1,y1+32);
PB->Canvas->LineTo(x1-8,y1+32);
PB->Canvas->LineTo(x1+8,y1+32);
}
}
//---------------------------------------------------------------------------
void TForm2::DrawL(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+17,y1);
PB->Canvas->LineTo(x1+20,y1-8);
PB->Canvas->LineTo(x1+23,y1);
PB->Canvas->LineTo(x1+26,y1-8);
PB->Canvas->LineTo(x1+29,y1);
PB->Canvas->LineTo(x1+32,y1-8);
PB->Canvas->LineTo(x1+35,y1);
PB->Canvas->LineTo(x1+52,y1);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+17);
PB->Canvas->LineTo(x1-8,y1+20);
PB->Canvas->LineTo(x1,y1+23);
PB->Canvas->LineTo(x1-8,y1+26);
PB->Canvas->LineTo(x1,y1+29);
PB->Canvas->LineTo(x1-8,y1+32);
PB->Canvas->LineTo(x1,y1+35);
PB->Canvas->LineTo(x1,y1+52);
}
}
void __fastcall TForm2::Button1Click(TObject *Sender)
{
PB->Canvas->MoveTo(30,50);
PB->Canvas->LineTo(30,20);
PB->Canvas->LineTo(56,20);
PB->Canvas->MoveTo(108,20);
PB->Canvas->LineTo(134,20);
PB->Canvas->LineTo(134,50);
PB->Canvas->MoveTo(82,102);
PB->Canvas->LineTo(30,102);
PB->Canvas->MoveTo(82,102);
PB->Canvas->LineTo(134,102);
DrawE(30,50,1); //Источник ЭДС
int i;
int j;
j=-1;
for(i=0;i<=5;i=i+1)
{ //массив типов элементов
a[i]=StrToFloat(Form1->StringGrid1->Cells[i][0]);
switch(i)
{
case 0:
switch(a[i])
{
case 2:
DrawL(30,50,0); //1й элемент
break;
case 3:
DrawR(30,50,0); //1й элемент
break;
}
break;
case 1:
switch(a[i])
{
case 2:
DrawL(82,50,1); //2й элемент;
break;
case 3:
DrawR(82,50,1); //2й элемент;
break;
}
break;
case 2:
switch(a[i])
{
case 2:
DrawL(82,50,0); //3й элемент;
break;
case 3:
DrawR(82,50,0); //3й элемент;
break;
}
break;
case 3:
switch(a[i])
{
case 2:
DrawL(56,20,0); //4й элемент;
break;
case 3:
DrawR(56,20,0); //4й элемент;
break;}
break;
case 4:
switch(a[i])
{
case 2:
DrawL(134,50,1);//5й элемент
break;
case 3:
DrawR(134,50,1);//5й элемент
break;}
break;
}
}
for(i=0;i<=5;i=i+1)
{
b[i]=StrToFloat(Form1->StringGrid2->Cells[i][0]);
}
}
//--------------------------------------------------------------------------
void TForm2::DrawE(int x1, int y1, int rotate)
{
if (rotate==0)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1+22,y1);
PB->Canvas->LineTo(x1+22,y1-8);
PB->Canvas->LineTo(x1+22,y1+8);
PB->Canvas->MoveTo(x1+52,y1);
PB->Canvas->LineTo(x1+32,y1);
PB->Canvas->LineTo(x1+32,y1+18);
PB->Canvas->LineTo(x1+32,y1-18);
}
if (rotate==1)
{
PB->Canvas->MoveTo(x1,y1);
PB->Canvas->LineTo(x1,y1+24);
PB->Canvas->LineTo(x1+18,y1+24);
PB->Canvas->LineTo(x1-18,y1+24);
PB->Canvas->MoveTo(x1,y1+52);
PB->Canvas->LineTo(x1,y1+32);
PB->Canvas->LineTo(x1-8,y1+32);
PB->Canvas->LineTo(x1+8,y1+32);
}
}
//---------------------------------------------------------------------------
void __fastcall TForm2::FormMouseMove(TObject *Sender, TShiftState Shift,
int X, int Y)
{
Button1Click (Button1);
}
//---------------------------------------------------------------------------
void __fastcall TForm2::Button5Click(TObject *Sender)
{
n=3;
X=new float [n] ;
for (int i=0; i
{
for (int j=0; j
{
A[i][j]=NULL;
}
X[i]=NULL;
}
StringGrid5->Cells[0][0]=FloatToStr(b[0]+b[1]);
StringGrid5->Cells[0][1]=FloatToStr(-b[1]);
StringGrid5->Cells[0][2]=FloatToStr(-b[0]);
StringGrid5->Cells[1][0]=FloatToStr(-b[1]);
StringGrid5->Cells[1][1]=FloatToStr(b[1]+b[2]+b[4]);
StringGrid5->Cells[1][2]=FloatToStr(-b[2]);
StringGrid5->Cells[2][0]=FloatToStr(-b[0]);
StringGrid5->Cells[2][1]=FloatToStr(-b[2]);
StringGrid5->Cells[2][2]=FloatToStr(b[0]+b[2]+b[3]);
StringGrid5->Cells[3][0]=FloatToStr(-b[5]);
StringGrid5->Cells[3][1]=0;
StringGrid5->Cells[3][2]=0;
}
//---------------------------------------------------------------------------
void __fastcall TForm2::Button6Click(TObject *Sender)
{
for (int m=1; m<10; m++)
{
StringGrid5->Cells[0][0]=FloatToStr((b[0]+b[1])/(1+6*0.001*m));
StringGrid5->Cells[0][1]=FloatToStr(-b[1]/(1+6*0.001*m));
StringGrid5->Cells[0][2]=FloatToStr(-b[0]/(1+6*0.001*m));
StringGrid5->Cells[1][0]=FloatToStr(-b[1]/(1+6*0.001*m));
StringGrid5->Cells[1][1]=FloatToStr((b[1]+b[2]+b[4])/(1+6*0.001*m));
StringGrid5->Cells[1][2]=FloatToStr(-b[2]/(1+6*0.001*m));
StringGrid5->Cells[2][0]=FloatToStr(-b[0]/(1+6*0.001*m));
StringGrid5->Cells[2][1]=FloatToStr(-b[2]/(1+6*0.001*m));
StringGrid5->Cells[2][2]=FloatToStr((b[0]+b[2]+b[3])/(1+6*0.001*m));
StringGrid5->Cells[3][0]=FloatToStr(-b[5]);
StringGrid5->Cells[3][1]=0;
StringGrid5->Cells[3][2]=0;
Memo1->Lines->Clear ();
for (int i=0; i
{
for (int j=0; j
{
TryStrToFloat(StringGrid5->Cells[j][i],A[i][j]);
}
}
Memo1->Lines->Add (" Решение системы методом Гаусса: ");
Memo1->Lines->Add ("");
if (!fl1) {
Memo1->Lines->Add ("Матрица приводится к ступенчатому виду: ");
l=0;
for (int i=0; i
{
for (int j=n-1; j>i; j--)
{
if (A[j-1][l]
{
for (int k=0; k
{
r=A[j][k] ;
A[j][k]=A[j-1][k] ;
A[j-1][k]=r;
}
l=0;
}
else
{
if (A[j-1][l]==A[j][l])
{
l++;
j++;
}
if (l==n+1)
{
j--;
l=0;
}
}
}
}
for (int k=0; k
{
for (int i=k; i
{
r=A[i][k] ;
for (int j=k; j
{
A[i][j]=A[i][j]/r;
}
}
for (int i=k+1; i
{
for (int j=k; j
{
A[i][j]=A[i][j]-A[k][j];
}
}
}
X[n-1]=A[n-1][n]/A[n-1][n-1] ;
for (int i=n-2; i>=0; i--)
{
r=A[i][n] ;
for (int j=i+1; j<=n-1; j++)
r=r-A[i][j]*X[j];
X[i]=r/A[i][i];
}
String s="";
for (int i=0; i
{
s="";
for (int j=0; j
{
s+=FloatToStr (A[i][j])+" ";
}
Memo1->Lines->Add(s);
}
Memo1->Lines->Add("");
Memo1->Lines->Add("Величины контурных токов: ");
for (int i=0; i
{
if (X[i]!=NULL)
{
Memo1->Lines->Add ("I"+IntToStr(i+1)+IntToStr(i+1) +" = "+FloatToStr(X[i])+",А");
}
else
{
Memo1->Lines->Add("Нет корней!");
break;
}
}
Memo1->Lines->Add("");
Memo1->Lines->Add("Величины токов в ветвях равны: ");
Memo1->Lines->Add ("I0=" + FloatToStr(-X[0])+",А" );
Memo1->Lines->Add ("I1="+FloatToStr(-X[0]+X[2])+",А");
Memo1->Lines->Add ("I2="+FloatToStr(X[1]-X[0])+",А");
Memo1->Lines->Add ("I3="+FloatToStr(-X[1]+X[2])+",А");
Memo1->Lines->Add ("I4="+FloatToStr(-X[2])+",А");
Memo1->Lines->Add ("I5="+FloatToStr(-X[1])+",А");
this->Series1->AddXY(m,-X[0],"",clTeeColor)
this->Series2->AddXY(m,-X[0]+X[2],"",clTeeColor);
this->Series3->AddXY(m,X[1]-X[0],"",clTeeColor);
this->Series4->AddXY(m,-X[1]+X[2],"",clTeeColor);
this->Series5->AddXY(m,-X[2],"",clTeeColor)
this->Series6->AddXY(m,-X[1],"",clTeeColor);
}}
}
//---------------------------------------------------------------------------
void __fastcall TForm2::Button2Click(TObject *Sender)
{
float x,y;
this->Series1->Clear();
for (x=0;x<10;x+=0.0001)
{
y=2*x;
this->Series1->AddXY(x,y,"",clTeeColor);
}
}
//---------------------------------------------------------------------------
Приложение Б
(обязательное)
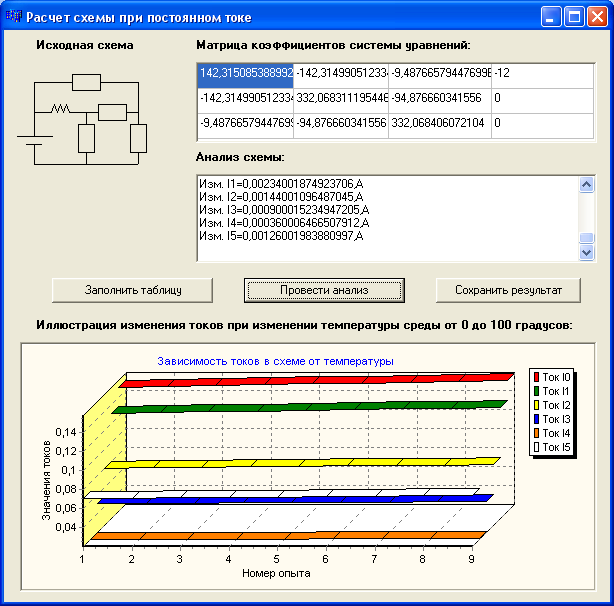
Приложение В