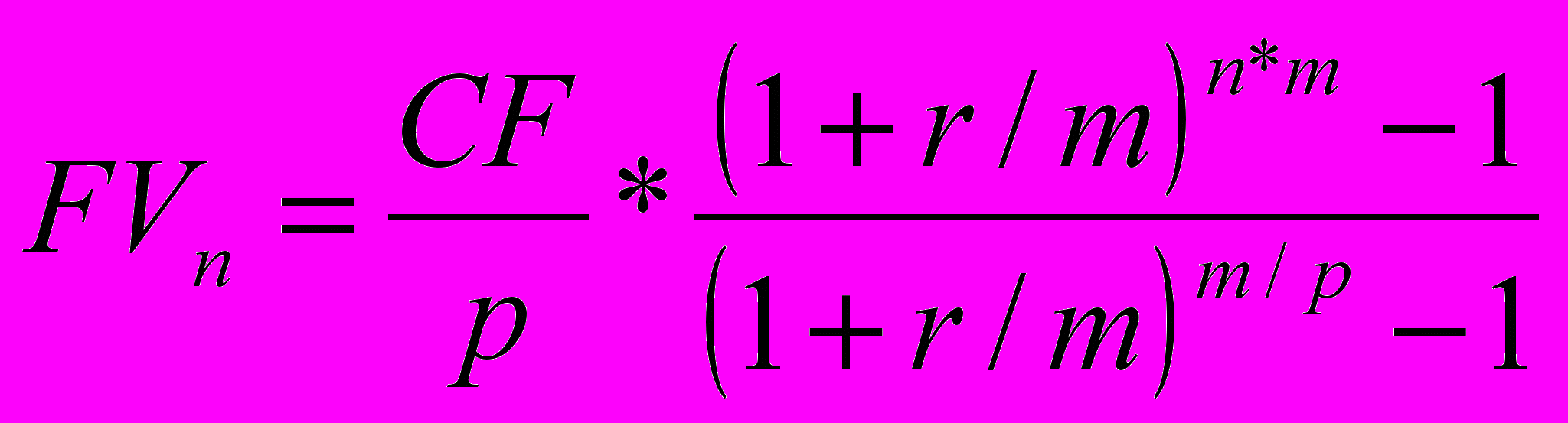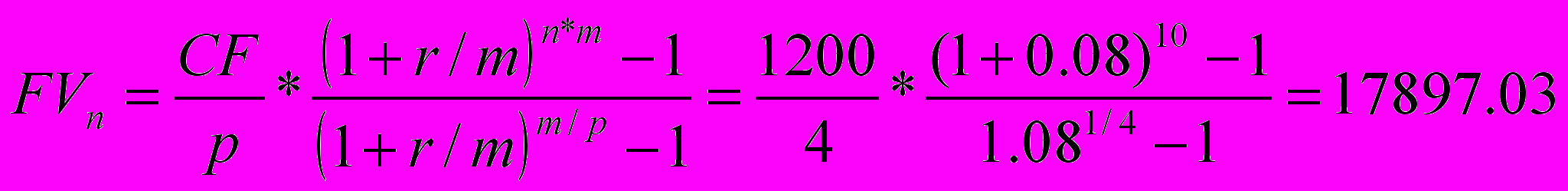Задача 1
| Вид материала | Задача |
- Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
- Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
- Разновозрастная итоговая проектная задача 1-4 классы, 87.27kb.
- Программа дисциплины Алгоритмы на графах Семестр, 13.21kb.
- Гиперкомплексных Динамических Систем (гдс) задача, 214.67kb.
- Домашнее задание по Теории информационных процессов и систем, 267.24kb.
- Задача линейного программирования Задача о «расшивке узких мест», 5.51kb.
- Программа учебной дисциплины вариационные методы в физике (спецкурс, дисциплины, 147.31kb.
- Варианты контрольных работ контрольная работа №1 (3 семестр), 237.84kb.
- Ручаевского Дмитрия Александровича. Карасик Л. В 1997-98 уч год. Основная часть Античная, 202.33kb.
Экономика информационного бизнеса и информационных систем Лекция 2
Задача 2.1
Через сколько лет удвоится сумма, положенная в банк под 10% годовых, по схеме:
А) простых процентов
Б) сложных процентов
а) FV=PV*(1+r*n)
n=
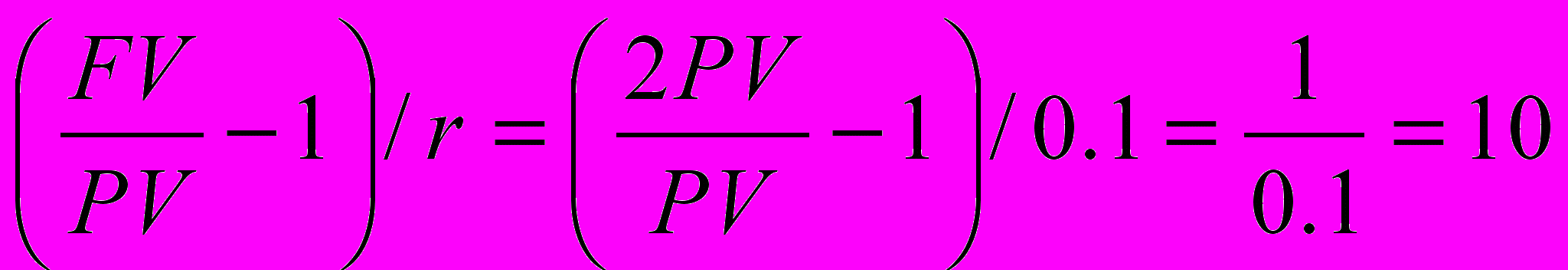летб)
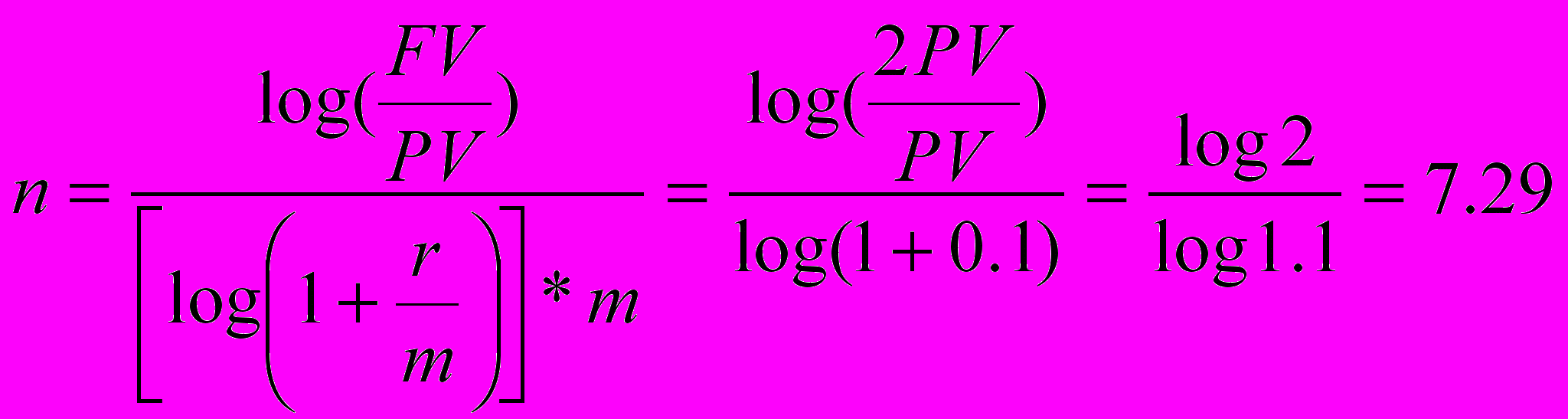летЗадача 2.2
По вкладу 10000р. помещенному в банк под 5% годовых (проценты ежегодно) выплачено 12762,82. Найти срок проведения операции.
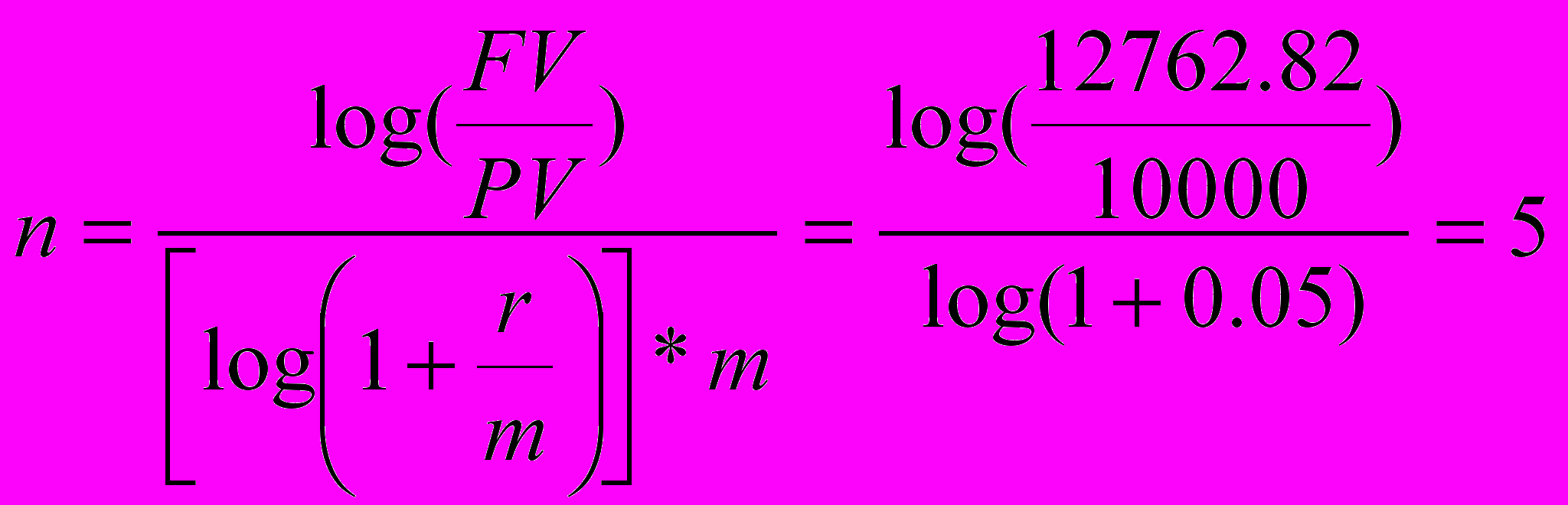лет=КПЕР (ставка, платеж CF, нз, бз, тип)=КПЕР(0,05/m;0;-10000;12762,82)
Доходность операции
Задача 2.3
Ставка банка по срочным валютным депозитам составляет 18% годовых. Определить реальную доходность вклада (т.е. эффективную ставку
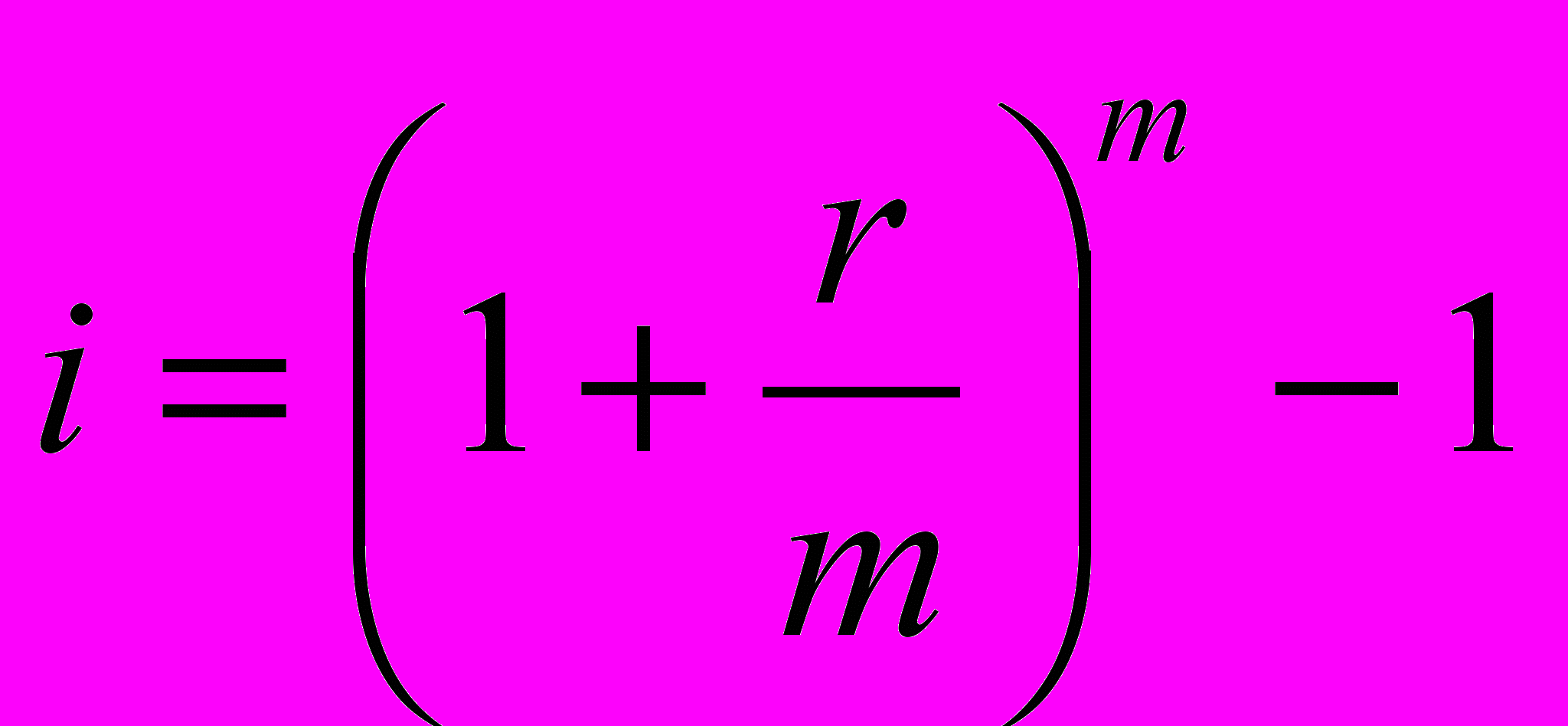), если % выплачиваются:а) ежемесячно: i=(0.18/12+1)12-1=19.56%
б) ежеквартальная: i=(1+0,18/4)4-1=0,1925=19,25%
в) полугодовая: i=(1+0,18/2)2-1=0,1881=18,81%
г) раз в год: i=(1+0,18/1)2-1=0,18=18%
Денежный поток в виде серии равных платежей (аннуитетов) или рента
Денежный поток – движение денежных средств, возникновение отдельных платежей или множества выплат и поступлений, распределенных во времени.
CASH FLOW – CF {CF0,CF1,…,CFn} – численный ряд, состоящий из последовательности распределенных во времени платежей.
CF1 = разность между притоком и оттоком (расходом) денежных средств, может иметь отрицательное и положительное значение.
Аннуитет – регулярный финансовый поток.
Рента- финансовый поток, идущий через одинаковые промежутки времени.
r/m - Процентная ставка, равная отношению номинальной ставки r к количеству периодов начисления m, называется периодической.
Периодическая ставка процентов может использоваться в вычислениях только в том случае, если число платежей в году равно числу начислений процентов.
Будущая стоимость простого аннуитета
Если (p=1, m=1)
Если % начисляется в конце года – обычные платежи - постнумерандо
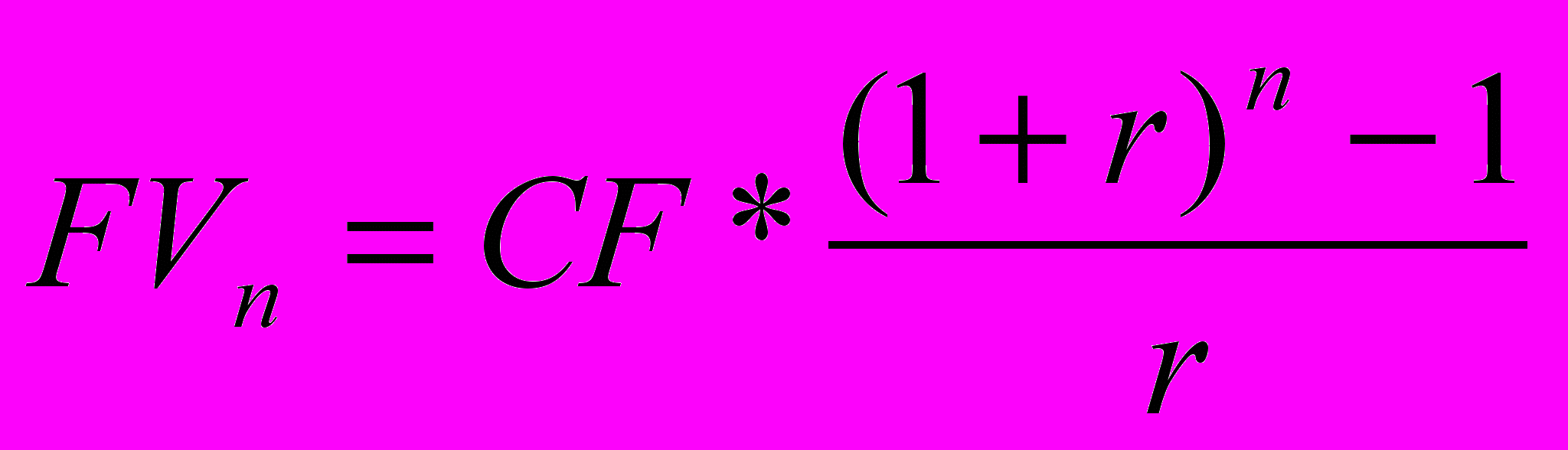
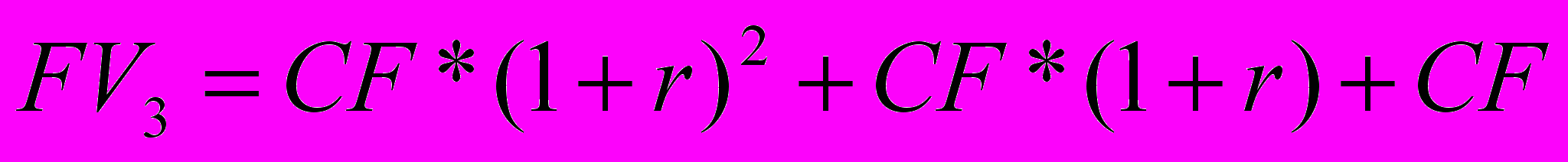
Если % начисляется в начале года – обязательные платежи - пренумерандо
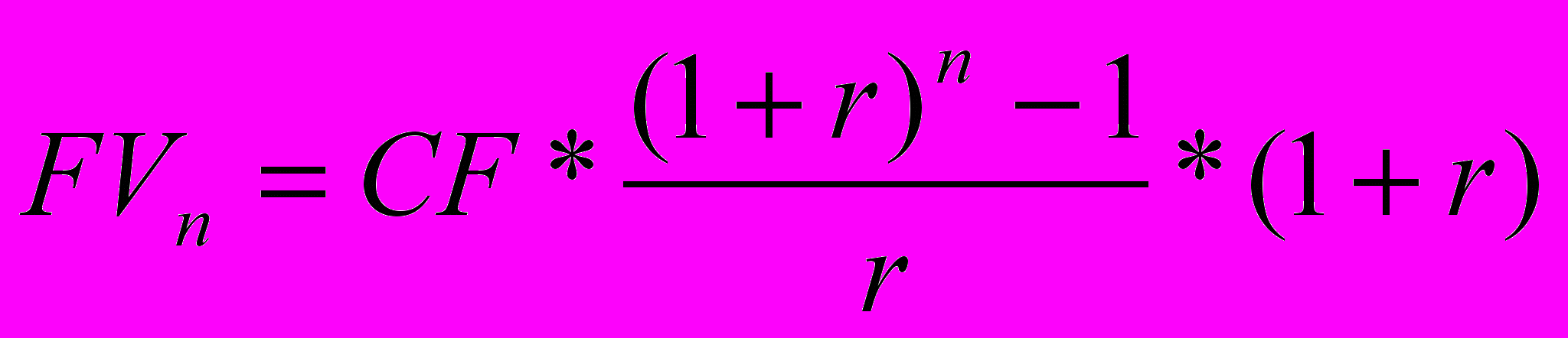
Если (p=1, m>1)
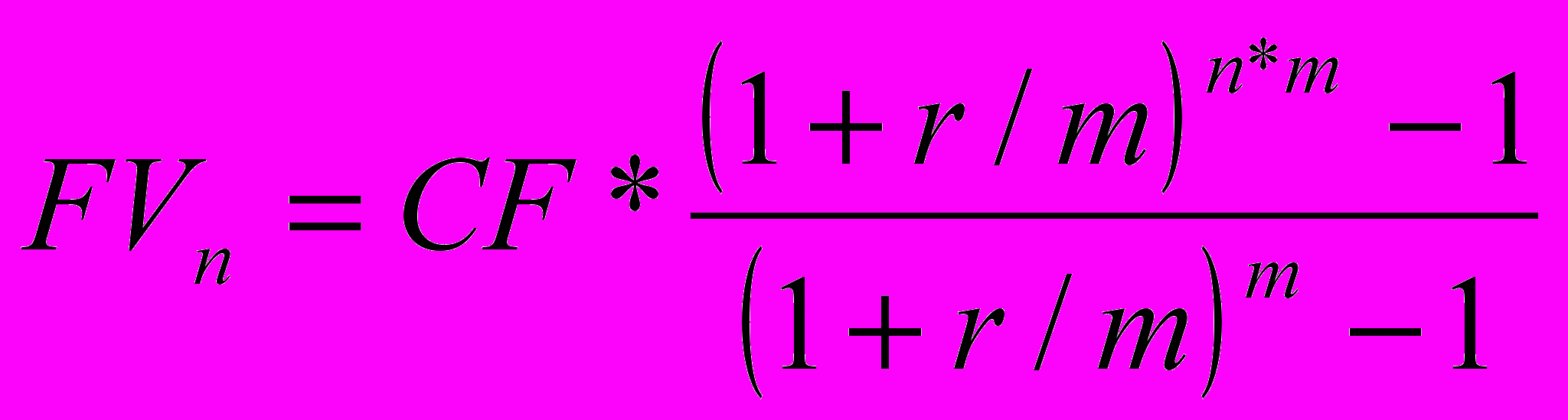
- Если сумма вносится регулярно, но чаще, чем раз в год (р>1), где: р – число раз поступлений в год отдельных платежей, а проценты начисляются m раз в год:
(р>1, m>1, p=m)
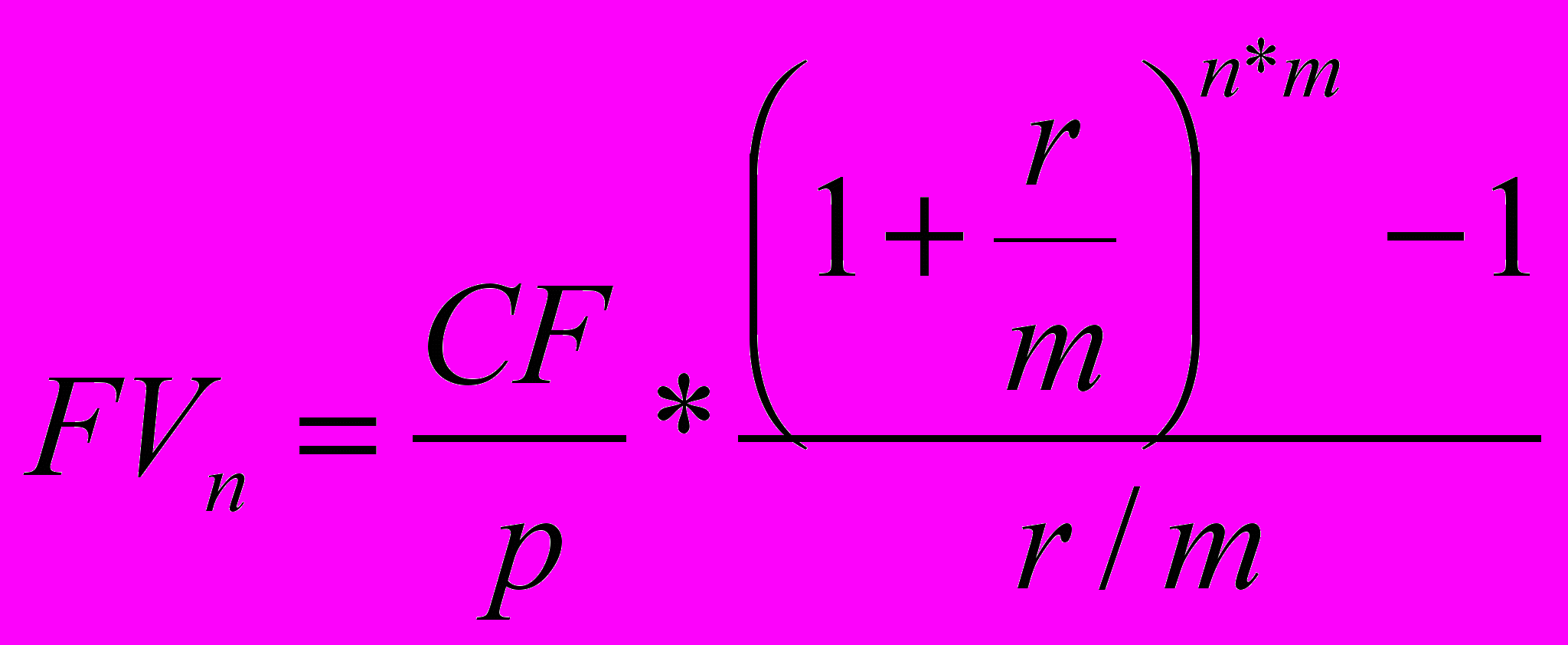, СF/р – сумма разового платежа.2. Если вложения чаще, чем капитализация (p>m, m=1)
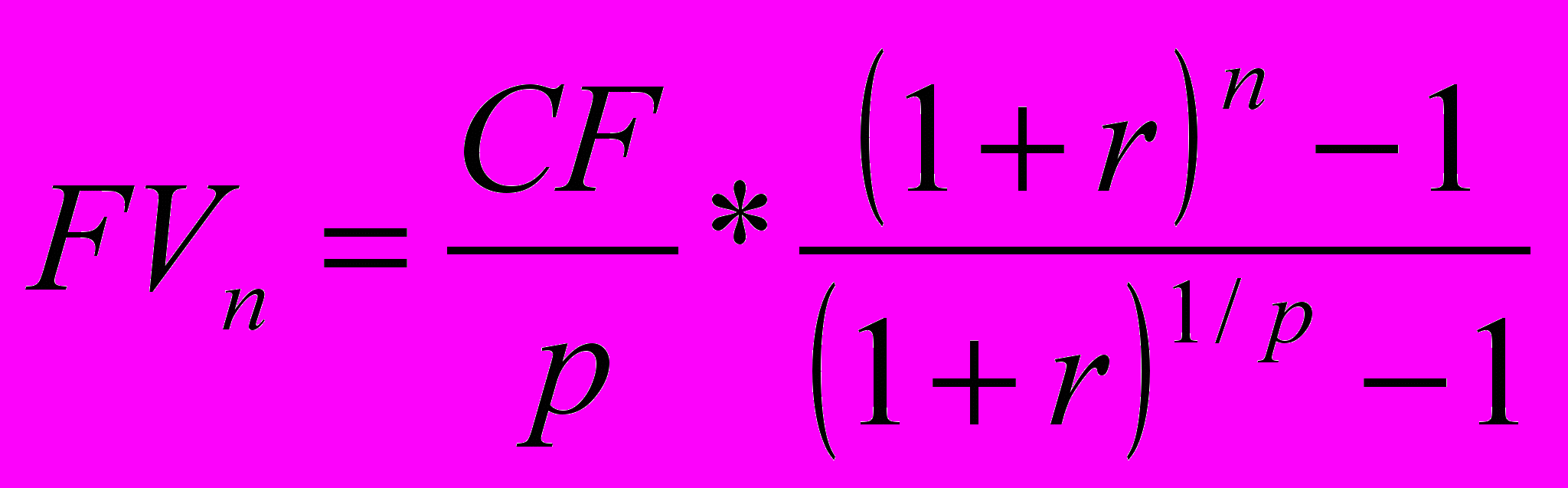
3. Если (p>m, m>1)
Текущая (современная) стоимость простого аннуитета PV
(эк. смысл) - это сумма всех составляющих платежей денежного потока, дисконтированных на момент начала операции.
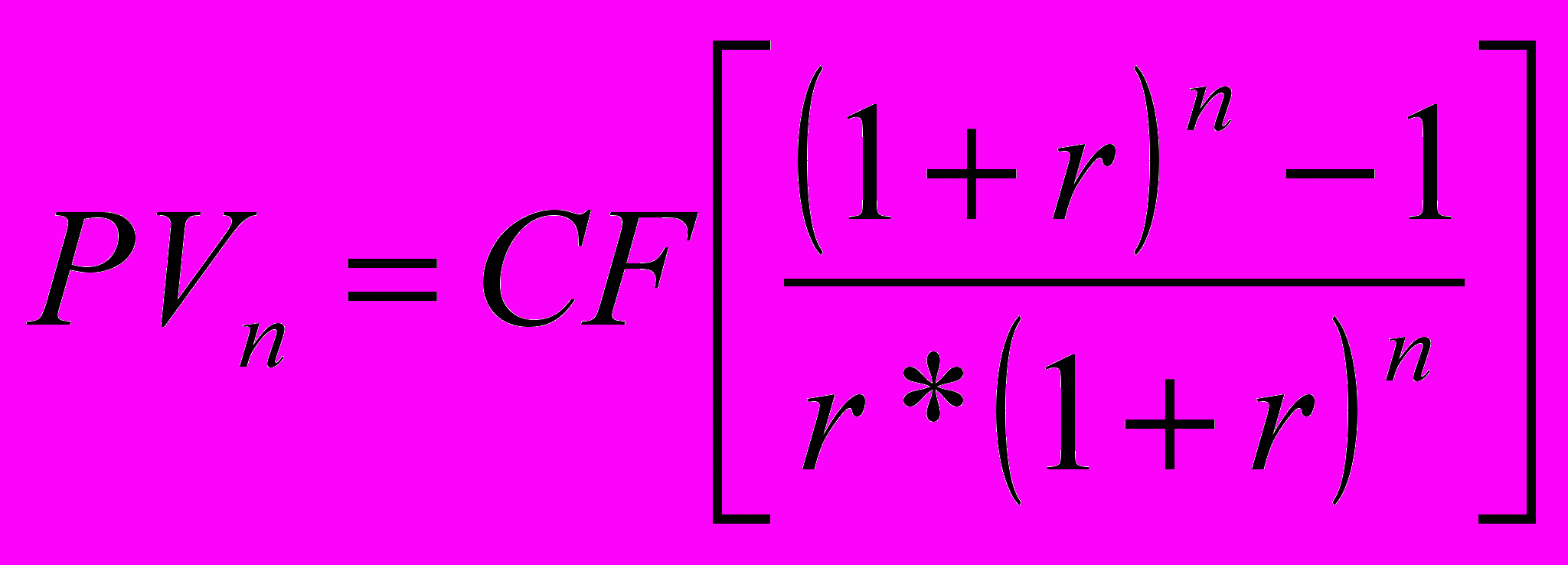
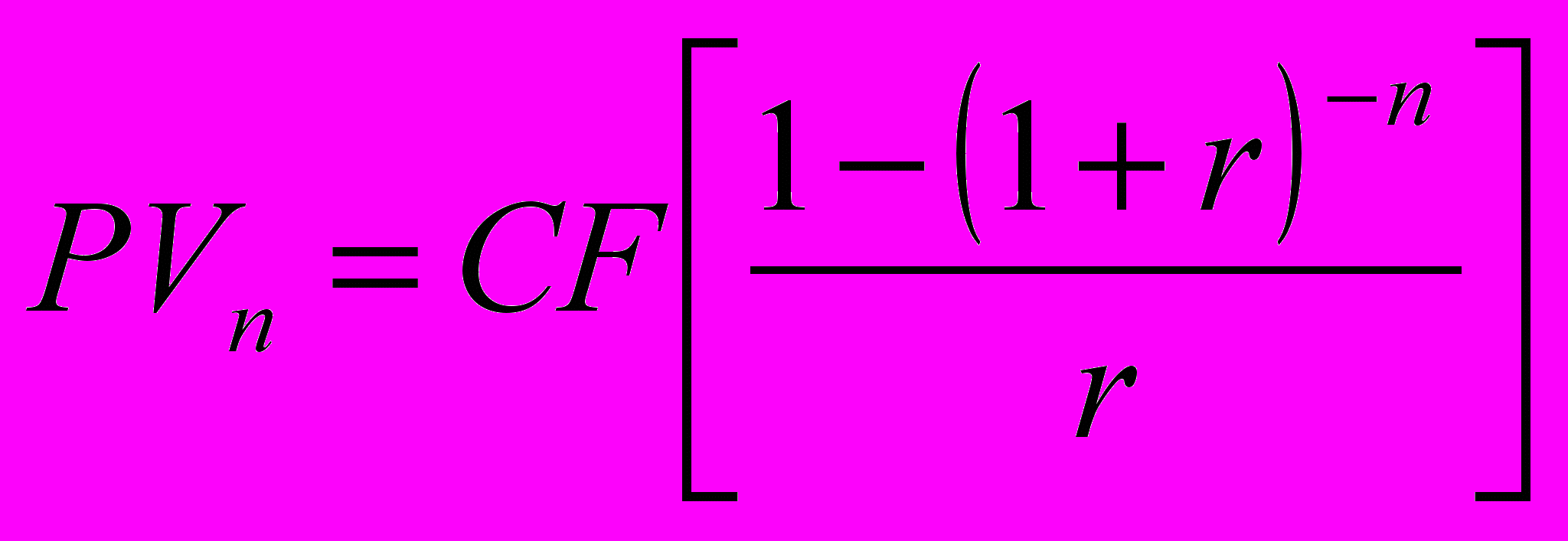
PV – современная стоимость аннуитета на 1 ден. единицу.
Если выплаты сумм аннуитета и начислений %% совпадают во времени, j=m:
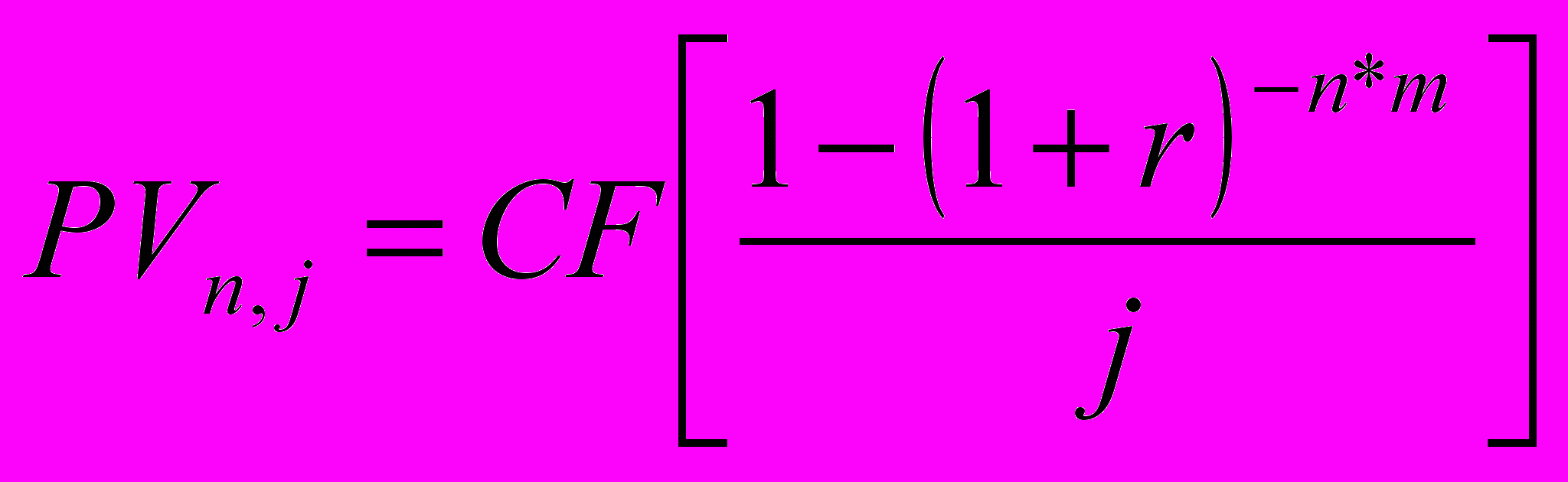
Исчисление суммы платежа CF, ставки r и длительности операций n:
Если известна FV
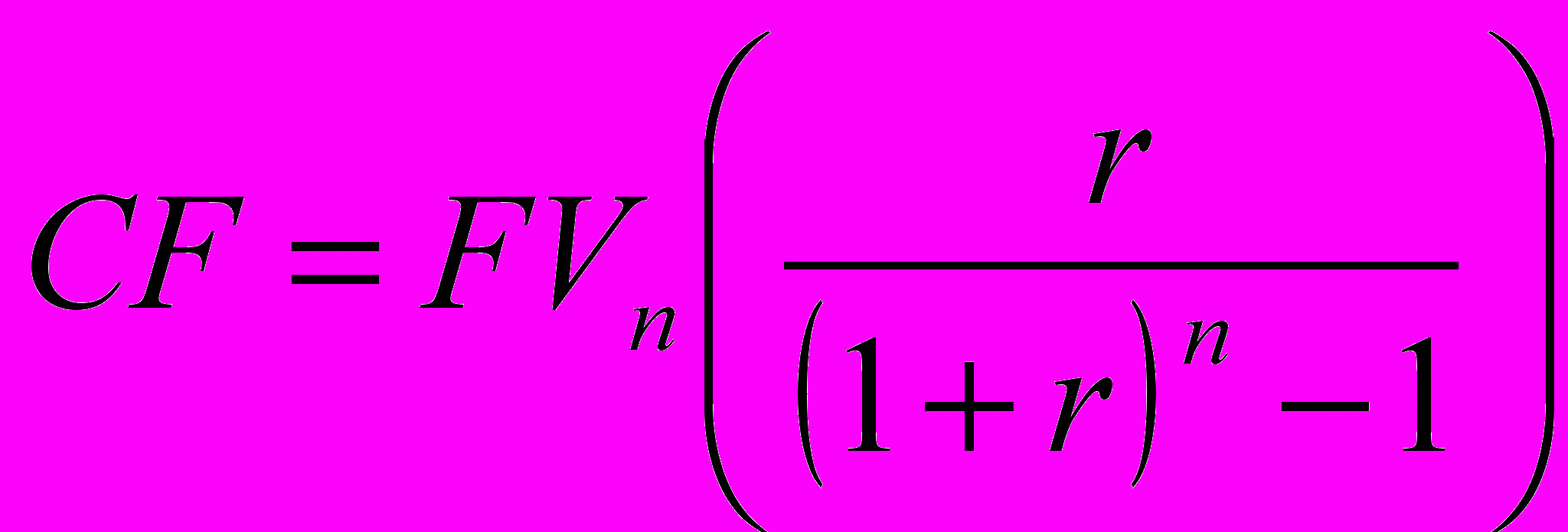
где:
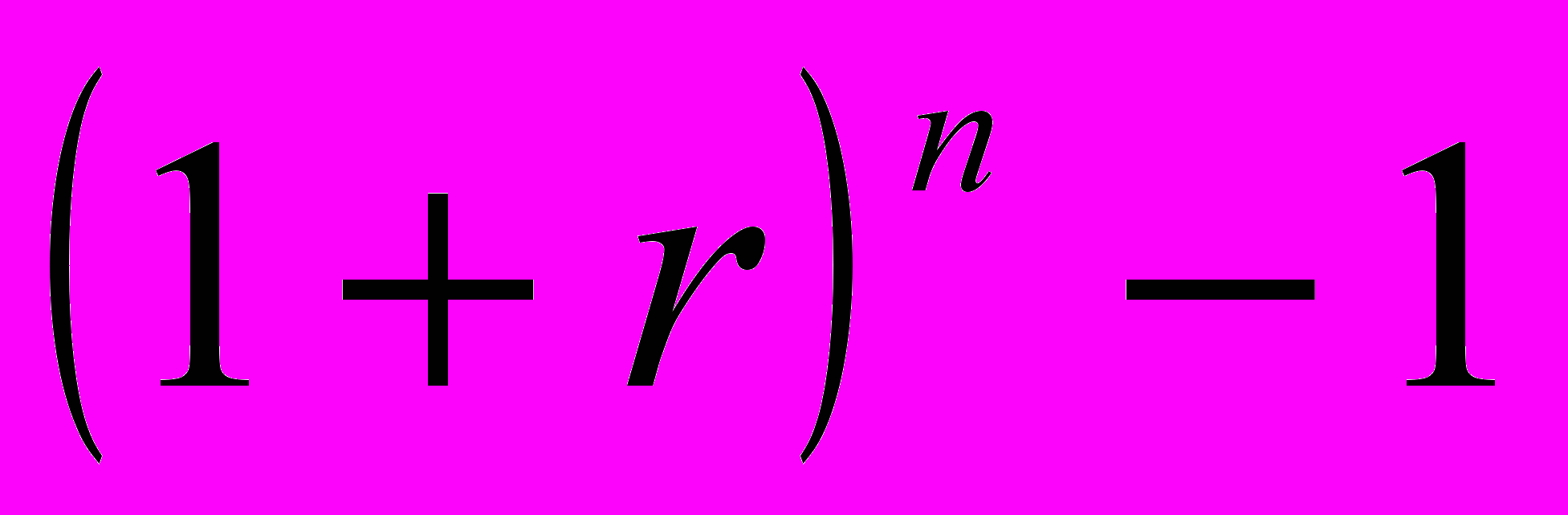- коэффициент погашения или накопления фонда – sinking fund factor.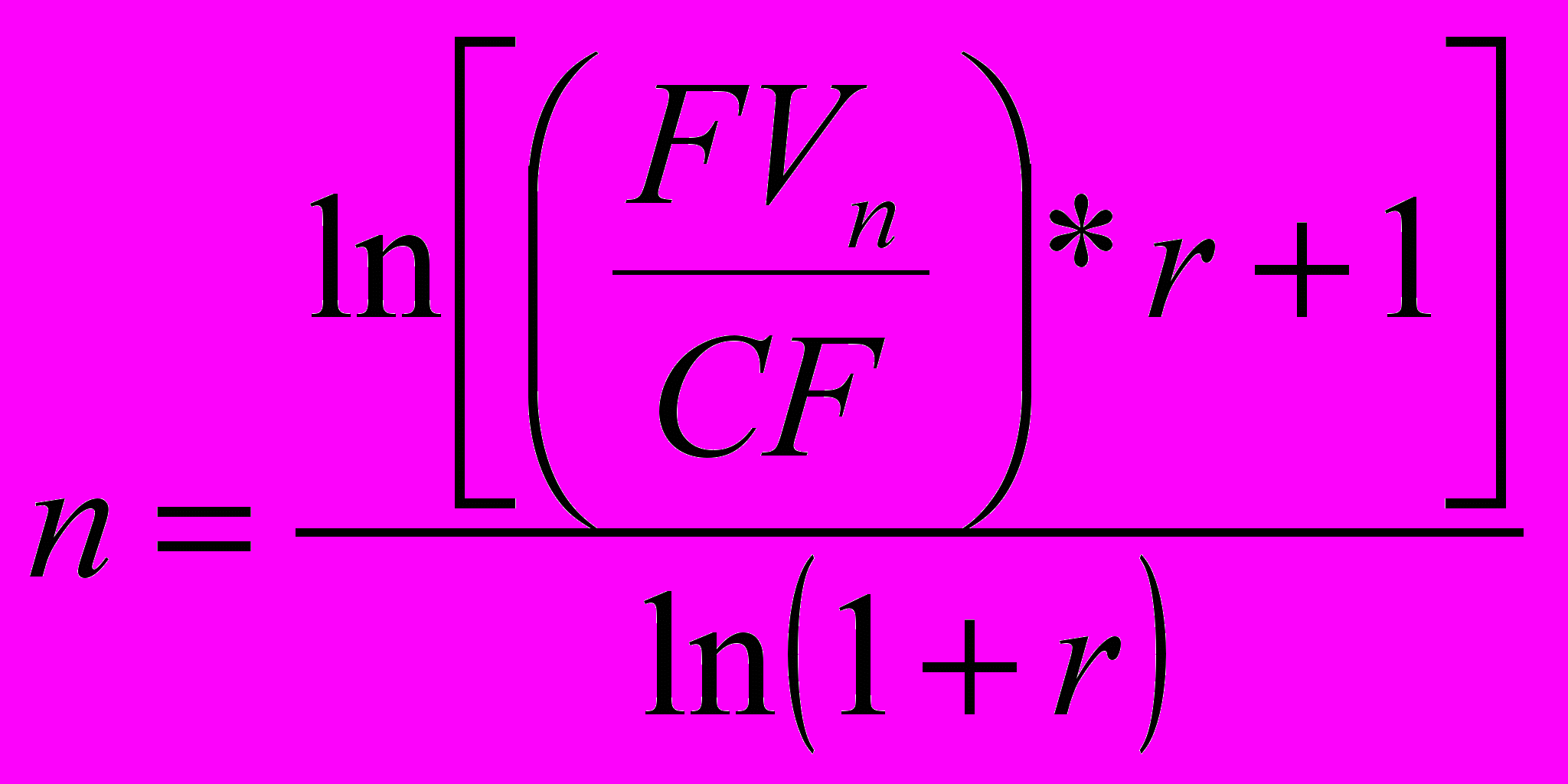
Если известна РV
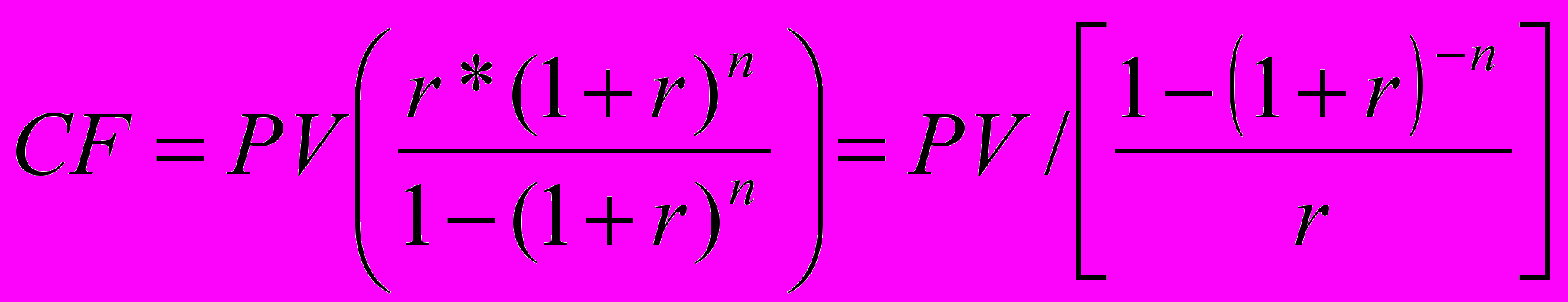
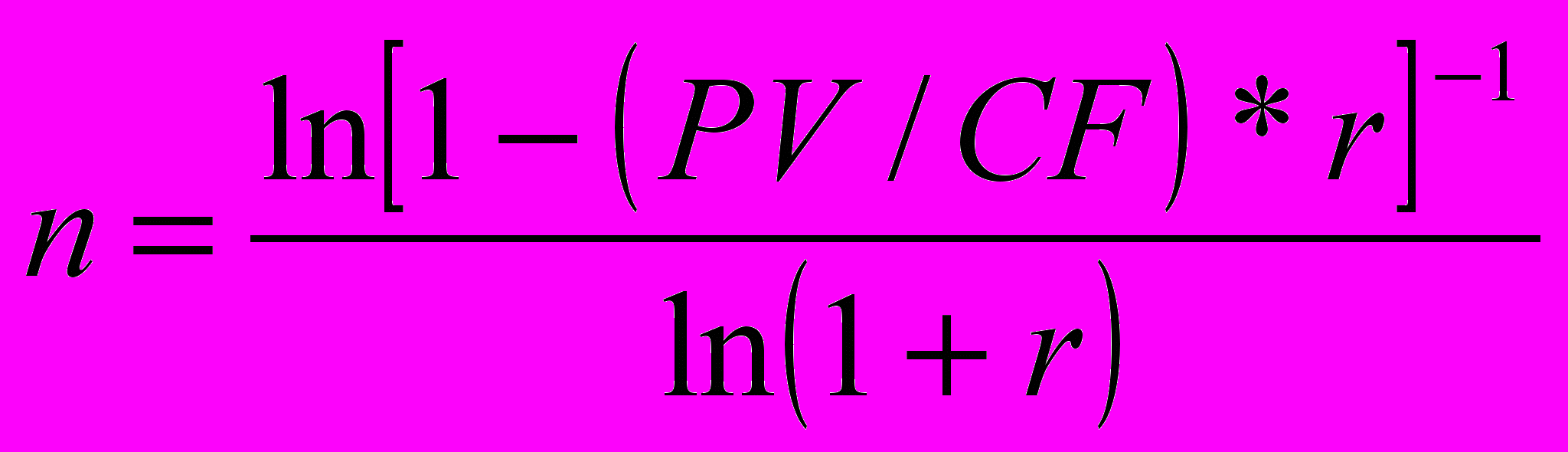
где:
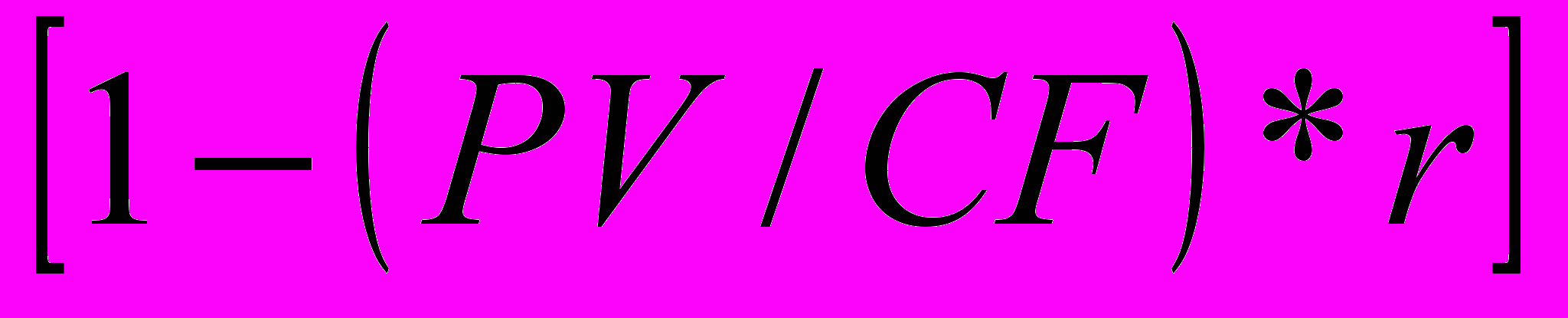- коэффициент восстановления или возмещения капитала - capital recovery factor.Задача 2.4
Финансовая компания создает фонд для погашения своих облигаций путем ежегодных помещений в банк суммы в 10000$ под 10% годовых.
Какова будет величина фонда к концу 4-го года?
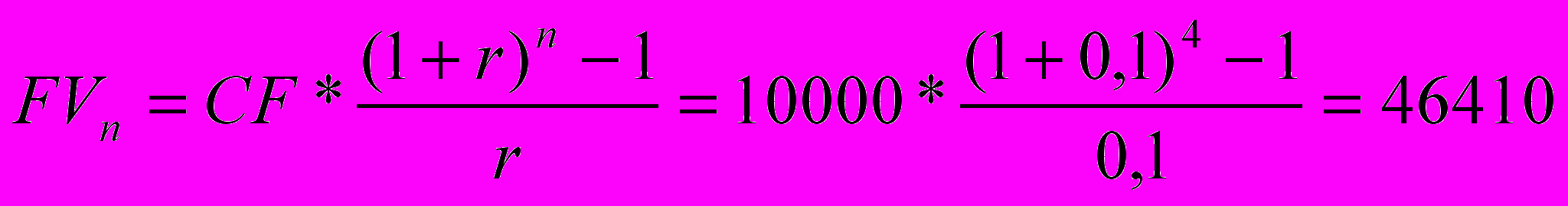
Задача 2.5
Есть 2 варианта инвестирования средств в течении 4 лет.
- в начале каждого года под 26% годовых
- в конце каждого года под 38% годовых
ежегодно вносится 300.000 рублей.
Определить сколько денег окажется на счете в конце 4-го года?
И какой вариант выгоднее.
1)
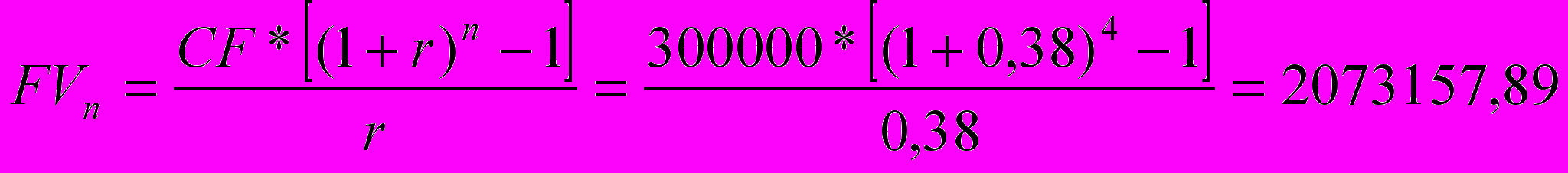
2)
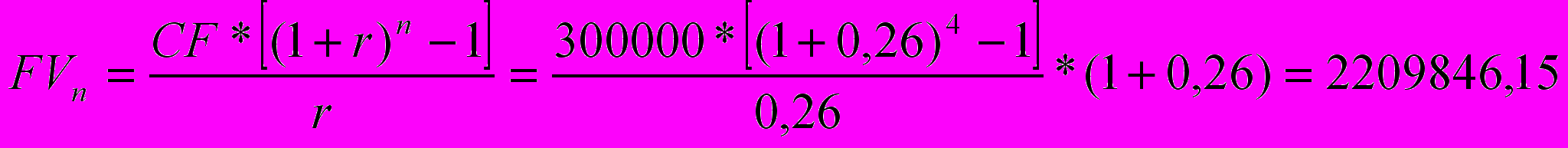
Какой из вариантов выгоднее? – 1)
Задача 2.6
Фирма взяла кредит в 100000$ на 5 лет под 12% годовых. Проценты начисляются ежеквартально и подлежат выплате вместе с основной суммой долга по истечению срока. Существует альтернатива взять кредит под 11% но выплачиваемых ежемесячно. Какой вариант лучше?
PV = 100.000
N=5
R = 12 and 11
M = 4 and 12
-----
FV - ?
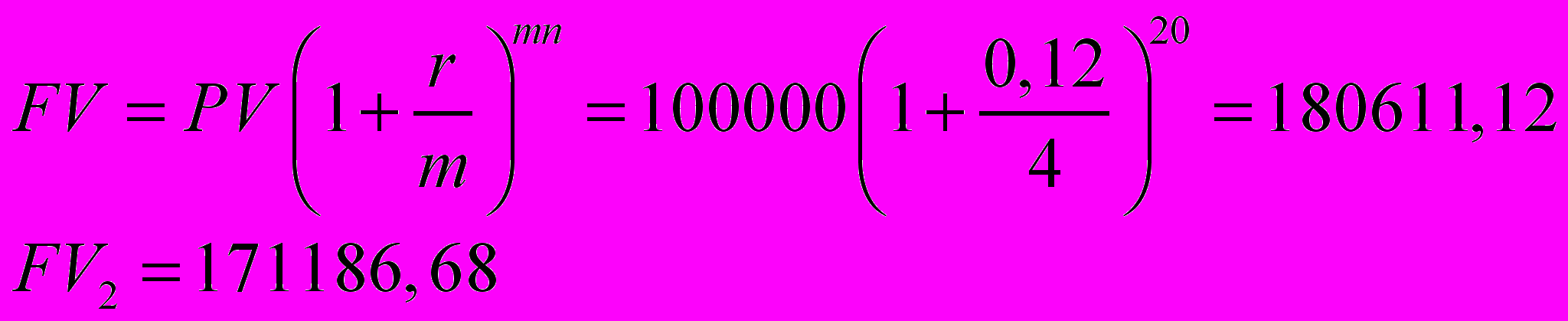
Задача 2.7
Фирма ежеквартально перечисляла в банк 300$. В течении 10 лет под 8 % годовых. Подсчитать сколько к концу 10-го года у них будет на счете.
(p>m, m>1)
(p>m, m=1)
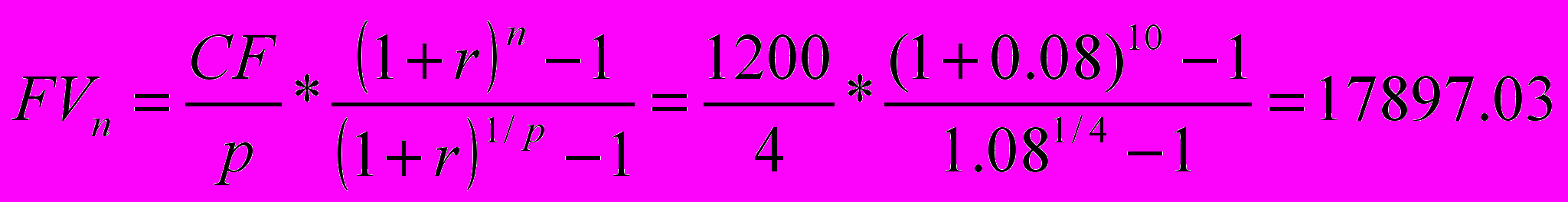
Задача 2.8
В целях привлечения клиентов банк начисляет проценты 4 раза в год под 8 % годовых. В течении 10 лет клиент вкладывал на счет 1000$ в конце каждого года.
Сколько на его счете будет в конце 10-го года.
Какая сумма была бы на его счете, при начислении процентов 1 раз в год?
m=4
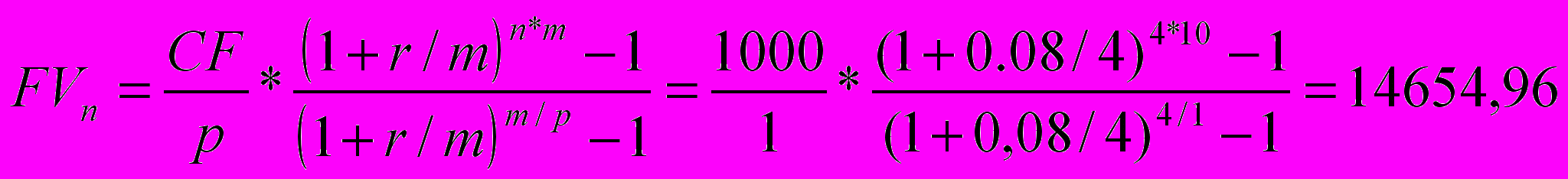
m=1
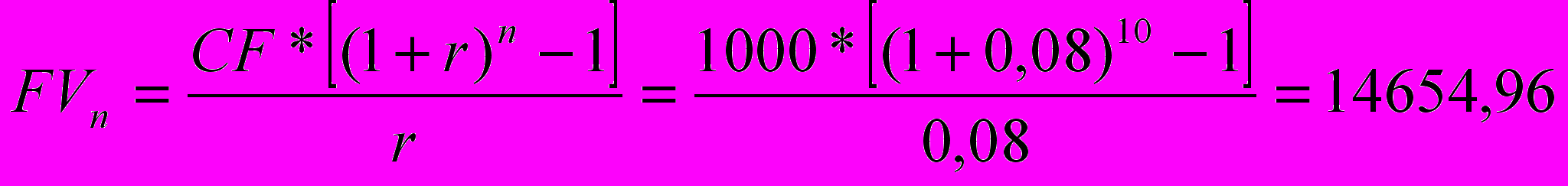
#9
ДОМАШНЕЕ ЗАДАНИЕ:
Задача Д 2.1
Рассчитать через сколько лет вклад размером 2.200.000 достигнет 1.000.000.000 если процентная ставка 16,79% производится ежеквартально
Задача Д 2.2
Для погашения задолженности единовременным платежом через 5 лет должником кредитном учреждением создается амортизационный фонд. Фонд предполагает начисление процентов исходя из 75%.
Определить размер равных взносов в конце полугодия (CF/P)
Р=2
M=4
Будущая стоимость фонда равна 10.000.000
Задача Д 2.3
Для обеспечения будущих расходов создается фонд. Средства фондов поступают в виде постоянной годовой ренты постномеранд. Размер разового платежа 16.000.000 рублей. НА поступившие взносы начисляются 11,18% годовых.
Определить когда величина фонда будет равна 600.000.000.
www.inf-man.ru