Рабочая программа для студентов I и II курсов экономических специальностей
| Вид материала | Рабочая программа |
- Рабочая программа учебной дисциплины (курса) «Обучение письменной речи, фсо», 113.73kb.
- Методические указания для практических занятий студентов экономических специальностей, 694.85kb.
- Рабочая программа для студентов I-II курсов всех специальностей роат, 93.95kb.
- Рабочая программа для студентов I-II курсов всех специальностей роат, 94.93kb.
- Рабочая программа для студентов специальности 080111 Маркетинг, цикл дс, экономический, 712.01kb.
- Рабочая программа, методические указания и контрольные задания для студентов всех специальностей, 707.03kb.
- Рабочая программа, методические указания и контрольные задания для студентов всех специальностей, 760.87kb.
- Учебное пособие для студентов экономических специальностей, 337.14kb.
- Рабочая программа для студентов I, II и III курсов всех специальностей очной формы, 84.23kb.
- Методическое пособие для выполнения курсовых работ для студентов экономических специальностей, 841.62kb.
МПС РОССИИ
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
________________________________________________________________________________
Одобрено кафедрой «Высшая математика»
Заведующий кафедрой
__________________(Джинчвелашвили Г.А.)
«_____» __________________ 2002 г.
УТВЕРЖДЕНО
Декан факультета
«Управление процессами перевозок»
_____________(Биленко Г.М.)
«_______»____________2002 г.
М А Т Е М А Т И К А
Рабочая программа
для студентов I и II курсов экономических специальностей
060400. Финансы и кредит (Ф),
060500 . Бухгалтерский учет, анализ и аудит (БУ),
060700. Национальная экономика (НЭ),
060800. Экономика и управление на предприятии (железнодорожный транспорт) (Э),
061100. Менеджмент организации (МО),
061500. Маркетинг (М),
351400. Прикладная информатика (в экономике) (ЭИ).
РГОТУПС
Москва – 2002
Рабочая программа составлена на основании примерной учебной программы дисциплины «Математика», утвержденной Министерством образования Российской Федерации для направления экономические науки.
Составитель: канд. техн. наук, доцент В.Б. Карпухин.
Рецензент: канд. физ.-мат. наук, доцент Л.Д. Блистанова.
Курс – I, II; семестры – 1,2,3,4.
Всего часов – 500(МО,М), 600(Ф,БУ,Э), 710(ЭИ), 850(НЭ).
Лекционные занятия – 32(МО,М), 44(Ф,БУ,Э), 56(ЭИ), 60(НЭ).
Практические занятия – 32(МО,М), 44(Ф,БУ,Э), 48(ЭИ), 64(НЭ).
Контрольные работы (количество) – 5(МО,М), 6(Ф,БУ,Э), 7(ЭИ), 8(НЭ).
Самостоятельная работа – 361(МО,М), 422(Ф,БУ,Э), 501(ЭИ), 606(НЭ).
Зачеты – 1 и 3 семестры.
Экзамены – 2 и 4 семестры.
Рабочая программа
1. Цель и задачи дисциплины
Дисциплина «Математика» имеет своей целью дать студентам фундаментальную математическую подготовку для формирования математического мышления и освоения специальности на высоком научно-методическом уровне.
Профессиональная подготовленность экономиста во многом зависит от того, освоил ли он современный математический аппарат и умеет ли использовать его при анализе сложных экономических процессов и принятии решений.
Задачи практической и теоретической экономики очень разнообразны. К ним относятся прежде всего методы сбора и обработки статистической информации, а также оценка состояния и перспективы развития экономических процессов. Применяются различные способы использования полученной информации – от простого логического анализа до составления сложных экономико-математических моделей и разработки математического аппарата их исследования. Неопределенность экономических процессов, значительный случайный разброс и большой объем получаемой информации предполагают необходимость привлечения к исследованию математических задач теории вероятностей и математической статистики. Наряду с моделированием экономистам необходимо изучать теорию оптимизации, которая представлена математическими методами исследования операций, в том числе линейным, нелинейным и динамическим программированием. Отмеченные направления требуют знания основополагающего математического аппарата: основ линейной и векторной алгебры, математического анализа, теории вероятностей, математической статистики, математического программирования и дискретной математики.
2. Содержание дисциплины
Введение
Представленная рабочая программа дисциплины «Математика» включает разделы, изучаемые экономистами различных специализаций – от финансовых и общеэкономических до экономической информатики. По каждой теме в квадратных скобках приведена ссылка на учебные пособия, указаны главы, параграфы, типовые примеры и задачи для самостоятельного решения. Первые 10 разделов изучаются студентами всех экономических специальностей. Содержание курса математики, отражающее специфику требований Государственных образовательных стандартов к различным экономическим специальностям, отмечено в скобках сокращенными обозначениями специальностей в названиях изучаемых для этих специальностей тем. В основе изучаемого учебного материала использованы рекомендованные Министерством образования Российской Федерации учебники для студентов высших учебных заведений, обучающихся по экономическим специальностям:
1) Общий курс высшей математики для экономистов /Под ред. В.И. Ермакова. – М.: ИНФРА–М,2000.
2) Сборник задач по высшей математике для экономистов /Под ред. В.И. Ермакова . – М.: ИНФРА–М,2001.
3) Красс М.С. Математика для экономических специальностей.– М.: ИНФРА–М,1999.
4) Математические методы принятия решений в экономике /Под ред. В.А. Колемаева /ГУУ.– М.: ЗАО « Финстатинформ», 1999.
5) Колемаев В.А. Математическая экономика. – М.: ЮНИТИ, 1998.
В процессе обучения рекомендуется также использовать современные версии пакетов прикладных программ для математических расчетов: MATH, MATLAB, MathCAD, Maple, Derive, Excel.
Раздел 1. Элементы линейной алгебры и аналитической геометрии
1.1. Прямоугольная и аффинная системы координат. Метод координат.
[5, гл.3, §1–3, задачи 1–40, гл.10, §1, 2, задачи 1–21], [Доп. 5, гл.4, 4.9, 4.19], [Доп. 6, гл.4, §2, 3].
1.2. Комплексные числа, действия с ними. Изображение комплексных чисел на плоскости. Модуль и аргумент комплексного числа.
Алгебраическая и тригонометрическая формы записи комплексного числа. Формула Эйлера. Показательная форма записи комплексного числа. Корни из комплексных чисел.
[2, 4.1, задачи 4.1–4.13], [5, гл.9, задачи 1–50], [6, 16.1, 16.2, упражнения 16.5–16.8].
1.3. Векторы. Линейные операции над векторами. Направляющие косинусы и длина вектора. Условие коллинеарности двух векторов.
[1, А, 2.1, 2.3], [2, 1.1, задачи 1.1–1.16], [5, гл.10, §3, задачи 22–40].
1.4. Скалярное произведение векторов и его свойства. Длина вектора и угол между двумя векторами. Условие ортогональности двух векторов.
[1, А, 2.2, 2.3], [2, 1.2, задачи 1.17–1.32], [5, гл.10, §4, задачи 41–62].
1.5. Система векторов. Разложение вектора по системе векторов. Линейная зависимость и независимость, базисы и ранг системы векторов. Пространство
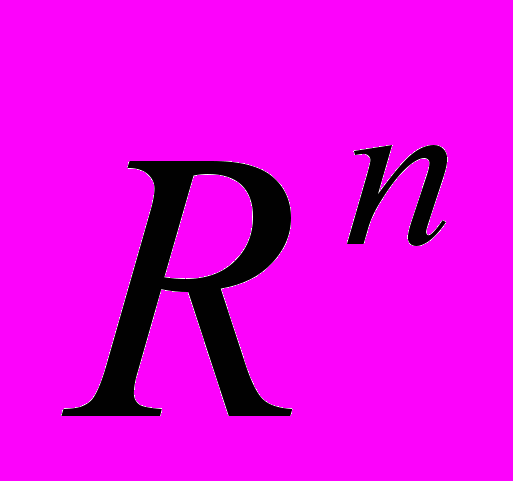. Ортогональность.[1, А, 2, 2.4–2.9], [2, 7.1–7.5, задачи 7.1–7.108].
1.6. Матрицы. Действия с матрицами. Обратная матрица. Ранг матрицы.
[1, А, 3, 3.1–3.5], [2, 5.1–5.3, задачи 5.1–5.68].
1.7. Определители. Свойства определителей. Алгебраические дополнения и миноры. Вычисление определителя разложением по строке (столбцу).
[1, А, 4.1–4.4], [2, 4.2–4.5, задачи 4.14–4.45].
1.8. Системы линейных уравнений. Метод Гаусса. Теорема Кронекера–Капелли. Формулы Крамера.
[1, А, 1, 1.1–1.5; 5, 5.1, 5.2], [2, 6.1, 6.2, задачи 6.1–6.36].
1.9. Однородные системы линейных уравнений. Фундаментальная система решений.
[1, А, 5, 5.3], [2, 7.6, задачи 7.109, 7.111–7.119, 7.127].
1.10. Общее решение системы линейных уравнений в векторной форме.
[1, А, 5, 5.4], [2, 7.6, 7.110, 7.120–7.126].
1.11. Уравнение линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.
[1, А, 6.1,6.2], [2, 2.1, задачи 2.1–2.33].
1.12. Кривые второго порядка: окружность, эллипс, гипербола, парабола, их геометрические свойства и уравнения.
[1, А, 6.1], [2, 3.1–3.4, задачи 3.1–3.40].
1.13. Уравнения плоскости и прямой в прямоугольной системе координат. Условия параллельности и перпендикулярности. Углы между двумя плоскостями, между двумя прямыми, между прямой и плоскостью. Прямые и плоскости в аффинном пространстве.
[1, А, 6.2–6.8], [2, 2.2, задачи 2.34–2.79], [Доп. 5, гл.4, 4.9, 4.19].
1.14. Поверхности второго порядка. Геометрические свойства этих поверхностей, исследование их формы методом сечений.
[3, 9.5].
1.15. Евклидово пространство. Неравенство Коши–Буняковского. Ортогональный базис. Процесс ортогонализации. Разложение вектора по ортогональному базису.
[2, 8.1–8.5, задачи 8.1–8.56].
1.16. Собственные значения и собственные векторы матриц и их свойства. Теорема о базисе пространства
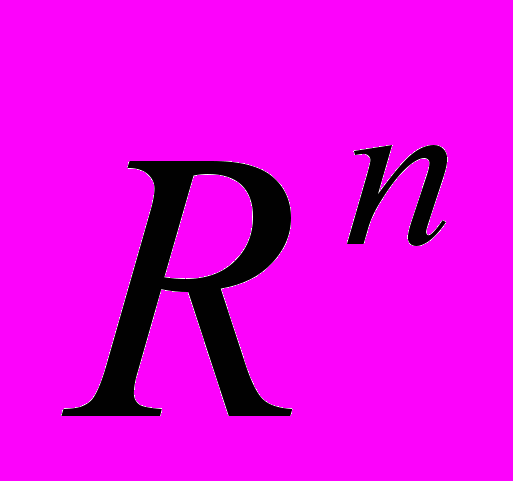из собственных векторов матрицы. Собственные векторы симметрической матрицы.[1, А, 7, 7.1–7.5], [2, 9.1–9.3, задачи 9.1–9.41].
1.17. Квадратичные формы в
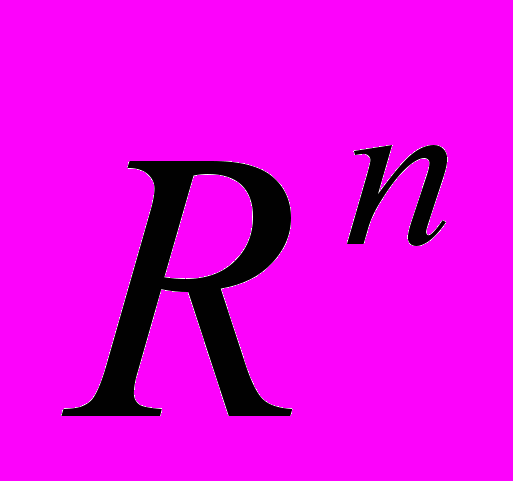. Понятие, канонический базис. Условие Якоби. Положительно и отрицательно определенные квадратичные формы. Критерий Сильвестра.[1, А, 8, 8.1–8.4], [2, 9.4, задачи 9.58–9.78].
Раздел 2. Введение в математический анализ
2.1. Множества. Операции над множествами. Числовые множества. Грани множеств. Множества в
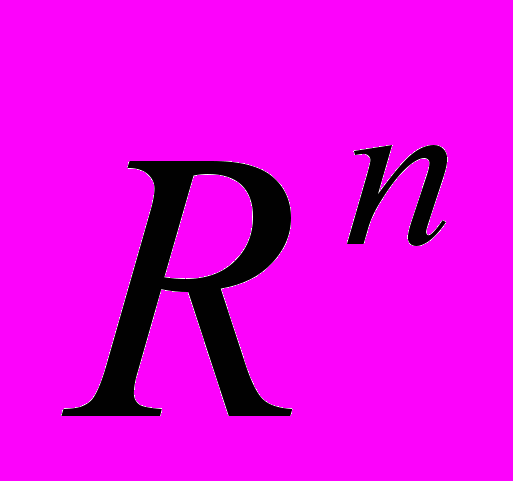. Выпуклые множества и их свойства. Соответствие множеств. Счетные и несчетные множества. Отношения. Отношения тождества и упорядоченности.[1, В, 1.1–1.4], [5,гл.1, §1, задачи 1–11,§2, задачи 12–22, §3, задачи 23–30].
2.2. Функция. Функциональное отношение. Соответствие. Способы задания. Основные элементарные функции, их свойства и графики.
[1, В, 2.1], [2, 10.1, задачи 10.1–10.55,10.2, задачи 10.56–10.85].
2.3. Числовые последовательности. Предел числовой последовательности. Стабилизация десятичных знаков у членов последовательности, имеющей предел.
Бесконечно малые и бесконечно большие величины. Свойства сходящихся последовательностей.
[1, В, 2.2, 2.3], [2, 11.1, задачи 11.1–11.18].
2.4. Алгебраические композиции числовых последовательностей и их пределы. Композиции с неопределенностью. Признаки существования предела монотонной ограниченной последовательности. Первый и второй замечательные пределы. Лемма Кантора. Теорема Больцано–Вейерштрасса. Признак Больцано–Коши.
[1, В, 2.4, 2.5], [2, 11.2, задачи 11.19–11.31].
2.5. Монотонные функции. Композиция и суперпозиция функций.
Предел функции в точке. Предел функции в бесконечности. Пределы монотонных функций.
Непрерывность функций в точке. Непрерывность основных элементарных функций. Типы разрывов.
[1, В, 3.1, 3.2], [2, 11.3, задачи 11.32–11.45, 11.5, задачи 11.54–11.58]. [5, гл.4, §2, задачи 213–305].
2.6. Сравнение бесконечно малых функций
[2, 11.4, задачи 11.46–11.53], [5, гл.4, §3, задачи 306–376].
2.7. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, существование промежуточных значений.
[1, В, 3.3].
Раздел 3. Дифференциальное исчисление функций одной переменной
3.1. Производная функции, ее геометрический смысл и смысл в прикладных задачах (скорость, плотность). Эластичность функции.
[1, В, 4.1, 4.3], [5, гл.5, §1, задачи 1–10].
3.2. Правила нахождения производной. Производная сложной и обратной функции. Дифференцирование функций, заданных неявно и параметрически.
[1, В, 4.2], [2, 12.1, задачи 12.1–12.75, 12.6, задачи 12.138–12.149], [5, гл.5, §2, задачи 11–145].
3.3. Понятие функции, дифференцируемой в точке. Дифференциал функции и его геометрический смысл.
[1, В, 4.4], [5, гл.5, §3, задачи 146–161].
3.4. Производные и дифференциалы высших порядков.
[1, В, 4.5], [2, 12.2, задачи 12.76–12.96, 12.5, задачи 12.115–12.137].
3.5. Теоремы Ферма, Ролля, Лагранжа, Коши, их применение. Правило Лопиталя.
[1, В, 4.6], [5, гл.5,§6, задачи 212–266], [2, 12.7, задачи 12.150–12.197].
3.6. Многочлен и формула Тейлора. Представление функций ехр(х), sin(x), cos(x), ln(1+x), (1+х)α по формуле Тейлора.
[1, В, 4.7], [5, гл.5,§6, задачи 2.67–2.79], [2, 12.7, задачи 12.198–12.204].
Раздел 4. Применение дифференциального исчисления для исследования функций и построения их графиков
4.1. Условия монотонности функции. Экстремумы функции, необходимое условие. Достаточные условия. Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке.
[1, В, 4.8], [2, 12.7, задачи 12.205–12.244].
4.2. Исследование выпуклости функции. Точки перегиба.
[1, В, 4.8], [2, 12.7, задачи 12.245–12.253].
4.3. Асимптоты функций.
[1, В, 4.9], [2, 12.7, задачи 12.254–12.261].
4.4. Общая схема исследования функции и построения ее графика.
[2, 12.7, задачи 12.262–12.290].
4.5. Уравнение касательной и нормали к плоской кривой в данной точке.
[2, 12.3, задачи 12.97–12.109].
Раздел 5. Неопределенный интеграл
5.1. Первообразная функция. Неопределенный интеграл и его свойства. Таблица интегралов.
[1, В, 6.1], [2, 14.1, задачи 14.1–14.17], [5, гл.6, §1].
5.2. Методы интегрирования. Замена переменной, интегрирование по частям. Интегрирование рациональных выражений, тригонометрических функций, некоторых иррациональных функций. Понятие о неберущихся интегралах.
[1, В, 6.2], [6, гл.10, 10.9], [2, 14.2, задачи 14.18–14.154], [5, гл.6, §2,задачи 1–253].
Раздел 6. Определенный интеграл
6.1. Задачи, приводящие к понятию определенного интеграла. Определенный интеграл, его геометрический смысл и свойства.
[1, В, 7.1, 7.2].
6.2. Формула Ньютона–Лейбница, ее применение для вычисления определенных интегралов.
[1, В, 7.3], [2, 15.1, задачи 15.1–15.21].
6.3. Замена переменной в определенном интеграле, интегрирование по частям.
[1, В, 7.3], [2, 15.2, 15.3, задачи 15.22–15.41].
6.4. Приложения определенных интегралов.
[1, В, 7.4], [2, 15.4, задачи 15.42–15.67].
6.5. Несобственные интегралы. Интегрирование неограниченных функций и по бесконечному промежутку. Несобственные интегралы от положительных функций. Признаки сравнения.
[1, В, 8.1–8.3], [2, 15.5, задачи 15.68–15.104].
6.6. Двойной и тройной интегралы, их свойства. Вычисление кратных интегралов повторным интегрированием.
[1, В, 9.1–9.3], [2, 15.6, задачи 15.105–15.120].
Раздел 7. Функции нескольких переменных
7.1. Функции нескольких переменных. Область определения. Предел функции. Непрерывность.
[1, В, 5.1], [2, 13.1, задачи 13.1–13.21].
7.2. Частные производные. Полный дифференциал, его геометрический смысл, связь с частными производными, применение в приближенных вычислениях.
[1, В, 5.2], [2, 13.3, задачи 13.59–13.76]. [2, 13.2, задачи 13.22–13.42].
7.3. Частные производные и полные дифференциалы высших порядков. Независимость смешанных производных от порядка дифференцирования.
[1, В, 5.3], [2, 13.4, задачи 13.77–13.99].
7.4. Производная по направлению. Градиент и его свойства.
[2, 13.2, задачи 13.43–13.58].
7.5. Экстремумы функции нескольких переменных. Необходимое условие экстремума. Наибольшее и наименьшее значения функции в ограниченной замкнутой области.
[1, В, 5.4], [2, 13.5, задачи 13.100–13.107].
7.6. Условный экстремум. Метод множителей Лагранжа. Примеры применений при поиске оптимальных решений.
[1, В, 5.4], [2, 13.6, задачи 13.108–13.115].
Раздел 8. Ряды
8.1. Понятие числового ряда и его сходимости. Критерий Коши сходимости числового ряда. Необходимое условие сходимости. Свойства сходящихся рядов.
[1, В, 10.1], [2, 17.1, задачи 17.1–17.14].
8.2. Признаки сходимости рядов: общий признак, признак сравнения, признак Коши, признак Даламбера, интегральный признак Коши.
[1, В, 10.2], [2, 17.2, задачи 17.15–17.37].
8.3. Понятия знакопеременного ряда, абсолютно сходящегося ряда, условно сходящегося ряда. Теорема Дирихле. Теорема Римана.
[1, В, 10.2], [2, 17.3, задачи 17.38–17.4].
8.4. Понятие знакочередующегося ряда. Признак Лейбница.
[1, В, 10.2], [5, гл.8, §3, задачи 86–102].
8.5. Понятие функционального ряда. Область сходимости. Критерий Коши равномерной сходимости. Признак Вейерштрасса.
[1, В, 11.1], [2, 17.4 задачи 17.47–17.56].
8.6. Свойства равномерно сходящихся рядов.
[1, В, 11.2].
8.7. Степенные ряды. Теорема Абеля. Радиус сходимости и способы его определения. Свойства степенных рядов.
[1, В, 11.3], [2, 17.5, задачи 17.57–17.69].
8.8. Интегрирование и дифференцирование степенных рядов.
[1, В, 11.4].
8.9. Ряды Тейлора и Маклорена. Применение рядов к приближенным вычислениям.
[1, В, 11.5], [2, 17.6, задачи 17.70–17.101].
Раздел 9. Обыкновенные дифференциальные
и разностные уравнения
9.1. Дифференциальные уравнения первого порядка. Основные понятия: определение, решение, общее решение, частное решение дифференциального уравнения первого порядка. Теорема Коши о существовании и единственности решения (без доказательства). Интегральная кривая. Начальные условия. Задача Коши. Особые точки. Геометрический смысл уравнения первого порядка. Элементы качественного анализа.
[3, гл.18, п.18.1], [6, гл.12, п.12.1, 12.2, 12.3], [2, 16.1, задачи 16.1–16.12].
9.2. Дифференциальные уравнения первого порядка. Виды уравнений и методы решения. Уравнения с разделяющимися переменными. Неполные уравнения. Линейные уравнения, однородные и неоднородные.
[3, гл.18, п.18.2], [6, гл.12, п.12.4, 12.5, 12.6], [2, 16.2, задачи 16.13–16.44], [5,гл.14, §1, задачи 1–77].
9.3. Дифференциальные уравнения второго порядка. Основные понятия. Теорема Коши о существовании и единственности решения (без доказательства). Задача Коши. Уравнения, допускающие понижение порядка.
[3, гл.19, п.19.1], [2,16.3, задачи 16.45–16.60], [6, гл.12, п.12.7].
9.4. Дифференциальные уравнения второго порядка. Линейные уравнения, однородные и неоднородные.
[3, гл.19, п.19.1], [5, §2, задачи 78–117].
9.5. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Краевая задача.
[3, гл.19, п.19.1], [6, гл.12, п.12.8], [2, 16.4, задачи 16.61–16.83].
9.6. Дифференциальные уравнения высших порядков. Система уравнений первого порядка. Нормальная форма. Теорема Коши. Задача Коши и краевая задача для уравнения n–го порядка. Линейные уравнения n–го порядка. Линейные уравнения n–го порядка с постоянными коэффициентами.
[3, гл.19, п.19.2], [5,§4, задачи 208–228].
9.7. Линейные обыкновенные разностные уравнения. Основные понятия. Сетки и сеточные функции. Однородные и неоднородные уравнения. Свойства решений.
[3, гл.21, п.21.1].
9.8. Решение линейных обыкновенных разностных уравнений с постоянными коэффициентами. Примеры. Системы линейных разностных уравнений первого порядка.
[3, гл.21, п.21.2], [Доп. 3, гл.6, §6.9].
Раздел 10. Теория вероятностей и математическая статистика
10.1. Случайные события. Алгебра событий. Классическое и статистическое определение вероятности события.
1, С, 1.1–1.3, 2,19.1, 7,15.1, Доп. 10, гл. 1, §1.
10.2. Теоремы сложения и умножения вероятностей. Теорема сложения вероятностей несовместных событий. Условная вероятность. Теорема умножения вероятностей. Теорема сложения вероятностей совместных событий.
1,С,2.1–2.4,2,19.2,7, 15.12, Доп. 10, гл.2, §1.
10.3. Основные формулы для вероятностей событий. Формула полной вероятности. Формула Байеса. Формула Бернулли. Формула Пуассона.
1,С, 3.1–3.4,2,19.3–19.5,7,15.3,Доп. 10, гл.2,§2–4,гл.3,§1.
10.4. Виды случайных величин. Распределение дискретной случайной величины. Математическое ожидание и дисперсия числа
появления события в независимых испытаниях. Начальные и центральные моменты.
1,С,4.1–4.6,2,20.1,20.2,7,16.1,Доп. 10,гл,4,§1–4.
10.5. Непрерывные случайные величины. Функция и плотность распределения вероятностей. Квантиль. Математическое ожидание и дисперсия. Мода и медиана. Моменты.
1,С,5.1,5.2,2,21.1,21.2,7,16.3,1–4,Доп. 10,гл.6,§1–3.
10.6. Равномерное распределение. Экспоненциальное распределение. Нормальное распределение. Функция Лапласа.
1,С,5.3–5.5,2,21.3–21.5,7,16.3,5,6,Доп. 10,гл.6,§4–6.
10.7. Системы случайных величин. Распределение двумерной случайной величины. Ковариация и коэффициент корреляции. Линейная регрессия.
1,С,6.1–6.3, 2,22.1,22.2,Доп. 10, гл.8,§ 1–4.
10.8. Закон распределения вероятностей для функций случайных величин
7,18.1,Доп. 10, гл.7 ,§1,2
10.9. Закон больших чисел. Неравенство Чебышева. Центральная предельная теорема и ее следствия.
1,С, 7.1,7.2,7,17.1,Доп. 10, гл.5,§ 1,2.
10.10. Статистические методы обработки экспериментальных данных. Генеральная совокупность и выборка. Типы выборок. Статистическое распределение выборки. Эмпирическая функция распределения. Гистограмма.
1,С,8.1–8.3,2,23.1–23.3,7,16.4,18.2,1Доп. 10, гл.9,§1–3.
10.11. Статистические оценки. Несмещенные, эффективные и состоятельные оценки. Выборочная средняя и выборочная дисперсия. Анализ смещенности выборочной средней и выборочной дисперсии. Начальный и центральный эмпирические моменты. Число степеней свободы. Основные законы распределения статистических оценок.
1,С,9.1–9.5,9.10,2,24.1,Доп. 9, гл. 16, §1–13.
10.12. Точечная и интервальная оценки. Доверительный интервал. Метод моментов и метод наибольшего правдоподобия для точечной оценки параметров распределения.
1,С, 9.6–9.8,2,24.2,24.3,7,18.2,2,3,Доп. 10, гл. 10, §1–3.
10.13. Доверительный интервал для оценки математического ожидания и среднего квадратического отклонения нормального распределения.
1,С, 9.9,9.11,2,24.4,7,18.2,4,Доп. 10, гл. 10, §4.
10.14. Проверка статистических гипотез. Статистическая гипотеза. Ошибки первого и второго рода. Статистический критерий проверки нулевой гипотезы. Сравнение двух дисперсий нормальных генеральных совокупностей, сравнение выборочной средней с математическим ожиданием, сравнение выборочной дисперсии с генеральной дисперсией, сравнение двух математических ожиданий.
1,С, 10.1–10.3,2,25.1–25.4,Доп. 10, гл. 13, §1–6.
10.15. Проверка гипотезы о распределении генеральной совокупности. Критерий Пирсона.
1,С, 10.4,2,25.5,Доп. 10, гл. 13,§16–21.
10.16. Зависимости между случайными величинами. Типы зависимостей. Регрессионный анализ. Выборочное уравнение регрессии. Отыскание параметров выборочного уравнения регрессии по несгруппированным и сгруппированным данным.
1,С,11.1–11.3,2,26.1,26.2,7,18.3,Доп. 10, гл. 12,§1–3.
10.17. Дисперсионный анализ. Понятие о дисперсионном анализе. Факторная и остаточная дисперсии.
1,С,12.1,12.2,2,27,Доп. 10, гл. 14, §1,2.
Раздел 11. Экономико–математические методы
11.1. Математическое программирование (Ф,БУ,НЭ,МО)
11.1.1. Математическая модель задачи математического и линейного программирования. Примеры составления математических модолей экономических задач. Каноническая форма и приведение к ней общей задачи линейного программирования.
1,D, 1,1.1–1.4,2,28,28.1,28.2.
11.1.2. Графический метод решения задач линейного программирования. Задачи сдвумя и с
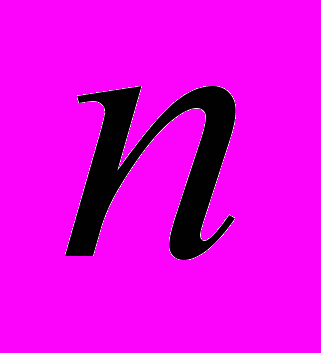переменными. Свойства решений задач линейного программирования. Многоугольники и многогранники. Экстремум целевой функции. Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками.1,D, 2,2.1,2.2,3,3.1–3.3,2,29,29.1,29.2.
11.1.3. Симплексный метод решения задач линейного программирования. Нахождение начального опорного решения и переход к новому опорному решению. Преобразование целевой функции. Улучшение опорного решения. Алгоритм симплексного метода. Метод искусственного базиса и особенности его алгоритма.
1,D, 4,4.1–4.6,2,30,30.1–30.3.
11.1.4. Теория двойственности. Виды математических моделей двойственных задач. Правила составления двойственных задач. Первая и вторая теоремы двойственности. Двойственный симплексный метод и его алгоритм. Постоптимальный анализ.
1,D,5,5.1–5.7,2,31,31.1–31.4.
11.1.5. Транспортная задача линейного программирования. Формулировка, математическая модель, необходимое и достаточное условия разрешимости, свойство системы ограничений, опорное решение. Методы построения начального опорного решения. Переход от одного опорного решения к другому. Распределительный метод. Метод потенциалов и его алгоритм. Особенности решения транспортных задач с неправильным балансом. Транспортная задача с ограничениями на пропускную способность. Транспортная задача по критерию времени. Применение траспортной задачи для решения экономических задач.
1,D, 6,6.1–6.14,2,32,32.1–32.4.
11.1.6. Целочисленное программирование. Метод Гомори. Метод ветвей и границ.
1,D,7,7.1,7.2,2,33.
11.1.7. Нелинейное программирование. Выпуклые функции и множества. Задача выпуклого программирования. Методы решения задачи нелинейного программирования. Теорема Куна–Таккера. Примеры экономических задач.
10, гл.3,§3.1–3.6,4, гл.28,§28.1–28.4.
11.1.8. Динамическое программирование. Принцип оптимальности и реккурентные соотношения Беллмана. Примеры экономических задач.
4, гл. 29,§29.1,29.2,10, гл. 5,§5.4, гл. 6, §6.7,Доп. 11, гл.1,§1.4, п. 1.4.6,26, гл. 5,27, гл. 10.
11.2. Теория игр (Ф,БУ,ЭИ)
11.2.1. Конфликтные ситуации. Кооперативные игры. Оптимальность по Парето. Переговорное множество.
10, гл. 8,§8.1–8.3.
11.2.2. Матричные игры. Игры с нулевой суммой. Условия игры. Чистые и смешанные стратегии. Определение оптимальных стратегий и цены игры. Решение игр в чистых стратегиях и седловые точки матрицы игры. Решение игр с матрицами размера
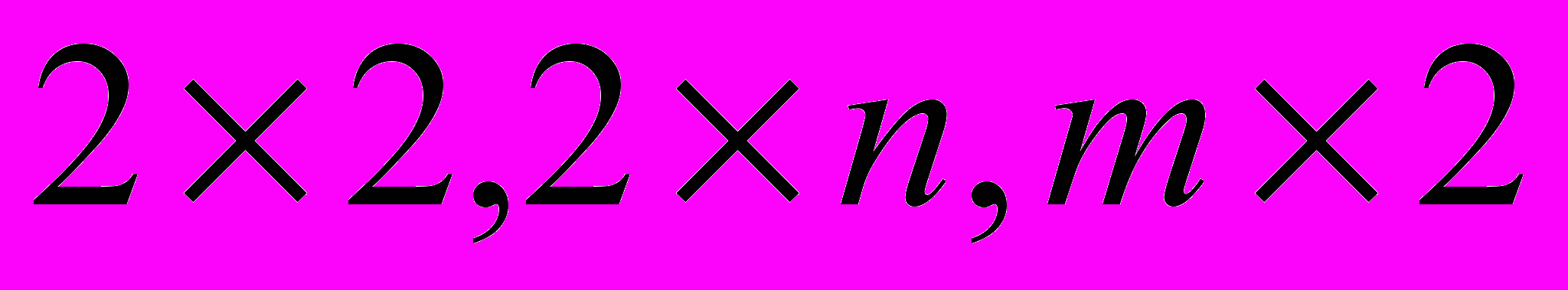. Сведение матричной игры к задаче линейного программирования.10, гл. 8, §8.4,4, гл. 31, §31.1–31.4.
11.2.3. Игры с природой. Критерии выбора оптимальной стратегии. Примеры экономических задач.
4, гл. 31, §31.5–31.7,9, гл. 8, §8.4
11.3. Теория графов (Ф,БУ,ЭИ)
11.3.1. Основные понятия и виды графов. Аналитическое описание графа. Численные характеристики графов. Операции над графами. Методы графа. Матрица смежностей вершин, матрица инциденций, матрица циклов.
10, гл. 4, §4.1,4.2.
11.3.2. Кратчайший путь, кратчайшее дерево, критический путь на графе и алгоритмы их нахождения. Примеры.
10, гл. 4,§4.3–4.5,4, гл. 30, §30.1, 30.2,9 гл. 3, §3.6.
11.3.3. Потоки на сетях. Теорема и алгоритм Форда–Фалкерсона нахождения потока наибольшей величины. Пропускная способность разреза.
10, гл. 4,§4.6.
11.4. Элементы теории марковских процессов и систем массового обслуживания (Ф,БУ,НЭ,МО,Э,М,ЭИ)
11.4.1. Цепи Маркова. Вероятности переходов и состояний. Классификация состояний. Эргодическая теорема. Процессы гибели и рождения, вероятности состояний.
11, раздел 2, гл.1, §1–5.
11.4.2. Системы массового обслуживания с ожиданием, отказами, ограниченным накопителем, ограниченным временем ожидания. Замкнутые, разомкнутые, многофазные системы массового обслуживания. Стохастические сети.
11, раздел 2, гл. 2, §6–13,9, гл. 8, §8.3,4, гл. 32, § 32.1–32.5.
Раздел 12. Экономико–математические модели (Ф,БУ)
12.1. Моделирование в экономике и его использование в развитии и формализации экономической теории. Математическая модель и ее основные элементы. Основные типы моделей.
8, Введение,Доп. 8, гл.1,§1.1–1.3.
12.2. Функции полезности, спроса и предложения. Кривые и поверхности безразличия. Кривые «доход–спрос», «объем производства–доход», «объем производства – издержки». Модель поведения потребителя. Уравнение Слуцкого. (Ф,БУ,НЭ,МО).
8, гл. 3, §3.1,3.2,Доп. 8, гл. 2,§2.5, гл. 9, §9.1–9.3.
12.3. Эластичность функции и ее геометрический смысл. Свойства эластичности. Применение эластичности в экономическом анализе.
Доп. 8, гл. 5, §5.1–5.3.
12.4. Производственные функции. Понятие, свойства, предельные и средние значения. Зависимость между темпами прироста показателей выпуска и затрат ресурсов. Функция Кобба–Дугласа. Функции с бесконечной и постоянной эластичностью замещения.
8, гл.1, §1.1,Доп. 8, гл. 10, §10.1–10.5.
12.5. Модели оптимизации производства. Основные понятия. Функции спроса на ресурсы в случаях долговременного и краткосрочного промежутка. Комбинация ресурсов, максимизирующая объем выпуска при ограничении на затраты. Комбинация ресурсов, минимизирующая издержки при фиксированнном объеме выпуска. (Ф,БУ,НЭ,МО).
Доп. 8, гл. 11, §11.1.–11.5.
12.6. Модели поведения фирмы в условиях несовершенной и совершенной конкуренции. Показатели экономического роста. Простейшая модель равновесия. Равновесие Курно. Равновесие и неравновесие Стакельберга. Модели установления равновесной цены. Паутинообразная модель. Модель Эванса. Модель общего экономического равновесия Вальраса. Модель расширенного воспроизводства Маркса.
8, гл. 4, §4.1, 4.2, гл. 5, §5.1, 5.2,Доп. 8, гл. 12, §12.1–12.3,Доп. 11, гл. 2, §2.3, п. 2.3.1, 2.3.2.
12.7. Статическая и динамическая модели межотраслевого баланса. Балансовый метод. Принципиальная схема межотраслевого баланса. Модель Леонтьева. Модель Неймана.
8, гл. 1, §1.2, гл. 2, §2.6,9, §6.1–6.5.
12.8. Общие модели развития экономики. Циклы экономического развития. Виды экономического роста. Классическая модель рыночной экономики. Модель Кейнса. Однофакторные модели экономического роста. Многофакторные модели экономического роста. Модель Солоу. Модель Эрроу. Монетаристский и кейнсианский подходы к прогнозированию и регулированию рыночной экономики.
Доп. 11, гл.2, §2.1,2.2, п. 2.2.1–2.2.3,8 гл. 2, §2.1–2.3, гл. 6, §6.1,6.2,Доп. 8, гл. 12,§12.4.
Раздел 13. Численные методы (Э,М,ЭИ)
13.1. Влияние на вычисляемые результаты ошибок во входных днных и погрешностей округления при выполнении арифметических операций. Элементы теории погрешностей. Погрешность функции. Прямая и обратная задачи.
12, введение,13, предварительные замечания, стр. 7–10,14, гл. 1, §1–4, Доп. 13, гл.1, §1,2.
13.2. Численное решение систем линейных уравнений. Прямые и итерационные методы. Схема исключения неизвестных. Метод простых итераций.
18, гл. 4, §4.3,13, лекция 2, стр.21–30; лекция 3, стр 35–42, 14, гл.2, §1–3,Доп. 14, гл. 3, §3.1–3.3; гл. 4, §4.1–4.3.
13.3. Численное решение нелинейных уравнений и их систем. Методы половинного деления, Ньютона, простых итераций, релаксаций, хорд.
1,В, 13, 13.4,18, гл 4, §4.4.,13, лекция 1, стр. 11–18 лекция 3, стр. 35–42, 14, гл. 4§1–6;гл.5.§1–3,Доп. 13, гл 5, §18,19,Доп. 14, гл. 6, §6.1–6.3.
13.4. Интегрированные и приближение функций. Полиноминальная интерполяция. Многочлены Чебышева. Многочлены наилучшего равномерного приближения. Приближение сплайнами.
1, В, 13,13.1,13.5, 18, гл. 4, §4.1,4.2,12, гл.2,§1,13, лекция 5, стр. 57–65,14, гл.6, §1–5,Доп. 13, гл.2, §3.4,6.7, Доп. 14, гл. 1, §1.1–1.3.
13.5. Численное дифференцирование и интегрирование. Погрешность формул численного дифференцирования. Неустойчивость численного дифференцирования. Задачи и алгоритмы приближенного вычисления интегралов. Погрешность и устойчивость квадратурных формул.
1,В, 13, 13.3,18, гл. 4, §4.5,12, гл. 2, §2,13, лекция 6, стр. 70–80,14, гл.7, стр. 132–138, гл. 8, §1–3,Доп. 13, гл. 2, §5, гл.3, §8–11,Доп. 14, гл.2,§2.1–2.3.
13.6. Численные методы решения обыкновенных дифференциальных уравнений. Задача Коши. Методы Эйлера. Методы Рунге–Кутты. Разностная аппроксимация краевой задачи, линейный и нелинейный случаи. Устойчивость и сходимость.
1,В,13,13.2,18, гл. 4, §4.6,12, гл. 5,§1,13, лекция 7, стр 84–91, лекция 8, стр. 98–108,14, гл. 9, §1–6, гл. 10, §1–6,Доп. 13, гл. 7, §23–25, Доп. 14, гл. 9, §9.1–9.3.
13.7. Задачи минимизации функций. Поиск минимума функции многих переменных. Методы решения задач оптимизации.
Доп. 14, гл. 7, §7.1–7.3.
13.8. Обзор и анализ численных методов, применяемых в пакетах прикладных программ.
15,16,17.
Раздел 14. Элементы дискретной математики (ЭИ)
14.1. Элементы комбинаторики. Перестановки, размещения и сочетания. Бином Ньютона. Свойства биномиальных коэффициентов. Полиномиальная формула. Понятие о комбинаторном анализе.
19;21; Метод. пос. 10;26.
14.2. Элементы классической математической логики. Предмет классической математической логики. Предмет логики высказываний. Логические операции над высказываниями. Понятие формулы алгебры высказываний. Равносильность и классификация формул. Логические эквивалентности. Определение булевой алгебры. Примеры. Законы булевой алгебры. Переключательные функции (ПФ). Определение различных типов ПФ. Полностью и не полностью определенные ПФ. Способы задания ПФ. Специальные разложения ПФ. Минимизация ПФ. Теорема о функциональной полноте. Примеры функционально полных базисов. Моделирование алгебры высказываний релейно–контактными схемами. Задача анализа и синтеза. Минимизация булевых функций. Алгебра предикатов. Кванторы. Применение нормальных форм в программировании. Примеры формальных (аксиоматических) систем. Исчисления. Исчисление высказываний. Исчисление предикатов. Непротиворечивость. Полнота.
19;20;21;23;Метод пос. 7;8;11.
14.3. Обычные (четкие) множества и нечеткие подмножества, их спецификации. Понятие множества. Четкие множества и нечеткие подмножества. Операции над четкими множествами. Диаграммы Эйлера–Венна. Степень принадлежности элемента множеству. Операции над нечеткими подмножествами. Нечеткое включение и равенство множеств. Четкие конечные множества и нечеткие подмножества. Число подмножеств данного четкого конечного множества. Упорядоченные четкие конечные множества. Множество всех нечетких подмножеств и его свойства.
19;21;22;23;24;25; Метод пос 9;10.
14.4. Элементы теории алгоритмов. Интуитивное понятие алгоритма и его спецификации. Понятие об (обычном) четком и нечетком алгоритме. Формализация понятия четкого алгоритма. Рекурсивные функции. Понятие о примитивно–рекурсивной функции. Функции, вычисляемые на машинах Тьюринга, нормальные алгоритмы Маркова. Тезисы Черча, Тьюринга, Маркова. Эффективные алгоритмы. Разрешимые и неразрешимые проблемы. Понятие сложности вычислений. Схемы алгоритмов. Схемы потоков данных.
19;21;22;23;24; Доп. 17; Метод. пос. 11.
Раздел 15. Элементы теории неопределенности (ЭИ)
Матрицы последствий и риска. Принятие решений в условиях полной неопределенности. Правило Вальда. Правило Сэвиджа. Правило Гурвица. Принятие решений в условиях частичной непределнности. Максимизация и минимизация среднего ожидаемого риска. Риск как среднее квадратическое отклонение. Байесовский подход к принятию решений.
10, гл. 7, §7.1–7.5.
Раздел 16. Дополнительные темы
16.1 Алгебраические структуры (ЭИ).
Группы, кольца, поля. Понятие изоморфизма. Нечеткие алгебраические структуры. Нечеткий группоид, нечеткий моноид.
Доп. 18, 2.4.1.6, Доп. 19, §1.1*,2,3,5,Доп. 20, гл. 13,Метод пос. 9.
16.2 Элементы теории функций комплексной переменной (Э,М).
Элементарные функции комплексной переменной. Производная. Условия Коши–Римана. Дифференцируемость. Понятие о конформном отображении. Интеграл от функции комплексного переменного. Ряд Тейлора.
18, гл.3,§3.2–3.5,Доп. 2,ч.2, гл. 7, §1–5.
16.3. Элементы гармонического анализа (Э,М).
Периодические величины Тригонометрический ряд. Ортогональность системы тригонометрических функций. Ряд Фурье. Сходимость ряда Фурье. Ряды Фурье для четных и нечетных функций. Ряд Фурье с произвольным периодом.
1,В,11.6,3, гл. 8, §8.5,Доп. 2, ч.2, гл.3,§8.
16.4. Элементы векторного анализа (Э,М,ЭИ).
Скалярное поле. Поверхности и линии уровня. Градиент скалярного поля. Векторное поле. Векторные линии. Поток векторного поля через поверхность. Дивергенция. Соленоидальное поле. Теорема Остроградского. Циркуляция векторного поля. Ротор. Теорема Стокса. Потенциальное поле. Оператор Гамильтона. Оператор Лапласа.
Доп. 21, лекции 45, 49–52, Доп. 6, гл. 6, 9.1–9.5,Доп. 22, гл. 29, 29.1–29.8.
16.5. Элементы функционального анализа (Э,М).
Метрические пространства. Линейные (векторные) пространства. Нормированные и полунормированные пространства. Банаховы, евклидовы и гильбертовы пространства. Топологические пространства. Обощенные функции.
Метод. пос. 1,II,1–5,Доп. 23, гл.4,§18–21.
3. Перечень тем лекционных (л) и практических занятий (п.з.)
| Тема | часы, вид занятий |
| Раздел 1 Системы линейных уравнений. Метод Гаусса. Теорема Кронекера–Капелли. Формулы Крамера. Однородные системы линейных уравнений. Общее решение системы линейных уравнений в векторной форме. Уравнение линий на плоскости. Кривые второго порядка: Поверхности второго порядка. Евклидово пространство. Неравенство Коши–Буняковского. Ортогональный базис. Собственные значения и собственные векторы матриц и их свойства. Квадратичные формы в 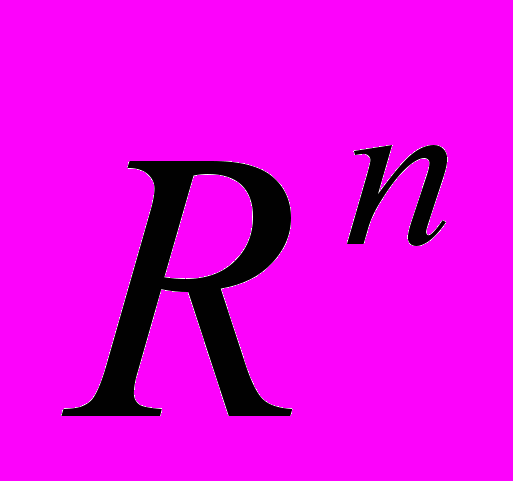. Условие Якоби. Критерий Сильвестра.Раздел 2. Множества. Операции над множествами. Отношения тождества и упорядоченности. Числовые последовательности. Бесконечно малые и бесконечно большие величины. Алгебраические композиции числовых последовательностей и их пределы. Лемма Кантора. Теорема Больцано–Вейерштрасса. Признак Больцано–Коши. Монотонные функции. Композиция и суперпозиция функций. Предел функции в точке. Предел функции в бесконечности. Непрерывность функций. Сравнение бесконечно малых функций Раздел 3 Понятие функции, дифференцируемой в точке. Дифференциал функции и его геометрический смысл. Производные и дифференциалы высших порядков. Теоремы Ферма, Ролля, Лагранжа, Коши, их применение. Правило Лопиталя. Многочлен и формула Тейлора. Представление функций по формуле Тейлора. Раздел 4. Условия монотонности функции. Экстремумы функции, необходимое условие. Достаточные условия. Исследование выпуклости функции. Точки перегиба. Асимптоты. Общая схема исследования функции и построения ее графика. Уравнение касательной и нормали к плоской кривой в данной точке. Раздел 5 Первообразная функция. Неопределенный интеграл и его свойства. Таблица интегралов. Методы интегрирования. Раздел 6 Несобственные интегралы. Двойной и тройной интегралы, их свойства и вычисление. Раздел 7 Функции нескольких переменных. Область определения. Предел. Непрерывность. Частные производные. Полный дифференциал Производная по направлению. Градиент и его свойства. Экстремумы. Метод множителей Лагранжа. Раздел 8. Понятие числового ряда и его сходимости. Признаки сходимости. Знакопеременный ряд. Теорема Дирихле. Теорема Римана. Знакочередующийся ряд. Признак Лейбница. Функциональный ряд. Область сходимости. Признак Вейерштрасса. Свойства равномерно сходящихся рядов. Раздел 9 Дифференциальные уравнения первого порядка. Теорема Коши о существовании и единственности решения. Задача Коши. Особые точки. Элементы качественного анализа. Виды уравнений и методы решения. Система уравнений первого порядка. Нормальная форма. Теорема Коши. Задача Коши и краевая задача для уравнения n-го порядка. Линейные уравнения n-го порядка с постоянными коэффициентами. Линейные обыкновенные разностные уравнения. Основные понятия. Сетки и сеточные функции. Однородные и неоднородные уравнения. Свойства решений. Системы линейных разностных уравнений первого порядка. Раздел 10 Случайные события. Классическое и статистическое определение вероятности. Теоремы сложения и умножения вероятностей. Основные формулы для вероятностей событий. Формула полной вероятности. Формула Байеса. Формула Бернулли. Формула Пуассона. Случайные величины и их описание. Равномерное, экспоненциальное, нормальное распределения. Функция Лапласа. Системы случайных величин. Корреляция и регрессия. Закон распределения вероятностей для функций случайных величин. Закон больших чисел. Неравенство Чебышева. Центральная предельная теорема. Проверка гипотез о параметрах и видах распределения. Критерий Пирсона. Раздел 11. Задача линейного программирования. Графический метод решения Симплексный метод решения Теория двойственности. Первая и вторая теоремы. Двойственный симплексный метод и его алгоритм. Нелинейное программирование. Теорема Куна–Таккера Динамическое программирование. Принцип оптимальности Беллмана. Примеры задач. Конфликтные ситуации. Кооперативные игры. Матричные игры. Сведение матричной игры к задаче линейного программирования. Игры с природой. Марковские процессы. Эргодическая теорема. Процессы гибели и рождения, Системы массового обслуживания Стохастические сети. Радел 12 Модели поведения фирмы в условиях совершенной и несовершенной конкуренции. Показатели экономического роста. Модель общего экономического равновесия. Модель расширенного воспроизводства Маркса. Раздел 13 Теория погрешностей. Прямая и обратная задачи. Численное решение систем линейных уравнений Схема исключения неизвестных. Метод итераций. Численное решение обыкновенных дифференциальных уравнений. Задача Коши. Методы Эйлера. Методы Рунге–Кутты. Разностная аппроксимация Устойчивость и сходимость. Обзор и анализ численных методов, применяемых в пакетах прикладных программ. Раздел 14 Логические исчисления. Законы булевой алгебры. Минимизация булевых функций. Исчисление предикатов. Элементы теории алгоритмов. Понятие о четком и нечетком алгоритме. Рекурсивные функции. Функции, вычисляемые на машинах Тьюринга. Тезисы Черча, Тьюринга, Маркова. Схемы алгоритмов. Схемы потоков данных. Раздел 15. Элементы теории неопределенности. Правила Вальда, Сэвиджа, Гурвица. Принятие решений в условиях полной и частичной неопределенности. Байесовский подход к принятию решений. Раздел 16 Алгебраические структуры Группы, кольца, поля. Нечеткие алгебраические структуры. Элементы гармонического анализа. Периодические величины. Ряды Фурье. Элементы функционального анализа. Метрические пространства. Банаховы, евклидовы и гильбертовы пространства. Топологические пространства. Обощенные функции. | 2 (л) 2 (п.з.) 2 (л) 2 (л) 2 (л) 2 (л) 2 (л) 4 (п.з) 4 (п.з) 4 (п.з) 2 (л) 2 (л) 2 (л) 2(л) 4( п.з.) 2(л) 4 (п.з) 2 (л) 4(п.з) 4 (п.з) 2( л) 2 (л) 4 (п.з.) 2 (л) 2 (л) 4 (п.з.) 4 (п.з.) 2 (л) 2 (л) 2 (л) 2 (л) 2 (л) 4 (п.з.) 2 (л) |
4. Перечень тем самостоятельных занятий
| Тема | Часы |
| Раздел 1 Метод координат. Комплексные числа, действия с ними. Векторы. Линейные операции над векторами. Скалярное произведение векторов и его свойства. Система векторов. Разложение вектора по системе векторов. Матрицы. Действия с матрицами. Обратная матрица. Ранг матрицы. Определители. Свойства определителей. Раздел 2 Функция. Основные элементарные функции, их свойства и графики. Свойства функций, непрерывных на отрезке. Раздел 3 Производная функции, ее геометрический смысл и смысл в прикладных задачах (скорость, плотность). Эластичность функции. Правила нахождения производной. Раздел 6 Определенный интеграл. Формула Ньютона–Лейбница, Замена переменной в определенном интеграле, интегрирование по частям. Приложения определенных интегралов. Раздел 8 Степенные ряды. Теорема Абеля. Радиус сходимости и способы его определения. Интегрирование и дифференцирование степенных рядов. Ряды Тейлора и Маклорена. Применение рядов к приближенным вычислениям. Раздел 9 Дифференциальные уравнения второго порядка. Теорема Коши о существовании и единственности решения. Задача Коши. Линейные уравнения, однородные и неоднородные. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Краевая задача. Раздел 10 Генеральная совокупность и выборка. Эмпирическая функция распределения. Статистические оценки. Точечная и интервальная оценки. Основные законы распределения статистических оценок. Метод моментов и метод наибольшего правдоподобия. Регрессионный анализ. Выборочное уравнение регрессии. Дисперсионный анализ. Факторная и выборочная дисперсии. Раздел 11 Транспортная задача линейного программирования. Метод потенциалов Примеры решения экономических задач. Основные понятия и виды графов. Операции над графами. Матрицы графов. Кратчайший путь, кратчайшее дерево, критический путь на графе. Примеры. Потоки на сетях. Теорема и алгоритм Форда–Фалкерсона. Пропускная способность разреза. Раздел 12 Математическая модель и ее основные элементы. Моделирование в экономике. Функции полезности, спроса и предложения. Уравнение Слуцкого. Применение эластичности в экономическом анализе. Производственные функции. Функция Кобба–Дугласа. Модели оптимизации производства. Комбинация ресурсов, оптимизирующая объем выпуска и издержки. Статическая и динамическая модель межотраслевого баланса. Модель Леонтьева. Модель Неймана. Общие модели развития экономики. Классическая модель рыночной экономики. Модель Кейнса. модели экономического роста. Модель Солоу. Раздел 13 Численное решение нелинейных уравнений и их систем. Методы половинного деления, Ньютона, простых итераций, релаксаций, хорд. Интерполирование и приближение функций. Полиномиальная интерполяция. Приближение сплайнами. Численное дифференцирование и интегрирование. Неустойчивость численного дифференцирования. Погрешность и устойчивость квадратурных формул. Задачи минимизации функций. Поиск минимума функции многих переменных. Раздел 14 Элементы комбинаторики. Перестановки, сочетания и размещения. Бином Ньютона. Полиномиальная формула. Четкие множества и нечеткие подмножества, Операции над четкими множествами. Операции над нечеткими множествами. Упорядоченные четкие конечные множества. Множество всех нечетких подмножеств и его свойства. Раздел 16. Элементы теории функций комплексной переменной. Условия Коши–Римана. Интеграл от функции комплексного переменного. Ряд Тейлора. Элементы векторного анализа. Скалярные и векторные поля. Дивергенция. Соленоидальное поле. Теорема Остроградского. Циркуляция. Ротор. Теорема Стокса. Потенциальное поле. Оператор Гамильтона. Оператор Лапласа. | 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 |
5. Информационно–методическое обеспечение дисциплины
5.1. Учебные пособия
Основные
1. Общий курс высшей математики для экономистов. Учебник / Под редакцией проф. В.И. Ермакова.–М.:ИНФРА–М,2000.
2. Сборник задач по высшей математике для экономистов. Учебное пособие / Под редакцией проф. В. И. Ермакова.–М.:ИНФРА–М,2001.
3. Красс М.С. Математика для экономических специальностей. Учебник. –М.: ИНФРА–М, 1999.
4. Красс М.С., Чупрынов Б.П.. Основы математики и ее приложения в экономическом образовании. Учебник.–М.: Дело, 2000.
5. Шипачев В.С. Задачник по высшей математике. Учебное пособие для вузов.–М.:Высшая школа,1998.
6. Высшая математика для экономистов. Учебник для вузов/Под редакцией проф. Н.Ш. Кремера.–М.: ЮНИТИ,2000
7. Малыхин В.И. Математика в экономике. Учебное пособие.–М.:ИНФРА–М,2001.
8. Колемаев В.А. Математическая экономика. Учебник для вузов.–М.:ЮНИТИ, 1998.
9. Экономико–математические методы и прикладные модели. Учебное пособие для вузов /Под редакцией В.В. Федосеева.–М.:ЮНИТИ,2002.
10. Математические методы принятия решений в экономике. Учебник / Под редакцией В.А. Колемаева.–М.:ЗАО «Финстатинформ», 1999.
11. Чернов В.П., Ивановский В.Б. Теория массового обслуживания. Учебное пособие для вузов/Под редакцией А.Ф. Тарасюка.–М.: ИНФРА–М,2000.
16. Кирьянов Д.В. Самоучитель MathCAD 2001.– СПб.:БХВ–Петербург,2001.
17. Манзон Б.М. Maple 5 Power Edition. –М.: Инф.–изд. дом «Филинъ», 1998.
20. Мендельсон Э. Введение в математическую логику.–М.: Наука,1999.
22. Ерусалимский Я.М. Дискретная математика: теория, задачи, приложения.–М.: Вузовская книга,1999.
26. Конюховский П.В. Математические методы исследования операций в экономике.–СПб:2000.
27. Киселев В.Ю. Экономико–математические методы и модели.–Иваново: 1998.
29. Джон Г. Мэтьюз, Куртис Д. Финк. Численные методы. Использование MATLAB.–М.: Издательский дом «Вильямс», 2001.
Дополнительные
1. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов. Т. I,II.–М:Интеграл–Пресс,2000.
2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Учебное пособие для втузов. Ч.1,2.–М.:Высшая школа,1999.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Учебник Ч.2.–М.:Финансы и статистика,1999.
4. Солодовников А.С. Бабайцев В.А., Браилов А.В., Шандра И.Г. Математика в экономике. Учебник Ч.1.–М.:Финансы и статистика,1998.
5. Кожухов И.Б., Прокофьев А.А. Справочник по математике.–М.:Лист 1999.
6. Куринной Г.Ч. Математика. Справочник.–Харьков: Фолио; М.: ООО «Издательство АСТ»,2000.
7. Справочник по математике для экономистов /Под редакцией проф. В.И. Ермакова.–М.: Высшая школа,1987.
8. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. Учебник.–М.: МГУ им. М.В. Ломоносова, издательство «ДНС», 1997.
9. Гмурман В.Е. Теория вероятностей и математическая статистика.–М.: Высшая школа, 2002.
10. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике.–М. Высшая школа,2002.
11. Монахов А.В. Математические методы анализа экономики. Учебное пособие. –СПб : Питер,2002.
12. Хачатрян С.Р. Прикладные методы математического моделирования экономических систем. Научно–методическое пособие.–М: Издательство «Экзамен»,2002.
13. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. Учебное пособие/ Под редакцией В.А. Садовничего.–М.: Высшая школа,2000.
14. Самарский А.А., Вабищевич П.А., Самарская Е.А. Задачи и упражнения по численным методам. Учебное пособие.–М.:Эдиториал УРСС,2000.
15. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование. Учебное пособие для вузов.–М.:Высшая школа,1980.
17. Кук Д., Бейз Г. Компьютерная математика.–М.: Мир, 1992.
18. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов.–М.:Наука,1986.
19. Мантуров О.В., Матвеев Н.М. Курс высшей математики Ч.1.–М.: Высшая школа, 1997.
20. Петрова В.Т. Лекции по алгебре и геометрии.–М.:Владос,1999.
21. Власов В.Г. Конспект лекций по высшей математике.–М.: Айрис,1996.
22. Гусак А.А., Гусак Г.М. Справочник по высшей математике.–Минск: Наука и техника, 1991.
23. Кудрявцев Л.Д., Кутасов А.Д., Чехлов В.И., Шабунин М. И. Сборник задач по математическому анализу. Функции нескольких переменных. Учебное пособие для вузов/Под редакцией Л.Д. Кудрявцева.– СПб: 1994.
12. Амосов А.А., Дубинский Ю.А., Копченов Н.А. Вычислительные методы для инженеров.–М.:Высшая школа,1994.
13. Косарев В.И. 12 лекций по вычислительной математике (вводный курс).Учебное пособие для вузов.–М.:Издательство МФТИ, 1995.
14. Сборник задач по методам вычислений. Учебное пособие для вузов /Под редакцией П.И. Монастырного.–М.: Физматлит, 1994.
15. Очков В.Ф. MathCAD PLUS 6.0 для студентов и инженеров.–М.: ТОО фирма Компьютерпресс,1996.
18. Мантуров О.В. Курс высшей математики. Уравнения математической физики. Теория функций комплексного переменного. Численные методы. Теория вероятностей. Учебник для вузов.–М.: Высшая школа,1991.
19. Горбатов В.А. Основы дискретной математики. Учебное пособие для вузов.–М.: Высшая школа,1986.
21. Кузнецов О.П., Адельсон–Вельский Г.М. Дискретная математика для инженеров.–М.: Энергоатомиздт,1989.
23. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов.–М.:Физматлит,1995.
24. Яблонский С.В. Введение в дискретную математику.–М.: Высшая школа,2002.
25. Кофман А., ХилАлуха Х. Введение теории нечетких множеств в управлении предприятиями.– Минск: Высшая школа, 1992.
28. Марков А.А., Нагорный Н.М. Теория алгоритмов.–М: Высшая школа,1996.
29. Шестаков А.А., Синдаловский Г.Х. Множества и пространства. Учебное пособие. –М.:РГОТУПС,1997.
30. Павленко Л.И. Векторная алгебра и ее применение в задачах аналитической геометрии. Учебное пособие. –М.:ВЗИИТ, 1984.
31. Масленникова З.Г. Матрицы и их применение. Решение систем методом Гаусса. Учебное пособие. –М.: ВЗИИТ,1994.
32. Синдаловский Г.Х. Высшая математика . Элементы линейной алгебры. Линейные преобразования (операторы) и квадратичные формы. Методические указания для студентов I курса. –М.:РГОТУПС,1998.
33. Романков В.В., Петунин А.П. Элементы теории игр. Учебное пособие –М.: ВЗИИТ, 1993
34. Шестаков А.А. Основы дискретной математики. Рабочая программа, методические указания и контрольные задания для студентов-заочников III курса специальности ЭВМ.–М.: ВЗИИТ,1987.
35. Шестаков А.А., Малышева И.А. Основы дискретной математики и дискретный анализ. Раздел «Элементы математической логики». Методические указания для студентов I курса специальности МОИ и III курса специальности ЭВМ.–М.: ВЗИИТ, 1986.
36. Шестаков А.А., Дружинина О.В. Дискретная математика. Элементы нечеткой логики. Учебное пособие.–М.: РГОТУПС,2002.
37. Шестаков А.А., Дунаева О.В. Дискретная математика. Четкие и нечеткие множества. Алгебраические структуры и коды. Часть I. Учебное пособие.–М.: РГОТУПС, 1998.
38. Дружинина О.В. Дискретная математика. Рабочая программа и задания на контрольную работу для студентов II курса специальности ЭВМ. –М: РГОТУПС, 2002.
39. Дружинина О.В. Математическая логика и теория алгоритмов. Рабочая программа и задание на контрольную работу для студентов II курса специальности ЭВМ.–М.: РГОТУПС, 2002.
40. Гушель Н.П. Начальные понятия комбинаторики. Учебное пособие.–М: ВЗИИТ, 1992.
5.2. Перечень компьютерных программ
1. Программа MATH. Обучение, контроль знаний, проверка решений задач.
2. Пакет прикладных программ MathCAD. Решение задач.
3. Пакет прикладных программ DERIVE. Решение задач.
4. Пакет прикладных программ Maple V R4. Решение задач.