Обзор средств matlab и ToolBox'ов для приближения данных

Вид материала

Содержание

Работа с разбросанными данными
Триангуляция Делоне
Построение диаграммы Вороного

Подобный материал:

1 2 3 4

Работа с разбросанными данными

В MATLAB входят функции для работы с разбросанными данными, т.е. например в двумерном случае это данные z_i, заданные в точках (x_i, y_i)_i=1,2,...,k. Эти функции позволяют решать следующие задачи.

Интерполировать разбросанные данные различными способами. Для данных, определенных в точках на плоскости, возможно кусочно-постоянное приближение по ближайшему соседу, кусочно-линейное приближение и более гладкое приближение с непрерывными производными (функция griddata). Данные, определенные в точках трехмерного и n-мерного пространства могут быть приближены по ближайшему соседу и при помощи кусочно-линейных функций (функции griddata3 и griddatan). Значение интерполянта возвращается на ортогональной сетке, накрывающей точки, в которых заданы разбросанные данные.
Строить выпуклую оболочку множества точек на плоскости, в трехмерном и n-мерном пространстве (функции convhull, convhulln).
Строить триангуляцию Делоне для множества точек на плоскости, в трехмерном и n-мерном пространстве ( функции delaunay, delaunay3, delaunayn).
Строить диаграмму Вороного для множества точек на плоскости, в трехмерном и n-мерном пространстве (функции voronoi, voronoin).
Визуализировать выпуклую оболочку, триангуляцию Делоне и диаграмму Вороного (функции triplot, trimesh, trisurf, tetramesh).
Для заданной точки определять ближайшую точку к ней из заданного множества точек на плоскости (функция dsearch).
Для заданной точки определить содержащий ее треугольник из триангуляции Делоне (функция tsearch), или сиплекс в n-мерном случае (функция tsearchn).
Решать такие задачи, как:
- нахождение площади многоугольника (функция polyarea);
- площади пересечения четырехугольников (функция rectint).

Нахождение выпуклой оболочки множества точек и ее визуализация

Выпуклая оболочка conv(P) множества точек, принадлежащих n-мерному пространству Rⁿ, определяется как наименьшее выпуклое множество, содержащее все эти точки. Выпуклое множество, порожденное точками (p_i)_i=1,2,...,k, определяется как множество точек:

p = a₁p₁ + a₂p₂ + ... + a_kp_k

где все a_i >/= 0 и a₁ + a₂ + ... + a_k = 1 (здесь точки отождествляются с векторами, выходящими из начала координат).

В двумерном случае есть простая интуитивно понятная аналогия. Пусть на плоскости лежат точки (вбиты гвозди), мы натягиваем вокруг них веревку.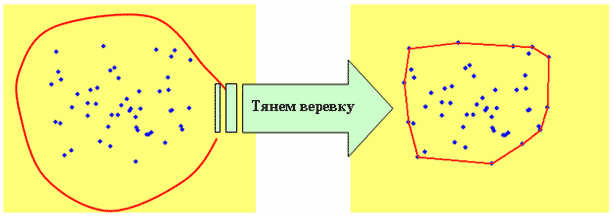

То, что получится, и будет выпуклой оболочкой (на правом рисунке ее граница изображена красным цветом). Все точки из множества находятся либо внутри выпуклой оболочки, либо на ее границе.

Выпуклая оболочка является пересечением конечного числа полупространств (полупространство - часть пространства, лежащая по одну сторону от гиперплоскости). В двумерном случае гиперплоскости это линии, а в трехмерном случае - плоскости.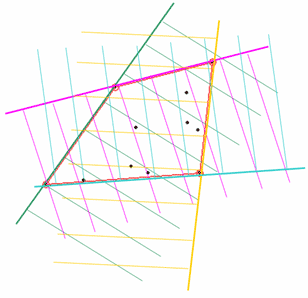

Для построения выпуклой оболочки в MATLAB служит функция convhull. Ее входными аргументами являются вектора с координатами абсцисс и ординат точек, а выходными аргументами являются номера точек, образующих вершины выпуклой оболочки. В следующем примере генерируется набор из 100 точек с координатами, изменяющимися случайным образом от 0 до 1, затем при помощи функции convhull строится выпуклая оболочка. Номера точек, являющихся вершинами выпуклой оболочки, заносятся в массив kvert. Затем вершины выпуклой оболочки выделяются круглыми маркерами и рисуется сама выпуклая оболочка

x=rand(1,100);

y=rand(1,100);

figure

plot(x,y,'k.')

hold on

axis([-0.5 1.5 -0.5 1.5])

kvert=convhull(x,y)

pause(0.3)

plot(x(kvert(1)),y(kvert(1)),'ro')

for k=2:length(kvert)

plot([x(kvert(k-1)) x(kvert(k))],[y(kvert(k-1)) y(kvert(k))],'r')

plot(x(kvert(k)),y(kvert(k)),'ro')

pause(0.3)

end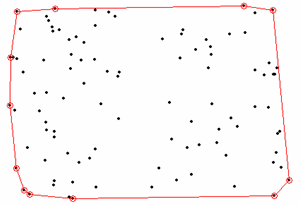

Если функцию convhull вызвать со вторым дополнительным выходным аргументом, то в него запишется площадь выпуклой оболочки

>> [kvert, s] = convhull(x, y);

>> s

s =

0.9164

Для построения выпуклой оболочки точек из трехмерного пространства и пространств более высоких размерностей используется функция convhulln. Координаты точек задаются в строках двумерного массива, который указывается в качестве входного аргумента функции convhulln. Она возвращает двумерный массив, каждая строка которого содержит номера точек из исходного множества, образующих грань выпуклой оболочки (в двумерном случае грань - отрезок, соединяющий соседние вершины выпуклой оболочки).

В качестве примера приведем построение выпуклой оболочки точек, которые случайным образом распределены в кубе [0,1]x[0,1]x[0,1]. Координаты точек генерируются при помощи функции rand и записываются в вектор-столбцы. Из этих столбцов создается матрица, которая указывается в качестве входного аргумента функции convhulln. Функция convhulln возвращает матрицу из трех столбцов, каждый из которых содержит номера точек исходного множества, образующих некоторую грань выпуклой оболочки. Для визуализации выпуклой оболочки применяется функция trimesh, которая строит полигональный объект (patch) и возвращает указатель на него. Вид этого полигонального объекта можно изменять по своему усмотрению, включая прозрачность и цвет граней, маркеры в вершинах и т.д. Когда выпуклая оболочка найдена, то все исходное множество точек разбивается на два подмножества - точки, которые являются вершинами выпуклой оболочки, и внутренние точки. В приводимом ниже примере рядом с точками этих типов размещаются подписи разного цвета с номерами точек. Для этого используется функция text. При этом возникает вопрос, как определить номера точек, попавших внутрь выпуклой оболочки исходного множества, и тех, которые принадлежат вершинам выпуклой оболочки. Как уже говорилось, номера вершин записаны в выходном аргументе функции convhulln (двумерном массиве с тремя столбцами). Однако, они встречаются в разных строках этого массива и не по одному разу. Поэтому для выделения номеров точек, попавших в вершины выпуклой оболочки, можно поступить так: последовательно объединить содержимое столбцов матрицы с номерами вершин, воспользовавшись функцией union. Поскольку данная функция производит объединение в смысле объединения множеств, то повторы элементов исключаются. Аналогично, для нахождения номеров точек, попавших внутрь выпуклой оболочки, можно применить функцию setdiff, которая находит разность множеств. В нашем случае из множества номеров всех точек следует вычесть номера точек, образующих вершины выпуклой оболочки.

% задаем двадцать точек

k=20;

% генератору случайных чисел задаем начальное состояние

rand('state',0);

% генерируем координаты точек множества и записываем их в

% вектор-столбцы x, y, и z

x=rand(k,1);

y=rand(k,1);

z=rand(k,1);

% образуем двумерный массив с координатами точек множества

X=[x y z];

% находим номера точек, образующих треугольные грани выпуклой оболочки

% множества

kvert=convhulln(X)

% визуализируем выпуклую оболочку при помощи функции trisurf

figure('Color','w')

h=trisurf(kvert,X(:,1),X(:,2),X(:,3))

hold on

% устанавливаем прозрачность граней, красные ребра

% и круглые красные маркеры в вершинах выпуклой оболочки

set(h,'FaceAlpha',0.1,'FaceColor','g',...

'EdgeColor','r','Marker','o','MarkerSize',10)

% находим номера точек, являющихся вершинами выпуклой оболочки,

% и записываем их в kv

kv=union(kvert(:,1),kvert(:,2))

kv=union(kv,kvert(:,3))

% подписываем номера вершин выпуклой оболочки

ht=text(x(kv), y(kv), z(kv),num2str(kv))

set(ht,'BackgroundColor','r','VerticalAlignment','Top',...

'FontWeight','bold')

% находим номера точек, попавших внутрь оболочки, и записываем их в kinner

kinner=setdiff(1:k,kv)

% рисуем точки, попавшие внутрь оболочки, круглыми синими маркерами

plot3(x(kinner),y(kinner),z(kinner),'Color','b','LineStyle','none',...

'Marker','o','MarkerSize',10)

% помещаем рядом с точками, попавшими внутрь оболочки, их номера

ht=text(x(kinner), y(kinner), z(kinner),num2str(kinner'))

set(ht,'BackgroundColor','y','VerticalAlignment','Top',...

'FontWeight','bold','Color','b')

В результате выполнения этих команд на оси графического окна выводится выпуклая оболочка, ее пронумерованные вершины и пронумерованные точки, попавшие внутрь выпуклой оболочки, в соответствии с их номерами в исходном множестве: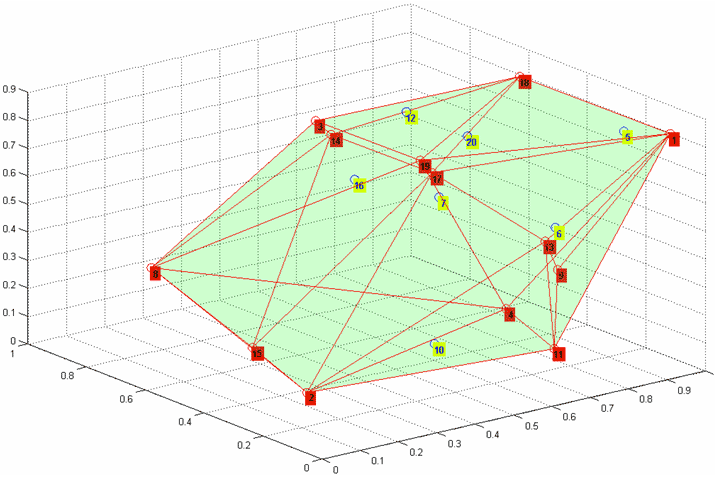

Вместо функции trisurf можно использовать функцию trimesh, которая в отличие от trimesh не заливает грани цветами.

При вызове функции convhulln(X) со вторым дополнительным выходным аргументом, в нем возвращается объем выпуклой оболочки

>> [kvert,V]=convhulln(X);

>> V

V =

0.2582

В MATLAB для построения выпуклой оболочки используется функция qconvex пакета Qhull (ссылка скрыта). Эти функция поддерживает ряд опций для задания некоторых параметров алгоритма построения выпуклой оболочки, которые можно задавать и в функциях convhull, convhulln.

Алгоритмы построения выпуклой оболочки, в том числе и алгоритм Quickhull, описаны, например, на ссылка скрыта. Там же приведено несколько ссылок на статьи с описаниями алгоритмов построения выпуклой оболочки множества точек.

Для визуализации выпуклой оболочки точек трехмерного пространства не обязательно использовать функцию trisurf. Вместо нее можно самому сконструировать полигональный объект с заданными способами заливки цветом ребер и граней и их прозрачностью.

Одним из способов задания полигонального объекта является указание его вершин и матрицы, содержащей номера вершин каждой грани, т.е. как раз той матрицы, которая возвращается функцией convhulln. При этом, в частности, можно указать цвет каждой вершины и способ заливки граней цветом, например плавное изменение цвета от вершины к вершине, как это сделано в следующем примере. Полигональный объект создается при помощи функции patch. При его создании используются свойства полигонального объекта:

Vertices - матрица из трех столбцов, в строки которой записаны координаты вершин полигонального объекта;
Faces - матрица, каждая строка которой содержит номера вершин, образующих различные грани полигонального объекта
FaceVertexCData - цвета вершин, в примере они задаются в формате RGB, цвет устанавливается зеленый, а его оттенок зависит от высоты точки над плоскостью xy.
FaceColor - способ заливки граней полигонального объекта цветом, в примере используется значение 'interp', т.е. плавное изменение цвета от вершины к вершине.

При визуализации выпуклой оболочки множества точек из трехмерного пространства при помощи функции patch необходимо самому устанавливать трехмерный вид осей, т.к. patch относится к низкоуровневым граничным функциям, которые не изменяют вид осей.

% Задание множества точек

k=30;

rand('state',0)

x=rand(k,1);

y=rand(k,1);

z=rand(k,1);

X=[x y z];

% Построение выпуклой оболочки

kvert=convhulln(X);

figure('Color','w')

% Задание цвета вершин

VColor=[zeros(size(z)) z zeros(size(z))];

% Создание полигонального объекта

patch('Vertices',X,'Faces',kvert,'FaceVertexCData',VColor,'FaceColor','interp')

% Установка трехмерного вида осей.

view(3)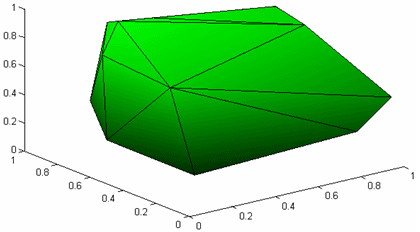

Триангуляция Делоне

Если задан набор точек на плоскости, то задача триангуляции такого набора состоит в соединении всех точек непересекающимися отрезками так, чтобы новых отрезков уже нельзя было добавить без пересечения с имеющимися, например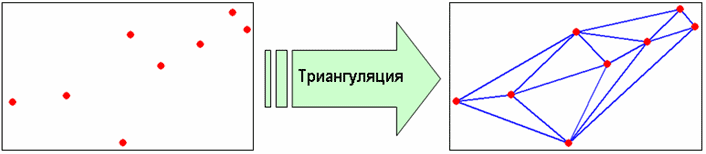

В этом примере видно, что триангуляция может быть неединственная, например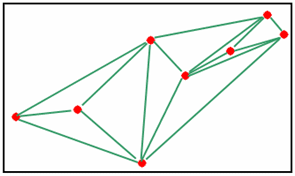

также является триангуляцией.

Важный в приложениях класс триангуляций составляют триангуляции Делоне. Триангуляция называется триангуляцией Делоне, если внутрь окружности, описанной вокруг каждого треугольника, не попадают точки множества. В предыдущих примерах триангуляция, построенная синими линиями, является триангуляцией Делоне, т.к. она удовлетворяет этому определению (см. левый рисунок, на котором окружности нарисованы не для всех треугольников только для того, чтобы не загромождать рисунок). Триангуляция, построенная зелеными линиями, не удовлетворяет условию Делоне (см. правый рисунок).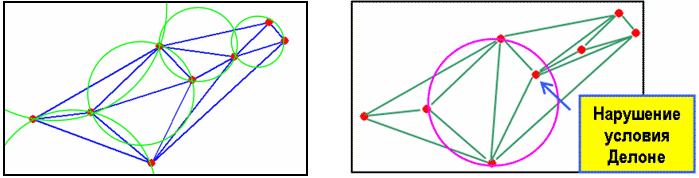

Триангуляция Делоне может быть неединственной (в случае, когда четыре точки множества лежат на одной окружности), например обе триангуляции одного и того же набора точек, приведенные ниже, являются триангуляциями Делоне.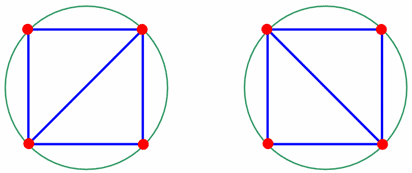

Можно показать, что триангуляция Делоне:

обладает максимальной суммой минимальных углов треугольников среди всех триангуляций множества точек;
минимальной суммой радиусов описанных вокруг всех треугольников окружностей по сравнению со всевозможными другими триангуляциями.

В Интернет о триангуляции Делоне можно почитать, например, на сайте ссылка скрыта (в разделе геометрия), где приведены ссылки на несколько доступных для скачивания источников с описаниями алгоритмов триангуляции.

Для построения триангуляции Делоне множества точек на плоскости в MATLAB используется функция delaunay, входными аргументами которой являются вектора с координатами точек, а выходным аргументом - матрица из трех столбцов, каждая строка которой содержит номера точек, образующие вершины треугольников. Для визуализации триангуляции удобно использовать функцию triplot, входными аргументами которой являются матрица, возвращаемая функцией delaunay, и два вектора с координатами точек. Функция triplot возвращает указатель на создаваемый ею полигональный объект, который в дальнейшем можно изменять по своему усмотрению.

Построим триангуляцию Делоне следующего множества точек

x = [4.4 8.9 8.1 4.5 0.1];

y = [6.9 6.1 0.7 1.9 0.2];

Отображаем их маркерами в графическом окне

figure('Color','w')

plot(x,y,'Marker','.','MarkerEdgeColor','r','MarkerSize',35,'LineStyle','none')

axis equal

axis off

hold on

Вызываем функцию delaunay для построения триангуляции

T = delaunay(x,y)

Рисуем триангуляцию при помощи функции triplot и устанавливаем линиям толщину 2пт.

h=triplot(T,x,y)

set(h,'LineWidth',2)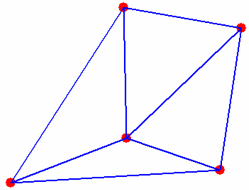

Легко убедиться, что построенная триангуляция действительно подходит под определение триангуляции Делоне. Построим для каждого треугольника описанную вокруг него окружность. Для этого обойдем треугольники (строки матрицы T) в цикле и по известным формулам вычислим координаты центра и радиус описанной вокруг него окружности. Сами окружности нарисуем при помощи функции rectangle, которая позволяет скруглять углы для получения эллипсов и кругов:

[m,n]=size(T); % определяем размер матрицы T

% Проходим по треугольникам в цикле

for k=1:m

% Записываем в p1, p2, p3 номера точек, являющихся вершинами текущего треугольника

p1=T(k,1);

p2=T(k,2);

p3=T(k,3);

% Находим координаты центра (xc, yc) описанной окружности

a=(y(p2)-y(p1))/(x(p2)-x(p1));

b=(y(p3)-y(p2))/(x(p3)-x(p2));

xc=(a*b*(y(p1)-y(p3))+b*(x(p1)+x(p2))-a*(x(p2)+x(p3)))*0.5/(b-a)

yc=-1/a*(xc-(x(p1)+x(p2))*0.5)+(y(p1)+y(p2))*0.5;

% Находим радиус

r=sqrt((xc-x(p1))2+(yc-y(p1))2);

% строим описанную окружность

rectangle('Curvature',[1 1],'Position',[xc-r, yc-r, 2*r, 2*r])

end

В результате убеждаемся, что триангуляция является триангуляцией Делоне.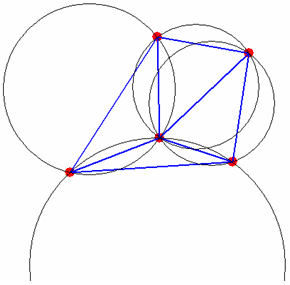

Триангуляцию удобно использовать для визуализации функций, заданных на непрямоугольной области определения. Сначала функция вычисляется в точках этой области, затем строится триангуляция Делоне множества точек на плоскости. После этого применяется функция trimesh, либо функция trisurf для визуализации:

% генерируем точки на плоскости

rand('state',0);

r=rand(1,500);

t=rand(1,500);

x = 2*r.*sin(2*pi*t)-1;

y = 2*r.*cos(2*pi*t)-1;

% вычисляем значение функции

z = exp(-x.2-y.2).*sin(pi*x).*y;

% находим триангуляцию Делоне

T = delaunay(x,y)

% строим поверхность двумя способами

figure('Color','w')

subplot(1,2,1)

trimesh(T,x,y,z)

subplot(1,2,2)

trisurf(T,x,y,z)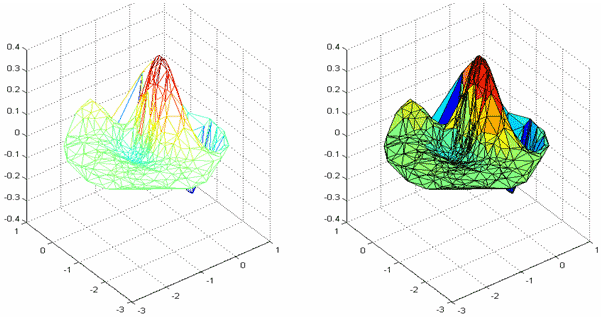

В трехмерном случае триангуляция Делоне определяется аналогично, только строятся тетраэдры, а сферы, описанные вокруг каждого тетраэдра, не должны содержать внутри себя точек из триангулируемого множества. Для построения триангуляции точек трехмерного пространства используется функция delaunay3, во входных аргументах которой задаются векторы с координатами точек триангулируемого множества. Выходным аргументом функции delaunay3 является матрица из четырех столбцов, каждый из которых содержит номера вершин симплекса (тетраэдра) триангуляции. Для визуализации триангуляции в трехмерном пространстве удобно применять функцию tetramesh, первым входным аргументом которой является матрица, возвращаемая delaunay3, а вторым входным аргументом - матрица, каждая строка которой содержит координаты точек триангулируемого множества. Функция tetramesh возвращает указатель на создаваемый ею полигональный объект, свойства которого можно изменять.

% генерируем набор из девяти точек в трехмерном пространстве

rand('state',0);

x = rand(9,1);

y = rand(9,1);

z = rand(9,1);

% Строим триангуляцию Делоне

T = delaunay3(x,y,z);

% Визуализируем тетраэдры

figure('Color','w')

h=tetramesh(T,[x y z])

% Задаем маркеры в вершинах и прозрачность граней

set(h,'Marker','.','MarkerEdgeColor','r','MarkerSize',30,'FaceAlpha',0.6)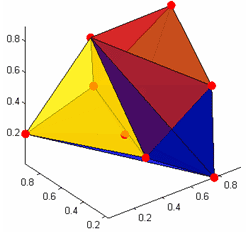

Для построения триангуляции в пространствах размерности больше трех применяется функция delaunayn. Ее входным аргументом является матрица, каждая строка которой содержит координаты точки из заданного множества, а в выходном аргументе возвращается матрица, в строках которой записаны номера точек, которые являются вершинами симплексов триангуляции.

Функции delaunay, delaunay3 и delaunayn используют функцию qdelaunay пакета Qhull (ссылка скрыта), которая позволяют задавать ряд опций для управления процессом триангуляции.

Построение диаграммы Вороного

Если на плоскости задано множество различных точек (x_i,y_i)_i=1,2,...,k, то диаграмма Вороного определяется как деление плоскости на k ячеек (по числу точек), каждая ячейка содержит одну точку из исходного набора и для любой ячейки выполняется следующее свойство. Ячейка, которая содержит точку (x_i,y_i), содержит также все точки плоскости, которые ближе к (x_i,y_i), чем к любой другой точке из исходного набора. Для примера приведем диаграмму Вороного, на которой точки множества заданы красным цветом, а сама диаграмма синими линиями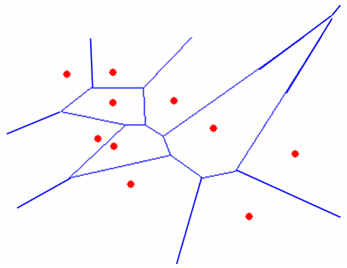

Можно рассматривать точки как ретрансляционные вышки, а многоугольники как соты, которые обслуживаются своими вышками. Если человек едет на машине и разговаривает по мобильному телефону, то при перемещении от одной соте к другой используется соответствующая ретрансляционная вышка.

Каждая ячейка диаграммы, содержащая (x_i,y_i), называется многоугольником Вороного, соответствующим точке (x_i,y_i), ребра и вершины, соответственно, ребра диаграммы Вороного и вершины диаграммы Вороного.

Приведем некоторые свойства диаграммы Вороного, которые доказываются довольно просто в предположении, что никакие четыре точки исходного множества не лежат на одной окружности (см. например, классическую монографию, переведенную на русский язык: Ф.Препарата, М.Шеймос. Вычислительная геометрия: Введение. М. "Мир". 1989).

Ребро диаграммы Вороного является отрезком прямой, перпендикулярной отрезку, соединяющему некоторые две точки из исходного набора, и проходящей ровно через середину этого отрезка. Каждое ребро принадлежит ровно двум многоугольникам.
Каждый ближайший сосед некоторой точки из исходного множества определяет ребро в многоугольнике Вороного.
Вершины диаграммы Вороного являются точками пересечения ровно трех ребер диаграммы Вороного.
Если провести окружность с центром в вершине диаграммы Вороного, проходящую через три точки из исходного множества, которые принадлежат смежным с вершиной многоугольникам, то внутри нее не будут содержаться никакие точки из исходного множества.
Очевидно, часть многоугольников диаграммы Вороного неограниченна. Многоугольник является неограниченным тогда и только тогда, когда соответствующая ему точка из исходного множества лежит на границе выпуклой оболочки всех точек множества.
Диаграмма Вороного для множества из k точек содержит не более 2k-5 вершин и 3k-6 ребер.
Между диаграммой Вороного и триангуляцией Делоне есть прямая связь (см. следующий раздел Как связаны выпуклая оболочка, триангуляция Делоне и диаграмма Вороного).

Для построения диаграммы Вороного заданного множества точек плоскости в MATLAB используется функция voronoi, которая допускает несколько вариантов вызова.

voronoi(x,y) - отображает в графическом окне множество точек, координаты которых заданы в массивах x и y, и диаграмму Вороного этого множества точек. Ребра, соответствующие бесконечным ячейкам, не строятся.
voronoi(x,y,T) - делает то же самое, что и voronoi(x,y), но не вычисляет предварительно триангуляцию Делоне, а использует триангуляцию, заданную в массиве T. Для получения массива T следует предварительно вызвать функцию delaunay так: T = delaunay(x,y) (см. раздел Триангуляция Делоне).
voronoi(hax,...) - работает аналогично предыдущим вариантам, только строит диаграмму Вороного на осях с указателем hax.
voronoi(...,'LineSpec') - позволяет задать цвет и стиль линий, используемых для построения диаграммы Вороного, а так же маркеры в вершинах. Например voronoi(x, y, 'ko:') рисует ребра черными пунктирными линиями и помещает круглые маркеры в вершинах диаграммы.
h = voronoi(...) - возвращает вектор указателей на линии, которыми прорисовываются ребра диаграммы.
[vx, vy] = voronoi(...) - возвращает координаты начальной и конечной точки каждого ребра (т.е. вершин диаграммы) в массивах vx и vy, которые являются матрицами из двух строк. Соответствующие координаты записаны в столбцах матриц, причем каждый столбец соответствует ребру диаграммы. При таком способе обращения к функции voronoi диаграмма Вороного не строится. Ее можно построить так: plot(vx,vy), а затем добавить исходные точки отобразив их некоторыми маркерами: hold on, plot(x,y,'.'). Для построения одновременно и диаграммы Вороного и множества точек все можно объединить в одну команду: plot(vx, vy, x, y, '.').
Для получения диаграммы в виде закрашенных многоугольников следует использовать функцию voronoin, которая предназначена для построения диаграммы Вороного для точек из трехмерного пространства и пространства более высоких размерностей (об этом чуть ниже).

Для построения диаграммы Вороного в функции voronoi предварительно строится триангуляция Делоне множества точек (см. раздел Триангуляция Делоне), для чего вызывается функция delaunay пакета MATLAB. Она в свою очередь, основана на функции qdelaunay пакета Qhull (ссылка скрыта), которая реализует алгоритм Quickhull и позволяют задавать ряд опций для управления процессом триангуляции. Поэтому в функции voronoi, допустимо задание тех же самых опций, что и в delaunay. Они указываются в массиве ячеек строк последним входным аргументом в voronoi.

Приведем пример, в котором демонстрируется построение диаграммы Вороного для случайно сгенерированного набора из восьми точек и то обстоятельство, что точки, соответствующие бесконечным многоугольникам, лежат в вершинах выпуклой оболочки исходного множества точек. Точки рисуются красным цветом, грани диаграммы Вороного зеленым цветом, а грани выпуклой оболочки черным цветом. Для построения выпуклой оболочки применяется функция convhull (см. Нахождение выпуклой оболочки множества точек и ее визуализация).

% генерируем случайный набор из восьми точек

rand('state',0);

x = rand(8,1);

y = rand(8,1);

% строим диаграмму Вороного

figure('Color','w')

h=voronoi(x,y);

% устанавливаем зеленый цвет линий многоугольников и толщину 2пт

set(h,'Color','g','LineWidth',2)

hold on

% строим набор точек красными маркерами

plot(x,y,'Marker','.','MarkerEdgeColor','r','MarkerSize',30, 'LineStyle', 'none')

% ищем выпуклую оболочку заданного набора точек

k = convhull(x,y);

% рисуем выпуклую оболочку черными линиями

plot(x(k),y(k),'k')

% ищем пределы по осям x и y, которые содержат координаты заданных точек

% и вершины диаграммы Вороного

X=get(h,'XData');

Y=get(h,'YData');

m=length(X)-1;

XX=cell2mat(X(1:m-1));

YY=cell2mat(Y(1:m-1));

xmin=min([XX(:);x]); xmax=max([XX(:);x]);

ymin=min([YY(:);y]); ymax=max([YY(:);y]);

% задаем пределы осей и делаем их невидимыми

axis([xmin xmax ymin ymax])

axis off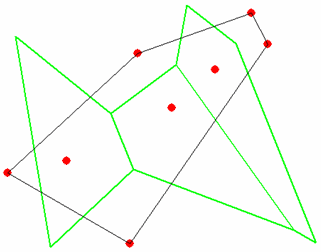

Для построения диаграммы Вороного в трехмерном пространстве и в пространствах большей размерности предназначена функция voronoin. Ее интерфейс оказывается полезным и при визуализации диаграммы Вороного для множества точек плоскости. Если координаты каждой точки множества записаны в строках массива X (т.е. число его столбцов совпадает с размерностью пространства), то

[V,C] = voronoin(X)

возвращает следующие массивы

Двумерный числовой массив V, содержащий координаты вершин диаграммы Вороного. Координаты каждой вершины записываются в строки массива V, причем первая строка всегда содержит Inf (т.е. бесконечность) и соответствует "бесконечно удаленной вершине", что нужно для отличия бесконечных ячеек диаграммы Вороного от конечных.
Вектор ячеек C, каждая ячейка которого содержит числовой вектор с номерами вершин, образующих ячейки диаграммы Вороного. Если один из элементов этого равняется единице (т.е. номеру бесконечно удаленной вершины, добавленной первой в массив V), то соответствующая ячейка диаграммы Вороного является неограниченной.

Используя массивы V и C, возвращаемые функцией voronoin, можно самостоятельно выбрать один из способов визуализации конечных ячеек диаграммы Вороного. Единственное, для каждой конечной ячейки придется построить выпуклую оболочку по ее вершинам (ячейки диаграммы Вороного являются выпуклыми политопами). Для этого можно использовать функцию convhulln (см. раздел Нахождение выпуклой оболочки множества точек и ее визуализация).

В следующем примере поясняется построение конечных ячеек диаграммы Вороного для точек трехмерного пространства.

% генерируем восемь случайных точек

k=8

rand('state',0)

x=rand(k,1);

y=rand(k,1);

z=rand(k,1);

% отображаем точки на графике

figure('Color','w')

plot3(x,y,z,'Marker','.','MarkerEdgeColor','r','MarkerSize',10, 'LineStyle', 'none')

axis off

% записываем координаты каждой точки в строку матрицы

X=[x y z];

% строим диаграмму Вороного

[V,C]=voronoin(X);

% отображаем содержимое массива V с координатами вершин диаграммы Вороного

V

% отображаем содержимое массива С с номерами вершин для каждой ячейки

for k=1:length(C)

disp(C{k})

end

%проходим по ячейкам диаграммы

for k=1:length(C)

if all(C{k}~=1)

% выбираем только конечные ячейки (в множество их вершин не входит первая вершина,

% соответствующая бесконечно удаленной точке

VertCell = V(C{k},:);

% строим выпуклую оболочку вершин конечной ячейки

KVert = convhulln(VertCell);

% отображаем ее при помощи полигонального объекта с полупрозрачными гранями

patch('Vertices',VertCell,'Faces',KVert,'FaceColor','g','FaceAlpha',0.5)

pause(1)

end

end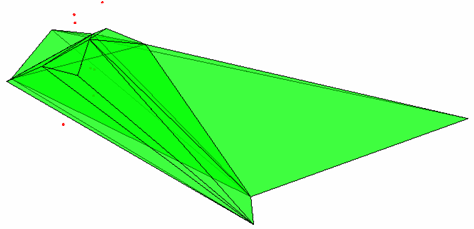

В результате получаем следующий массив V с координатами вершин диаграммы Вороного, в котором первая строка соответствует бесконечно удаленной точке

V =

Inf Inf Inf

1.6786 -1.3247 -0.8356

-0.0413 1.4857 0.2195

0.7505 0.4797 0.7848

0.6998 0.4013 1.4033

0.2062 0.3564 0.4473

0.0184 0.8389 0.4706

0.5013 0.5008 0.7148

0.7016 1.5308 0.5868

0.7426 0.7456 0.6857

0.0122 1.4615 0.2417

4.4104 -2.1563 -0.0837

1.1532 0.2007 0.6310

1.7639 -1.1568 -0.6208

Массив C с номерами вершин ячеек получается такой:

1 4 5 9 10 12 13

1 5 6 7 8

2 3 4 6 7 8 10 11 13 14

1 3 4 5 7 8 9 10 11

1 2 3 9 11 12 14

9 10 11 12 13 14

1 2 4 5 6 8 12 13 14

1 2 3 6 7

Его содержимое говорит о том, что есть только две ячейки конечных размеров - вторая и шестая, поскольку множество их вершин не содержит первой с бесконечными значениями координат.

Функция voronoin оказывается полезной не только для построения диаграммы Вороного в случае пространств, размерности больше трех. Поскольку она возвращает номера вершин, образующих ячейки и их координаты, то ее можно применять для визуализации диаграммы Вороного полигональными объектами для множества точек плоскости и получать закрашенные ячейки.

% генерируем случайные точки

rand('state',0);

x = rand(22,1);

y = rand(22,1);

% отображаем их красными маркерами

figure('Color','w')

plot(x,y,'Marker','.','MarkerEdgeColor','r','MarkerSize',10, 'LineStyle', 'none')

axis off

% находим вершины и многоугольники диаграммы Вороного

[V,C]=voronoin([x y]);

% проходим в цикле по многоугольникам

for k=1:length(C)

if all(C{k}~=1)

% конечные многоугольники рисуем полигональными объектами

VertCell = V(C{k},:)

patch('XData',VertCell(:,1),'YData',VertCell(:,2),'FaceColor','g','FaceAlpha',0.5)

pause(0.1)

end

end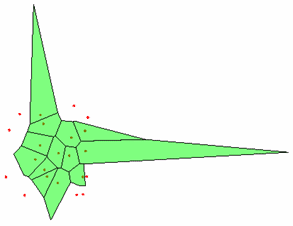

Blog

Обзор средств matlab и ToolBox'ов для приближения данных

Содержание

Работа с разбросанными данными