Обзор средств matlab и ToolBox'ов для приближения данных
| Вид материала | Обзор |
- Структура программы пакета MatLab Простые переменные и основные типы данных в MatLab, 615.94kb.
- Окно элементов управления toolbox окно элементов управления ToolBox, 76.09kb.
- Isbn 5-7262-0634 нейроинформатика 2006, 93.81kb.
- Система управления базами данных это комплекс программных и языковых средств, необходимых, 150.5kb.
- Лабораторна робота №1 операцiї з матрицями. Графічні засоби matlab, 206.02kb.
- Возможности реляционной модели данных по отображению сложных структур данных, 155.27kb.
- «Применение matlab для моделирования физических процессов», 123.4kb.
- Статистические методы и анализ данных, 190.46kb.
- Методические указания к курсовому проектированию по курсу базы данных для студентов, 852.24kb.
- Учебной дисциплины «Базы данных» для направления 010200. 62 «Математика и компьютерные, 55.58kb.
Пример 1. Интегрирование полинома, приближающего данные. Напомним, что исходные табличные данные содержались в массивах x = 0:0.25:2; y = sin(exp(x)); рабочей среды. Требуется проинтегрировать полином пятого порядка, приближающий их в смысле наименьших квадратов, коэффициенты которого хранятся в векторе c5. Для этого сначала воспользуемся функцией polyint для получения вектора с коэффициентами полинома, являющегося его первообразной В качестве входного аргумента функции polyint задается вектор коэффициентов интегрируемого полинома, а возвращает она вектор коэффициентов его первообразной, длина которого на единицу больше (т.к. степень первообразной на единицу выше степени исходного полинома), причем коэффициент первообразной при нулевой степени равен нулю. >> Ic5 = polyint(c5) Ic5 = -0.1280 1.1633 -3.0118 2.4982 -0.5071 0.8553 0 Теперь для вычисления определенного интеграла от полинома, приближающего данные в смысле наименьших квадратов, осталось найти разность значений первообразной в правой и левой точках интервала, на котором заданы данные. Для этого применим функцию polyval, вызвав ее с двумя входными аргументами - вектором с коэффициентами первообразной Ic5 и значением аргумента, при котором ее надо вычислить, т.е. x(end) и x(1). >> I = polyval(Ic5, x(end)) - polyval(Ic5, x(1)) I = 0.5113 Задача решена. Пример 2. Поиск корней полинома, приближающего табличные данные. Найдем корни полинома пятой степени, приближающего наши табличные данные x = 0:0.25:2; y = sin(exp(x)); в смысле наименьших квадратов, который мы построили средствами приложения Basic Fitting, и отобразим вещественные корни на графике с данными и приближением. Для этого воспользуемся функцией root, которая возвращает вектор, содержащий все корни полинома, включая комплексные. Ее входным аргументом является вектор коэффициентов полинома: >> r=roots(c5) r = 4.6289 1.8786 1.1178 -0.0262 + 0.3375i -0.0262 - 0.3375i Нам подходят только второй и третий корни, поскольку только они принадлежат отрезку [0, 2] на котором определены данные. Осталось нанести их на график с данными и приближением, например красными маркерами-звездочками. Следует только предварительно выполнить hold on для того, чтобы графики данных и полиномиального приближения сохранились на осях: >> hold on >> plot([r(2) r(3)], 0, '*r') 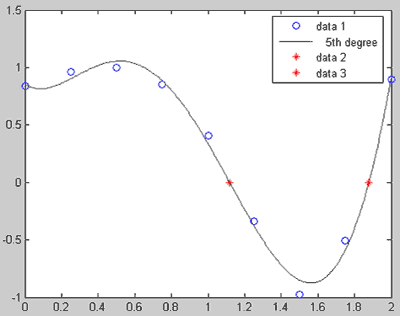 В легенде появились строки data 2 и data 3, поскольку приложение Basic Fitting считает, что мы добавили новые данные. Эти строки легко изменить, перейдя в режим редактирования легенды двойным щелчком мыши. Для отделения вещественных корней полинома, попадающих в отрезок [0, 2] можно было воспользоваться логическим индексированием, сформировав подходящее условие. Это удобно, когда корней много или требуется автоматизировать процесс выбора нужных корней. В нашем случае условие отбора корней является составным - требуется проверить, что корень является вещественным, больше или равен нуля и меньше или равен двум: >> R = r(imag(r)==0 & r>=0 & r<=2) R = 1.8786 1.1178 Более подробные сведения о логическом индексировании, операциях сравнения и условных операторов содержатся в справочной системе MATLAB в разделах:
Описанные выше примеры были посвящены экспорту полиномиальных приближений из приложения Basic Fitting в рабочую среду MATLAB в виде структуры. Информация о сплайнах так же передается в рабочую среду в структуре, которая содержит больше полей, чем в случае с полиномом. Экспортируем кубический сплайн, интерполирующий наши данные x = 0:0.25:2; y = sin(exp(x)); выбрав spline interpolant в раскрывающемся списке Fit на панели Numerical results (если сплайна нет, то его предварительно следует построить, см. Приближение данных полиномами по методу наименьших квадратов и сплайнами в приложении Basic Fitting). После нажатия на кнопку Save to workspace появляется диалоговое окно сохранения Save Fit to Workspace, в нем можно ввести имя для структуры, в которую будет записана информация о сплайне и имя переменной для значения среднеквадратичной нормы ошибки. Норма ошибки в данном случае равна нулю, поскольку сплайн интерполяционный, и соответствующий флаг окно сохранения Save Fit to Workspace можно сбросить. Введем имя для структуры sp3 и нажмем кнопку ОК. В рабочей среде создалась структура (о чем вывелось сообщение в командное окно "Variables have been created in the current workspace"), выведем ее >> sp3 sp3 = type: 'spline' coeff: [1x1 struct] Структура sp3 содержит два поля: поле type с информацией о том, что это сплайн, и поле coeff, которое также является структурой. Запишем его содержимое в новую структуру s3 >> s3 = sp3.coeff s3 = form: 'pp' breaks: [0 0.2500 0.5000 0.7500 1 1.2500 1.5000 1.7500 2] coefs: [8x4 double] pieces: 8 order: 4 dim: 1 Это формат представления сплайна принятый в MATLAB и Spline Toolbox. Ряд функций, предназначенных для работы со сплайнами (поиск корней, интегрирование и т. д.), требуют задания сплайна именно в этом формате. Смысл полей структуры следующий:
Проделаем с кубическим сплайном, записанным в структуру s3, те же самые действия, что описаны выше для полинома пятой степени, приближающего данные по методу наименьших квадратов: найдем его корни и проинтегрируем на том отрезке, на котором определены данные. Пример 3. Интегрирование интерполяционного кубического сплайна, приближающего табличные данные. Для вычисления определенного интеграла от сплайна по отрезку [0, 2], на котором определены данные воспользуемся функциями fnint и fnval, входящими в Spline ToolBox. Функция fnint вычисляет первообразную для сплайна, принимающую нулевое значение на левой границе интервала. Её входным аргументом является приведенная выше структура с информацией об интегрируемом сплайне, а возвращает результат она в том же самом формате - в виде структуры с полями, имеющими те же названия. Разумеется, значение поля order для первообразной будет на единицу большей. >> Is3 = fnint(s3) Is3 = form: 'pp' breaks: [0 0.2500 0.5000 0.7500 1 1.2500 1.5000 1.7500 2] coefs: [8x5 double] pieces: 8 order: 5 dim: 1 Функция fnval предназначена для нахождения значений сплайна в заданных точках, ее входными аргументами являются: структура со сплайном и значение аргумента (или вектор значений). >> I=fnval(Is3,2)-fnval(Is3,0) I = 0.5348 Полученный результат немного отличается от того, что был получен при интегрировании полинома, поскольку эти приближения не совпадают. Пример 4. Поиск корней сплайна, приближающего табличные данные. Для решения этой задачи воспользуемся функцией fnzeros, входящей в состав Spline ToolBox. Если в качестве ее входного аргумента указать структуру со сплайном, то она вернет матрицу, состоящую из двух строк, которая строка которой содержит информацию о корнях сплайна. Вычисление корней производится на всем промежутке задания сплайна. Смысл элементов возвращаемой матрицы в данном случае простой:
Для нашего сплайна, информация о котором записана в структуре s3, результат будет следующим: >> r = fnzeros(s3) r = 1.1453 1.8551 1.1453 1.8551 Т.е. корни сплайна имеют значения 1.1453 и 1.8551. Работа с несколькими наборами данных Приложение Basic Fitting позволяет работать с несколькими наборами данных. Их можно или сразу отобразить в графическом окне, либо добавлять данные при запущенном приложении Basiс Fitting (выполнив предварительно hold on для того, чтобы предыдущие данные не удалились с осей графического окна). Каждый набор данных автоматически получает имя: data1, data2 и т. д. Для перехода к требуемому набору следует использовать раскрывающийся список Select data приложения Basic Fitting. Для смены имени существует два способа:
Если графики данных построены в нескольких графических окнах, то для каждого из окон следует запустить свою копию приложения Basic Fitting, которая позволит работать с данными именно этого графического окна. Если графики данных построены на разных осях в пределах одного графического окна, к примеру: figure x = 0:0.25:2; sublot(2,1,1) plot(x, sin(x), 'o') sublot(2,1,2) plot(x, cos(x), 'o') то запуск приложения Basic Fitting позволит приближать данные, построенные на всех осях. Какие функции MATLAB и методы используются в приложении Basic Fitting Приложение Basic Fitting служит графической оболочкой для следующих функций MATLAB: spline - для построения кубических сплайнов с граничным условием отсутствия узла (not-a-knot condition). Смысл этих условий пояснен в разделе Интерполяция одномерных данных сплайнами. pchip - для построения сплайнов, сохраняющих форму данных, т.е. кубических полиномов Эрмита. Кубические полиномы Эрмита описаны в разделе Интерполяция сплайнами, сохраняющими форму (кубическими полиномами Эрмита). polyfit - для приближения данных полиномами в смысле наименьших квадратов. Применение метода наименьших квадратов для приближения данных описано в разделе Приближение полиномами в смысле наименьших квадратов. norm - для вычисления среднеквадратичной нормы ошибки. Приближение полиномами в смысле наименьших квадратов В этом разделе мы рассмотрим применение функции polyfit для приближения данных полиномами в смысле наименьших квадратов, визуализацию результата функцией polyval и получение ошибки приближения (см. разд. Приближение полиномами в смысле наименьших квадратов). Кроме того, мы обсудим метод наименьших квадратов и его вычислительные свойства (см. разд. Метод наименьших квадратов), поскольку довольно часто задача о приближении данных оказывается плохо обусловленной, что может привести к значительному ухудшению качества приближения (см. разд. Когда функция polyfit выдает предупреждения, плохая обусловленность, центрирование и масштабирование данных). Функция polyfit возвращает полином в виде вектора его коэффициентов, т.е. в стандартном для MATLAB виде, поэтому в конце этого раздела приведены функции для выполнения различных операций над полиномами в MATLAB и пример, в котором требуется проинтегрировать табличную функцию и найти ее корни (см. разд. Операции с полиномиальными приближениями). Задача о приближении данных полиномом в смысле наименьших квадратов Одним из способов приближения данных некоторой непрерывной функцией является приближение полиномом по методу наименьших квадратов. Для набора данных: 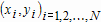 требуется найти такой полином степени  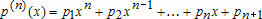 коэффициенты которого являются решением следующей задачи минимизации 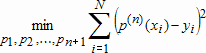 То есть, другими словами, разыскивается полином, который наименее уклоняется от заданных данных в том смысле, что сумма квадратов расстояний от заданных точек 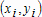 до до 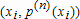 будет минимальной будет минимальной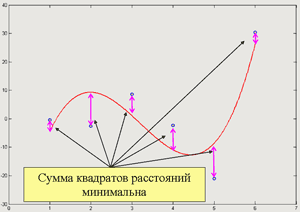 Степень полинома должна быть меньше количества заданных точек для того, чтобы такой полином был единственным. Например, если заданы три точки, то их можно приблизить либо полиномом нулевой или первой степени (прямая), либо параболой. Причем, парабола будет точно проходить через три заданные точки (сумма квадратов расстояний окажется равной нулю), поскольку три коэффициента квадратичного полинома однозначно определяются из трех условий прохождения через заданные точки. В данном случае, мы получим уже не приближение данных, а их интерполяцию. На практике, обычно применяются полиномы не очень высоких степеней. В MATLAB для приближения данных в смысле наименьших квадратов используется функция polyfit, во входных аргументах которой указываются вектора с данными, а выходным является вектор коэффициентов полинома, начиная со старшей степени. Функция polyfit может быть вызвана и с большим числом входных и выходных аргументов, что может потребоваться для улучшения качества приближения и получения некоторой дополнительной информации о нем. Подробнее об этом написано в разделах алгоритм, решение системы, когда появляются предупреждения, центрирование и масштабирование и как использовать polyval. Поставим задачу приблизить данные, которые заданы массивами x и y: >> x = [0.1 0.3 0.45 0.5 0.79 1.1 1.89 2.4 2.45]; >> y = [-3 -1 0.9 2.4 2.5 1.9 0.1 -1.3 -2.6]; полиномами первой, третьей и пятой степени. Используем функцию polyfit, указав в ее входных аргументах вектора с данными и степени полиномов. Сами коэффициенты запишем в вектора p1, p3 и p5, соответственно: >> p1 = polyfit(x, y, 1) p1 = -0.6191 0.6755 >> p3 = polyfit(x, y, 3) p3 = 2.2872 -12.1553 17.0969 -4.5273 >> p5 = polyfit(x, y, 5) p5 = -6.0193 33.9475 -62.4220 35.9698 4.7121 -3.8631 Итак, мы получили полиномы: 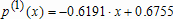 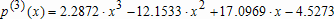 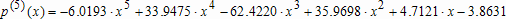 Для построения графиков этих полиномов следует найти их значения в промежуточных точках, принадлежащих интервалу, на котором заданы данные, т.е. между x(1) и x(end). Сгенерируем 100 точек, равномерно расположенных на области определения данных, при помощи функции linspace >> xx = linspace(x(1), x(end), 100); вычислим в них значения полиномов 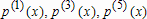 при помощи функции polyval и запишем найденные значения в вектора yy1, yy3, yy5 соответственно. Входными аргументами функции polyval в самом простом случае являются вектор коэффициентов полинома и вектор значений независимой переменной, для которых требуется вычислить значения полинома, а выходным - вектор значений полинома при помощи функции polyval и запишем найденные значения в вектора yy1, yy3, yy5 соответственно. Входными аргументами функции polyval в самом простом случае являются вектор коэффициентов полинома и вектор значений независимой переменной, для которых требуется вычислить значения полинома, а выходным - вектор значений полинома>> yy1 = polyval(p1, xx); >> yy3 = polyval(p3, xx); >> yy5 = polyval(p5, xx); Для наглядности построим графики полиномов и разместим заданные массивами x и y точки круглыми маркерами >> plot(x, y, 'o', xx, yy1, xx, yy3, xx, yy5) Кроме этого, при помощи функции legend разместим справа от осей легенду, в которой укажем соответствие линий полиномам: >> legend('DATA', '{\itp}{(1)}({\itx})', '{\itp}{(3)}({\itx})', '{\itp}{(5)}({\itx})',-1) При создании легенды использовались возможности интерпретатора TeX (см. ссылка скрыта). В результате получается график, приведенный ниже 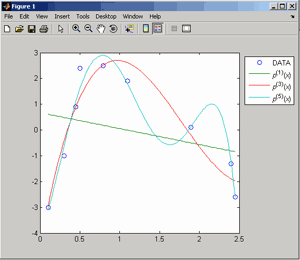 Для того, чтобы узнать, насколько далеко отстоит график полинома от заданных точек, т.е. какая была допущена ошибка при приближении данных, следует вызывать функцию polyfit с двумя выходными аргументами. В первый из них запишется вектор коэффициентов построенного полинома, а во второй структура с информацией о приближении, например: >> [p3, S3] = polyfit(x, y, 3) приводит к выводу в командное окно того же самого вектора коэффициентов кубического полинома, что получился в предыдущем примере, и структуры S3 с полями R, df и normr: p3 = 2.2872 -12.1553 17.0969 -4.5273 S3 = R: [4x4 double] df: 5 normr: 1.7201 Поле normr содержит ошибку в среднеквадратичной норме, т.е. значение 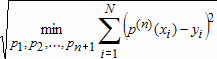 (если работа со структурами незнакома, то достаточно понять, что для записи содержимого поля структуры в некоторую переменную надо отделять имя структуры от имени поля точкой, т.е. >> r = S3.normr). В поле df содержится разность между числом точек и числом коэффициентов полинома. Повышение степени полинома приводит к уменьшению ошибки, однако качество приближения не всегда улучшается. Например, для наших данных полином восьмой степени обеспечивает практически нулевую ошибку (вычислительные погрешности возникают в ходе алгоритма нахождения коэффициентов) >> [p8, S8] = polyfit(x, y, 8) S8 = R: [9x9 double] df: 0 normr: 2.2382e-010 однако приближает данные намного хуже, чем полином седьмой степени, что можно видеть из графика, на котором представлены данные и два приближения: >> [p7, S7] = polyfit(x, y, 7) >> yy7 = polyval(p7, xx); >> yy8 = polyval(p8, xx); >> plot(x, y, 'o', xx, yy7, xx, yy8) >> legend('DATA', '{\itp}{(7)}({\itx})', '{\itp}{(8)}({\itx})',-1) 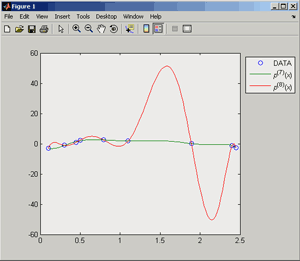 Так происходит потому, что полином восьмой степени является интерполяционным полиномом, который как правило, плохо подходит для приближения данных. Дальнейшее увеличение степени полинома ни к чему хорошему не приведет, например при построении полинома девятой степени >> [p9, S9] = polyfit(x, y , 9) выведется предупреждение о том, что такой полином не единственный Warning: Polynomial is not unique; degree >= number of data points. Приближение полиномом девятой степени окажется еще хуже, чем интерполяция полиномом восьмой степени: >> yy9 = polyval(p9, xx); >> plot(x, y, 'o', xx, yy8, xx, yy9) >> legend('DATA', '{\itp}{(8)}({\itx})', '{\itp}{(9)}({\itx})',-1) 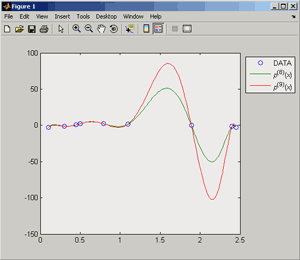 В следующем разделе мы рассмотрим реализацию метода наименьших квадратов для построения полиномиального приближения. Метод наименьших квадратов Напомним, что задача приближения данных 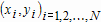 полиномом некоторой степени  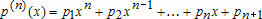 состоит в решении задачи минимизации 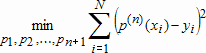 Запишем полином в виде 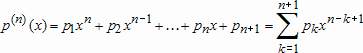 Тогда задача о построении полиномиального приближения сводится к поиску минимума следующей функции 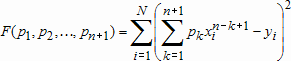 по переменным 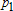 , , 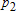 , ... , , ... , 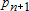 . Функция . Функция 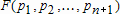 является квадратичной функцией (с неотрицательными коэффициентами при квадратах неизвестных), поэтому ее минимум достигается в той точке, где выполняются следующие условия: является квадратичной функцией (с неотрицательными коэффициентами при квадратах неизвестных), поэтому ее минимум достигается в той точке, где выполняются следующие условия: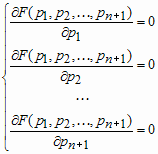 Взяв частные производные от 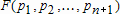 по по 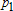 , , 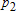 , ... , , ... , 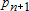 и приравняв их к нулю, получаем систему линейных алгебраических уравнений из ( и приравняв их к нулю, получаем систему линейных алгебраических уравнений из (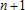 )-го уравнения для нахождения искомых коэффициентов )-го уравнения для нахождения искомых коэффициентов 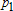 , , 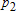 , ... , , ... , 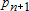 полинома полинома  -ой степени, наилучшим образом в смысле наименьших квадратов приближающего данные -ой степени, наилучшим образом в смысле наименьших квадратов приближающего данные 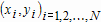 . Эта система имеет вид: . Эта система имеет вид: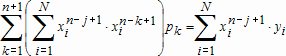 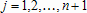 или в матричном виде 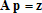 где 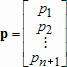 а элементы матрицы 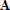 и вектора правой части системы и вектора правой части системы  выражаются формулами выражаются формулами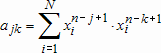 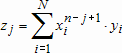 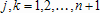 В принципе, ее можно решить и получить искомые коэффициенты полинома (это называется методом нормальных уравнений), однако в функции polyfit реализован несколько другой подход, более устойчивый к вычислительным ошибкам. Формируется прямоугольная матрица 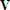 из из 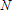 строк и ( строк и (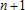 )-го столбца, элементами которой являются степени )-го столбца, элементами которой являются степени 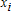 : :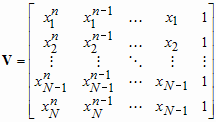 (Если 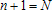 , то матрица , то матрица 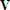 с точностью до перестановки столбцов в обратном порядке является известной матрицей Вандермонда). Несложно заметить, что матрица с точностью до перестановки столбцов в обратном порядке является известной матрицей Вандермонда). Несложно заметить, что матрица 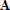 нашей системы линейных алгебраических уравнений и матрица нашей системы линейных алгебраических уравнений и матрица 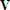 связаны между собой следующим образом: связаны между собой следующим образом: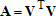 Аналогично, вектор  правой части системы уравнений правой части системы уравнений 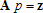 так же выражается через вектор так же выражается через вектор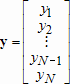 следующим образом: 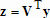 В функции polyfit при помощи функции qr пакета MATLAB разыскивается QR-разложение матрицы 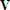 , т.е. находятся такая ортогональная матрица , т.е. находятся такая ортогональная матрица 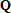 (квадратная матрица (квадратная матрица 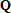 называется ортогональной, если произведение называется ортогональной, если произведение 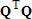 является единичной матрицей) и верхняя треугольная матрица является единичной матрицей) и верхняя треугольная матрица 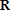 , что , что 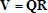 (более точно, ищется только первые (более точно, ищется только первые 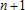 столбцов матрицы столбцов матрицы 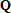 и не вся матрица и не вся матрица 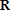 , а только первые , а только первые 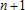 ее строк и столбцов). Далее система линейных уравнений ее строк и столбцов). Далее система линейных уравнений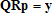 решается так:
Ошибка приближения, т.е. значение 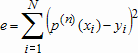 для найденного полинома 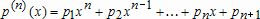 вычисляется по формуле 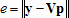 где евклидова норма вектора находится при помощи функции norm. Функция polyfit может возвращать норму ошибки и матрицу 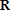 . Для этого ее следует вызвать с двумя выходными аргументами. В первом выходном аргументе (векторе) возвращаются найденные коэффициенты полинома, а второй выходной аргумент является структурой со следующими полями: . Для этого ее следует вызвать с двумя выходными аргументами. В первом выходном аргументе (векторе) возвращаются найденные коэффициенты полинома, а второй выходной аргумент является структурой со следующими полями:
Например, для записи евклидовой нормы ошибки приближения в переменную e можно использовать следующие команды: [p, S] = polyfit(x,y,4); e = S.normr В ряде случаев функция polyfit может выдавать предупреждения, об этом подробно написано в следующем разделе. Когда функция polyfit выдает предупреждения, плохая обусловленность, центрирование и масштабирование данных Функция polyfit выдает предупреждения в нескольких случаях.
Большое число обусловленности может быть в нескольких случаях. Во-первых матрица 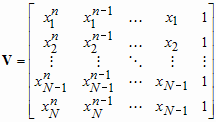 при 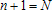 , как уже было замечено, является матрицей Вандермнода (с точностью до перестановки столбцов). Если точки , как уже было замечено, является матрицей Вандермнода (с точностью до перестановки столбцов). Если точки 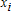 , в которых заданы значения данных , в которых заданы значения данных 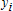 , равномерно распределены на отрезке [0, 1], то число обусловленности матрицы , равномерно распределены на отрезке [0, 1], то число обусловленности матрицы 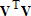 с ростом N ведет себя как число обусловленности матрицы Гильберта, которая является классическим примером плохо обусловленной матрицы с экспоненциально растущим числом обусловленности. Тогда число обусловленности матрицы с ростом N ведет себя как число обусловленности матрицы Гильберта, которая является классическим примером плохо обусловленной матрицы с экспоненциально растущим числом обусловленности. Тогда число обусловленности матрицы 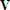 , совпадающее по значению с числом обусловленности множителя , совпадающее по значению с числом обусловленности множителя 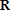 , входящего в QR-разложение , входящего в QR-разложение 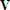 , будет вести себя как квадратный корень из числа обусловленности матрицы , будет вести себя как квадратный корень из числа обусловленности матрицы 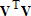 . Для N равномерно распределенных на отрезке [0, 1] точек . Для N равномерно распределенных на отрезке [0, 1] точек 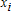 зависимость числа обусловленности матрицы зависимость числа обусловленности матрицы 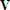 от N (при от N (при 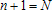 ) в полулогарифмической шкале представлена на следующем графике ) в полулогарифмической шкале представлена на следующем графике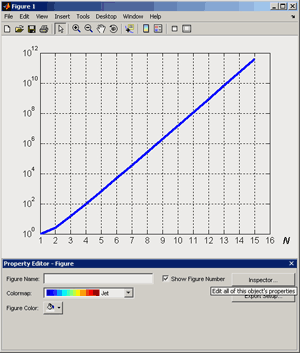 из которого видно, что даже для небольших значений число обусловленности будет превосходить 1010 и функция polyfit выдаст предупреждение о большой обусловленности, например: >> N = 13; >> x = linspace(0,1,N); >> y = sin(x); >> p = polyfit(x, y, N-1) Warning: Polynomial is badly conditioned. Remove repeated data points or try centering and scaling as described in HELP POLYFIT. Для получения предыдущего графика число обусловленности прямоугольной матрицы 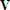 вычислялось как отношение ее наибольшего сингулярного числа к наименьшему, т.е. вычислялось как отношение ее наибольшего сингулярного числа к наименьшему, т.е. 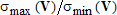 , где , где 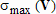 и и 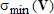 - максимальные и минимальные числа на диагонали матрицы - максимальные и минимальные числа на диагонали матрицы 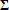 , входящей в сингулярное разложение матрицы , входящей в сингулярное разложение матрицы 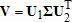 , где , где 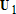 и и 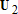 - ортогональные матрицы. Сами сингулярные числа определялись при помощи функции svd. Поскольку в функции polyfit используется сверху оценка для числа обусловленности, возвращаемая функцией condest, то предупреждение о превышении порога 1010 оценкой для числа обусловленности может наступить раньше. Для сравнения числа обусловленности матрицы - ортогональные матрицы. Сами сингулярные числа определялись при помощи функции svd. Поскольку в функции polyfit используется сверху оценка для числа обусловленности, возвращаемая функцией condest, то предупреждение о превышении порога 1010 оценкой для числа обусловленности может наступить раньше. Для сравнения числа обусловленности матрицы 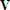 , полученного при помощи svd, и его оценки сверху, возвращаемой функцией condest, приведен следующий график , полученного при помощи svd, и его оценки сверху, возвращаемой функцией condest, приведен следующий график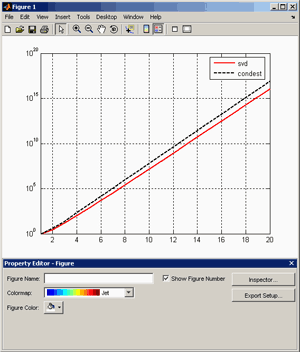 Если степень полинома  не в точности равна не в точности равна 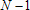 , но близка к числу точек N, в которых заданы данные, то число обусловленности тоже будет велико, как видно из следующего графика , но близка к числу точек N, в которых заданы данные, то число обусловленности тоже будет велико, как видно из следующего графика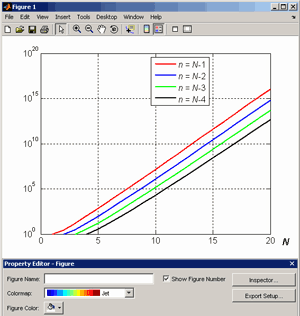 К примеру, приближение данных, заданных в двадцати равноотстоящих точках на отрезке [0, 1] полиномом тринадцатой степени уже приведет к предупреждению о плохой обусловленности: >> N = 20; >> x = linspace(0, 1, N); >> y = sin(x); >> p = polyfit(x, y, 13) Warning: Polynomial is badly conditioned. Remove repeated data points or try centering and scaling as described in HELP POLYFIT. Следующий пример демонстрирует, к чему может привести большая обусловленность, если исходные данные заданы с ошибкой 10-3. Данные задаются на отрезке [0,1] в двадцати равномерно расположенных точках 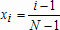 , , 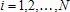 , , 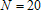 . Заданные значения . Заданные значения 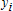 в них являются значениями функции в них являются значениями функции 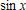 . Сначала производится приближение этих данных полиномом восемнадцатой степени по методу наименьших квадратов, затем в данные вносится ошибка порядка 10-3 и снова строится приближение полиномом восемнадцатой степени по методу наименьших квадратов. При этом функция polyfit каждый раз выдает предупреждение о плохой обусловленности. . Сначала производится приближение этих данных полиномом восемнадцатой степени по методу наименьших квадратов, затем в данные вносится ошибка порядка 10-3 и снова строится приближение полиномом восемнадцатой степени по методу наименьших квадратов. При этом функция polyfit каждый раз выдает предупреждение о плохой обусловленности.% определяем данные в 20-и точках N = 20; x = linspace(0,1,N); y = sin(x); % приближаем данные по методу наименьших квадратов полиномом 18-ой степени n=18; p = polyfit(x, y, n) % строим график данных и полинома xx = linspace(x(1), x(end), 100); yy = polyval(p, xx); plot(x, y, 'o', xx, yy) % вносим в данные ошибку порядка 0.001 ye = y + 0.001*rand(size(y)); % приближаем данные по методу наименьших квадратов полиномом 18-ой степени pe = polyfit(x, ye, n) % строим график полинома yy = polyval(pe, xx); hold on plot(xx, yy, 'm') legend('data', '{\itp}{(18)} for data', '{\itp}{(18)} for data + 10{-3}',-1) 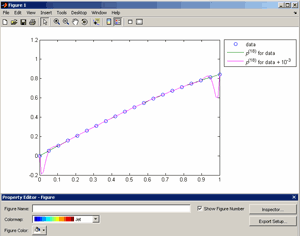 Более того, разница между коэффициентами полиномов, применяемых для приближения исходных и возмущенных данных составляет величину порядка 1010, >> max(abs(p-pe)) ans = 3.0239e+010 Приближение же полиномом третьей степени даст разницу коэффициентов порядка 10-3, в чем несложно убедиться, присвоив в предыдущем примере переменной n значение 3. Еще один источник появления сообщения о плохой обусловленности - повторяющиеся точки 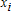 , в которых определены исходные данные. В этом случае столбцы матрицы , в которых определены исходные данные. В этом случае столбцы матрицы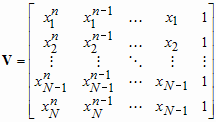 становятся линейно зависимыми, ее ранг получается меньше, чем 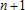 и мы получаем задачу метода наименьших квадратов неполного ранга. Если степень полинома больше или равна рангу, то задача не будет иметь единственного решения. Это демонстрирует следующий простой пример. Если есть две точки с координатами и мы получаем задачу метода наименьших квадратов неполного ранга. Если степень полинома больше или равна рангу, то задача не будет иметь единственного решения. Это демонстрирует следующий простой пример. Если есть две точки с координатами 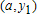 и и 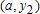 , то существует бесконечно много прямых, одинаково хорошо приближающих их в смысле наименьших квадратов, как видно из следующего рисунка , то существует бесконечно много прямых, одинаково хорошо приближающих их в смысле наименьших квадратов, как видно из следующего рисунка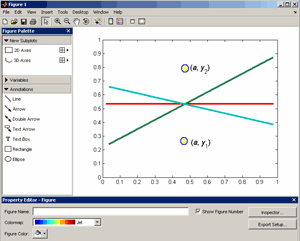 В качестве примера рассмотрим приближение данных x = [1 2 2 3 3 3 4]; y = [1 5 4 3 4 3 4]; в смысле наименьших квадратов полиномом четвертой степени p = polyfit(x, y, 4); Warning: Polynomial is badly conditioned. Remove repeated data points or try centering and scaling as described in HELP POLYFIT. 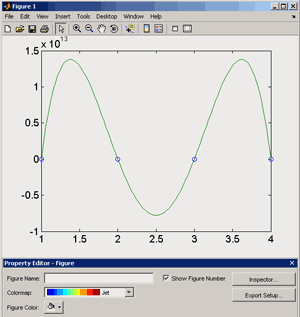 В таком случае можно усреднить данные, заданные в повторяющихся точках, и удалить повторяющиеся точки и сами данные, воспользовавшись например следующими операторами: for k=1:length(x) - 1 % проходим по массиву x % находим индексы элементов массива x, совпадающих с x(k) ind = find(x == x(k)); if length(ind)>1 % есть элементы, совпадающие с x(k) % удаляем их из массива x x(ind(2:end))=[]; % усредняем соответствующие элементы в массиве y y(ind(1)) = mean(y(ind)); % удаляем лишние элементы из массива y y(ind(2:end)) = []; end end Вычислительные погрешности, неизбежно возникающие в ходе алгоритма, могут привести к тому, что при различных, но достаточно близких точках, произойдет потеря точности. В качестве примера рассмотрим приближение данных y = [1 5 5.03 3 2.99 3 4]; заданных в двух наборах точек: x1 = [1 2 2.01 3 3.01 3.02 4]; x2 = [1 2 2.000001 3 3.000001 3.0000002 4]; полиномом четвертой степени. При приближении данных, определенных в x1, полиномиальное приближение получается хорошее, а в случае с x2 появляется предупреждение о плохой обусловленности и результат получается очень плохой, как видно из следующих графиков (на левом - результаты для набора (x1, y), на правом - для (x2, y)) 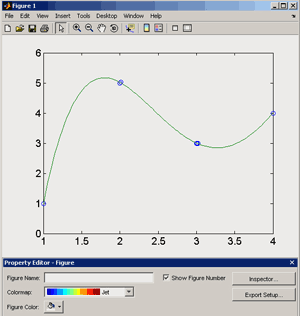 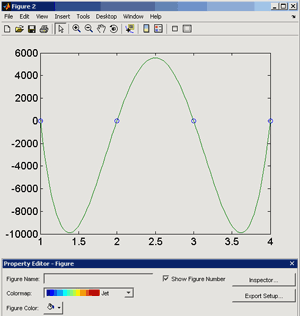 Последний источник возникновения плохой обусловленности при приближении в смысле наименьших квадратов - немасштабированные данные. Например, при приближении данных x = [51 52 53 54 55 56 57]; y = [1.2 3.4 2.9 4.4 4.5 5.1 4.2]; полиномом четвертой степени получаем предупреждение о плохой обусловленности >> p = polyfit(x, y, 4) Warning: Polynomial is badly conditioned. Remove repeated data points or try centering and scaling as described in HELP POLYFIT. хотя степень полинома невелика и в массиве x нет совпадающих или близких точек, в которых определены значения данных, как было описано выше. Продемонстрируем на простом примере, как зависит число обусловленности матрицы системы линейных алгебраических уравнений метода наименьших квадратов 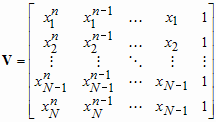 понимаемое в смысле отношения ее наибольшего сингулярного числа к наименьшему, т.е. 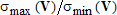 , где , где 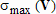 и и 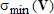 - максимальные и минимальные числа на диагонали матрицы - максимальные и минимальные числа на диагонали матрицы 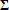 , образующей сингулярное разложение матрицы , образующей сингулярное разложение матрицы 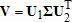 с ортогональными матрицами с ортогональными матрицами 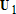 и и 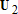 . Пусть данные заданы в семи равномерно отстоящих друг от друга на отрезке [0, 1] точках . Пусть данные заданы в семи равномерно отстоящих друг от друга на отрезке [0, 1] точках 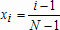 , , 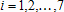 . Исследуем, как зависит число обусловленности матрицы . Исследуем, как зависит число обусловленности матрицы 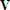 от передвижения отрезка, т.е. как будет вести себя обусловленность метода наименьших квадратов, применяемого для семи равномерно отстоящих друг от друга точках на отрезке от передвижения отрезка, т.е. как будет вести себя обусловленность метода наименьших квадратов, применяемого для семи равномерно отстоящих друг от друга точках на отрезке 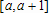 с увеличением с увеличением  . Как видно из следующего графика, число обусловленности растет достаточно быстро . Как видно из следующего графика, число обусловленности растет достаточно быстро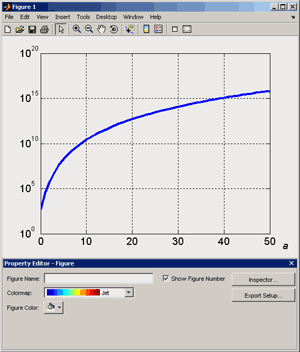 В таких случаях для улучшения вычислительных свойств полиномиальных приближений по методу наименьших квадратов рекомендуется прибегать к предварительной обработке данных - их центрированию и масштабированию (нормализации), которая сводится к простой замене 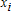 на на 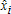 , вычисляемые для , вычисляемые для 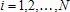 по формуле по формуле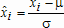 где 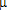 и и  соответственно - среднее значение и среднеквадратичное отклонение, вычисляемые по формулам соответственно - среднее значение и среднеквадратичное отклонение, вычисляемые по формулам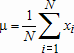 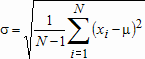 Это преобразование не нужно делать самому, его выполняет функция polyfit, если обратиться к ней с тремя выходными аргументами. В третьем аргументе вернется вектор из двух компонент, первой из них будет среднее 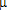 , а второй - среднеквадратичное отклонение , а второй - среднеквадратичное отклонение  . Этот вектор понадобится в дальнейшем при вычислении значений полинома при помощи функции polyval, его следует указывать в качестве четвертого входного аргумента (третий входной аргумент задается, если требуется получить оценку ошибки приближения, что относится к статистическим методам анализа данных, см. пример в справочной системе в разделе MATLAB: Mathematics: Data Analysis and Statistics: Case Study: Curve Fitting). Для того, чтобы пропустить третий входной аргумент функции polyval, будем использовать пустой массив. . Этот вектор понадобится в дальнейшем при вычислении значений полинома при помощи функции polyval, его следует указывать в качестве четвертого входного аргумента (третий входной аргумент задается, если требуется получить оценку ошибки приближения, что относится к статистическим методам анализа данных, см. пример в справочной системе в разделе MATLAB: Mathematics: Data Analysis and Statistics: Case Study: Curve Fitting). Для того, чтобы пропустить третий входной аргумент функции polyval, будем использовать пустой массив.В нашем предыдущем примере для приближения данных x = [51 52 53 54 55 56 57]; y = [1.2 3.4 2.9 4.4 4.5 5.1 4.2]; полиномом четвертой степени в смысле наименьших квадратов следовало использовать именно такие обращения к функциям polyfit и polyval, предполагающее центрирование и масштабирование исходных данных: x = [51 52 53 54 55 56 57]; y = [1.2 3.4 2.9 4.4 4.5 5.1 4.2] [p, S, mu] = polyfit(x, y, 4) xx = linspace(x(1), x(end), 200); yy = polyval(p, xx, [], mu); plot(x, y, 'o', xx, yy) 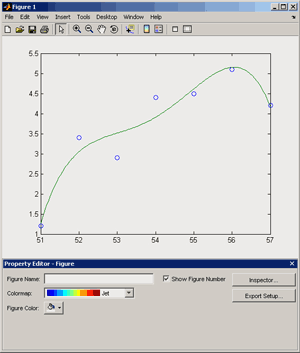 Применение масштабирования в этом примере существенно улучшило вычислительные свойства метода наименьших квадратов и в ходе работы функции polyfit сообщения о плохой обусловленности выведено не было. Операции с полиномиальными приближениями Функция polyfit возвращает вектор коэффициентов полинома, приближающий данные в смысле наименьших квадратов. В этом векторе коэффициенты полинома записываются начиная с коэффициента при старшей степени, т.е. в соответствии с соглашением, принятым в MATLAB. Это позволяет применить ряд функций для дальнейших операций с полученными полиномиальными приближениями. Одна из этих функций polyval, предназначенная для вычисления значений полинома в заданных точках была описана в предыдущих разделах, в том числе и для случая, когда к данным применялось центрирование и масштабирование (см. Задача о приближении данных полиномом в смысле наименьших квадратов и когда функция polyfit выдает предупреждения, плохая обусловленность, центрирование и масштабирование данных). В MATLAB возможно производить следующие операции над полиномами: Умножение полиномов и деление с остатком при помощи функций conv и deconv. Пусть, например, требуется найти произведение и отношение следующих полиномов: 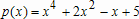 и и 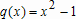 Задаем их векторами коэффициентов >> p = [1 0 0 2 -1 5]; >> q = [1 0 -1]; и применяем функцию conv, входными аргументами которой являются вектора коэффициентов перемножаемых полиномов, а выходным - вектор коэффициентов результирующего полинома: >> P = conv(p, q) P = 1 0 1 -1 3 1 -5 т.е. 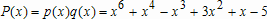 Деление полиномов при помощи deconv требует указания двух аргументов, в первый из которых записываются коэффициенты частного от деления, а во второй - коэффициенты полинома, являющегося остатком от деления: >> [R, r] = deconv(p, q) R = 1 0 3 r = 0 0 0 -1 8 т.е. 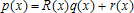 , где , где 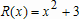 , , 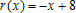 , что несложно проверить перемножением при помощи conv и сложением: , что несложно проверить перемножением при помощи conv и сложением: >> conv(R, q) + r ans = 1 0 2 -1 5 Получаются в точности коэффициенты исходного полинома. Кстати, функция deconv возвращает коэффициенты остатка от деления в векторе (в нашем примере r), длина которого всегда совпадает с длиной вектора коэффициентов делимого (в нашем примере p), а если степень остатка меньше степени делимого, то вектор с коэффициентами остатка дополняется нулями. Это позволило нам выполнить операцию сложения в выражении conv(R, q) + r без ошибки, поскольку складывались два вектора одинаковой длины. Сложение и вычитание полиномов. Для корректного сложения и вычитания полиномов разных степеней следует дополнить наименьший вектор нулями справа до длины наибольшего. Этот процесс можно автоматизировать при помощи такой последовательности операторов: >> d = length(q)-length(p); >> s = [zeros(1,d) p] + [zeros(1,-d) q] s = 1 0 3 -1 4 Аналогично производится и вычитание полиномов. MATLAB является объектно-ориентированной системой, поддерживающей создание классов. Можно было создать собственный класс для полиномов и перегрузить операции сложения и умножения (см. раздел справочной системы MATLAB: Programming: Classes and Objects: Example A Polynomial Class). Интегрирование и дифференцирование полиномов. Для нахождения коэффициентов полиномов, являющихся производной и неопределенным интегралом от заданного полинома предназначены функции polyder и polyint. Для полинома 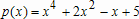 заданного вектором коэффициентов >> p = [1 0 0 2 -1 5]; функция polyder возвращает вектор коэффициентов первой производной: >> p1 = polyder(p) p1 = 4 0 4 -1 т.е. 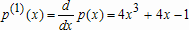 Кроме этого, функция polyder умеет вычислять производную от произведения и отношения двух полиномов. Если функция polyder вызывается с двумя входными аргументами (векторами с коэффициентами полиномов), то она возвращает производную от произведения полиномов, например: >> dP = polyder(p, q) dP = 6 0 4 -3 6 1 возвращает то же самое, что и >> polyder(conv(p, q)) ans = 6 0 4 -3 6 1 Для нахождения производной от отношения полиномов следует вызывать функцию polyder с двумя выходными аргументами, в первый из которых записываются коэффициенты числителя производной отношения полиномов, а во второй - знаменателя, например для полиномов 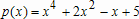 и и 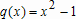 заданных их векторами коэффициентов >> p = [1 0 0 2 -1 5]; >> q = [1 0 -1]; >> [P,Q] = polyder(p, q) P = 2 0 -4 1 -14 1 Q = 1 0 -2 0 1 возвращается 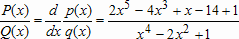 Для вычисления первообразной полинома, принимающей в нуле значение ноль используется обращение к функции polyint с одним входным коэффициентом - вектором коэффициентов интегрируемого полинома, например возвращаемый вектор >> I = polyint(p) I = 0.2000 0 0.6667 -0.5000 5.0000 0 содержит коэффициенты полинома 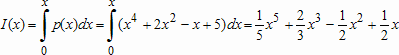 а при обращении >> I = polyint(p,100) I = 0.2000 0 0.6667 -0.5000 5.0000 100.0000 вычисляются коэффициенты полинома 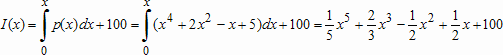 Нахождение корней полинома. Для вычисления всех корней полинома, включая и комплексные, предназначена функция roots, которая возвращает их в виде вектор-столбца. Например, для полинома 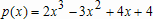 >> p = [2 -3 4 4]; возвращается >> r = roots(p) r = 1.0545 + 1.4739i 1.0545 - 1.4739i -0.6090 При использовании функции roots следует соблюдать некоторую осторожность, поскольку алгоритм нахождения корней не всегда гарантирует хорошую точность. Корни полинома разыскиваются как собственные числа сопровождающей матрицы, которая для полинома 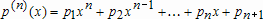 определяется следующим образом (заполнена только верхняя строка и нижняя поддиагональ, а все остальные элементы сопровождающей матрицы равны нулю) 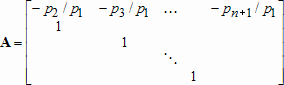 Собственные числа матрицы вычисляются функцией eig пакета MATLAB, однако не всегда из-за вычислительных погрешностей они будут совпадать с хорошей точностью с корнями полинома. Продемонстрируем это на следующем примере. При помощи функции poly создадим вектор коэффициентов полинома с заданными корнями, например: >> p = poly([1e-16 1.3 2.3 3.3 4.3 5.3 6.3 7.3 1e16]); и решим обратную задачу о нахождении его корней. >> format short e >> r = roots(p) r = 1.0000e+016 8.1590e+000 +1.3736e+000i 8.1590e+000 -1.3736e+000i 5.2418e+000 +3.1452e+000i 5.2418e+000 -3.1452e+000i 1.6492e+000 +2.5042e+000i 1.6492e+000 -2.5042e+000i 0 0 Результат не соответствует действительности. Однако, если решать эту задачу при помощи функции fzero, входящей в MATLAB, то корни найдутся верно. Такое решение реализовано в функции test с подфункцией polynom, которая вычисляет значение исследуемого полинома. function test r = fzero(@polynom, 0) r1 = fzero(@polynom, 1) r2 = fzero(@polynom, 2) r3 = fzero(@polynom, 3) r4 = fzero(@polynom, 4) r5 = fzero(@polynom, 5) r6 = fzero(@polynom, 6) r7 = fzero(@polynom, 7) R = fzero(@polynom,[10 1e20]) function y=polynom(x) p = poly([1e-16 1.3 2.3 3.3 4.3 5.3 6.3 7.3 1e16]); y = polyval(p,x); В результате работы функции test все корни [1e-16 1.3 2.3 3.3 4.3 5.3 6.3 7.3 1e16] находятся c хорошей точностью: >> test r = 9.999999548218181e-017 r1 = 1.299999999999999e+000 r2 = 2.299999999999998e+000 r3 = 3.299999999999994e+000 r4 = 4.300000000000304e+000 r5 = 5.300000000000961e+000 r6 = 6.299999999997263e+000 r7 = 7.300000000000616e+000 R = 1.000000000000000e+016 Нахождение характеристического полинома матрицы. Функция poly, которую в предыдущем примере мы применяли для построения полинома по его корням, умеет также вычислять коэффициенты характеристического полинома матрицы. Для этого ее входным аргументом должна быть матрица, а в выходном аргументе (векторе) она возвращает коэффициенты характеристического полинома в виде, принятом в MATLAB, т.е. начиная с коэффициента при старшей степени. Например, для матрицы 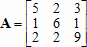 характеристический полином 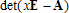 равен равен 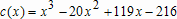 >> A = [5 2 3; 1 6 1; 2 2 9]; >> c = poly(A) c = 1.0000 -20.0000 119.0000 -216.0000 Для проверки можно воспользоваться теоремой Кэли-Гамильтона, которая утверждает, что матрица является корнем своего характеристического полинома. Для вычисления значения полинома от матрицы удобно применить функцию polyvalm (которая отличается от функции polyval тем, что вычисляет значение полинома не поэлементно для каждого элемента заданной матрицы, а в смысле матричных произведений) >> polyvalm(c, A) ans = 1.0e-012 * 0.0853 0.1137 0.1990 0.0426 0.0284 0.1137 0.1421 0.1990 0.3126 Т.е. функция polyvalm находит значение 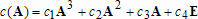 >> c(1)*A3+c(2)*A2+c(3)*A+c(4)*eye(3) ans = 1.0e-012 * 0.0853 0.1705 0.2274 0.0284 -0.0284 0.0853 0.1705 0.1705 0.3126 То, что в результате получается матрица, элементы которой не являются в точности нулями, а имеют порядок 10-12, обусловлено вычислительными погрешностями. Упомянем еще одну функцию residual, которая осуществляет преобразование между представлениями отношения двух полиномов. 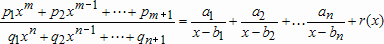 Пример. Интегрирование данных и поиск их корней. Рассмотрим простой пример, требуется проинтегрировать табличные данные, найти их корни и отметить их на графике. В качестве данных возьмем таблицу значений функции 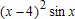 на отрезке [-1, 8] в равномерно отстоящих точках с шагом 0.5 на отрезке [-1, 8] в равномерно отстоящих точках с шагом 0.5x = -1:0.5:8; y = (x-4).2.*sin(x); Приблизим наши данные полиномом седьмой степени в смысле наименьших квадратов, используя функцию polyfit p = polyfit(x, y, 7); и вычислим значение полинома в 100 промежуточных точках функцией polyval, задав сами промежуточные точки функцией linspace >> xx = linspace(x(1), x(end), 100) >> yy = polyval(p, xx); Отобразим данные маркерами и полученное полиномиальное приближение сплошной линией на одних осях >> plot(x, y, 'o', xx, yy) Найдем все корни полинома, приближающего наши данные в смысле наименьших квадратов, при помощи функции roots >> r = roots(p) r = 8.6530 -2.0428 6.3088 4.2151 + 0.6798i 4.2151 - 0.6798i 3.1963 -0.0115 Воспользуемся логическим индексированием для отделения интересующих нас корней, т.е. тех, которые являются вещественными и принадлежат отрезку, на котором заданы данные R = r((r==conj(r))&(r>=x(1))&(r<=x(end))) R = 6.3088 3.1963 -0.0115 Отобразим их на графике круглыми маркерами красного цвета hold on plot(R, polyval(p, R), 'ro') 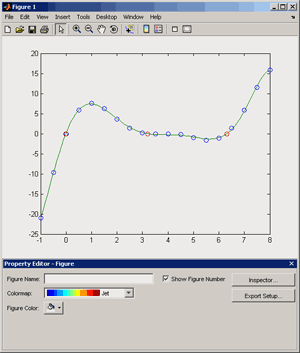 |

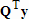 ;
; 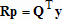 и находится вектор
и находится вектор 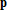 , содержащий коэффициенты
, содержащий коэффициенты